Multivariate Control Chart and Lee–Carter Models to Study Mortality Changes

Abstract

The mortality structure of a population usually reflects the economic and social development of the country. The purpose of this study was to identify moments in time and age intervals at which the observed probability of death is substantially different from the pattern of mortality for a studied period. Therefore, a mortality model was fitted to decompose the historical pattern of mortality. The model residuals were monitored by the $T^2$ multivariate control chart to detect substantial changes in mortality that were not identified by the model. The abridged life tables for Colombia in the period 1973–2005 were used as a case study. The Lee–Carter model collects information regarding violence in Colombia. Therefore, the years identified as out-of-control in the charts are associated with very early or quite advanced ages of death and are inversely related to the violence that did not claim as many victims at those ages. The mortality changes identified in the control charts pertain to changes in the population’s health conditions or new causes of death such as COVID-19 in the coming years. The proposed methodology is generalizable to other countries, especially developing countries.

1. Introduction

The analysis of mortality and its temporal trends allows a country to understand the dynamics of its population and provides a fundamental guide for establishing economic and social policy. There are a wide variety of mortality models to understand those dynamics. According to Alexopoulos et al. [1], the best-known mortality model, and the most successful in terms of generating extensions, is the Lee–Carter (LC) model. This model was built to decompose the historical pattern, obtaining the trends of mortality and its relationship with the population’s age.

The LC model proposed in 1992 by Lee and Carter [2] and its different extensions or variants have been applied for modeling and forecasting mortality in insurance and population studies. In this sense, most applications have been done in developed countries. Callot et al. [3] proposed a modification of the LC model that facilitates the separation of the deterministic and stochastic dynamics; and empirical illustrations of mortality data for the United States, Japan, and France were provided to demonstrate the advances of the modified model. Carfora, Cutillo, and Orlando [4] proposed a quantitative comparison of the leading mortality models (including the basic LC model) to evaluate both their goodness of fit and their forecasting performance on Italian population data. Booth et al. [5] compared five variants or extensions of the Lee–Carter method for mortality forecasting for populations of 10 developed countries (Australia, Canada, Denmark, England, Finland, France, Italy, Norway, Sweden, and Switzerland). Salhi and Loisel [6] proposed a multivariate approach for forecasting pairwise mortality rates of related populations and realized a comparison with the classical LC model for data for England and Wales. Recently, some research proposed alternative procedures to the classic LC model to obtain the mortality rate. Postigo-Boix et al. [7] presented polynomial functions where the amount of data required to establish the mortality rate is considerably reduced.

There are also successful applications of the LC model and its different versions for the mortality data of Central America and South America. Examples include the works by Andreozzi [8] and Belliard and Willians [9] for Argentina; García-Guerrero [10] for Mexico; Lee and Rofman [11] for Chile; Aguilar [12] for Costa Rica; and Díaz et al. [13] for Colombia. These papers show the usefulness of the LC models in analyzing and modeling mortality in developing countries.

As noted, until now, most of the papers have focused on modeling the dynamics of mortality. However, the Lee–Carter model will capture the overall pattern of mortality behavior of the population in the age profile and over time with an excellent or regular fit. The analyst can describe this pattern and the changes in mortality when analyzing the estimates obtained for the model parameters. Typically, the model does not correctly reproduce observed mortality, and some of the information on that phenomenon may remain in the residuals vector. It is precisely here that the control chart plays an important role: attempting to discover some other substantial changes in mortality behavior which have not already been collected by the model.

Therefore, in this paper, we go beyond modeling mortality and propose the use of the residuals of LC models to monitor and identify situations of substantial change in the mortality trend. The purpose of the study was to determine whether death probability changed significantly over a studied period. Therefore, times (years) and age intervals with death probabilities which significantly differ from the trend pattern determined by the LC models were identified. For this task, we used a $T^2$ control chart implemented on the residuals of LC models complemented with the Mason, Tracy, and Young (MTY) decomposition [14] to detect the age range where the change occurred.

A control chart is a straightforward graphical tool, initially proposed by Shewhart in 1927 [15], to verify the temporal stability of a parameter of interest in the probability distribution of a random variable. In this way, the univariate control chart monitors a single variable. Then, in 1947, Hotelling [16] extended the application of control charts for simultaneous control of two or more random variables, creating the $T^2$ multivariate control chart.

Although control charts were initially proposed to monitor industrial processes (statistical quality control), many papers evidenced their application to other areas of knowledge. For example, in medicine, Woodall [17] mentioned that control charts are linked to health care surveillance. The recent review work of Vetter and Morrice [18] proposed the use of control charts as a tool that allows health professionals to understand and communicate performance data and improve quality for patient care, anesthesiology, perioperative medicine, critical care, and pain management. Some papers report their use to monitor hospital performance indicators [19], clinical variables in patients [20], and chronic and infectious diseases [21,22,23], and for monitoring the effectiveness of surgical procedures [24].

Additionally, the literature has evidenced the use of control charts for mortality data. Chamberlin et al. [25] proposed using control charts to determine whether the severity of illnesses of patients and mortality rates changed significantly over the five years from 1986 to 1990. Marshall and Mohammed [26] used control charts to monitor mortality rates after coronary artery bypasses. More recently, Urdinola and Rojas-Perilla [27] proposed to use this approach to identify the under-registration of adult mortality in Colombia.

Studies on mortality are important for countries like Colombia, considering that it is in the group of Latin American countries with the highest mortality rates [28]. In addition, its rapid increase in violent crime over the last century must be taken into account. According to Gaviria [29], the homicide rate began its upward trend in the late 1970s and had more than tripled by the early 1990s. For this period, the homicide rate in Colombia was three times those of Brazil and Mexico, seven times that of the United States and 50 times that of a typical European country.

In our context, the fitted mortality models for abridged life tables are designed to simultaneously predict a vector of mortality rates. Therefore, each time a prediction is made, a vector of estimated mortality rates is obtained, one for each age interval, and consequently, a residual vector is generated. The residuals measure the departures between the current mortality rate and the expected rate according to the model. A high residual indicates that the current mortality does not correspond to the observed trend. Consequently, it is suspected that there is a change in the population’s mortality for a specific age range.

According to this, life table monitoring is a multivariate control problem which consists of simultaneously monitoring p random variables (each observed residual is a random variable). Therefore, we propose to monitor the residuals of the mortality model with a $T^2$ control chart, and only for the years identified as out-of-control, use the first term of the MTY decomposition to identify the age range involved in the out-of-control signal.

The proposed methodology is illustrated with the mortality data of Colombia, obtained from “The Latin America Human Mortality Database“ [30]. Primarily, Colombia has presented a series of demographic phenomena in the last 60 years, such as the progressive increase of the population, which is reflected by a change of the population pyramid, and an increase in life expectancy, which is primarily associated with the drop in mortality rate and the aging of the population. Although the methodology is illustrated through this particular case, our proposal is standard and generalizable to other similar contexts that require sociodemographic explanations of the “anomalies“ detected with control charts.

This paper has the following structure: Section 2 presents the methodology, including definitions of life tables, Lee–Carter models, and standardized deviance residuals, and descriptions of the control charts that were used and the MTY decomposition. Section 3 describes Colombian mortality data, and the results obtained in the monitoring of those data; and Section 5 provides the main conclusions of the paper.

2. Methodology

In this section, we briefly describe the life tables and Lee–Carter (LC) and Lee–Carter with two terms (LC2) models. Then, more carefully, we present the $T^2$ Hotelling chart for individual observations and the MTY decomposition. These theoretical elements support our proposal to study substantial changes in the mortality of developing countries.

2.1. Life Tables

Period life tables, also known as mortality tables, are a demographic analysis tool that summarizes the information of mortality incidence for a population for a given period. Life tables are classified according to the length of the age interval in which the data are presented: “complete“ when containing data for every single age from birth to the last applicable age, and “abridged“ when containing data at age intervals, generally 5 years of age for most of the age range [31]. The basic life table functions are $m_x$, $q_x$, $l_x$, $d_x$, $L_x$, $T_x$, and $e_x$. However, the life table does not always publish all of these functions. The interpretation of the life table functions in a complete table would be as follows [32]:

• The death rate or mortality rate $m_x$; the occurrence of deaths expressed per person-year at each age x.

For a fictitious cohort with an incidence of mortality according to the mortality rates that have been defined:

• The probability of death $q_x$ is the likelihood that deaths occur in a certain period at each age x.
• The number of survivors $l_x$ is the number of individuals from the fictitious cohort that reach the age of x.
• The number of deaths $d_x$ is the number of deaths within the fictitious cohort at each age x.
• The stationary population $L_x$ is the total time lived for all individuals of the fictitious generation that are x years old.
• The total years lived $T_x$ is the total amount of years lived for all individuals of the fictitious generation aged x or more.
• The life expectancy at birth $e_x$ is the average number of years that survivors have left to live at age x.

The abridged life table shows estimates based on mortality data from vital statistics and population size obtained from population censuses. Censuses are conducted approximately every 10 years in some countries, such as Argentina, Brazil, and Mexico, among others, and some censuses are carried out with intervals longer than 10 years, as is the case in Colombia [33]. Developing countries, due to misstatements regarding vital registrations related to age during mortality collection, often build the mortality table with age intervals.

In an abridged life table, the interpretation of the functions is similar to the case of the complete life table, except that the ${}_n{m}_x$, ${}_n{q}_x$, ${}_n{d}_x$, and ${}_n{L}_x$ values relate to age interval $[x,x+n)$:

• The probability of death ${}_n{q}_x$ is calculated from the death rate ${}_n{m}_x$:
  ${\displaystyle {}_n{q}_x=\frac{n·{}_n{m}_x}{1+(n-{}_n{a}_x)·{}_n{m}_x}}$, where $a_x$ is the average number of years lived by individuals dying in the age interval and n is the amplitude of the age interval.
• The number of deaths ${}_n{d}_x$ is the number of individuals from the fictitious generation who died during the age interval $[x,x+n)$.
• The stationary population ${}_n{L}_x$ is the total time lived for all individuals of the fictitious generation of $[x,x+n)$ years old.

The intervals commonly used to group ages in an abridged life table are $[0;1);[1;5);[5;10);[10;15);\dots ;$ until the final open interval, because usually preferred ages are those which end in multiples of five in a declaration of death. To ensure a broader view of the dynamics of mortality in a population, it is additionally necessary to visualize the temporal trend of the incidence of mortality. For this, dynamic life tables are used, which correspond to the collection of period life tables, complete or abridged, obtained for each year of a time interval. Hereafter, the total number of age intervals for each period will be denoted by p, and the total number of periods analyzed will be denoted by m.

2.2. Lee–Carter Models

Lee and Carter [2] proposed a simple method for modeling and forecasting mortality: a model of age-specific death rates with a time component and a fixed relative age component, and a time series model (an autoregressive integrated moving average (ARIMA)) of the time component. This method offers three significant advantages: it is a parsimonious demographic model combined with standard statistical time-series methods, forecasting is based on persistent long-term trends, and probabilistic confidence intervals are provided for the forecasts [34].

The Lee–Carter model (LC) expresses the age-specific death rate as a measure depending on both the age of individuals, x, and the time period, t. The classical LC model is expressed as follows:

$$ln\left(m_{xt}\right)=a_x+b_x{k}_t+{ϵ}_{xt},$$

(1)

where $a_x$ is an age-specific parameter that is independent of time (it describes the general mortality profile according to age), $b_x$ is an age-specific parameter that represents how rapidly or slowly mortality at each age varies when the general level of mortality changes, and $k_t$ is the general mortality index which depends on time and reflects the general level of mortality. The errors ${ϵ}_{xt}$ are assumed to be independent, identically distributed $N(0,{\sigma }^2)$ random variables.

The LC model has a structure which is invariant under some linear transformations of the parameters. For example, for any value of constant c, it is verified that

$$\begin{array}{ccc}\hfill (a_x,b_x,k_t)& \mapsto & (a_x,b_x/c,c{k}_t)\hfill \\ \hfill (a_x,b_x,k_t)& \mapsto & (a_x+c{b}_x,b_x,k_t-c).\hfill \end{array}$$

To ensure the identifiability of the model, Lee and Carter [2] proposed including the following constraints in the model: ${\sum }_x{b}_x=1$ and ${\sum }_t{k}_t=0$.

A modification to the Lee–Carter model, called the Lee–Carter model with two terms (LC2), was developed by Renshaw and Haberman [35]. They indicated that the interaction between age and time can be better captured by adding terms to the LC model. The LC2 model is expressed as follows:

$$ln\left(m_{xt}\right)=a_x+b_x^1{k}_t^1+b_x^2{k}_t^2+{ϵ}_{xt}.$$

(2)

In this paper, we adjust Equations (1) and (2) with the adequacy proposed by Debón, Montes and Puig [36], who suggest modeling the logit death probability $q_{xt}$ considering a binomial distribution for the death rate. Thus, the LC model is expressed as:

$$\mathrm{logit}\left(q_{xt}\right)=ln\left(\frac{q_{xt}}{1-q_{xt}}\right)=a_x+b_x{k}_t+{ϵ}_{xt}$$

with constraints ${\sum }_x{b}_x=1$, $k_{t_0}=0$; and the LC2 model

$$\mathrm{logit}\left(q_{xt}\right)=a_x+b_x^1{k}_t^1+b_x^2{k}_t^2+{ϵ}_{xt}$$

with constraints ${\sum }_x{b}_x^i=1(i=1,2)$ and $k_{t_0}^1=k_{t_0}^2=0$. Details about this fitting using R can be found in Debón et al. [37]. Finally, the LC models are based on historical mortality patterns, and if the trends do not continue to hold, then the models will no longer be valid [38].

2.3. Standardized Deviance Residuals

Residuals are the basis of most diagnostic methods and are often used to analyze the goodness of fit of mortality models. However, as we mentioned before, residuals can identify moments in time and age intervals at which the observed probability of death is substantially different from the pattern of mortality for a period of time. With this objective, we propose using a Hotelling $T^2$ multivariate control chart.

In the goodness-of-fit analysis of mortality models, deviance residuals are often used [36,39,40], taking into account that patterns in the residuals could indicate that the model does not adequately describe all the characteristics of the data [41]. The deviance residuals based on a binomial distribution for the number of deaths at age x are as follows:

$$r_{xt}=sign(d_{xt}-{\widehat{d}}_{xt})\sqrt{\frac{2}{\widehat{\varphi }}\left[d_{xt}log\left(\frac{d_{xt}}{\widehat{d_{xt}}}\right)+(l_{xt}-d_{xt})log\left(\frac{l_{xt}-d_{xt}}{l_{xt}-{\widehat{d}}_{xt}}\right)\right]},$$

where $d_{xt}$ denotes the observed number of deaths, ${\widehat{d}}_{xt}$ is the deaths estimated by the model, $l_{xt}$ is the number of persons living at the beginning of the indicated age interval, and $\widehat{\varphi }$ is an empirical scaling factor estimated by the expression

$$\widehat{\varphi }=\frac{D(d_{xt},{\widehat{d}}_{xt})}{(m·p)-\nu }.$$

Further, $D(d_{xt},{\widehat{d}}_{xt})$ is the total model deviance, $m·p$ is the number of observations in the data, and $\nu$ is the effective number of parameters [41].

The deviance residuals are usually symmetrical, but their variance and scale are not standard. Therefore, to correct these situations, deviance residuals are usually standardized.

The standardized deviance residuals are defined by

$$st{r}_{xt}=\frac{r_{xt}}{\sqrt{(1-h_{xt})}}$$

where $h_{xt}$ is the leverage, the distance between an observation $(x,t)$ and the center of the observations.

The standardized deviance residuals are distributed by a standard normal distribution with unit variance when the fitted model is satisfactory. For this reason, the values of these residuals will generally lie between $-2$ and 2 [42]. Moreover, these residuals satisfied the assumptions of the Hotelling $T^2$ control charts. Given the above, the standardized deviance residuals were used to monitor the mortality trend.

2.4. Hotelling $T^2$ Control Charts for Standardized Deviance Residuals

The control charts are useful to determine whether a process has been in a state of statistical control by examining historical data [43]. Specifically, the multivariate control charts are used for process-monitoring problems in which several related variables are of interest.

Hotelling [16] proposed the $T^2$ control chart to meet the objective of simultaneous monitoring of $p\ge 2$ random variables, which generally have some non-negligible degree of association. Under the assumption that the vector $\mathit{X}={(X_1,X_2,\dots ,X_p)}^{\prime }$ follows a p-variate normal distribution, $\mathit{X}\backsim N_p(\mu ,\Sigma )$, with known mean vector $\mu ={({\mu }_1,{\mu }_2,\dots ,{\mu }_p)}^{\prime }$ and covariances matrix $\Sigma$, the statistic:

$$T^2={(\mathit{X}-\mu )}^{\prime }{\Sigma }^{-\mathit{1}}(\mathit{X}-\mu )$$

(3)

follows a chi-square distribution with degrees of freedom p.

The $T^2$-chart is then a chart of the statistic $T^2$ vs. the observation number, with an upper control limit (UCL) located at ${\chi }_{(\alpha ,p)}^2$, which represents the upper $\alpha$ percentile of the chi-square distribution. Here, $\alpha$ is the desired type I error probability.

Since $\mathit{\mu }$ and $\mathbf{\Sigma }$ are often unknown, these parameters should be estimated from a reference sample composed by m observations of $\mathit{X}$. The sample mean vector ($\overline{\mathit{X}}$) and covariance matrix (S), obtained from the reference sample, are the estimators of $\mathit{\mu }$ and $\mathbf{\Sigma }$, respectively, for Equation (3).

According to Tracy [44], when $\mathit{\mu }$ and $\mathbf{\Sigma }$ are estimated, the Hotelling $T^2$ statistic

$$T^2={(\mathit{X}-\overline{\mathit{X}})}^{\prime }{\mathbf{S}}^{-\mathit{1}}(\mathit{X}-\overline{\mathit{X}})\backsim \frac{{(m-1)}^2}{m}{B}_{(p/2,(m-p-1)/2)},$$

where $B_{(p/2,(m-p-1)/2)}$ represents a beta distribution with parameters $p/2$ and $(m-p-1)/2$. This distribution depends on the number of variables p and the sample size m, which must satisfy $m>p+1$ [45].

Therefore, the upper control limit (UCL) for the $T^2$-chart should be located at:

$$\mathrm{UCL}=\frac{{(m-1)}^2}{m}{B}_{(\alpha ,p/2,(m-p-1)/2),}$$

where $B_{(\alpha ,p/2,(m-p-1)/2)}$ is the upper $\alpha$ percentile of a beta distribution with parameters $p/2$ and $(m-p-1)/2$.

When a point exceeds the upper control limit in a $T^2$ chart, it is interpreted as a signal of change in the distribution of $\mathit{X}$. Then, it is recommended to carry out an investigation to find the causes that produce the signal or apply some procedure to identify the causal variable(s) of the signal, as the $T^2$ chart itself cannot do this.

In our proposal, the changes in the dynamics of mortality are evaluated through monitoring the p-dimensional vector of standardized deviance residuals ${\mathit{R}}_{\mathit{t}}={(st{r}_{1t},st{r}_{2t},\dots ,st{r}_{xt},\dots ,st{r}_{pt})}^{\prime }$, which was obtained from a Lee–Carter model adjusted for a reference sample of m consecutive periods ($t=1,2,3,\dots ,m$). In this particular application, the mean vector $\overline{{\mathit{R}}_{\mathit{t}}}$ and the covariance matrix ${\mathbf{S}}_{\mathbf{R}}$ are estimated from the reference sample of the m historical standardized residuals vectors. Under this approach, the Hotelling’s $T^2$ statistic takes the form:

$$T^2={(\mathit{R}-\overline{\mathit{R}})}^{\prime }{{\mathbf{S}}_{\mathbf{R}}}^{-\mathit{1}}(\mathit{R}-\overline{\mathit{R}}).$$

In this application context, an observation that exceeds the control limit of Hotelling’s $T^2$ chart is interpreted as a departure from the mortality trend pattern reproduced by fitting any Lee–Carter model. Consequently, this period is labeled as out-of-control, a substantial change in mortality dynamics is suspected, and the second phase of analysis investigates the age intervals that may be involved in the out-of-control diagnosis.

As can be seen, the proposal for multivariate control is more flexible in its assumptions than the usual analysis of residuals, since the condition of complete independence imposed on the error term is now relaxed. Under the multivariate control approach, each set of p-residuals, associated with the p-intervals of age for a particular year, form a vector of random p-variables that are not necessarily independent, nor identically distributed. Therefore, the multivariate control chart allows the methodology to be applied even when the model presents local fitting problems. Note that a particular case of the multivariate strategy is constituted when the p-residuals are independent and identically distributed.

Another difference between these strategies for identifying anomalies is related to the number of assessments made in the hypothesis test. In the residuals analysis, each residual is checked individually against tolerable limits of variation, which implies making a set of $m\times p$ comparisons. Conversely, under the multivariate approach, the comparison against the control limit is done for each p-dimensional observation: that is, a comparison for each year. Then, the multivariate control chart reduces the number of comparisons to m, which reduces the probability of global type I error. As is known, the probability of global error increases exponentially according to the overall number of comparisons made simultaneously [45].

Finally, it should be noted that the performance of a Hotelling $T^2$ control chart is related to the number of periods m that make up the observation period to which Lee–Carter’s model fits. For the Hotelling $T^2$ control chart, m defines the sample size used to estimate the parameters of the multivariate probability distribution of standardized residuals vector. In this sense, through simulation studies, Champ and Jones-Former [46] showed that when the sample size m is small, the true-false alarm rate of multivariate control charts is usually substantially higher than the established nominal rate. A recommendation of these authors is to use broader control limits. The estimation error effect on the false alarm rate is absorbed without substantially affecting the chart’s performance in detecting changes.

2.5. MTY Decomposition

Several approaches are presented for the problem of interpreting a multivariate signal. Mason, Tracy, and Young [14] proposed the MTY method of decomposition to find the causes that produce the signal. The MTY method decomposes the $T^2$ Hotelling statistics into p additive orthogonal components, each of which reveals the contribution of the individual process variable and the relative joint contribution of the same process variable.

For the case of p variables, there are $p!$ different possible MTY decompositions. One such decomposition is given by

$$T^2=T_1^2+T_{2.1}^2+T_{3.1,2}^2+\dots +T_{p.1,2,\dots ,p-1}^2=T_1^2+\sum _{j=2}^p{T}_{j.1,2,\dots ,j-1}^2.$$

The first term of decomposition is called the unconditional term and corresponds to the $T^2$ statistic calculated for the variable $j=1,2,3,\dots ,p$. The expression is the following:

$$T_j^2={\left(\frac{st{r}_j-\widehat{{\mu }_j}}{\widehat{{\sigma }_j}}\right)}^2$$

where $\widehat{{\mu }_j}$ and $\widehat{{\sigma }_j}$ are the mean and standard deviation estimates of the standardized deviance residuals $st{r}_j$ obtained with the m historical observations of $st{r}_j$. In our context, the unconditional term measures the standardized distance between observed mortality in an age interval and the expected pattern according to the model. Thus, when a signal of change is emitted by the $T^2$ statistic, the unconditional term’s high value indicates that the signal of change may be related to the age range j.

The other terms, called the conditional terms, are calculated as

$$T_{j1,2,\dots ,k}^2={\left(\frac{st{r}_j-{\widehat{\mu }}_{j|1.2,\dots ,k}}{{\widehat{\sigma }}_{j|1.2,\dots ,k}}\right)}^2$$

where ${\widehat{\mu }}_{j|1.2,\dots ,k}$ and ${\widehat{\sigma }}_{j|1.2,\dots ,k}$ are the mean and conditional standard deviation estimates of $st{r}_j$, respectively.

These parameters can be estimated through the estimation of a linear regression model ($st{r}_j$ as a response variable and ${str}_1,{str}_2,\dots ,{str}_k$ as predictors) with the m historical observations of the standardized deviance residuals vector. When the unconditional term’s calculation yields a high value, this is an indication that the signal may be associated with a change in the correlation structure of the variables being monitored. In our application context, where the monitoring variables correspond to the standardized deviance residuals of a Lee–Carter model, the interpretation of this kind of change does not make practical sense. For this reason, their analysis is not considered in our proposal.

An appropriate F distribution can describe the probability distribution for the unconditional term on the MTY decompositions:

$$T_j^2\sim \left(\frac{m+1}{m}\right)F_{(1,m-1)}.$$

Using these distributions, for a specified $\alpha$ level and a reference sample of size m, the upper control limits for the unconditional term are obtained as follows:

$$\mathrm{UCL}=\left(\frac{m+1}{m}\right)F_{(\alpha ,1,m-1)}$$

where $F_{(\alpha ,1,m-1)}$ is the upper $\alpha$ percentile of the F distribution with degree of freedom $(1,m-1)$.

As a result, one can use the F distribution to determine when an individual unconditional term of the decomposition is significantly broad and contributes to the signal. In essence, a significant value for an unconditional term implies that the designated variable is out-of-control [45]. For our proposal, we use only the unconditional term of the MTY decomposition to identify the age range involved in the mortality change signal.

Finally, it is essential to note that our proposal for mortality surveillance based on implementing a multivariate control chart presents some advantages with respect to the simple exercise of verifying model fit through residuals analysis. Usually, the residuals analysis is carried out to validate the distributional assumptions established a priori about the errors in the mortality model: mean zero, homoscedasticity, independence, and equality of probability distribution. Under the established assumptions, the residuals are treated as $m\times p$ independent observations of a random variable of zero mean and constant variance. Implicitly, this is equivalent to assuming that the model’s goodness of fit is the same for any age interval and any instant in time, which is usually not satisfied in practice. In an application with real data, the model often fits very well for certain age intervals, but overestimates or underestimates other intervals’ mortality rates. In these cases, there will be a natural difference in error distribution for certain age intervals. Under a residuals analysis, this situation will be identified as a model fitting problem, limiting its use.

On the other hand, our multivariate control proposal is oriented to identify moments of time and age intervals, in which the probability of observed death is substantially different from the mortality pattern that has been collected by the adjusted model. Under this strategy, changes in mortality can be identified in either the model or the control chart.

3. Analysis of Mortality Data from Colombia

3.1. Description of the Data

The data used in this paper were taken from abridged life tables which we constructed for Colombia for the period 1973–2005 for both men and women using information available in “The Latin America Human Mortality Database” [30]. The available population data correspond to the last four censuses (1973, 1985, 1993, and 2005), and so the information was completed using linear interpolation. Based on death and population data, it was possible to calculate the functions of the life abridged tables for Colombia from 1973 to 2005. Ages are grouped accordingly: $[0;1);[1;5);[5;10);[10;15);\dots ;[80;85)$ for each sex. Díaz-Rojo and Debón-Aucejo [47] describe in detail the method of obtaining the abridged life tables.

3.2. Fitting LC and LC2 Models

In a previous paper [13], different mortality models were fitted, with the Lee–Carter (LC) and Lee–Carter with two terms (LC2) models providing the best fits. In the statistical software R [48], the LC models can be fitted using the gnm package [49].

Considering a large number of estimated parameters in the LC and LC2 models for men and women, the estimates obtained for the parameters of the two models are presented in Figure 1 and Figure 2. Some characteristics of the mortality and its differences between men and women are noted.

In Figure 1a, the parameter $a_x$ shows the usual phases of population mortality: for both sexes, the probability of death is high in the early years and decreases slowly until age 15, then increases as the population ages. This parameter also shows the phenomenon known as the “young adult mortality hump”, which describes the excess mortality for a time period for young adults. For Colombian data, this hump phenomenon is observed in a very marked way in men between 20 and 40 years of age.

The $k_t$ mortality index presents different structures in its behavior during the analyzed period (see Figure 1b). There is a decline from 1973 to 1978 and then a remarkable rise for 1981. There is also a peak around 1985. The decrease in mortality is more pronounced for women than men, which can be explained by improved health and living conditions. For men, this slope is lower because they were more exposed to the war events of the 80s and 90s. The most considerable difference between the sexes occurs in the last years of the period analyzed.

The parameter $b_x$ indicates how the mortality of each age x responds to changes in $k_t$ (see Figure 1c). In women, $b_x$ takes positive values for all ages, indicating that mortality has decreased for all ages. In men, the parameter takes negative values between the ages of 20 and 40, which means that despite the trend in the reduction of mortality observed at the general level during the study period, the subpopulation of men between the ages of 20 and 40 years presented the inverse phenomenon: their mortality increased, accentuating the hump effect on male mortality. This hump phenomenon has been mainly associated with the homicides due to the armed conflict [13].

In Figure 2, the parameters of the LC2 model are shown. Comparing Figure 1 and Figure 2 in (a–c), it is observed that, in general, the parameters $a_x$, $k_t$, and $b_x$ exhibit behavior which is similar to both models. The parameter $k_t^2$ presents values close to zero, although the values decrease considerably in both sexes between 1975 and 1980. This second term only has an effect for a few years at all ages, improving LC’s fit. The parameter $b_x^2$ has higher values at early ages of up to 15 years, then decreases rapidly, with a peak approaching zero for women around 20 years; for subsequent ages, the value remains almost constant for both sexes (see Figure 2d,e).

3.3. $T^2$ Chart to Identify Substantial Changes in Mortality Trend

The Hotelling $T^2$ control chart was used retrospectively to identify substantial mortality changes during the study period that were not collected by the Lee–Carter model. Information on these changes is found in the model residuals. In this application, the residual associated with each specific age interval is seen as a random variable. In this way, the p residuals of the Lee–Carter model form a vector of random variables, and in practice are not necessarily independent.

The monitoring was performed using standardized deviance residuals to guarantee the symmetry of the residuals’ vector distribution. Hotelling $T^2$ control charts were built using the qcc R package [50].

To estimate the upper control limit for the Hotelling $T^2$ control chart, ${\alpha }^{*}$ was adjusted (false alarm probability for each point). Since we represent a fixed set of m points in the chart, in this case with the years ($m=33$), ${\alpha }^{*}$ was calculated as follows:

$${\alpha }^{*}=1-{(1-\alpha )}^{\frac{1}{m}}$$

where $\alpha$ is the total probability of false alarm (set a priori at 0.05).

In Figure 3 and Figure 4, the Hotelling $T^2$ control charts for the residual vector of the LC and LC2 models are shown. The years whose residuals are outside the control limits can be observed.

Figure 3 shows that the LC model identifies the year 1991 as out-of-control for men, while two years are identified for women: 1979 and 1991.

For the residual vector of the LC2 models, the year 1991 is out-of-control for men, and for women, the years 1976 and 1991 were detected (see Figure 4).

In summary, the Hotelling $T^2$ control chart with LC and LC2 models identifies the year 1991 as out-of-control for both sexes. Moreover, the year 1979 is identified for women with the LC model and the year 1976 is identified for women with the LC2 model (see

Table 1. $T^2$ values for out-of-control points.

Model	Sex	Year	${\mathit{T}}^2$ Values
LC	Men	1991	29.67
	Women	1979	27.01
		1991	29.99
LC2	Men	1991	27.74
	Women	1976	27.47
		1991	29.59
$\alpha =0.05$, UCL = 26.99.

).

In this context, the out-of-control signal should be interpreted as a change in mortality not captured by the Lee–Carter model. Therefore, when the chart does not generate out-of-control signals, it should not be interpreted as meaning that no changes in mortality occur, but rather that these changes were most likely already captured by the model.

3.4. MTY Decomposition to Interpret the Out-Of-Control Signals

The ages related to the signals were explored by applying the MTY decomposition over the Hotelling $T^2$ control chart over the out-of-control signals.

Table 2. Unconditional terms of the MTY decomposition for out-of-control points.

	LC			LC2
	Men	Women		Men	Women
Age Interval	1991	1979	1991	1991	1976	1991
[0–1)	$4.80$ *	$4.78$ *	$5.27$ *	3.68	0.15	$12.58$ *
[1–5)	3.79	$7.21$ *	1.39	$17.38$ *	0.28	$14.47$ *
[5–10)	$15.42$ *	0.85	$9.95$ *	$18.80$ *	0.01	$22.06$ *
[10–15)	0.83	0.76	0.39	2.20	0.01	0.27
[15–20)	1.60	0.19	0.55	0.02	0.17	0.00
[20–25)	3.44	0.11	0.04	0.76	0.15	0.33
[25–30)	3.69	0.82	0.01	1.39	0.83	1.41
[30–35)	2.88	0.37	0.49	0.31	0.55	0.01
[35–40)	2.37	0.24	0.02	0.10	0.04	0.79
[40–45)	2.13	0.44	1.03	0.08	1.38	0.07
[45–50)	0.69	0.83	0.38	0.05	1.85	0.11
[50–55)	2.86	1.01	0.00	1.13	1.49	0.15
[55–60)	1.47	0.27	0.76	0.13	0.21	0.22
[60–65)	2.03	4.10	0.08	0.24	0.51	0.10
[65–70)	0.04	0.49	0.69	0.46	0.21	1.11
[70–75)	0.45	$6.05$ *	0.63	0.41	3.36	0.02
[75–80)	0.24	0.01	0.50	0.00	3.34	0.11
[80–85)	0.06	$9.25$ *	0.52	0.69	0.64	0.20
$\alpha =0.05$, UCL = 4.27, * Denotes significance.

shows a summary of the information obtained from the unconditional term of the MTY decomposition of signaling points for the residual vector of LC and LC2 models. For men, the residuals of both mortality models point to 1991 as outside the limits of control, where infant ages cause this alarm. In women, the LC model’s residuals indicate the years 1979 and 1991 as out-of-control; in both years, infant ages have a strong influence, in addition to the ages [70–75) and [80–85) for the year 1979.

The residuals of the LC2 model indicated the years 1976 and 1991 as outside the limits of control, and very young ages are related to this alarm. It should be noted that although the year 1976 was identified by the Hotelling $T^2$ control chart as being outside the control limits, no related ages were detected with the MYT decomposition, which could indicate a false alarm or an error of the MYT test [45].

It may also be noted that the change identified in the year 1976 was not generated by an abnormal variation in mortality in any of the specific age ranges; the anomaly was generated by a multivariate movement contrary to the correlation structure between the residuals of this year. This type of change has no practical interpretation, and therefore, its exploration is discarded in the proposed methodology.

4. Discussion

The obtained results were compared to a series of events registered in Colombia from a socio-demographic perspective.

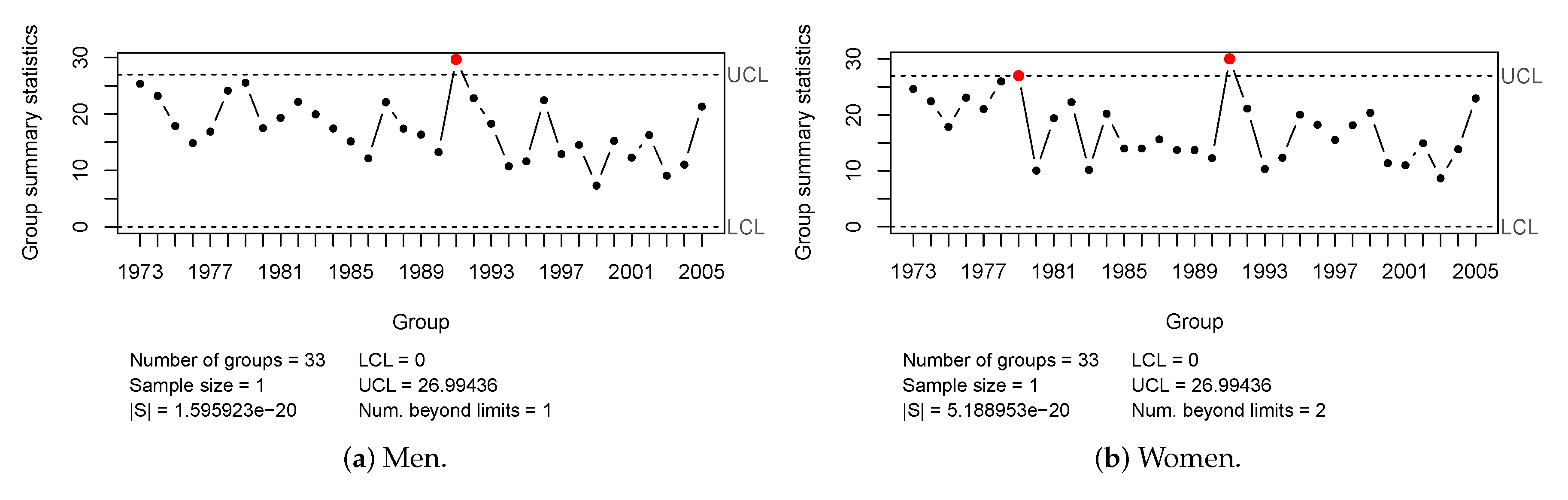
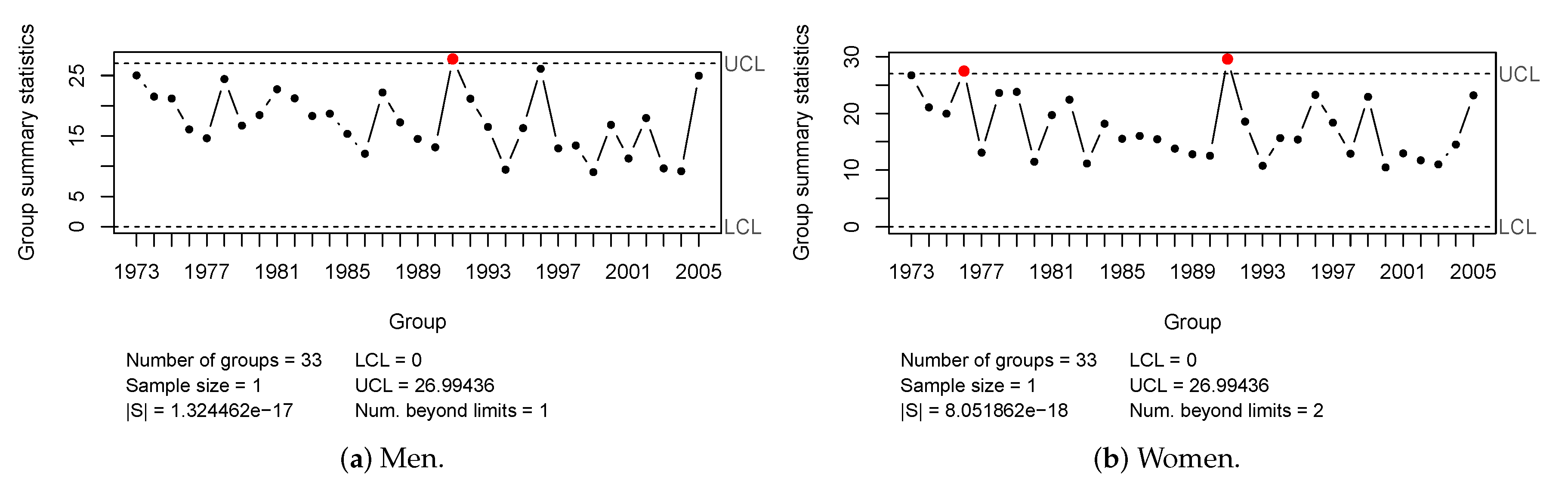
The alert detected with the residuals can be related to a change in the causes of death from an epidemiological point of view. Cristancho [51] mentions that according to the National Administrative Department of Statistics (DANE), homicide became the leading cause of death for men in the 1980s. In that decade, there was also an increase in mortality due to non-infectious diseases and external causes. External causes, especially for men, were associated with violence and accidents.

It should be noted that in the 1990s, the so-called emerging diseases increased in Colombia. In 1990, there was a massive dengue epidemic with a 40% fatality rate: its intensity decreased in 1991–1995 [52]. Additionally, in 1991 there was an epidemic outbreak of cholera [53].

In analyzing facts related to public health in Colombia, two crucial events were identified as out-of-control and related to the detected years. In 1975, the National Health System was established; in the period from 1990–2000, there were changes in mortality related to this Health System Reform.

On the other hand, with the Political Constitution of 1991, a new political administrative division was created in Colombia, creating new departments, which benefited the collection of information in the country’s southern region. The exhaustive work of this division in recovering information increased the number of registered deaths.

5. Conclusions

This paper demonstrates the usefulness of control charts as a tool to detect substantial changes in mortality behavior by monitoring residuals from mortality models. In some developing countries, data are presented in age groups because of misstatements related to age; usually, there is a preference for the declaration of the age of death to occur in multiples of five, and there are various other registration difficulties. Therefore, a question of interest in the demographic and actuarial fields is the use of residuals of a model to monitor the mortality of abridged life tables.

Previous works such as Urdinola and Rojas-Perilla [27] use control charts with only one measure per unit of time to monitor mortality data, which involves building numerous control charts and increasing the false alarm rate (out-of-control points). Instead, in this paper, we use a Hotelling $T^2$ multivariate control chart, which simultaneously monitors p random variables (age intervals) per unit of time, which dramatically reduces the number of charts to build. Further, this multivariate control chart considers the relationships between the residuals associated with different age intervals. The methodology we propose considers that mortality is a phenomenon that is not stable over time, but instead exhibits trends collected through Lee–Carter models. Consequently, the control charts applied to the residuals of these models can detect the other types of mortality changes that were not previously collected by the models.

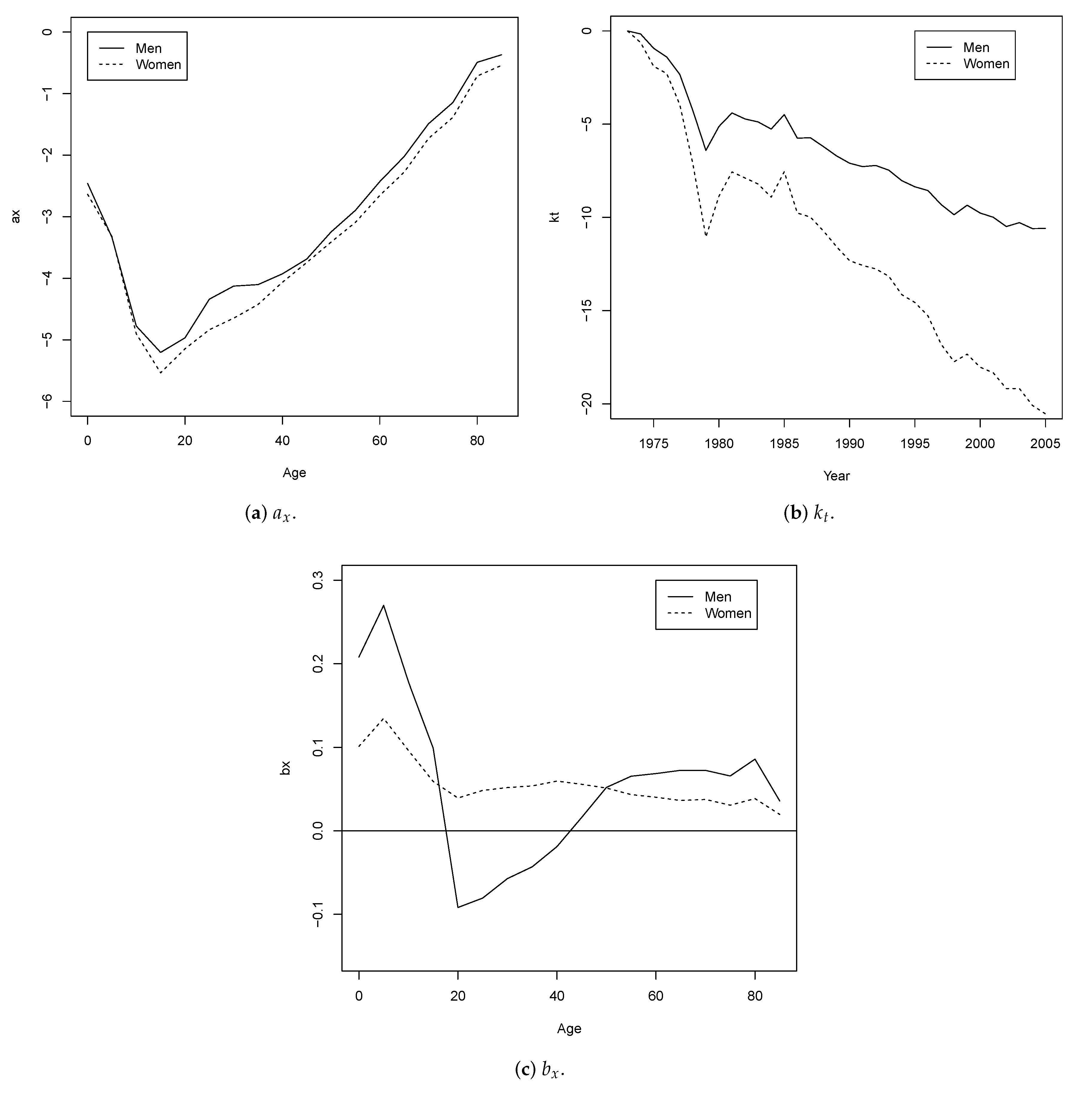
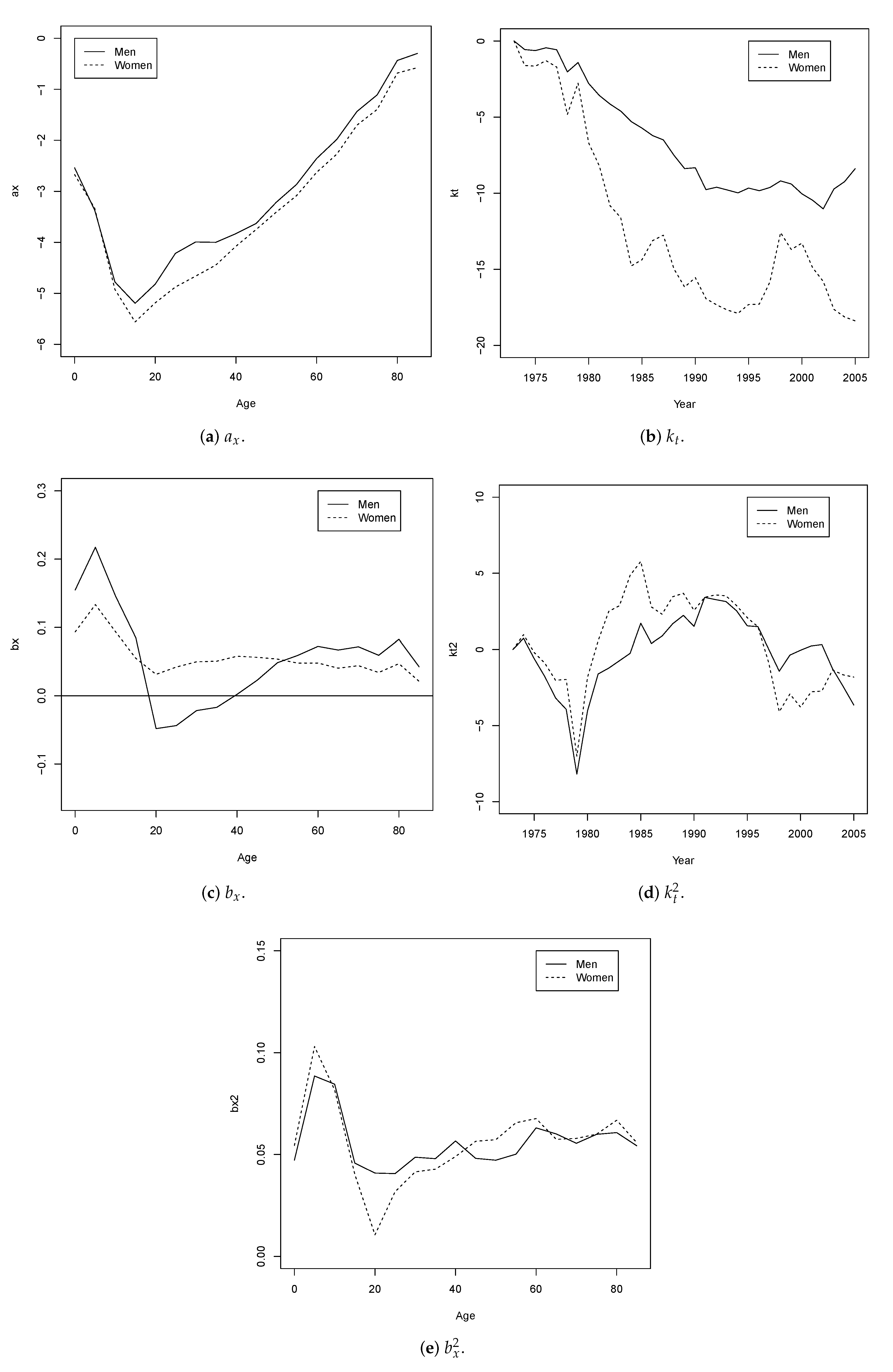
The LC and LC2 mortality models identified the principal characteristics of mortality in Colombia. The infant mortality is high and decreases slowly until the age of 15, after which it increases progressively as the population ages. The hump phenomenon is recorded in young adults, mainly in men. This phenomenon has been described before in other papers [13,54] and is mainly explained by the homicides related to internal armed conflict [55] and illicit activities such as illegal drug markets [29], as well as the availability of firearms [28].

The Hotelling $T^2$ control chart is an exciting option to monitor the residuals of the mortality models and thus identify the years in which the mortality differs from the patterns that are collected by the mortality model. With the combined use of Hotelling $T^2$ and MTY decomposition, the years and age range of that atypical pattern were identified. Two years were identified as out-of-control: 1991 for the residuals of both models for both men and women with an influence of very young ages, and the year 1979 for residuals from the Lee–Carter model for women with the influence of very young ages and very advanced ages.

The Lee–Carter model collects information regarding the phenomenon of violence in Colombia. Therefore, the years identified as out-of-control in the charts are associated with very early or quite advanced ages, which are inversely related to violence that did not claim as many victims at those ages. Besides, the mortality changes identified in the control charts pertain to changes in the population’s health conditions, or new causes of death such as COVID-19 in future investigations. Future studies to evaluate this combined methodology by adding information from new censuses for Colombia would be interesting.

Nevertheless, our proposal for mortality surveillance consists of two analysis tools that work sequentially; therefore, this study has limitations regarding models and control charts. In the first place, the model captures the time trend and the age profile of mortality in the population. Subsequently, the Hotelling $T^2$ control chart and the MTY decomposition identify those years and age ranges whose death probabilities differ substantially from the model trend. Therefore, the $T^2$ chart out-of-control signals are interpreted as possible changes in mortality according to the model trend. For example, the LC model is more straightforward than the LC2 one, as the LC2 model includes more particular additional change structures. The selection of one or the other model will entail a different characterization of the mortality trend, and consequently, a variation in the Hotelling $T^2$ control chart diagnosis.

Finally, we would like to point out that although this paper only applied control charts to the Colombian abridged life tables, the methodology can be extended to abridged life tables in any developing country. It might be useful to look at other datasets and examine whether conclusions are consistent for different countries.