Latent Class Regression Utilizing Fuzzy Clusterwise Generalized Structured Component Analysis
Abstract
1. Introduction
2. GscaLCR Algorithm
2.1. Generalized Structured Component Analysis (GSCA)
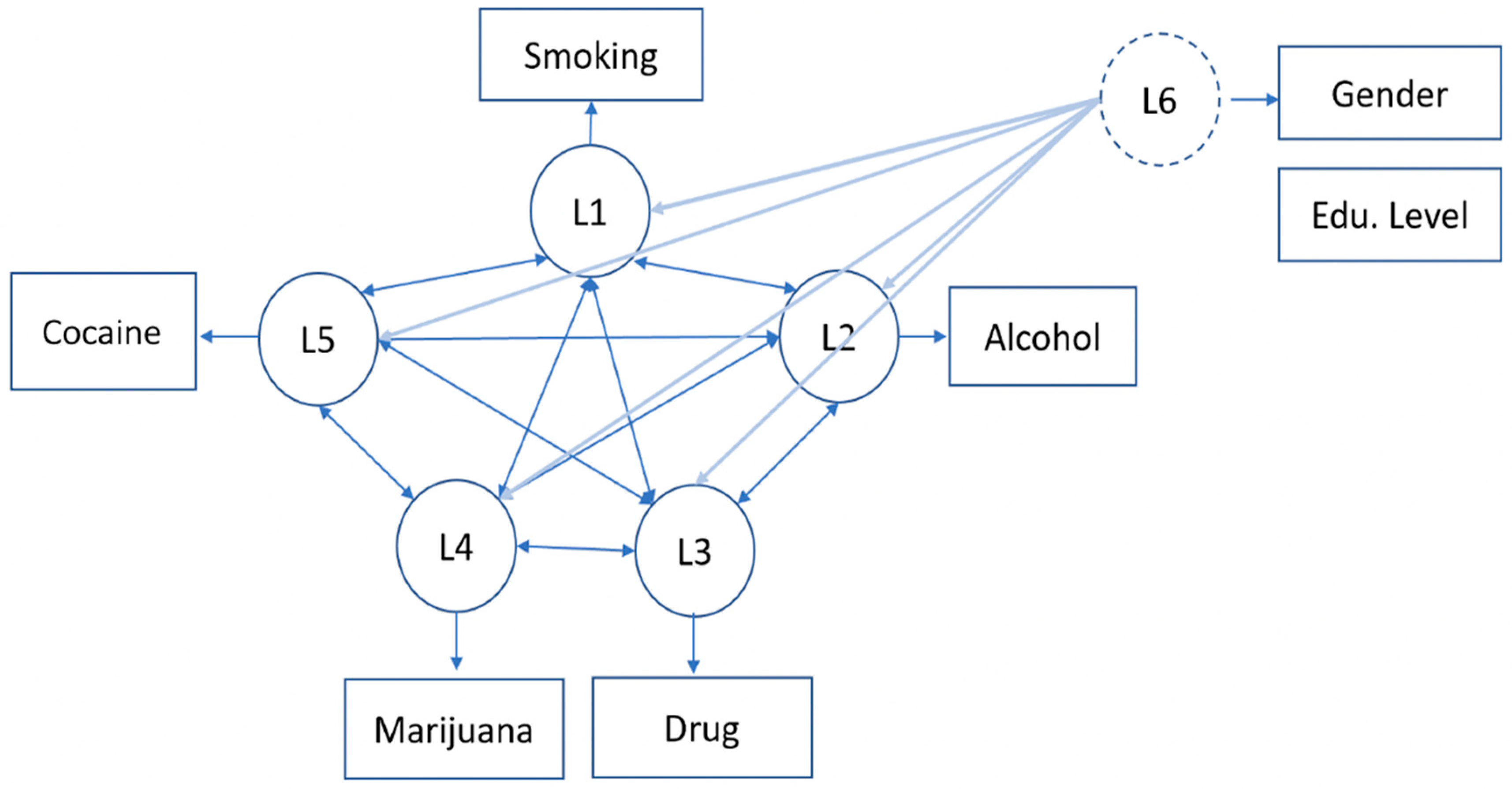
2.2. Generalized Structured Component Analysis for Latent Class Analysis (gscaLCA)
2.3. Latent Class Regression
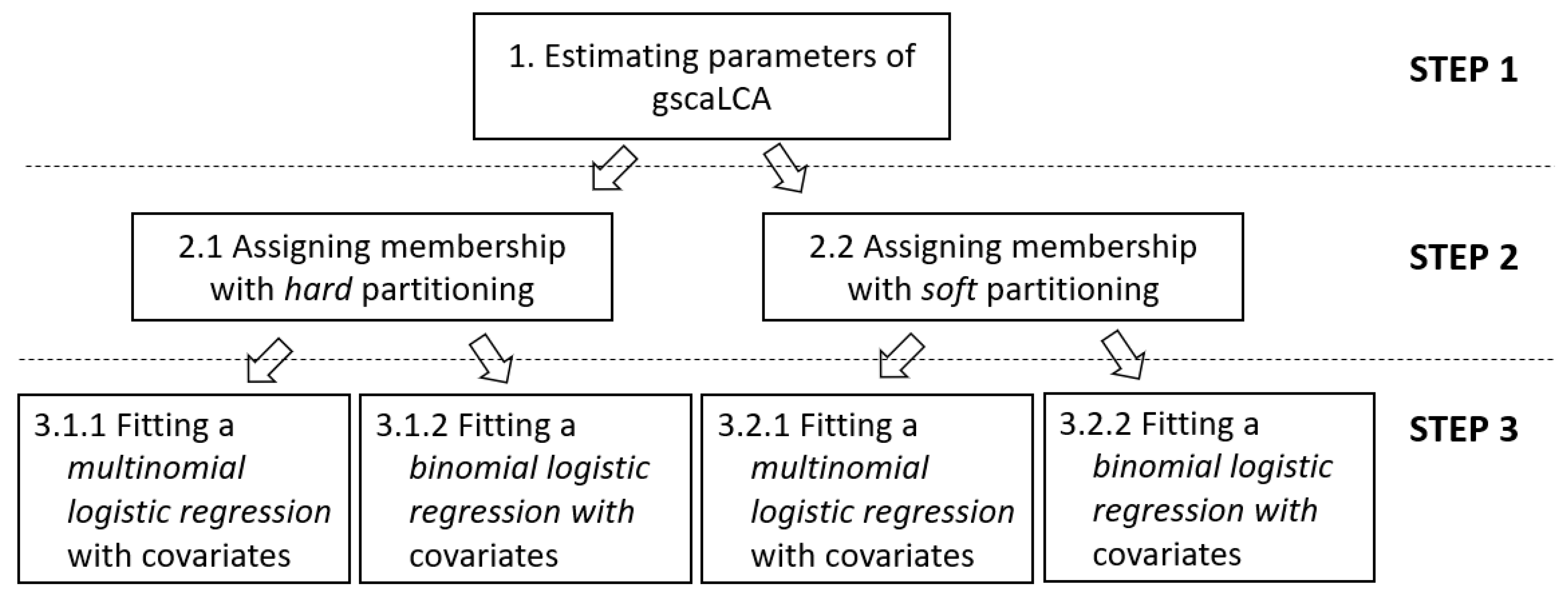
2.4. Generalized Structured Component Analysis for Latent Class Regression (gscaLCR)
2.4.1. Step 1: Estimate Parameters of gscaLCA
Step 1.1. Update the Parameters of Generalized Structured Component Analysis ( and ) in each cluster for fixed
Step 1.2. Update Membership Parameter for the Fixed and
2.4.2. Step 2: Assign Each Subject into a Latent Class Based on the Parameter Estimates from the Previous Step
2.4.3. Step 3: Fit a Regression Model with Covariates
3. An Illustration of Fitting gscaLCR into Empirical Data
3.1. Empirical Data
3.2. Method
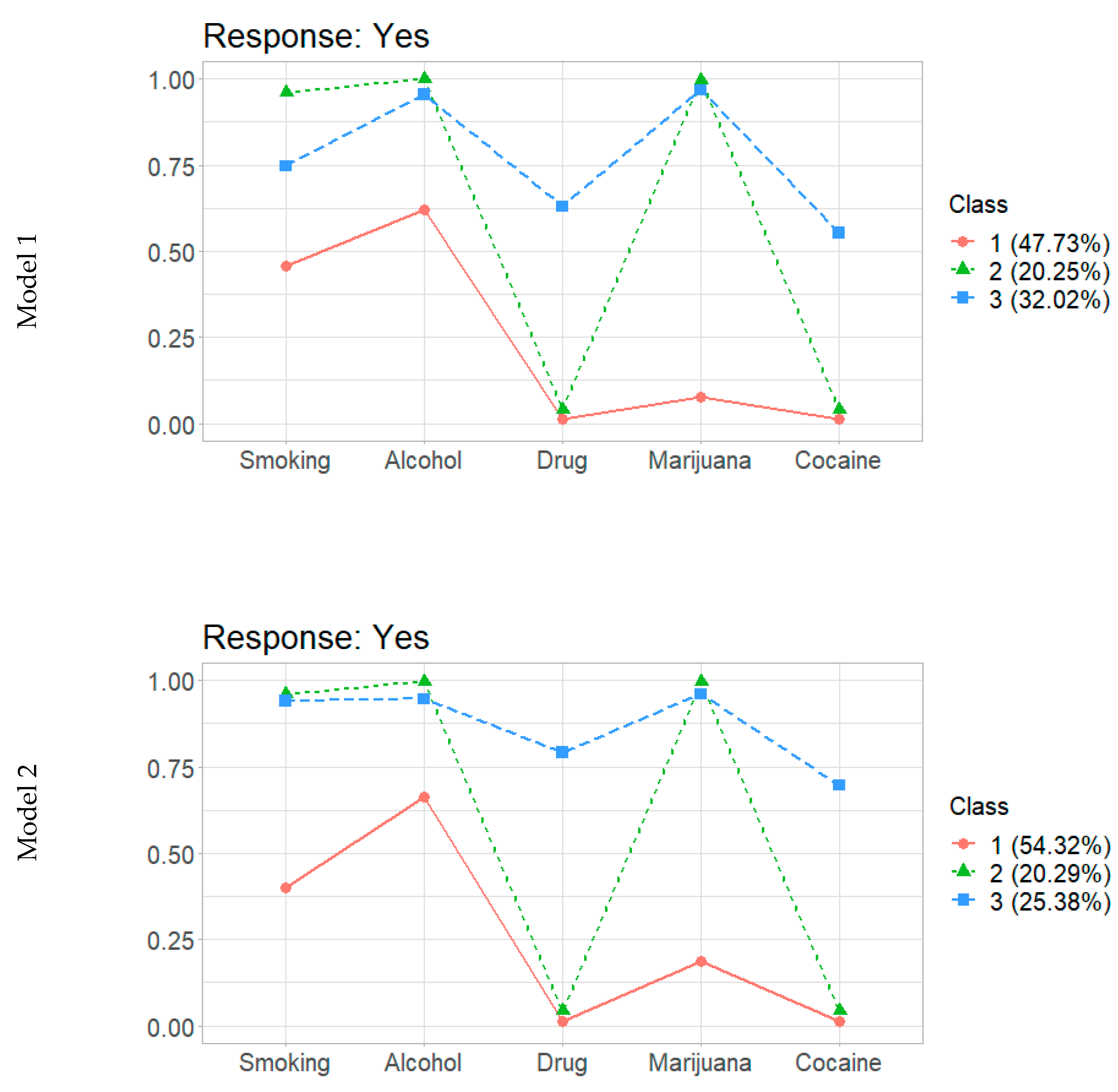
3.3. Results
3.3.1. Multinomial Logistic Regression: Hard Partitioning
3.3.2. Multinomial Logistic Regression: Soft Partitioning
3.3.3. Binomial Logistic Regression: Hard Partitioning
3.3.4. Binomial Logistic Regression: Soft Partitioning
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Lazarsfeld, P.; Henry, N. Latent Structure Analysis; Houghton Mifflin: Boston, MA, USA, 1968. [Google Scholar]
- McCutcheon, A. Latent Class Analysis; Sage Publications: Beverly Hills, CA, USA, 1987. [Google Scholar]
- Vermunt, J.K. Latent class modeling with covariates: Two improved three-step approaches. Polit. Anal. 2010, 18, 450–469. [Google Scholar] [CrossRef]
- Urick, A.; Bowers, A.J. What are the different types of principals across the United States? A latent class analysis of principal perception of leadership. Educ. Adm. Q. 2014, 50, 96–134. [Google Scholar]
- Lanza, S.T.; Cooper, B.R. Latent class analysis for developmental research. Child Dev. Perspect. 2016, 10, 59–64. [Google Scholar] [CrossRef] [PubMed]
- Xia, J.; Evans, F.H.; Spilsbury, K.; Ciesielski, V.; Arrowsmith, C.; Wright, G. Market segments based on the dominant movement patterns of tourists. Tour. Manag. 2010, 31, 464–469. [Google Scholar] [CrossRef]
- Doctor, S.M.; Liu, Y.; Whitesell, A.; Thwai, K.L.; Taylor, S.M.; Janko, M.; Emch, M.; Kashamuka, M.; Muwonga, J.; Tshefu, A.; et al. Malaria surveillance in the Democratic Republic of the Congo: Comparison of microscopy, PCR, and rapid diagnostic test. Diagn. Microbiol. Infect. Dis. 2016, 85, 16–18. [Google Scholar] [CrossRef] [PubMed]
- Formann, A.K.; Kohlmann, T. Latent class analysis in medical research. Stat. Methods Med. Res. 1996, 5, 179–211. [Google Scholar] [CrossRef]
- Jiang, Y.; Perry, D.K.; Hesser, J.E. Suicide patterns and association with predictors among Rhode Island public high school students: A latent class analysis. Am. J. Public Health 2010, 100, 1701–1707. [Google Scholar] [CrossRef]
- Harville, D.A. Maximum likelihood approaches to variance component estimation and to related problems. J. Am. Stat. Assoc. 1977, 72, 320–338. [Google Scholar] [CrossRef]
- Muthen, B.; Muthen, L. Mplus User’s Guide, 8th ed.; Muthen & Muthen: Los Angeles, CA, USA, 1998. [Google Scholar]
- Lanza, S.T.; Dziak, J.J.; Huang, L.; Wagner, A.; Collins, L.M. PROC LCA & PROC LTA Users’ Guide Version 1.3.2.; The Methodology Center, Penn State: University Park, PA, USA, 2015. [Google Scholar]
- Vermunt, J.K.; Magidson, J. Latent GOLD 4.0 User’s Guide; Statistical Innovations Inc.: Belmont, MA, USA, 2005. [Google Scholar]
- Linzer, D.A.; Lewis, J.B. poLCA: An R package for polytomous variable latent class analysis. J. Stat. Softw. 2011, 42, 1–29. [Google Scholar] [CrossRef]
- Dempster, A.; Laird, N.; Rubin, D. Maximum likelihood from incomplete data via the “EM” algorithm. J. R. Stat. Soc. Ser. B Methodol. 1977, 39, 1. [Google Scholar]
- Collins, L.M.; Lanza, S.T. Latent Class and Latent Transition Analysis: With Applications in the Social Behavioral, and Health Sciences (Vol. 718); Wiley Series in Probability and Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2010; ISBN 978-0-470-22839-5. [Google Scholar]
- Dziak, J.J.; Lanza, S.T.; Tan, X. Effect size, statistical power, and sample size requirements for the bootstrap likelihood ratio test in latent class analysis. Struct. Equ. Model. Multidiscip. J. 2014, 21, 534–552. [Google Scholar] [CrossRef] [PubMed]
- Gudicha, D.W.; Tekle, F.B.; Vermunt, J.K. Power and sample size computation for Wald tests in latent class models. J. Classif. 2016, 33, 30–51. [Google Scholar] [CrossRef]
- Ryoo, J.H.; Park, S.; Kim, S. Categorical latent variable modeling utilizing fuzzy clustering generalized structured component analysis as an alternative to latent class analysis. Behaviometrika 2020, 47, 291–306. [Google Scholar] [CrossRef]
- Hwang, H.; Takane, Y. Generalized structured component analysis. Psychometrika 2004, 69, 81–99. [Google Scholar] [CrossRef]
- Harris, K.M.; Udry, J.R. National Longitudinal Study of Adolescent to Adult Health (Add Health) 1994–2008; Inter-University Consortium for Political and Social Research (ICPSR): Ann Arbor, MI, USA, 2018. [Google Scholar] [CrossRef]
- Hwang, H.; Takane, Y. Generalized Structured Component Analysis: A Component-Based Approach to Structural Equation Modeling; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- De Leeuw, J.; Young, F.W.; Takane, Y. Additive structure in qualitative data: An alternating least squares method with optimal scaling features. Psychometrika 1976, 41, 471–503. [Google Scholar] [CrossRef]
- Jung, K.; Takane, Y.; Hwang, H.; Woodward, T.S. Dynamic GSCA (Generalized Structured Component Analysis) with applications to the analysis of effective connectivity in functional neuroimaging data. Psychometrika 2012, 77, 827–848. [Google Scholar] [CrossRef]
- Hwang, H.; DeSarbo, W.S.; Takane, Y. Fuzzy clusterwise generalized structured component analysis. Psychometrika 2007, 72, 181. [Google Scholar] [CrossRef]
- Young, F.W. Quantitative analysis of qualitative data. Psychometrika 1981, 46, 357–388. [Google Scholar] [CrossRef]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Springer: Boston, MA, USA, 1981; ISBN 978-1-4757-0452-5. [Google Scholar]
- Bezdek, J.C. Numerical taxonomy with fuzzy sets. J. Math. Biol. 1974, 1, 57–71. [Google Scholar] [CrossRef]
- Dunn, J.J. A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters. J. Cybern. 1974, 3, 32–57. [Google Scholar] [CrossRef]
- Wedel, M.; Steenkamp, J.-B.E. A clusterwise regression method for simultaneous fuzzy market structuring and benefit segmentation. J. Mark. Res. 1991, 28, 385–396. [Google Scholar] [CrossRef]
- Maulik, U.; Saha, I. Automatic fuzzy clustering using modified differential evolution for image classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3503–3510. [Google Scholar] [CrossRef]
- Aliahmadipour, L.; Torra, V.; Eslami, E. On hesitant fuzzy clustering and clustering of hesitant fuzzy data. In Fuzzy Sets, Rough Sets, Multisets and Clustering; Torra, V., Dahlbom, A., Narukawa, Y., Eds.; Studies in Computational Intelligence; Springer: Cham, Switzerland, 2017; Volume 671, pp. 157–168. [Google Scholar]
- Cacciola, M.; La Foresta, F.; Morabito, F.C.; Versaci, M. Advanced use of soft computing and eddy current test to evaluate mechanical integrity of metallic plates. NDT E Int. 2007, 40, 357–362. [Google Scholar] [CrossRef]
- Dayton, C.M.; Macready, G.B. Concomitant-variable latent-class models. J. Am. Stat. Assoc. 1988, 83, 173–178. [Google Scholar] [CrossRef]
- Dayton, C.M.; Macready, G.B. Use of categorical and continuous covariates in latent class analysis. In Applied Latent Class Analysis; Hagenaars, J., McCutcheon, A.L., Eds.; Cambridge University Press: Cambridge, UK, 2002; pp. 213–233. ISBN 0-521-59451-0. [Google Scholar]
- DeSarbo, W.S.; Oliver, R.L.; Rangaswamy, A. A simulated annealing methodology for clusterwise linear regression. Psychometrika 1989, 54, 707–736. [Google Scholar] [CrossRef]
- Wedel, M.; Kistemaker, C. Consumer benefit segmentation using clusterwise linear regression. Int. J. Res. Mark. 1989, 6, 45–59. [Google Scholar] [CrossRef]
- Van der Heijden, P.G.M.; Dessens, J.; Bockenholt, U. Estimating the concomitant-variable latent-class model with the EM algorithm. J. Educ. Behav. Stat. 1996, 21, 215–229. [Google Scholar] [CrossRef]
- Vermunt, J.K. LEM: A General Program for the Analysis of Categorical Data. Ph.D. Thesis, Tilburg University, The Netherlands, 1997. [Google Scholar]
- Yamaguchi, K. Multinomial logit latent-class regression models: An analysis of the predictors of gender-role attitudes among Japanese women. Am. J. Sociol. 2000, 105, 1702–1740. [Google Scholar] [CrossRef]
- Skrondal, A.; Laake, P. Regression among factor scores. Psychometrika 2001, 66, 563–575. [Google Scholar] [CrossRef]
- Bolck, A.; Croon, M.; Hagenaars, J. Estimating latent structure models with categorical variables: One-step versus three-step estimators. Polit. Anal. 2004, 12, 3–27. [Google Scholar] [CrossRef]
- Croon, M. Ordering the classes. In Applied Latent Class Analysis; Hagenaars, J., McCutcheon, A.L., Eds.; Cambridge University Press: Cambridge, UK, 2002; pp. 137–162. ISBN 0-521-59451-0. [Google Scholar]
- Gordon, G.J. Approximate Solutions to Markov Decision Processes. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 1999. (No. CMU-CS-99-143). [Google Scholar]
- Hruschka, H. Market definition and segmentation using fuzzy clustering methods. Int. J. Res. Mark. 1986, 3, 117–134. [Google Scholar] [CrossRef]
- Dias, J.G.; Vermunt, J.K. A bootstrap-based aggregate classifier for model-based clustering. Comput. Stat. 2008, 23, 643–659. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2019. [Google Scholar]
- Hwang, H.; Takane, Y.; Jung, K. Generalized structured component analysis with uniqueness terms for accommodating measurement error. Front. Psychol. 2017, 8, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Ryoo, J.H.; Hwang, H. Model evaluation in generalized structured component analysis using confirmatory tetrad analysis. Front. Psychol. 2017, 8, 916. [Google Scholar] [CrossRef] [PubMed]
| Model 1 | Estimate | Standard Error | z Value | Pr (>|z|) | ||
|---|---|---|---|---|---|---|
| Hard Partitioning | Class 2/Class 1 | (Intercept) | −0.836 | 0.100 | −8.403 | <0.001 ** |
| Gender(F) | −0.240 | 0.076 | −3.173 | 0.002 ** | ||
| Edu. Level | 0.029 | 0.022 | 1.316 | 0.188 | ||
| Class 3/Class 1 | (Intercept) | −0.165 | 0.085 | −1.948 | 0.051 | |
| Gender(F) | −0.545 | 0.065 | −8.341 | <0.001 ** | ||
| Edu. Level | 0.014 | 0.019 | 0.716 | 0.474 | ||
| Soft Partitioning | Class 2/Class 1 | (Intercept) | −0.374 | 0.108 | −3.458 | <0.001 ** |
| Gender(F) | −0.275 | 0.082 | −3.353 | 0.001 ** | ||
| Edu. Level | 0.005 | 0.024 | 0.194 | 0.846 | ||
| Class 3/Class 1 | (Intercept) | 0.163 | 0.099 | 1.634 | 0.102 | |
| Gender(F) | −0.640 | 0.076 | −8.375 | <0.001 ** | ||
| Edu. Level | −0.024 | 0.023 | −1.043 | 0.297 | ||
| Model 2 | ||||||
| Hard Partitioning | Class 2/Class 1 | (Intercept) | −0.876 | 0.098 | −8.933 | <0.001 ** |
| Gender(F) | −0.211 | 0.074 | −2.845 | 0.004 ** | ||
| Edu. Level | 0.003 | 0.022 | 0.117 | 0.907 | ||
| Class 3/Class 1 | (Intercept) | −0.209 | 0.088 | −2.365 | 0.018 * | |
| Gender(F) | −0.598 | 0.069 | −8.685 | <0.001 ** | ||
| Edu. Level | −0.063 | 0.021 | −3.081 | 0.002 ** | ||
| Soft Partitioning | Class 2/Class 1 | (Intercept) | −0.824 | 0.131 | −6.287 | <0.001 ** |
| Gender(F) | −0.167 | 0.099 | −1.693 | 0.090 | ||
| Edu. Level | −0.004 | 0.029 | −0.153 | 0.878 | ||
| Class 3/Class 1 | (Intercept) | 0.082 | 0.110 | 0.744 | 0.457 | |
| Gender(F) | −0.646 | 0.085 | −7.590 | <0.001 ** | ||
| Edu. Level | −0.061 | 0.025 | −2.403 | 0.016 * | ||
| Model 1 | Model 2 | ||||
|---|---|---|---|---|---|
| Male | Female | Male | Female | ||
| Multinomial Logistic Regression | Odds | ||||
| Class 2/Class 1 | 0.4857 | 0.3820 | 0.4214 | 0.3412 | |
| Class 3/Class 1 | 0.8958 | 0.5194 | 0.6337 | 0.3485 | |
| Binomial Logistic Regression | Percentage | ||||
| Class 1 | 41.98% | 52.59% | 48.59% | 59.13% | |
| Class 2 | 20.43% | 20.12% | 20.43% | 20.12% | |
| Class 3 | 37.58% | 27.28% | 30.83% | 20.62% | |
| Model 1 | Estimate | Standard Error | z Value | Pr (>|z|) | ||
|---|---|---|---|---|---|---|
| Hard Partitioning | Class 2/Class 1 | (Intercept) | −0.245 | 0.075 | −3.272 | 0.001 ** |
| Gender(F) | 0.427 | 0.057 | 7.451 | <0.001 ** | ||
| Edu. Level | −0.020 | 0.017 | −1.177 | 0.239 | ||
| Class 3/Class 1 | (Intercept) | −1.454 | 0.093 | −15.640 | <0.001 ** | |
| Gender(F) | −0.019 | 0.071 | −0.270 | 0.787 | ||
| Edu. Level | 0.024 | 0.021 | 1.138 | 0.255 | ||
| Soft Partitioning | Class 2/Class 1 | (Intercept) | 1.743 | 0.175 | 9.988 | <0.001 ** |
| Gender(F) | 0.353 | 0.134 | 2.632 | 0.008 ** | ||
| Edu. Level | −0.027 | 0.038 | −0.719 | 0.472 | ||
| Class 3/Class 1 | (Intercept) | 0.555 | 0.149 | 3.738 | <0.001 ** | |
| Gender(F) | −0.131 | 0.114 | −1.151 | 0.250 | ||
| Edu. Level | 0.068 | 0.034 | 2.023 | 0.043 * | ||
| Model 2 | ||||||
| Hard Partitioning | Class 2/Class 1 | (Intercept) | −0.186 | 0.075 | −2.474 | 0.013 |
| Gender(F) | 0.426 | 0.057 | 7.422 | <0.001 ** | ||
| Edu. Level | 0.033 | 0.017 | 1.966 | 0.049* | ||
| Class 3/Class 1 | (Intercept) | −1.446 | 0.093 | −15.578 | <0.001 ** | |
| Gender(F) | −0.019 | 0.071 | −0.268 | 0.789 | ||
| Edu. Level | 0.022 | 0.021 | 1.079 | 0.281 | ||
| Soft Partitioning | Class 2/Class 1 | (Intercept) | 0.804 | 0.143 | 5.603 | <0.001 ** |
| Gender(F) | 0.548 | 0.112 | 4.881 | <0.001 ** | ||
| Edu. Level | 0.051 | 0.033 | 1.545 | 0.122 | ||
| Class 3/Class 1 | (Intercept) | −0.480 | 0.145 | −3.313 | 0.001 ** | |
| Gender(F) | 0.083 | 0.110 | 0.757 | 0.449 | ||
| Edu. Level | 0.039 | 0.032 | 1.203 | 0.229 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.; Kim, S.; Ryoo, J.H. Latent Class Regression Utilizing Fuzzy Clusterwise Generalized Structured Component Analysis. Mathematics 2020, 8, 2076. https://doi.org/10.3390/math8112076
Park S, Kim S, Ryoo JH. Latent Class Regression Utilizing Fuzzy Clusterwise Generalized Structured Component Analysis. Mathematics. 2020; 8(11):2076. https://doi.org/10.3390/math8112076
Chicago/Turabian StylePark, Seohee, Seongeun Kim, and Ji Hoon Ryoo. 2020. "Latent Class Regression Utilizing Fuzzy Clusterwise Generalized Structured Component Analysis" Mathematics 8, no. 11: 2076. https://doi.org/10.3390/math8112076
APA StylePark, S., Kim, S., & Ryoo, J. H. (2020). Latent Class Regression Utilizing Fuzzy Clusterwise Generalized Structured Component Analysis. Mathematics, 8(11), 2076. https://doi.org/10.3390/math8112076





