Abstract
Metaheuristics have become a widely used approach for solving a variety of practical problems. The literature is full of diverse metaheuristics based on outstanding ideas and with proven excellent capabilities. Nonetheless, oftentimes metaheuristics claim novelty when they are just recombining elements from other methods. Hence, the need for a standard metaheuristic model is vital to stop the current frenetic tendency of proposing methods chiefly based on their inspirational source. This work introduces a first step to a generalised and mathematically formal metaheuristic model, which can be used for studying and improving them. This model is based on a scheme of simple heuristics, which perform as building blocks that can be modified depending on the application. For this purpose, we define and detail all components and concepts of a metaheuristic (i.e., its search operators), such as heuristics. Furthermore, we also provide some ideas to take into account for exploring other search operator configurations in the future. To illustrate the proposed model, we analyse search operators from four well-known metaheuristics employed in continuous optimisation problems as a proof-of-concept. From them, we derive 20 different approaches and use them for solving some benchmark functions with different landscapes. Data show the remarkable capability of our methodology for building metaheuristics and detecting which operator to choose depending on the problem to solve. Moreover, we outline and discuss several future extensions of this model to various problem and solver domains.
1. Introduction
Metaheuristics (MHs) are well-known alternatives to exact methods, which are excessively rigid and sometimes unsuitable for most practical applications. Even so, MHs are not as recent as we thought—we have been using them since we started understanding the world [1]. Heuristics (and metaheuristics), as well as mathematics, are akin to pre-loaded and hidden tools that our brains contain, and which have been barely uncovered by us. Nevertheless, MHs have evolved as a concept (more slowly than mathematics) passing through several paradigms and “novelty” phases over the last century [2,3]. The scientific community has developed several powerful algorithms under the metaheuristic scheme, which have been combined by several researchers to explore other methods. These procedures were oft-named (now less) as “new” or “novel” metaheuristics. This, after all, is not entirely accurate and represents a bad practise [4,5]. However, the literature contains a plethora of information for researchers and practitioners to plough and structure MHs as a scientific field. Such a “revolution” is currently ongoing as Sörensen et al. described in their overview of the MH history [1].
It is challenging to find a standard metaheuristic model or framework that allows designers to focus on studying different strategies to coin powerful and problem-specific methods. For instance, a researcher could propose a brand new method inspired by pink dolphins based on his/her environment, whilst, coincidentally, another researcher from a distant country reports a mathematically similar procedure but inspired in greater kudu bulls. (This is a fictional example. We do not know if such metaheuristics exist.) Therefore, how can we notice their similarities without running extensive computations? How can we compare these methods against others? Can we identify and classify them based only on their mathematical procedures? Before describing some approaches for such a model, we must accept that the No-Free-Lunch theorem [6] reigns supreme. Hence, there is not a MH with remarkable performance for all problem domains. One of the most popular approaches to a generalised model can be found in Genetic Algorithms (GAs), which is defined as a family because different genetic operators can be chosen for a particular implementation [7]. This arrangement also exists for other metaheuristics, such as Differential Evolution (DE) algorithms [8]. In both cases (i.e., GAs and DEs), the iterative procedure is represented by two or three operations over a population (a collection of probes) exploring a problem domain after being initialised. Note that operations within a family may have the same objective. Still, they differ in how much additional information is required to generate a new candidate solution. For example, DE/rand-to-best-and-current/3/exp implements more elaborate mutation and crossover operations than DE/rand/1/bin [8]. Recall the general convention DE/x/y/z, where x stands for the particular vector positions involved in the perturbation of each individual, y indicates the number of vector position differences regarded in the perturbation, and z means the kind of crossover employed after mutation. Plus, a distinct strategy for exploring MHs is by using Genetic Programming (GP) to choose between alternative operations, from those proposed in the literature. For instance, Miranda et al. redesigned the well-known Particle Swarm Optimisation (PSO) via a GP-based design schemes to solve 60 continuous benchmark problems [9]. However, this strategy is not straightforward enough to extend it to other metaheuristics. Another relevant methodology for combining MHs and then generating powerful optimisation algorithms is hybridisation [10,11]. A hybrid is not only a combination of two or more metaheuristics, but it can also contemplate non-heuristic-based algorithms, e.g., Nelder–Mead Simplex [12]. Nonetheless, hybrid methods are under the umbrella of the metaheuristics. Hassan and Pillay proposed a procedure, powered by a GA, for automating the design of a hybrid metaheuristic for a given template, and with a predefined collection [13]. More related examples, based on design patterns, can also be found in the literature [14,15]. These focus on tuning specific operators into a metaheuristic template. Further quite exciting strategies, which also go beyond the metaheuristic model, are hyper-heuristics (HHs) [16]. These methods combine heuristics to render a procedure capable of solving a given optimisation problem. Some authors have taken advantage of this fact for setting a process by selecting two or more simple heuristics to provide MHs with excellent performance in particular problems [17]. Nevertheless, there is not a concrete mathematical model that serves as a guideline for systematic and rigorous research on metaheuristics. Based on the aforementioned section, we can infer three exciting facts: (i) A metaheuristic is formed by operators no matter their nature; (ii) These operators are combined following a blueprint; (iii) These operators possess parameters that can be pre- or post- tuned when assembling the metaheuristic.
In this work, we consider these facts, as well as further inferences from several MHs of the state-of-the-art. Our goal: to take a step towards a generalised metaheuristic model. This formal model will facilitate comparisons and avoid reinventing the wheel when studying metaheuristics. Moreover, it will provide a standardised framework to automate metaheuristic generation. We focus our modelling, in this preliminary work, in the particular case of solving continuous optimisation problems with population-based methodologies. However, as we remark, the proposed model can be extended to any problem and procedure by addressing their particular circumstances. For example, to implement this model for metaheuristics in integer programming, the simple heuristics must search within an integer space instead of a continuous one. To illustrate our model, as a proof-of-concept, we select four well-known metaheuristics and employ their components as building blocks for generating new metaheuristics. These MHs are tested on some benchmark problems with different landscape domains.
This paper has three major contributions, as follows:
- Presents the first approach to a formal mathematical model to describe a metaheuristic in terms of building blocks for tackling continuous optimisation problems. It provides standardisation for researchers to easily identify the similarities and differences between metaheuristics, preventing researchers from reinventing the wheel.
- Highlights the effectiveness of combining building blocks to generate metaheuristics to provide problem-specific solutions.
- Yields a methodology to investigate the effect of search operators.
The remainder of this document is organised as follows. Section 2 introduces the theoretical foundations, where we detail all the concepts employed to develop the proposed model. Subsequently, Section 3 explains the derivation of the model, starting from the basics and increasing in complexity as the section progresses. Here, we include a full description of each component in the model, as well as their properties and graphical representation based on the signal-flow diagram from control theory. Section 4 shows how this model can be applied to the metaheuristics, reported in the literature to deal with continuous optimisation problems, for obtaining their building blocks (simple heuristics). Then, Section 5 exemplifies how to use such building blocks to spawn metaheuristics systematically and formally, via the proposed model. These MHs are implemented to solve several benchmark continuous optimisation problems with different dimensionalities and features. Finally, Section 6 summarises the most relevant conclusions and lays out some paths for future work.
2. Theoretical Foundations
In this section, we begin by presenting the foundations of the proposed model, which is detailed in the forthcoming lines. Several of these concepts may seem trivial, but some of them have slightly different definitions depending on the discipline that uses them. For example, “heuristic” and “metaheuristic” may be interchangeable terms in some combinatorial problems, such as Job-Shop Scheduling or Knapsack. However, they may have distinctive meanings in other areas. Thus, and to avoid controversies, we describe the rules and definitions adopted for formulating the standard model, in this first approach, focused on continuous optimisation problems.
2.1. Optimisation
Optimisation is one of the most common abstract procedures that all living species on earth, conscious or unconscious, perform in their daily activities. In layman terms, it mainly refers to the decisions made to achieve the best result of a problem or event. In this work, we use the definition of an optimisation problem given by a feasible domain and an objective function to minimise. These two components are described below.
Definition 1
(Minimisation problem). Let be a feasible domain, since is an arbitrary domain, and let be an objective function to be minimised, known as cost function, defined on a set such as . Thus, a minimisation problem represented with the tuple is stated as
where is the optimal vector (or solution) that minimises the objective function within the feasible domain, i.e., .
Remark 1
(Particular domain). This feasible domain is somehow a general representation of any domain delimited by simple constraints, which can be extended to a more complex one by considering constraints of different nature.
Remark 2
(Maximisation problem). In several applications, the objective function models the revenue, profit or utility of a process, so this function needs to be maximised. Let be the utility function such that we can state the optimisation problem with (1) by using a simple transformation such as .
Remark 3
(Multi-objective problem). When dealing with several objective functions, one must handle several considerations about the optimal solution. Nevertheless, in one way or another, it is always possible to transform the objective set into a single objective optimisation function such that it can be enclosed in (1).
In this work, we focus on continuous optimisation problems from the mathematical programming models according to the classification presented by Talbi [18] and Rao [19]. For these problems, we say that with D as the dimensionality of the problem. In many practical engineering applications, the problem domain is known a priori and its dimensionality is related to the number of design variables [19].
2.2. Heuristics
Heuristics are procedures designed to interact (create, evaluate or modify) a (candidate) solution, using a certain level of knowledge, for a given problem domain. The keyword “designed” indicates that the rules followed by such a procedure are based on practical experience, an inspirational source, or just a systematic process. The most popular implementation of heuristics are related to combinatorial optimisation problems [16], whilst there is relatively scarce information for continuous ones [20]. For the sake of clarity, we categorise the heuristics into three groups, taking as a starting point the ideas of [16,20]. These categories are based on the word “procedure”, from the Definition given at the beginning of this paragraph. Generally speaking, this involves a sequence of actions to do something. Such a sequence may contain a single instruction or multiple instructions that do not necessarily follow a sequential pattern. Thus, a heuristic is said to be low-level, when it comprises a single fixed action; mid-level, when it describes a sequence of fixed instructions; high-level, when it is a configuration of variable orders. These categories are related to simple heuristics, metaheuristics, and hyper-heuristics, respectively. It is not infrequent to find some authors who use “heuristics” to refer to “metaheuristics”, and others call the partial solutions of a “hyper-heuristic” a “metaheuristic”. All of them are surprisingly right, but it is quite tricky: one must know the conditions in which they are working to avoid an unnecessary headache. These types of heuristics are certainly heuristics per se, although they operate in different conditions and domains. However, since most heuristics use a set of search agents or populations, we must first establish the following concepts:
Definition 2
(Population). Let be a finite set of N candidate solutions for an optimisation problem , cf. Definition 1, at time t in an iterative procedure, i.e., . Then, denotes the n-th candidate solution or search agent of, say, the population of size N.
Definition 3
(Best solution). Let be an arbitrary set of solutions, which can be designated as—e.g., the entire population , the n-th neighbourhood , and the historical evolution of the n-th candidate . Therefore, let be the best solution in —i.e., .
3. Formulation
Consider the simplest case of continuous optimisation: the quadratic problem (), defined as
and solved with the well-known Newton method, based on a gradient operator , given by
since and are the gradient and Hessian of evaluated in the position found at the iteration t. It is common knowledge that it only requires one step to update the initial position to the optimum. To illustrate this, we first determine and as shown,
since is the identity matrix. By evaluating these terms in and plugging into (4), we obtain
As mentioned, this approach requires only one step to reach the optimum located at , no matter what the initial position was.
In the next step, we consider an arbitrary but continuous and differentiable objective function . We can still use the Newton heuristic after calculating and . It is also known that, under such conditions, this operator requires a good initial position to ensure its convergence to the optimum [19]. So, we need to somehow provide such a position—for example, by using a random generator, an outcome from another search operator, or just empirical information. Without loss of generality, it can be assumed that an initialisation operator performs such a task, which gives
Therefore, the first position is found by using the Newton search operator as follows
since ∘ is the operator composition. Hence, it is straightforward to specify how to determine the t-th candidate solution by applying the Newton operator consecutively—i.e.,
As may be seen, when implementing a sequence of operations (iterated operators), one expects to reach the optimal solution after iterations, . However, that is not true even in the example above, which is a small step forward from the simplest case, where any local optimum could serve as a stagnation pit. For that reason, a metric, convergence measurement, or simply an iteration counter should be considered as a stopping criterion. In general terms, we say that this functionality is fulfilled by a finalisation heuristic that evaluates one or more criteria for choosing which operator comes next. Considering the present example, can be represented as
where is a criteria evaluation function, and is the identity operator, such that . Bear in mind that the argument of in (9), , indicates the operator which will be chosen if returns zero.
Revisiting (8) and including this finalisation heuristic, we obtain the candidate solutions for each iteration , as follows,
Notice that each iteration depends on the decision, this operator resolves whether applying or according to the criteria verification , as specified in (9). Assuming that the T-th iteration corresponds to the candidate solution where convergence criteria are fulfilled, the step yields
which means the T-th candidate solution is close to the optimal solution, , according to a criterion specified for .
Therefore, three kinds of operators are required to describe the Newton method for solving any continuous and differentiable optimisation problem. These are the initialisation operator , the search operator , and the finalisation operator . A key point of using the last two operators is recursion, which can be inducted from (10). So, taking into account the previous analysis, we can represent the Newton method based on these operators, and as the triple (3-tuple),
Note that the disposition in the triple is causal in terms of the operator to apply, while the composition on the right-hand side is anti-causal. Thus, rewriting (11) in terms of , we have that
Now, let us consider an arbitrary continuous problem which may not be differentiable. In this case, this gradient-based operator cannot be implemented as before, so we must select a suitable operator to accomplish the optimisation work. For a given search operator , carefully chosen from the literature or designed to address this particular problem, we can easily extend the expression in (12), as follows
At this point, we consider a further assumption: is possibly incapable of dealing with a challenging problem by itself. Hence, we rethink the extension of (14) considering a sequence of search operators, represented as a set , to replace in (14). However, applying this set requires that we perform a sequence of composition operations, such as , which is also an operator, say ; in other words, the operators are closed under the composition. So, it is not necessary to use a complex notation for , which can be a single operator or the result of an operator sequence. Furthermore, Equation (14) represents any optimisation method based on search operators, or even, just operators. As we illustrate in the following sections, this expression is powerful enough to describe almost all metaheuristics reported in the literature, at least for continuous optimisation problems, whilst also serving for designing new ones.
The remainder of this section details the operators (or simple heuristics) and formally defines the first approach to the generalised metaheuristic model, which is the goal of this work. Without loss of generality, such a model is given in (14), though it can also be extended to hyper-heuristics. Lastly, several examples of operators and metaheuristics from the literature are discussed.
3.1. Simple Heuristics
As we may notice, the operators , , and are simple heuristics (SHs). What does that mean? They are the atomic units or building blocks in terms of search techniques that directly interact with either the problem domain, the solution state, or both. SHs are commonly categorised as constructive and perturbative. As their names suggest, a constructive heuristic generates new candidate solutions from scratch whereas a perturbative heuristic modifies existing ones [21]. Although these categories enclose the initialisation and search operators, , we deem it necessary to consider an additional one to describe the finalisation operator .
Definition 4
(Simple Heuristic). Let be a set of simple heuristics, or heuristic space, with a composition operation and an identity heuristic . Let be subsets of heuristics that produce a new solution, modify an existing solution, and choose between two operators, respectively.
Definition 5
(Initialiser). Let be a simple heuristic that generates a candidate solution within the search space from scratch—i.e., . represents an arbitrary domain, for which the case of continuous optimisation corresponds to . Then, let be the set of initialisers that satisfies the following properties:
- Composition: ;
- Last-hit: ;
- Associative: ;
- Non-commutative: .
The most common initialiser in the literature is to randomly place an agent within the feasible search space—e.g., using the uniform distribution.
Remark 4
(Last-hit). Note that using the second property into the third, we get . This is the essential part of an initialiser because it generates a new candidate solution within the feasible region . So, if multiple initialisers are applied in the same composition sequence, only the effect of the last one is preserved, the others are neglected.
Definition 6
(Search Operator). Let be a simple heuristic that modifies a candidate position , i.e., . Then, let be the set of search operators that satisfies the following properties:
- Composition: ;
- Identity element: ;
- Inverse element: ;
- Associative: ;
- Non-commutative: .
Remark 5
(Perturbators and Selectors). A search operator mostly comprises two basic operations: perturbation and selection. Hence, let be simple heuristics that modify () and update () the current solution called perturbator and selector, respectively. A perturbator always precedes a selector, so a search operator corresponds to . In many implementations, selectors may require additional information to operate—for example, the current best position in the population and a neighbourhood. Some examples of selection criteria found in the literature are Direct, Greedy, and Metropolis update.
Remark 6
(Inverse Element). The inverse element (heuristic) for could be hard to be determined analytically, mainly because h can use random numbers sampled from different distributions and unpredictable decisions, for example. Nevertheless, this element is readily available when, in a practical implementation, it is needed to recover a previous candidate solution after applying a search operator. In simple terms, this element serves to represent a step back in a solution process.
Definition 7
(Finaliser). Let be a simple heuristic that evaluates the current solution quality and chooses which search operator to apply. To do so, it uses information about the solution state (e.g., the current solution, its fitness value, the current iteration, the previous candidate solutions, and other measurements) in a criteria function . Then, is called a finaliser and is defined as
since and are two search operators selected according to . When , the identity operator, the finaliser can be specified as .
Remark 7
(Features). Regard that finalisers are somewhat more intricate than the other heuristics. They can be interpreted as condition-controlled loops (while-loops) because of their recursion behaviour when the criteria function is not satisfied. These simple heuristics are commonly used as strategies to control a search procedure.
Lastly, we have introduced several key concepts about simple heuristics assuming that they generate, modify, and evaluate a single candidate solution. This behaviour is frequently observed in several combinatorial domains, as well as in “classical” algorithms of a different nature, such as the Newton method and Simulated Annealing. However, this can be impractical for modern methods designed for touring the problem domain using a population of points (agents, probes, particles, amongst others). Nevertheless, the described way of representing simple heuristics covers either using a single point , a group of N points (cf. Definition 2), or even subgroups, as discussed below.
3.2. First Approach to a Generalised Metaheuristic Model
Metaheuristics are commonly defined as just heuristics or master strategies which control simple heuristics. Amongst these methods, one can list some widely recognised techniques because they have proven their capabilities in several implementations [3,5]. Some examples include Simulated Annealing (SA), Genetic Algorithm (GA), Differential Evolution (DE), Particle Swarm Optimisation (PSO), Cuckoo Search Algorithm (CSA), Deterministic Spiral Optimisation Algorithm (DSOA), and Symbiotic Organism Search (SOS) [22]. Nonetheless, these methods can be represented, as mentioned at the beginning of this section, by considering the simple heuristic components from Section 3.1. In the following definitions, we outline how these “building blocks” serve to describe well-known metaheuristics or to construct new ones, not under a particular bio-inspirational source of knowledge, but in a mathematical sense.
Definition 8
(Metaheuristic). Let be an iterative procedure called metaheuristic that renders an optimal solution for a given optimisation problem , cf. Definition 1. A metaheuristic can be mathematically defined in terms of three basic components as shown,
since is an initialiser, is a finaliser, and is a search operator, according to Definition 4.
Remark 8.
(Cardinality) An inherent property of metaheuristics is the cardinality, which is defined as the number of search operators it implements, i.e., disregarding the initialiser and finaliser; ergo . By way of standardisation, we denote a metaheuristic and its cardinality as , where .
Figure 1 depicts an example of an arbitrary metaheuristic using a block-diagram representation, which is very illustrative in terms of the SHs used. This kind of representation is suitable for basic metaheuristics, where the number of search operators is somehow small, but not flexible enough for intricate configurations. For instance, think about a population that is split into neighbourhoods, which search within the problem domain through different operators.
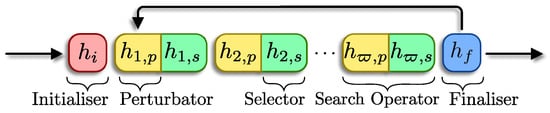
Figure 1.
Block-diagram of a metaheuristic composed by an initialiser , perturbators and selectors , , and a finaliser .
Therefore, we propose an alternative representation based on signal-flow diagrams from control theory. This allows for a more general representation of a metaheuristic closed under the Definition 8. Table 1 shows the three essential components from simple heuristics. For these diagrams, the line represents the state of the problem solution. Such a line begins with an initialiser (first row), which is displayed as an arrow to indicate causality. But the line can also pass through a search operator, depicted as a circular node (second row). When the finaliser (third row) deems it appropriate, the process ends. Otherwise, the current solution returns to a search operator (feedback dashed stroke).

Table 1.
Elements based on signal-flow diagrams for representing simple heuristics.
With these elements, we can reproduce most metaheuristics reported in the literature, or even go beyond that and into creating new ones. Figure 2a displays the representation for a common metaheuristic with a search operator , according to Definition 8. Bear in mind that this SO can be either a single operator or an equivalent of any SO configuration. For instance, Figure 2b illustrates a cascade sequence of SOs, whereas Figure 2c represents a parallel configuration of SOs. The former is pretty simple and easy to find in methods like PSO, SA, and DSOA with , and DE, GA, and CSA with . The latter is not as exotic. The most straightforward example of this configuration is PSO, including neighbourhoods or swarm topologies. Hence, and are search operators that split and merge, respectively. The population (of candidate solutions) into these subpopulations, are modified by the same SO—i.e., . In this example, the cardinality equals three. Notice that such a split is shown in Figure 2c with thinner strokes. Another example case of this configuration is Artificial Bee Colony (ABC), where the “swarm” is divided into three kinds of agents which perform specific functions [23]. Now, according to Figure 2a, is it possible to state a metaheuristic with either multiple initialisers, finalisers, or both? The short answer is yes. However, we can not guarantee that such a MH outperforms others from the literature. So, appropriate experiments must be carried out.
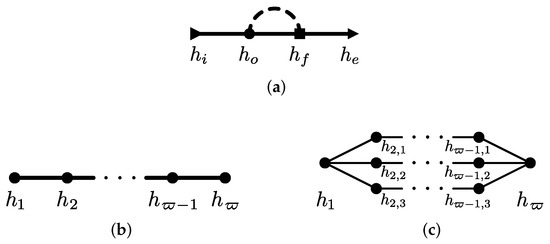
Figure 2.
Example of (a) the metaheuristic representation based on signal-flow diagrams, where can be obtained from (b) a cascade or (c) a parallel composition.
4. Analysis of Selected Metaheuristics
In this section, we use the components discussed for the generalised model approach to describe four selected well-known metaheuristics from the literature. These are Simulated Annealing (SA) [24], Particle Swarm Optimisation (PSO) [25,26], Genetic Algorithm (GA) [27], and Differential Evolution (DE) [8]. Because some MHs employ similar selectors, and to avoid repeating information, we first present three of the most common selectors found in the literature.
Consider a candidate position obtained through any perturbator from the current position of the n-th agent and further information about the solution state, such as the fitness difference between the candidate and current solutions, , amongst others. Thence, is accepted to be the new position via a selector , as is now described.
Definition 9
(Direct selection). The new position for the n-th agent is straightforwardly designated equal to —i.e.,
Definition 10
(Greedy selection). The new position for the n-th agent is assigned equal to if it improves the current position (i.e., ), thus
where the sign “≤” prefers to escape or overcome a large plateaux [8].
Definition 11
(Metropolis selection). The new position for the n-th agent is set equal to if it improves the current position (i.e., ). Should it be worsened (), is selected with a given probability of acceptance, as shown in
since is the Boltzmann’s constant and is the temperature which decreases slowly, such as , with as the initial temperature, as the decreasing (cooling) ratio, and as the current iteration [28]. Some default values used for these parameters are , , and . It is worth noting that this is only a flavour of this selection scheme, and there are several variations of it in the literature [29].
Furthermore, and before going into detail, we regard that the continuous problem domain is normalised between −1 and 1—i.e., . Additionally, we consider that all MHs use an initialiser based on a Random Sampling perturbator and a Direct selector (Definition 9).
Definition 12
(Random Sampling). A candidate solution is obtained through
where is a vector of i.i.d. random numbers with .
4.1. Simulated Annealing (SA)
SA was introduced by Kirkpatrick et al. for solving combinatorial optimisation problems [24], but it has also been implemented in other domains [28,29]. It was the first metaheuristic inspired in a nonlinear physical process—i.e., the annealing—which refers to the thermal treatment of materials for promoting its recrystallisation [30]. This technique is mainly composed of one Search Operator based on the Random Search perturbator and the Metropolis selector (Definition 11). This perturbator is described as follows.
Definition 13
(Random Search). A candidate solution is determined by a random search operation, as shown in
where is the step size factor and is a vector of i.i.d. random numbers with either or another probability distribution, such as the normal standard and symmetric Lévy stable ones.
4.2. Particle Swarm Optimisation (PSO)
Kennedy and Eberhart proposed PSO as a population-based methodology that takes advantage of social and individual interactions between agents for exploring a problem domain [25]. Swarm particles have two primary components, position and velocity, which are updated on each iteration via a simple kinematic expression [26]. In terms of search operators, PSO only implements one that comprises the Swarm Dynamic perturbator and the Direct selector (Definition 9).
Definition 14
(Swarm Dynamic). The candidate position for the n-th agent is determined via the swarm dynamic operation, such as
where corresponds to the velocity of this individual. This velocity can be calculated via different approaches, and PSO variants with slight to radical changes being prolific. The simplest and most common one, broadly implemented in several practical problems, corresponds to
since are velocity scale coefficients, , , are known as the self and swarm confidence coefficients, respectively, and are i.i.d. random vectors with , [31]. stands the previous velocity of the n-th agent, whilst and are the best position found by each individual and by the entire population, respectively.
Remark 9
(Velocity Approach). Two approaches branch out from (23) by carefully selecting the coefficient values—i.e., inertial and constricted—as shown below.
- Inertial approach: is called inertia weight and (they are neglected). In several implementations, is employed as a fixed parameter, but in others, it is defined as a time-dependent function, or a uniform random variable [32,33].
- Constrained approach: since χ is known as the constriction factor determined bywhere is the Heaviside step function with , , and [26,32].
4.3. Genetic Algorithm (GA)
GA was developed by Holland, De Jong, and others in the early ages of computing machines [34,35]. This algorithm comprises a sequence of two search operators inspired on the evolutionary mechanisms of genes of organisms [27]. The first SO consists of the Genetic Crossover perturbator and the Direct selector (Definition 9), and the second one of the Genetic Mutation perturbator and the Greedy selector (Definition 10); these perturbators are detailed next.
Definition 15
(Genetic Crossover). This operator works on a ranked version of the population w.r.t. the cost function value—i.e., with . Many authors refer to such a preliminary adjustment as natural selection [27]. Subsequently, a candidate position is rendered by a genetic crossover operation through
where and are mutually exclusive indices from the population—i.e., , and is a mask vector. Besides, is the mating pool size since is the portion of the best ranked agents from the population of size N. The parent indices and are obtained via a pairing scheme, whereas the mask vector is determined by a crossover mechanism.
Remark 10
(Pairing Scheme). Let and be the parent indices chosen by using a pairing scheme from the mating pool. Consider that indicates a positive integer randomly chosen between a and b, with , by sampling a given probability distribution ; when is unspecified, it is assumed to be the uniform distribution—i.e., . The most common pairing schemes from the literature for determining , are listed below [27,34].
- Random pairing:
- Rank weighting pairing:
- Roulette wheel pairing:
- Tournament pairing:since and .
Remark 11
(Crossover Mechanism). The mask vector is commonly assumed in the range , as we do in this work. However, some researchers incorporate values beyond such a range. This vector can be determined via diverse crossover mechanisms [27]. The most common ones are presented below.
- Single-point crossover:
- Two-points crossover:
- Uniform crossover:
- Blend crossover:
- Linear crossover:
Definition 16
(Genetic Mutation). This operator also works on a ranked version of the population w.r.t. the cost function value—i.e., with . Hence, the candidate position is found by implementing a genetic mutation such as
where is a mask vector, is the spatial step size, and are vectors of i.i.d. random numbers with distribution and , respectively, is the elite portion of the population (i.e., the top ranked individuals), and is the mutation probability. Furthermore, most researchers implement different probability distributions for mutating agents in continuous optimisation [27]. Some feasible options are the normal standard distribution and the symmetric Lévy stable distribution .
4.4. Differential Evolution (DE)
DE was proposed by Price and Storn for solving global optimisation problems [36]. This technique is considered as a stochastic population-based direct search algorithm whose performance depends mainly on the chosen mutation and crossover strategies [8,37]. They are different from those of GA and implemented in reverse order. Differential operators can be interpreted as particular cases, in a weak sense, of the genetic ones. Hence, the first operator comprises the Differential Mutation perturbator and the Direct selector (Definition 9), and the second one is based on the Differential Crossover perturbator and the Greedy selector (Definition 10).
Definition 17
(Differential Mutation). The candidate position is determined by using the differential mutation operator as displayed
where is the target vector which depends on the mutation scheme, stands the number of random differences or perturbations, and is a constant factor, . Plus, is an integer with uniform random distribution between 1 and N, where N is the population size, then with .
Remark 12
(Mutation Scheme). The most representative schemes for determining in a differential mutation, according to [8], are:
- rand:
- best:
- current-to-best:
- rand-to-best-and-current:
Since is the best position found in the population, and and parameters are determined according to the previous definition.
Definition 18
(Differential Crossover). The candidate position is achieved by performing the differential crossover operation given by
where ⊙ is the Hadamard–Schur’s product, and is the crossover mask vector calculated, such as , by employing as the element-wise Heaviside step function with , is a vector of i.i.d. uniformly random variables in , , and is the crossover probability that depends of the constant .
Remark 13
(Crossover Type). The crossover probability indicates if an element mutates, and its formula varies according to the crossover type [38], as described below.
- Binomial crossover:
- Exponential crossover:
4.5. Summary
In this section, we described four well-known metaheuristics in terms of the proposed model—i.e., their search operators—which are composed by a perturbator and a selector (Definition 6). Figure 3 illustrates them and details their simple heuristics. To complement the information, Table 2 summarises the corresponding control parameters. We classify such parameters as those of variation and tuning. The former group concerns those parameters that can dramatically change the behaviour of the operator, and the latter corresponds to those that refine the search procedure. According to the variation parameters, the analysed perturbators can easily be regarded as families of simple heuristics. For instance, consider the Random Search perturbator; two (or more) implementations can be made by varying only the probability distribution function to use—e.g., Uniform, Normal, or Lévy distribution.
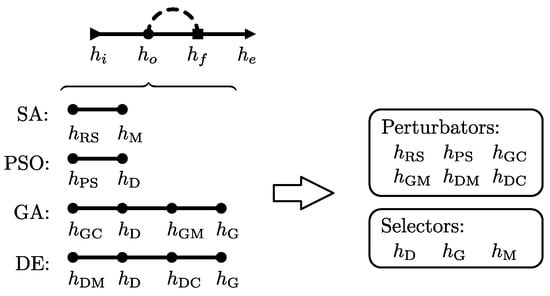
Figure 3.
Representation of the selected metaheuristics using the proposed model and their search operators (perturbators and selectors).

Table 2.
Search operators extracted from four well-known metaheuristics in the literature. Values or ranges for variation and tuning parameters, as well as selectors, are chosen from those commonly employed in the literature.
5. Numerical Examples
In this section, we illustrate as a proof-of-concept how to use the proposed model for the metaheuristics tackling continuous optimisation problems. As a disclaimer, the scope of this work is not to show which metaheuristic performs best, nor to conduct a comprehensive study about their features. Those works are undoubtedly vital. Nevertheless, they must be carried out as independent research, as is customary in the literature. We invite the reader to consult [39], where we implemented an approach based on hyper-heuristics to tailor metaheuristics using the same, but not so formal, building block idea. Instead, our purpose is to provide researchers and practitioners with a modular and formal way to explore innovative methodologies and topologies.
We implemented the perturbators and selectors indicated in Table 2 using the parameter values displayed in Table 3. We defined twenty metaheuristics, ten of cardinality one, and the other ten of cardinality two, using the same random initialiser as commented above. Table 4 details the search operators that give place to those metaheuristics, according to the conventional topology (see Figure 3). It is worth mentioning that the last column of Table 4 provides a possible name, following a systematic nomenclature, for each one of these configurations, except for the well-known metaheuristics such as SA, PSO, GA, and DE. This nomenclature is quite simple and can be defined with two rules. First, the perturbator is written in a capital letter, whereas the selector initial is given in lowercase. Second, whenever there are two or more search operators, they are concatenated with a dash. Moreover, Table 5 presents the selected problems that we tackled with the aforementioned metaheuristics, each of them over search spaces in two, ten, and fifty dimensions. All optimisation procedures performed 100 iterations and were repeated 50 times for guaranteeing statistical significance.

Table 3.
Parameters chosen for each implemented perturbator.

Table 4.
Metaheuristics built by defining the cascade sequence of search operators.

Table 5.
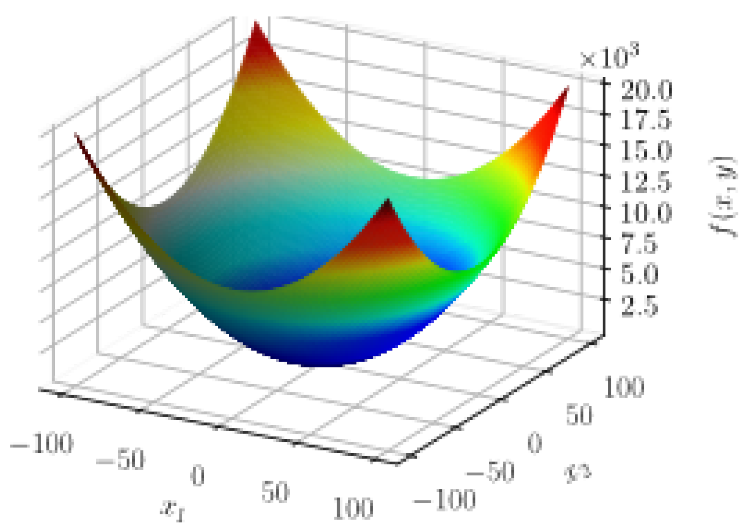
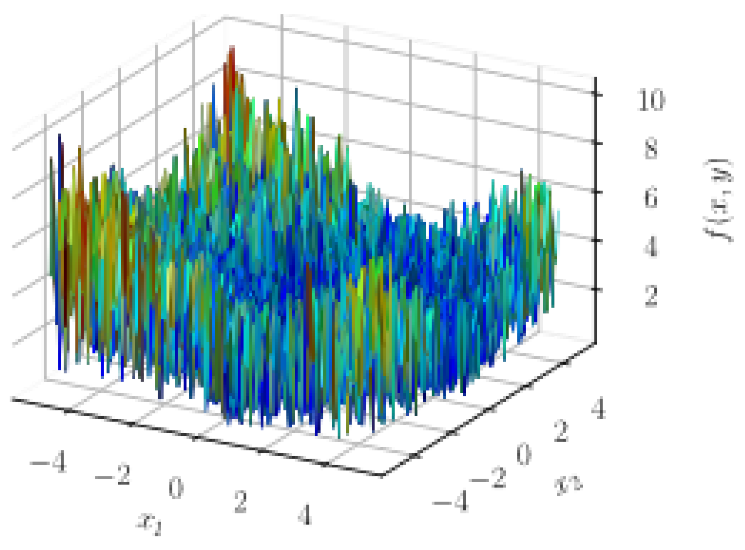
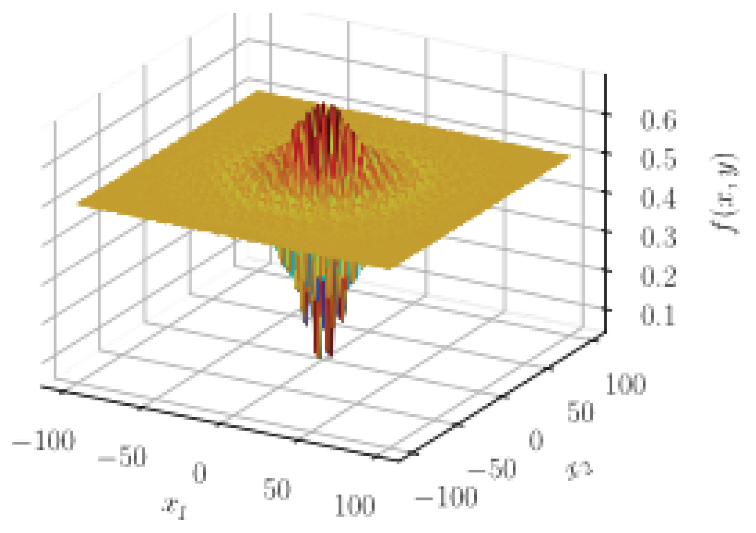
Selected benchmark functions.
All the numerical experiments were carried out on a personal laptop computer with Intel Core i5 dual-core processor @ 2 GHz and 8 Gb LPDDR3 RAM @ 1867 MHz. They were coded in Python v3.7 using the package CUSTOMHyS v1.0 (freely available at https://github.com/jcrvz/customhys.git), which facilitates the implementation of metaheuristics through search operators as building blocks.
Figure 4 shows the fitness orders obtained for each problem when solved through all 20 MHs. The first problem, Sphere, corresponds to the simplest one. When considering the two-dimensional case, Figure 4a, it is easy to identify search operator configurations that behave undesirably. This is the simplest case used in the literature. However, not all metaheuristics report a low fitness order. For example, the MH comprising the Differential Crossover (DC) perturbator and the Greedy (g) selector achieved a fitness order above two for most runs—i.e., . On the contrary, the PSO variant using the Metropolis selector (PSm) stands out, even over the vanilla PSO. Another point worthy of remark is that the metaheuristic PSO-DCg, which has a cardinality of two, improves the performance of PSO. Notice that the second search operator is the worst one when it is used as a standalone metaheuristic. However, it seems to act like a refiner when it is applied as a second step; remember that this one comes from DE, where it is also the second SO. The combination of PSO and SA, in any order, renders better results than using these metaheuristics by themselves. When increasing the number of dimensions, Figure 4a, performances remain somewhat stable. In this case (Sphere 10D), PSOm also renders the best fitness values, surmounting the other metaheuristics in almost 50% of the tests. For the last case—i.e., when the number of dimensions is 50 (Figure 4a)—we detect that this metaheuristic is no longer the best. GA achieves the lowest fitness values, followed by GCd, GCm, GCd-DCg, and GCd-SA. Recall that GA can be rewritten as GCd-GMg. Therefore, it is evident that those MHs with distinctive low fitness values include the Genetic Crossover perturbator, which seems to have significant capabilities for big dimensional problems. It is also curious to note that this simple heuristic does not exhibit a significant performance for the scenarios with low dimensionality—i.e., two and ten dimensions.
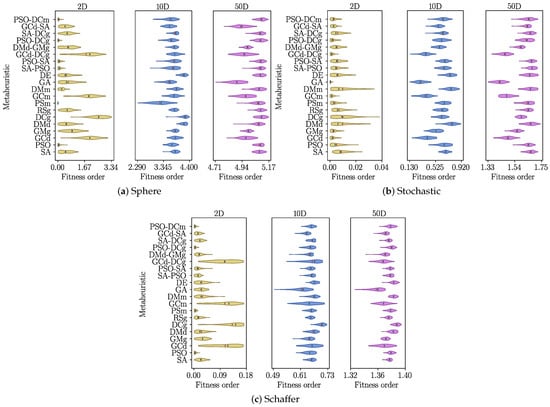
Figure 4.
Violin-plots of the fitness orders, , obtained for each metaheuristic built when solving a given problem. Mean and median are indicated by the red and green vertical strokes, respectively.
The aforementioned pattern is easily observed for the Stochastic function in all dimensions—cf. Figure 4b. Notice that even for the two-dimensional case, GA beats the other metaheuristics. Are methods based on Genetic Crossover a better option for high-dimensional smooth problems and noisy multi-modal problems? This is an interesting fact that seems to arise from these problems. However, it is a hypothesis that still needs to be proven. Indeed, Figure 4c shows the results obtained for the function Schaffer N3, which exhibits a landscape that is somehow between that of the other two (see Table 5). For the two-dimensional case, also shown in Figure 4c, there is a marked difference between GCd, DCg, GCm, and GCd-DCg, and the others. These three render the largest (worst) fitness orders. They all share the base of a crossover perturbator, either a genetic or differential one. However, when combining them with search operators of a different nature, the undesired behaviour seems to be alleviated, as shown by DE (or DMd-DCg), DMd-GMg, PSO-DCg, SA-DCg, GCd-SA, and PSO-DCm. Despite this, the best results were obtained by using PS-based metaheuristics, such as PSO, PSm, PSO-DCg, and PSO-DCm. Lastly, by visually analysing the 10D and 50D cases in Figure 4c, it is easy to recognise a pattern. Although the Genetic Crossover perturbations play a role for achieving the lowest fitness orders, in this case, benefits start at ten dimensions. Note that GA also finds the best solution for these problems.
It is important to remark that the above discussion was focused on the lowest value that each MH reaches. Such a value may be somewhat related to the accuracy, but keeping in mind that it occurs with a certain probability. Regarding Figure 4, one notices that for higher dimensions, the violins for low values are much longer than those for the two-dimensional case. This fact is attributed to the precision of the method. For example, results for SA in Figure 4c at 50D, provide more confidence than those for GA; but SA does not have the same chance of reaching lower fitness orders. At this point, the trade-off between accuracy and precision becomes evident, which has been discussed in plenty of works [43,44,45]. A straightforward solution for this issue consists of defining a metric for deciding which metaheuristic to choose as the best one. A simple but meaningful measurement is the sum of the median and the interquartile range, as proposed in [39]. So, we rank all MHs studied for each particular problem and dimension through this criterion, obtaining Figure 5. This heatmap heeds which methodology outperforms the others (number one), and also shows the worst metaheuristic (number twenty). Several inferences stem from these data. For instance, GCd-SA performs the best when tackling the ten-dimensional Schaffer N3 function, which is quite hard to observe from the 10D case in Figure 4a. Nonetheless, it makes sense as its mean and median performances are quite similar to that of GA, which was visually chosen as the best one. Even so, the performance of GCd-SA spans over a region more than 50% smaller; hence, it is more precise.
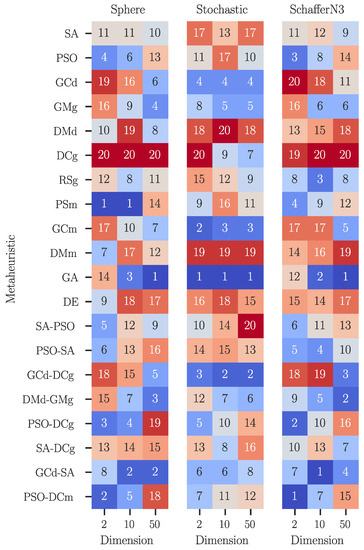
Figure 5.
Rank of the metaheuristics based on the median and interquartile range of the fitness values obtained when solving Sphere, Stochastic, and Schaffer N3, both for 2, 10, and 50 dimensions.
Finally, it is essential to observe how these metaheuristics perform through each step of their solving procedure. So, we select some illustrative cases from Figure 5. Figure 6 displays the fitness evolution when solving three problems: Sphere 2D, Stochastic 10D, and Schaffer N3 50D. These problems can be interpreted as a low, medium, and great difficulty, respectively. Similarly, we choose metaheuristics at the first, tenth, and twentieth positions of their corresponding ranking (Figure 5). For each problem, we plot fitness evolution in green, blue, and red strokes, which correspond to the best, mid, and lowest-ranked solvers, respectively. Each curve stands as one of the 50 runs carried out for each problem. It is noteworthy that the worst election of search operator for building metaheuristics exhibits a stagnation behaviour. A critical and highly undesired convergence can be observed in the most straightforward problem, the two-dimensional Sphere function, where the DCg-based metaheuristic does not evolve at any iteration; see Figure 6a. Such a dynamic is also noticed in the fifty-dimensional Schaffer N3 in Figure 6c. Apart from this, the best performing MH displays convergence curves that evolve with a desirable pattern, as Figure 6a,b show. Another critical remark emerges from the GA curves in Figure 6c, where only five runs reach fitness values below 21, before the 100 iterations mark. This figure also depicts the stagnation of more than half of the runs after the 25th iteration. Such a dynamic confirms the information provided by the corresponding violin plot in Figure 4c.
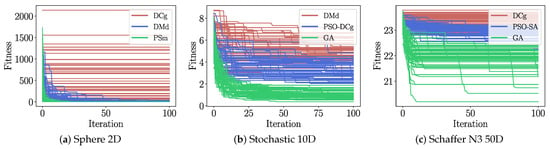
Figure 6.
Fitness evolution for some selected metaheuristics solving the problems Sphere 2D, Stochastic 10D, and Schaffer N3 50D. Green, blue, and red strokes are used for the best, mid, and lowest ranked solvers, respectively.
6. Summary
This work introduced the first approach to a generalised metaheuristic model, which serves as a standard model for studying and improving existing metaheuristics (MHs) for continuous optimisation problems. We described this model based on building blocks given from simple heuristics, which are specified as to avoid controversies with other definitions. We revisited several MHs and detected their essential parts, in terms of heuristics and how they interact throughout the search procedure. These simple heuristics were classified into three groups: initialisers, search operators (SOs), and finalisers. We also identified that a perturbator and a selector yield a search operator. Our model underlines the rules for considering not only one SO, but any given number. Indeed, along with the theoretical framework proposed for this model, we introduced a graphical representation based on signal-flow diagrams, where SOs are the central elements. We realised that our model is not only capable of describing well-known metaheuristics, but it serves to explore other alternatives, such as hyper-heuristics. It is also flexible enough to allow for more complex topologies of Search Operators, such as those in parallel, for example. We analysed four well-known metaheuristics from the literature and detected their SOs based on the proposed model. These MHs were Simulated Annealing (SA), Particle Swarm Optimisation (PSO), Genetic Algorithm (GA), and Differential Evolution (DE). Therefore, as a numerical example, we employed these operators to build twenty metaheuristics (including the four original ones), in terms of the proposed model. The MHs comprised ten MHs of cardinality one, and ten of cardinality two, where cardinality is defined as the number of search operators in cascade. We used these MHs for solving three benchmark continuous problems in three different dimensionalities, as a proof-of-concept. Our data revealed that some search operators have the ability to deal with a certain kind of problem, rendering outstanding performances. Additionally, this led to the conclusion that other search operators perform poorly when used as standalone metaheuristics, but become excellent when combined with another operator.
This model provides a great starting point for several future investigations. The most direct one is the automated generation of problem-specific metaheuristics by using either Hyper-Heuristics (HHs) or Machine Learning (ML) algorithms. Moreover, it is possible to explore non-heuristic-based Search Operators (SOs), such as Neural Networks. Additionally, the model allows investigating different topologies for the SOs, as well as inferring the behavioural patterns of a SO for problem characteristics through Data Science (DS) strategies. These possible paths will contribute to enhancing and proposing not only better metaheuristics but heuristic-based methods. For instance, the proposed model can be extended with ease to implement Hyper-Heuristics (HHs) for solving any optimisation problem. In this work, we focused on continuous optimisation problems, which are immersed in many practical applications, though not all. For example, Integer Programming (IP) and Combinatorial Optimisation (CO) problems are not included here. Even so, an extension to cover IP should be relatively straightforward as it shares many similarities with the proposed model. However, a meticulous analysis must be carried out for CO problems. It is well-known that metaheuristics are dependent on the problem domain nature, but such a dependency is a heritage from the search operators that compose them. Hence, for defining metaheuristics to tackle any problem from a particular domain, the proposed framework can be adjusted with ease by analysing the operators of the proposed metaheuristics in such a domain. With that in mind, another domain worth mentioning for future works is the multi-objective optimisation problems. In these, we need to adjust the selectors to classify or sort, as Pareto-based algorithms do, the population between dominated and non-dominated. Recall that selectors are responsible for guiding the search step-by-step for the whole search procedure.
Author Contributions
Conceptualisation, J.M.C.-D., I.A. and J.C.O.-B.; methodology and software, J.M.C.-D., I.A. and J.C.O.-B.; validation, J.M.C.-D., I.A. and J.C.O.-B.; formal analysis and investigation, J.M.C.-D., I.A. and J.C.O.-B.; resources, J.M.C.-D., I.A., J.C.O.-B., H.T.-M. and Y.S.; data curation, J.M.C.-D., I.A., J.C.O.-B., H.T.-M. and N.P.; writing—original draft preparation, J.M.C.-D., I.A. and J.C.O.-B.; writing—review and editing, J.M.C.-D., I.A., J.C.O.-B., H.T.-M., Y.S. and N.P.; visualisation, J.M.C.-D., I.A. and J.C.O.-B.; supervision, H.T.-M. and N.P.; project administration, I.A. and H.T.-M.; funding acquisition, I.A. and H.T.-M. All authors have read and agreed to the published version of the manuscript.
Funding
The research was supported by the Research Group in Intelligent Systems at the Tecnológico de Monterrey (México), the Project TEC-Chinese Academy of Sciences, and by the CONACyT Basic Science Project with grant number 287479.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DC | Differential Crossover |
| DE | Differential Evolution |
| DM | Differential Mutation |
| GA | Genetic Algorithm |
| GC | Genetic Crossover |
| GM | Genetic Mutation |
| MH | Metaheuristic |
| PS | Particle Swarm |
| PSO | Particle Swarm Optimisation |
| RS | Random Search |
| SA | Simulated Annealing |
| SH | Simple Heuristic |
| SO | Search Operator |
References
- Sörensen, K.; Sevaux, M.; Glover, F. A history of metaheuristics. Handb. Heuristics 2018, 2-2, 791–808. [Google Scholar] [CrossRef]
- Sotoudeh-Anvari, A.; Hafezalkotob, A. A bibliography of metaheuristics-review from 2009 to 2015. Int. J. Knowl.-Based Intell. Eng. Syst. 2018, 22, 83–95. [Google Scholar] [CrossRef]
- Dokeroglu, T.; Sevinc, E.; Kucukyilmaz, T.; Cosar, A. A survey on new generation metaheuristic algorithms. Comput. Ind. Eng. 2019, 137, 106040. [Google Scholar] [CrossRef]
- Sörensen, K. Metaheuristics—The metaphor exposed. Int. Trans. Oper. Res. 2015, 22, 3–18. [Google Scholar] [CrossRef]
- Hussain, K.; Salleh, M.N.M.; Cheng, S.; Shi, Y. Metaheuristic research: A comprehensive survey. Artif. Intell. Rev. 2019, 52, 2191–2233. [Google Scholar] [CrossRef]
- Adam, S.P.; Alexandropoulos, S.A.N.; Pardalos, P.M.; Vrahatis, M.N. No Free Lunch Theorem: A Review. In Approximation and Optimization; Demetriou, I., Pardalos, P., Eds.; Springer: Cham, Switzerland, 2019; pp. 57–82. [Google Scholar] [CrossRef]
- Kumar, S.; Jain, S.; Sharma, H. Genetic algorithms. In Advances in Swarm Intelligence for Optimizing Problems in Computer Science; Taylor and Francis Group: Abingdon, UK, 2018; pp. 27–52. [Google Scholar]
- Das, S.; Mullick, S.S.; Suganthan, P.N. Recent advances in differential evolution-An updated survey. Swarm Evol. Comput. 2016, 27, 1–30. [Google Scholar] [CrossRef]
- Miranda, P.B.; Prudêncio, R.B.; Pappa, G.L. H3AD: A hybrid hyper-heuristic for algorithm design. Inf. Sci. 2017, 414, 340–354. [Google Scholar] [CrossRef]
- Raidl, G.R. A unified view on hybrid metaheuristics. In International Workshop on Hybrid Metaheuristics; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–12. [Google Scholar]
- Talbi, E.G. A taxonomy of hybrid metaheuristics. J. Heuristics 2002, 8, 541–564. [Google Scholar] [CrossRef]
- Barzinpour, F.; Noorossana, R.; Niaki, S.T.A.; Ershadi, M.J. A hybrid Nelder–Mead simplex and PSO approach on economic and economic-statistical designs of MEWMA control charts. Int. J. Adv. Manuf. Technol. 2012. [Google Scholar] [CrossRef]
- Hassan, A.; Pillay, N. Hybrid metaheuristics: An automated approach. Expert Syst. Appl. 2019, 130, 132–144. [Google Scholar] [CrossRef]
- Krawiec, K.; Simons, C.; Swan, J.; Woodward, J. Metaheuristic design patterns: New perspectives for larger-scale search architectures. In Handbook of Research on Emergent Applications of Optimization Algorithms; IGI Global: Hershey, PA, USA, 2018; pp. 1–36. [Google Scholar]
- Stützle, T.; López-Ibáñez, M. Automated design of metaheuristic algorithms. In Handbook of Metaheuristics; Springer: Cham, Switzerland, 2019; pp. 541–579. [Google Scholar]
- Burke, E.K.; Hyde, M.R.; Kendall, G.; Ochoa, G.; Özcan, E.; Woodward, J.R. A classification of hyper-heuristic approaches: Revisited. In Handbook of Metaheuristics; Springer: Cham, Switzerland, 2019; pp. 453–477. [Google Scholar]
- Del Ser, J.; Osaba, E.; Molina, D.; Yang, X.S.; Salcedo-Sanz, S.; Camacho, D.; Das, S.; Suganthan, P.N.; Coello Coello, C.A.; Herrera, F. Bio-inspired computation: Where we stand and what’s next. Swarm Evol. Comput. 2019, 48, 220–250. [Google Scholar] [CrossRef]
- Talbi, E.G. Metaheuristics: From Design to Implementation; Wiley Publishing: Hoboken, NJ, USA, 2009; Volume 74. [Google Scholar]
- Rao, S.S. Engineering Optimization: Theory and Practice, 4 ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; p. 829. [Google Scholar]
- Pillay, N.; Qu, R. Hyper-Heuristics: Theory and Applications; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Woumans, G.; De Boeck, L.; Beliën, J.; Creemers, S. A column generation approach for solving the examination-timetabling problem. Eur. J. Oper. Res. 2016, 253, 178–194. [Google Scholar] [CrossRef]
- Kar, A.K. Bio inspired computing–a review of algorithms and scope of applications. Expert Syst. Appl. 2016, 59, 20–32. [Google Scholar] [CrossRef]
- Karaboga, D.; Gorkemli, B.; Ozturk, C.; Karaboga, N. A comprehensive survey: Artificial bee colony (ABC) algorithm and applications. Artif. Intell. Rev. 2014, 42, 21–57. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization (PSO). In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Clerc, M.; Kennedy, J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space. Evol. Comput. IEEE Trans. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Ahn, C.W. Practical Genetic Algorithms; Wiley-Interscience: Hoboken, NJ, USA, 2006; Volume 18, pp. 7–22. [Google Scholar] [CrossRef][Green Version]
- Delahaye, D.; Chaimatanan, S.; Mongeau, M. Simulated Annealing: From Basics to Applications. In Handbook of Metaheuristics, 3rd ed.; Gendreau, M., Potvin, J.Y., Eds.; Springer: Cham, Switzerland, 2019; Chapter 1; pp. 1–35. [Google Scholar] [CrossRef]
- Franzin, A.; Stützle, T. Revisiting simulated annealing: A component-based analysis. Comput. Oper. Res. 2019, 104, 191–206. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S. Modern meta-heuristics based on nonlinear physics processes: A review of models and design procedures. Phys. Rep. 2016, 655, 1–70. [Google Scholar] [CrossRef]
- Bonyadi, M.R.; Michalewicz, Z. Particle swarm optimization for single objective continuous space problems: A review. Evol. Comput. 2017, 25, 1–54. [Google Scholar] [CrossRef]
- Imran, M.; Hashim, R.; Khalid, N.E.A. An overview of particle swarm optimization variants. Procedia Eng. 2013, 53, 491–496. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Ji, G. A comprehensive survey on particle swarm optimization algorithm and its applications. Math. Probl. Eng. 2015, 2015, 931256. [Google Scholar] [CrossRef]
- Goldberg, D.; Holland, J. Genetic algorithms and machine learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Dianati, M.; Song, I.; Treiber, M. An introduction to genetic algorithms and evolution strategies. Sadhana 2002, 24, 293–315. [Google Scholar]
- Price, K.; Storn, R. Differential Evolution—A Simple and Efficient Adaptive Scheme for Global Optimization Over Continuous Space; Technical Report; International Computer Science Institute: Berkeley, CA, USA, 1995. [Google Scholar]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Zaharie, D. A Comparative Analysis of Crossover Variants in Differential Evolution. In Proceedings of the International Multiconference on Computer Science and Information Technology, IMCSIT 2007, Wisła, Poland, 15–17 October 2007; pp. 171–181. [Google Scholar]
- Cruz-Duarte, J.M.; Amaya, I.; Ortiz-Bayliss, J.C.; Conant-Pablos, S.E.; Terashima-Marín, H. A primary study on hyper-heuristics to customise metaheuristics for continuous optimisation. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–8. [Google Scholar]
- Jamil, M.; Yang, X.S. A literature survey of benchmark functions for global optimisation problems. Int. J. Math. Model. Numer. Optim. 2013, 4, 150. [Google Scholar] [CrossRef]
- Al-Roomi, A.R. Unconstrained Single-Objective Benchmark Functions Repository. 2015. Available online: https://www.al-roomi.org/benchmarks/unconstrained (accessed on 16 November 2020).
- Ardeh, M.A. Benchmark Function Toolbox. 2016. Available online: http://benchmarkfcns.xyz/fcns (accessed on 16 November 2020).
- Abualigah, L.M.; Khader, A.T.; Hanandeh, E.S. A new feature selection method to improve the document clustering using particle swarm optimization algorithm. J. Comput. Sci. 2018, 25, 456–466. [Google Scholar] [CrossRef]
- Pillai, D.S.; Rajasekar, N. Metaheuristic algorithms for PV parameter identification: A comprehensive review with an application to threshold setting for fault detection in PV systems. Renew. Sustain. Energy Rev. 2018, 82, 3503–3525. [Google Scholar] [CrossRef]
- Deng, W.; Zhao, H.; Zou, L.; Li, G.; Yang, X.; Wu, D. A novel collaborative optimization algorithm in solving complex optimization problems. Soft Comput. 2017, 21, 4387–4398. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).