Optimal Replenishment Policy for Deteriorating Products in a Newsboy Problem with Multiple Just-in-Time Deliveries
Abstract
1. Introduction
- We derive the optimal wholesale price and production strategies for a newsboy problem model.
- We incorporate product deterioration into the newsboy problem model.
- We simultaneously include repair cost, warranty cost, setup cost, item cost, storage cost, and JIT delivery.
1.1. Literature Review
2. Problem Description, Assumptions, and Notation
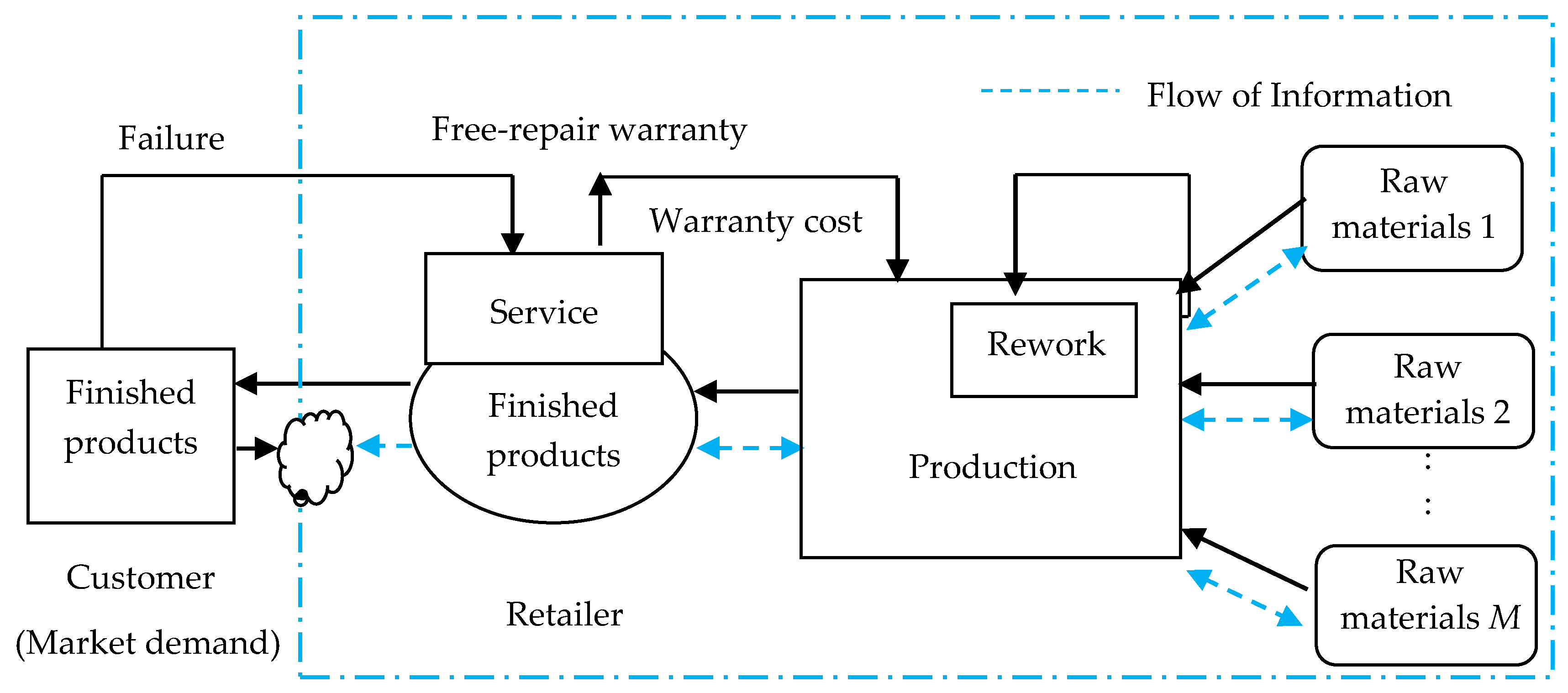
2.1. Problem Description
2.2. Assumptions
- Total orders are calculated by the manufacturer based on the retailer’s orders according to the production lot size for the following cycle while the demand is considered unknown.
- Material inventory is controlled through periodic reviews; backlogging is forbidden to prevent shortages.
- A static wholesale price is set by the manufacturer during replenishment, and the newsboy rule is followed by the retailer to regulate the order quantity with reference to the average demand, total salvage cost, and wholesale price.
- The lead-time for raw materials is fixed, and the transportation time is considered to be zero.
- The production rate is larger than the demand rate.
- The deterioration rate is constant, and the deterioration rate is considered only after the product has been received into inventory.
- No information gaps are considered during negotiations.
- Replenishment is instantaneous.
- The production procedure is initially controlled; after intervention, it may vary between controlled and out of control. The intervention time imperfect production process is distributed exponentially with known mean and variance.
- Imperfect production is not identified until the completion of an inspection process.
- JIT production and JIT multiple-delivery strategies are considered.
2.3. Notations
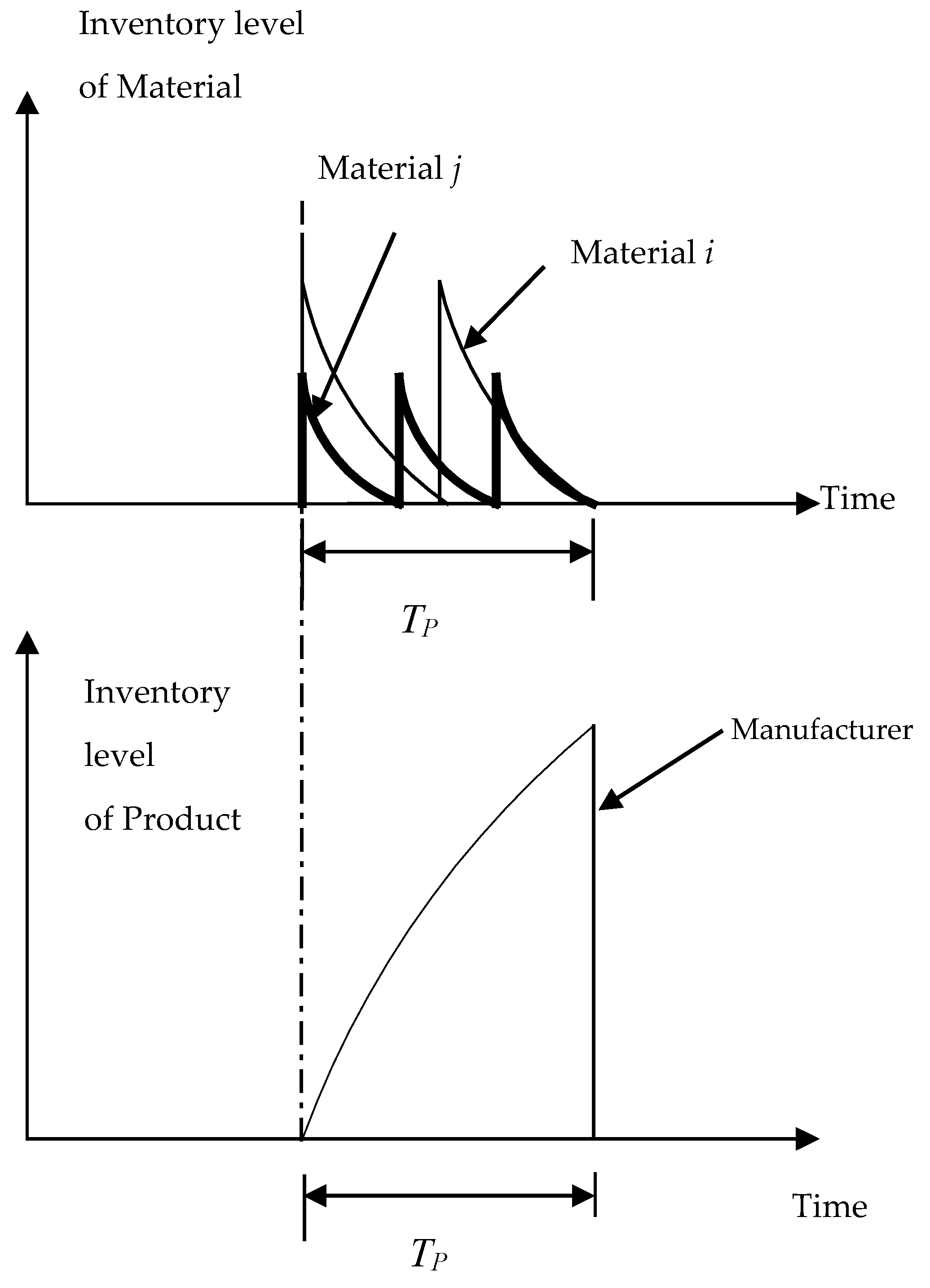
3. Model Development
3.1. Mathematical Form of the Model
3.2. Manufacturing Cost
3.3. Material Cost
4. Theoretical Derivations
4.1. The Sufficient Condition
4.2. Algorithm
5. Numerical Examples and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Bhuniya, S.; Sarkar, B.; Pareek, S. Multi-Product Production System with the Reduced Failure Rate and the Optimum Energy Consumption under Variable Demand. Mathematics 2019, 7, 465. [Google Scholar] [CrossRef]
- Tayyab, M.; Sarkar, B.; Yahya, B. Imperfect Multi-Stage Lean Manufacturing System with Rework under Fuzzy Demand. Mathematics 2019, 7, 13. [Google Scholar] [CrossRef]
- Mashud, A.H.M. A deteriorating inventory model with different types of demand and fully backlogged shortages. Int. J. Logis. Sys. Manag. 2020, 36, 16–45. [Google Scholar] [CrossRef]
- Wee, H.M.; Kuo, T.C.; Huang, Y.D.; Lin, Y.J. Two-stage newsboy problem for fashion products considering revenue sharing and return policies. J. Indust. Prod. Eng. 2013, 30, 500–509. [Google Scholar] [CrossRef]
- Yang, P.; Pai, S.; Yang, L.; Wee, H.M. Constrained optimization of newsboy problem with return policy. Appl. Mat. Inf. Sci. 2012, 6, 635–641. [Google Scholar]
- Gallego, G.; Moon, I. The distribution-free newsboy problem–review and extensions. J. Oper. Res. Soc. 1993, 44, 734–825. [Google Scholar] [CrossRef]
- Nagare, M.; Dutta, P.; Cheikhrouhou, N. Extended distribution-free newsvendor models with demand updates using experts’ judgment. Int. Trans. Oper. Res. 2019. [Google Scholar] [CrossRef]
- Kalpana, P.; Kaur, A. Single-period inventory models with multiple ordering opportunities: A review. Int. J. Logist. Syst. Manag. 2012, 13, 209–229. [Google Scholar] [CrossRef]
- Moon, I.; Choi, S. Distribution free newsboy problem with balking. J. Oper. Res. Soc. 1995, 46, 537–542. [Google Scholar] [CrossRef]
- Mashud, A.H.M.; Khan, M.A.-A.; Uddin, M.S.; Islam, M.N. A non-instantaneous inventory model having different deterioration rate with stock and price dependent demand under partially backlogged. Unce. Sup. Cha. Manag. 2018, 6, 49–64. [Google Scholar] [CrossRef]
- Mashud, A.H.M.; Hasan, M.R.; Wee, H.M.; Daryanto, Y. Non-instantaneous deteriorating inventory model under the joined effect of trade-credit, preservation technology and advertisement policy. Kybernetes 2019, 49, 1645–1674. [Google Scholar] [CrossRef]
- Mashud, A.H.M.; Wee, H.M.; Sarkar, B.; Chiang Li, Y.H. A sustainable inventory system with the advanced payment policy and trade-credit strategy for a two- warehouse inventory system. Kybernetes 2020. [Google Scholar] [CrossRef]
- Mashud, A.H.M.; Wee, H.M.; Huang, C.V. Preservation technology investment, trade credit and partial backordering model for a non-instantaneous deteriorating inventory. RAIRO Oper. Res. 2019. (In press) [CrossRef]
- Ghare, P.M.; Schrader, S.F. A model for exponentially decaying inventory. J. Ind. Eng. 1963, 14, 238–243. [Google Scholar]
- Covert, R.P.; Philip, G.C. An EOQ model for items with Weibull distribution deterioration. AIIE Trans. 1973, 5, 323–326. [Google Scholar] [CrossRef]
- Raafat, F.; Wolfe, P.M.; Eldin, H.K. An inventory model for deteriorating items. Comput. Ind. Eng. 1991, 20, 89–94. [Google Scholar] [CrossRef]
- Wee, H.M. Economic production lot size model for deteriorating items with partial back-ordering. Comput. Ind. Eng. 1993, 24, 449–458. [Google Scholar] [CrossRef]
- Wee, H.M.; Jong, J.F. An integrated multi-lot-size production inventory model for deteriorating items. Manag. Syst. 1998, 5, 97–114. [Google Scholar]
- Perez, F.; Torrres, F. An integrated production-inventory model for deteriorating items to evaluate JIT purchasing alliances. Int. J. Ind. Eng. Comput. 2019, 10, 51–66. [Google Scholar] [CrossRef]
- Yang, P.C.; Wee, H.M. An integrated multi-lot-size production inventory model for deteriorating item. Comput. Oper. Res. 2003, 30, 671–682. [Google Scholar] [CrossRef]
- Lau, A.H.L.; Lau, H.S. The effects of reducing demand uncertainty in a manufacturer-retailer channel for single-period products. Comput. Oper. Res. 2002, 29, 1583–1602. [Google Scholar]
- Lariviere, M.; Porteus, E.L. Selling to the newsvendor: An analysis of price-only contracts. Manuf. Serv. Op. Manag. 2001, 3, 293–305. [Google Scholar] [CrossRef]
- Malek, L.L.A.; Ziegler, H. Age dependent perishability in two-echelon serial inventory systems. Comput. Oper. Res. 1988, 15, 227–239. [Google Scholar] [CrossRef]
- Yoo, S.H.; Kim, D.; Park, M.S. Economic production quantity model with imperfect-quality items, two-way imperfect inspection and sales return. Int. J. Prod. Econ. 2009, 121, 255–265. [Google Scholar] [CrossRef]
- Sarkar, B.; Ullah, M.; Kim, N. Environmental and economic assessment of closed-loop supply chain with remanufacturing and returnable transport items. Comput. Ind. Eng. 2017, 111, 148–163. [Google Scholar] [CrossRef]
- Eppen, G.D. Effect of centralization on expected costs in a multi-location newsboy problem. Manag. Sci. 1979, 25, 498–503. [Google Scholar] [CrossRef]
- Alfares, H.K.; Elmorra, H.H. The distribution-free newsboy problem: Extensions to the shortage penalty case. Int. J. Prod. Econ. 2005, 93–94, 465–477. [Google Scholar] [CrossRef]
- Cherikh, M. On the effect of centralization on expected profits in a multi-location newsboy problem. J. Oper. Res. Soc. 2000, 51, 755–761. [Google Scholar] [CrossRef]
- Choi, T.M.; Li, D.; Yan, H. Optimal two-stage ordering policy with Bayesian information updating. J. Oper. Res. Soc. 2003, 54, 846–859. [Google Scholar] [CrossRef]
- Dutta, P. A multi-product newsboy problem with fuzzy customer demand and a storage space constraint. Int. J. Oper. Res. 2010, 8, 230–246. [Google Scholar] [CrossRef]
- Zhou, Y.W.; Wang, S.D. Manufacturer-buyer coordination for newsvendor products with two ordering opportunities and partial back orders. Eur. J. Oper. Res. 2009, 198, 958–974. [Google Scholar] [CrossRef]
- Yu, Y.; Zhu, J.; Wang, C. A newsvendor model with fuzzy price-dependent demand. Appl. Math. Model. 2013, 37, 2644–2661. [Google Scholar] [CrossRef]
- Rossi, R.; Prestwich, S.; Tarim, S.A.; Hnich, B. Confidence-based optimization for the newsvendor problem under binomial, Poisson and exponential demand. Eur. J. Oper. Res. 2014, 239, 674–684. [Google Scholar] [CrossRef]
- Dutta, P.; Chakraborty, D. Incorporating one-way substitution policy into the newsboy problem with imprecise customer demand. Eur. J. Oper. Res. 2010, 200, 99–110. [Google Scholar] [CrossRef]
- Sakakibara, S.; Flynn, B.; Schroeder, R.; Morris, W. The impact of Just-in-Time manufacturing and its infrastructure on manufacturing performance. Manag. Sci. 1997, 43, 1246–1257. [Google Scholar] [CrossRef]
- Nassimbeni, G. Factors underlying operational purchasing practices: Results of a research. Int. J. Prod. Econ. 1995, 42, 275–288. [Google Scholar] [CrossRef]
- Reese, J.; Geisel, R. A comparison of current practice in German manufacturing industries. Eur. J. Purch. Supply. Manag. 1997, 42, 275–288. [Google Scholar] [CrossRef]
- Gunasekaran, A. Just-in-time purchasing: An investigation for research and application. Int. J. Prod. Econ. 1999, 59, 77–84. [Google Scholar] [CrossRef]
- Batrancea, I.; Rathnaswamy Malar, M.; Gaban, L.; Fatacean, G.; Tulai, H.; Bircea, I.; Rus, M.I. An Empirical Investigation on Determinants of Sustainable Economic Growth. Lessons from Central and Eastern European Countries. J. Ris. Fin. Manag. 2020, 13, 146. [Google Scholar] [CrossRef]
- Batrancea, I.; Rathnaswamy Malar, M.; Batrancea, L.; Nichita, A.; Gaban, L.; Fatacean, G.; Tulai, H.; Bircea, I.; Rus, M.I. A Panel Data Analysis on Sustainable Economic Growth in India, Brazil, and Romania. J. Ris. Fin. Manag. 2020, 13, 170. [Google Scholar] [CrossRef]
- Larissa, B.; Maran, R.M.; Ioan, B.; Anca, N.; Mircea-Iosif, R.; Horia, T.; Gheorghe, F.; Ema Speranta, M.; Dan, M.I. Adjusted Net Savings of CEE and Baltic Nations in the Context of Sustainable Economic Growth: A Panel Data Analysis. Ris. Fin. Manag. 2020, 13, 234. [Google Scholar]
- Batrancea, I.; Batrancea, L.; Nichita, A.; Gaban, L.; Masca, E.; Fatacean, G.; Moscviciov, A. An econometric approach on production, costs and profit in Romanian coal mining enterprises. Eco. Rese. 2019, 32, 1019–1036. [Google Scholar] [CrossRef]
- Kung, K.Y.; Huang, Y.D.; Wee, H.M.; Daryanto, Y. Production-inventory system for deteriorating items with machine breakdown, inspection and partial backordering. Mathematics 2019, 7, 616. [Google Scholar] [CrossRef]
- Hsu, J.T.; Hsu, L.F. An EOQ model with imperfect quality items, inspection errors, shortage backordering, and sales returns. Int. J. Prod. Econ. 2013, 143, 162–170. [Google Scholar] [CrossRef]
- Salameh, M.K.; Jaber, M.Y. Economic production quantity model for items with imperfect quality. Int. J. Prod. Econ. 2000, 64, 59–64. [Google Scholar] [CrossRef]
- Lee, H.L.; Rosenblatt, M.J. Simultaneous determination of production cycle and inspection schedules in a production system. Manag. Sci. 1987, 33, 1125–1136. [Google Scholar] [CrossRef]
- Hota, S.K.; Sarkar, B.; Ghosh, S.K. Effects of unequal lot size and variable transportation in unreliable supply chain management. Mathematics 2020, 8, 357. [Google Scholar] [CrossRef]
- Daryanto, Y.; Wee, H.M.; Widyadana, G.A. Low Carbon Supply Chain Coordination for Imperfect Quality Deteriorating Items. Mathematics 2019, 7, 234. [Google Scholar] [CrossRef]
- Daryanto, Y.; Wee, H.M. Low carbon economic production quantity model for imperfect quality deteriorating items. Int. J. Ind. Eng. Eng. Manag. 2019, 1, 1–8. [Google Scholar] [CrossRef]
- Shaw, B.K.; Sangal, I.; Sarkar, B. Joint Effects of Carbon Emission, Deterioration, and Multi-Stage Inspection Policy in an Integrated Inventory Model. In Optimization and Inventory Management; Springer Nature: Singapore, 2020; pp. 195–208. [Google Scholar] [CrossRef]
- Hasan, R.; Mashud, A.H.M.; Daryanto, Y.; Wee, H.M. A non-instantaneous inventory model of agricultural products considering deteriorating impacts and pricing policies. Kybernetes 2020. [Google Scholar] [CrossRef]
- Yeh, R.H.; Ho, W.T.; Teng, S.T. Optimal production run length for products sold with warranty. Eur. J. Oper. Res. 2000, 120, 575–582. [Google Scholar] [CrossRef]
- Wang, C.H.; Sheu, S.H. Optimal lot size for products under free-repair warranty. Eur. J. Oper. Res. 2003, 149, 131–141. [Google Scholar] [CrossRef]
- Wang, C.H. The impact of a free-repair warranty policy on EMQ model for imperfect production system. Comput. Oper. Res. 2004, 31, 2021–2035. [Google Scholar] [CrossRef]
- Lin, T.Y. Effect of warranty and quantity discounts on a deteriorating production system with a Markovian production process and allowable shortages. J. Ind. Manag. Optim. 2017, 13. [Google Scholar] [CrossRef]
- Ullah, M.; Khan, I.; Sarkar, B. Dynamic Pricing in a Multi-Period Newsvendor Under Stochastic Price-Dependent Demand. Mathematics 2019, 7, 520. [Google Scholar] [CrossRef]
- Chung, J.C.; Wee, H.M. An integrated production-inventory deteriorating model for pricing policy considering imperfect production, inspection planning and warranty-period- and stock-level-dependent demand. Int. J. Syst. Sci. 2008, 39, 823–837. [Google Scholar] [CrossRef]
- Spiegel, M.R. Applied Differential Equations; Prentice-Hall: Englewood Cliffs, NJ, USA, 1960. [Google Scholar]
| μc | The mean demand | Ratio of non-conforming products when the procedure is under control | |
| σ | Standard deviation parameter | Ratio of non-conforming products when the procedure is out of control | |
| Retailer’s selling price of products | CR | Per unit cost for rework procedure | |
| Per unit value of lost sale amount | Cw | Per unit cost for item warranty | |
| Per unit value of salvage amount | Gm | Per unit target profit | |
| Crj | Item cost of material j per unit | u | Per unit item production cost |
| Per unit transportation cost | H | Per unit holding cost for manufacturer | |
| Per unit ordering items cost | The variation of lead-time for material j (=maximum lead-time -average lead-time) | ||
| CS | Cost of setup for production | Cmj | Ordering cost for material j |
| P | Production rate | hdmj | Additional cost to handle the material j |
| Θ | Rate of deterioration | hdmj | Additional cost to handle the material j |
| K | Duration of warranty | Hrj | Holding cost for materials |
| A0 | Constant ordering cost | Quantity of material j required per unit product | |
| F | Constant transportation cost | rj | The decrease fraction for material j |
| Per unit purchase cost | Constant coefficient of selling price | ||
| Constant coefficient of lost sale amount | Constant coefficient of salvage amount | ||
| Constant coefficient of transportation cost | Constant coefficient of ordering cost |
| Parameters | Example 1 | Example 2 |
|---|---|---|
| μc | 700 | 800 |
| σ | 60 | 70 |
| L1 | 0.64 | 0.64 |
| L2 | 0.6 | 0.6 |
| L3 | 0.58 | 0.58 |
| L4 | 0.04 | 0.04 |
| L5 | 0.05 | 0.05 |
| CS | 1200 | 1000 |
| P | 1200 | 1200 |
| θ | 0.01 | 0.01 |
| μ | 0.015 | 0.015 |
| K | 2 | 2 |
| 0.01 | 0.01 | |
| 0.015 | 0.012 | |
| 0.8 | 0.8 | |
| 0.9 | 0.8 | |
| A0 | 230 | 230 |
| F | 600 | 600 |
| 1/320 | 1/360 | |
| 1/220 | 1/240 | |
| CR | 40 | 40 |
| Cw | 100 | 90 |
| Gm | 25 | 25 |
| u | 2 | 2 |
| H | 4 | 4.5 |
| 0.002 | 0.0027 | |
| 0.0025 | ||
| Cm1 | 285 | 300 |
| Cm2 | 310 | |
| hdm1 | 13 | 10 |
| hdm2 | 13 | |
| Cr1 | 5 | 4 |
| Cr2 | 4.6 | |
| Hr1 | 3.5 | 3 |
| Hr2 | 4 | |
| 3 | 2 | |
| 3 | ||
| r1 | 0.0015 | 0.001 |
| r2 | 0.001 |
| Value of n* | |||
|---|---|---|---|
| Example 1 | n* ( 2.68) = 3 | 59.74 | 23,397.27 |
| Example 2 | (, ) (2.26, 3.14) = (2,3) | 76.62 | 39,671.64 |
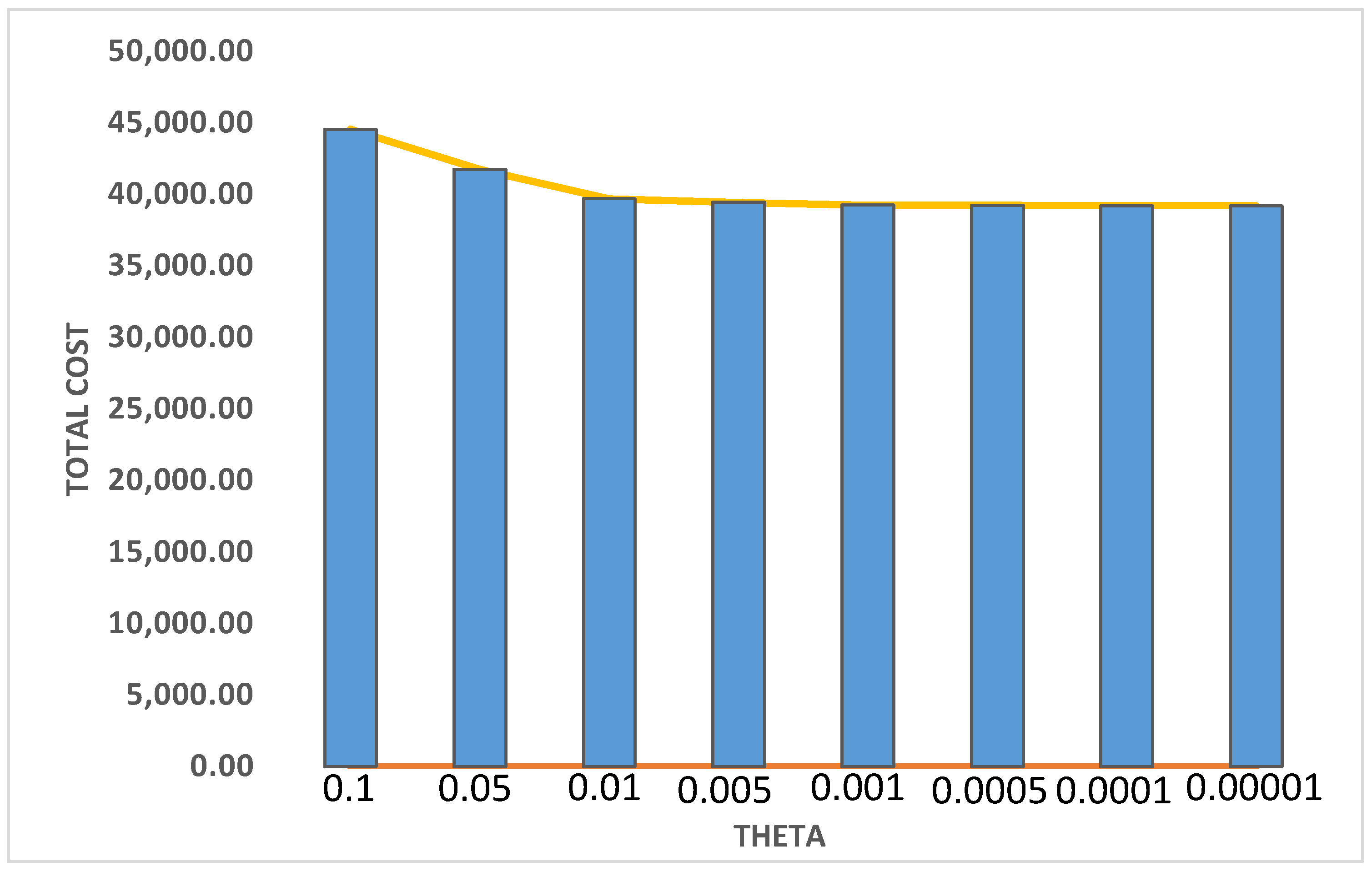
| θ | Ordering Sizes | |||
|---|---|---|---|---|
| 0.10 | (3,4) | 79.77 | 848.42 | 44,527.24 |
| 0.05 | (3,3) | 77.95 | 803.77 | 41,737.19 |
| 0.01 | (2,3) | 76.62 | 771.58 | 39,671.64 |
| 0.005 | (2,3) | 76.47 | 767.42 | 39,427.24 |
| 0.001 | (2,3) | 76.35 | 764.35 | 39,233.91 |
| 0.0005 | (2,3) | 76.33 | 763.96 | 39,209.88 |
| 0.0001 | (2,3) | 76.32 | 763.66 | 39,190.68 |
| 0.00001 | (2,3) | 76.32 | 763.59 | 39,186.36 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mashud, A.H.M.; Wee, H.-M.; Huang, C.-V.; Wu, J.-Z. Optimal Replenishment Policy for Deteriorating Products in a Newsboy Problem with Multiple Just-in-Time Deliveries. Mathematics 2020, 8, 1981. https://doi.org/10.3390/math8111981
Mashud AHM, Wee H-M, Huang C-V, Wu J-Z. Optimal Replenishment Policy for Deteriorating Products in a Newsboy Problem with Multiple Just-in-Time Deliveries. Mathematics. 2020; 8(11):1981. https://doi.org/10.3390/math8111981
Chicago/Turabian StyleMashud, Abu Hashan Md, Hui-Ming Wee, Chiao-Ven Huang, and Jei-Zheng Wu. 2020. "Optimal Replenishment Policy for Deteriorating Products in a Newsboy Problem with Multiple Just-in-Time Deliveries" Mathematics 8, no. 11: 1981. https://doi.org/10.3390/math8111981
APA StyleMashud, A. H. M., Wee, H.-M., Huang, C.-V., & Wu, J.-Z. (2020). Optimal Replenishment Policy for Deteriorating Products in a Newsboy Problem with Multiple Just-in-Time Deliveries. Mathematics, 8(11), 1981. https://doi.org/10.3390/math8111981