Machinery Failure Approach and Spectral Analysis to Study the Reaction Time Dynamics over Consecutive Visual Stimuli: An Entropy-Based Model
Abstract
1. Introduction
2. Description of the Sample and Visual Stimuli Experiments
2.1. Participants
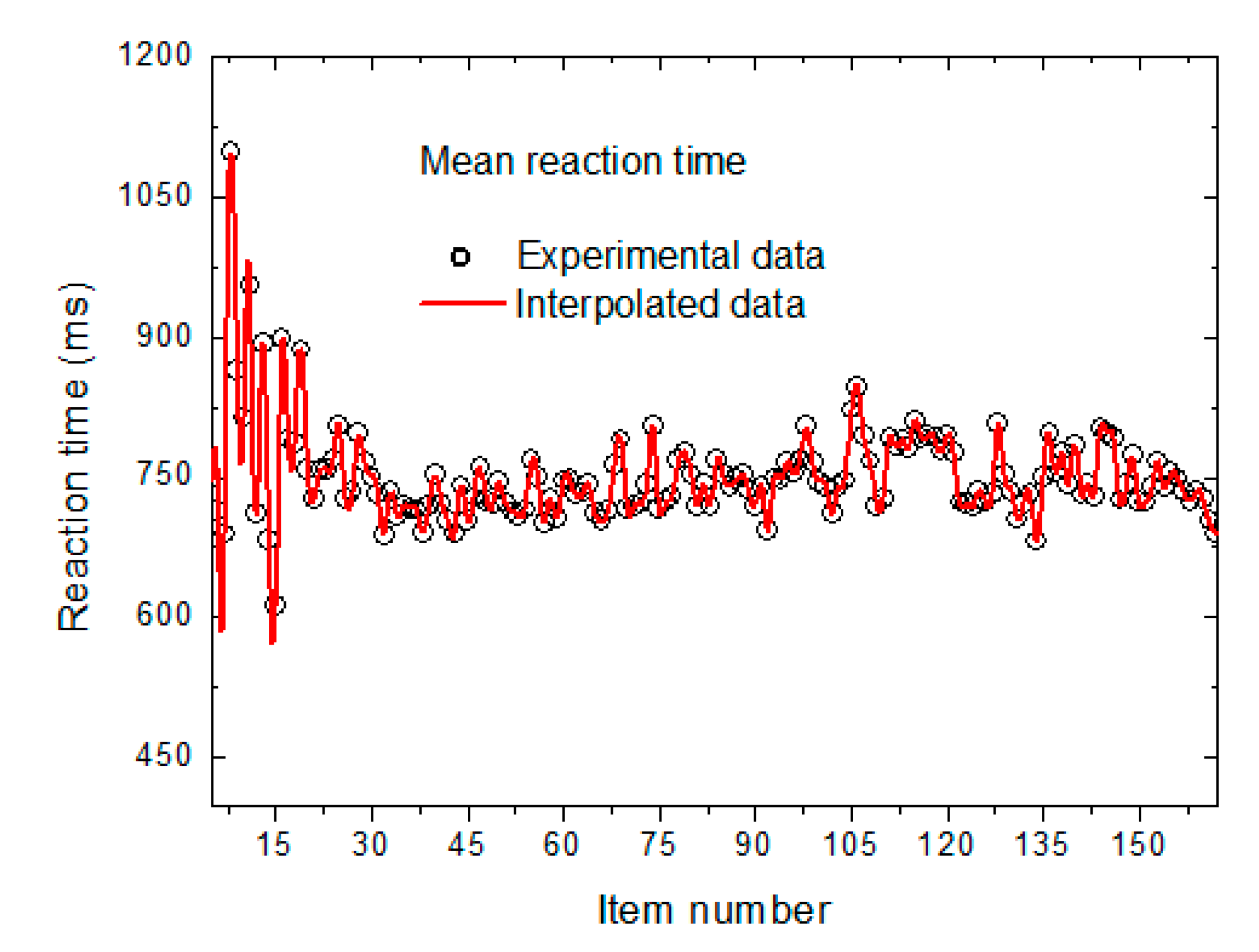
2.2. Reaction Time Experiments
3. Methodology
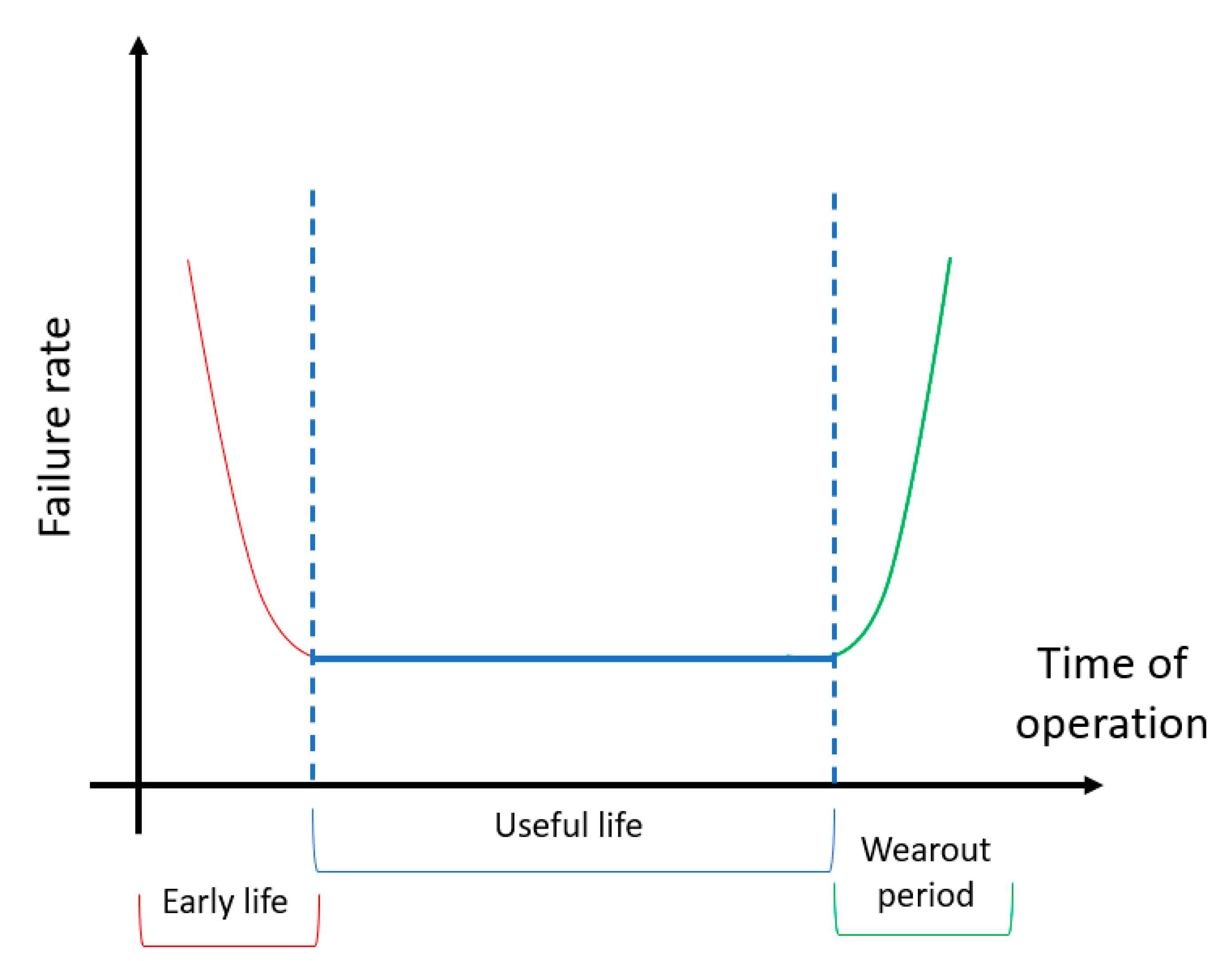
Failures Entropy Based Model
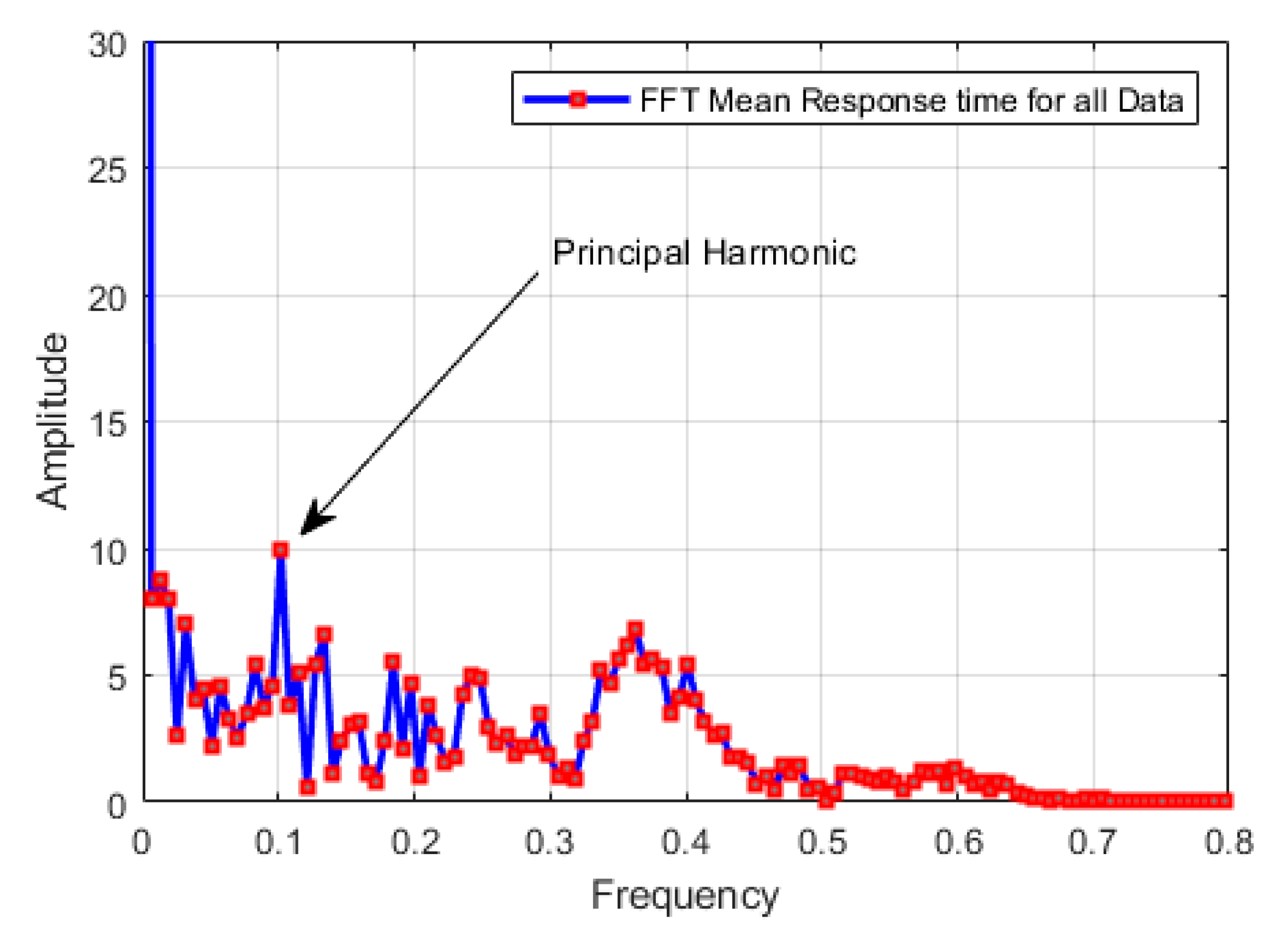
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Thorpe, S.J.; Fize, D.; Marlot, C. Speed of processing in the human visual system. Nature 1996, 381, 520–522. [Google Scholar] [CrossRef] [PubMed]
- Krajbich, I.M.; Bartling, B.; Hare, T.A.; Fehr, E. Rethinking fast and slow based on a critique of reaction-time reverse inference. Nat. Commun. 2015, 6, 7455. [Google Scholar] [CrossRef] [PubMed]
- Barinaga, M. Neuroscience: Neurons Put the Uncertainty Into Reaction Times. Science 1996, 274, 344. [Google Scholar] [CrossRef] [PubMed]
- Tuch, D.S.; Salat, D.H.; Wisco, J.J.; Zaleta, A.K.; Hevelone, N.D.; Rosas, H.D. Choice reaction time performance correlates with diffusion anisotropy in white matter pathways supporting visuospatial attention. Proc. Natl. Acad. Sci. USA 2005, 102, 12212–12217. [Google Scholar] [CrossRef] [PubMed]
- Colonius, H.; Diederich, A. Measuring multisensory integration: From reaction times to spike counts. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Ritchie, J.B.; De Beeck, H.O. Using neural distance to predict reaction time for categorizing the animacy, shape, and abstract properties of objects. Sci. Rep. 2019, 9, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Castro-Palacio, J.C.; Fernández de Córdoba, P.; Isidro, J.M.; Navarro-Pardo, E.; Selvas Aguilar, R. Percentile study of Chi distribution. Application to response time data. Mathematics 2020, 8, 514. [Google Scholar] [CrossRef]
- Hernaiz-Guijarro, M.; Castro-Palacio, J.C.; Pardo, E.N.; Isidro, J.M.; Castellá, P.F.D.C.; Guijarro, H.; Palacio, C.; Pardo, N.; Córdoba, F.-D. A Probabilistic Classification Procedure Based on Response Time Analysis Towards a Quick Pre-Diagnosis of Student’s Attention Deficit. Mathematics 2019, 7, 473. [Google Scholar] [CrossRef]
- Ruhai, G.; Weiwei, Z.; Zhong, W. Research on the Driver Reaction Time of Safety Distance Model on Highway Based on Fuzzy Mathematics. In Proceedings of the IEEE 2010 International Conference on Optoelectronics and Image Processing (ICOIP), Haikou, China, 11–12 November 2010; pp. 293–296. [Google Scholar]
- Yamagishi, T.; Matsumoto, Y.; Kiyonari, T.; Takagishi, H.; Li, Y.; Kanai, R.; Sakagami, M. Response time in economic games reflects different types of decision conflict for prosocial and proself individuals. Proc. Natl. Acad. Sci. USA 2017, 114, 6394–6399. [Google Scholar] [CrossRef]
- Badau, D.; Baydil, B.; Badau, A. Differences among Three Measures of Reaction Time Based on Hand Laterality in Individual Sports. Sports 2018, 6, 45. [Google Scholar] [CrossRef]
- Abbasi-Kesbi, R.; Memarzadeh-Tehran, H.; Deen, M.J. Technique to estimate human reaction time based on visual perception. Health Technol. Lett. 2017, 4, 73–77. [Google Scholar] [CrossRef]
- Gmehlin, D.; Fuermaier, A.B.M.; Walther, S.; Debelak, R.; Rentrop, M.; Westermann, C.; Sharma, A.; Tucha, L.; Koerts, J.; Tucha, O.; et al. Intraindividual Variability in Inhibitory Function in Adults with ADHD—An Ex-Gaussian Approach. PLoS ONE 2014, 9, e112298. [Google Scholar] [CrossRef]
- Adamo, N.; Hodsoll, J.; Asherson, P.; Buitelaar, J.K.; Kuntsi, J. Ex-Gaussian, Frequency and Reward Analyses Reveal Specificity of Reaction Time Fluctuations to ADHD and Not Autism Traits. J. Abnorm. Child Psychol. 2019, 47, 557–567. [Google Scholar] [CrossRef]
- Shahar, N.; Teodorescu, A.R.; Karmon-Presser, A.; Anholt, G.E.; Meiran, N. Memory for Action Rules and Reaction Time Variability in Attention-Deficit/Hyperactivity Disorder. Biol. Psychiatry Cogn. Neurosci. Neuroimaging 2016, 1, 132–140. [Google Scholar] [CrossRef] [PubMed]
- Castellanos, F.X.; Sonuga-Barke, E.J.; Scheres, A.; Di Martino, A.; Hyde, C.; Walters, J.R. Varieties of Attention-Deficit/Hyperactivity Disorder-Related Intra-Individual Variability. Biol. Psychiatry 2005, 57, 1416–1423. [Google Scholar] [CrossRef]
- Johnson, K.A.; Kelly, S.P.; Bellgrove, M.A.; Barry, E.; Cox, M.; Gill, M.; Robertson, I.H. Response variability in Attention Deficit Hyperactivity Disorder: Evidence for neuropsychological heterogeneity. Neuropsychologia 2007, 45, 630–638. [Google Scholar] [CrossRef]
- Di Martino, A.; Ghaffari, M.; Curchack, J.; Reiss, P.; Hyde, C.; Vannucci, M.; Petkova, E.; Klein, D.F.; Castellanos, F.X. Decomposing Intra-Subject Variability in Children with Attention-Deficit/Hyperactivity Disorder. Biol. Psychiatry 2008, 64, 607–614. [Google Scholar] [CrossRef]
- Vaurio, R.; Simmonds, D.J.; Mostofsky, S.H. Increased intra-individual reaction time variability in attention-deficit/hyperactivity disorder across response inhibition tasks with different cognitive demands. Neuropsychologia 2009, 47, 2389–2396. [Google Scholar] [CrossRef]
- Tarantino, V.; Cutini, S.; Mogentale, C.; Bisiacchi, P.S. Time-on-Task in Children with ADHD: An ex-Gaussian Analysis. J. Int. Neuropsychol. Soc. 2013, 19, 820–828. [Google Scholar] [CrossRef] [PubMed]
- Moret-Tatay, C.; Perea, M. Is the go/no-go lexical decision task preferable to the yes/no task with developing readers? J. Exp. Child Psychol. 2011, 110, 125–132. [Google Scholar] [CrossRef]
- World Medical Association. Declaration of Helsinki: Ethical Principles for Medical Research Involving Human Subjects. J. Am. Med. Assoc. 2013, 310, 2191–2194. [Google Scholar] [CrossRef]
- Rueda, M.; Fan, J.; McCandliss, B.D.; Halparin, J.D.; Gruber, D.B.; Lercari, L.P.; Posner, M.I. Development of attentional networks in childhood. Neuropsychologia 2004, 42, 1029–1040. [Google Scholar] [CrossRef] [PubMed]
- Forster, K.I.; Forster, J.C. DMDX: A Windows display program with millisecond accuracy. Behav. Res. Methods Instrum. Comput. 2003, 35, 116–124. [Google Scholar] [CrossRef] [PubMed]
- Moret-Tatay, C.; Leth-Steensen, C.; Irigaray, T.Q.; Argimon, I.I.L.; Gamermann, D.; Abad-Tortosa, D.; Oliveira, C.; Sáiz-Mauleón, B.; Vázquez-Martínez, A.; Navarro-Pardo, E.; et al. The Effect of Corrective Feedback on Performance in Basic Cognitive Tasks: An Analysis of RT Components. Psychologica Belgica 2016, 56, 370–381. [Google Scholar] [CrossRef]
- Moreno-Cid, A.; De Valencia, S.U.; Moret-Tatay, C.; Irigaray, T.Q.; Argimon, I.I.L.; Murphy, M.; Szczerbinski, M.; Martínez-Rubio, D.; Beneyto-Arrojo, M.J.; Navarro-Pardo, E.; et al. The role of age and emotional valence in word recognition: An ex-gaussian analysis. Stud. Psychol. 2015, 57, 83–94. [Google Scholar] [CrossRef]
- Moret-Tatay, C.; Moreno-Cid, A.; Argimon, I.I.L.; Irigaray, T.Q.; Szczerbinski, M.; Murphy, M.; Vázquez-Martínez, A.; Molina, J.V.; Sáiz-Mauleón, B.; Navarro-Pardo, E.; et al. The effects of age and emotional valence on recognition memory: An ex-Gaussian components analysis. Scand. J. Psychol. 2014, 55, 420–426. [Google Scholar] [CrossRef]
- Fan, J.; McCandliss, B.D.; Sommer, T.; Raz, A.; Posner, M.I. Testing the Efficiency and Independence of Attentional Networks. J. Cogn. Neurosci. 2002, 14, 340–347. [Google Scholar] [CrossRef]
- Posner, M.I.; Dehaene, S. Attentional networks. Trends Neurosci. 1994, 17, 75–79. [Google Scholar] [CrossRef]
- Posner, M.I.; Raichle, M.E. Images of Mind; Scientific American Library: New York, NY, USA, 1994. [Google Scholar]
- Martínez, M.E.I.; Garcia-Gomez, J.M.; Sáez, C.; Castellá, P.F.D.C.; Conejero, J.A. Feature Extraction and Similarity of Movement Detection during Sleep, Based on Higher Order Spectra and Entropy of the Actigraphy Signal: Results of the Hispanic Community Health Study/Study of Latinos. Sensors 2018, 18, 4310. [Google Scholar] [CrossRef]
- Ho, T.S.; Rabitz, H. A general method for constructing multidimensional molecular potential energy surfaces from ab initio calculations. J. Chem. Phys. 1996, 104, 2584–2597. [Google Scholar] [CrossRef]
- Castro-Palacio, J.C.; Nagy, T.; Meuwly, M. Computational study of the O(3P) + NO(2π) reaction at temperatures relevant to the Hypersonic Flight Regime. J. Chem. Phys. 2014, 141, 164319. [Google Scholar] [CrossRef]
- Unke, O.T.; Castro-Palacio, J.C.; Bemish, R.; Meuwly, M. Collision-induced rotational excitation in N+2 (2Σ+g, v = 0)–Ar: Comparison of computations and experiment. J. Chem. Phys. 2016, 144, 224307. [Google Scholar] [CrossRef] [PubMed]
- Denis-Alpizar, O.; Inostroza, N.; Castro Palacio, J.C. Rotational relaxation of CF^+ (X^1 Sigma) in collision with He (1^S). Mon. Not. R. Astron. Soc. 2018, 473, 1438–1443. [Google Scholar] [CrossRef]
- Castro-Palacio, J.C.; Bemish, R.J.; Meuwly, M. Communication: Equilibrium rate coefficients from atomistic simulations: The O(3P) + NO(2π) = O2(X3Σg) + N(4S) reaction at temperatures relevant to the hypersonic flight regime. J. Chem. Phys. 2015, 142, 091104. [Google Scholar] [CrossRef]
- Unke, O.T.; Meuwly, M. Toolkit for the Construction of Reproducing Kernel-Based Representations of Data: Application to Multidimensional Potential Energy Surfaces. J. Chem. Inf. Model. 2017, 57, 1923–1931. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, F.J.T.E.; Baoming, G.; De Almeida, A.T. Reliability and Operation of High-Efficiency Induction Motors. In Proceedings of the IEEE Transactions on Industry Applications, Calgary, AB, Canada, 5–8 May 2015; Volume 52. [Google Scholar] [CrossRef]
- Tavner, P.; Ran, L.; Penman, J.; Sedding, H. Condition Monitoring of Rotating Electrical Machines; Bibliovault OAI Repository, University of Chicago Press: Chicago, IL, USA, 2008. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iglesias-Martínez, M.E.; Hernaiz-Guijarro, M.; Castro-Palacio, J.C.; Fernández-de-Córdoba, P.; Isidro, J.M.; Navarro-Pardo, E. Machinery Failure Approach and Spectral Analysis to Study the Reaction Time Dynamics over Consecutive Visual Stimuli: An Entropy-Based Model. Mathematics 2020, 8, 1979. https://doi.org/10.3390/math8111979
Iglesias-Martínez ME, Hernaiz-Guijarro M, Castro-Palacio JC, Fernández-de-Córdoba P, Isidro JM, Navarro-Pardo E. Machinery Failure Approach and Spectral Analysis to Study the Reaction Time Dynamics over Consecutive Visual Stimuli: An Entropy-Based Model. Mathematics. 2020; 8(11):1979. https://doi.org/10.3390/math8111979
Chicago/Turabian StyleIglesias-Martínez, Miguel E., Moisés Hernaiz-Guijarro, Juan Carlos Castro-Palacio, Pedro Fernández-de-Córdoba, J. M. Isidro, and Esperanza Navarro-Pardo. 2020. "Machinery Failure Approach and Spectral Analysis to Study the Reaction Time Dynamics over Consecutive Visual Stimuli: An Entropy-Based Model" Mathematics 8, no. 11: 1979. https://doi.org/10.3390/math8111979
APA StyleIglesias-Martínez, M. E., Hernaiz-Guijarro, M., Castro-Palacio, J. C., Fernández-de-Córdoba, P., Isidro, J. M., & Navarro-Pardo, E. (2020). Machinery Failure Approach and Spectral Analysis to Study the Reaction Time Dynamics over Consecutive Visual Stimuli: An Entropy-Based Model. Mathematics, 8(11), 1979. https://doi.org/10.3390/math8111979







