Variational Inference over Nonstationary Data Streams for Exponential Family Models †
Abstract
:1. Introduction
2. Related Work
3. Preliminaries
3.1. Conjugate Exponential Models
3.2. Variational Inference
3.3. Variational Inference over Data Streams
3.4. Exponential Forgetting in Variational Inference
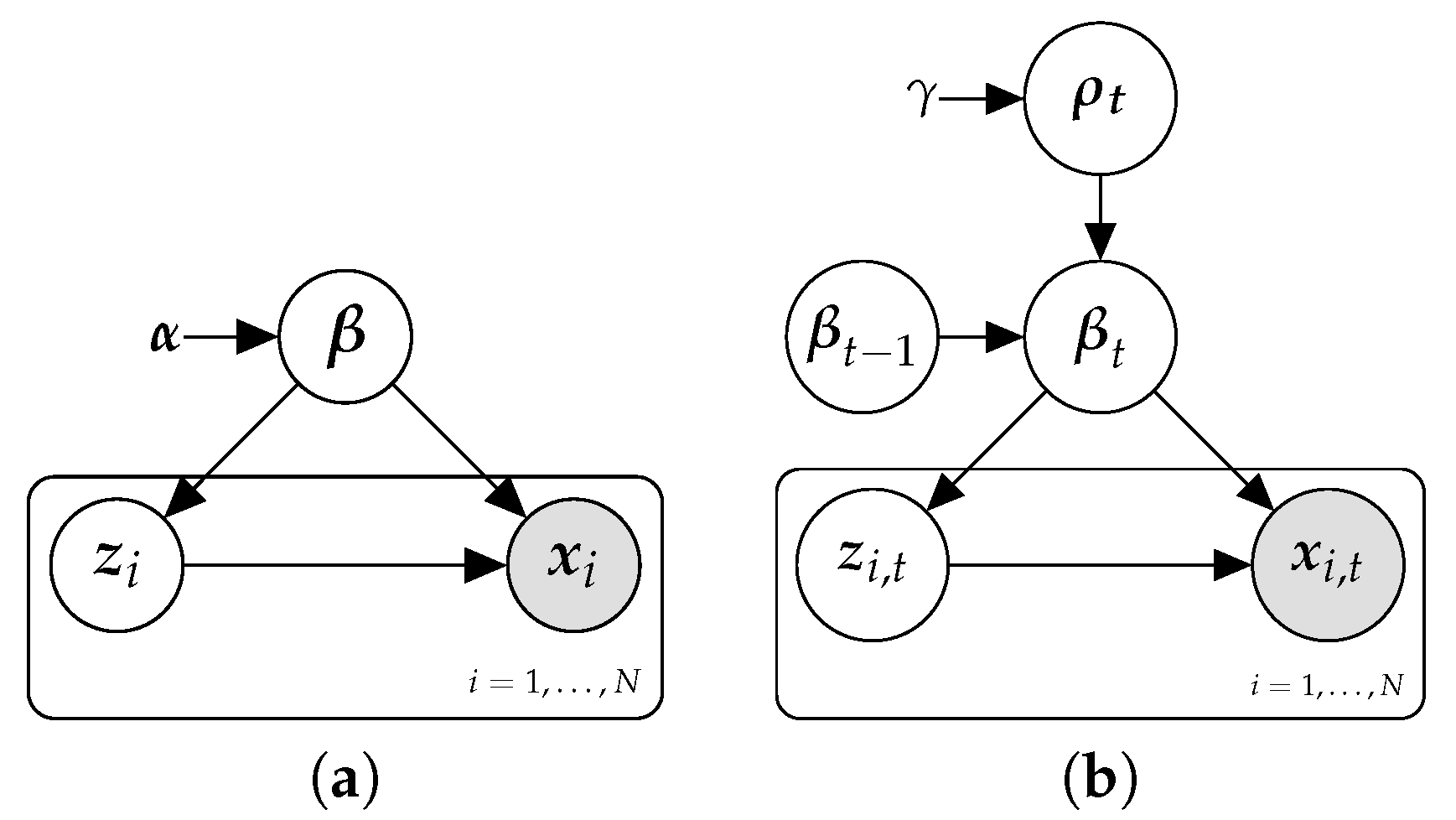
4. Implicit Transition Models
4.1. Exponential Forgetting as Implicit Transition Models
4.2. Power Priors as Implicit Transition Models
5. Hierarchical Power Priors
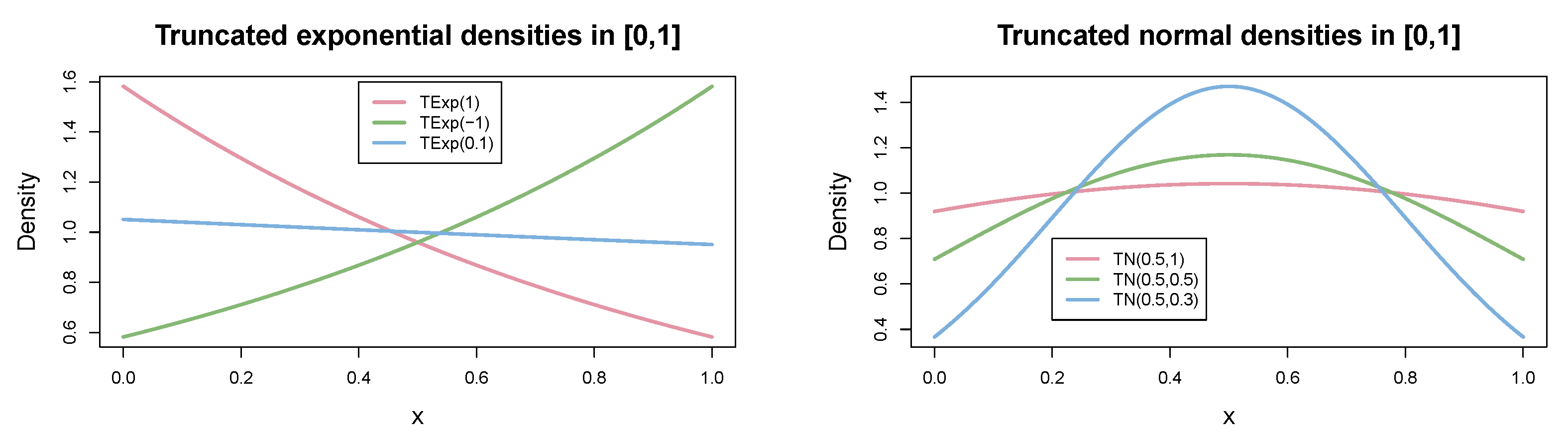
5.1. A Hierarchical Prior over the Forgetting Rate
5.2. The Double Lower Bound
| Algorithm 1 Streaming variational Bayes (SVB) with Hierarchical Power Priors (SVB-HPP). |
| Input: A data batch xt, the variational posterior in previous time step λt−1. |
| Output: (λt, ϕt, ωt), a new update of the variational posterior. |
| 1: λt ← λt−1. |
| 2: . |
| 3: Randomly initialize ϕt. |
| 4: repeat |
| 5: (λt, ϕt) = arg minλt,ϕt |
| 6: |
| 7: Update according to Equation (28) or Equation (29). |
| 8: until convergence |
| 9: return (λt,ϕt,ωt) |
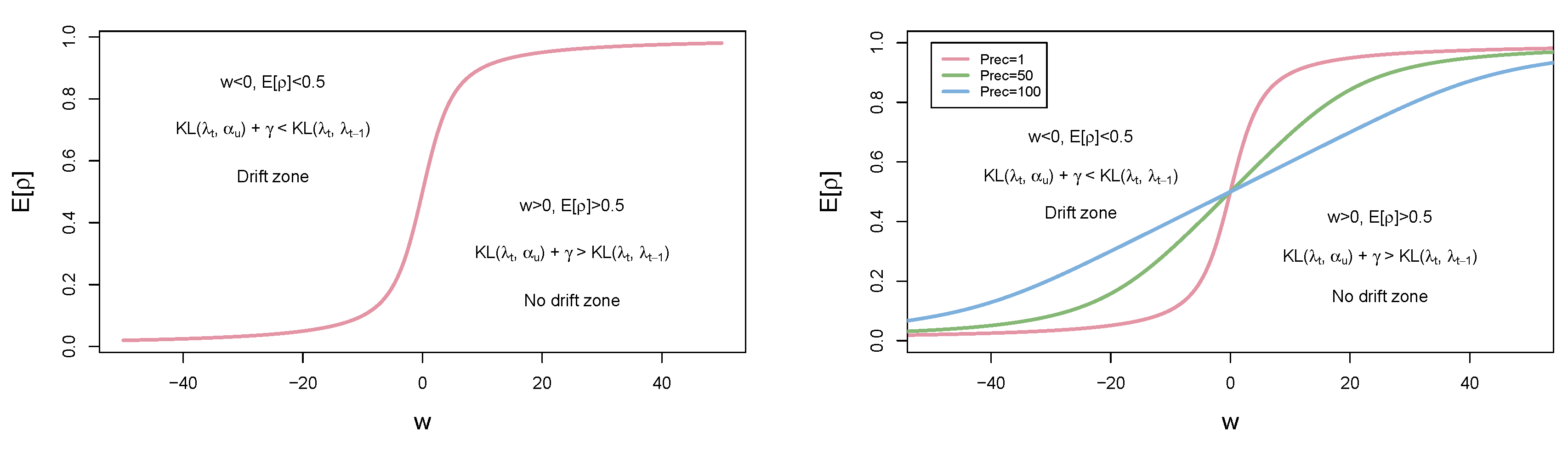
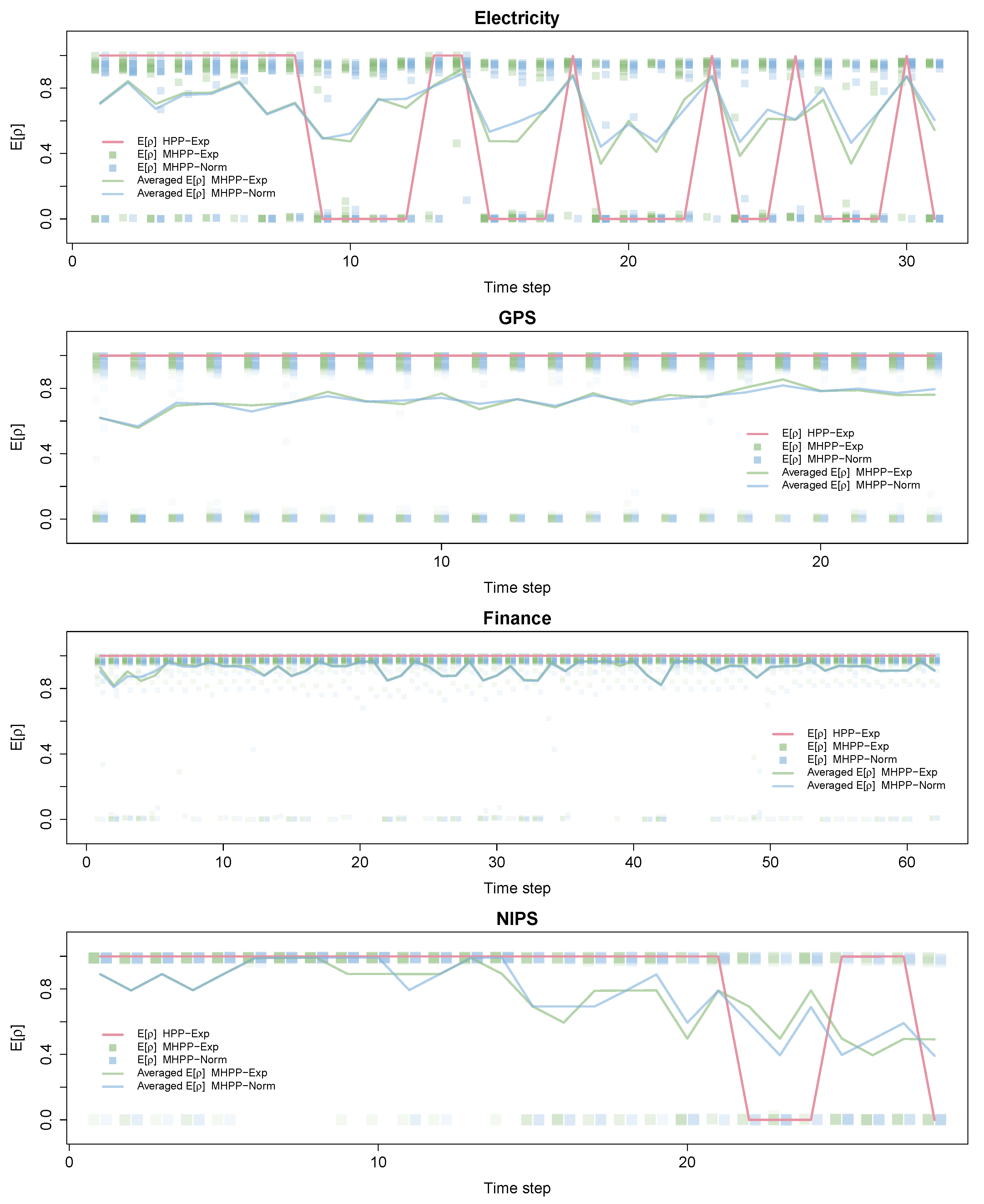
5.3. Towards a Measure of Concept Drift
5.4. The Multiple Hierarchical Power Prior Model
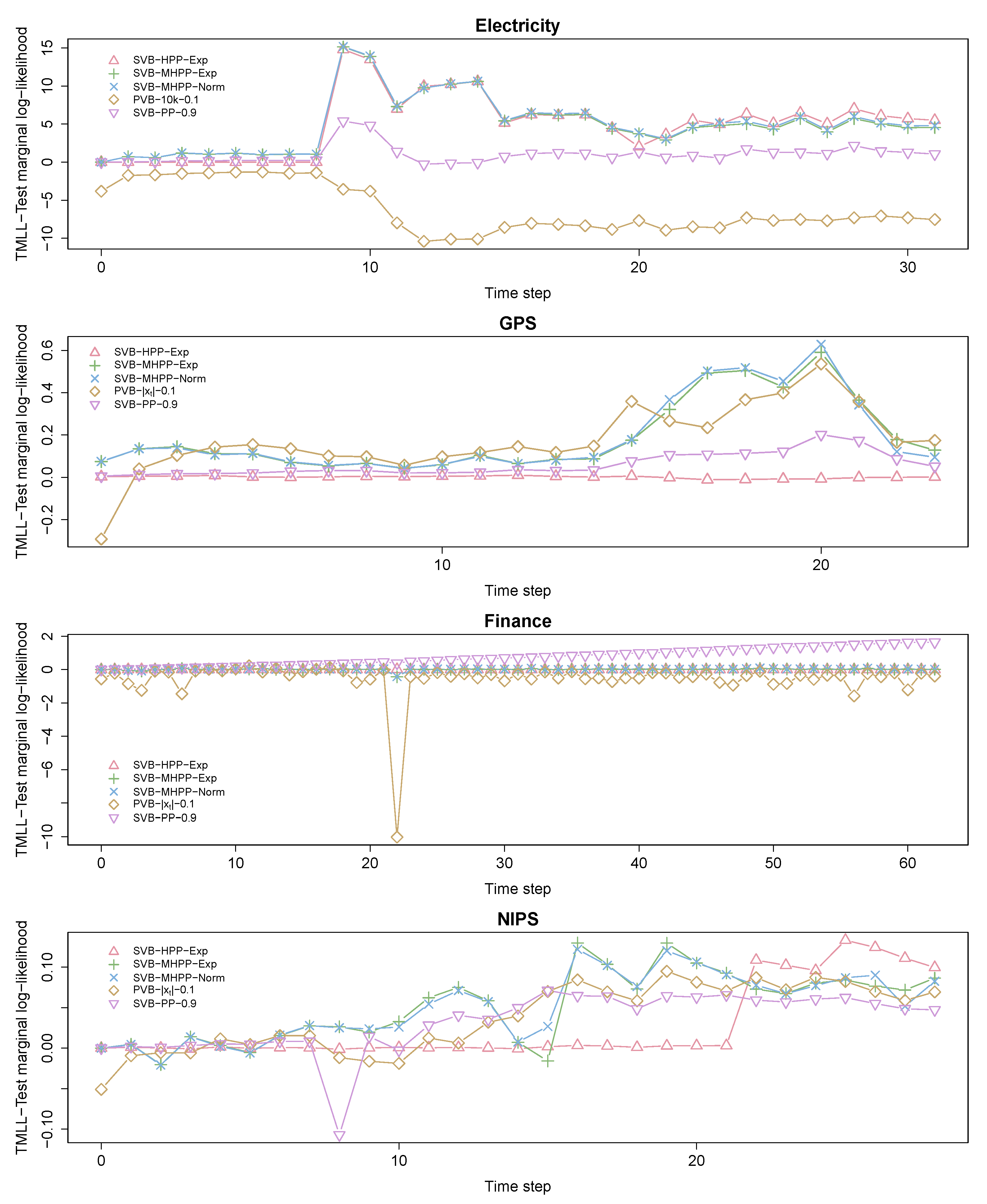
6. Results
- Streaming variational Bayes (SVB) as described in Section 3.3.
- Four versions of Population Variational Bayes (PVB) (We do not compare with SVI because SVI is a special case of PVB when M is equal the total size of the stream.) resulting from combining the values of the population size parameter (Section 6.1) and (Section 6.2) with the learning rate values and . In the four cases, the mini-batch size was set to 1000. Note that, however, for the LDA case, we set rather than in Section 6.2 and use a mini-batch size of 1000 instead of .
- Two versions of the SVB method with power priors (SVB-PP) or fixed exponential forgetting (as described in Section 4.1) with or .
- Three versions of our method based on the SVB method with adaptive exponential forgetting using hierarchical power priors (as described in Section 5):
- SVB-HPP-Exp using a single shared with a truncated exponential distribution as a prior over with (i.e., close to uniform).
- SVB-MHPP-Exp using separate for each parameter (as described in Section 5.4) with truncated exponential distributions as priors over each with .
- SVB-MHPP-Norm using also separate for each parameters but with truncated normal distributions as priors over each . In this case, we use and learn the variance using the empirical Bayes approach described at the end of Section 5.2.
6.1. Evaluation Using an Artificial Data Set
6.2. Evaluation Using Real Data Sets
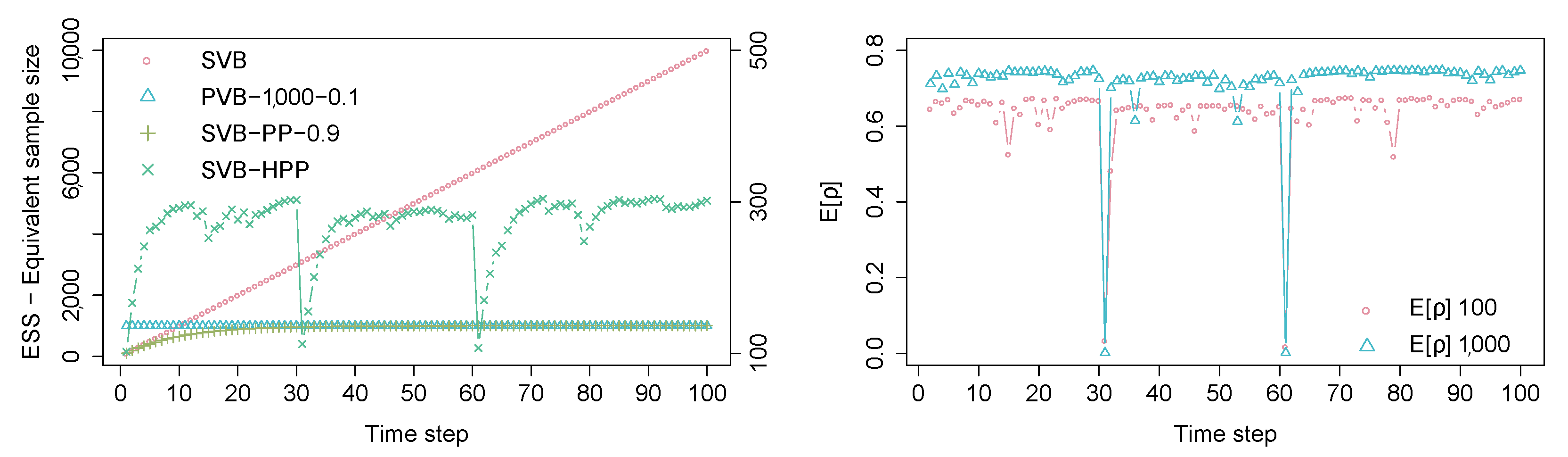
6.3. Discussion of Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proofs
Appendix B. Probabilistic Models Used in the Experimental Evaluation
Appendix B.1. Electricity Model

Appendix B.2. GPS Model

Appendix B.3. Financial Model

References
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Gelfand, A.E.; Smith, A.F. Sampling-based approaches to calculating marginal densities. J. Am. Stat. Assoc. 1990, 85, 398–409. [Google Scholar] [CrossRef]
- Gama, J.; Žliobaitė, I.; Bifet, A.; Pechenizkiy, M.; Bouchachia, A. A survey on concept drift adaptation. ACM Comput. Surv. 2014, 46, 1–37. [Google Scholar] [CrossRef]
- Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent Dirichlet allocation. J. Mach. Learn. Res. 2003, 3, 993–1022. [Google Scholar]
- Borchani, H.; Martínez, A.M.; Masegosa, A.R.; Langseth, H.; Nielsen, T.D.; Salmerón, A.; Fernández, A.; Madsen, A.L.; Sáez, R. Modeling concept drift: A probabilistic graphical model based approach. In International Symposium on Intelligent Data Analysis; Springer: Cham, Switzerland, 2015; pp. 72–83. [Google Scholar]
- Rabiner, L.R.; Juang, B.H. An introduction to hidden Markov models. IEEE ASSP Mag. 1986, 3, 4–16. [Google Scholar] [CrossRef]
- Bishop, C.M. Latent variable models. In Learning in Graphical Models; Springer: Dordrecht, The Netherlands, 1998; pp. 371–403. [Google Scholar]
- Blei, D.M. Build, compute, critique, repeat: Data analysis with latent variable models. Annu. Rev. Stat. Its Appl. 2014, 1, 203–232. [Google Scholar] [CrossRef] [Green Version]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Tipping, M.E.; Bishop, C.M. Probabilistic principal component analysis. J. R. Stat. Soc. Ser. B Stat. Methodol. 1999, 61, 611–622. [Google Scholar] [CrossRef]
- Koller, D.; Friedman, N. Probabilistic Graphical Models: Principles and Techniques; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational inference: A review for statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef] [Green Version]
- Hamilton, J.D. Time Series Analysis; Princeton University Press: Princeton, NJ, USA, 1994; Volume 2. [Google Scholar]
- Triantafyllopoulos, K. Inference of dynamic generalized linear models: On-line computation and appraisal. Int. Stat. Rev. 2009, 77, 430–450. [Google Scholar] [CrossRef]
- Chen, X.; Irie, K.; Banks, D.; Haslinger, R.; Thomas, J.; West, M. Scalable Bayesian Modeling, Monitoring, and Analysis of Dynamic Network Flow Data. J. Am. Stat. Assoc. 2018, 113, 519–533. [Google Scholar] [CrossRef] [Green Version]
- Aminikhanghahi, S.; Cook, D.J. A survey of methods for time series change point detection. Knowl. Inf. Syst. 2017, 51, 339–367. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adams, R.P.; MacKay, D.J. Bayesian online changepoint detection. arXiv 2007, arXiv:0710.3742. [Google Scholar]
- Gaber, M.M.; Zaslavsky, A.; Krishnaswamy, S. Mining data streams: A review. ACM Sigmod Rec. 2005, 34, 18–26. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Data Streams: Models and Algorithms; Springer: New York, NY, USA, 2007; Volume 31. [Google Scholar]
- Gama, J.; Rodrigues, P.P. An overview on mining data streams. In Foundations of Computational, Intelligence; Springer: Berlin/Heidelberg, Germany, 2009; Volume 6, pp. 29–45. [Google Scholar]
- Aggarwal, C.C. Managing and Mining Sensor Data; Springer: New York, NY, USA, 2013. [Google Scholar]
- Papadimitriou, S.; Sun, J.; Faloutsos, C. Streaming pattern discovery in multiple time-series. In Proceedings of the 31st International Conference on Very Large Data Bases, VLDB Endowment, Trondheim, Norway, 30 August–2 September 2005; pp. 697–708. [Google Scholar]
- Honkela, A.; Valpola, H. On-line variational Bayesian learning. In Proceedings of the 4th International Symposium on Independent Component Analysis and Blind Signal Separation, Nara, Japan, 1–4 April 2003; pp. 803–808. [Google Scholar]
- McInerney, J.; Ranganath, R.; Blei, D. The population posterior and Bayesian modeling on streams. In Advances in Neural Information Processing Systems 28; Curran Associates, Inc.: Montreal, QC, Canada, 2015; pp. 1153–1161. [Google Scholar]
- Hoffman, M.D.; Blei, D.M.; Wang, C.; Paisley, J. Stochastic variational inference. J. Mach. Learn. Res. 2013, 14, 1303–1347. [Google Scholar]
- Broderick, T.; Boy, N.; Wibisono, A.; Wilson, A.C.; Jordan, M.I. Streaming variational Bayes. In Advances in Neural Information Processing Systems 26; Curran Associates, Inc.: Lake Tahoe, NV, USA, 2013; pp. 1727–1735. [Google Scholar]
- Ibrahim, J.G.; Chen, M.H. Power prior distributions for regression models. Stat. Sci. 2000, 15, 46–60. [Google Scholar]
- Ibrahim, J.G.; Chen, M.H.; Sinha, D. On optimality properties of the power prior. J. Am. Stat. Assoc. 2003, 98, 204–213. [Google Scholar] [CrossRef]
- Ozkan, E.; Smidl, V.; Saha, S.; Lundquist, C.; Gustafsson, F. Marginalized adaptive particle filtering for nonlinear models with unknown time-varying noise parameters. Automatica 2013, 49, 1566–1575. [Google Scholar] [CrossRef]
- Kárnỳ, M. Approximate Bayesian recursive estimation. Inf. Sci. 2014, 285, 100–111. [Google Scholar] [CrossRef]
- Shi, T.; Zhu, J. Online Bayesian passive-aggressive learning. J. Mach. Learn. Res. 2017, 18, 1–39. [Google Scholar]
- Williamson, S.; Orbanz, P.; Ghahramani, Z. Dependent Indian buffet processes. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; pp. 924–931. [Google Scholar]
- Blei, D.M.; Lafferty, J.D. Dynamic topic models. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 113–120. [Google Scholar]
- Williamson, S.; Wang, C.; Heller, K.; Blei, D. The IBP compound Dirichlet process and its application to focused topic modeling. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Perrone, V.; Jenkins, P.A.; Spano, D.; Teh, Y.W. Poisson random fields for dynamic feature models. J. Mach. Learn. Res. 2017, 18, 1–45. [Google Scholar]
- Brown, L.D. Fundamentals of Statistical Exponential Families: With Applications in Statistical Decision Theory; Institute of Mathematical Statistics: Hayward, CA, USA, 1986. [Google Scholar]
- Bernardo, J.M.; Smith, A.F. Bayesian Theory; John Wiley & Sons: New York, NY, USA, 2009; Volume 405. [Google Scholar]
- Heckerman, D.; Geiger, D.; Chickering, D.M. Learning Bayesian networks: The combination of knowledge and statistical data. Mach. Learn. 1995, 20, 197–243. [Google Scholar] [CrossRef] [Green Version]
- Masegosa, A.R.; Martinez, A.M.; Langseth, H.; Nielsen, T.D.; Salmerón, A.; Ramos-López, D.; Madsen, A.L. Scaling up Bayesian variational inference using distributed computing clusters. Int. J. Approx. Reason. 2017, 88, 435–451. [Google Scholar] [CrossRef]
- Winn, J.M.; Bishop, C.M. Variational message passing. J. Mach. Learn. Res. 2005, 6, 661–694. [Google Scholar]
- Olesen, K.G.; Lauritzen, S.L.; Jensen, F.V. aHUGIN: A system creating adaptive causal probabilistic networks. In Proceedings of the Eighth International Conference on Uncertainty in Artificial Intelligence, Stanford, CA, USA, 17–19 July 1992; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1992; pp. 223–229. [Google Scholar]
- Lauritzen, S.L. Propagation of probabilities, means, and variances in mixed graphical association models. J. Am. Stat. Assoc. 1992, 87, 1098–1108. [Google Scholar] [CrossRef]
- Sato, M.A. Online model selection based on the variational Bayes. Neural Comput. 2001, 13, 1649–1681. [Google Scholar] [CrossRef]
- Harries, M. Splice-2 Comparative Evaluation: Electricity Pricing; NSW-CSE-TR-9905; School of Computer Siene and Engineering, The University of New South Wales: Sydney, Australia, 1999. [Google Scholar]
- Zheng, Y.; Li, Q.; Chen, Y.; Xie, X.; Ma, W.Y. Understanding mobility based on GPS data. In Proceedings of the 10th International Conference on Ubiquitous Computing, UbiComp ’08, Seoul, Korea, 21–24 September 2008; ACM: New York, NY, USA, 2008; pp. 312–321. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, L.; Xie, X.; Ma, W.Y. Mining interesting locations and travel sequences from GPS trajectories. In Proceedings of the 18th International Conference on World Wide Web, WWW ’09, Madrid, Spain, 20–24 April 2009; ACM: New York, NY, USA, 2009; pp. 791–800. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Y.; Xie, X.; Ma, W.Y. GeoLife: A collaborative social networking service among user, location and trajectory. IEEE Data Eng. Bull. 2010, 33, 32–39. [Google Scholar]
- Wainwright, M.J.; Jordan, M.I. Graphical models, exponential families, and variational inference. Found. Trends® Mach. Learn. 2008, 1, 1–305. [Google Scholar] [CrossRef] [Green Version]


| Data Set | SVB | PVB | SVB-PP | SVB-HPP | SVB-MHPP | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | Exp | Exp | Norm | ||||
| Electricity | −44.91 | −51.01 | −52.19 | −51.11 | −61.70 | −43.92 | −44.80 | −40.05 | −40.02 | −39.91 |
| GPS | −1.98 | −2.10 | −2.77 | −1.97 | −4.49 | −1.94 | −1.97 | −1.97 | −1.86 | −1.86 |
| Finance | −19.84 | −22.29 | −22.57 | −20.40 | −20.73 | −19.05 | −19.78 | −19.83 | −19.83 | −19.82 |
| NIPS | −4.07 | −4.04 * | −4.21 * | −4.01 | −4.12 | −4.02 | −4.06 | −4.01 | −4.00 | −4.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masegosa, A.R.; Ramos-López, D.; Salmerón, A.; Langseth, H.; Nielsen, T.D. Variational Inference over Nonstationary Data Streams for Exponential Family Models. Mathematics 2020, 8, 1942. https://doi.org/10.3390/math8111942
Masegosa AR, Ramos-López D, Salmerón A, Langseth H, Nielsen TD. Variational Inference over Nonstationary Data Streams for Exponential Family Models. Mathematics. 2020; 8(11):1942. https://doi.org/10.3390/math8111942
Chicago/Turabian StyleMasegosa, Andrés R., Darío Ramos-López, Antonio Salmerón, Helge Langseth, and Thomas D. Nielsen. 2020. "Variational Inference over Nonstationary Data Streams for Exponential Family Models" Mathematics 8, no. 11: 1942. https://doi.org/10.3390/math8111942





