1. Introduction
The analysis of rankings of scores (
cardinal rankings) or, particularly, rankings composed of natural numbers (
ordinal rankings), have been studied from different perspectives attending to the ultimate goal of the researchers or practitioners (see [
1]). When the interest is on obtaining a
consensus score that summarizes the opinion of various judges, the used mathematical tools are usually aimed to find a ranking that minimizes a given
distance metric (see the seminal paper [
2,
3] for some properties of different metrics). In such a case, we say that a
distance metric minimizes disagreement. We can place in this area the methods called
voter systems,
ranking aggregation, and others (see the detailed review in [
4]).
When the interest is focused on comparing two series of rankings, one of the key points is to obtain a measure that describes the
evolution of the series. In this case, we have a series of rankings such that each one of them prioritizes the elements based on the scores obtained at a particular time (see [
5]). For example,
sports rankings belong to this category. Obviously, at the end of a season, there is no need to find a consensus ranking since, by the nature of sports leagues, it is the last ranking that serves to summarize the result of the overall season. The same happens with the Stock Market, the richest people rankings made by the Fortune magazine [
6], university rankings (e.g., [
7,
8]), songs rankings based on the number of downloads, streaming, or sales (see [
9]), etc. Our work is focused on a series of rankings behavior.
The terminology applied to rankings is not unique. For example, in [
10] the term
partial is used to indicate rankings in which ties are presented, while in [
11] the term
partial indicates that not all the objects are compared. In this paper, we use the terminology coined in [
4,
12]. We talk of
complete rankings when all the objects are compared (as in a football league) and
incomplete when there are absent objects (as in a Top k ranking). We explicitly use the terms
with ties or
without ties to indicate whether we consider the presence of tied objects in the rankings. We recall that in [
11] the term
linear order is used when all objects are compared and no ties are allowed (that is, for us,
complete rankings with no ties) and the term
weak ordering when all objects are compared, but ties are allowed (that is, for us,
complete rankings with ties).
Incomplete rankings appear in multiple areas. For example, in national or European grant calls, judges evaluate only a subset of the applications, and therefore each judge handles an incomplete ranking. The same happens in literary contests, where each judge only reads a small number of manuscripts. In the case of the results shown by search engines, it is clear that only the first Top k web pages are displayed, being, as a consequence, an incomplete ranking.
We use, and extend, the results of some previous papers. Some concepts are taken from [
5], where a method to compare series of complete rankings with no ties was presented, and from [
13], where a method to compare series of complete rankings with ties was analyzed. We also make reference to [
14], where some theoretical aspects where studied. In all these works, there are two main ingredients:
- 1.
The use of generalizations of the classical concept of Kendall’s
coefficient of disagreement [
15,
16,
17];
- 2.
The use of graphs associated to the series of rankings as a tool to visualize and also to help in the definition the coefficients that summarize the “behaviour” of the series of rankings.
Regarding to extensions of Kendall’s
coefficient, the first attempt to incorporate an axiomatic distance metric was in [
2], followed by the works [
11,
18,
19].
More recently, in [
4] these previous works were revised and a new axiomatic framework for incomplete rankings was introduced. To the best of our knowledge, the last paper devoted to an axiomatic study for incomplete rankings is [
12], where it is shown as an extension of Kendall’s
coefficient to the case of incomplete rankings with ties.
Kendall’s
has been extensively used, and some extensions can be found in the literature up to the present day on [
10,
12,
20]. In particular, Kendall’s
has been recently reviewed for ophthalmic research in [
21] and it is a tool used in neuroscience studies—e.g., [
22]—and in bioinformatics [
23].
Regarding the use of graphs to represent a series of rankings, we recall, in particular, that a graph can be used to describe the crossings between two rankings. This graph is called a
permutation graph (see [
24,
25]). When a graph is defined to show the
consecutive crossings between a series of
m rankings, it is called a
Competitivity graph [
5]. This concept corresponds to that of
intersection graph of a concatenation of permutation diagrams in graph theory (see [
26]). For more relations on graphs associated with rankings, see [
14].
In this paper, we take some results of [
4,
12] as our starting point to develop two coefficients to describe the evolution of a series of
incomplete rankings with ties. When applied to the case of only two rankings, our measures reduce to the measures given in [
4,
12].
We also extend the study of a series of complete rankings with ties developed in [
13] to the case of incomplete rankings with ties. We make use of the standard modern notation in the field of rankings mainly based on [
10,
12,
27], among others.
We take as our starting point the definition of
of [
12] that is based on the computation of a certain sum of the form
that involves the terms of some matrix
A and
B that indicate the relative positions of the elements of two rankings. In Theorem 1, we give an expression of this sum as a function of the type of interactions between a pair of elements
from one ranking to the next one (e.g., interchanges from tie to untie, absence of one of the elements in one ranking, crossings, etc.). This result allows for writing
(and
) in terms of the interactions of the elements of the rankings.
On the one hand, this theoretical result also allows a computation of the sum without computing explicitly the involved matrices. On the other hand, it allows for interpreting the interactions of a series of rankings by using a permutation graph or, more generally speaking, a competitivity graph. The edges are weighted to represent the weight of the corresponding interactions and the whole series of rankings.
We define two coefficients
and
for series of incomplete rankings with ties by using an analogy based on previous well-established definitions. We recall that, in the field of incomplete rankings, “intuition” is usually used for some measures over others since when you handle an incomplete ranking, there is no unique form to interpret the results (see this kind of reasoning in [
4,
12]). In our case, our measures’ behaviour is checked by ensuring that they are well normalized and that they reduce to well-known cases in limit situations.
Finally, other contributions of the paper are placed on a practical field. We give a methodology to study the movements of rankings (of songs) in Spotify by using two different approaches: the cases of series of incomplete rankings without ties and series of incomplete rankings with ties.
The structure of the paper is as follows. In
Section 2, we recall Kendall’s
and give the fundamental relations that will be useful throughout the paper. In
Section 3, we recall the notation and basic results for the case of two incomplete rankings with ties allowed.
In
Section 4, we give the fundamental theoretical result of the paper and some remarks that give insight both into the validity and application of this result. In
Section 5, we recall some definitions from [
13] to measure the evolution of
m complete rankings with ties. In
Section 6, we present two coefficients, denoted as
and
to characterize the evolution of
m incomplete rankings with ties and some examples are given. In
Section 7, we illustrate the applicability of the new coefficients by using some real data obtained from Spotify charts. Finally, in
Section 8, we outline the main conclusions of the paper.
2. Preliminaries
In [
16] it is shown that Kendall’s
coefficient (also called
measure of disarray) associated with two rankings with the same number of elements
n, can be written in the form
where
s is the minimum number of interchanges required to transform one ranking into the other. This coefficient is a measure of the intensity of rank correlation. The coefficient can also be written as
where
P is the number of pair of elements that maintain its relative order when passing from the first ranking to the second one (that is, the first element is above or below the second in both rankings) and
Q is the number of pairs of elements that interchange its order (that is, in one ranking, the first element is above the second and, in the other ranking, the first element is below the second, or vice-versa).
Note that
Q and
s are equal. Furthermore, this quantity can be identified with the number of
crossings or
inversions when passing from the first ranking to the second. For this reason, throughout the paper, we will keep in mind that Equation (
1) gives the equivalence between the number of crossings and the associated
. This will be important in what follows since we will deal with different extensions of Kendall’s
coefficient and since one of our preferred tools will be counting the number of crossings, as in [
5].
We recall from [
27] that a
distance metric can be transformed into a correlation coefficient
by the formula
where
is the maximum possible distance between two rankings. We recall that a distance metric between two rankings
and
is a non-negative real function
f, such that it is
symmetric (
, for any pair of rankings),
regular (
) and satisfying the
triangle inequality (
, for any rankings
a,
b, and
c). Note that Equation (
1) is of this form, since
is the maximum number of crossings between two given rankings. The same happens with the Spearman’s
coefficient. In [
16] the Spearman’s
for two ordinal complete rankings
and
with
is defined by
and this is of the form (
3) since it is easy to show that the maximum value of
occurs when one ranking is the reverse of the other and, as a consequence, the maximum value of the
distance metric is
(see [
3] for this and other properties of distance metrics).
We also recall that a permutation graph (called
competitivity graph in [
5]) is associated with two rankings over the same elements in such a way that the nodes represent the elements and two nodes and are connected with an edge if they cross their positions when passing from one ranking to the other.
In this way, it is clear that the number of edges of this graph is, precisely,
s. Furthermore, another quantity (borrowed from graph theory) is also introduced in [
5]: the
Normalized Mean Strength ; that is, the normalized sum of the weights of the edges of a weighted graph. When considering only two rankings and its corresponding
competitivity graph, we have the following relation
that gives the equivalence between the
Normalized Mean Strength and Kendall’s
for two rankings. Note that
and
. We consider that the measure
is more intuitive than
since it allows us to interpret the movements or
activity of a series of rankings as a percentage.
3. Coefficients for Two Incomplete Rankings with Ties
In this section, we recall some definitions used in [
4,
12]. We will use the next three ingredients in order to define a coefficient to compare two rankings:
- 1.
A vector to define the ordinal ranking (including the description of absent elements and tied elements);
- 2.
A matrix to indicate the relative positions of the elements of the ranking (including absent and tied elements);
- 3.
A formula to define the coefficients for a pair of rankings by using the entries of their associate matrices defined in the previous step.
Let
be the objects to be ranked, with
. The ranking is given by
where
is the position of
in the ranking. Note that if
, then
and
are tied. If
is not ranked, then it is denoted as
. We also define the set
We define an
matrix
, with entries
associated to
as follows:
According to [
12], we define the coefficients
and, when
where
is the number of common ranked elements
to
and
. That is:
Example 1. Let , and let us consider two rankings and . Then, represents the incomplete ranking with ties , where indicate tied elements. Analogously, represents the ranking . Note that and .
Note that
with complete rankings and no ties reduces to the classic Kendall’s
given by (
1), while
is a renormalization of
, verifying
.
As we will see, Definition 6 in
Section 6, is based on an analogy with Equation (
1). To that end, it will be necessary to count all the possible cases when passing from
to
(interactions between the relative positions of pair of elements such as crossings, pass from tie to untie, from being in the ranking to quitting it, etc.). We do this in the next section.
4. Main Result
The following result is the fundamental theoretical result of this paper. This result will allow us to write
and
in terms of the interactions of the rankings’ elements. It opens the possibility of giving weights to the interactions, as is a common practice in modern definitions of Kendall’s tau [
10]. This result also constitutes our starting point to define a coefficient for a series of more than two incomplete rankings. This theorem also allows giving insight into the differences between
and
. Some other consequences are detailed in the remarks below and in Corollary 1.
Theorem 1. Given two vectors , representing incomplete rankings of n elements with ties, represented as in (
5)
, and their corresponding matrices and defined by (
6)
, it holds thatwhere s is the number of crossings—that is, the number of pairs —such that and , or and .
is the number of pairs that are tied in only one ranking (from tie to untie or viceversa), that is, such that and , or and .
In the definitions of s, and , it is assumed that and are different from •. For the cases when one or more • may appear, the following notation holds:
is the number of entries such that ;
is the number of entries, such that and ;
is the number of entries, such that and .
Finally, it is also needed to define as the number of entries, such that and .
Proof of Theorem 1. For each pair we will evaluate each term in the expression . The case gives .
Thus, we focus on pairs
with
. There is a total number of
of these pairs. It is useful to consider the basic cell of the pair
with
.
where
and
can be natural numbers or a • if the element
k is not ranked in
or
.
Let us study first the cases that can appear when no • is present in the basic cell.
The Complete Case (C):
That is , for all . We distinguish four types of basic cells.
Type C.1: Not crossing, and no ties in a nor in b.
For example:
So that, we have
and
and two cases can appear:
- C.1.1.
If , then .
- C.1.2.
If , then .
Type C.2: Crossing.
Again, we have and and two more cases can appear:
- C.2.1.
If , then .
- C.2.2.
If , then .
Type C.3: From tie to untie or viceversa.
We have or . Therefore, four cases can appear:
- C.3.1.
If then .
- C.3.2.
If then .
- C.3.3.
If then .
- C.3.4.
If then .
Type C.4: From tie to tie.
For example:
That is, we have:
, and then
.
We denote the number of pairs of each case using the terminology of
Table 1. Note that
is
the number of pairs that are tied in both rankings, that is, such that
and
. Note also that
is the number of pairs that go from tie to untie or viceversa.
The Incomplete Case (I):
There is at least one • in the basic cell. In other words, there is some k such that , or , or both. We distinguish seven cases:
Type I.1: Four • That is
, or graphically
Then . Let us denote by the number of null rows that appear in the matrix with columns and . Therefore, we have pairs of this type.
Type I.2: Three •. That is, a cell of one of these forms
where ∗ is a number (not a •). Therefore, we have four cases, but all are similar to this one:
and
. Then,
.
Denoting the number of rows of the form in the matrix , and the number of rows of the form in the same matrix, it is clear that the number of pairs of this type is: .
Type I.3: Two •, one on each ranking. That is, any cell of one of these forms
These four cases can be reduced to two:
- I.3.1.
If , then .
- I.3.2.
If , then .
Denoting by the number of rows of the form in the matrix , it is clear that the number of pairs of this type is .
Type I.4: Tied in one ranking and two • in the other. For example,
That is, we have two cases, which are similar to this
, and then
.
Let us denote by
the number of different natural numbers in
and by
be the number of different natural numbers in
. Let
be the number of rows of the form
in that matrix, for
and, analogoulsly, let
be the number of rows of the form
in the matrix
for
. Then, it is straightforward to see that the number of cases of this type is given by
Type I.5: Tied in one ranking, one • in the other. For example
We have the following 4 cases:
- I.5.1.
If , then .
- I.5.2.
If , then .
- I.5.3.
If , then .
- I.5.4.
If , then .
Let be the number of rows of the form (where ∗ can be i) in the same matrix, with .
Analogously, let
be the number of rows of the form
(where ∗ can be
i) in the matrix
. Then, it is straightforward to see that the number of cases of this type is given by
Type I.6: Two • in one ranking and different numbers in the other.
We have here only two cases:
- I.6.1.
If then .
- I.6.2.
If then .
Then, it is easy to see that the number of pairs
of this type is
where we have subtracted the number of cases of the type I.4.
Type I.7: Only one • and no ties.
For example, they are cases of the form
We can have four cases that are similar to these
- If
then .
- If
then .
Let
be number of rows of the form
(where ∗ can be
i) in the same matrix, with
and, analogously, let
be the number of rows of the form
(where ∗ can be
i) in the matrix
, with
. Then, the number of pairs
of this type is given by
where we have subtracted the number of cases of the type I.5.
In
Table 2 we overview the number of cases for each type of the incomplete case.
To end the proof, we add the contributions for all the cases, complete (C) and incomplete (I), to the sum
and we obtain
Now, taking into account that all the cases must amount up to the total number of pairs we have
where
is the sum of all the cases in
Table 2. By plugging
into (
12), we finally get
where
□
In the next example, we illustrate the previous result.
Example 2. Given the rankings and , then , , , , , (corresponding to the pairs and ), (corresponding to the pair ), (corresponding to the pair ), , , , , , , , , , , , and, .
From the parameters of Table 3, we obtain . Thus, it is easy to check that as stated in Theorem 1. The number of pairs is 45, corresponding to the following cellsand the number of cases of each type for the incomplete case appearing on Theorem 1 are shown in Table 3. Remark 1. By using (
10)
and (
7)
we obtainthat can be thought of an extension of (
1)
to the case of two incomplete rankings with ties. This formula is one of the original contributions of this paper. Note that the term is known since it is given by (
11)
. This formula will be useful in Section 6 to define our measure of correlation for a series of incomplete rankings with ties. Remark 2. For two complete rankings with ties allowed, Equation (
10)
simplifies to If we recall the definition of the distance of Kemeny and Snell [2] depending on a matrix such thatby following a similar procedure as in the proof of Theorem 1 it is easy to show thatand by using (
15)
we getthat it is in agreement with the results shown in [27], but we obtain it as a particular case of Theorem 1. Remark 3. The common number of ranked elements in and that we denote as in (
9)
is precisely . Moreover, by using thatLet us check that given by (
11)
can be rewritten as To that end, it is needed to use that and To see how it is, we first note that Second, we can simplify, by using (
20)
Third, note that, by using (
20)
, Now, by using (
21)
–(
23)
we have that given by (
11)
becomesand sincewe getthat is to sayand the proof is done. Note also that, by using (
13)
, we have: . This last remark motivates the next result.
Corollary 1. Given two vectors , representing incomplete rankings of n elements with ties and their corresponding matrices and , it holds thatwhere is the number of common ranked elements in both rankings—see (
9)
—s is the number of crossings, that is, the number of pairs , such that and or and , and is the number of pairs that are tied in only one ranking (from tie to untie or viceversa
), that is, such that and , or and . With (
24), it is easy to obtain the maximum and minimum of the expression
. When
and
we have
that is the maximum value of
. Analogously, by taking
, that is the maximum number of crossings and consequently
, we obtain from (
24)
that is the minimum value of
. These facts, that are in agreement with the results shown in [
12], explain why
defined by (
8) takes values in
.
Remark 4. By using (
7)
and (
24)
we obtainand from (
8)
and (
25)
we get Remark 5. As we have pointed out in (
3)
, a distance metric
can be transformed into a correlation coefficient by the formula Note that in expression (
14)
, when , the quantity is not the maximum value of the distance metric
(see Example 6). This problem does not appear with the use of since, by using (
26)
we can identify a “distance metric” given by and its maximum value is achieved when (and consequently ) and has the value of Therefore, should be preferred over in terms of normalization (see [12] for other considerations). This fact will be useful for the definition that we will introduce in Section 6. In the next examples, we illustrate the two previous remarks. Note that when
and
then, by (
26),
and it is not affected by the presence of • in the rankings. By analogy with (
4), we denote the
Normalized Mean Strength of
a and
b as
Example 3. Let and . It is easy to obtain: , , , , and .
Example 4. Let and . It is easy to obtain: , , , , and .
The next example shows the results when a ranking is compared to itself and its reverse ranking for the case of complete rankings (note that since ).
Example 5. Let and . Then The next example shows that does not take its limit values when the rankings are incomplete and that is not defined when there are no elements in common in both rankings.
Example 6. Let , , , and , Then Our main practical result in this paper is the definition of a measure to deal not only with two rankings and , as we have seen so far, but with a series of incomplete rankings with ties in which, in practical situations, some kind of time evolution is presented (e.g., a sport ranking during a session where there may be ties or inclusion/elimination of teams, charts of songs ordered on a daily/weekly basis, etc.). In order to define this measure, it will be useful to recall some concepts defined for complete rankings.
6. New Coefficients for Series of Incomplete Rankings with Ties
Given a series of incomplete rankings with ties, for each pair of rankings and we can use Definitions 1–4 straightforwardly to also apply for a series of incomplete rankings by assuming that there is no penalty for the case of absent elements (regarding Definitions 1 and 2) and that these absent elements (denoted by `•’) do not contribute to either ties or to crossings after ties (regarding Definitions 3 and 4). That is, those definitions are applied as they are, ignoring the effect of the absent elements.
Keeping this in mind and, in analogy with (
14), given a series of
m incomplete rankings we could include the effect of the incomplete cases by defining
with
where
is the number of incomplete cases when passing from ranking
to ranking
. Note that the explicit form of
for each pair of consecutive rankings is given by (
11) in Theorem 1 and Corollary 1. The value of
depends on
. We have seen in Remark 5 that the definition of
corresponds to take
as the value corresponding to
(and that is the reason why
is not well normalized). We can translate here the same reasoning and formalize it in the next definition.
Definition 5. Given m incomplete rankings with ties of n elements we define the corrected evolutive Kendall’s τ coefficient for the series with penalty parameters and as follows:where is given by Definition 4, and is given by (
11).
Here we have the same drawback as we showed for
in Remark 5:
is not properly normalized and it cannot get the values
if any
. Therefore, in analogy with (
26), we introduce a new coefficient in the following definition.
Definition 6. Given m incomplete rankings with ties of n elements, such that , for all , we define the scaled corrected evolutive Kendall’s τ coefficient for the series with penalty parameters and as follows:where is given by Definition 4 and withwhere denotes the common ranked elements between and . Note that we need that, for some i, .
Remark 8. In the limit case of m complete rankings with ties, note that Equation (
37)
collapses to Equation (
32)
. Note also that is affected by the crossings, the pass from tie to untie (or viceversa) and the long crossings
(crossings after ties given by , given by Definition 3), due to the term . The effect of the elements that are out of the rankings appear explicitly by the term that does not take into account the position in nor in . is well normalized, that is . Example 8. Let . Given the series of incomplete rankings with ties , , and , an easy computation shows and thus . Note that .
Example 9. Let . Given the series of incomplete rankings with ties , , and , it is easy to obtain that and thus . Note that .
As we have seen in the above definitions, the importance of Theorem 1 and Corollary 1 consists of giving the explicit formula for
to allow for the computation of the coefficient
for the series of
m incomplete rankings with ties. Note that
. For the particular case when the rankings are complete, we have
for all the pairs of consecutive rankings and
, for
, and therefore Equation (
36) reduces to the complete case given by Equation (
33), that is,
collapses to
.
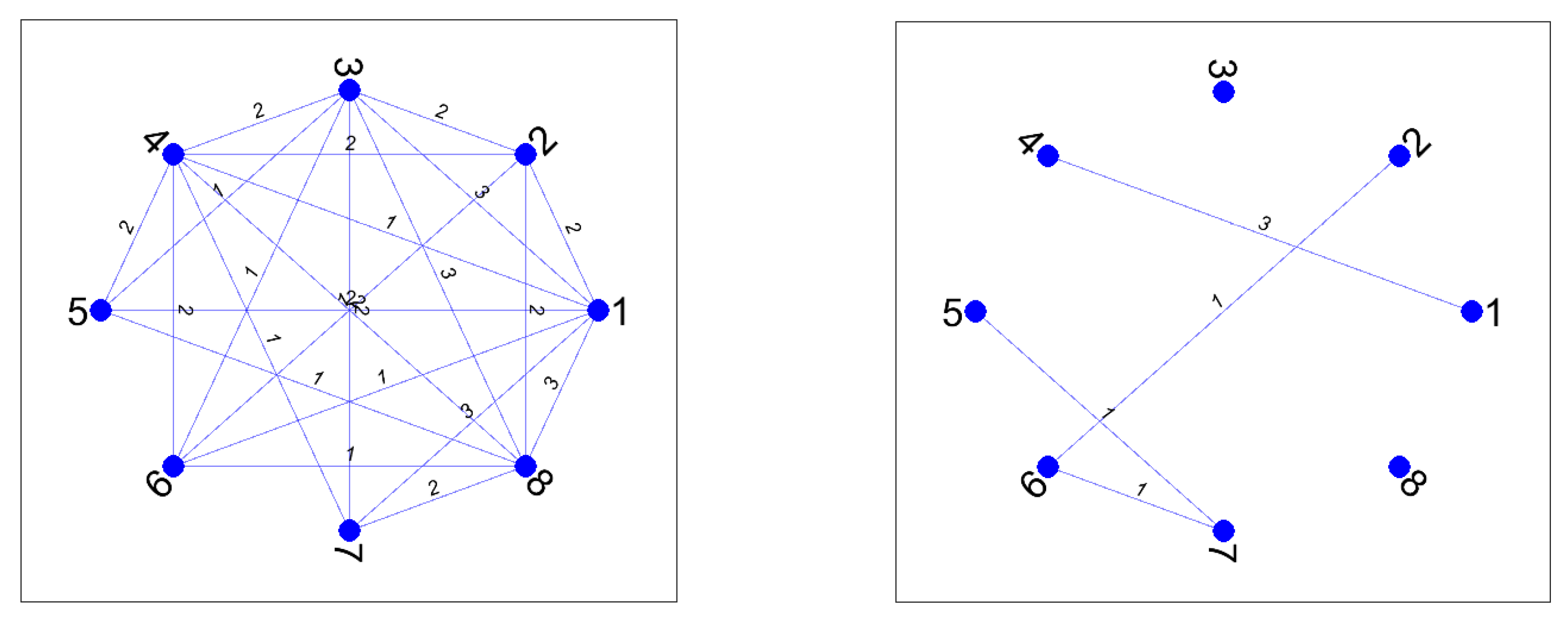
Another contribution of Theorem 1 and Definition 6 is that they are useful to describe the behavior of the series of m rankings in terms of a competitivity graph. We can define a weighted graph for each one of the interactions between the elements when passing from to : crossings, passing from tie to untie (or vice-versa), and crossing after ties. Moreover, for each kind of graph, we can add the contributions of all the pairs of consecutive rankings to obtain a projected graph for any interaction (crossings, passing from tie to untie (or vice-versa), and crossing after ties). The procedure is the following: First, we construct an undirected graph for each pair of rankings by identifying each element i as a node and defining an edge between i and j by the rule: there is an edge connecting with weight when this weight is nonzero. By adding the pairs of undirected graphs we obtain a projected graph with a total sum of weights . By adding the crossing after ties term to the projected graph we have all the ingredients appearing on Definition 6. We show this procedure by using the next example with and .
Example 10. Given the series of incomplete rankings with tiesthe corresponding areIn this example we have , and an easy computation leads to the parameters shown in Table 4. For each pair of consecutive rankings it is easy to compute the parameters defined in Theorem 1: , , , , s, , and . Then, by using Equation (
10)
in Theorem 1 we can obtain, for any pair of rankings, the value . is the number of common elements, given by (
9)
. The coefficient is given by (
35)
, and the coefficient is given by (
36)
. In analogy with (
4)
we can define the corresponding normalized mean strengths given byandFinally, in Table 4 we include the coefficients and given by (
7)
and (
8)
, respectively. These last coefficients are included to show that our new coefficients and reduce to them when only a pair of rankings are considered. To compute our new coefficients
and
for the whole series of rankings
to
we need some previous parameters. First, we need the value
To compute
, given by (
31), we need to know, previously, the value of the
crossing after ties coefficients
, given by Definition 3. Note that the unique long crossing occurs for the pair
: the elements tagged as 1 and 4 are such that 4 is above 1 in
, both elements are tied in rankings
and
, and, finally, 4 is below 1 in ranking
. Note, for example, that the pair
does not accomplish the conditions of crossing after ties. Therefore the only term that contributes to
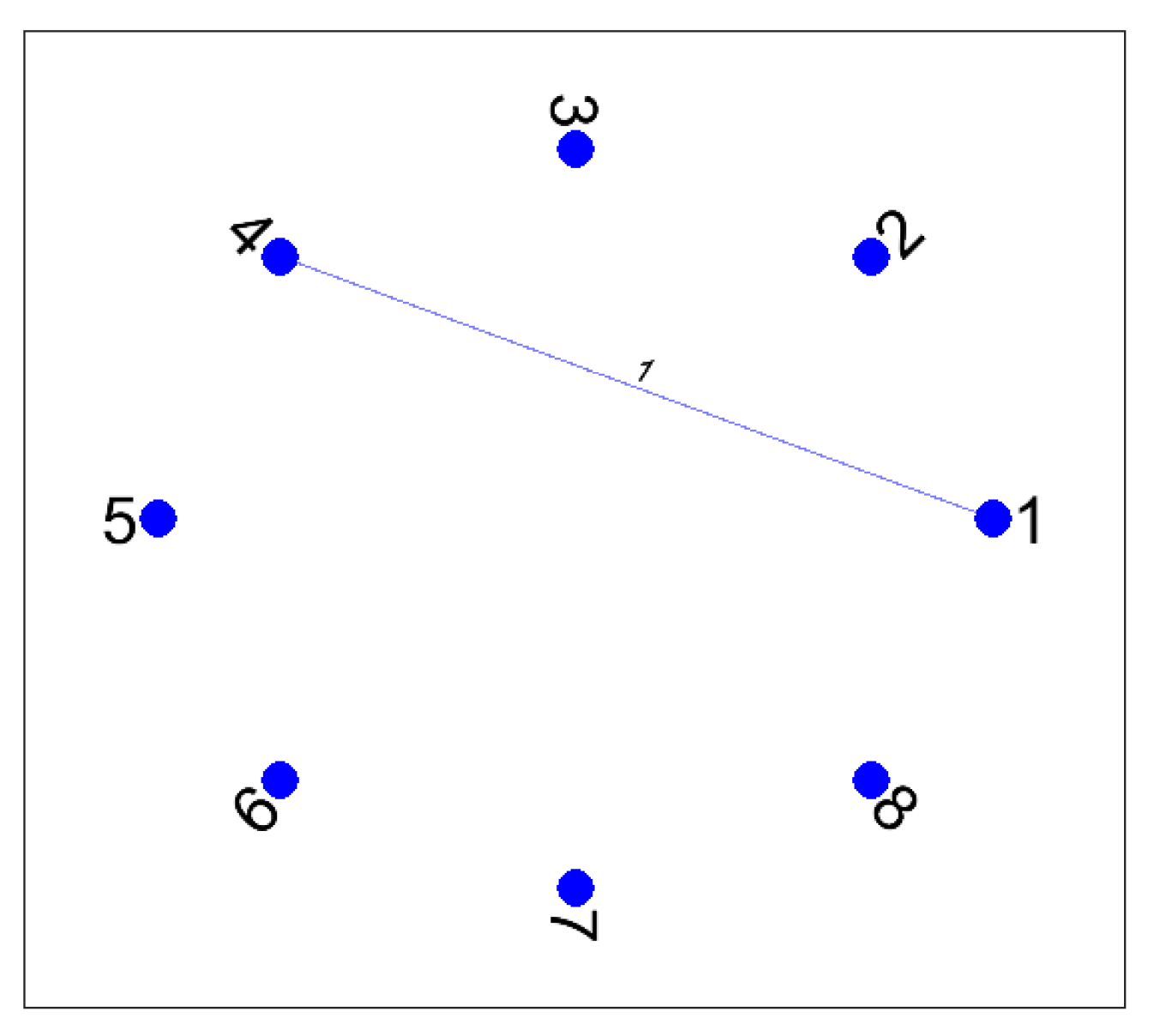
is
.
With respect to
, given by (
30), we need to compute the terms
, given by (
28), for any pair of consecutive rankings. A detailed computation shows that, in this example, we have 42
crossings and 6 cases of
tie to untie or viceversa. The precise pairs of elements that contribute to these cases are shown in the corresponding projected weighted graphs in
Figure 1. The
crossing after ties case is represented in
Figure 2.
Therefore we have all the ingredients to compute
. That is
and, by Remark (7), we know that
By using (
35), we obtain
that corresponds to an equivalent normalized mean strength
Finally, regarding
, we have
that corresponds to
All in all, we conclude that
is a proper coefficient for the evaluation of
m incomplete rankings with ties and can be considered as a natural extension of the coefficient
presented in [
12]. In the next section we apply the new coefficients
and
to real rankings appearing on Spotify charts.
7. Results
Spotify is one of the major music streaming services worldwide, with 299 million monthly active users, as of July 2020 [
28]. The company Spotify Technology S.A. has been listed on the New York Stock Exchange since 2018. As of September 2020, the company offers a catalog of 60 million tracks and operates in 92 countries from Albania to Vietnam [
29]. Spotify divides the monthly active users into four regions [
30]: Europe (35%), North America (26%), Latin America (22%) and rest of the world (17%). The app is available on several devices, such as computers, smartphones, tablets, wearable devices, etc. The users can choose between a free service (called
Freemium or
Ad-Supported) or a
Premium service. In any case, the user can listen by streaming any song of the catalog (that is, the user does not own the song’s digital file, but can listen to it). It is accepted that music streaming services have transformed the entire music market—see [
31]—and they have evolved very fast, changing their services and capabilities. For example, Spotify has signed some partnerships with Microsoft [
32], Sony [
33] and Facebook [
34] among other big companies. There exists a large amount of literature about Spotify, but it is mainly focused on Economics and Music. To the best of our knowledge, a small number of papers are devoted to the mathematical aspects of the rankings produced by Spotify. Among these papers, we have [
35,
36]. A paper that studies the relationship between personality and type of music is [
37]. See [
38] for more details about Spotify.
Like other services on the Internet, Spotify provides some chart lists (song rankings) based on the platform’s number of streamings. To this kind of rankings belongs the Top 200 (see [
39,
40,
41]), that is one of the topics of our study. Another ranking that we are interested in is called
Viral 50 which is an evolution of the original Social 50 ranking (see [
42,
43,
44]) that incorporated in the song chart the effect of the social sharing of a track by Spotify users. This sharing included platforms such as Facebook and Twitter. It is not completely clear for us how this rank is computed, but it aims to gather
fresh songs that acquire high impact on social networks by new release promotions, special apparitions on tv-shows, music festivals, tours, etc. (see [
45] for an example of how a viral song transformed into a Top 100 song in 2013).
Due to the situation caused by the COVID-19 pandemic, the live music business reflected some drawbacks, such as festivals being cancelled worldwide, a reduction in public-performance licensing, and other related factors—see [
46]. As an example, Warner Music Group Corp showed a total revenue fall of
in the first quarter of 2020 compared to the first quarter of 2019 [
47]. Spotify also reported some impact on their business, but in the first quarter of 2020, it seemed that the consumption recovered and monthly active users increased faster in the first quarter of 2020 than in the same period of 2019 [
30]. Some perturbations in Spotify streaming were also reported by the music analytic company Chartmetric that observed a change in the type of consumption of Spotify streamings by music genre in the period between 3 March 2020 to 9 April 2020, concluding that it seemed that it had been a
pandemic-induced lifestyle change [
48].
With regard to the Top 50 viral, it is reasonable to think that the fact that many artists (such as Lady Gaga, Alicia Keys, and Cardi B. [
46]) have postponed big releases may have decreased the movements in these charts.
7.1. Method to Convert Spotify Lists into Incomplete Rankings
Both Spotify Top 200 and Viral 50 lists can be treated as incomplete rankings since some elements (songs) quit the list and some others that appear on the list (new songs). Let us call any of these rankings as Top k rankings. In order to handle these Top k rankings, our methodology consists of the following steps:
- 1.
Select a set of m lists with k entries in each .
- 2.
Denote as n the number of different songs that appear on these m lists. We tag these songs from 1 to n, following the order they first appear, reading the lists from the first to the last one, and each list from top to bottom. Denote the tagged version of , for , including all the n songs.
- 3.
Denote a vector with entries from 1 to n. The first k values correspond to the elements in .
- 4.
Construct the rankings for , in the following form:
- (a)
The first k entries of are copied from ;
- (b)
The rest of the entries form a vector and come from the the elements that quit from plus the elements that, being in , are not included in .
These elements preserve their relative order. This order is not important since these elements are not included in the Top k ranking .
- 5.
From each
, we construct the corresponding incomplete ranking
given by (
5).
Example 11. Let us consider three Top 4 lists () and construct the corresponding three rankings (). Here we have and .We have denoted as the elements beyond the k position in each ranking . The rankings are constructed looking at from positions 1 to 4. Since the elements that do no belong to are in , we tagged them as •. 7.2. Comparison of Two Series of Top 200 Rankings
From the site [
49] we downloaded the series of Top 200 (Global) rankings corresponding to the following time intervals:
The term
Global means that the charts were produced from streaming on Spotify from all over the world. By using the methodology explained in the previous section, we convert the 18 downloaded rankings to a series of incomplete rankings (with no ties)
, and we compute our parameters. This is repeated for each considered year. The results are shown in
Table 5.
In
Table 5 we have denoted by
the average of
for
, that is the mean number of common elements from each pair of consecutive rankings. We see that the number of songs involved in the 2019 series is
, which is lower than the 2020 series number. This fact could indicate that there was more
activity in the 2020 series since more new songs appeared than the previous year. By extension, we can also conclude that the
activity on Spotify of the users was higher in the 2020 series.
The same tendency is observed by looking at and . Our coefficients and corroborate this intuition since they take higher values in the 2020 Series than in the 2019 Series. Analogously, by looking at and , we see a decrease when comparing the 2019 Series with the 2020 Series. Recall that the coefficients and introduced in this paper offer a measure of the movements in the rankings, since they take into account the number of crossings and, in this case, that we do not have ties, due to the effect of absent elements.
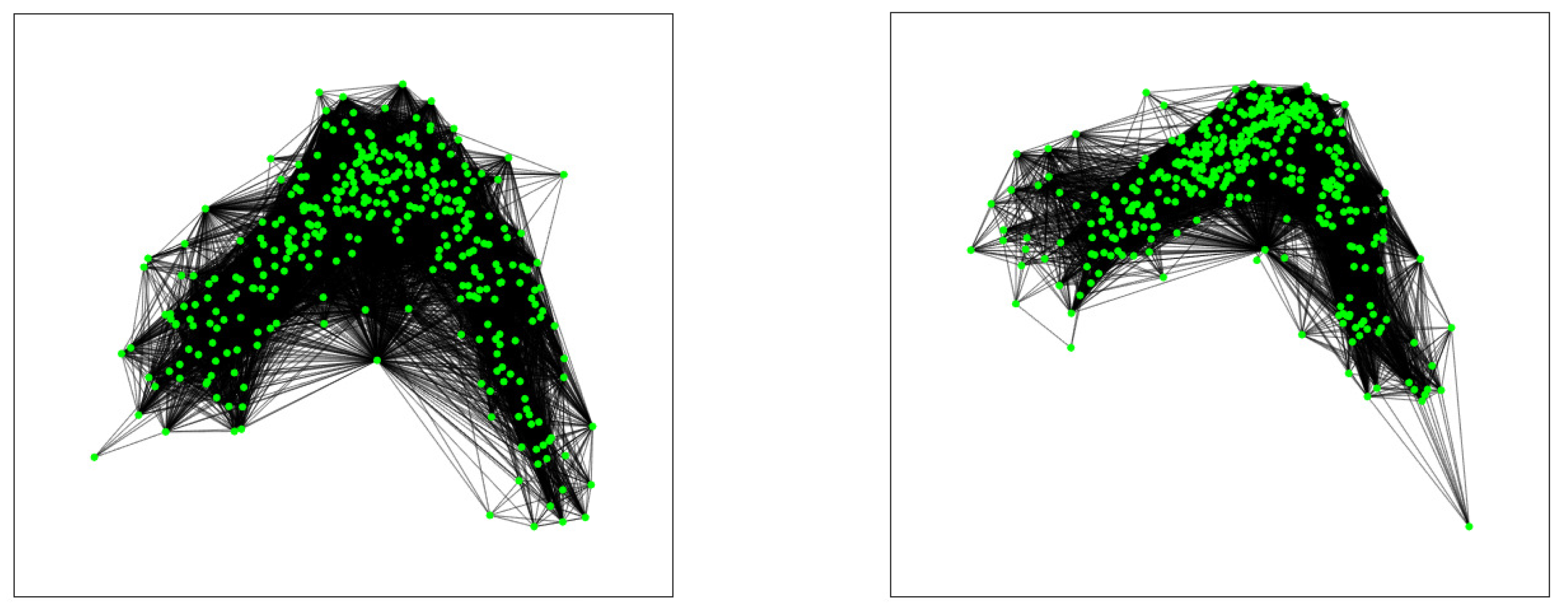
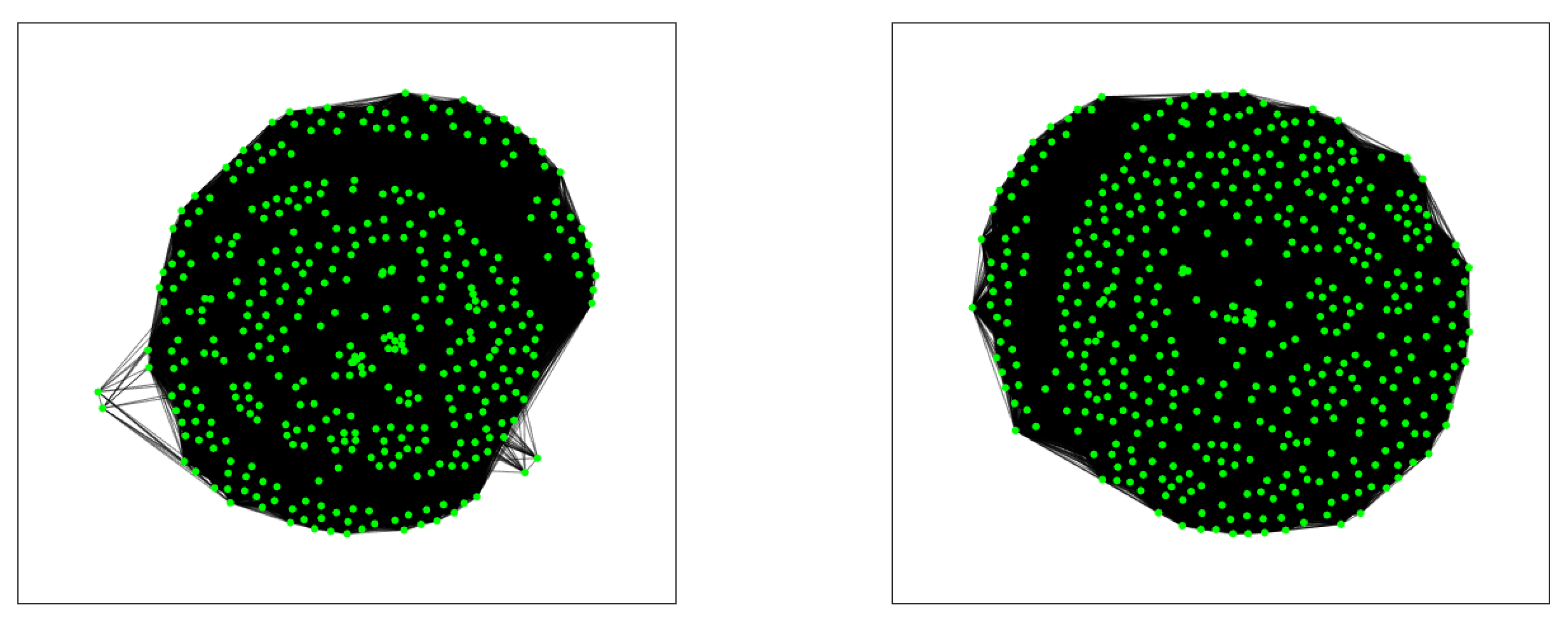
In the same manner, as we did in Example 10, we can construct the projected graph corresponding to the crossings for each series. We show these graphs in
Figure 3, that have been plotted with MATLAB by using the option ”subspace”.
7.3. Comparison of Two Series of Viral-50 Rankings
From the site [
50], we downloaded the series of Viral 50 (Global) weekly rankings corresponding to the following periods:
For each considered year, we convert the 18 downloaded rankings to a series of incomplete rankings (with no ties)
, and we computed again the aforementioned parameters. The results are shown in
Table 6.
The number of songs involved in the 2019 series is , that is greater than the number involved in the 2020 series. This fact could indicate that there was less viral activity in the 2020 series since fewer new songs appeared than the previous year. The same tendency is observed at . This intuition is corroborated by our coefficients. and since they take lower values in the 2020 series than in the 2019 series. We also see an increase in and when comparing the 2019 series with the 2020 series.
If we compare these results with those obtained in the previous section, we conclude that Spotify’s viral activity was negatively affected by the Pandemic. This may seem reasonable since many events that produce sharing in Social Networks, such as shows, new releases, and performances, were postponed during these months, as we have already discussed. We again plot the projected graph corresponding to the crossings for each series in
Figure 4.
7.4. Comparison of a Series of Top 200 and a Series of Viral 50 Rankings
Given that our coefficients
,
,
, and
are normalized, we can compare series of rankings of different type. Looking at
Table 5 and
Table 6, we conclude (e.g., looking at
) that the Viral-50 rankings present more activity than the Top 200 rankings. For example in the 2019 series the value of
is
for the Viral-50 rankings, and only
for the Top 200 rankings. This conclusion seems reasonable, taking into account that the Viral-50 rankings are constructed by looking at the behaviours of songs that may rapidly change, since they are viral phenomena.
7.5. Comparison of the Evolution of Two Series of Incomplete Ranking with Ties
Spotify charts Top 200 do not present ties, but we can construct incomplete rankings with ties if we take into account the Top 200 ranking and the rest of the songs that appear in the whole studied interval. In detail, to obtain a series of incomplete rankings with ties from a Top 200 series on Spotify, we will consider the whole list of tracks along with the m rankings and focus on what happens in positions greater than 200. Using the terminology used in Example 11 we consider the elements that appear on the rankings, denoted as , . In this ranking we consider the following:
- (i)
All the tracks in are tied. That is where is a row vector of 200 entries of the type •, and is the row vector of all-ones, with entries, being n the total number of different tracks in the m rankings.
- (ii)
For , we consider that in we have (at most) two buckets of tied elements. In one bucket we have the elements (if any) that come from . In the other bucket, we consider the rest of the elements of
The next example with a series of Top 4 charts illustrates this methodology.
Example 12. Let us consider the series of seven Top 4 tracks with elements given by the rankingsfrom these rankings we construct the rankings and to obtain the rankings in the form Now, we consider the rankings as a series of incomplete rankings with ties with the convention explained above and we compute the corresponding vectors to obtain the rankings Note that, since there are at most two buckets, the entries of belong to the set . Note also that in there is only one bucket.
By using this methodology, we have converted the series of rankings studied in
Section 7.2 to the corresponding series
with ties. The parameters obtained are shown in
Table 7.
If we look at
n,
,
, and
in
Table 7, we conclude that there has been more activity in the 2020 Series than in the 2019 Series. However, by looking at
(and
), the conclusion seems to be the reverse. Here we see, therefore, that
and
can present different tendencies. This is related to the form in which they are normalized, as we have commented in Remark 5 and in
Section 6. These results provide an example of how the transformation from
to
is not linear, since
increases from 2019 to 2020 but
decreases in the same period.
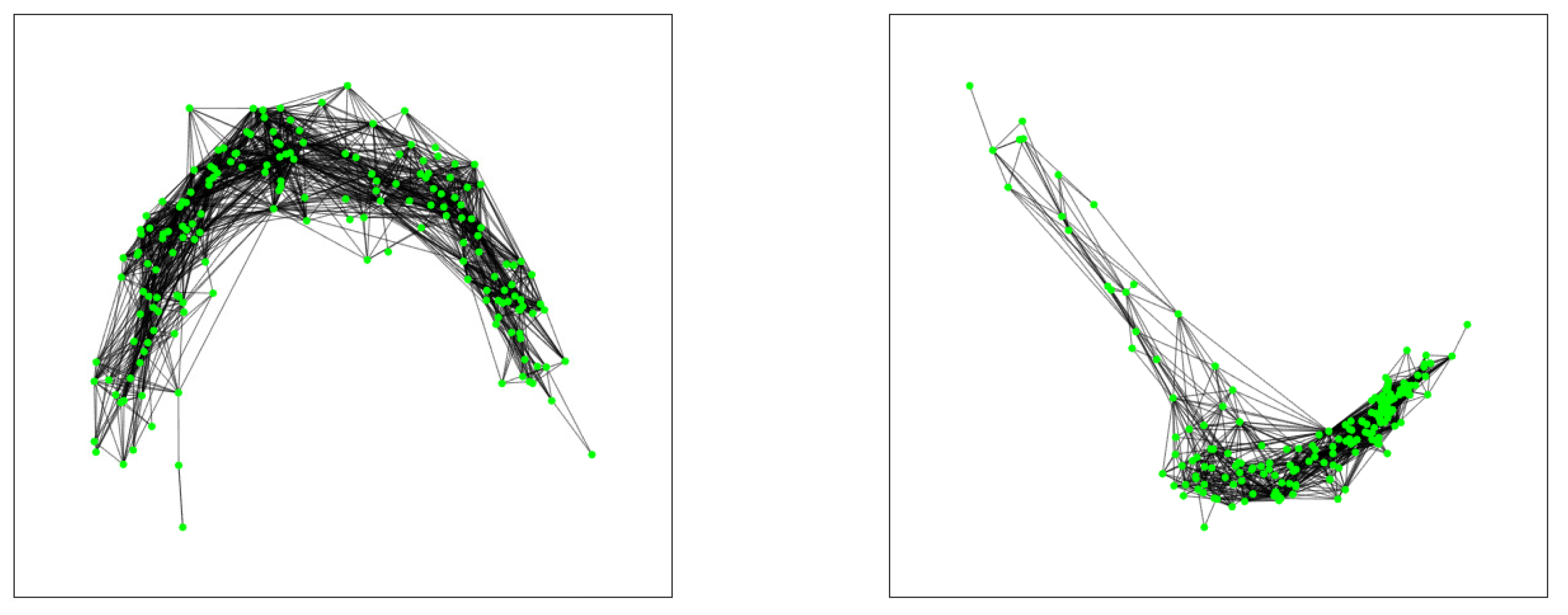
In
Figure 5, we show the plot of the giant component corresponding to the projected graph showing the interactions of the form
tie to untie or viceversa. That is, there is a link between elements (nodes)
i and
j when the pair
goes from tie to untie (or vice versa) in any pair of consecutive rankings
and
. We see many more interactions of this type in the 2020 series than in the 2019 series.
In
Figure 6, we show the plot of the giant component corresponding to the projected graph showing the interactions of the form
tie to tie, that is, there is a link between elements (nodes)
i and
j when the pair
goes from tie to tie in any pair of consecutive rankings
and
. We also see many more interactions of this type in the 2020 series than in the 2019 series.
Therefore, and taking into account the values of
Table 7, we can conclude (for this artificial model of incomplete ranking with ties) that there was more activity in the 2020 series than in the 2019 series.
We have shown the application of the new coefficients introduced in this work, as long as the utility of the visualizations based on the projected graph plots of the (evolutive) competitive graph associated to a series of incomplete rankings with or without ties.