Modeling of Artificial Groundwater Recharge by Wells: A Model Stratified Porous Medium

Abstract

In recent years, groundwater levels have been decreasing due to the demand in agricultural and industrial activities, as well as the population that has grown exponentially in cities. One method of controlling the progressive lowering of the water table is the artificial recharge of water through wells. With this practice, it is possible to control the amount of water that enters the aquifer through field measurements. However, the construction of these wells is costly in some areas, in addition to the fact that most models only simulate the well as if it were a homogeneous profile and the base equations are restricted. In this work, the amount of infiltrated water by a well is modeled using a stratified media of the porous media methodology. The results obtained can help decision-making by evaluating the cost benefit of the construction of wells to a certain location for the recharge of aquifers.

1. Introduction

Infiltration wells are used to contribute to the evacuation of rains in urban areas and also as a mechanism to recharge aquifers in regions where they present an unsustainable abatement [1,2,3,4]. Their construction must be analyzed from several angles: objectives of artificial recharge, available technological options, chemical quality of the water, social factors, place, quantity of water to contribute, among others [5,6,7,8,9].

In the literature, several numerical and analytical solutions can be found to model the flow of water in the porous medium, however, the models present restrictions to estimating the properties of soils, in addition to considering the stratum of the soil well profile as a homogeneous medium [1,10,11,12,13,14].

The artificial recharge capacity in a well is measured as the amount of water that infiltrates the soil during a specific period of time, and varies depending on the number of strata in the soil in which it was built. In this way, if you want to know the amount of water that the entire well contributes, you must evaluate the infiltration rate in all the strata to have a better knowledge about the contributions to the aquifer and the behavior of the system as a whole.

The phenomenon of infiltration in porous media can be studied from the general principles of the conservation of mass and momentum. The equation that results from the application of the first principle is:

$$\frac{\partial \mathsf{\theta }}{\partial \mathrm{t}}=-\nabla \cdot \overrightarrow{\mathrm{q}}.$$

(1)

Darcy’s law generalized to partially saturated porous media is used as a dynamic equation [15]:

$$\overrightarrow{\mathrm{q}}=-\mathrm{K}\nabla \mathrm{H},$$

(2)

where H is the hydraulic potential and is the sum of the pressure potential (ψ) and the gravitational potential assimilated to the vertical coordinate (z) oriented, in this case, as positive upwards. The pressure potential is positive in the saturated zone and negative in the unsaturated zone, since it is agreed that the zero pressure corresponds to the atmospheric pressure; θ = θ (ψ) is the volumetric water content, also called moisture content, and is a function of the water pressure, θ (ψ) is known as the retention curve or soil moisture characteristic; $\overrightarrow{\mathrm{q}}$ = (q_x, q_y, q_z) is the flow of water per unit of soil surface or Darcy flow, with its components in a rectangular system; (x, y, z) are the spatial coordinates in a rectangular or Cartesian system, $\mathrm{t}$ is time; $\nabla$ is the gradient operator; K = K (ψ) is the hydraulic conductivity as a function of the water pressure.

Thus, the general equation of flow in a porous medium results from the combination of Equations (1) and (2):

$$\frac{\partial \mathsf{\theta }}{\partial \mathrm{t}}=\nabla \cdot \left[\mathrm{K}\left(\mathsf{\psi }\right)\nabla \left(\mathsf{\psi }+\mathrm{z}\right)\right].$$

(3)

This equation presents two independent variables, θ and ψ, but since there is a relationship between them, the specific capacity defined as the slope of the retention curve is introduced. The chain rule is applied and the equation with the dependent variable pressure is established, known as the Richards equation [16]:

$$\mathrm{C}\left(\mathsf{\psi }\right)\frac{\partial \mathsf{\psi }}{\partial \mathrm{t}}=\nabla \cdot \left[\mathrm{K}\left(\mathsf{\psi }\right)\nabla \mathsf{\psi }\right]+\frac{\partial \mathrm{K}}{\partial \mathsf{\psi }}\frac{\partial \mathsf{\psi }}{\partial \mathrm{z}}; \mathrm{C}\left(\mathsf{\psi }\right)=\frac{\partial \mathsf{\theta }}{\partial \mathsf{\psi }}.$$

(4)

In this work a methodology is presented to obtain the water infiltration rate by partially or totally filled artificial recharge wells. The equations have been adapted to be used in a homogeneous stratified medium, taking into account the soil characteristics of each strata in the profile of the well.

2. Materials and Methods

2.1. The Richards and Kirchhoff Equations in Spherical and Cylindrical Coordinates

In some problems the analysis is simplified if Equation (4) is written in cylindrical or spherical coordinates. The Richards equation [16] in cylindrical coordinates (r, φ, z) is as follows:

$$\mathrm{C}\left(\mathsf{\psi }\right)\frac{\partial \mathsf{\psi }}{\partial \mathrm{t}}=\frac{1}{\mathrm{r}}\frac{\partial }{\partial \mathrm{r}}\left[\mathrm{r}\mathrm{K}\left(\mathsf{\psi }\right)\frac{\partial \mathsf{\psi }}{\partial \mathrm{r}}\right]+\frac{1}{{\mathrm{r}}^2}\frac{\partial }{\partial \mathsf{\phi }}\left[\mathrm{K}\left(\mathsf{\psi }\right)\frac{\partial \mathsf{\psi }}{\partial \mathsf{\phi }}\right]+\frac{\partial }{\partial \mathrm{z}}\left[\mathrm{K}\left(\mathsf{\psi }\right)\frac{\partial \mathsf{\psi }}{\partial \mathrm{z}}\right]+\frac{\partial \mathrm{K}}{\partial \mathsf{\psi }}\frac{\partial \mathsf{\psi }}{\partial \mathrm{z}},$$

(5)

where r is the radius and φ is the azimuth: r² = x² + y², x = r cos φ, y = r sin φ.

In spherical coordinates (ρ, ϑ, φ) the Richards equation is written as:

$$\begin{array}{c}\mathrm{C}\left(\mathsf{\psi }\right)\frac{\partial \mathsf{\psi }}{\partial \mathrm{t}}=\frac{1}{{\mathsf{\rho }}^2}\frac{\partial }{\partial \mathrm{r}}\left[{\mathsf{\rho }}^2\mathrm{K}\left(\mathsf{\psi }\right)\frac{\partial \mathsf{\psi }}{\partial \mathsf{\rho }}\right]+\frac{1}{{\mathsf{\rho }}^2\sin \mathsf{\vartheta }}\frac{\partial }{\partial \mathsf{\vartheta }}\left[\sin \mathsf{\vartheta }\mathrm{K}\left(\mathsf{\psi }\right)\frac{\partial \mathsf{\psi }}{\partial \mathsf{\vartheta }}\right]\\ +\frac{1}{{\mathsf{\rho }}^2{\sin }^2\mathsf{\vartheta }}\frac{\partial }{\partial \mathsf{\phi }}\left[\mathrm{K}\left(\mathsf{\psi }\right)\frac{\partial \mathsf{\psi }}{\partial \mathsf{\phi }}\right]+\frac{\partial \mathrm{K}}{\partial \mathsf{\psi }}\frac{\partial \mathsf{\psi }}{\partial \mathrm{z}}\end{array}$$

(6)

where ρ is the radio, ϑ is the polar angle and φ is the azimuth: ρ² = x² + y² + z², x = ρ sin ϑ cos φ, y = ρ sin ϑ sin φ, z = ρ cos ϑ.

In a symmetric well with respect to the z axis, the radius r takes this axis as its origin, and Equation (5) is very useful for the infiltration analysis when it is assumed that the pressure does not depend on the azimuth, that is, when the heterogeneity is presented by layers. In this case the equation simplifies to the following:

$$\mathrm{C}\left(\mathsf{\psi }\right)\frac{\partial \mathsf{\psi }}{\partial \mathrm{t}}=\frac{1}{\mathrm{r}}\frac{\partial }{\partial \mathrm{r}}\left[\mathrm{r}\mathrm{K}\left(\mathsf{\psi }\right)\frac{\partial \mathsf{\psi }}{\partial \mathrm{r}}\right]+\frac{\partial }{\partial \mathrm{z}}\left[\mathrm{K}\left(\mathsf{\psi }\right)\frac{\partial \mathsf{\psi }}{\partial \mathrm{z}}\right]+\frac{\partial \mathrm{K}}{\partial \mathsf{\psi }}\frac{\partial \mathsf{\psi }}{\partial \mathrm{z}},$$

(7)

which has only two spatial coordinates (r, z).

The equation in spherical coordinates presents a very particular importance when, in the analysis of a problem, it is considered that the medium is homogeneous and isotropic, that is, when the phenomenon does not depend on either the colatitude or the azimuth:

$$\mathrm{C}\left(\mathsf{\psi }\right)\frac{\partial \mathsf{\psi }}{\partial \mathrm{t}}=\frac{1}{{\mathsf{\rho }}^2}\frac{\partial }{\partial \mathsf{\rho }}\left[{\mathsf{\rho }}^2\mathrm{K}\left(\mathsf{\psi }\right)\frac{\partial \mathsf{\psi }}{\partial \mathsf{\rho }}\right]+\frac{\partial \mathrm{K}}{\partial \mathsf{\psi }}\frac{\partial \mathsf{\psi }}{\partial \mathrm{z}},$$

(8)

in which only two spatial coordinates are presented (ρ, z).

Furthermore, in some particular problems involving homogeneous porous media, the analysis is simplified if the potential Kirchhoff flow is defined by:

$$\mathsf{\Phi }={\displaystyle \underset{-\infty }{\overset{\mathsf{\psi }}{\int }}\mathrm{K}\left(\overline{\mathsf{\psi }}\right)\mathrm{d}\overline{\mathsf{\psi }}}={\displaystyle \underset{{\mathsf{\theta }}_{\mathrm{r}}}{\overset{\mathsf{\theta }}{\int }}\mathrm{D}\left(\overline{\mathsf{\theta }}\right)\mathrm{d}\overline{\mathsf{\theta }}},$$

(9)

from which it follows that:

$$\frac{\mathrm{d}\mathsf{\Phi }}{\mathrm{d}\mathsf{\psi }}=\mathrm{K}\left(\mathsf{\psi }\right); \frac{\mathrm{d}\mathsf{\Phi }}{\mathrm{d}\mathsf{\theta }}=\mathrm{D}\left(\mathsf{\theta }\right),$$

(10)

where D (θ) is the hydraulic diffusivity, in analogy with the diffusion of gases, which is expressed as D(θ) = K(θ)/C(θ), considering, now, that both the hydraulic conductivity and the specific capacity are functions of the volumetric content moisture.

The water transfer equation in porous media as a dependent variable for moisture content, Equation (3), is as follows:

$$\frac{\partial \mathsf{\theta }}{\partial \mathrm{t}}=\nabla \cdot \left[\mathrm{D}\left(\mathsf{\theta }\right)\nabla \mathsf{\theta }\right]+\frac{\mathrm{d}\mathrm{K}}{\mathrm{d}\mathsf{\theta }}\frac{\partial \mathsf{\theta }}{\partial \mathrm{z}},$$

(11)

which presents the structure of a nonlinear Fokker–Planck equation [17], the linear version of which is widely known in diffusion problems.

In terms of the potential Kirchhoff flow, Equation (11) becomes:

$$\frac{1}{\mathrm{D}\left(\mathsf{\Phi }\right)}\frac{\partial \mathsf{\Phi }}{\partial \mathrm{t}}={\nabla }^2\mathsf{\Phi }+\frac{\mathrm{d}\mathrm{K}}{\mathrm{d}\mathsf{\Phi }}\frac{\partial \mathsf{\Phi }}{\partial \mathrm{z}}.$$

(12)

Kirchhoff’s equation in cylindrical coordinates (r, φ, z), where r is the radius and φ is the azimuth, is:

$$\frac{1}{\mathrm{D}\left(\mathsf{\Phi }\right)}\frac{\partial \mathsf{\Phi }}{\partial \mathrm{t}}=\frac{1}{\mathrm{r}}\frac{\partial }{\partial \mathrm{r}}\left(\mathrm{r}\frac{\partial \mathsf{\Phi }}{\partial \mathrm{r}}\right)+\frac{1}{{\mathrm{r}}^2}\frac{{\partial }^2\mathsf{\Phi }}{\partial {\mathsf{\phi }}^2}+\frac{{\partial }^2\mathsf{\Phi }}{\partial {\mathrm{z}}^2}+\frac{\mathrm{d}\mathrm{K}}{\mathrm{d}\mathsf{\Phi }}\frac{\partial \mathsf{\Phi }}{\partial \mathrm{z}}.$$

(13)

In spherical coordinates (ρ, ϑ, φ) the Kirchhoff equation is written as follows:

$$\begin{array}{c}\frac{1}{\mathrm{D}\left(\mathsf{\Phi }\right)}\frac{\partial \mathsf{\Phi }}{\partial \mathrm{t}}=\frac{1}{{\mathsf{\rho }}^2}\frac{\partial }{\partial \mathsf{\rho }}\left({\mathsf{\rho }}^2\frac{\partial \mathsf{\Phi }}{\partial \mathsf{\rho }}\right)+\frac{1}{{\mathsf{\rho }}^2\sin \mathsf{\vartheta }}\frac{\partial }{\partial \mathsf{\vartheta }}\left(\sin \mathsf{\vartheta }\frac{\partial \mathsf{\Phi }}{\partial \mathsf{\vartheta }}\right)\\ +\frac{1}{{\mathsf{\rho }}^2{\sin }^2\mathsf{\vartheta }}\frac{{\partial }^2\mathsf{\Phi }}{\partial {\mathsf{\phi }}^2}+\frac{\mathrm{d}\mathrm{K}}{\mathrm{d}\mathsf{\Phi }}\frac{\partial \mathsf{\Phi }}{\partial \mathrm{z}}\end{array}.$$

(14)

These formulations are only applicable in homogeneous media, and, if these are isotropic, they are written respectively in cylindrical coordinates as follows:

$$\frac{1}{\mathrm{D}\left(\mathsf{\Phi }\right)}\frac{\partial \mathsf{\Phi }}{\partial \mathrm{t}}=\frac{1}{\mathrm{r}}\frac{\partial }{\partial \mathrm{r}}\left(\mathrm{r}\frac{\partial \mathsf{\Phi }}{\partial \mathrm{r}}\right)+\frac{{\partial }^2\mathsf{\Phi }}{\partial {\mathrm{z}}^2}+\frac{\mathrm{d}\mathrm{K}}{\mathrm{d}\mathsf{\Phi }}\frac{\partial \mathsf{\Phi }}{\partial \mathrm{z}},$$

(15)

and in spherical coordinates:

$$\frac{1}{\mathrm{D}\left(\mathsf{\Phi }\right)}\frac{\partial \mathsf{\Phi }}{\partial \mathrm{t}}=\frac{1}{{\mathsf{\rho }}^2}\frac{\partial }{\partial \mathsf{\rho }}\left({\mathsf{\rho }}^2\frac{\partial \mathsf{\Phi }}{\partial \mathsf{\rho }}\right)+\frac{\mathrm{d}\mathrm{K}}{\mathrm{d}\mathsf{\Phi }}\frac{\partial \mathsf{\Phi }}{\partial \mathrm{z}}.$$

(16)

2.2. The Hydrodynamic Characteristics of Porous Media

In order to solve the mass or energy transfer equations of water in porous media, aside from specifying the limit conditions, it is necessary to know the hydrodynamic characteristics formed by the water retention curve θ (ψ) and the hydraulic conductivity curve either as a function of the water pressure, K(ψ), or as a function of the moisture content K(θ). The analysis is greatly simplified if these curves are represented with analytical functions.

The retention curve can be represented with the equation of van Genuchten [18]:

$$\Theta \left(\mathsf{\psi }\right)={\left[1+{\left(\frac{\mathsf{\psi }}{{\mathsf{\psi }}_{\mathrm{d}}}\right)}^{\mathrm{n}}\right]}^{-\mathrm{m}},$$

(17)

where m > 0 and n > 0 are two shape parameters (dimensionless), ψ_d is a characteristic value of the water pressure and Θ is the effective degree of saturation defined by:

$$\Theta =\frac{\mathsf{\theta }-{\mathsf{\theta }}_{\mathrm{r}}}{{\mathsf{\theta }}_{\mathrm{s}}-{\mathsf{\theta }}_{\mathrm{r}}},$$

(18)

in which θ_r is the residual moisture content defined such that K(θ_r) = 0 and θ(ψ$\to$-$\infty$) = θ_r [19]; θ_s is the moisture content at saturation, assimilated to the total porosity of the soil (ϕ), when under saturation conditions no air is trapped in the interstices of the porous medium: θ_s = ϕ. In general, θ_r = 0 can be assumed [20].

A closed way to represent the conductivity curve can be obtained using prediction models of the same from the retention curve. In the literature we can find various works, but given the condition of the phenomenon we are studying, this work uses one of the fractal models proposed, calibrated and validated by Fuentes et al. [20]. The results found by [20] shows a better adjustment between observed and estimated data by the function given by:

$$\mathrm{K}(\Theta )={\mathrm{K}}_{\mathrm{s}}{\left[{\displaystyle \underset{0}{\overset{\Theta }{\int }}\frac{{\mathsf{\vartheta }}^{\mathrm{s}-1}\mathrm{d}\mathsf{\vartheta }}{{\left|\mathsf{\psi }\left(\mathsf{\vartheta }\right)\right|}^{2\mathrm{s}}}}/{\displaystyle \underset{0}{\overset{1}{\int }}\frac{{\mathsf{\vartheta }}^{\mathrm{s}-1}\mathrm{d}\mathsf{\vartheta }}{{\left|\mathsf{\psi }\left(\mathsf{\vartheta }\right)\right|}^{2\mathrm{s}}}}\right]}^2,$$

(19)

where K_s is the hydraulic saturation conductivity and s = D/E, with D the fractal dimension of the porous medium and E = 3 the Euclid dimension of the physical space where the medium is embedded, related to the total porosity through the relation:

$${\left(1-\mathsf{\varphi }\right)}^{\mathrm{s}}+{\mathsf{\varphi }}^{2\mathrm{s}}=1.$$

(20)

The introduction of Equation (17) in Equation (19) leads to the following equation to represent the hydraulic conductivity curve, accepting the relationship between the parameters as indicated:

$$\mathrm{K}(\Theta )={\mathrm{K}}_{\mathrm{s}}{\left[1-{\left(1-{\Theta }^{1/\mathrm{m}}\right)}^{\mathrm{s}\mathrm{m}}\right]}^2; 0<\mathrm{s}\mathrm{m}=1-2\mathrm{s}/\mathrm{n}<1.$$

(21)

The solution of the transfer equation in its different forms is generally numerical [21,22]. However, in some simplified cases, characteristics of the solution can be obtained analytically [23,24,25].

3. Results and Discussion

3.1. Conceptual Model

To analyze the infiltration in steady-state wells, it is necessary to write the Darcy flows in the radial and vertical directions:

$${\overrightarrow{\mathrm{q}}}_{\mathrm{r}}=-{\mathrm{K}}_{\mathrm{s}}\frac{\partial \mathsf{\psi }}{\partial \mathrm{r}}\widehat{\mathrm{r}},$$

(22)

$${\overrightarrow{\mathrm{q}}}_{\mathrm{z}}=-\left({\mathrm{K}}_{\mathrm{s}}\frac{\partial \mathsf{\psi }}{\partial \mathrm{z}}+{\mathrm{K}}_{\mathrm{s}}\right)\widehat{\mathrm{k}},$$

(23)

where $\widehat{\mathrm{r}}$ and $\widehat{\mathrm{k}}$ are unitary vectors in the r and z directions respectively.

Flow through the wall and bottom of the well is defined by:

$${\mathrm{Q}}_{\mathrm{s}}={\displaystyle \underset{{\mathrm{A}}_{\mathrm{p}}}{\int }{\overrightarrow{\mathrm{q}}}_{\mathrm{r}}\cdot \mathrm{d}{\mathrm{A}}_{\mathrm{p}}}+{\displaystyle \underset{{\mathrm{A}}_{\mathrm{b}}}{\int }{\overrightarrow{\mathrm{q}}}_{\mathrm{z}}\cdot \mathrm{d}{\mathrm{A}}_{\mathrm{b}}},$$

(24)

where dA_p y dA_b are, respectively, the differential areas in the wall and at the bottom of the well defined by:

$$\mathrm{d}{\mathrm{A}}_{\mathrm{p}}=\left(2\mathsf{\pi }\mathrm{R}\mathrm{d}\mathrm{z}\right)\widehat{\mathrm{r}},$$

(25)

$$\mathrm{d}{\mathrm{A}}_{\mathrm{b}}=\left(2\mathsf{\pi }\mathrm{r}\mathrm{D}\mathrm{r}\right)\left(-\widehat{\mathrm{k}}\right).$$

(26)

Equation (24), considering Equations (22), (23), (25) and (26), is written as follows:

$${\mathrm{Q}}_{\mathrm{s}}=-2\mathsf{\pi }\mathrm{R}{\mathrm{K}}_{\mathrm{s}}{\displaystyle \underset{0}{\overset{\mathrm{H}}{\int }}{\frac{\partial \mathsf{\psi }}{\partial \mathrm{r}}|}_{\mathrm{r}=\mathrm{r}}\mathrm{d}\mathrm{z}}+2\mathsf{\pi }{\mathrm{K}}_{\mathrm{s}}{\displaystyle \underset{0}{\overset{\mathrm{R}}{\int }}{\frac{\partial \mathsf{\psi }}{\partial \mathrm{z}}|}_{\mathrm{z}=0}\mathrm{r}\mathrm{d}\mathrm{r}}+\mathsf{\pi }{\mathrm{K}}_{\mathrm{s}}{\mathrm{R}}^2.$$

(27)

Introducing the dimensionless variables:

$${\mathrm{z}}^{\ast }=\frac{\mathrm{z}}{\mathrm{H}}; {\mathrm{r}}^{\ast }=\frac{\mathrm{r}}{\mathrm{R}} ; {\mathsf{\psi }}^{\ast }=\frac{\mathsf{\psi }}{\mathrm{H}};$$

(28)

Equation (27) is written as follows:

$${\mathrm{Q}}_{\mathrm{s}}={\mathrm{Q}}_{\mathrm{o}}+\mathsf{\pi }{\mathrm{K}}_{\mathrm{s}}{\mathrm{R}}^2; {\mathrm{Q}}_{\mathrm{o}}=\frac{2\mathsf{\pi }{\mathrm{K}}_{\mathrm{s}}{\mathrm{H}}^2}{\mathrm{C}};$$

(29)

where C is a coefficient defined as:

$$\frac{1}{\mathrm{C}}=-{\displaystyle \underset{0}{\overset{1}{\int }}{\frac{\partial {\mathsf{\psi }}^{\ast }}{\partial {\mathrm{r}}^{\ast }}|}_{{\mathrm{r}}^{\ast }=1}\mathrm{d}{\mathrm{z}}^{\ast }+{\left(\frac{\mathrm{R}}{\mathrm{H}}\right)}^2{\displaystyle \underset{0}{\overset{1}{\int }}{\frac{\partial {\mathsf{\psi }}^{\ast }}{\partial {\mathrm{z}}^{\ast }}|}_{{\mathrm{z}}^{\ast }=0}{\mathrm{r}}^{\ast }\mathrm{d}{\mathrm{r}}^{\ast }}}.$$

(30)

To find this coefficient it is necessary to know ψ (r, z).

3.2. The Glover Model

According to Glover [26], in a first approximation, the steady-state pressure flow through an infiltration well in a homogeneous and isotropic porous medium can be described with Laplace’s equation in spherical coordinates that describes the pressure in the absence of gravitational gradients. From Equation (8) we have:

$${\nabla }^2\mathsf{\psi }=\frac{1}{{\mathsf{\rho }}^2}\frac{\partial }{\partial \mathsf{\rho }}\left({\mathsf{\rho }}^2\frac{\partial \mathsf{\psi }}{\partial \mathsf{\rho }}\right)=0,$$

(31)

which must be subject to border conditions:

$$\mathsf{\psi }={\mathsf{\psi }}_{\mathrm{R}}; \mathsf{\rho }=\mathrm{R}$$

(32)

$$\mathsf{\psi }=0; \mathsf{\rho }\to \infty .$$

(33)

Integration of Equation (31) leads to ψ = −c₁ρ⁻¹ + c₂, where c₁ and c₂ are integration constants; the Equation (33) implies c₂ = 0 and the Equation (32) c₁ = −ψ_R R, ergo ψ = ψ_R (R/ρ). The Darcy flux is q_ρ = − K_s ∂ψ/∂ρ = K_s ψ_R (R/ρ²), when ρ = R, q_R = K_s ψ_R/R; the flow through the surface of the sphere of radius R is q_o = 4πR²q_R = 4πK_sRψ_R; this flow from the point source in the center of the sphere is the variable of interest. Since ψ_RR = q_o/4πK_s, it is better to set the pressure variation around the source flow to continue with the Glover approach:

$$\mathsf{\psi }=\frac{{\mathrm{q}}_{\mathrm{o}}}{4\mathsf{\pi }{\mathrm{K}}_{\mathrm{s}}\mathsf{\rho }}.$$

(34)

If h represents the position of the center of the sphere from the base, then the spherical coordinate (ρ) and the cylindrical coordinate (r) are related by:

$$\mathsf{\rho }=\sqrt{{\mathrm{r}}^2+{\left(\mathrm{z}-\mathrm{h}\right)}^2}.$$

(35)

The pressure in terms of the cylindrical coordinates is obtained by introducing Equation (35) into Equation (34):

$$\mathsf{\psi }=\frac{{\mathrm{q}}_{\mathrm{o}}}{4\mathsf{\pi }{\mathrm{K}}_{\mathrm{s}}\sqrt{{\mathrm{r}}^2+{\left(\mathrm{z}-\mathrm{h}\right)}^2}}.$$

(36)

To provide a series of point sources whose magnitude increases with depth, an expression similar to that originally proposed by Glover, we have:

$$\mathrm{d}{\mathrm{q}}_{\mathrm{o}}=\mathrm{B}\left({\mathrm{h}}_{\mathrm{c}}-\mathrm{h}\right)\mathrm{d}\mathrm{h},$$

(37)

where B is a parameter to be determined and h_c defines the range of the sources h_o ≤ h ≤ h_c and sinks h_c < h ≤ h_s.

The total flow is found by integrating Equation (37):

$${\mathrm{Q}}_{\mathrm{o}}=\mathrm{B}{\displaystyle \underset{{\mathrm{H}}_{\mathrm{o}}}{\overset{{\mathrm{h}}_{\mathrm{s}}}{\int }}\left({\mathrm{h}}_{\mathrm{c}}-\mathrm{h}\right)\mathrm{d}\mathrm{h}}=\frac{1}{2}\mathrm{B}{\mathrm{H}}^2\left[{\left({\mathrm{h}}_{\mathrm{c}}^{\ast }-{\mathrm{h}}_{\mathrm{o}}^{\ast }\right)}^2-{\left({\mathrm{h}}_{\mathrm{c}}^{\ast }-{\mathrm{h}}_{\mathrm{s}}^{\ast }\right)}^2\right]$$

(38)

hence parameter B is deduced:

$$\mathrm{B}=\frac{2{\mathrm{Q}}_{\mathrm{o}}}{{\mathrm{H}}^2\left[{\left({\mathrm{h}}_{\mathrm{c}}^{\ast }-{\mathrm{h}}_{\mathrm{o}}^{\ast }\right)}^2-{\left({\mathrm{h}}_{\mathrm{c}}^{\ast }-{\mathrm{h}}_{\mathrm{s}}^{\ast }\right)}^2\right]}$$

(39)

where h* = h/H for all subscripts.

From Equations (36), (37) and (39) we have:

$$\mathrm{d}\mathsf{\psi }=\frac{{\mathrm{Q}}_{\mathrm{o}}\left({\mathrm{h}}_{\mathrm{c}}-\mathrm{h}\right)}{2\mathsf{\pi }{\mathrm{K}}_{\mathrm{s}}{\mathrm{H}}^2\left[{\left({\mathrm{h}}_{\mathrm{c}}^{\ast }-{\mathrm{h}}_{\mathrm{o}}^{\ast }\right)}^2-{\left({\mathrm{h}}_{\mathrm{c}}^{\ast }-{\mathrm{h}}_{\mathrm{s}}^{\ast }\right)}^2\right]\sqrt{{\mathrm{r}}^2+{\left(\mathrm{z}-\mathrm{h}\right)}^2}}\mathrm{d}\mathrm{h}$$

(40)

the integration of which leads to:

$$\mathsf{\psi }=\frac{{\mathrm{Q}}_{\mathrm{o}}}{2\mathsf{\pi }{\mathrm{K}}_{\mathrm{s}}{\mathrm{H}}^2\left[{\left({\mathrm{h}}_{\mathrm{c}}^{\ast }-{\mathrm{h}}_{\mathrm{o}}^{\ast }\right)}^2-{\left({\mathrm{h}}_{\mathrm{c}}^{\ast }-{\mathrm{h}}_{\mathrm{s}}^{\ast }\right)}^2\right]}{\left[\left({\mathrm{h}}_{\mathrm{c}}-\mathrm{z}\right)\mathrm{a}\sinh \left(\frac{\mathrm{z}-\mathrm{h}}{\mathrm{r}}\right)+\sqrt{{\mathrm{r}}^2+{\left(\mathrm{z}-\mathrm{H}\right)}^2}\right]}_{\mathrm{h}={\mathrm{h}}_{\mathrm{s}}}^{\mathrm{h}={\mathrm{h}}_{\mathrm{o}}},$$

(41)

ergo:

$$\mathsf{\psi }=\frac{{\mathrm{Q}}_{\mathrm{o}}}{2\mathsf{\pi }{\mathrm{K}}_{\mathrm{s}}{\mathrm{H}}^2}\frac{\left[\begin{array}{l}\left({\mathrm{h}}_{\mathrm{c}}-\mathrm{z}\right)\mathrm{a}\sinh \left(\frac{\mathrm{z}-{\mathrm{h}}_{\mathrm{o}}}{\mathrm{r}}\right)-\left({\mathrm{h}}_{\mathrm{c}}-\mathrm{z}\right)\mathrm{a}\sinh \left(\frac{\mathrm{z}-{\mathrm{h}}_{\mathrm{s}}}{\mathrm{r}}\right)\\ +\sqrt{{\mathrm{r}}^2+{\left(\mathrm{z}-{\mathrm{h}}_{\mathrm{o}}\right)}^2}-\sqrt{{\mathrm{r}}^2+{\left(\mathrm{z}-{\mathrm{h}}_{\mathrm{s}}\right)}^2}\end{array}\right]}{\left[{\left({\mathrm{h}}_{\mathrm{c}}^{\ast }-{\mathrm{h}}_{\mathrm{o}}^{\ast }\right)}^2-{\left({\mathrm{h}}_{\mathrm{c}}^{\ast }-{\mathrm{h}}_{\mathrm{s}}^{\ast }\right)}^2\right]}.$$

(42)

At the point on the boundary (r, z) = (R, 0) we have ψ = H, which allows obtaining the expression of the flow, Equation (29):

$${\mathrm{Q}}_{\mathrm{o}}=\frac{2\mathsf{\pi }{\mathrm{K}}_{\mathrm{s}}{\mathrm{H}}^2}{\mathrm{C}},$$

(43)

where the form coefficient is defined by:

$$\mathrm{C}=\frac{{\mathrm{h}}_{\mathrm{c}}^{\ast }\left[\mathrm{a}\sinh \left(\frac{\mathrm{H}}{\mathrm{R}}{\mathrm{h}}_{\mathrm{s}}^{\ast }\right)-\mathrm{a}\sinh \left(\frac{\mathrm{H}}{\mathrm{R}}{\mathrm{h}}_{\mathrm{o}}^{\ast }\right)\right]+\sqrt{{\left(\frac{\mathrm{R}}{\mathrm{H}}\right)}^2+{\mathrm{h}}_{\mathrm{o}}^{\ast 2}}-\sqrt{{\left(\frac{\mathrm{R}}{\mathrm{H}}\right)}^2+{\mathrm{h}}_{\mathrm{s}}^{\ast }{}^2}}{{\left({\mathrm{h}}_{\mathrm{c}}^{\ast }-{\mathrm{h}}_{\mathrm{o}}^{\ast }\right)}^2-{\left({\mathrm{h}}_{\mathrm{c}}^{\ast }-{\mathrm{h}}_{\mathrm{s}}^{\ast }\right)}^2}.$$

(44)

Glover formula is derived from Equation (44) by making ${\mathrm{h}}_{\mathrm{c}}^{\ast }$ = 1, ${\mathrm{h}}_{\mathrm{o}}^{\ast }$ = 0 y ${\mathrm{h}}_{\mathrm{s}}^{\ast }$ = 1:

$$\mathrm{C}=\mathrm{a}\sinh \left(\frac{\mathrm{H}}{\mathrm{R}}\right)+\frac{\mathrm{R}}{\mathrm{H}}-\sqrt{{\left(\frac{\mathrm{R}}{\mathrm{H}}\right)}^2+1}.$$

(45)

3.3. The Reynolds and Elrick Model

This model proposed by Reynolds and Elrick [27] assumes ${\mathrm{h}}_{\mathrm{c}}^{\ast }$ = 1/2, ${\mathrm{h}}_{\mathrm{i}}^{\ast }$ = 0 y ${\mathrm{h}}_{\mathrm{s}}^{\ast }$ = 1/2:

$$\mathrm{C}=4\left[\frac{1}{2}\mathrm{a}\sinh \left(\frac{\mathrm{H}}{2\mathrm{R}}\right)+\frac{\mathrm{R}}{\mathrm{H}}-\sqrt{{\left(\frac{\mathrm{R}}{\mathrm{H}}\right)}^2+\frac{1}{4}}\right].$$

(46)

3.4. A Model for Stratified Porous Media

Glover’s model can be adapted for the case of stratified porous media. The well is considered to be in a medium composed of N layers of thickness P_j, j = 1,2, …, N; the total hydraulic head, denoted as H_T, is the height of the water column counted from the base of the well to the upper border of the N-th stratum.

The flow infiltrated by the walls of the j-th stratum is provided by Equation (43) modified as:

$${\mathrm{Q}}_{\mathrm{o}\mathrm{j}}=\frac{2\mathsf{\pi }{\mathrm{K}}_{\mathrm{s}\mathrm{j}}{\mathrm{p}}_{\mathrm{j}}^2}{{\mathrm{C}}_{\mathrm{j}}},$$

(47)

where K_sj and C_j are the saturated hydraulic conductivity and the shape coefficient of the j-th stratum, respectively.

The shape coefficient is derived from Equation (44) denoting by H_j the hydraulic head at the base of the j-th stratum:

$${\mathrm{C}}_{\mathrm{j}}={\mathrm{h}}_{\mathrm{p}\mathrm{j}}^{\ast }\frac{{\mathrm{h}}_{\mathrm{C}\mathrm{j}}^{\ast }\left[\mathrm{a}\sinh \left(\frac{{\mathrm{p}}_{\mathrm{j}}}{\mathrm{R}}{\mathrm{h}}_{\mathrm{s}\mathrm{j}}^{\ast }\right)-\mathrm{a}\sinh \left(\frac{{\mathrm{p}}_{\mathrm{j}}}{\mathrm{R}}{\mathrm{h}}_{\mathrm{o}\mathrm{j}}^{\ast }\right)\right]+\sqrt{{\left(\frac{\mathrm{R}}{{\mathrm{P}}_{\mathrm{j}}}\right)}^2+{\mathrm{h}}_{\mathrm{o}\mathrm{j}}^{\ast 2}}-\sqrt{{\left(\frac{\mathrm{R}}{{\mathrm{P}}_{\mathrm{j}}}\right)}^2+{\mathrm{h}}_{\mathrm{s}\mathrm{j}}^{\ast }{}^2}}{{\left({\mathrm{h}}_{\mathrm{c}\mathrm{j}}^{\ast }-{\mathrm{h}}_{\mathrm{o}\mathrm{j}}^{\ast }\right)}^2-{\left({\mathrm{h}}_{\mathrm{c}\mathrm{j}}^{\ast }-{\mathrm{h}}_{\mathrm{s}\mathrm{j}}^{\ast }\right)}^2},$$

(48)

where ${\mathrm{h}}_{\mathrm{P}\mathrm{j}}^{\ast }$ = P_j/H_j, ${\mathrm{h}}_{\mathrm{c}\mathrm{j}}^{\ast }$ = h_cj/P_j, ${\mathrm{h}}_{\mathrm{o}\mathrm{j}}^{\ast }$ = h_oj/P_j, ${\mathrm{h}}_{\mathrm{s}\mathrm{j}}^{\ast }$ = h_sj/P_j. It is noted that h_cj, h_oj y h_sj are calculated from the base of the j-th stratum.

The Reynolds and Elrick model assumes ${\mathrm{h}}_{\mathrm{c}}^{\ast }$ = 1/2, ${\mathrm{h}}_{\mathrm{o}}^{\ast }$ = 0 y ${\mathrm{h}}_{\mathrm{s}}^{\ast }$ = 1/2 and therefore:

$${\mathrm{C}}_{\mathrm{j}}=4\left[\frac{1}{2}\mathrm{a}\sinh \left(\frac{{\mathrm{P}}_{\mathrm{j}}}{2\mathrm{R}}\right)+\frac{\mathrm{R}}{{\mathrm{p}}_{\mathrm{j}}}-\sqrt{{\left(\frac{\mathrm{R}}{{\mathrm{P}}_{\mathrm{j}}}\right)}^2+\frac{1}{4}}\right]{\mathrm{h}}_{\mathrm{P}\mathrm{j}}.$$

(49)

The total flow is obtained as:

$$\mathrm{Q}={\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{N}}{\mathrm{Q}}_{\mathrm{o}\mathrm{j}}}+\mathsf{\pi }{\mathrm{R}}^2{\mathrm{K}}_{\mathrm{s}1}$$

(50)

where the flow at the bottom of the well has been added.

3.5. Aplications

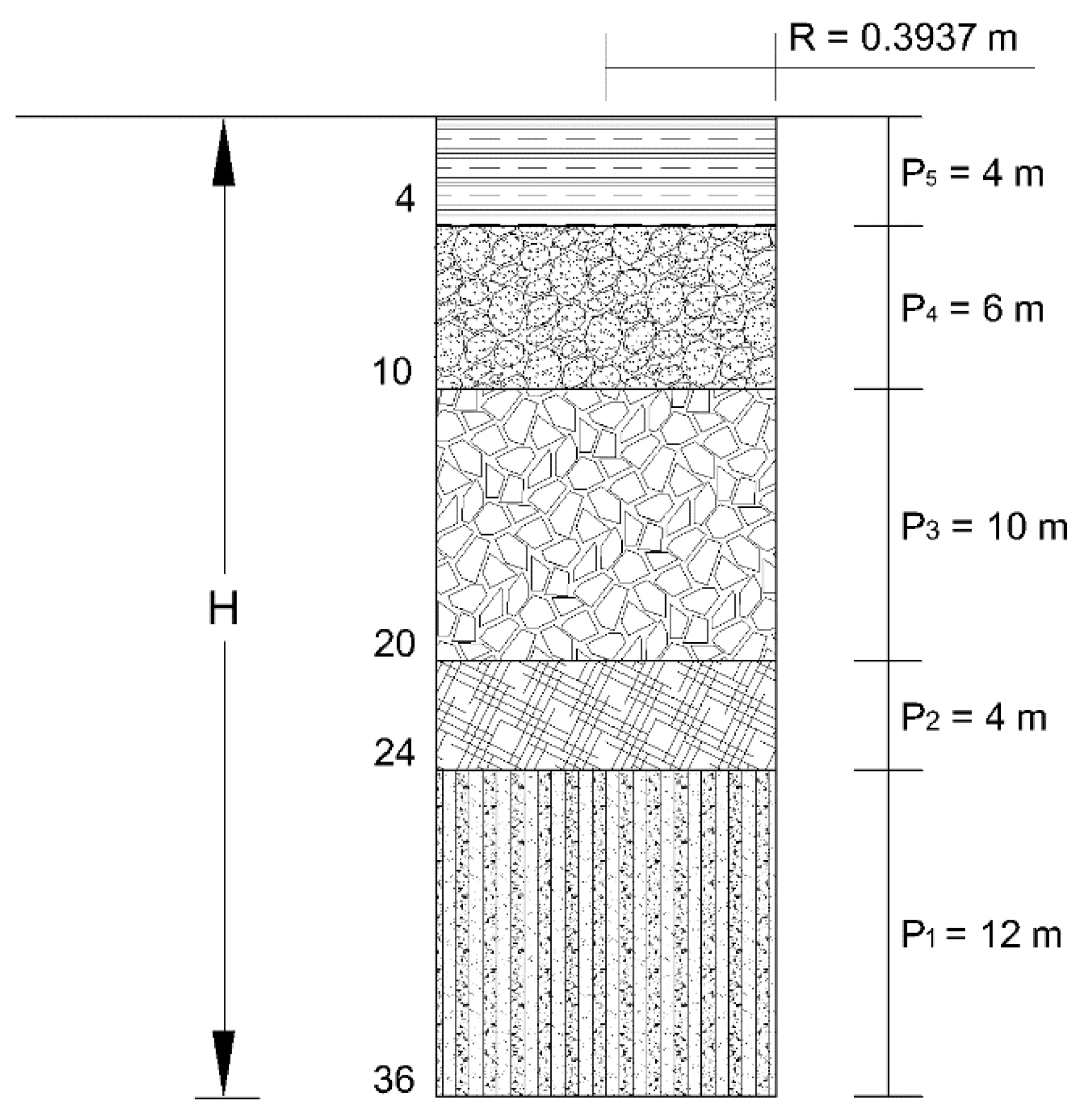
To show the versatility of the solution, data obtained from an infiltration well built on the Queretaro Valley aquifer of radio are used: R = 0.3937 m (15.5″) and depth P_T = 36 m; Five strata were located in the profile (Figure 1). As drilling was carried out, the infiltration tests per stratum were carried out until the permanent regime was reached. The measured data are concentrated in

Table 1. Calculation of hydraulic conductivity per stratum, Equation (43).

Stratum	H (m/s)	Q (L/s)	C	Ks (m/d)
1	12	0.02841	4.9632	0.0134
2	4	0.33681	3.0113	0.8592
3	10	0.81158	4.6239	0.5142
4	6	1.01448	3.7017	1.4231
5	4	1.62317	3.0113	4.1405

, and the saturated hydraulic conductivity calculated from Equation (43) is also shown.

Table 2. Calculation of the flow per stratum corresponding to a full well, Equations (47) and (49).

Stratum	P (m)	Ks (m/d)	H (m)	C	Q (L/s)
1	12	0.0134	36	1.6544	0.085
2	4	0.8592	24	0.5019	1.992
3	10	0.5142	20	2.3119	1.617
4	6	1.4231	10	2.2210	1.677
5	4	4.1405	4	3.0113	1.600
Equivalent	36	0.5231	36	7.0749	6.972

shows the flow rates calculated for each stratum when the well is full. In the last row is the total flow, Equation (50), and the saturated hydraulic conductivity corresponding to an equivalent homogeneous stratum.

The artificial volume that can be recharged to the aquifer is 6972 L/s (602.3808 m³/day), however, stratum 1 only contributes 1.22% of the entire volume and is the deepest layer of the entire well (12 m). With these data, the cost benefit is analyzed and the decision is made to drill wells to a depth of 24 m with the understanding that we would contribute only 595.0318 m³/day to the aquifer but we reduce time and money.

The time to drill the well up to 36 m is 27 days at a cost of 25,457 USD. Therefore, if you choose to build two, the time taken would be 60 days with a total of 50,915 USD. Conversely, if you only drill to a depth of 24 m, the time taken is 7 days and a cost of 13,376 USD, which gives us a total cost of 53,504 USD for four wells drilled in 30 days. This is due to the fact that the material in the last 12 m is basalt and drilling progress is slower.

Regarding the volumes of recharge to the aquifer, with the four wells in the same area it would be 2380.1272 m³/day compared to 1204.7616 m³/day that we would obtain with only two at a depth of 36 m. Finally, the cost-benefit of annual recharge in the aquifer would be 16.24 m³/USD invested in four wells, compared to the 8.64 m³/USD that you have if you choose two wells.

4. Conclusions

In recent years the construction of artificial wells to recharge aquifers has been very popular in Mexico, however, as has been demonstrated in this work, the construction of a well at a greater depth does not necessarily give us a greater volume of recharge. The lack of information to calculate the total volumes has led to decisions being made with unscientific bases and, on several occasions, it has resulted in not achieving the expectations for which they were built.

This work provides a tool for knowing the behavior of the water infiltration rate in the porous medium in stratified media to artificially recharge an aquifer through wells. The analysis takes into account all the characteristics of the soil profiles that construct the well, resulting in the cost-benefit analysis of the complete operation to make a better decision.

It is widely demonstrated in the literature that several experimental tests are needed to know the behavior of this phenomenon, and that in order to know the process in detail, other factors that are not analyzed here must be taken into account: preferential flow in heterogeneous soils, trapped air, sediment deposit, among others.

When exploration drilling is done to propose a series of wells to recharge the aquifer, the data from the first layer is usually measured to simulate the behavior of the entire profile as a homogeneous stratum. However, as verified in this work, it is necessary to know the behavior of the entire well by stratum so that pertinent decisions are made, since a deeper well does not necessarily imply a greater volume of recharge to the aquifer.