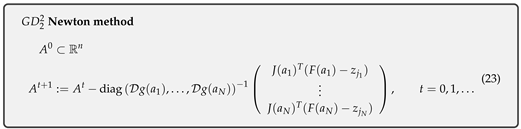1. Introduction
Multi-objective optimization problems (MOPs), i.e., problems where multiple incommensurable and conflicting objectives have to be optimized concurrently, arise in many fields such as engineering and finance (e.g., [
1,
2,
3,
4,
5]). One important characteristic is that there is typically not one single solution to be expected for such problems (as it is the case for “classical” scalar optimization problems (SOPs)), but rather an entire set of solutions. More precisely, if the MOP contains
k conflicting objectives, one can expect the solution set (the Pareto set respectively its image, the Pareto front) to form at least locally a manifold of dimension
[
6]. Many numerical methods take this fact into account and generate an entire (finite) set of candidate solutions so that the decision maker (DM) obtains an overview of the possible realizations of his/her project. For such set based multi-objective optimization algorithms a natural question that arises is the goodness of the obtained solution set
A (i.e., the relation of
A to the Pareto set/front of the underlying MOP). For this, several performance indicators have been proposed over the last decades such as the Hypervolume indicator (HV, [
7]), the Generational Distance (GD, [
8]), the Inverted Generational Distance (IGD, [
9]), R2 [
10], DOA [
11], and the averaged Hausdorff distance
[
12,
13]. Each such indicator assigns to a given set of candidate solutions an indicator value according to the given MOP. Hence, if the MOP and the size of the candidate solution set are fixed, the detection of the “best” candidate solution can be expressed by the problem
where
I denotes the chosen performance indicator (to be minimized),
the domain of the objective functions, and
N the size of the candidate solution set. Since
contains
N elements, it is also a vector in
. Problem (
1) can hence be regarded as a SOP with
decision variables.
A popular and actively researched class of set based multi-objective algorithms is given by specialized evolutionary algorithms, called multi-objective evolutionary algorithms (MOEAs, e.g., [
14,
15,
16,
17]). MOEAs evolve entire sets of candidate solutions (called populations or archives) and are hence capable of computing finite size approximations of the entire Pareto set/front in one single run of the algorithm. Further, they are of global nature, very robust, and require only minimal assumptions on the model (e.g., no differentiability on the objective or constraint functions). MOEAs have caught the interest of many reseachers and practitioners during the last decades, and have been applied to solve many real-world problems coming from science and engineering. It is also known, however, that none of the existing MOEAs converges in the mathematical sence which indicates that they are not yet tapping their full potential. In [
18], it has been shown that for any strategy where
children are chosen from
parents, there is no guarantee for convergence w.r.t. the HV indicator. Studies coming from mathematical programming (MP) indicate similar results for any performance indicator (e.g., [
19,
20]) since
strategies in evolutionary algorithms are equivalent to what is called cyclic search in MP.
In this work, we propose the set based Newton method for Problem (
1), where we will address the averaged Hausdorff distance
as indicator. Since
is defined via
and
, we will also consider the respective set based
and
Newton methods. To this end, we will first derive the (set based) gradients and Hessians for all indicators, and based on this define and discuss the resulting set based Newton methods for unconstrained MOPs. Numerical results on some benchmark test problems indicate that the method indeed yields local quadratic convergence on the entire set of candidate solutions in certain cases. The Newton methods are tested on aspiration set problems (i.e., the problem to minimize the distance of a set of solutions toward a given utopian reference set
Z and the given unconstrained MOP). Further, we will show how the
Newton method can be used in a bootstrap manner to compute finite size approximations of the entire Pareto front of a given problem in certain cases. The method can hence in principle be used as standalone algorithm for the treatment of unconstrained MOPs. On the other hand, the results also show that the Newton methods—as all Newton variants—are of local nature and require good initial solutions. In order to obtain a fast and reliable solver a hybridization with a global strategy—e.g., with MOEAs since the proposed Newton methods can be viewed as particular “
” strategies—seems to be most promising which is, however, beyond the scope of this work.
The remainder of this work is organized as follows: In
Section 2, we will briefly present the required background needed for the understanding of this work. In
Section 3,
Section 4 and
Section 5, we will present and discuss the set based
,
and
Newton methods, respectively. Finally, we will draw our conclusions and will give possible paths for future work in
Section 6.
2. Background and Related Work
Continuous unconstrained multi-objective optimization problems are expressed as
where
,
denotes the map that is composed of the individual objectives
,
, which are to be minimized simultaneously.
If objectives are considered, the resulting problem is termed a bi-objective optimization problem (BOP).
For the definition of optimality in multi-objective optimization, the notion of dominance is widely used: for two vectors
we say that
a is
less thanb (in short:
), if
for all
. The definition of
is analog. Let
, then we say that
x dominates
y (
) w.r.t (
2) if
and
. Else, we say that
y is non-dominated by
x. Now we are in the position to define optimality of a MOP. A point
is called Pareto optimal (or simply optimal) w.r.t. (
2) if there exists no
that dominates
. We denote by
P the set of all optimal solutions, also called Pareto set. Its image
is called the Pareto front. Under mild conditions on the MOP one can expect that both sets form at least locally objects of dimension
[
6].
The averaged Hausdorff distance
for discrete or discretized sets is defined as follows: let
and
, where
, be finite sets. The values
and
are defined as
where
p is an integer and where the distance of a point
to a set
B is defined by
. The averaged Hausdorff distance
is simply the maximum of these two values,
We refer to [
21] for an extension of the indicators to continuous sets. We stress that all of these three indicators are entirely distance based and are in particularly not Pareto compliant. A variant of IGD that is weakly Pareto compliant is the indicator DOA. Here, we are particularly interested in multi-objective reference set problems. That is, given a finite reference set
, we are interested in solving the problem
where I is one of the indicators
,
, or
, and
N is the size of the approximation.
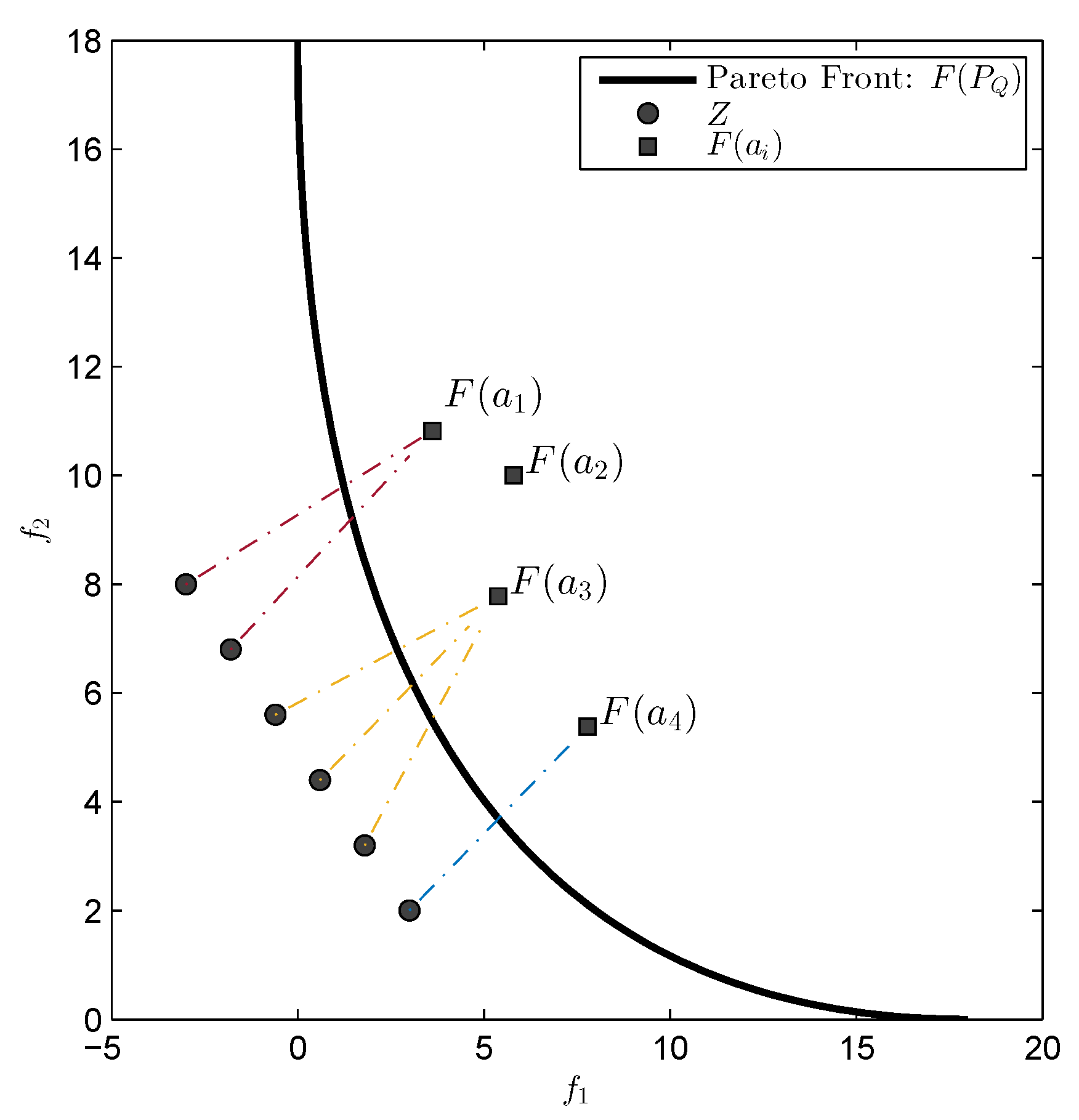
Probably the most important reference set in our context is the Pareto front itself. For this case,
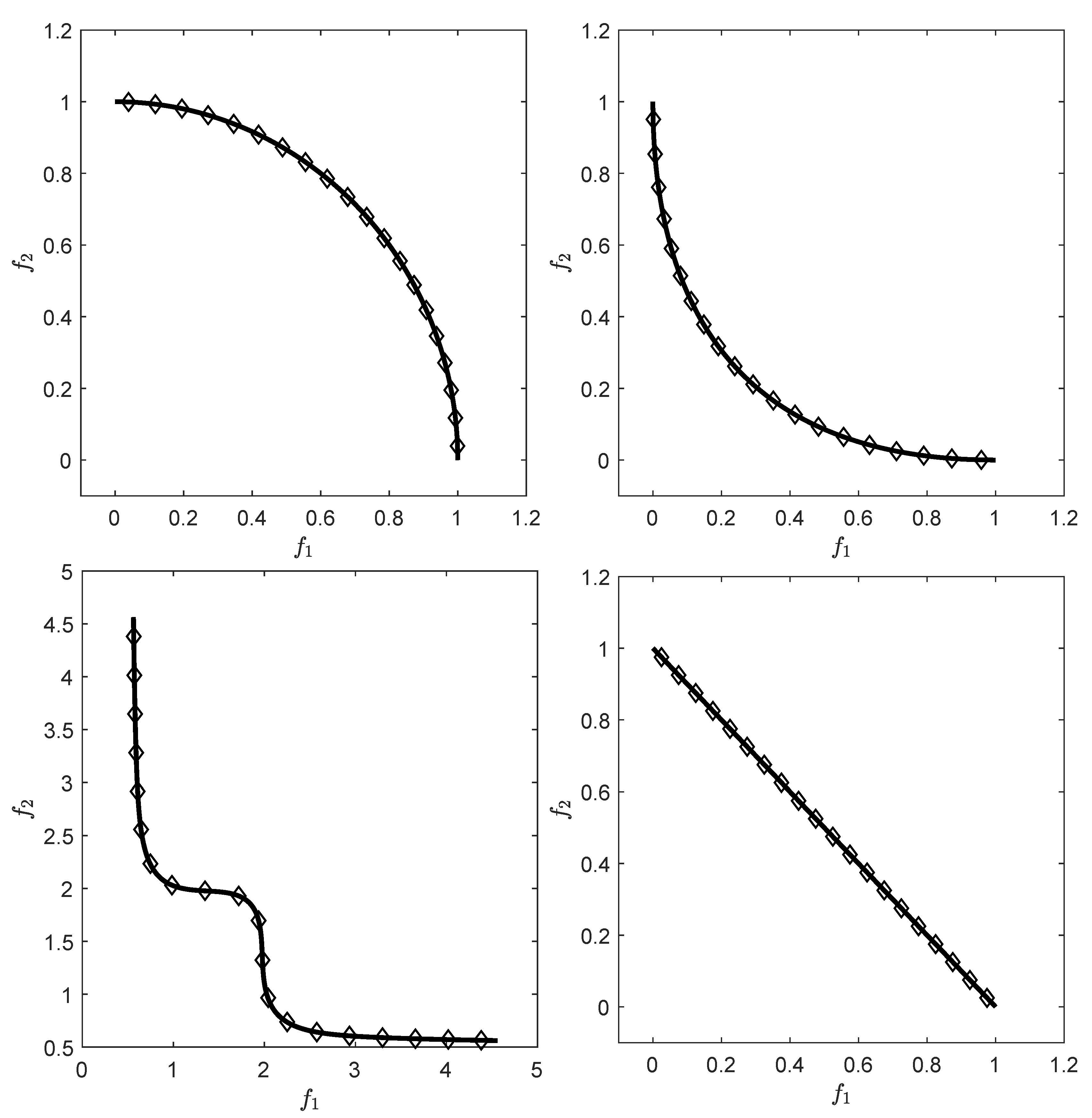
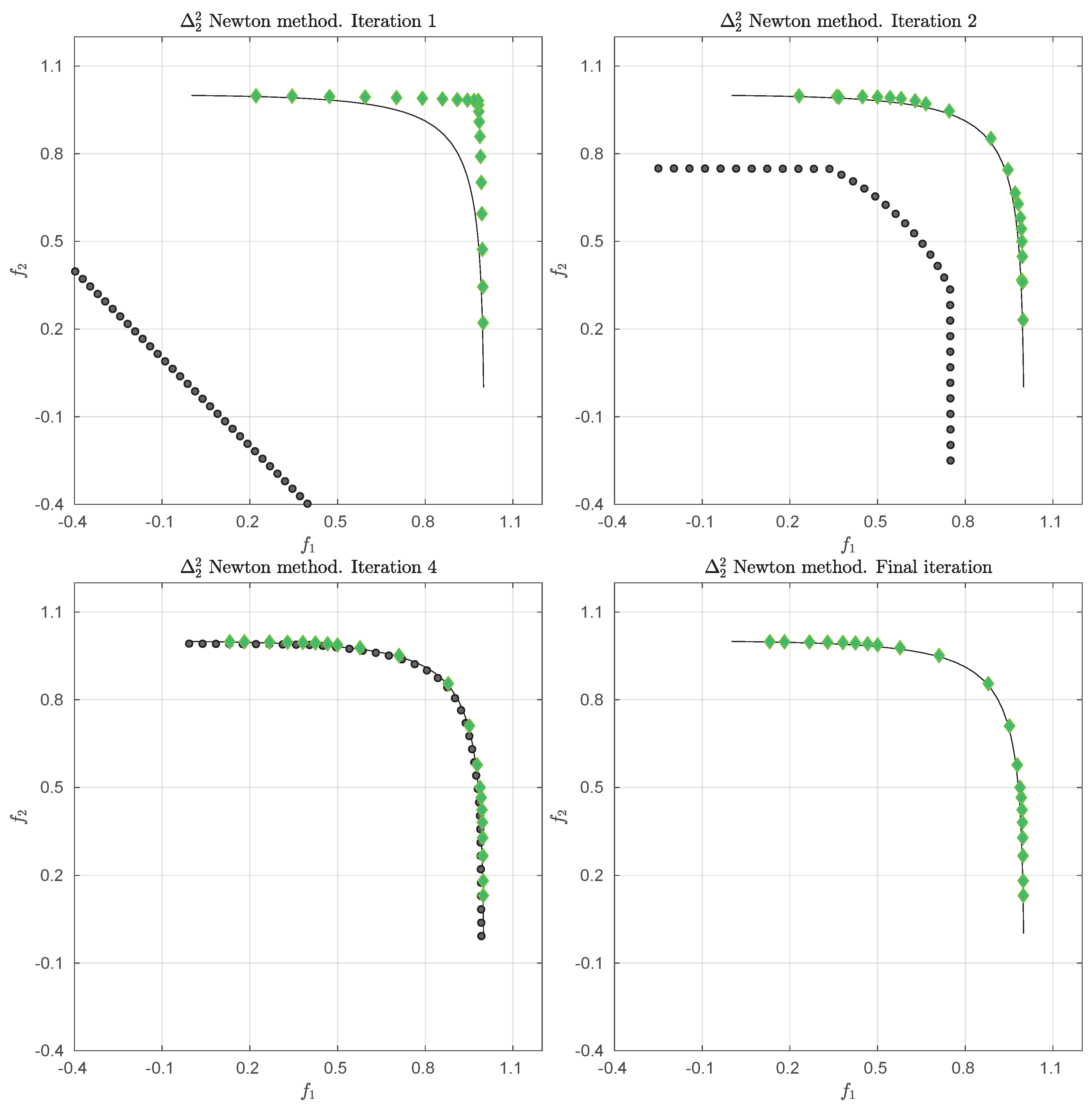
prefers, roughly speaking, evenly spread solutions along the Pareto front and is hence e.g., in accord with the terms spread and convergence as used in the evolutionary multi-objective optimization (EMO) community for a “suitable” performance indicator. As an example,
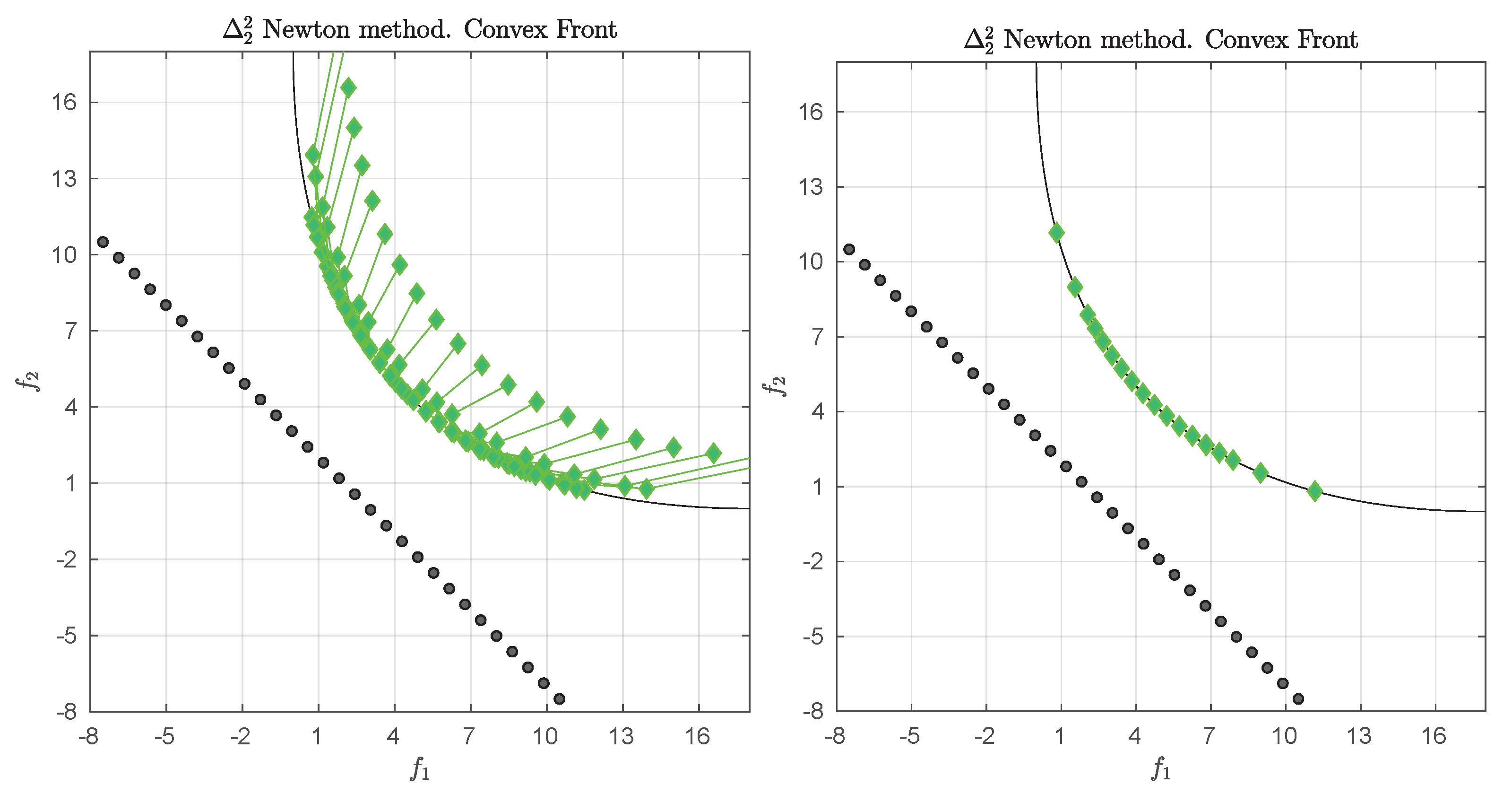
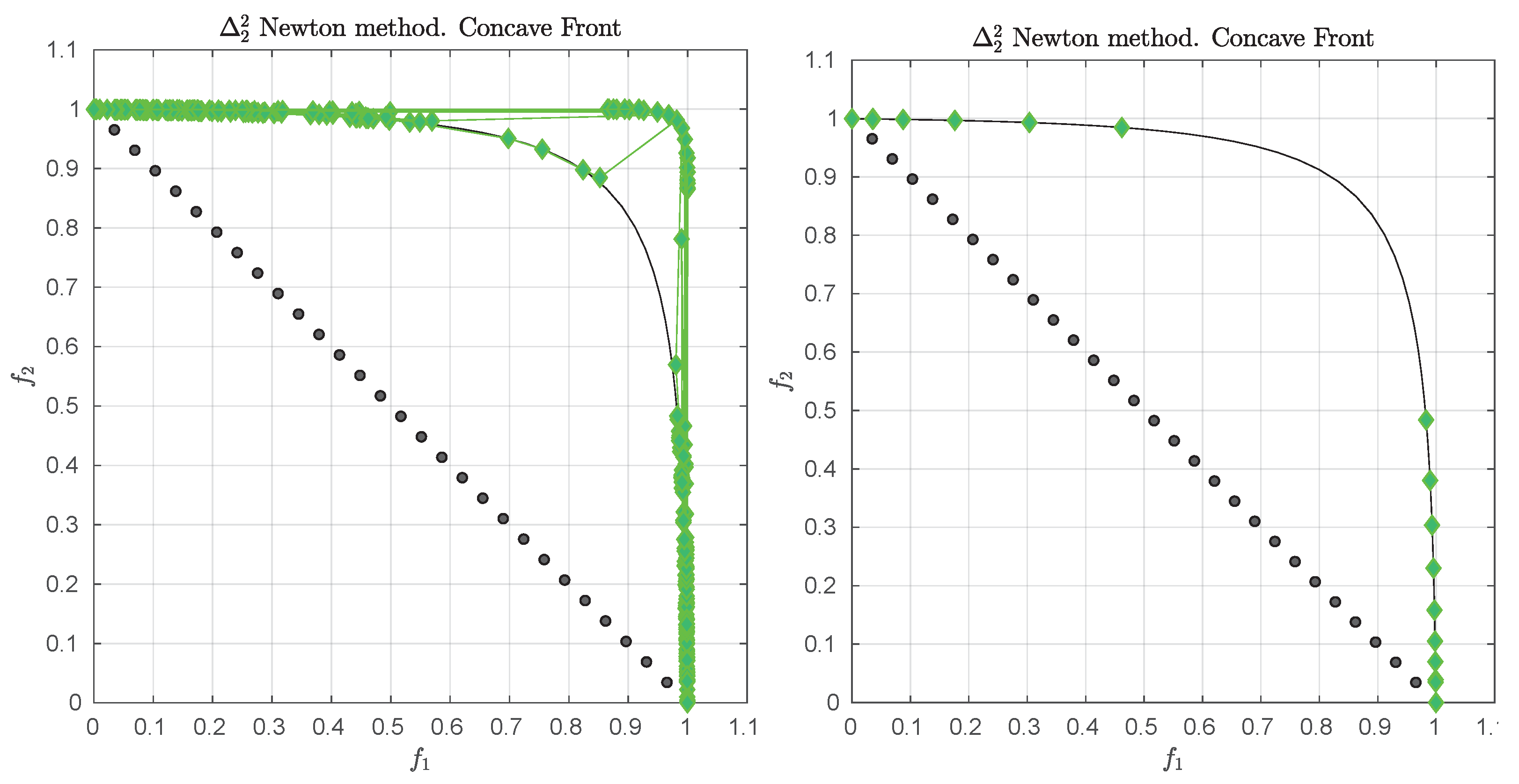
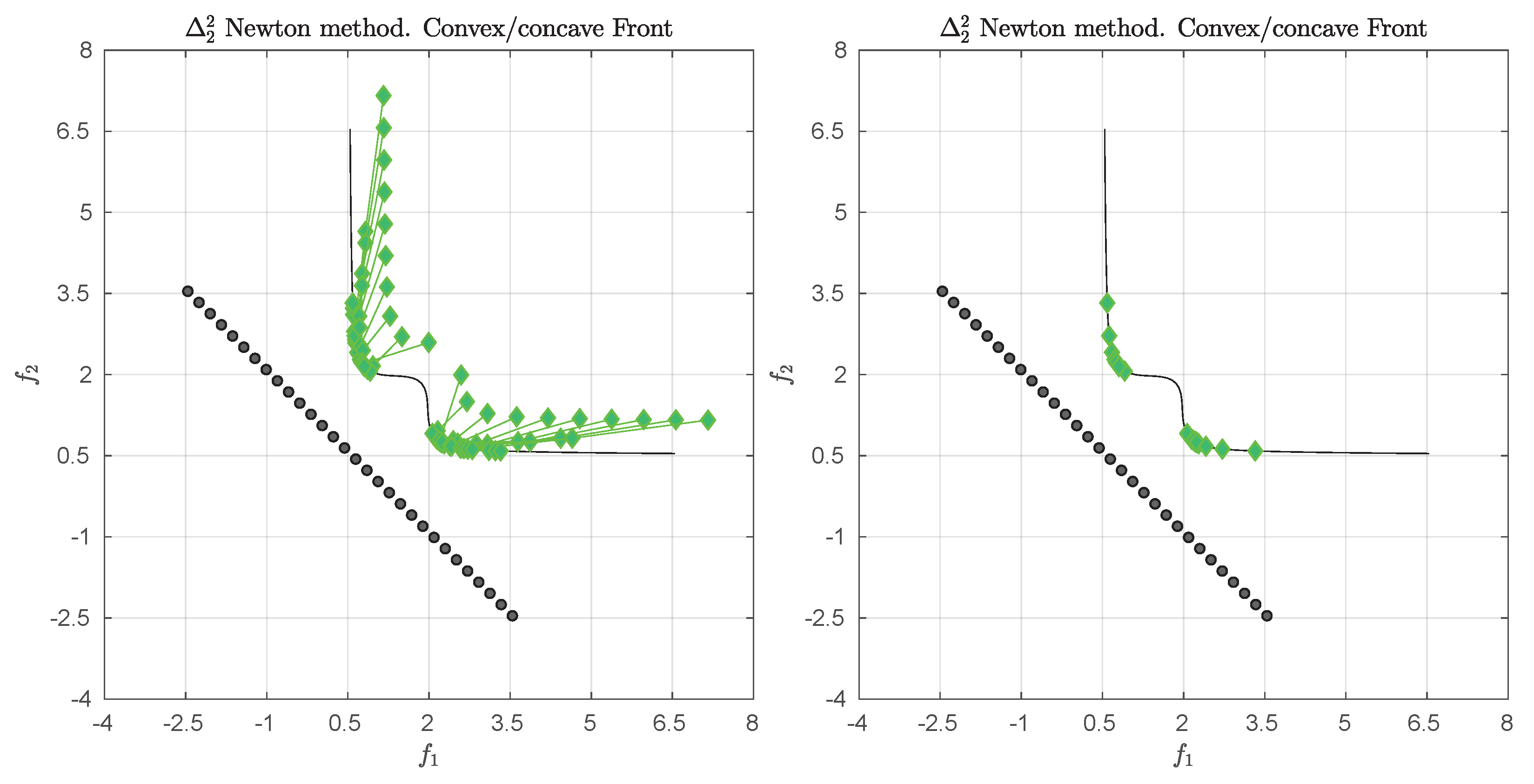
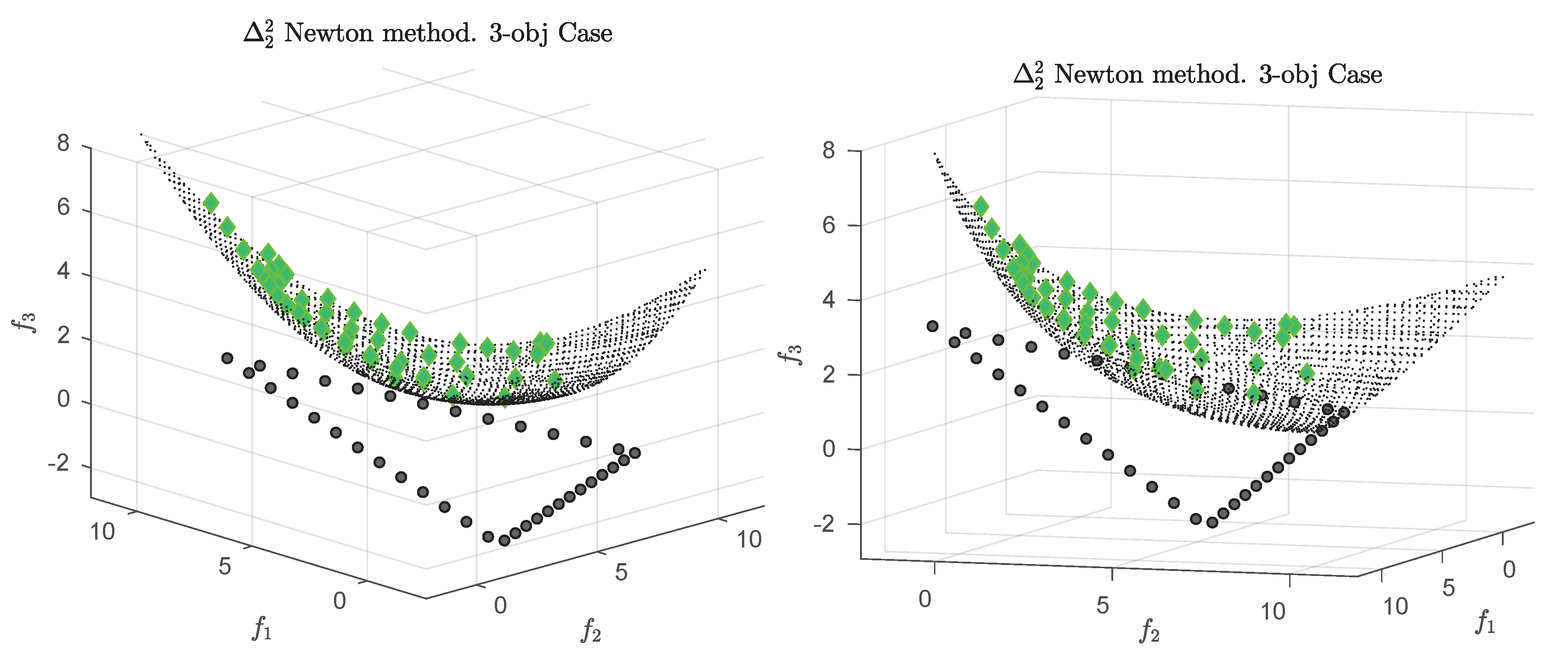
Figure 1 shows some “best approximations” in the
sense (i.e., when using
) for MOPs with different shapes of the Pareto front. More precisely, each subfigure shows a fine grain (
) approximation of the Pareto front of the underlying problem (using dots), as well as the best approximations in the
sense (using diamonds). The latter are (numerical) solutions of (
5) for
, and where
Z has been chosen as the Pareto front approximation.
If
is a subset of the
it means that each of its element
is an element of the
. Hence, the
set can in a natural way also be identified as a point or vector in the higher dimensional space
, i.e.,
. That is, the optimization problem (
5) can be identified as a “classical” scalar optimization problem that is defined in
-dimensional search space. A necessary condition for optimality is hence given by the Karush–Kuhn–Tucker conditions, e.g., for unconstrained problems we are seeking for sets
A for those the (set based) gradient vanishes. In order to solve this root finding problem, one can e.g., utilize the Newton method. If we are given a performance indicator
I together with the derivatives
and
on a set
A, the Newton function is hence given by
There exist many methods for the computation of Pareto optimal solutions. For example, there are mathematical programming (MP) techniques such as scalarization methods that transform the MOP into a sequence of scalar optimization problems (SOPs) [
22,
23,
24,
25,
26]. These methods are very efficient in finding a single solution or even a finite size discretization of the solution set. Another sub-class of the MP techniques is given by continuation-like methods that take advantage of the fact that the Pareto set forms—at least locally—a manifold. Methods of this kind start from a given initial solution and perform a search along the solution manifold [
6,
27,
28,
29,
30,
31,
32,
33].
Next there exist also set oriented methods that are capable of obtaining the entire solution set in a global manner. Examples for the latter are subdivision [
34,
35,
36] and cell mapping techniques [
37,
38,
39]. Another class of set based methods is given by multi-objective evolutionary algorithms (MOEAs) that have proven to be very effective for the treatment of MOPs [
14,
16,
40,
41,
42,
43]. Some reasons for this include that are very robust, do not require hard assumptions on the model, and allow to compute a reasonable finite size representation of the solution set already in a single run.
Methods that deal with single reference points for multi-objective problems can be found in [
26,
44,
45]. The first work that deals with a set based approach using a problem similar to the one in (
5) can be found in [
46], where the authors apply the steepest descent method on the Hypervolume indicator [
47]. In [
48], the Newton method is defined where as well the Hypervolume indicator has been used. In [
49], a multi-objective Newton method is proposed that detects single Pareto optimal solutions for a given MOP. In [
50], a set based Newton method is proposed for general root finding problems and for convex sets.
3. GDp Newton Method
In the following sections we will investigate the set based Newton methods for , , and . More precisely, we will consider the p-th powers, , of these indicators as this does not change the optimal solutions. In all cases, we will first derive the (set based) derivatives, and then investigate the resulting Newton method. For the derivatives, we will focus on which is related to the Euclidean norm, and which hence represents the most important performance indicator of the indicator families. However, we will also state the derivatives for general integers p.
Let
be a candidate set for (
2), and
be a given reference set. The indicator
measures the averaged distance of the image of
A and
Z:
Hereby, we have used the notation
and assume
Z to be fixed for the given problem (and hence, it does not appear as input argument).
3.1. Derivatives of
3.1.1. Gradient of
In the following, we have to assume that for every point
there exists exactly one closest element in
Z. That is,
there exists an index
such that:
Otherwise, the gradient of
is not defined at
A. If condition (
9) is satisfied, then (
7) can be written as follows:
and for the special case
we obtain
The gradient of
at
A is hence given by
where
denotes the Jacobian matrix of
F at
for
. We call the vector
the
i-th sub-gradient ( The sub-gradient is defined here as part of the gradient that is associated to an element
a of
A, and is not equal to the notion of the sub-gradient known in non-smooth optimization. ) of
with respect to
. Note that the sub-gradients are completely independent of the location of the other archive elements
.
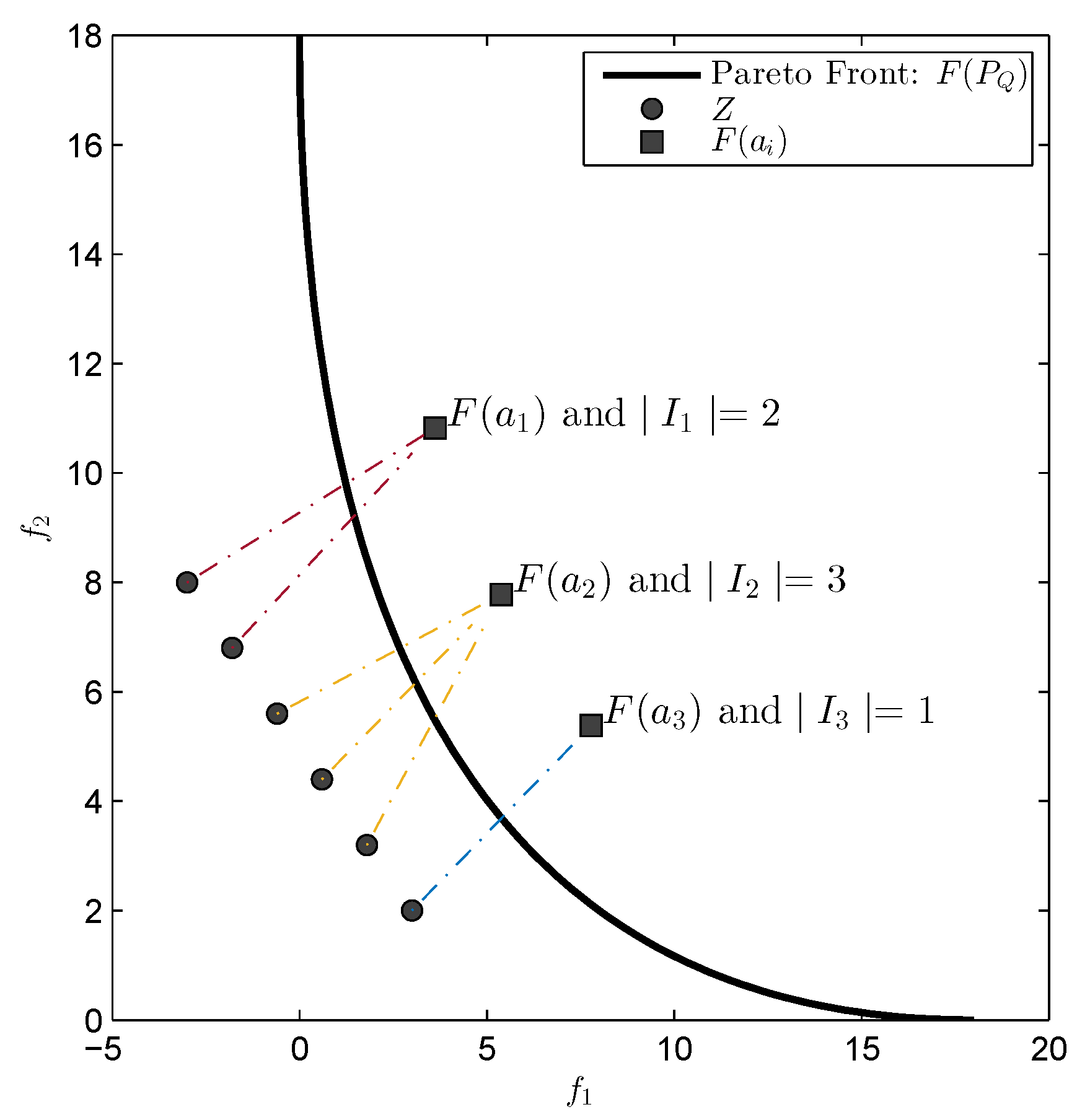
If the given MOP is unconstrained, then the first order necessary condition for optimality is that the gradient of
vanishes. This is the case for a set
A if all sub-gradients vanish
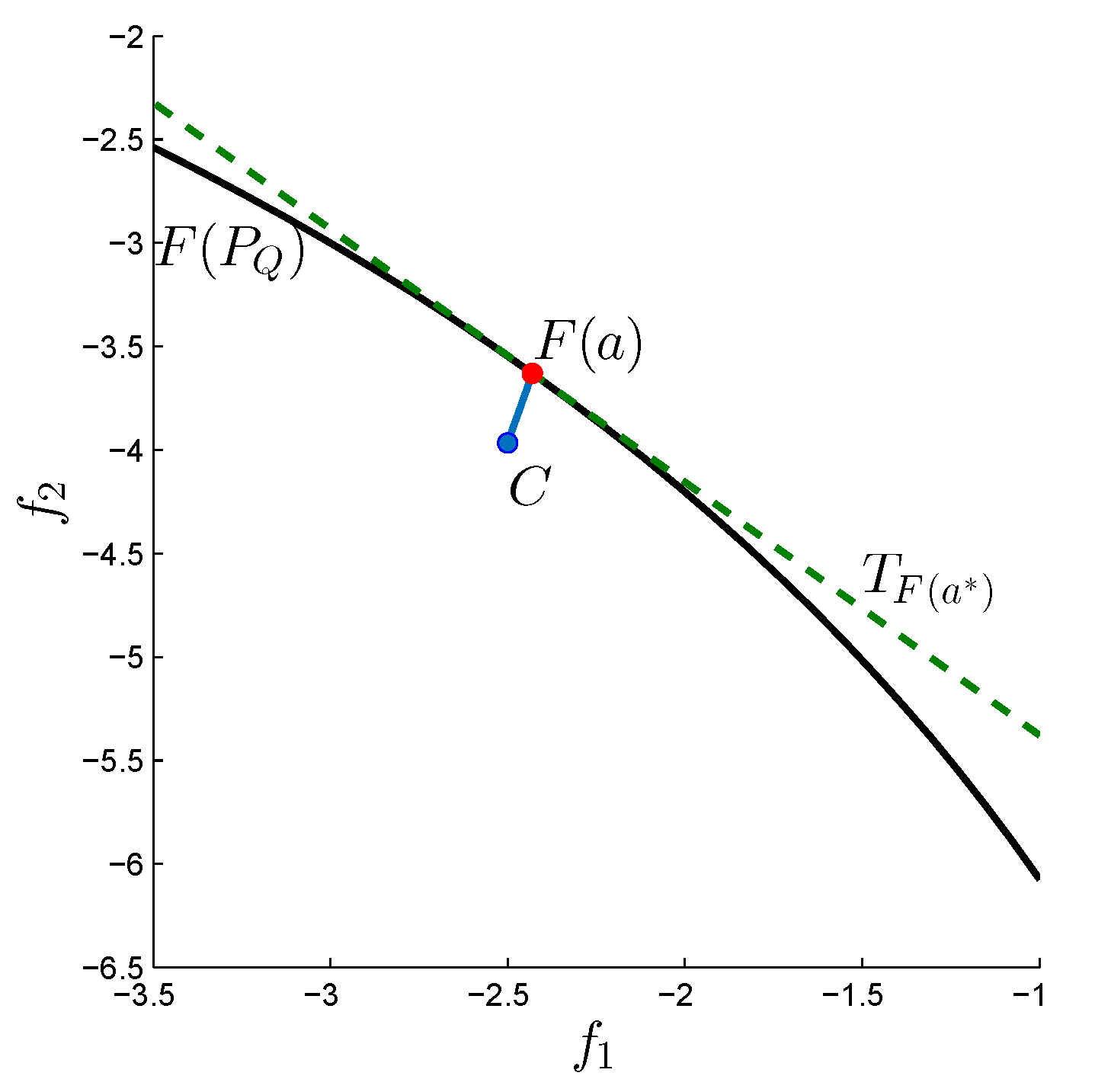
This happens if for each either
- (i)
that is, if the image of is equal to one of the elements of the reference set. This is for instance never the case if Z is chosen utopian.
- (ii)
If
, we have
for a vector
. The point
is hence a critical point since
. Furthermore, if
(e.g., if
Z is again utopian) then
is even a Karush–Kuhn–Tucker point. See
Figure 2 for a geometrical interpretation of this scenario.
3.1.2. Hessian of
We first define the map
as
where
is as in (
15). In order to find an expression of the Hessian matrix, we now derive Equation (
16) as follows:
where
Thus, the Hessian matrix of
is
which is a block diagonal matrix.
3.2. Gradient and Hessian for General
As mentioned above, we focus here on the special case
. The above derivatives, however, can be generalized for
as follows (assuming that
Z is an utopian finite set to avoid problems when
): the gradient is given by
and the Hessian by
where
for
3.3. -Newton Method
After having derived the gradient and the Hessian we are now in the position to state the set based Newton method for the indicator:
The Newton iteration can in practice be stopped at a set
if
for a given tolerance
. In order to speed up the computations one may proceed due to the structure of the (sub-)gradient as follows: for each element
of a current archive
A with
one can continue the Newton iteration with the smaller set
(and later insert
into the final archive).
We are particularly interested in the regularity of
at the optimal set, i.e., at a set
that solves problem (
5) for
. This is the case since if the Hessian is regular at
—and if the objective function is sufficiently smooth—we can expect the Newton method to converge locally quadratically [
51].
Since the Hessian is a block diagonal matrix it is regular if all of its blocks
are regular. From this we see already that if
Z is not utopian, we cannot expect quadratic convergence: assume that one point
is feasible, i.e., that there exists one
such that
. We can assume that
x is also a member of the optimal set
, say
. Then, we have that the weight vector
is zero, and hence that
. Thus, the block matrix reduces to
those rank is at most
k. The block matrix is hence singular, and so is the Hessian of
at
.
In the case all individual objectives are strictly convex, the Hessian is positive definite (and hence regular) at every feasible set A, and we can hence expect local quadratic convergence.
Proposition 1. Let a MOP of the form (2) be given whose individual objectives are strictly convex, and let Z be a discrete utopian set. Then, the matrix is positive definite for all feasible sets A. Proof. Since
is block diagonal, it is sufficient to consider the block matrices
Let
. Since
Z is utopian, it is
, and all of its elements are non-negative. Further, since all individual objectives
are strictly convex, the matrices
are positive definite, and hence also the matrix
. Since
is positive semi-definite, we have for all
since
and
. Therefore, each
,
, is positive definite and hence also the matrix
. □
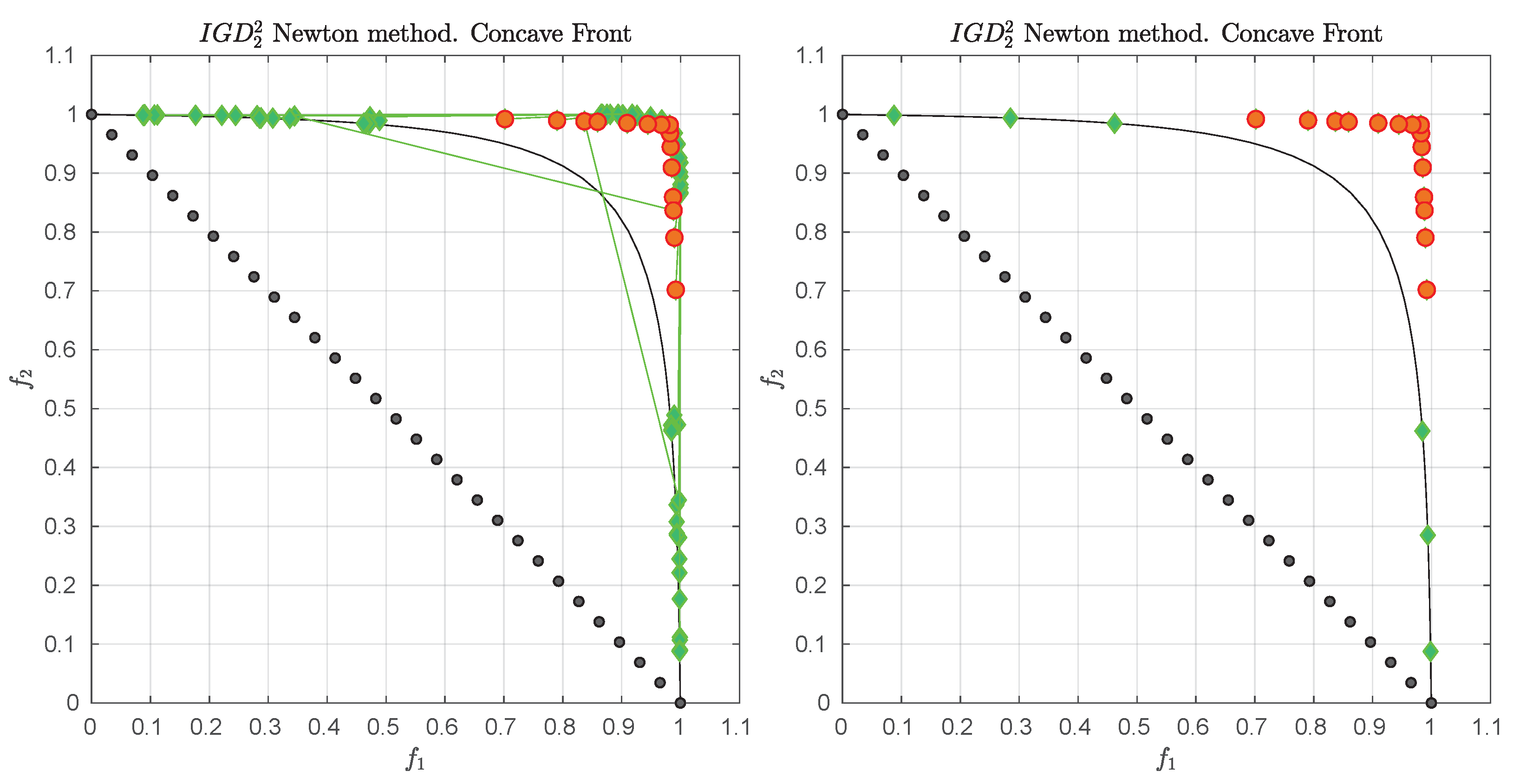
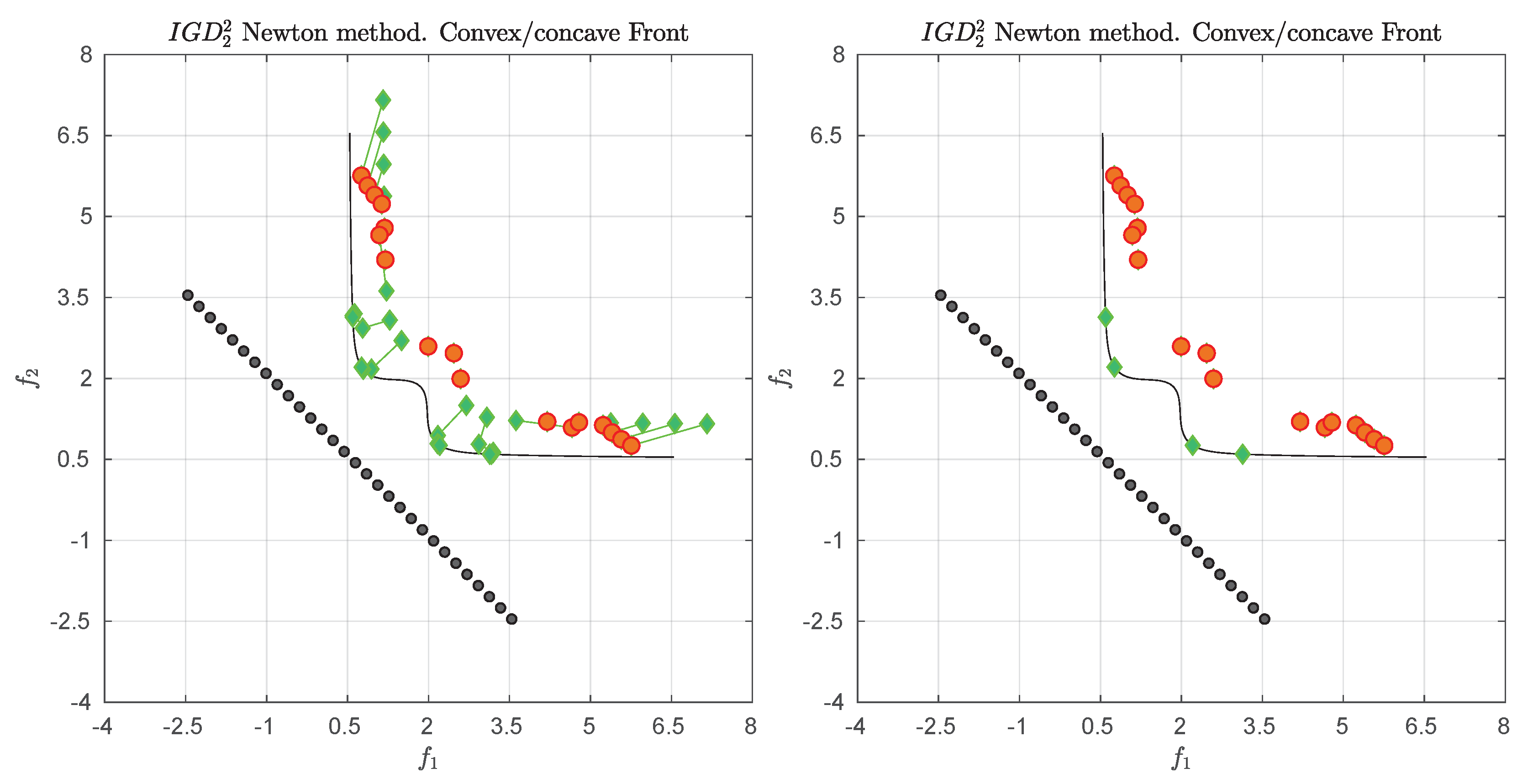
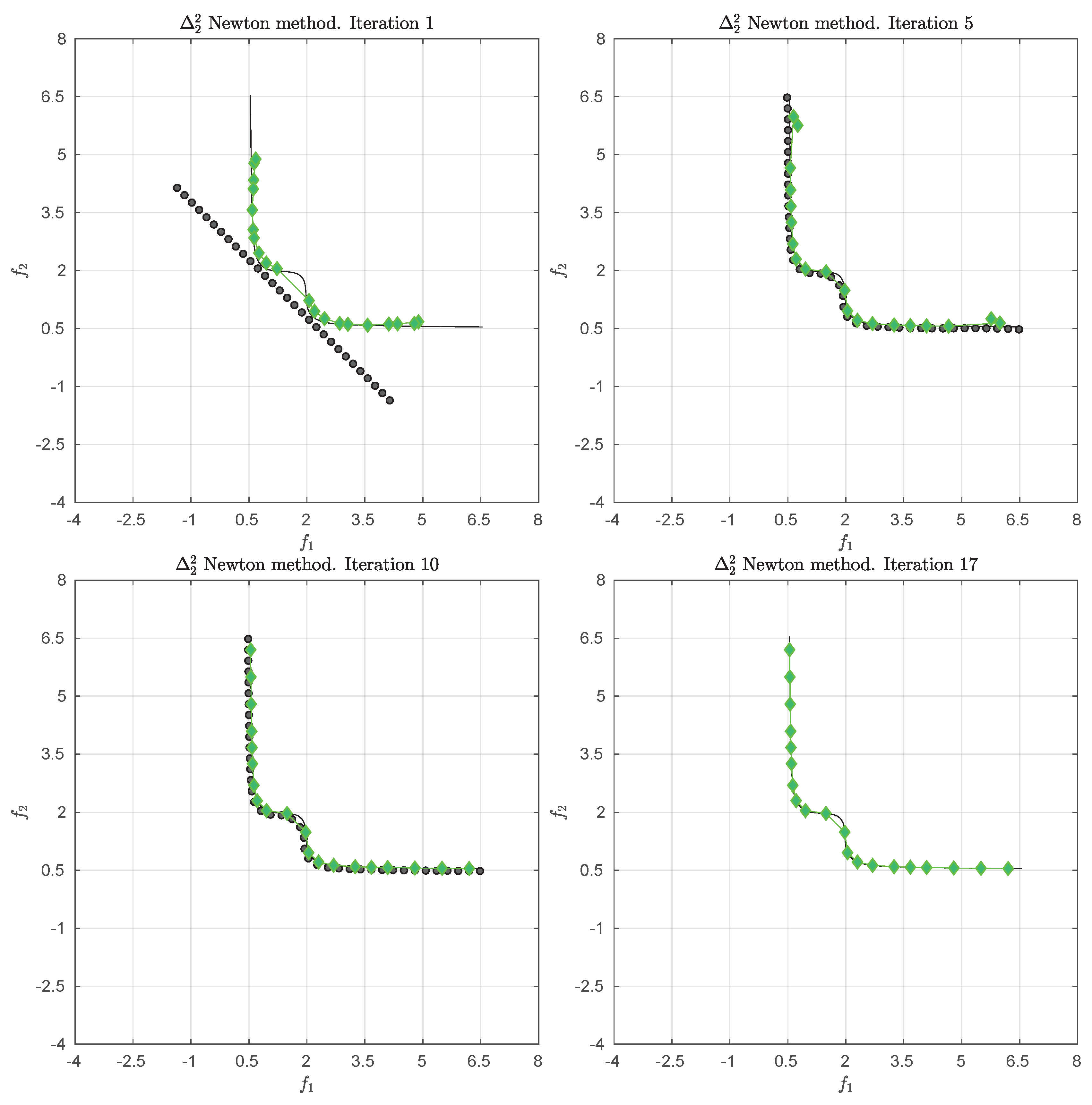
3.4. Example
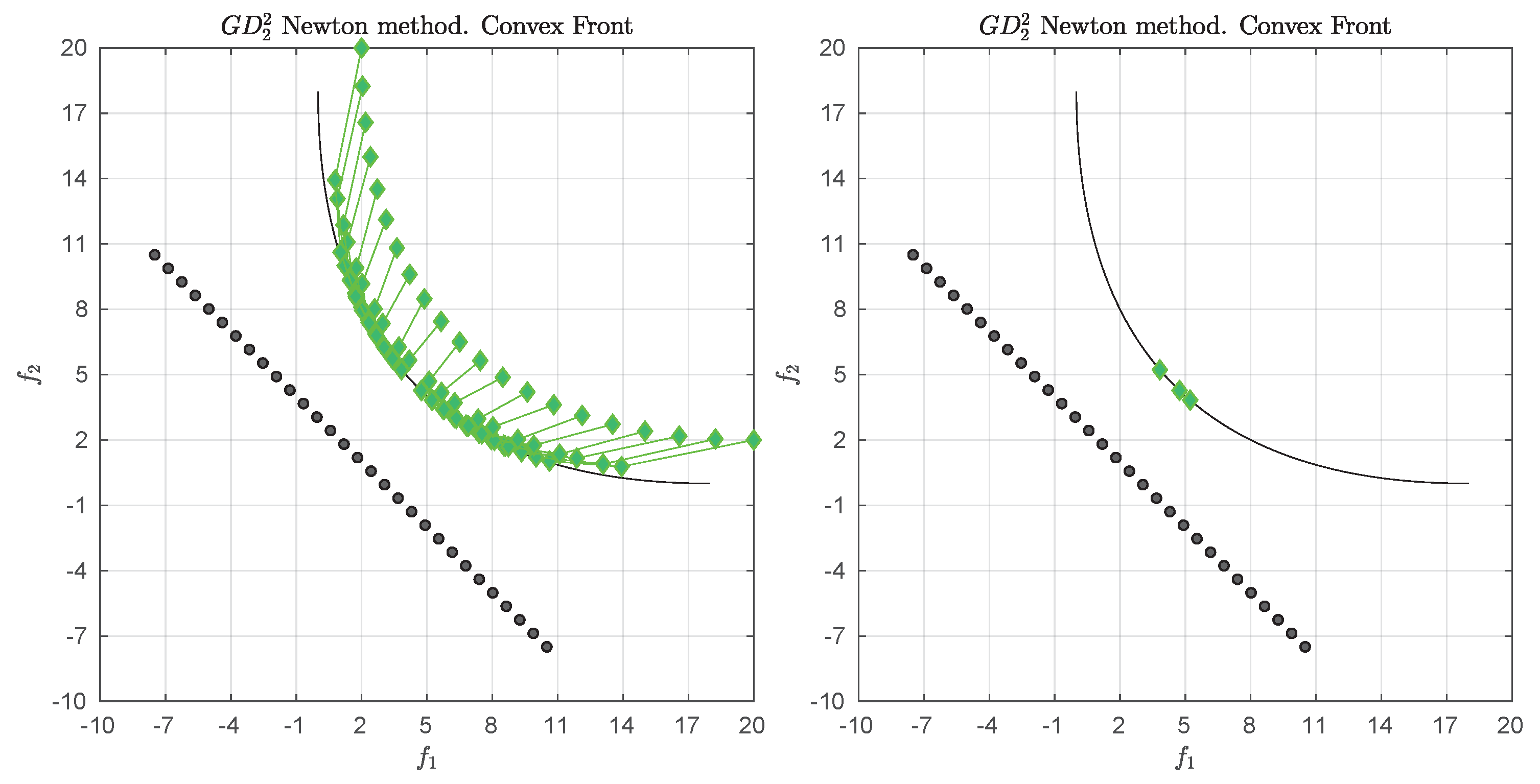
We consider the following convex bi-objective problem
Figure 3 shows the Pareto front of this problem together with the reference set
Z that contains 30 elements (black dots). The set
Z is a discretization of the convex hull of individual minima (CHIM, [
23]) of the problem that has been shifted left down. Further, it shows the images of the Newton steps of an initial set
that contains 21 elements. As it can be seen, all images converge toward three solutions that are placed in the middle of the Pareto front (which is owed to the fact that
Z is discrete. If
Z would be continuous, all images would converge toward one solution). This example already shows that the
Newton method is of restricted interest as standalone algorithm. The method will, however, become important as part of the
-Newton method as it will become apparent later on.
Table 1 shows the respective
values plus the norms of the gradients which indicate quadratic convergence. The second column indicates that the images of the archives converge toward the Pareto front as anticipated.