1. Introduction
Blockchain was developed in 2009 by grouping, all at once, some well-known technologies. Its core idea was to create a new electronic cash system [
1] able to replace the existing payment methods. For several years, the project remained in the shadow and some minor improvements have been done. Later, the fintech industry began to realise the potentiality of this technology. Starting from the original Nakamoto’s paper, many experts designed their own project. In this survey, we discuss three consensus mechanisms which constitute the basis of some of the most interesting projects without focusing on a specific project. Our goal is not to provide a detailed overview of every blockchain on the market, such as Bitcoin or Ethereum, but we would rather focus on the consensus mechanism because, in our humble opinion, this is worthy to create a critical thinking of the blockchain technology. Furthermore, to avoid focusing on a specific project (e.g., Tezos) will allow us to provide a framework that could be useful to compare blockchain technologies, regardless of other projects that may arise in the future. We focused on Proof-of-Work because it was the first idea of consensus in the blockchain framework and it is still widely adopted; the Proof-of-Stake that was the first to implement a selection of participants based on their stakes; and the Pure Proof-of-Stake that claims to solve the Trilemma problem. To the best of our knowledge, these are amongst the most interesting consensus protocols, despite the fact that there are many other consensus that we do not discuss here, such as proof of authority, proof of space, proof of burn, proof of elapsed time, etc.
Only in the first half of 2017, there were counted more than 20,000 blockchain projects which sprang out on the GitHub platform [
2]. According to the China Academy of Information and Communications Technology (CAICT), only eight percent of these projects are still alive and they last, on average, 15 months [
3].
Nowadays, the blockchain industry competes in a heterogeneous environment in which many solutions try to solve the so-called Trilemma problem, establishing them as the leading blockchain technology. The Trilemma problem was firstly introduced by Vitalik Buterin (the founder of the Ethereum blockchain) and it stands for security, decentralization, and scalability. Buterin claims that with the actual blockchains proposal, the Trilemma is hard to achieve and the existing blockchains do not guarantee these three properties at the same time [
4].
With the aim to provide a solution to the Trilemma problem, researches have been conducted. The project called Algorand, provided by the MIT professor Silvio Micali, is noteworthy. Micali has proposed a new interesting approach that claims to solve the Trilemma problem by reaching the consensus with good performances [
5]. The consensus problem is fundamental for any distributed system to prevent malicious users to get control of the network. The consensus used by the first blockchain implementation was called Proof-of-Work and it is still widely adopted by the industry. Three years later, a totally different approach called Proof-of-Stake took place, becoming the main alternative to the Proof-of-Work consensus model. Today, people may study the blockchain for two aims: for cryptocurrencies applications or as a technology able to integrate web-based applications adding decentralization as a feature already implemented by blockchains—for example, applications to support the rental market. In both cases, the blockchains have to perform well, reaching a high throughput and scaling to hundreds of thousands of users. Unfortunately, today there is not a blockchain design officially recognized by all as the best solution for the industry sector but there are many variants and flavors. Some proposals may perform well in private networks, while other ones should be employed in a different context (for example in public networks). Hence, everything depends from our specific needs.
This survey has been written with the aim to provide a framework to compare three of the most interesting public consensus procedures: the Proof-of-Work, the Proof-of-Stake, and the Pure Proof-of-Stake. The paper is organized as follows. In
Section 2, we present some cryptographic preliminaries, needed to understand Blockchain technology. In
Section 3, we introduce the blockchain technology’s future vision.
Section 4 goes deeper in the technology architecture and gives a taxonomy-based analysis, while in
Section 5, we propose a high-level review of the above consensus models. Finally, the reader will get an analysis using the CAP theorem in
Section 6 and a performance comparison in
Section 7.
2. Cryptographic Preliminaries
As the number of devices deployed over the Internet has grown, the need for securely connecting these devices to the network has become a colossal factor. Encryption is needed to guarantee data privacy in communication channels and it is the process of converting information into a pseudorandom code to prevent unauthorized access, so that only the intended receiver can decrypt, and so read, the message. Thus, encryption algorithms avoid data leaks [
6]. To securely communicate, the sender and the receiver need to privately share the key. Long ago, keys were shared through a piece of paper or by other means, but anyway in person, and this posed overtime significant logistic problems. It was just in 1977 that a secure key-exchange scheme, based on the discrete logarithm problem, was presented in modern cryptography by Diffie and Hellman. The problem with the discrete logarithm, though, is that in order to become secure, keys must be quite large. In a real scenario, keys must be implemented in devices where we cannot rely on much computing power to generate keys of sufficient size. Here is where elliptic curves come to show their strengths.
Hashing and asymmetric key encryption techniques are predominantly used for securing the blockchain and for efficient validation and verification. These techniques depend on several complex proven algorithms. A high-level view of the application of these algorithms, and the critical role they play in securing the decentralized chain, consists in public-key cryptography, secure hashing, transaction integrity, and block integrity. Indeed, they are fundamental to manage the integrity of the transactions and the blocks in a blockchain.
Note that symmetric key encryption has some issues. As an example, the key distribution: how to distribute the key to the participants?
These issues are further exacerbated in a blockchain decentralized network where participants are unknown to each other.
Instead of a single secret key, proper of symmetric cryptography, the blockchain uses public key cryptography, which employs two different keys that take care of the mentioned issue of symmetric key encryption. The most popular implementation of public key cryptography is the Rivest–Shamir–Adleman (RSA) algorithm. A common application of RSA is the password-less user authentication—for example, for accessing a virtual machine on Amazon cloud. Though RSA is very commonly used in many applications, blockchains need a more efficient and secure algorithm. Efficiency is a critical requirement since public key cryptography is frequently used in many different operations in blockchain protocol. The elliptic curve cryptography family of algorithms is used in the Bitcoin blockchain as well as in the Ethereum blockchain for generating the key pair. The reason why elliptic curve cryptography is preferred to RSA is that it is computationally harder to break than RSA for a given number of bits: a 256 bit ECC key pair is equal in strength to about 3072 bits of a RSA key pair. Bitcoin, Ethereum, and most blockchains use ECC-based algorithms for their encryption needs.
In what follows, we will recap the main cyptographic primitives used in the blockchain and deepen on the issues highlighted above.
2.1. Elliptic Curves
In the mid-1980s, Miller and Koblitz introduced elliptic curves into cryptography [
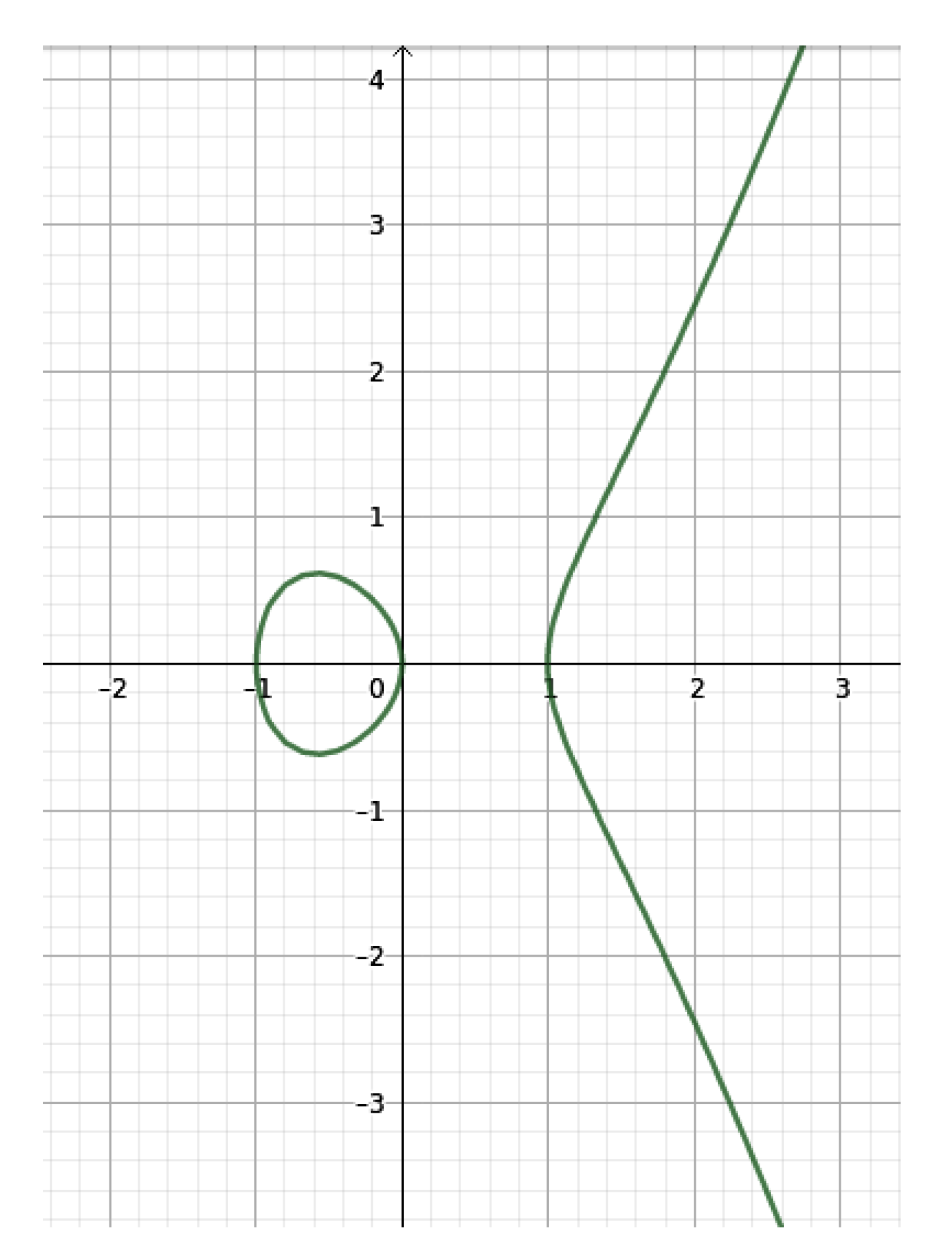
7]. One of the advantages of elliptic curve cryptography is that elliptic curves do not require big keys. For example, a 313-bit key with an elliptic curve system is just hard to break as it is to break a 4096-bit Diffie–Hellman key. We can define an elliptic curve E as a nonsingular algebraic projective curve with genus one, described by the so-called Weierstrass equation, with coefficients on a given ground field (see
Figure 1).
Elliptic curves are abelian curves. This means that it is possible to define a group law on their points, namely an operation (addition of points) which makes the points form an abelian group. The idea is that, thanks to Bézout’s Theorem, given the elliptic curve and a line through two of its points (or tangent to the curve in a point), there is exactly a third intersection between the curve and the line. The symmetric of this third intersection with respect to the x axis gives the sum of the given points (or the sum of the given point with itself). Of course, scalar multiplication means summing a point (or its opposite if the scalar coefficient is negative) with itself as many times as given by the absolute value of the given scalar. This operation generates the difficult problem providing security to elliptic curve cryptography, namely the elliptic curve discrete logarithm problem (ECDLP). The elliptic curve discrete logarithm problem states that, given a base point G (a generator for a subgroup of the group of points on a fixed curve) and another element of the subgroup generated by G, , it is infeasible to recover the value k. Let us explain how this is applied in a real case scenario. If Bob and Alice want to communicate, they need to establish a key to exchange information. They first agree on an elliptic curve over a field and on a base point G, giving the needed subgroup. Bob then starts the key exchange by generating a random value n that is essentially his private key and then computes a point B as . Alice picks randomly her private key m and computes A as . Then, they both share their computed values A and B and Bob calculates P as , while Alice computes P as . Notice that they come to the same result without sharing any secret key n or m. Thanks to the discrete logarithm, nobody can reverse engineering the procedure and roll back to figure out the common key. The process has some downsides though. For example, the algorithm fails if there is not sufficient randomness or if the actors use a bad random number generator. Despite all, today, several applications benefit from the elliptic curve’s properties to ensure safety.
2.2. Symmetric and Asymmetric Cryptography
In literature, there are many encryption algorithms designed and developed to securely share information and protect users against threats. We can classify these algorithms in two categories [
8] namely: (1) symmetric and (2) asymmetric algorithms. The main difference between these encryption schemes is in their keys. We give in what follows a very quick overview on these two categories of cryptographic algorithms. It is important to highlight their differences and to point out that blockchains are essentially based on asymmetric cryptography.
Symmetric Cryptography
A symmetric algorithm is also the simplest kind of encryption that involves only one secret key. Such key is used both for encryption and decryption and it must be shared between sender and receiver before transmitting any message. When the message is encoded using the key, it is possible to obtain the plaintext only using the same secret key. Thus, the message is safe as long as the private key is secretly and securely stored. These algorithms can cipher the message one bit at a time as in stream ciphers (e.g., KASUMI) or one block at a time such as in block ciphers [
9], such as AES, RC6, and BlowFish [
8]. To eliminate the chance of encrypting identical blocks in the same way, block ciphers make use of an initialization vector (IV), which is needed also in some modes of operation.
Asymmetric Cryptography
By contrast, asymmetric schemes can overcome the problem of sharing the secret key [
10]. An asymmetric scheme is a relatively new kind of encryption that relies on a key pair: (1) a private key that is privately stored; and a (2) public key that is well-known by all. While one key is used to encrypt the message, the other key is needed to roll back to the original plaintext. In a nutshell, if we encrypt the message using a private key, the only way to obtain the plaintext is by using the corresponding public key, and vice-versa if we encrypt the plaintext using the public key, we shall use the secret key to bring the message back to the original value. The problem, though, is that the entire procedure is computationally intensive [
9]. With the spread of public-key models, further relevant cryptographic primitives gained more attention: the hash functions and the digital signature. In the remaining part of this section, we want to discuss these two models.
2.3. Hash Functions
Broadly speaking, hash functions are used to map a string of arbitrary data into a fixed-size set of bits [
11]. Basically, no matter how long the original message is, the output will always be a string of a fixed length. The output provided by hash functions—called digest—is extremely useful for a variety of purposes. For example, to save disk space by storing only a fraction of the original message or to speed up information retrieval using a short code to access data within a constant time. Hash functions are also commonly used for message authentication and message integrity [
12] to detect errors by means of appending the digest at the end of the message and using the values as parity bits [
11]. To the best of our knowledge, cryptographic hash functions are used to implement digital signatures as described in the next section. According to Sobti and Geetha [
12], this general definition of hash functions is provided:
Definition 1. A hash function is a function , that maps a string of arbitrary length from a domain to a string of a fixed length message digest.
We can group the hash functions in two classes: (1) keyed hashing functions and (2) un-keyed hashing functions. The former use a secret key along with the message to produce the digest. The latter do not use any secret key.
One-way hash functions form a well-known class of un-keyed hash functions. In cryptography, they find place in numerous applications where one-wayness is needed. For example, they can be used to detect unwarranted modifications of a file by simply calculating the checksum that may be attached to the message. A canonical example comes if we wish to design a users’ authentication system storing the passwords in a publicly available file. The file is readable by everyone, but it contains only a set of digests from which it is infeasible to get the original passwords.
A contribution to understand the one-way hash functions has been given by Jueneman et al. in 1983 [
13], and we report the following definition (see [
14]):
A hash function H can be applied to any block of arbitrary size.
An output y is of a fixed length.
Given an input x, it is easy to compute .
Given an output y, it is computationally infeasible to find an x such that .
This last property is also known as preimage resistance [
13,
14] and determines the one-wayness of a function by stating that it computationally infeasible to find an input which hashes to a fixed specific output. There is one more property that states as follows:
This fifth property is called second preimage resistance or weak collision resistance. This is a weakness indicator of a cipher. A stronger version, called strong collision resistance, requires that it is computationally infeasible to find two inputs , having the same digest. It is a well-known fact that strong collision implies weak collision.
2.4. Digital Signatures
One of the main tools to record data onto a blockchain is the digital signature. Just like the handwritten signature, digital signatures are used to bind an identity to digital data. We might think of it as an electronic verification of the sender that mainly serves three purposes:
Authentication. Digital signature are used to authenticate the source of the message demonstrating that the message was sent by the claimed sender.
Non-repudiation. The sender cannot deny at a later time that he/she indeed signed that information.
Integrity. The message was not altered during transmission.
Digital signatures are commonly used in cases where it is important to detect forgery and tampering and, of course, it is extremely popular with email users.
To explain how digital signatures are created, we consider a simplified version of a signature scheme. Of course it depends on the single protocol, but our aim here is to explain the role of the public and the private key. Let us suppose that our typical sender Bob wants to send a digitally signed document to Alice. Bob creates two keys, public and private key, according to the chosen encryption scheme. We know from the previous section that the private key should remain private, while Bob will provide his public key to the receiver Alice. Besides these keys, Bob needs to define a hashing algorithm and the document to be certified. The document runs through the hashing algorithm to create the digest. The digest is then encrypted with Bob’s private key which finally allows to output the digital signature of the document. Hence, the digital signature is a combination of the content of the document it certifies and the author’s private key. Any variation to the content of the document will create a different signature. Bob packs up both the digital signature and the document in plaintext and sends it to Alice.
Alice can decrypt the digital signature with Bob’s public key to also get the document and its digest. Alice will run the document through the same hashing algorithm that Bob previously used which would output a digest. Finally, Alice compares the two digests, one based on the digital signature and the other one, based on the content of the document. If the document is untampered and the signature is authentic, the digests should be the same. If both digests match, then, the digital signature is verified. Otherwise, the signature is not valid and this clearly indicates that some unwanted practice involved the message.
Of course, the entire procedure is not safe against information disclosure because the document is sent in plaintext. If we want to protect the document’s contents, a further layer of encryption needs to be added.
3. What Is the Blockchain
The blockchain is a decentralized technology that allows users to exchange transactions (e.g., digital assets). Technically, it is a distributed ledger replicated over a network of peers where each peer locally stocks a copy of the ledger. Data on that ledger can be readable and writable by everyone, but it is stored in such a way that modifying the committed transactions’ history is hard from a computational point of view. Therefore, the blockchain is created in such a way that past data cannot be altered nor removed. As its name suggests, “blockchain” stands for chain of blocks because every block that contains a subset of the entire records’ list, is linked to the next one forming a chain.
People might handle the same blockchain for several purposes. For example, a blockchain comes handy in the financial sector to insure the shipping industry [
15]. It is also useful in electronic cash payments to substitute banknotes or credit cards [
16] or for tracking the supply chain [
17].
When we think about a blockchain, we should imagine this technology as a result of assembling different existing technologies. Comparing to the Web, it is an application needing the Internet to work, and it must be remarked that there are applications exploiting both the Web and the blockchain potentialities [
18]. Regarding the blockchain, we should remark an important difference compared to the Web. While the Web is essentially centralized, in the sense that we rely on a central authority to manage the data, the blockchain is intrinsically decentralized. This means that the data is broadcast to all peers, which manage it on their own.
For software architects, it requires shifting from a client-server model to a more decentralized paradigm in which every participant to the network (usually called node) is both a client and a server. This is probably one of the best features that we profit from a blockchain. Keeping this in mind, we may rethink the opportunities that the blockchain gives us for creating new ways to rewrite business applications [
18].
The reader must be aware that the blockchain applied to the business process is still an experiment [
15] and as it was for the Web, a large part of its success will depend on from the ability and commitment of the stakeholders to create a list of critical issues and solve them one after another.
A noteworthy aspect of the blockchain is its trust. The greatest inventions of the past have been driven by the need to fill a gap, and in the case of blockchain, it is actually a gap of trust. The importance of trust is associated with the need of two parties to trust each other in commercial transactions. Without a blockchain, a trusted third party is required. Actually, by running a decentralized procedure, two parties agree without involving any intermediaries, simplifying the business processes.
The blockchain also guarantees pseudo-anonymity. Nodes are identified by a unique address that is required to operate on that blockchain. This address is visible by all, but it is never explicitly associated with any identity which therefore remains hidden. To improve anonymity, periodically addresses are recreated, decreasing the chance for a user of being tracked. For this reason, this new stage of the Web, will be mostly about trust, decentralization, and pseudo-anonymity.
According to [
19], in 2018, there have been over 2216 confirmed data breaches. More and more companies have suffered a cyber attack, making us reassess the way how we protect customers’ data. Cloud storage services seem a typical approach for those who require availability and scalability but they are particularly prone to security issues. Threats come from the heterogeneity of both hardware and software components which are present in the cloud infrastructure. A way to mitigate these threats is to identify any access violation in a reliable manner [
20]. Unfortunately, the control of any access violation comes at the cost of tracking all data transactions. Hence, a different approach could be employed, adopting a storage model based on trust and decentralization [
21], such as the blockchain. In fact, sundry stakeholders with different objectives might use the blockchain to prevent data breaches thanks to its inherent security. It might work well, but this is not always the solution that best meets their needs. Actually, adopting a blockchain rather than a cloud storage drive does not give any advantage, for the following two reasons [
22]. Firstly, the cost for replicating a huge amount of data to all nodes. Secondly, the world has plenty of equally secure solutions at lower costs.
Usually, business firms should get a strict analysis of the costs and benefits of the blockchain technology before implementing it. There is always a trade-off to consider between positive and negative aspects that should be taken into account. The blockchain may not lead to any benefit compared with the actual business models [
23]. However, it provides a strong contribute in situations in which to keep track of assets, whatever they are (digital assets or physical goods), is essential.
Centrality is another issue that we want to prevent. We said that the blockchain is natively decentralized but there are cases in which centralization comes out, leading to a more insecure network. When centrality comes, an attacker may potentially control the network status deciding which transactions are going to be validated or discarded. For example, in Bitcoin, the nodes’ trend is to join their computational power in so-called mining pools in order to increase their rewards. Unfortunately, these pools jeopardize the decentralization of the blockchain making it risky for all users on the network to send transactions. However, this is not only a Bitcoin-related concern. Several other Bitcoin-derived blockchains (e.g., Bitcoin Cash), are dealing with the same problem. Hence, the main concern for a blockchain designer is to guarantee security avoiding centrality. From this point of view, designing a stable consensus procedure plays a central role.
In
Section 4, we are going to explain the drawbacks of the blockchain technology in details. At this point, the reader will not be surprised to see that different (but complementary) definitions of what a blockchain is, can be given [
18]. We already gave a technical definition as a distributed shared ledger and business-wise as an exchange network for assets transactions. Now, we can give a third one, as a tool to replace notaries or other trusted parties in a dispute.
5. The Consensus Problem
The first blockchain (Bitcoin) relied on the proof of work to secure transactions. Proof of work is a consensus algorithm which requires a participant node to prove that the work done and submitted by it is accurate, therefore giving them the right to add more transactions to the blockchain. The consensus’s main purpose is to allow a group of peers to agree on a single state of the ledger, avoiding two problems: (1) the double-spending (refer to
Section 4.1) and (2) the creation of forks.
To understand what a fork is and why it matters, we should consider two main factors: (1) the propagation latency of both blocks and data transactions and (2) the coexistence of many leaders in the network. The former affects the list of data transactions that a node receives: a user close to the data source obtains data transactions earlier than a node located in proximity of the network boundary. The latter will impact the number of leaders that are in charge of generating the next block. Ideally, a well-designed consensus procedure should allow the presence of only one leader at a time. These two factors combined together—the propagation latency and the multiple leaders—might end up into a weird situation in which leaders propagate divergent blocks through the network. As a consequence, the nodes receive more than one block at a time and they are not able to discriminate either the correct block or the block that should be get rid of. In this uncertainty situation, nodes behave by temporarily adding all correct blocks to the chain and creating a fork. Afterwards, the nodes just continue by adding the subsequent blocks to the chain. When a block is covered by enough other blocks (in Bitcoin a transaction must be followed by at least 6 blocks), the nodes come to an agreement by pruning the orphan branch, according to the longest chain rule (see
Section 4.1). When the chain gets pruned, several situations may arise. From discarding a valid transaction that will be later re-proposed, increasing the transaction confirmation latency, up to validate invalid blocks. Taking advantage from this behaviour, some malicious parties might double-spend their digital assets with the aim to get them validated by the consensus procedure. This behaviour might cause severe consequences.
A consensus procedure has to guarantee safety and liveness. Safety states that the algorithm should not do anything wrong, while liveness ensures that eventually something good happens. Contextualizing to the blockchain, safety guarantees that forks should not happen, while liveness guarantees that all non-faulty nodes eventually terminate and output a decision without any external intervention to restart the system. Unfortunately, due to an impossibility result from Fischer et al. [
40], no deterministic algorithm solves the consensus problem in an asynchronous system. Roughly speaking, in an asynchronous distributed system, no deterministic consensus algorithm can satisfy both safety and liveness while preserving fault-tolerance. Due to this, different blockchains, such as Bitcoin, prioritize liveness over safety while others, like Stellar [
41], prioritize safety over liveness. Wanting to achieve both safety and liveness, one needs to add more computational power to the system using, for example, randomization, failures detectors, leader elections, different timing assumptions etc. [
42].
Consensus is also crucial in any distributed system to allow overall reliability in the presence of faulty nodes. A fault simply implies an unexpected behaviour of the nodes that can result in [
31]: (1) fail-stop failures or (2) Byzantine failures. The former happens if a node halts informing the users that a failure has happened, while the latter happens when a malicious node sends conflicting information to the observers. Most of the distributed applications assume to have fail-stop failures, since assuming Byzantine failures would make the system too complex in situations where it is not needed [
43]. Roughly speaking, a system satisfies a
t-fault tolerant condition when no more than
t nodes become faulty during some interval of interest.
A first practical solution to the Byzantine faults was given by Lamport in 1982 with the analogy called the Byzantine general’s problem. [
44]. The best way to explain the analogy is through a historic tale. The depicted scenario consists of an army that has besieged the city [
45]. The army has
n divisions with
, and each division has a lieutenant. In particular there is a commanding general plus
n lieutenants that are close to the enemy target. The commanding general must take a decision whether to attack or retreat and send the order to the other lieutenants. Be aware that the army has a good chance to win if and only if a majority of
of the lieutenants agrees to the same overall decision (attack or retreat). In order to find the agreement, the lieutenants propagate the commanding general’s decision to the other members, but there might be some traitors among them, including the commanding general. These traitors are assumed to misbehave and send conflicting messages to the others with the aim to prejudice the consensus. At the end of the day, we would like that a small number of traitors cannot influence the commanding general’s decision and everyone agrees to the same order.
It is possible to prove that the Byzantine general’s problem is still unsolved if we have only two lieutenants. In this case, a tie breaker is needed to reach a majority otherwise the nodes will continue sending conflicting messages. As an example, a lieutenant A receives a message from the commanding general ordering to attack. At the same moment, he receives another message from the lieutenant B, saying to retreat. They never come to an agreement and thus, the consensus cannot be reached. Based on this, we can provide the following theorem:
Theorem 1 ([
44])
. If t is the number of traitors for any value of , the Byzantine general’s problem has not a solution when less than members are employed. This theorem means that to have a solution to the Byzantine general’s problem at least
of the members must be loyal. Unfortunately, the number of messages exchanged between the parties grows quadratically with the number of members of the network. Therefore, increasing the number of lieutenants comes at a cost of increasing the complexity of finding an agreement. Back to our blockchain, the lieutenants are the nodes, while the commanding general is the leader, in charge of delivering the next block. Both of them can communicate over a bi-directional channel and both of them can potentially be traitors. In the case of blockchain, the leader does not propagate any order but rather a block. The nodes check that all transactions in the block are correct and have not already been spent. Then, they propagate their vote through the network. The main idea is that every node should reach a final consensus on the state of the shared ledger. Such types of approaches that allow an arbitrary (or Byzantine) behaviour of a small number of nodes without affecting the outcome, are called Byzantine Fault Tolerance protocols (BFT) [
46]. The BFT protocol can be applied to every distributed system, including the blockchain, to allow overall reliability in asynchronous networks.
5.1. BFT Protocol
We present a quick review of the protocol. The basic version of the BFT works in two steps called pre-commit and commit. These two steps are applied for each block proposed by the leader increasing the overall latency of the protocol. Firstly, an elected leader proposes a block to the whole network. The nodes receive the block and (if it is correct) they reply with a pre-commit message to all participants. The first step ends up when a
majority of the nodes acknowledges the pre-commit message. Soon after this step, the nodes send a commit message and halt waiting the
majority of the commit messages. Receiving the majority of commit messages means that all nodes have come to an agreement [
47].
According to [
42], a Byzantine agreement protocol satisfies:
Strong validity. If all correct processes propose the same value v, then no correct process decides a value different from v.
Agreement. No two correct processes decide differently.
Termination. Every correct process eventually decides some value.
Integrity. No correct process decides twice
A weaker notion of validity can be also defined, namely weak validity, such that if all processes are correct and propose the same value v, then no correct process decides a value different from v. Furthermore, if all processes are correct and some process decides v, then v was proposed by some process.
According to [
33], we can split the blockchain consensus procedures between two classes: permissionless and permissioned. These two properties involve who can partake to the consensus procedure and they have nothing to do with the previously mentioned public, private and consortium blockchains (
Section 4.3). Permissionless means that the membership to the group of who participates to the consensus procedure is open. The most famous permissionless blockchains are Bitcoin and Ethereum. We call a blockchain consensus procedure permissioned when the participants who run the consensus are pre-selected by a central authority. So far, we have seen that there are public permissionless blockchains in which anyone joins the network and participates to the consensus procedure and public permissioned blockchains, in which only a specific group of nodes is in charge of running the consensus procedure.
By contrast, there are private (or consortium) permissioned blockchains that usually run inside an organization’s intranet. Here, only a specific group of people joins the network and participates to the consensus. Many of the projects under the Hyperledger umbrella [
35] are private-permissioned, in which to join the network the node must sign in to a trusted third party. Last but not least, there are also private-permissionless blockchains [
48]. Typically, saying private and permissionless sounds weird but actually, they do exist. In a private-permissionelss network, the blockchain runs inside the organization itself because, as the name suggests, the network is still private. That said, to partake to the consensus the node simply informs the organizer of their existence.
Since 2009, when the blockchain idea came to the forefront, several consensus methods were proposed in which the user must show proof of the work done to reach that consensus. In the next part of this section we are going to discuss the mainstream consensus proof called Proof-of-Work and how a revisited version of the Byzantine Fault Tolerance has been employed in other consensus procedures in order to ensure a better performance.
These proofs can be embedded into a three-levels hierarchical structure [
18] in which the discriminant among those levels is about the amount of technology required to grasp the consensus. As a matter of fact, the first layer is called Proof-in-a-Consensus and involves those proofs that are part of or affect the consensus protocol itself at low-level. In this case, to change the proof, we should completely re-design our blockchain. In the middle tier of the pyramid, there is the Proof-as-a-Service, in which you prove your identity signing in into a service. Finally, in a Proof-in-a-Service the proof procedure depends from an external service and it is not strictly related with the blockchain design. An example is a blockchain employed for the voting system or the supply chain.
We will focus on the first layer, the one with more technology because it is independent from the specific application and it provides a better understanding of how a consensus would affect the blockchain’s performance.
We are going to introduce the so-called Proof-of-Work (PoW), Proof-of-Stake (PoS) and the Pure Proof-of-Stake. We have chosen to review these three Proof-in-a-consensus since in
Section 7 we will analyse how they perform. All of them have some peculiarities and can be employed in public blockchains but while the PoW was the original consensus procedure employed in a blockchain network, the PoS was the first to embrace a different approach to save energy. The Pure Proof-of-Stake (Pure PoS) instead, is a quite new project that has recently attracted a lot of attention thanks to its ability to get rid of many of the previously mentioned blockchains’ drawbacks.
5.2. Proof-of-Work
We introduce here the main concepts of the Proof-of-Work. We said that every time a new transaction is generated, it is delivered to all nodes who gather these data to be afterward inserted into the next block. As we said in
Section 4, transactions are ordered and pairwise hashed, forming a Merkle tree, so that only the root needs to be stored [
1]. In this way, a transaction verification is performed quickly by checking the consistency of the internal branch’s hashes.
In order to build the next block, each node must solve a cryptographic puzzle. The first who finds a solution to this complicated puzzle, becomes the leader in charge of closing and deliver the block. Therefore, the more rapidly you solve the puzzle, the more opportunity to generate the next block you have. This process is called mining and it is performed by so called miners. The role of miners is twofold. First, when computers solve the puzzle, they produce new coins, and secondly, miners make the payment on the network trustworthy and secure, by verifying its transaction information. The leader receives a reward as a result of his activity to generate the block. This reward is the incentive the network provides to keep the nodes loyal. As long as the majority of the honest nodes are encouraged to find a solution to the puzzle, the majority of the CPU power would be in honest hands. This preserves the safety of the system. Hence, increasing the number of miners, decreases the chance for malicious nodes to control the 51% of the CPU power, making any attempt of defrauding the network practically infeasible.
By contrast, in case of malicious nodes that take control of the entire network (majority of the CPU power), or a significant part of it, attackers can propose invalid transactions and switch off the trust the system relies on. Practically, attackers continue to propose the new blocks and no honest node can revert this trend. Hence, attackers can defraud the network and double spend any transaction they wish.
We can distinguish two types of nodes: full nodes, also called miners, and accounts. Full nodes run the consensus and validate transactions, while accounts are linked to a wallet. People with an account can spend their digital coins and deliver transactions, but they do not play any role in the consensus. As result, this type of node does not waste energy to solve the cryptographic puzzle.
The cryptographic puzzle consists in looking for a number (nonce) such that hashing that number together with the block header, the obtained result will start with a prescribed number of zeroes. If the required number of zero bits is not found, the procedure will continue by incrementing the nonce. The entire procedure guarantees that, in the fastest possible time, only one node can close the block and become the leader. Finally, when a solution to the puzzle is found, the leader broadcasts the block to all nodes to verify the transaction’s validity. In real scenarios, forks do happen due to some network delays but peers implicitly accept the block by working on extending the longest chain and pruning the shortest branch.
The entire procedure is safe and the transactions are tamperproof. An attacker might change a previously validated transaction only re-executing the hash function for all the subsequent blocks. Therefore, while the chain continues to grow, the attackers must chase and pass the last block added to the chain. The probability that an attacker reaches the last block drops exponentially as the number of blocks the attacker has to catch up increases [
1]. This means, if someone can control the majority of the CPU power on the network, it has more opportunity to control the whole network.
The Proof-of-Work comes with some drawbacks, mainly centralization and energy consumption. Every time a node generates the next block it gets a reward that is the incentive the blockchain provides in order to keep the nodes loyal. From here, miners start to increase their opportunity to get a reward by creating the so-called mining pools. The idea is that many miners share their computational power and so also the earnings from the block they mine together. If one of these mining pools could reach the 51% of the entire CPU power, all we said about the blockchain’s decentralization would be missing. Hence, this is a form of centralization that should be avoided.
Finally, the mining process requires a huge amount of energy. According to [
49], the entire process is CPU intensive and requires a lot of energy consumption that is analogous to gold miners expending resources. From here, the name miner was given to the nodes that try to solve the puzzle. For example, the energy consumption per year of the Bitcoin network is estimated to be similar to a country like Ireland or Hong Kong. The study [
50] shows that the expenses to earn one dollar worth of bitcoin are three times that required to mine gold. Furthermore, the high energy consumption will have a strong environmental impact and might influence how people will approach this technology in the years to come.
Proof-of-Work comes with some more threats. It is not our ambition to investigate all the PoW drawbacks, but we should clarify that the entire procedure is prone to generate forks. The presence of these forks impacts the transaction confirmation time. In fact, to be sure that a transaction has been approved, a user must wait until the transaction is followed by enough blocks that are part of the longest chain.
Despite all, the PoW is still the most popular choice in achieving distributed consensus [
51] because it has been widely tested. In order to fix its issues, a number of patches were applied and other consensus procedures have been designed as alternatives to the Proof-of-Work.
5.3. Proof-of-Stake
The Proof-of-Work has some drawbacks so the blockchain designers have developed a new consensus procedure, known as Proof-of-Stake (PoS). The term “stake” highlights the number of tokens a user bets in order to partake to the validation process. The concept was firstly introduced in 2012 by Peercoin [
52] and since then, several other blockchains were based on the same idea.
The protocol is quite simple: a node partakes to the consensus procedure (it generates or validates the next block) proportionally to the stakes it bets. The more you bet in, the more influence you have on validating the next block. The nodes do not need to compete with each other for solving a mathematical puzzle, resulting in a more efficient and energy saving procedure. As incentive to keep the nodes loyal, the leader receives a reward for propagating the block. According to [
53], there are two types of PoS design:
Chain-based Proof-of-Stake. Periodically, a leader is elected in a semi-random fashion and delivers the next block to be added to the chain. Hence, a global clock is required to mark the time.
Consortium consensus—Byzantine fault tolerance (BFT) protocol. A node gets elected in a semi-random fashion and a voting procedure runs in order to find the consensus. In the voting procedure, every node counts proportionally to the stake it bets. Differently from the chain-based PoS, the Byzantine fault tolerance is required in asynchronous networks.
There are two types of nodes. A node can just have an account and start to spend coins or it can also participate in the consensus, vote and eventually propose a block. Be aware that only the leader proposes a new block. A node becomes the leader in a two-step procedure. (1) The first step takes into account the amount of money a user deposits into the system. (2) The second phase adds some kind of randomness to this process.
Particularly, to avoid that wealthy nodes may get richer receiving the reward for delivering invalid transactions, a random election model is adopted. But to make matters worse every blockchain implements its own method or a combination of them. Some blockchains use a combination of lowest hash value and highest stake, others a coin age selection where tokens staked for a long time will give more profits. Unfortunately, this last method has a drawback. Nodes are more incentivized to keep the tokens for a long time rather than to spend them and this is in contrast with the philosophy of a savvy blockchain’s designer, due to problems related to stagnation of money [
54].
The PoS suffers from the nothing-at-stake problem. In fact, with the PoS, participants get a reward voting for what ends up of being the “correct” block. This activity of voting consists of checking that all data transactions are not being double-spent. This verification is not computationally intensive and the parties can easily misbehave by voting for all blocks. Practically, with the aim to get a reward, nodes start supporting several branches of the chain because it is effortless. This bad behaviour favours malicious parties and makes the final agreement hard to find. At first, no individual disincentive was in place to avoid the nothing-at-stake problem. Later, a solution was implemented with the second generation of the PoS, in which nodes supporting multiple branches were penalized by losing their own stake or a part of them.
Nowadays, some famous blockchains are migrating toward a PoS consensus such as Ethereum [
53], but other are more reluctant on using the PoS because it has still not been widely tested. Like for the PoW, greedy stakeholders might take control of the majority of the stakes and jeopardize the network. Therefore, other solutions were coming out with the aim to provide a response for these issues.
5.4. Pure Proof-of-Stake
Pure Proof-of-Stake (Pure PoS) is a new consensus procedure implemented by the public blockchain called Algorand. Differently from the previously mentioned PoW and PoS, the Algorand’s team has redesigned the consensus procedure from scratch with the ambition to solve many of the problems that affect the Proof-of-Work and the Proof-of-Stake. Therefore, the entire procedure promises to be energy saving and completely decentralized.
Anyone can join the network and as long as they have money, they can partake to the consensus procedure. Particularly, the members of the network can belong to one of these categories: normal user, a leader or a committee member. This information might change a little depending on which implementation of Pure PoS we are considering. For example, Algorand, which was the first to rely on Pure Proof-of-Stake, identifies two types of nodes, called relay nodes and non-relay nodes. Relay nodes are primarily used to route the network traffic to a set of connected non-relay nodes. Non-relay nodes only connect to other relay nodes and cannot be used to route the network traffic. Both types of nodes can access the ledger and participate in the consensus. By the way, Algorand recommends that only non-relay nodes participate in consensus. By default, relay nodes store the entire history of the ledger, while to reduce disk space requirement, non-relay nodes maintain just a limited number of blocks (usually 1000 blocks). To understand the difference between these categories, let us explain at high level how the entire procedure works.
The Algorand consensus works in rounds and for each round two phases are highlighted. During the first phase every participant runs a sortition function to elect the leader. As usual, the leader is in charge of proposing the next block. In the second phase, a subset of members is pseudo-randomly selected to become part of a committee group and runs the Algorand Agreement —BA★— [
55]. As the name suggests, the BA★ is a customized version of the BFT protocol revisited by Algorand’s team. The committee members are elected (using the same Sortition function as before) based on their weights. Practically, every participant has a weight that is proportional to the stake it owns. Participants with high weights have more chances get elected as committee members. The committee members vote for the proposed block and may influence the final decision on that block. Hence, to preserve the correctness of the network, stakeholders (honest participants) are incentivized to become leaders or committee members.
At this point, two questions need an answer. First, how does the Sortition function work?
We might see the Sortition function as a fair lottery that cannot be manipulated by malicious parties. The lottery elects the leader as well as the committee members and takes into account the number of tokens owned by each node, in the same way the PoS does. Hence, if a node owns a lot of tokens, its chance to be elected increases. The key factor of the Sortition function is the so-called “Verifiable Random Function” (VRF) [
56], which is a random number generator that takes a public seed and the node’s role to generate a random value. Sortition returns three values: a random number generated by the VRF, a proof that the output provided by the VRF is correct and a number
j that expresses the probability of a node to become a committee member. Typically, every participant is elected proportionally to the coins it owns. Every other node can later verify the validity of the value
j using a VerifySortition function. We should take into account that the entire procedure is energy saving, such as for the PoS [
57].
The second question that we left behind is, how does the Algorand Agreement BA★ work?
Once a leader is elected, he propagates the block to the committee members who run the BA★. The main innovation of this new consensus protocol is the property called Player Replaceability [
58]. The Player Replaceability allows Algorand to rely on a different subset of users for each round, still continuing to reach an agreement. Therefore, in the beginning of each round nobody knows in advance who will be elected to run the consensus. In this way, nodes are protected against targeted attacks because the attacker will not know in advance who is going to win the lottery.
During the BA★ three kinds of messages are exchanged between the committee members [
59]: a CERT-VOTE, a SOFT-VOTE, and a NEXT-VOTE. When a majority of votes is received a node switches its status from SOFT-VOTE to CERT-VOTE and stops propagating further messages. Moreover, the entire procedure assures a low number of forks. In order to avoid overwhelming the network, when a fork happens and two parties are not able to find an agreement, the Pure PoS switches to a so-called CommonCoin procedure that forces the nodes to accept one value between 0 or 1 with probability
. In this way, adversaries have a lower chance to manipulate the vote.
The previous mentioned PoS is also vulnerable to the Sybil attack. In this attack a node can create many addresses and splits his tokens between them to have a better chance to be part of the consensus procedure. With the Pure PoS instead, if you earn 1M tokens, they are implicitly divided by the system into 1 Million accounts containing 1 token for each and this makes the Sybil attacks practically unfeasible.
Hence, as a conclusion, the Pure Proof-of-Stake is certainly an interesting consensus procedure that makes things different with respect to the previous ones. Unfortunately, this blockchain is still in its early stages and it has not been properly tested in real scenarios. Hence, Algorand might provide a solution to solve the problems of centralization, security and scalability that affect the blockchains, but we must still fully understand if there are any downsides.
Table 1 summarizes the main strengths and weaknesses of each of the consensus procedures explained so far.
6. A Blockchain Analysis via CAP Theorem
In this section, we analyse the blockchain consensus procedures by taking into account three important properties that every shared database must deal with. Just like every distributed database, the blockchain employs these properties [
60]. The first database peculiarity is called consistency. Every time a commit happens, the ledger is updated and every node reads the same shared values. Secondly, databases do agree on availability. Hence, for each data demand, corresponds an answer. Finally, the network does not stop even if it is broken up (partition tolerance).
The prevailing idea of consistency in distributed systems is quite different from the one proposed during the early database stages by the ACID properties. The term ACID stands for: Atomicity, Consistency, Isolation, and Durability. In a nutshell, Atomicity means that all data transactions should not be left only partially completed. The Consistency property states that a transaction should not have adverse effect on the data previously recorded on the database. Isolation means that all data transactions should be carried out independently from the others. If a transaction fails, it should not affect the other transactions. The last property called Durability states that when an update is committed, data should be never removed nor revoked. Practically, once a commit happens, data should be hold on, even if the system fails or restarts. The cloud computing entirely changed this scenario and these ACID properties have not-well fitted this new distributed paradigm [
61]. In the blockchain, the actual idea of consistency is a little different from the original one and it is focused on maintaining a total ordering of data transactions in the shared ledger [
62].
Eric Brewer was the person who has introduced a milestone in the database systems’ theory. Such milestone is known as the CAP theorem [
62] and it claims that every distributed database system, such as the blockchain, cannot simultaneously guarantee more than two out of three of these properties (availability, consistency and partition tolerance).
To prove the theorem [
62], let us take a look at this first scenario in which both consistency and availability would be preserved as well as network partitioning. A network partition might be caused by some faulty nodes or a message delivery delay. When it happens, the network is teared up into isolated segments and a new transaction will be broadcast within the same partition, forcing the remaining part of the network to keep going on using an old copy of the ledger. As we see, in this case consistency cannot be preserved. To simultaneously pick partition tolerance and consistency, we should force the network to isolate the single partition and switch off the remaining part of the network. Clearly, this means to discard availability. Hence, the only way to preserve availability and consistency at the same time is to avoid such network’s behaviour in which a node can act maliciously and a network partition is created. However, partition tolerance is a fundamental property for any distributed system that cannot be postponed.
Since the blockchain must tolerate network partitioning, we must pick only one property between consistency and availability. Roughly speaking, choosing availability will make the system responsive but its data would be often outdated. Vice-versa, a consistent system would be more precise but it will introduce a higher latency.
So far, we used to the term consistency, but we could be more precise adopting the term strong consistency. In general, the strong consistency might bring to a more centralized network [
63] because all transactions should be written at the same time and a central authority is desirable to preserve the transactions ordering. Furthermore, according to the CAP theorem, if we pick strong consistency, we give up availability in favour of consistency and partition tolerance. To relax this constraint, several consistency paradigms have been defined and the blockchain designers have embraced the so-called weak or eventual consistency, in which availability as well as network partitioning are guaranteed. Thus, the blockchain does respect the CAP theorem and agrees on Partition Tolerance + Availability or Partition Tolerance + Availability + Eventual Consistency.
Back to our consensus procedures (starting from
Section 5.3), the Proof-of-Stake and the Pure Proof-of-Stake demand for a strong consistency in which a collision could happen and the system quickly converges to the same shared ledger using a voting-system. Practically, PoS and the Algorand Pure PoS do not allow the creation of forks and they guarantee consensus finality. It could be worthy to spend some time explaining what a consensus finality means. A proper definition of consensus finality has been given in [
46] and claims that once a node appends a block to the chain, nobody can remove the block neither the creator itself. Hence, adding a block to the ledger, means that the transactions in the block have been shortly confirmed. In this case, no time is wasted waiting for a response. Hence, BFT protocols guarantee consensus finality and if a collision happens, they shelve availability in favour of consistency and partition tolerance.
By contrast, in eventual consistency forks do happen because of nodes’ misbehaviour or some network delays and they are later resolved. The Proof-of-Work (and its heritages) refers to this consensus procedure in which availability is preserved as well as network partitioning and weak consistency. Here, consensus finality is not satisfied, that means, to receive a transaction confirmation, nodes must wait several blocks to significantly decrease the opportunity that their transaction is going to be revoked. Therefore, the PoW does not suit well the micro-payment systems since transactions have to take place in real time.
Some PoW-based blockchains like Bitcoin adopt an eventual consistency flavour but the ultimate trend is to move toward a strong consistency procedure in which the BFT quickly confirms the data transactions and the consensus finality is preserved. Despite all, the BFT protocol has some drawbacks related with poor scalability [
46]. Hence, we can conclude that there is not a best solution and everything depends on what we want to do.
7. A Throughput-Based Performance Comparison
In this section, we propose a framework to compare the performances—throughput and scalability—of the consensus procedures reviewed so far. When possible, the data have been gathered from academic journals [
46,
64,
65] or whitepapers [
57,
66]. When they were not available, we used blogs and community discussion forums [
67,
68] to complete our analysis. Firstly, let us introduce the concept of
data throughput. According to [
69,
70], the throughput is the average number of bits per second that a node can deliver or receive over a communication channel. It is a measure of the network performances related with the network ability to carry out messages. When we operate in a multi-hop network such as the blockchain, data transactions are delivered passing through several intermediate nodes. Each node should be able to buffer data, according to its buffer size, and send packets. In this case the network throughput depends from the theoretical upper bound of the buffer size and the network bandwidth. There are several devices that can be used to measure the throughput and they work by tracking the windows of packets over an end-to-end communication channel [
71]. In order to improve the throughput, a technique called sharding is employed. We will explain the sharding technique in
Section 7.4.
A second term that we want to emphasize is scalability. We all know what scalability is, but here we refer to the
structural scalability [
72]. The structural scalability is the ability of the network to enlarge the number of nodes that partake to the consensus or clients, without any struggle. One of the goals of the blockchain technology is to handle part of the business applications over its network to take advantage of its decentralization and security features. Actually, the main blockchain challenges are in the financial market, in which VISA and PayPal networks overwhelm any previous blockchain technology. VISA carries out 1667 transactions per seconds (tps) and PayPal 193 tps on average [
65,
73]. Generally, many leading credit-card companies declare a peak of 10,000 tps [
46], while, according to [
74], the VISA network can process 24,000 tps with a theoretical limit of 56,000 tps [
75].
The second market in which the blockchain must compete is in the web-based applications. Today, many centralized web application such as Facebook, are able to run 175,000 requests per second [
76]. Hence, if the blockchain wants to have a chance to compete or even replace these technologies (e.g., the electronic cash systems or the web-based applications), it should be able to manage the same number of tps that the fintech market does.
For these reasons a high throughput is desirable. Hence, permissionless blockchains expect to increase their performances, boosting the throughput. Unfortunately, a high throughput affects the overall consensus and leads to security threats because the network is more prone to generate forks (a definition of forks has been given in
Section 5). Hence, in the next section we propose a comparison of the state of the art of the blockchains’ performances by reviewing the throughput’s upper bound for the main consensus procedures [
73].
7.1. Proof-of-Work Performance Analysis
Throughput. In Bitcoin’s PoW, transactions are limited by the block size to an upper bound of 7 transactions per second with small transactions (200–250 bytes per transaction) [
46] and 6 blocks confirmation latency. That means, in the case of Bitcoin in which a new block is delivered every 10 min [
43], the nodes must wait, on average, 1 h to confirm a transaction [
64]. This is one of the main limitations to the PoW because it makes infeasible to process small payments. Up to 2016, the PoW-based blockchains performed 2 transactions per second on average with a transaction dimension of 500 bytes. By the way, the Ethereum PoW testnet declares a throughput of 11 tps [
77] while to Litecoin and Bitcoin Cash are attributed 56 and 60 tps [
74].
There are two ways to boost the network throughput. It can be done by magnifying the dimension of the block or increasing the frequency of the packet’s delivery. Unfortunately, these come at a cost of security issues that must be later handled by the blockchain. Increasing the block size would impact the latency and creates many forks to the chain because every block will take longer to propagate [
78]. In Bitcoin, the average block size was 87 KB in 2012 and 540 KB in 2015 with a latency of 87 s to reach the 90% of the network’s nodes. To avoid future blunders the block size has been limited to 1 MB [
65,
67,
74] and in any case, it cannot exceed the 4 MB to guarantee that every block could propagate quickly to the whole network [
64]. The block takes longer to propagate from the source to the network bounds, hence unfair situations may arise in which peripheral nodes receive 1 MB block 2.4 min later (on average) than the nodes close to the source [
64]. Since then, many conflicting situations may arise because the earlier you receive the block the more chance you have to solve the cryptographic puzzle.
Regarding frequency, a high blocks rate would favor the strongly connected nodes rather than the peripheral one. Hence, adversaries could take advantage of the weaker nodes and overtake the network [
65]. Taking the Bitcoin PoW network as a benchmark, the block frequency should not exceed a delivery rate of 5 blocks per minute.
Scalability. We should keep in mind the two categories of users: the clients that spend transactions and the miners in charge of generating the next block. PoW scales well up to thousands of clients and thousands of miners [
46] but we should remind that the miners’ trend is to generate mining pools in order to share their reward. Hence, we cannot really consider this kind of metric as representative of the PoW network ability to scale up to thousands of miners. We have already discussed about the centralization and the energy consumption problem in
Section 5.2.
7.2. Proof-of-Stake Performance Analysis
Throughput. The first blockchain employing the PoS chain-based was Peercoin in 2012 and it has been able to run 10 tps [
68]. Since 2017, Ethereum is migrating from the PoW to a chain-based PoS consensus procedure [
53]. Today, its network handles between 10 up to 20 tps [
73]. By contrast, the PoS consortium consensus (
Section 5.3) easily overtakes any previous PoW-based blockchain, performing tens of thousands of transactions per second [
46]. According to the Byzantine General’s problem shown in
Section 5, running a machine state replication protocol (e.g., the BFT) requires a large bandwidth because the number of messages grows quadratically in the number of nodes. Therefore, the set of forgers should be limited to just a bunch of nodes. The protocol tested on a small network composed with 4 nodes guarantees 113,000 tps, while enlarging the network to 64 nodes, the throughput factor dramatically degrades to 2400 tps. These values become one third with a transaction size of 500 bytes [
64]. However, they still perform significantly better than the PoW.
Scalability. PoS chain-based (
Section 5.3) scales up to thousands of users [
46] but it does not guarantee consensus finality as discussed in
Section 6. This is one of the reasons to shift toward a consortium consensus which by contrast, has a poor scalability (up to a bunch of nodes) [
46,
79]. In fact, scaling on thousands or even hundreds of nodes will significantly degrade the performance of the system. As observed in [
64] a configuration with 64 nodes was already limited by the network bandwidth bound.
7.3. Pure Proof-of-Stake Performance Analysis
Throughput. The Pure PoS can handle several thousands of transactions per second. The Algorand Agreement commits a transaction in about 12 s, independently from the block size. The protocol can manage a block size of 500 KB as well as 10 MB, resulting in a throughput of 750 MB per hour. That means, the Algorand’s network is about 125 times faster than the Bitcoin network [
57]. Unfortunately, these results come from a testnet of 50,000 nodes and they cannot be considered as final benchmark [
57]. Nowadays, the only blockchain project (namely Vault) that uses the Algorand infrastructure to move assets is actually in Beta [
66] hence, we do not have any statistics on a worldwide scenario. We are confident that in the future more analysis will be conducted and more data will be available to the reader.
Scalability. The Pure PoS scales well up to 500,000 nodes. The procedure selects a subset of representatives to run the Algorand Agreement. The size of the committees is preselected by a multi-round procedure and may vary for each round of the BFT (as we defined in
Section 5.4). Transactions are disseminated by gossip and confirmed within a minute. By the way, the network latency does not depend by the number of nodes who join the network but only from the size of a block and the width of the network [
57]. That means, increasing the number of nodes, the transactions are confirmed within a minute, while enlarging the block size to 10MB will increase the latency up to 50 s (always less than one minute). Finally, according to [
55], the latency will grow by widening the extension of the network. At the same time the dimension of the network grows logarithmically with the number of nodes.
7.4. Comparisons
Table 2 provides a comparison between the three consensus procedures studied so far based on their key features.
Type of consensus. In the PoW-based blockchains every node can become a miner and starts using its computational power to generate blocks and validate transactions (see
Section 5.2). As we said in
Section 5.2, they usually join some mining pools in order to share the rewards. By contrast, the consortium consensus Proof-of-Stake (refer to
Section 5.3) is permissioned and a trusted third party is needed to select a list of validators. These validators are in charge of verifying and validate the next block. Similarly to the PoW, the Pure Proof-of-Stake (
Section 5.4) is permissionless. The committee members are selected with a fair lottery and every node has an equal chance to become a validator.
Consensus finality (Section 6) and latency. In the PoW-based blockchains a user must accept a certain degree of uncertainty because many forks are generated and a branch might be later pruned from the chain. Hence, the consensus finality is not guaranteed and a node must wait up to 6 block time latency before considering its transaction as validated. This means that in the case of Bitcoin, a user must wait on average 1 h of time before considering the transaction as validated. Generally, in the consensus procedures that run the BFT protocol (or its variants) once a transaction is added to the chain, it is never revoked. Hence, the latency is limited by the network latency (in the case of the consortium PoS) and it is up to 1 min for the Pure PoS.
Throughput. The Algorand consensus overwhelms any previous consensus procedure. It achieves tens of thousands of transactions per second. We should keep in mind that this value is limited by the network bandwidth. In fact, the network bandwidth constitutes a bottleneck to the blockchains’ performances. The PoW is more prone to generate forks and this may impact the number of transactions per second that the blockchain guarantees as well as the size of the block. In the PoW the maximum block size is limited to 1 MB, while the Algorand Agreement is able to handle up to 10 MB blocks.
To increase throughput, a leading idea discussed in literature is
sharding [
80].
Sharding is a technique already used for database partitioning that breaks up very large data sets into smaller pieces, or shards, and stores them in separate machines. Thus, each node has no longer to process the entire network’s transaction load.
Blockchain uses sharding to divide data to a subset of nodes. Each subset (or shard) manages a different section of the entire chain. Instead of having every node to process all the data, nodes are broken up into smaller groups, and each group handles one part of the data in transaction processing. If the network has N nodes with K shards, the blockchain is partitioned in K sub-chains. Each sub-chain is then replicated at nodes. Thanks to this technique, the throughput is improved by a factor K. If K shards are taken, K times the throughput is, roughly, what we can have.
This solution comes up with drawbacks though, for example security. To mitigate this problem nodes should be randomly assigned to a different shard.
Scalability. When we talk about scalability, we refer to the subset of nodes in charge of generating or validate the next block. The PoW last trend is to employ thousands of miners working in mining pools. By contrast, the BFT protocol has a poor scalability (up to few dozens of nodes). To solve this blunder, the Pure PoS randomly selects a small portion of users to run the Algorand Agreement. The dimension of this small subset of nodes may vary accordingly to the network bandwidth.
7.5. Conclusions and Future Works
We introduced the blockchain as a new decentralized way to handle transactions. We provided a summary of their major strengths and weaknesses. However, there are many debates about the pros and cons of blockchain technology. Luther & White (2014) [
81] introduced some limitations of Proof-of-Work and discussed the entrepreneurial efforts that might enable bitcoin to become a more commonly accepted payment medium. We showed that a blockchain can be used for a variety of purposes, for example to substitute the fiat currency without the need of a central authority. By the way, this technology has some downsides. It could be worthy for the industry sector to have a guideline that allows them to orient themselves in the world of blockchain technologies. Therefore, we proposed a framework to compare blockchain’s consensus mechanisms based on some characteristics such as throughput, speed and scalability. Hopefully, this study could provide some hints for future studies in related fields and that we could contribute to this rapidly growing body.
As future work, the research could focus to study the effectiveness of the connection between the oracle and the blockchain network. How do we safely reach consensus if several IoT devices gather conflicting information from the external environment? For industrial applications where IoT devices are commonly used, sensors collect information coming from the outside world, IoT devices process these information and they should eventually agree on a single value before sending the result to the blockchain network. A way to deal with this problem is to run a consensus algorithm on the local network, and once they all agree on a single value, they can share the result to the blockchain. This is one of the hottest areas of research today. Future works may also consider different consensus protocols than the three presented in this Survey. We provided a brief and incomplete list of further consensus in the introduction, citing the proof-of-authority, proof-of-space, proof-of-burn, proof-of-elapsed time, just to name a few.