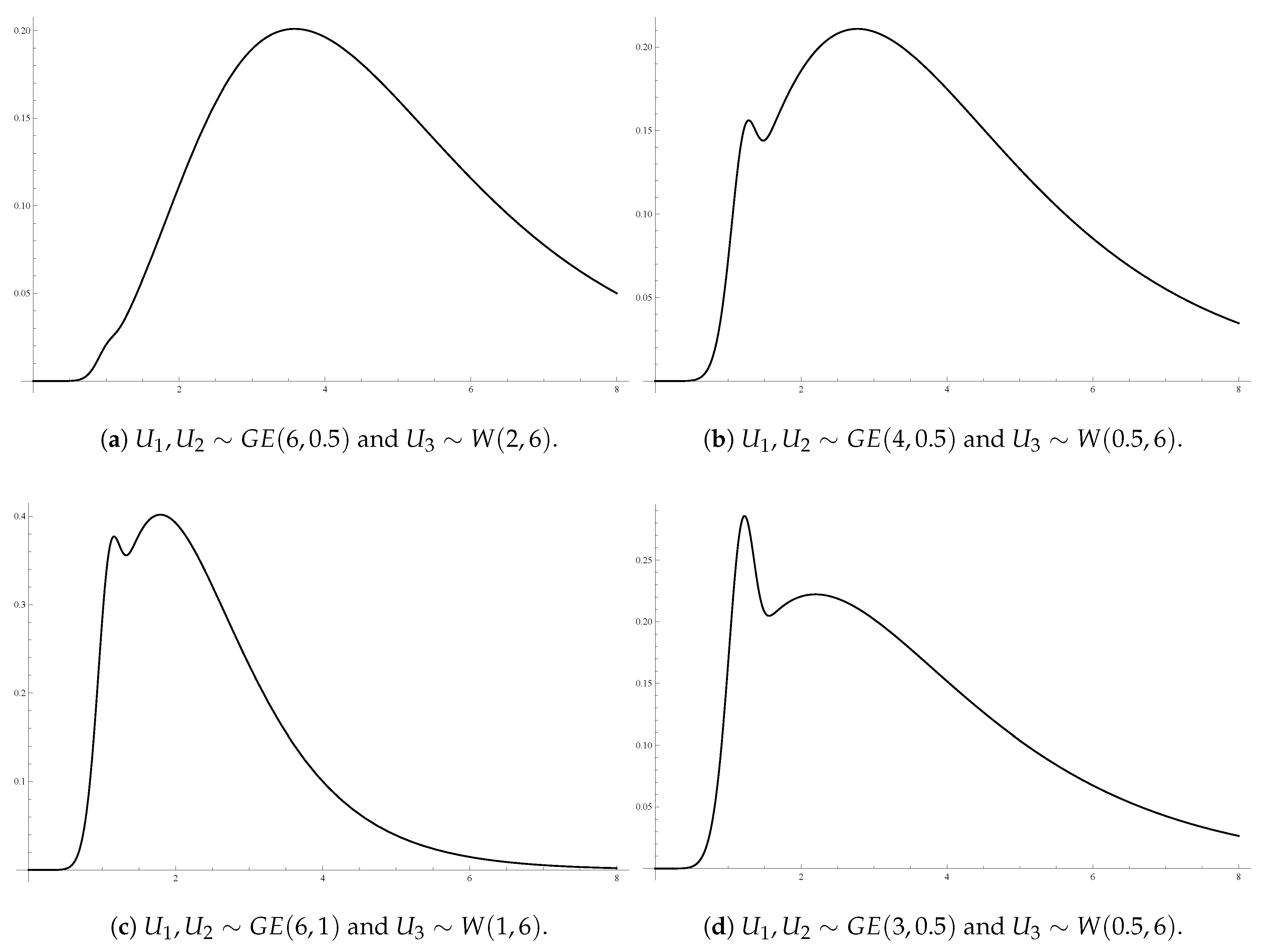1. Introduction
Gumbel [
1], Freund [
2], and Marshall and Olkin [
3] in their pioneering papers developed bivariate exponential distributions. Since then, an extensive amount of work has been done on these models and their different generalizations, which have played a crucial role in the construction of multivariate distributions and modeling in a wide variety of applications, such as physic, economy, biology, health, engineering, computer science, etc. Several continuous bivariate distributions can be found in Balakrishnan and Lai [
4], and some generalizations and multivariate extensions have been studied by Franco and Vivo [
5], Kundu and Gupta [
6], Franco et al. [
7], Gupta et al. [
8], Kundu et al. [
9], among others, and recently by Muhammed [
10], Franco et al. [
11], and El-Morshedy et al. [
12], also see the references cited therein.
Kundu and Gupta [
13] introduced a bivariate generalized exponential (BGE) distribution by using the trivariate reduction technique with generalized exponential (GE) random variables, which is based on the maximization process between components with a latent random variable, suitable for modeling of some stress and maintenance models. This procedure has also been applied in the literature to generate other bivariate distributions, for example, the bivariate generalized linear failure rate (BGLFR) given by Sarhan et al. [
14], the bivariate log-exponentiated Kumaraswamy (BlogEK) introduced by Elsherpieny et al. [
15], the bivariate exponentiated modified Weibull extension (BEMWE) given by El-Gohary et al. [
16], the bivariate inverse Weibull (BIW) studied by Muhammed [
17] and Kundu and Gupta [
18], the bivariate Dagum (BD) provided by Muhammed [
19], the bivariate generalized Rayleigh (BGR) depicted by Sarhan [
20], the bivariate Gumbel-G (BGu-G) presented by Eliwa and El-Morshedy [
21], the bivariate generalized inverted Kumaraswamy (BGIK) given by Muhammed [
10], and the bivariate Burr typeX-G (BBX-G) proposed by El-Morshedy et al. [
12]. Some associated inferential issues have been discussed in these articles, and all of them are based on considering the same kind of baseline components. In each of these bivariate models, the baseline components belong to the proportional reversed hazard rate (PRH) family with a certain underlying distribution (Gupta et al. [
22] and Di Crescenzo [
23]). It is worth mentioning that Kundu and Gupta [
24] extended the BGE model by using components within the PRH family, called a bivariate proportional reversed hazard rate (BPRH) family, and a multivariate extension of the BPRH model was studied by Kundu et al. [
9].
The main aim of this paper is to provide a more flexible generator of bivariate distributions based on the maximization process from an arbitrary three-dimensional baseline continuous distribution vector, i.e., not necessarily identical continuous distributions. Hence, this proposed generator allows researchers and practitioners to generate new bivariate distributions even by combining non-identically distributed baseline components, which may be interpreted as a stress model or as a maintenance model. We refer to the bivariate models from this generator as the generalized bivariate distribution (GBD) family, which contains as special cases the aforementioned bivariate distributions. Note that a two-dimensional random variable , belonging to the GBD family, has dependent components due to a latent factor, and its joint cumulative distribution function (cdf) is not absolutely continuous, i.e., the joint cdf is a mixture of an absolutely continuous part and a singular part due to the positive probability of the event , whereas the line has two-dimensional Lebesgue measure zero. In general, the maximum likelihood estimation (MLE) of the unknown parameters a GBD model cannot be obtained in closed form, and we propose using an EM algorithm to compute the MLEs of such parameters.
The rest of the paper is organized as follows. The construction of the GBD family is given in
Section 2, and we obtain its decomposition in absolutely continuous and singular parts and its joint probability density function (pdf). In
Section 3, several special bivariate models are presented. The cdf and pdf of the marginals and conditional distributions are derived in
Section 4, as well as for its order statistics. Some dependence and two-dimensional ageing properties for the GBD family, and stochastic properties of their marginals and order statistics are studied in
Section 5, as well as its copula representation and some related association measures. The EM algorithm is proposed in
Section 6, which is applied in
Section 7, for illustrative purposes, to find the MLEs of particular models of the GBD family in the analysis of two real data sets. Finally, the multivariate extension is discussed in
Section 8, as well as the concluding remarks. Some of the proofs are relegated to
Appendix A for a fluent presentation of the results, and some technical details of the applications can be found in
Appendix B.
2. The GBD Family
In this section, we define the generalized bivariate distribution family as a generator system from any three-dimensional baseline continuous distribution, and then we provide its joint cdf, decomposition, and joint pdf.
Let , , and be mutually independent random variables with any continuous distribution functions , and , respectively. Let and . Then, the random vector is said to be a GBD model with baseline distribution vector .
Theorem 1. Let be a GBD model with baseline distribution vector , then its joint cdf is given bywhere , for all . For instance, a stress model may lead to the GBD family, as in Kundu and Gupta [
13]. Suppose a two-component system where each component is subject to an individual independent stress, say
and
, respectively. The system has an overall stress
which has been equally transmitted to both the components, independent of their individual stresses. Then, the observed stress for each component is the maximum of both, individual and overall stresses, i.e.,
and
, and
is a GBD model.
Analogously, a GBD model is also plausible for a maintenance model. Suppose a system has two components, and it is assumed that each component has been maintained independently and there is also an overall maintenance. Due to component maintenance, the lifetime of the individual component is increased by a random time, say and respectively, and, because of the overall maintenance, the lifetime of each component is increased by another random time . Then, the increased lifetime of each component is the maximum of both individual and overall maintenances, and , respectively.
As mentioned before, a bivariate model belonging to the GBD family does not have an absolutely continuous cdf. Let us see now the decomposition of a GBD model as a mixture of bivariate absolutely continuous and singular cdfs, the proof is provided in
Appendix A.
Theorem 2. Let be a GBD model with baseline distribution vector . Then,whereandwith , are the singular and absolutely continuous parts, respectively, and In addition, due to the singular part
in (
2), the GBD family does not have a pdf with respect to the two-dimensional Lebesgue measure even when the distribution functions
,
, and
are absolutely continuous. However, it is possible to construct a joint pdf for
through a mixture between a pdf with respect to the two-dimensional Lebesgue measure and a pdf with respect to the one-dimensional Lebesgue measure (the proof is provided in
Appendix A).
Theorem 3. If is a GBD model with joint cdf given by (1), then the joint pdf with respect to μ, the measure associated with F, iswhereandwhen the pdf of exists, . 3. Special Cases
In this section, we derive new bivariate models from Theorem 1, taking into account particular baseline distribution vectors .
Note that, if the baseline components s belong to the same distribution family, say , then the proposed generator provides novel extended bivariate versions of that distribution . Furthermore, under certain restrictions on the underlying parameters of each , bivariate distributions given in the literature are obtained. From now on, it is assumed that all parameters of each are positive unless otherwise mentioned.
Extended bivariate generalized exponential model. A random variable
U follows a GE distribution,
(see Gupta and Kundu [
25]), if its cdf is given by
If
, then the GBD model with the GE baseline distribution vector is an extended BGE model with
and
parameter vectors, denoted as
, and its joint cdf is
where
.
As a particular case, if
,
,
given by Kundu and Gupta [
13].
Extended bivariate proportional reversed hazard rate model. If
with base distribution
, i.e., its cdf can be expressed as
(see Gupta et al. [
22] and Di Crescenzo [
23]), then the GBD model with PRH baseline distribution vector provides an extended BPRH model,
, with
parameter vector of the PRH components and
parameter vector of the underlying distributions
’s. From (
1), its joint cdf is given by
where
.
In particular, if the PRH components have the same base distribution,
, then
with baseline distribution
introduced by Kundu and Gupta [
24].
Extended bivariate generalized linear failure rate model. It is said that a random variable
U follows a GLFR distribution,
(see Sarhan and Kundu [
26]), if its cdf is given by
If
, then the GBD model with GLFRs baseline distribution vector is an extended BGLFR model,
, with parameters
,
, and
, having joint cdf
where
.
When
and
,
, it is obtained that
given by Sarhan et al. [
14].
Extended bivariate log-exponentiated Kumaraswamy model. Let
U be a random variable with logEK distribution,
(see Lemonte et al. [
27]), then its cdf
If
, then the GBD model with logEKs baseline distribution vector is an extended BlogEK model,
with parameters
,
, and
, and its joint cdf is given by
where
.
Clearly, it can be seen that
given by Elsherpieny et al. [
15], when
and
,
.
Extended bivariate exponentiated modified Weibull extension model. A random variable
U follows an EMWE distribution,
(see Sarhan and Apaloo [
28]), if its cdf can be expressed as
If
, then the GBD model with EMWEs baseline distribution vector is an extended BEMWE model,
with
and
,
, and
parameter vectors, and its joint cdf is given by
for
and
, where
.
Note that, if
,
and
,
, then
given by El-Gohary et al. [
16].
Extended bivariate inverse Weibull model. The cdf of the IW distribution (e.g., see Keller et al. [
29]) is defined by
If
, then the GBD model with IWs baseline distribution vector is an extended BIW model with
and
parameter vectors, denoted as
, and its joint cdf can be written as
where
.
In particular,
studied by Muhammed [
17] and Kundu and Gupta [
18], when
for
.
Extended bivariate Dagum model. It is said that a random variable
U follows a Dagum distribution [
30],
, if its cdf is given by
If
, then the GBD model with Dagum baseline distribution vector is an extended BD model with
,
and
parameter vectors, denoted as
, having joint cdf
where
.
Note that, when
and
for
, it is simplified to the model
defined by Muhammed [
19].
Extended bivariate generalized Rayleigh model. The cdf of the GR distribution, also called Burr type X model [
31], is
If
, then the GBD model with a GR baseline distribution vector is an extended BGR model with
and
parameter vectors,
, with joint cdf
where
.
Hence, if
,
, it is obtained that
given by Sarhan [
20].
Extended bivariate Gumbel-G model. Alzaatrech et al. [
32] proposed a transformed-transformer method for generating families of continuous distributions. From such method, it is said that a random variable
U follows a Gumbel-G model,
-
if its cdf can be expressed as
where
G is the transformer distribution with parameter vector
. If
-
, then the GBD model with Gu-Gs baseline distribution vector is an extended BGu-G model,
-
, with parameters
,
, and
, where
encompasses all parameter vectors of
G in each baseline component. Thus, its joint cdf is given by
for
,
, where
.
In particular, when
and
for
,
-
given by Eliwa and El-Morshedy [
21].
Extended bivariate generalized inverted Kumaraswamy model. A random variable
U is said to be a GIK distribution defined by Iqbal et al. [
33], if its cdf is given by
If
, then the GBD model with GIKs baseline distribution vector is an extended BGIK model,
, with parameters
,
, and
, and its joint cdf can be written as
where
.
It is straightforward to see that
analyzed by Muhammed [
10] when
and
for
.
Extended bivariate Burr type X-G model. From the transformed-transformer method of Alzaatrech et al. [
32], it is said that a random variable
U follows a Burr X-G model,
-
if its cdf can be expressed as
where
is the parameter vector of the transformer distribution
G.
If
-
, then the GBD model with BX-Gs baseline distribution vector is an extended BBX-G model,
-
, with parameters
, and
, where
encompasses all parameter vectors of
G in each baseline component. Then, its joint cdf can be expressed as
where
.
In particular, if
for
, then
-
introduced by El-Morshedy et al. [
12].
GBD models from different baseline components. In addition, a GBD model can be derived from baseline components s belonging to different distribution families, which allows one to generate new bivariate distributions.
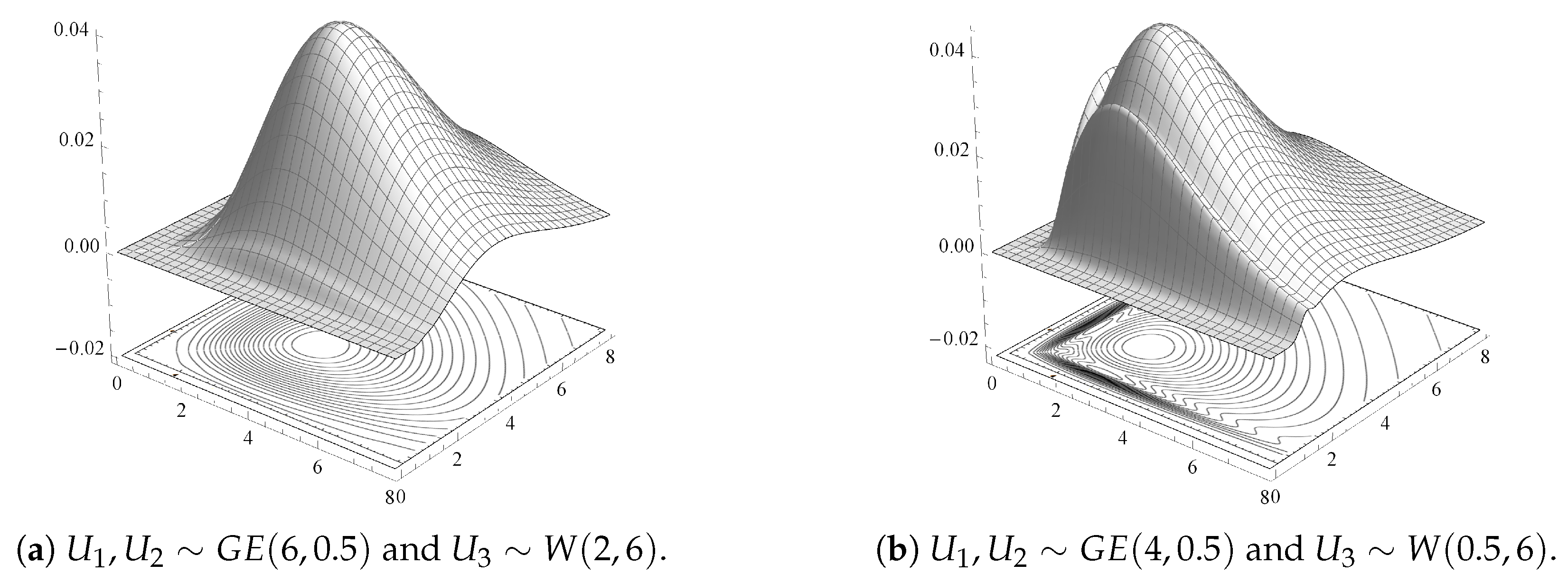
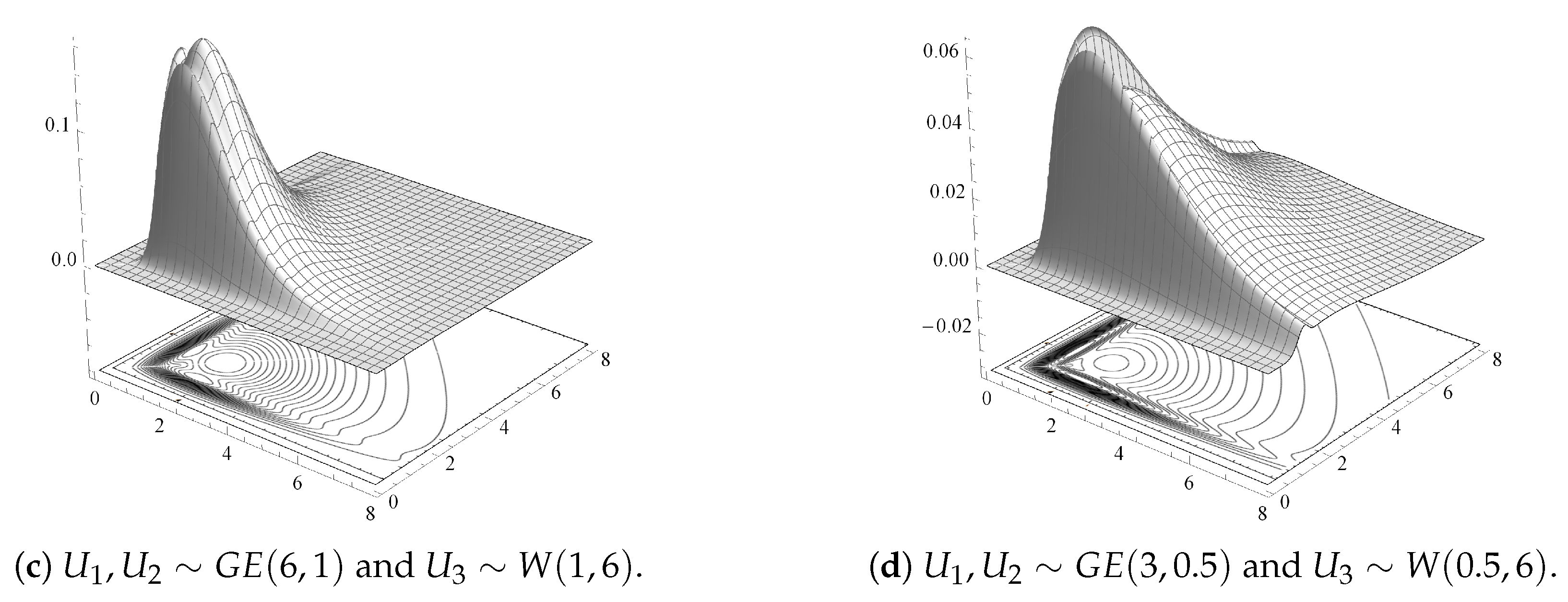
For illustrative purposes,
Figure 1a–d display 3D surfaces of different joint pdfs given by Theorem 3, along with their contour plots. Here,
and
are taken identically distributed
with different shape and scale parameter values, and
having a Weibull distribution with scale parameter
and shape parameter
,
.
Figure 1 shows that some of these GBD models are multi-modal bivariate models. It indicates a variety of shapes for the GBD family depending on the different baseline distribution components and for different parameter values.
5. Dependence and Stochastic Properties
In this section, we study various dependence and stochastic properties on the GBD family, its marginals and order statistics, and its copula representation. Notions of dependence and ageing for bivariate distributions can be found in Lai and Xie [
34] and Balakrishnan and Lai [
4]; see also Shaked and Shantikumar [
35] for univariate and multivariate stochastic orders.
5.1. GBD Model
Proposition 2. If model, then is positive quadrant dependent (PQD).
Proof. From (
1) and (
5), it is readily obtainable that
, which is equivalent to say that all random vector
, having a GBD model, is PQD. □
An immediate consequence of the PQD property is that
. Other important bivariate dependence properties are the following, whose proofs are provided in
Appendix A.
Proposition 3. Let be a random vector having a GBD model:
- 1.
is left tail decreasing (LTD).
- 2.
is left corner set decreasing (LCSD).
- 3.
Its joint cdf F is totally positive and of order 2 ().
Proof. Note that
F is
is equivalent to
is LCSD, which implies LTD (e.g., see Balakrishnan and Lai [
4]). Thereby, we only have to prove (3). From the definition of
property, it is equivalent to check that the following inequality holds:
for all
and
, where
, and
. Hence, from (
1), the inequality (
8) can be expressed as
where
,
,
and
. Moreover, one can observe that
.
Therefore, when
, i.e.,
, the inequality (
8) can be simplified as follows:
which is trivial, since
and
is a cdf. An analogous development follows for
, which completes the proof. □
Let us see now some results related to the reversed hazard gradient of a random vector from the GBD family, which is defined as an extension of the univariate case, see Domma [
36],
where each
represents the reversed hazard function of
,
, and assuming that
F is differentiable. In addition, it is said that
has a bivariate decreasing (increasing) reversed hazard gradient, BDRHG (BIRHG), if all components
s are decreasing (increasing) functions in the corresponding variables.
Proposition 4. If has a GBD model with baseline distribution vector , then its reversed hazard gradient is given byfor , when the reversed hazard function of , exists, . Proof. The proof is straightforward from the definition of reversed hazard rate function corresponding to the conditional cdf given by (1) of Theorem 4. □
Theorem 6. Let be a random vector having a GBD model. If s have decreasing reversed hazard functions (DRH), then .
Proof. It is straightforward from Proposition 4. □
Note that Theorem 6 provides the closure of the DRH property under the formation of a GBD model. Thus, the bivariate extension of a DRH distribution generated by the GBD family is BDRHG.
Nevertheless, it does not hold for the increasing reversed hazard (IRH) property, since both given in Proposition 4 have a negative jump discontinuity at for . Therefore, if , then cannot be BIRHG.
Finally, we present some interesting stochastic ordering results between bivariate random vectors of GBD type.
Theorem 7. Let and have GBD models with baseline distribution vectors and , respectively. If (), then .
Proof. The result immediately follows from the stochastic ordering between components and (
1), since
is equivalent to
, and the lower orthant ordering is defined by the inequality
for all
. □
Corollary 3. Let and with base distributions and (), respectively. If and (), then .
Proof. It is obvious that , i.e., , and then the proof readily follows from Theorem 7. □
Remark 1. From Corollary 3, if both EBPRH models are based on a common base distribution vector, (), then it is only necessary that to hold the lower orthant ordering.
5.2. Marginals and Order Statistics
Now, we study some stochastic properties of the marginals and the minimum and maximum order statistics of the GBD model.
Firstly, from (
5) and (
6), the reversed hazard function of the marginal
s can be expressed as
Therefore, the DRH (IRH) property is preserved to the marginals.
Theorem 8. If has a GBD model formed by (), then ().
Remark 2. Note that the IRH distributions have upper bounded support [37]. Thus, if any is not upper bounded, its reversed hazard function is always decreasing at the end, and then the marginal cannot be IRH. Therefore, it is necessary that () and they have the same upper bounds to be (). Example 1. Suppose s have extreme value distributions of type 3 with a common support, , whose cdf is defined byand otherwise. Its reversed hazard function is given bywhich is increasing (decreasing) in its support for . Thus, if (), then , and, consequently, (). Example 2. If has an EBGE model, then its marginals are , since given by (9) is the sum of two decreasing functions because of each is a with exponential baseline distributionwhich is evidently a decreasing function. Here, denotes an exponential random variable with mean . Remark 3. From (9), when the s have a common distribution , then the marginals with base distribution . Therefore, has the same monotonicity. In particular, if , then . Remark 4. From (9), if with the same base distribution , then with base , i.e., . Thus, Remark 3 also holds by using instead of . Secondly, the mean inactivity time (MIT), also called mean waiting time [
37], of a random variable
X is defined as
Thus, from (
5), the MIT of the marginal
s of a GBD model can be derived by
Here, we shall focus on two particular cases of GBD models, having baseline components with monotonous MIT, which is preserved by the marginals.
Example 3. Suppose , then its MIT can be expressed aswhich is an increasing MIT function (IMIT), i.e., . From (10), we obtain the MIT function of the marginals s for the bivariate exponential version of GBD type,Then, upon differentiation, has the same sign as the expression , which is positive, and therefore (). Example 4. Suppose , then its MIT can be expressed aswhere and are the cdf and pdf of a normal model with and , respectively. Moreover, taking into account that a random variable and its standardized version have PRH functions, and the standard normal distribution has the DRH property [38], we obtain that . Upon considering the cdf of s and (5), the marginal (). Thus, their MIT can be written aswhere for , and, consequently, On the other hand, the following stochastic orderings among the three baseline components of two GBD models are preserved by their corresponding marginals. The proof immediately follows from the definitions of the stochastic orderings.
Theorem 9. Let and have GBD models with base distribution vectors and , respectively.
- 1.
If (), then ().
- 2.
If (), then ().
Finally, we discuss some stochastic properties of the minimum and maximum order statistics of the GBD family. In this setting, from (
7), the reversed hazard function of the maximum statistic
of
of GBD type is determined by the sum of the reversed hazard rates of the baseline distribution vector:
when the pdf
of
exists,
. Hence, it is immediate the following result.
Theorem 10. If (), then .
Example 5. Suppose (). Then, the reversed hazard function of is given byand, therefore, if every , , then is increasing (decreasing) in x, i.e., . Example 6. If , then the maximum statistic of the EBGE model is , , since (11) is the sum of three decreasing functions. Remark 5. When s have a common distribution , the GBD model has a maximum statistic whose cdf is cube, and (11) can be written as . In particular, if , then . Remark 6. From Corollary 2, if with the same base distribution , with base and , i.e., . Thus, if and only if .
Furthermore, the MIT of the maximum statistic of a GBD model
can be derived by
for each specific baseline distribution vector
, when the integral exists. For instance, we will consider a particular case, similar to one used in Example 4.
Example 7. Suppose has a GBD model with and base distributions for , then each component , and consequently, for . Moreover, from Corollary 2, the maximum statistic with . Thus, which is obtained along the same line as Example 4, since Regarding the minimum statistic
of
of GBD type, some preservation results are also obtained based on its reversed hazard rate
, the proofs are given in
Appendix A, and from (
7)
can be written as
Theorem 11. If () and (), then .
Corollary 4. If () and , then .
Example 8. Suppose for and , then , and, consequently, from Corollary 4.
Remark 7. Note that, when s have a common distribution , (12) can be expressed as , and from Corollary 4, it is immediate to have that, if , then . Theorem 12. Let be a GBD model. Then, .
Proof. From (
11) and (
12), the statement is equivalent to
, which readily follows from Theorem 1.B.56 of Shaked and Shanthikumar [
35], since the baseline components
s are independent. □
5.3. Copula and Related Association Measures
Let us see now the copula representation of the GBD family and some related dependence measures of interest in the analysis of two-dimensional data.
It is well known that the dependence between the random variables
and
is completely described by the joint cdf
, and it is often represented by a copula which describes the dependence structure in a separate form from the marginal behaviour. In this setting, from Sklar’s theorem (e.g., see [
39]), if its marginal cdfs
s are absolutely continuous, then the joint cdf has a unique copula representation for
and reciprocally, if
is the inverse function of
(
), then there exists a unique copula
C in
, such that
Now, we can derive the copula representation for the joint cdf of the GBD family as a function of its base distribution vector
. In order to do this, by using (
5), the joint cdf (
1) can be expressed as
and taking
, the associated copula for an arbitrary base distribution vector
can be written as
where
which allows us to give an additional result.
Theorem 13. Let and be two GBD models with baseline distribution vectors and , respectively. If and have the same associated copula and , then .
Proof. It is immediate by using Theorem 6.B.14 of Shaked and Shanthikumar [
35] and (
5), since
implies
. □
Corollary 5. Let and be two GBD models with common baseline distributions, and , respectively. If , then .
Note that (
13) provides a general formula to establish the specific copula upon considering two particular continuous and increasing bijective functions
and
from
onto
. Fang and Li [
40] analyzed some stochastic orderings for an equivalent copula representation to (
13) with interesting applications in network security and insurance. In the last section, we shall use the bivariate copula representation (
13) to discuss the multivariate extension of the GBD family.
Furthermore, (
13) may be considered a generalization of the Marshall–Olkin copula, as displayed in the following results whose proofs are omitted.
Corollary 6. If has a GBD model with a common base distribution , then the copula representation of its joint cdf is Corollary 7. If has a GBD model with PRHs baseline distribution vector of the same base , i.e., , then the copula representation of its joint cdf is Some association measures for a bivariate random vector
of GBD type can be derived from the dependence structure described by the general expression (
13) for each particular pair of continuous and increasing bijective functions
and
determined by the specific baseline distribution vector. For instance, for the special GBD models given in Corollaries 6 and 7, the measures of dependence namely Kendall’s tau, Spearman’s rho, Blomqvist’s beta, and tail dependence coefficients, see Nelsen [
39] among others, can be calculated as follows.
Kendall’s tau. The Kendall’s
is defined as the probability of concordance minus the probability of discordance between two pairs of independent and identically distributed random vectors,
and
, as follows:
and it can be calculated through its copula representation
by
with
s uniform
random variables whose joint cdf is
C.
For example, if
has a GBD model with a common baseline
, upon substituting from the copula of Corollary 6 in (
14), it is easy to check that Kendall’s
.
Analogously, from the copula given in Corollary 7 of the GBD model for
components with a common base
, the Kendall’s
coefficient (
14) can be written as
Spearman’s rho. The Spearman’s
coefficient measures the dependence by three pairs of independent and identically distributed random vectors,
,
and
. It is defined as
which can be computed by its copula representation
by
Thus, if there is a common base distribution as in Corollary 6, the Spearman’s coefficient between and is .
In the case of
with a common base distribution
, from (
15) and Corollary 7, this association measure is
which coincides with one obtained by Kundu et al. [
9] for this specific GBD model,
. As remarked by Kundu et al. [
9] for the BPRH model, both coefficients,
and
, vary between 0 and 1 as
varies from 0 to
∞.
Blomqvist’s Beta. The Blomqvist’s
coefficient, also called the medial correlation coefficient, is defined as the probability of concordance minus the probability of discordance between
and its median point, say
, taking the following form:
and from the copula of its joint cdf
F, it can be expressed as
In the case of Corollary 6, it is immediate that the medial correlation coefficient between and is when it follows a GBD model with a common baseline distribution.
In the other case, from Corollary 7, the Blomqvist’s
coefficient (
16) is also readily obtainable between the marginals of a BPRH model:
which takes values between 0 and 1 as
varies from 0 to
∞.
Tail Dependence. The tail dependence measures the association of extreme events in both directions, the upper (lower) tail dependence
(
) provides an asymptotical association measurement in the upper (lower) quadrant tail of a bivariate random vector, given by (if it exists)
Similar to the above association coefficients, the tail dependence indexes can be calculated from the copula representation
of the joint cdf of
, as follows:
In particular, if
follows a GBD model with a common baseline distribution, upon substituting from the copula of Corollary 6 in (
17), it is easy to check that
and
.
In the case of
with the same base, from (
17) and Corollary 7, it is clear that the tail dependence indexes of the BPRH model are
and
which takes values between 0 and 1 as
varies from 0 to
∞.
6. Maximum Likelihood Estimation
In this section, we address the problem of computing the maximum likelihood estimations (MLEs) of the unknown parameters based on a random sample. The problem can be formulated as follows. Suppose
is a random sample of size
n from a GBD model, where it is assumed that, for
,
has the pdf
and
is of dimension
. The objective is to estimate the unknown parameter vector
. We use the following partition of the sample:
Based on the above observations, the log-likelihood function becomes
where
,
,
have been defined in Theorem 3.
Here, it is difficult to compute the MLEs of the unknown parameter vector
by solving a
optimization problem. To avoid that, we suggest using the EM algorithm, and the basic idea is based on considering a random sample of size
n from
, instead of the random sample of size
n from
. From the observed sample
, the sample
has missing values as shown in
Table 1. It is immediate that the MLEs of
,
and
can be obtained by solving the following three optimization problems of dimensions
,
and
, respectively,
which are computationally more tractable.
From
Table 1, if,
, then
is known, and
and
are unknown. Similarly, if
(
), then
(
) and
(
) are known. Hence, in the E-step of the EM algorithm, the ‘pseudo’ log-likelihood function is formed by replacing the missing
by its expected value,
, for
and
:
If
and
, then
If
and
, then
Therefore, we propose the following EM algorithm to compute the MLEs of . Suppose at the k-th iteration of the EM algorithm, the value of is ), then the following steps can be used to compute :
E-step
At the k-th step for , obtain the missing and as and , respectively. For obtain the missing and as and , respectively. Similarly, for , obtain the missing and as and , respectively.
Form the ’pseudo’ log-likelihood function as
, where
M-step
can be obtained by maximizing , and with respect to , and , respectively.
Mainly for illustrative purposes, two particular GBD models will be applied in the next section to show the usefulness of the above EM algorithm. Firstly, we shall consider a GBD model with baseline components having the same distribution type and different underlying parameters. Secondly, we shall use a GBD model with baseline components from different distribution families. The technical details of both of them can be found in
Appendix B.
8. Discussion and Conclusions
In this paper, we have presented the generalized bivariate distribution family by a generator system based on the maximization process from any three-dimensional baseline continuous distribution vector with independent components, providing bivariate models with dependence structure.
For the proposed GBD family, several distributional and stochastic properties have been established. The preservation of the PRH property for the marginals and the maximum order statistic has been obtained. The positive dependence has been shown between both marginals of the GBD models, some results about stochastic orders and on the preservation of the monotonicity of the reversed hazard function and of the mean inactivity time. Furthermore, the copula representation of the GBD model has been discussed, providing a general formula, and some related dependence measures have been also calculated for specific copulas of particular bivariate distributions of the GBD family. In addition, new bivariate distributions can be generated by combining independent baseline components from different distribution families, and several bivariate distributions given in the literature are derived as particular cases of the GBD family.
Note that, even in the simple case, the MLEs cannot be obtained in explicit forms, and it is required solving a multidimensional nonlinear optimization problem. We have proposed using an EM algorithm to compute the MLEs of the unknown parameters, and it is observed that the proposed EM algorithm perform quite satisfactorily in the two data analyses by using two different models of the GBD family. The experimental results summarized in
Table A1 disclose such efficiency of the EM algorithm with respect to a conventional numerical iterative procedure of the Newton-type. In more detail,
Table A1 presents the experimental results obtained by the Broyden–Fletcher–Goldfarb–Shanno algorithm for maximizing the log-likelihood function, available in the R package “maxLik” [
44].
It is worth mentioning that the bivariate copula representation (
13) allows us to discuss its multivariate extension. Let
s for
be a set of
mutually independent random variables with any continuous distribution functions, denoting by
the cdf of each
. Similarly to (
1), the joint cdf of the
q-dimensional random vector
with
is given by
which can be considered as a generator of
q-dimensional distribution models, called generalized multivariate distribution (GMD) family with baseline distribution vector
. Hence, the
q-dimensional copula representation of this GMD family can be expressed as
where
From these
q-dimensional joint cdf and copula, many distributional and stochastic properties established for the GBD family are extensible to the GMD family. Furthermore, by using this generator of multivariate distributions, the special bivariate models given in
Section 3 can be easily extended to the multivariate case, which contain multivariate versions of bivariate distributions given in the literature.