Abstract
Linear autonomous incommensurate systems that consist of two fractional-order difference equations of Caputo-type are studied in terms of their asymptotic stability and instability properties. More precisely, the asymptotic stability of the considered linear system is fully characterized, in terms of the fractional orders of the considered Caputo-type differences, as well as the elements of the linear system’s matrix and the discretization step size. Moreover, fractional-order-independent sufficient conditions are also derived for the instability of the system under investigation. With the aim of exemplifying the theoretical results, a fractional-order discrete version of the FitzHugh–Nagumo neuronal model is constructed and analyzed. Furthermore, numerical simulations are undertaken in order to substantiate the theoretical findings, showing that the membrane potential may exhibit complex bursting behavior for suitable choices of the model parameters and fractional orders of the Caputo-type differences.
1. Introduction
The domain of fractional calculus is regarded as an important tool in modelling various phenomena from different scientific and engineering fields [1,2,3,4,5,6]. Many recent research results conjecture that fractional-order systems lead to more precise results in a wide range of practical applications, relying on the fact that memory and hereditary properties of different processes may be successfully modeled while using fractional-order derivatives.
Stability and linearization results have been recently explored for continuous-time fractional-order systems in [7,8], as well as for discrete-time fractional systems [9,10]. The solutions of initial value problems that involve fractional-order Caputo-type and Riemann-Liouville-type difference equations with positive orders were given in [11], but a qualitative study regarding the stability properties of these types of equations or systems of several equations have not been explored. Stability results for linear systems with Caputo fractional-order difference equations with variable order of convolution type have been studied in [12], along with the recurrence formulas for the solutions of linear initial value problems for the considered fractional operators. Still, when compared to fractional-order differential equations [13,14,15,16,17,18], their discrete-time counterparts, namely fractional-order difference equations, have not received the same amount of attention, especially regarding their qualitative theory and, in particular, their stability and instability properties.
The most common and effective method used in the study of the stability properties of linear discrete-time fractional order systems is considered to be the -transform method. When taking into consideration the fact that fractional derivatives are successfully approximated by fractional h-differences of similar types, a link can be established between the stability properties of fractional-order differential systems and their discrete-time counterparts, i.e., fractional-order systems of difference equations.
In this paper, we explore the stability and instability properties for systems that consist of two fractional-order difference equations. The type of fractional-order difference operator chosen in this work is the fractional-order Caputo h-difference operator, as it has nonzero equilibrium points, while Grunwald-Letnikov or Riemann–Liouville operators only have the origin as equilibrium states [10]. As an application, we undertake a stability analysis of a fractional-order version of the discrete FitzHugh–Nagumo neuronal model [19], as illustrated by some numerical simulations. The occurrence of discrete Hopf and Flip bifurcations can also be remarked.
Recent experimental neuronal research [20,21] has indicated that fractional-order derivatives or differences may be incorporated in the mathematical modelling of neuronal dynamics. Fractional-order membrane potential dynamics have proven their utility in reproducing the electrical activity of neurons that were experimentally observed, as they are able to introduce capacitive memory effects [22]. Moreover, it has been suggested in [23] that a possible physical interpretation of the fractional order is that of the index of memory, which is in strong agreement with employing fractional-order operators in neuroscience modeling.
The paper is organized, as follows: we first introduce preliminary definitions regarding the Caputo fractional-order difference operator used, the formula of the -transform associated to the difference operator and we also recall the definitions for the notions of stability, asymptotic stability and asymptotic stability of order . Subsequently, we introduce the two-dimensional system of fractional-order difference equations of Caputo-type and deduce the associated characteristic equation while using the -transform method. Next, we explore stability and instability properties of the system in terms of the roots of the characteristic equation. A fractional-order-independent instability theorem is also proved, along with the necessary and sufficient fractional-order-dependent results. A discrete FitzHugh–Nagumo neuronal model is later investigated, as an application to the theoretical findings, followed by numerical simulations that reveal rich spiking behaviour.
2. Preliminaries
We first recall several definitions and properties regarding fractional-order difference operators, as introduced in [10,24], as well as the definition of the stability and/or instability of the trivial solution of a system of fractional-order difference equations. We restrict our attention to the Caputo-type h-difference operator of a fractional order , as it is a commonly used operator in applications.
Let , and be an arbitrary function.
Definition 1.
The operator
is called the forward h-difference operator.
We introduce a family of binomial functions on parameterized by and given by
with .
Definition 2.
Let be a function. The fractional h-sum of order is defined by
where “*” denotes the convolution operator, i.e.,
Definition 3.
Let . The operator denoted by is called the Caputo-type h-difference operator of order q for a function and it is given by
We recall the classical definition of the -transform associated to a sequence (see [25]).
Definition 4.
The - transform of a sequence is a complex function given by
where is a complex number for which the series converges absolutely.
Remark 1.
If , we obtain
The next proposition was proved in [26] and it will be useful in determining the characteristic equations that are associated to the considered system.
Proposition 1.
Let . Defining , where and , the -transform of is
where and .
The following n-dimensional fractional-order system is considered:
where and is a continuous function on the whole domain and Lipschitz-continuous with respect to the second variable, such that for any Let denote the unique solution of (1) satisfying the initial condition .
As in the case of the continuous counterpart explored in [27], we highlight the fact that, in general, because of the presence of the memory terms, the asymptotic stability of the null solution of system (1) will not be of exponential type [15,28]. Therefore, a particular type of non-exponential asymptotic stability, namely the notion of Mittag–Leffler stability was introduced for the case of fractional-order differential equations [29]. In the case of fractional-order difference systems, Mittag–Leffler stability was explored in [30]. In this paper, we focus our attention on a particular type of discrete Mittag–Leffler stability, specifically the -asymptotic stability, which pertains to the algebraic decay of the solutions.
Therefore, we recall the following definitions of notions of stability:
Definition 5.
- a.
- The trivial solution of (1) is called stable if for any there exists such that for every satisfying we have for any .
- b.
- The trivial solution of (1) is called asymptotically stable if it is stable and there exists , such that whenever .
- c.
- The trivial solution of (1) is called-asymptotically stableif it is stable and there exists , such that for any one has as
3. Stability Results for Systems of Two Fractional-Order Difference Equations
In what follows, we restrict our attention to the case of linear autonomous incommensurate fractional-order systems of the form:
where the system’s matrix is a real two-dimensional matrix, h is the discretization step, and are the fractional orders of Caputo forward difference operators.
By means of the -transform method, we obtain:
where the -transforms of x and y are denoted by and , respectively. This gives the following characteristic equation:
which is equivalent to
Observing that and multiplying the previous relation by , we obtain the characteristic function of the system (2):
In the remainder of the paper, we will denote .
Similarly to the continuous counterpart that was explored in [7,8], the next result can be obtained for the characterization of the stability and instability properties of system (2), with respect to the distribution of the roots of the characteristic function.
4. Fractional-Order Independent Results
We first explore several sufficient conditions that guarantee the instability of system (2), regardless of the choice of the fractional orders and .
Theorem 2
(Fractional-order independent instability results). System (2) is unstable for any choice of the fractional orders and if one of the following conditions hold:
- 1.
- ;
- 2.
- , and ;
- 3.
- and .
Proof.
- 1.
- Since and , because the function is continuous, it follows that it has at least one real root in the interval . From Theorem 1 it follows that system (2) is unstable.
- 2.
- We have:Because , and is a continuous function on , it follows that has at least one root in the interval and, consequently, from Theorem 1 system (2) is unstable.
- 3.
- If , with and thenDenoting , we have that and , therefore there exists such that . Hence, and as , it follows that has a real root in the interval . Thus, according to Theorem 1 system (2) is unstable.
□
5. Fractional-Order Dependent Results
In this section, let and , be arbitrarily fixed. In order to establish stability and instability conditions, the following curves and lines will be considered in the -plane:
- the line
- for , the smooth parametric curvewhere , for ,
- for , the line
We can easily prove the following lemmas, while using basic mathematical tools:
Lemma 1.
Let and be a complex-valued function, where . Then if and only if belongs to the line .
Proof.
is equivalent to the following equation
Dividing the previous equation by , we obtain:
Therefore, belongs to the line . □
Lemma 2.
Let . Subsequently, has a root z satisfying , if and only if belongs to the parametric curve .
Proof.
has a root on the unit circle if and only if there exists such that . Denoting , we first compute
Therefore, the equation is equivalent to
The following system is obtained by taking the real and imaginary parts of the terms in the above equation:
Solving this linear system with respect to the unknowns and we obtain:
Hence, . □
Lemma 3.
Let . Subsequently, has a root z satisfying , if and only if belongs to the line .
Proof.
For Equation (3) becomes
As in Lemma 2, has a root on the unit circle of the form , with if and only if the following relation holds:
By taking the real and imaginary parts of the previous equation, it follows that
The second relation of system (5) is equivalent to
which, combined with the first relation of (5) leads to
Substituting in Equation (6), it follows that belongs to the line . □
Lemma 4.
Let and let and denote the functions that define the parametric equations of the curve . The following properties holds:
- 1.
- Considering , it follows that belongs to the line ;
- 2.
- ;
- 3.
- , for all .
Proof.
The statements are proved in a straightforward manner.
Proof of Statement 1. Using the L’Hospital rule, we obtain:
Hence:
It follows that .
Proof of Statement 2. The proof is trivial and will be omitted; it follows from the fact that , for .
Proof of Statement 3. Dropping for simplicity the arguments of the functions and and applying the inequality of arithmetic and geometric means, we obtain:
as one can show, by elementary trigonometric inequalities, that
□
We have proved in Lemma 2 that, if , then the characteristic function admits a pair of complex conjugated roots on the unit circle and, therefore, in line with the classical theory of discrete dynamical systems, a discrete Hopf (Neimark–Sacker) bifurcation is expected to take place. Moreover, if , by Lemma 1, the characteristic function has a root , which is normally associated with a Flip bifurcation in the case of discrete dynamical systems (see [31]). Still, it is of high importance to underline that, for systems of fractional-order difference equations, there are no thorough results regarding their bifurcation theory, which remains yet to be investigated.
Lemma 5.
Let and . All of the roots of the equation
are in the interior of the unit disc if and only if .
Proof.
Let us denote . It is easy to see that , , and . Hence, if , the function has a real root in the interval . On the other hand, if , then the function has a real root in the interval .
Now let us consider and let us assume (using reductio ad absurdum) that the function has a root , such that . We may assume, without loss of generality, that . Let us consider and such that . Therefore:
Taking the real and imaginary parts, we obtain:
As and , we deduce that and , hence, .
Assuming that , we also obtain:
As , it follows that . Moreover, from Equation (7), we deduce that
which is a contradiction. Therefore, the only possibility is that , i.e., is a real root of Equation (7). We have , and, hence, the function f is increasing on . As and in this case, it follows that the function f does not have a root in the interval . In a similar way, as and , there are no roots in the interval either. Hence, our assumption is false, i.e., all the roots of the equation are in the interior of the unit disc (7). □
When taking into consideration the previous lemmas, as a main result of this section, the following fractional-order dependent stability theorem is given:
Theorem 3
(Fractional-order-dependent stability results). Let , and consider the discretization step h arbitrarily fixed such that
Proof.
Proof of statement 1. We will first show that, if , system (2) is asymptotically stable. Indeed, we consider
It is easy to see that is situated above the line , as:
Moreover, the point is in the third quadrant of the -plane satisfying . On the other hand, based on Lemma 4, the curve belongs to the region . Hence, it results that is situated below the curve . In conclusion, .
As , in this case, the characteristic Equation (3) becomes:
Based on inequality (8), for , with the convention , we have
Hence, it follows that for and, therefore, Lemma 5 implies that all roots of the characteristic Equation (9) are in the interior of the unit disc and, hence, system (2) is asymptotically stable. Therefore, system (2) is asymptotically stable, for any .
In what follows, the transversality condition will be verified, at the boundary of the domain . We consider and distinguish two cases.
Case 1. If , based on the parametric equations of the curve , it follows that there exists , such that . By Lemma 2, let denote the root of the characteristic function satisfying the relation
By the implicit function theorem, taking into consideration the characteristic Equation (3), we deduce:
where .
On one hand, we have:
On the other hand, it can be shown that
We obtain:
Therefore, this leads to:
A laborious but straightforward calculation (which can also by verified by symbolic computation tools) gives
In a similar manner, we compute , leading to the gradient vector:
Taking into account the parametric equations of the curve , it follows that the gradient vector is normal to the curve , pointing towards the region above the curve. Hence, the following transversality condition can be expressed in terms of the directional derivative:
for any vector pointing towards the region above the curve . Therefore, as the parameters vary and cross the curve into the region above the curve, becomes larger than 1.
Case 2. If , based on Lemma 1, we will now denote, by , the root of the characteristic function satisfying the relation
Following the same method as above, Equation (10) now provides:
As , it follows that
Hence:
In a similar manner, computing , we obtain the gradient vector:
It is easy to see that the vector is normal to the line . Moreover, as , i.e.,
the gradient vector is normal to the line , pointing towards the region that is below the line. Similarly as in the previous case, the transversality condition implies that, as the parameters vary and cross the line into the region below the line, becomes larger than 1.
Therefore, from the previously discussed case, we deduce that, as the parameters are varied and leave the domain , the asymptotic stability of the system (2) is lost.
Proof of statement 2. The proof follows the same lines as previously and, hence, it will be omitted.
We remark that inequality (8) plays an important role in the proof of Theorem 3, giving an upper bound for the discretization step h. Moreover, Figure 1 exemplifies the results that were obtained in Theorem 3, for several values of the discretization step h, when considering the fractional orders and and .
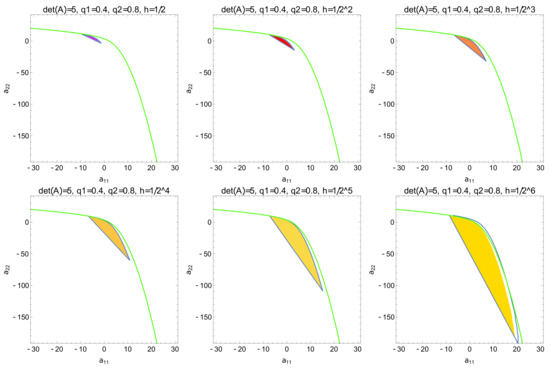
Figure 1.
Stability regions in the -plane, for several values of the discretization step h. The boundary of the stability region corresponding to the continuous-time counterpart [8] is represented by green curve.
6. A Discrete FitzHugh-Nagumo Neuronal Model
The FitzHugh–Nagumo neuronal model describes a biological neuron’s spiking behavior and it is a simplification of the well-known Hodgkin–Huxley model. Several studies have previously suggested that, at the neuronal membrane level, conductance adaptation is history dependent and, hence, its response can be described by a power-law function [21,22,32], leading to mathematical models that involve fractional-order differential equations [33]. Here, we consider a discretization of the fractional-order version of the FitzHugh–Nagumo model that was studied in [8]:
where v is the neuronal membrane potential, w represents a recovery variable, and I is an external excitation current. Moreover, and are the fractional orders of the Caputo h-difference operators, with .
It is important to emphasize that, in the numerical investigation of the continuous-time fractional-order FitzHugh–Nagumo model undertaken in [8], the well-known Adams–Bashforth– Moulton scheme was used [34]. Instead, in this section, we investigate the discrete-time model that was obtained by replacing the fractional-order Caputo derivatives with fractional-order h-differences of Caputo type.
Rewriting the second equation of system (11), we obtain:
where , and .
It follows that system (11) is a conductance-based system of the form:
with and is a linear function.
Similarly to the case of the continous version of the fractional-order FitzHugh–Nagumo neuronal model [8], the equilibrium states of the fractional-order neuronal model (12) can be determined. In order to investigate the stability of equilibrium states, the Jacobian matrix associated to system (12) at an arbitrary equilibrium state is:
where
Based on the results that were obtained in Theorem 3, the stability regions have been determined and transposed to the -plane for different values of the equilibrium membrane potential and several discretization steps. Figure 2 plots these regions.
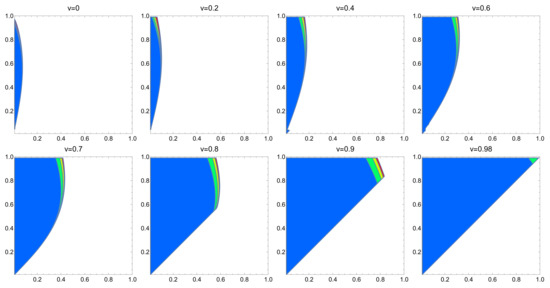
Figure 2.
Superposition of stability regions displayed in the -plane for equilibrium states of system (12) (with parameter values: , ), considering several values of the equilibrium membrane potential between 0 and , taking the discretization steps , , and 1, respectively (the smallest region plotted in blue corresponds to the largest step size ).
Taking , , , and as values for the parameters of system (11), the equilibrium potential is . In Figure 3, the evolution of the membrane potential can be observed, taking an initial condition from a small neighborhood of the equilibrium. We considered the value of the fractional order for the recovery variable to be and varied the value of the fractional order corresponding to the membrane potential . A Hopf bifurcation appears to be occurring for a value in the interval as for , we have an asymptotically stable behaviour and for , oscillations can be observed, depicting individual spikes that can be modulated by the fractional order and that complement the dynamic behavior displayed by classical integer order counterpart, as observable in the last image of Figure 3.
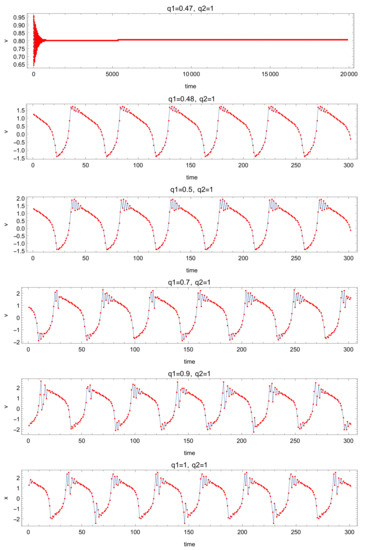
Figure 3.
Evolution of membrane potential of system (11), with parameter values , , , and for different values of the fractional orders.
7. Conclusions
Theoretical results regarding both asymptotic stability and instability properties of two-dimensional systems of autonomous linear fractional-order difference equations of Caputo type have been explored. The theoretical findings were later applied in the investigation of a fractional-order version of the well-known FitzHugh–Nagomo neuronal model. Moreover, numerical simulations revealed that the chaotic bursting and spiking behavior of the membrane potential of a biological neuron can be modulated by varying the corresponding fractional order of the system. This is in accordance with previous results that were published in the literature for other types of fractional-order neuronal models [22,35,36,37,38], where the spike frequency and amplitude reduction have also been observed as the fractional-order decreases (which is associated to a greater influence of the memory of the membrane potential).
Author Contributions
Conceptualization, O.B., E.K., D.M. and M.W.; methodology, O.B., E.K., D.M. and M.W.; software, O.B. and E.K.; validation, O.B., E.K., D.M. and M.W.; formal analysis, O.B., E.K., D.M. and M.W.; investigation, O.B., E.K., D.M. and M.W.; resources, O.B., E.K., D.M. and M.W.; data curation, O.B., E.K., D.M. and M.W.; writing—original draft preparation, O.B., E.K., D.M. and M.W.; writing—review and editing, O.B., E.K., D.M. and M.W.; visualization, O.B., E.K., D.M. and M.W.; supervision, E.K.; project administration, O.B. and E.K. All authors have read and agreed to the published version of the manuscript.
Funding
This article is based upon work from COST Action CA15225, a network supported by COST (European Cooperation in Science and Technology). The work was supported by Polish funds of National Science Center, granted on the basis of decision DEC-2016/23/B/ST7/03686.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cottone, G.; Paola, M.D.; Santoro, R. A novel exact representation of stationary colored Gaussian processes (fractional differential approach). J. Phys. A Math. Theor. 2010, 43, 085002. [Google Scholar] [CrossRef]
- Engheia, N. On the role of fractional calculus in electromagnetic theory. IEEE Antennas Propag. Mag. 1997, 39, 35–46. [Google Scholar] [CrossRef]
- Henry, B.I.; Wearne, S.L. Existence of Turing instabilities in a two-species fractional reaction-diffusion system. SIAM J. Appl. Math. 2002, 62, 870–887. [Google Scholar] [CrossRef]
- Heymans, N.; Bauwens, J.C. Fractal rheological models and fractional differential equations for viscoelastic behavior. Rheol. Acta 1994, 33, 210–219. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Relaxation-Oscillation and Fractional Phenomena. Chaos Solitons Fractals 1996, 7, 1461–1477. [Google Scholar] [CrossRef]
- Ionescu, C.; Lopes, A.; Copot, D.; Machado, J.T.; Bates, J. The role of fractional calculus in modeling biological phenomena: A review. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 141–159. [Google Scholar] [CrossRef]
- Brandibur, O.; Kaslik, E. Stability properties of a two-dimensional system involving one Caputo derivative and applications to the investigation of a fractional-order Morris-Lecar neuronal model. Nonlinear Dyn. 2017, 90, 2371–2386. [Google Scholar] [CrossRef]
- Brandibur, O.; Kaslik, E. Stability of two-component incommensurate fractional-order systems and applications to the investigation of a FitzHugh-Nagumo neuronal model. Math. Methods Appl. Sci. 2018, 41, 7182–7194. [Google Scholar] [CrossRef]
- Mozyrska, D.; Wyrwas, M. Explicit criteria for stability of fractional h-difference two-dimensional systems. Int. J. Dyn. Control 2017, 5, 4–9. [Google Scholar] [CrossRef]
- Mozyrska, D.; Wyrwas, M. Stability by linear approximation and the relation between the stability of difference and differential fractional systems. Math. Methods Appl. Sci. 2017, 40, 4080–4091. [Google Scholar] [CrossRef]
- Mozyrska, D.; Wyrwas, M. Fractional Linear Equations with Discrete Operators of Positive Order. Adv. Model. Control Non-Integer-Order Syst. Lect. Notes Electr. Eng. 2015, 320, 47–58. [Google Scholar]
- Mozyrska, D.; Wyrwas, M. Stability of Linear Systems with Caputo Fractional-, Variable-Order Difference Operator of Convolution Type. In Proceedings of the 2018 41st International Conference on Telecommunications and Signal Processing (TSP), Athens, Greece, 4–6 July 2018; pp. 1–4. [Google Scholar]
- Sabatier, J.; Farges, C. On stability of commensurate fractional order systems. Int. J. Bifurc. Chaos 2012, 22, 1250084. [Google Scholar] [CrossRef]
- Li, C.; Ma, Y. Fractional dynamical system and its linearization theorem. Nonlinear Dyn. 2013, 71, 621–633. [Google Scholar] [CrossRef]
- Čermák, J.; Kisela, T. Stability properties of two-term fractional differential equations. Nonlinear Dyn. 2015, 80, 1673–1684. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, D.; Zhang, H. Stability analysis on a class of nonlinear fractional-order systems. Nonlinear Dyn. 2016, 86, 1023–1033. [Google Scholar] [CrossRef]
- Kukushkin, M.V. Asymptotics of eigenvalues for differential operators of fractional order. Fract. Calc. Appl. Anal. 2019, 22, 658–680. [Google Scholar] [CrossRef]
- Kukushkin, M.V. On One Method of Studying Spectral Properties of Non-selfadjoint Operators. In Abstract and Applied Analysis; Hindawi: London, UK, 2020; Volume 2020. [Google Scholar]
- FitzHugh, R. Impulses and physiological states in theoretical models of nerve membrane. Biophys. J. 1961, 1, 445–466. [Google Scholar] [CrossRef]
- Anastasio, T.J. The fractional-order dynamics of brainstem vestibulo-oculomotor neurons. Biol. Cybern. 1994, 72, 69–79. [Google Scholar] [CrossRef]
- Lundstrom, B.N.; Higgs, M.H.; Spain, W.J.; Fairhall, A.L. Fractional differentiation by neocortical pyramidal neurons. Nat. Neurosci. 2008, 11, 1335–1342. [Google Scholar] [CrossRef]
- Weinberg, S.H. Membrane capacitive memory alters spiking in neurons described by the fractional-order Hodgkin-Huxley model. PLoS ONE 2015, 10, e0126629. [Google Scholar] [CrossRef] [PubMed]
- Du, M.; Wang, Z.; Hu, H. Measuring memory with the order of fractional derivative. Sci. Rep. 2013, 3, 3431. [Google Scholar] [CrossRef] [PubMed]
- Mozyrska, D.; Wyrwas, M. Stability of discrete fractional linear systems with positive orders. Sci. Direct 2017, 50, 8115–8120. [Google Scholar]
- Elaydi, S. An Introduction to Difference Equations; Springer Science & Business Media: New York, NY, USA, 2005. [Google Scholar]
- Mozyrska, D.; Wyrwas, M. The Z-transform method and delta type fractional difference operators. Discret. Dyn. Nat. Soc. 2015, 852734. [Google Scholar] [CrossRef]
- Brandibur, O.; Kaslik, E. Exact stability and instability regions for two-dimensional linear autonomous systems of fractional-order differential equations. arXiv 2019, arXiv:1910.07237. [Google Scholar]
- Gorenflo, R.; Mainardi, F. Fractional calculus, integral and differential equations of fractional order. In Fractals and Fractional Calculus in Continuum Mechanics; Carpinteri, A., Mainardi, F., Eds.; CISM Courses and Lecture Notes; Springer: Wien, Austria, 1997; Volume 378, pp. 223–276. [Google Scholar]
- Li, Y.; Chen, Y.; Podlubny, I. Mittag-Leffler stability of fractional order nonlinear dynamic systems. Automatica 2009, 45, 1965–1969. [Google Scholar] [CrossRef]
- Wyrwas, M.; Mozyrska, D. On Mittag–Leffler Stability of Fractional Order Difference Systems. Adv. Model. Control Non-Integer-Order Systems. Lect. Notes Electr. Eng. 2015, 320, 209–220. [Google Scholar]
- Kuznetsov, Y.A. Elements of Applied Bifurcation Theory; Springer Science & Business Media: New York, NY, USA, 2004; Volume 112. [Google Scholar]
- Mercik, S.; Weron, K. Stochastic origins of the long-range correlations of ionic current fluctuations in membrane channels. Phys. Rev. E 2001, 63, 051910. [Google Scholar] [CrossRef] [PubMed]
- Magin, R.L. Fractional calculus models of complex dynamics in biological tissues. Comput. Math. Appl. 2010, 59, 1586–1593. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.; Freed, A. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Teka, W.; Marinov, T.M.; Santamaria, F. Neuronal spike timing adaptation described with a fractional leaky integrate-and-fire model. PLoS Comput. Biol. 2014, 10, e1003526. [Google Scholar] [CrossRef]
- Teka, W.; Stockton, D.; Santamaria, F. Power-Law Dynamics of Membrane Conductances Increase Spiking Diversity in a Hodgkin-Huxley Model. PLoS Comput. Biol. 2016, 12, e1004776. [Google Scholar] [CrossRef] [PubMed]
- Teka, W.W.; Upadhyay, R.K.; Mondal, A. Spiking and bursting patterns of fractional-order Izhikevich model. Commun. Nonlinear Sci. Numer. Simul. 2018, 56, 161–176. [Google Scholar] [CrossRef]
- Mondal, A.; Sharma, S.K.; Upadhyay, R.K.; Mondal, A. Firing activities of a fractional-order FitzHugh-Rinzel bursting neuron model and its coupled dynamics. Sci. Rep. 2019, 9, 15721. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).