Unsteady Stagnation Point Flow of Hybrid Nanofluid Past a Convectively Heated Stretching/Shrinking Sheet with Velocity Slip
Abstract
1. Introduction
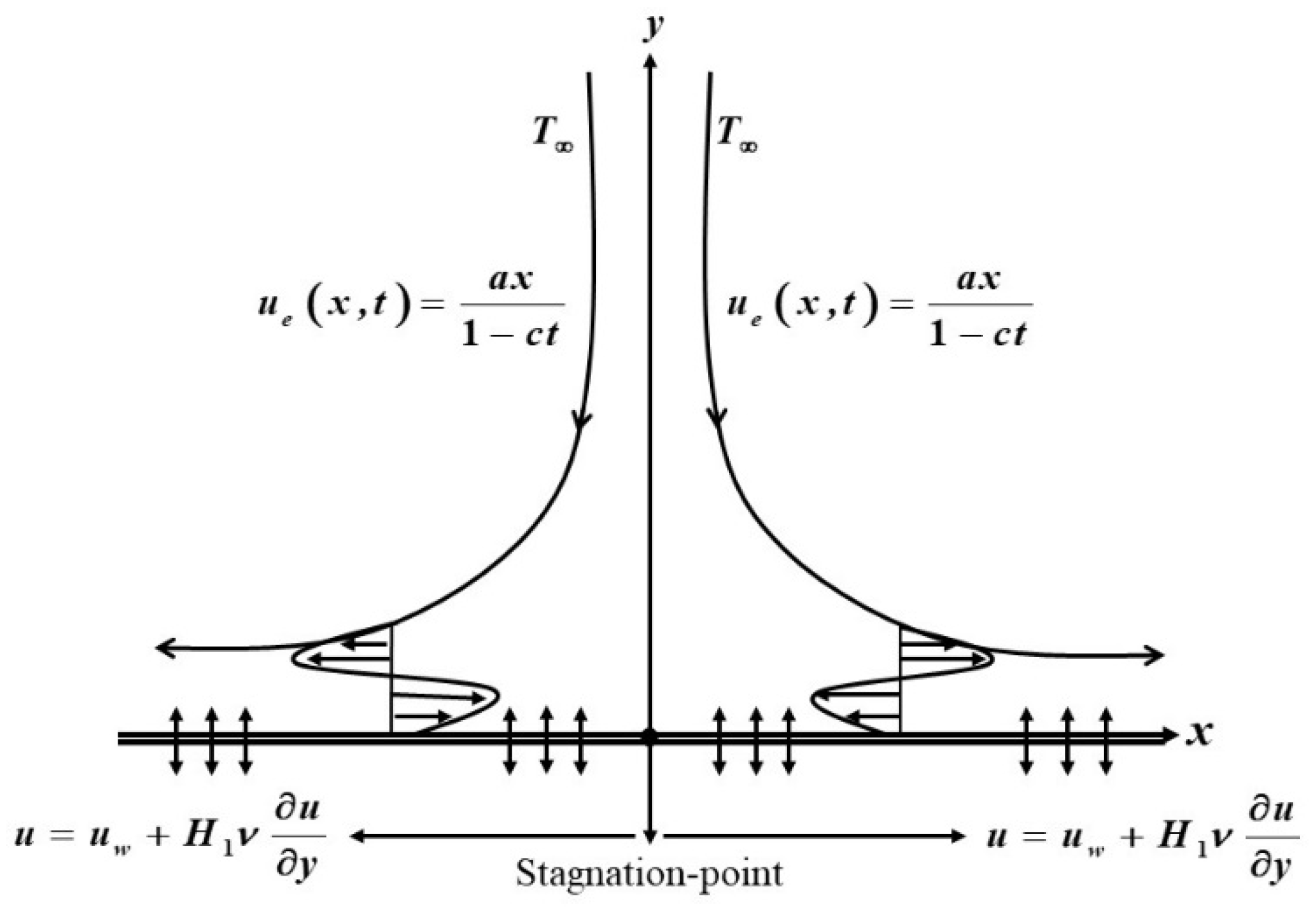
2. Mathematical Model
3. Analysis of Solution Stability
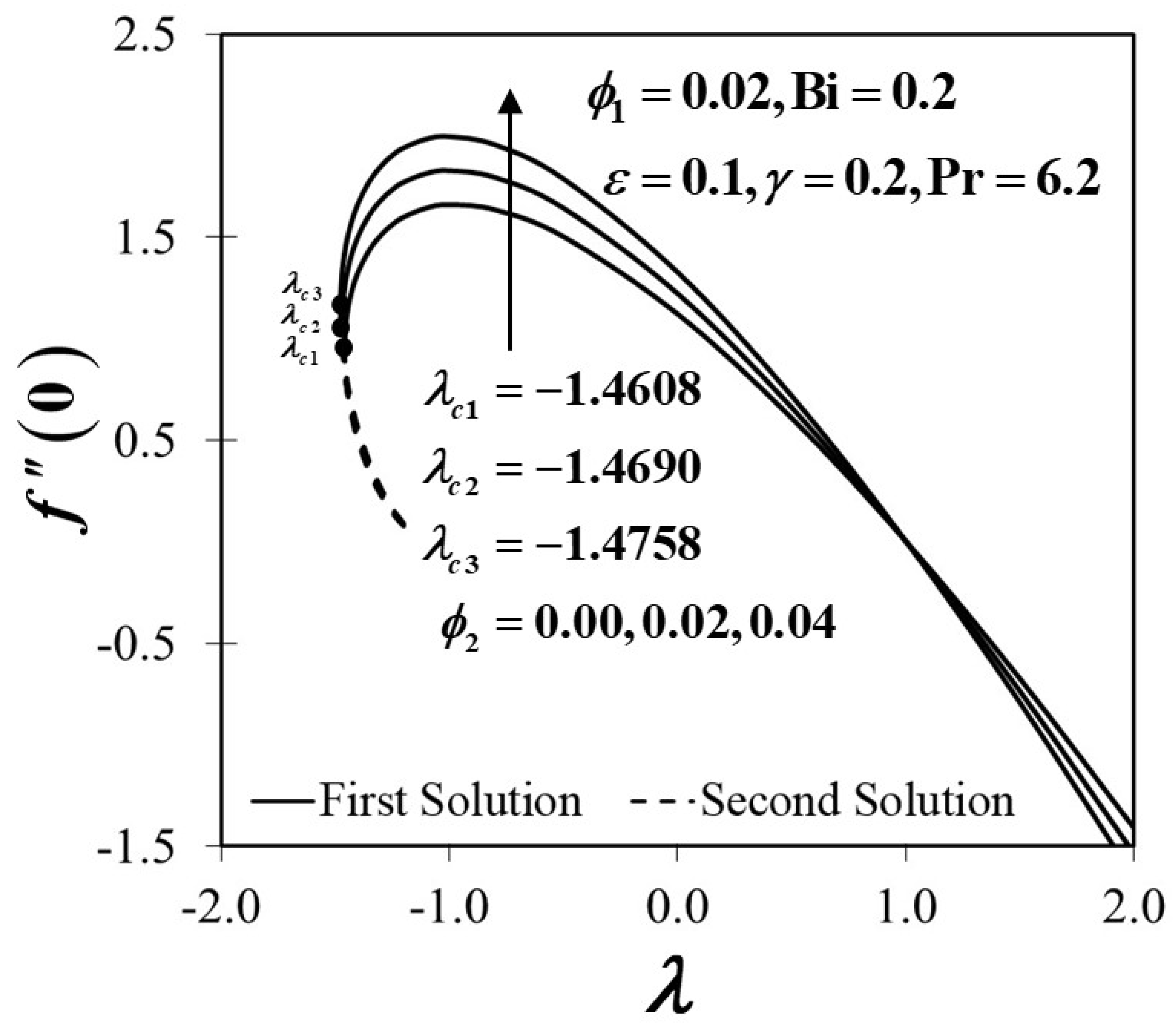
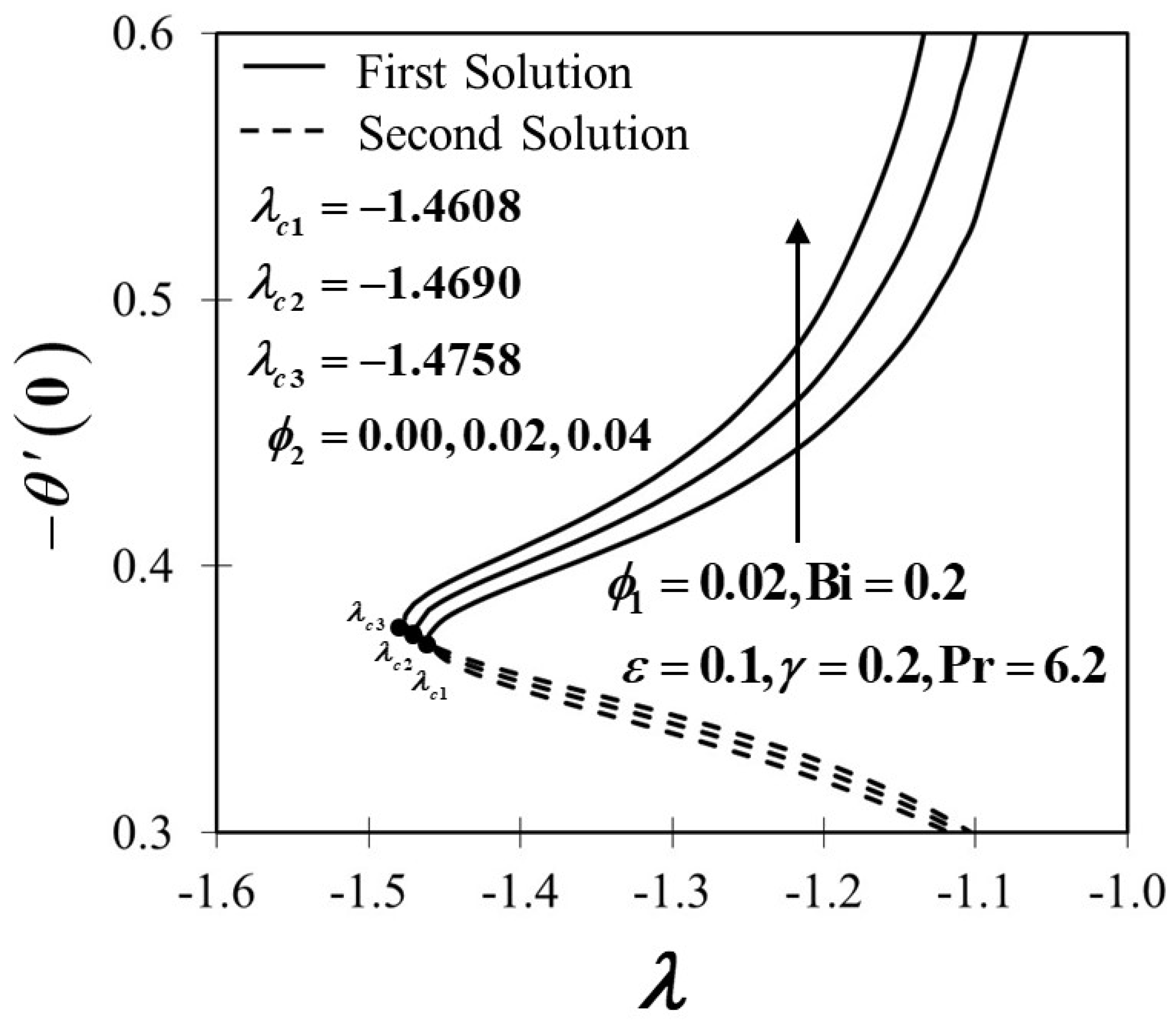
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Roman letters | |
| constant | |
| Bi | Biot number |
| skin friction coefficient | |
| specific heat at constant pressure | |
| velocity slip factor | |
| heat transfer coefficient | |
| dimensionless stream function | |
| thermal conductivity of the fluid | |
| local Nusselt number | |
| heat capacitance of the fluid | |
| Prandtl number | |
| local Reynolds number in axis | |
| time | |
| fluid temperature | |
| reference temperature | |
| ambient temperature | |
| velocities component in the and directions, respectively | |
| velocities of the free stream in | |
| velocities of the stretching/shrinking surface | |
| x, y | rtesian coordinates |
| Greek symbols | |
| stream function | |
| similarity variable | |
| dimensionless temperature | |
| unsteadiness parameter | |
| ratio of the velocity parameter | |
| velocity slip parameter | |
| dynamic viscosity of the fluid | |
| kinematic viscosity of the fluid () | |
| density of the fluid | |
| dimensionless time variable | |
| wall shear stress | |
| nanoparticle volume fractions for Al2O3 (alumina) | |
| nanoparticle volume fractions for Cu (copper) | |
| eigenvalue | |
| smallest eigenvalue | |
| Subscripts | |
| base fluid | |
| nanofluid | |
| hybrid nanofluid | |
| solid component for Al2O3 (alumina) | |
| solid component for Cu (copper) | |
| Superscript | |
| differentiation with respect to | |
References
- Schlichting, H.; Gersten, K. Boundary Layer Theory; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Smith, F.T. Steady and unsteady boundary layer separation. Annu. Rev. Fluid Mech. 1986, 18, 197–220. [Google Scholar] [CrossRef]
- White, F.M. Viscous Fluid Flow; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Elbashbeshy, E.M.A.; Bazid, M.A.A. Heat transfer over an unsteady stretching surface. Heat Mass Transf. 2004, 41, 1–4. [Google Scholar] [CrossRef]
- Bhattacharyya, K. Dual solutions in unsteady stagnation-point flow over a shrinking sheet. Chin. Phys. Lett. 2011, 28, 084702. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. The boundary layers of an unsteady stagnation-point flow in a nanofluid. Int. J. Heat Mass Transf. 2012, 55, 6499–6505. [Google Scholar] [CrossRef]
- Fan, T.; Xu, H.; Pop, I. Unsteady stagnation flow and heat transfer towards a shrinking sheet. Int. Commun. Heat Mass Transf. 2010, 37, 1440–1446. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Unsteady three-dimensional MHD non-axisymmetric Homann stagnation point flow of a hybrid nanofluid with stability analysis. Mathematics 2020, 8, 784. [Google Scholar] [CrossRef]
- Kamal, F.; Zaimi, K.; Ishak, A.; Pop, I. Stability analysis on the stagnation-point flow and heat transfer over a permeable stretching/shrinking sheet with heat source effect. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 2650–2663. [Google Scholar] [CrossRef]
- Basir, F.; Hafidzuddin, E.H.; Naganthran, K.; Chaharborj, S.S.; Kasihmuddin, M.S.M.; Nazar, R. Stability analysis of unsteady stagnation-point gyrotactic bioconvection flow and heat transfer towards the moving sheet in a nanofluid. Chin. J. Phys. 2020, 65, 538–553. [Google Scholar] [CrossRef]
- Jusoh, R.; Nazar, R.; Pop, I. Impact of heat generation/absorption on the unsteady magnetohydrodynamic stagnation point flow and heat transfer of nanofluids. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 557–574. [Google Scholar] [CrossRef]
- Zheng, Y.; Ahmed, N.A.; Zhang, W. Heat dissipation using minimum counter-flow jet ejection during spacecraft re-entry. Procedia Eng. 2012, 49, 271–279. [Google Scholar] [CrossRef][Green Version]
- Fisher, E.G. Extrusion of Plastics; Wiley: New York, NY, USA, 1976. [Google Scholar]
- Hiemenz, K. Die Grenzschicht an einem in den gleichförmigen Flüssigkeitsstrom eingetauchten geraden Kreiszylinder. Dinglers Polytech. J. 1911, 326, 321–324. [Google Scholar]
- Homann, F. Der Einfluss grosser Zähigkeit bei der Strömung um den Zylinder und um die Kugel. Z. Angew. Math. Mech. 1936, 16, 153–164. [Google Scholar]
- Howarth, L. CXLIV. The boundary layer in three-dimensional flow—Part II. The flow near a stagnation point. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1951, 42, 1433–1440. [Google Scholar]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I. Mixed convective stagnation point flow towards a vertical Riga plate in hybrid Cu–Al2O3/water nanofluid. Mathematics 2020, 8, 912. [Google Scholar]
- Khashi’ie, N.S.; Hafidzuddin, E.H.; Ariffin, N.M.; Wahi, N. Stagnation point flow of hybrid nanofluid over a permeable vertical stretching/shrinking cylinder with thermal stratification effect. CFD Lett. 2020, 12, 80–94. [Google Scholar]
- Fang, T.G.; Wang, F.J. Momentum and heat transfer of a special case of the unsteady stagnation-point flow. Appl. Math. Mech. Engl. 2020, 41, 51–82. [Google Scholar]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow towards a stagnation point on a stretching/shrinking cylinder. Sci. Rep. 2020, 10, 1–12. [Google Scholar]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. MHD mixed convection stagnation point flow of a hybrid nanofluid past a vertical flat plate with convective boundary condition. Chin. J. Phys. 2020, 66, 630–644. [Google Scholar]
- Wang, C.Y. Flow over a surface with parallel grooves. Phys. Fluids. 2003, 15, 1114–1121. [Google Scholar]
- Sharipov, F.; Seleznev, V. Data on internal rarefied gas flows. J. Phys. Chem. Ref. Data 1998, 27, 657–706. [Google Scholar]
- Hafidzuddin, E.H.; Nazar, R.; Arifin, N.M.; Pop, I. Effects of anisotropic slip-on three-dimensional stagnation-point flow past a permeable moving surface. Eur. J. Mech. B Fluids. 2017, 65, 515–521. [Google Scholar] [CrossRef]
- Pavlišič, A.; Huš, M.; Prašnikar, A.; Likozar, B. Multiscale modelling of CO2 reduction to methanol over industrial Cu/ZnO/Al2O3 heterogeneous catalyst: Linking ab initio surface reaction kinetics with reactor fluid dynamics. J. Clean. Prod. 2020, 275, 122958. [Google Scholar] [CrossRef]
- Navier, C.L. Memorie sur les lois du lois du mouvement des fluides. Mem. Acad. Sci. Inst. France 1827, 6, 298–440. [Google Scholar]
- Maxwell, J. On stresses in rarefied gases arising from inequalities of temperature. Philos. Trans. R. Soc. Lond. 1879, 27, 231–256. [Google Scholar]
- Wang, C.Y. Stagnation flows with slip: Exact solutions of the Navier-Stokes equations. Z. Fur Angew. Math. Und Phys. 2003, 54, 184–189. [Google Scholar] [CrossRef]
- Rao, I.J.; Rajagopal, K.R. Effect of the slip boundary condition on the flow of fluids in a channel. Acta Mech. 1999, 135, 113–126. [Google Scholar] [CrossRef]
- Jusoh, R.; Nazar, R.; Pop, I. Three-dimensional flow of a nanofluid over a permeable stretching/shrinking surface with velocity slip: A revised model. Phys. Fluids 2018, 30, 033604. [Google Scholar] [CrossRef]
- Yoshimura, A.; Prud’homme, R.K. Wall slip corrections for couette and parallel disk viscometers. J. Rheol. 1988, 32, 53–67. [Google Scholar] [CrossRef]
- Vajravelu, K.; Mukhopadhyay, S. Fluid Flow, Heat and Mass Transfer at Bodies of Different Shapes: Numerical Solutions; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Mukhopadhyay, S. Effects of slip-on unsteady mixed convective flow and heat transfer past a porous stretching surface. Nucl. Eng. Des. 2011, 241, 2660–2665. [Google Scholar] [CrossRef]
- Mahapatra, R.T.; Nandy, S.K. Slip effects on unsteady stagnation-point flow and heat transfer over a shrinking sheet. Meccanica 2013, 48, 1599–1606. [Google Scholar] [CrossRef]
- Majumder, M.; Chopra, N.; Andrews, R.; Hinds, B.J. Nanoscale hydrodynamics: Enhanced flow in carbon nanotubes. Nature 2005, 438, 930. [Google Scholar] [CrossRef]
- Noghrehabadi, A.; Pourrajab, R.; Ghalambaz, M. Effect of partial slip boundary condition on the flow and heat transfer of nanofluids past stretching sheet prescribed constant wall temperature. Int. J. Therm. Sci. 2012, 54, 253–261. [Google Scholar] [CrossRef]
- Van Gorder, R.A.; Sweet, E.; Vajravelu, K. Nano boundary layers over stretching surfaces. Commun. Nonlinear Sci. Numer. Simulat. 2010, 15, 1494–1500. [Google Scholar] [CrossRef]
- Dinarvand, S.; Rostami, M.N. Rotating Al2O3-H2O nanofluid flow and heat transfer with internal heating, velocity slip and different shapes of nanoparticles. Multidiscip. Model. Mater. Struct. 2020. Available online: https://doi.org/10.1108/MMMS-01-2020-0017 (accessed on 17 August 2020). [CrossRef]
- Seth, G.S.; Bhattacharyya, A.; Kumar, R.; Chamkha, A.J. Entropy generation in hydromagnetic nanofluid flow over a non-linear stretching sheet with Navier’s velocity slip and convective heat transfer. Phys. Fluids 2018, 30, 122003. [Google Scholar] [CrossRef]
- Rahman, J.U.; Khan, U.; Ahmad, S.; Ramzan, M.; Suleman, M.; Lu, D.; Inam, S. Numerical Simulation of Darcy–Forchheimer 3D Unsteady Nanofluid Flow Comprising Carbon Nanotubes with Cattaneo–Christov Heat Flux and Velocity and Thermal Slip Conditions. Processes 2019, 7, 687. [Google Scholar] [CrossRef]
- Reddy, R.C.S.; Reddy, P.S. A comparative analysis of unsteady and steady Buongiorno’s Williamson nanoliquid flow over a wedge with slip effects. Chin. J. Chem. Eng. 2020, 28, 1767–1777. [Google Scholar] [CrossRef]
- Reddy, J.V.R.; Sugunamma, V.; Sandeep, N. Thermophoresis and Brownian motion effects on unsteady MHD nanofluid flow over a slendering stretching surface with slip effects. Alex. Eng. J. 2018, 57, 2465–2473. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J. Enhancing thermal conductivity of fluids with nanoparticles. ASME Publ. Fed. 1995, 231, 99–103. [Google Scholar]
- Shah, T.R.; Ali, H.M. Applications of hybrid nanofluids in solar energy, practical limitations and challenges: A critical review. Sol. Energy 2019, 183, 173–203. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Hybrid nanofluids for heat transfer applications—A state-of-the-art review. Int. J. Heat Mass Transf. 2018, 125, 82–103. [Google Scholar]
- Gupta, M.; Singh, V.; Kumar, S.; Kumar, S.; Dilbaghi, N. Up to date review on the synthesis and thermophysical properties of hybrid nanofluids. J. Clean. Prod. 2018, 190, 169–192. [Google Scholar]
- Xian, H.W.; Azwadi, N.; Sidik, C.; Aid, S.R.; Ken, T.L.; Asako, Y. Review on preparation techniques, properties and performance of hybrid nanofluid in recent engineering applications. J. Adv. Res. Fluid Mech. Therm. Sci. 2018, 45, 1–13. [Google Scholar]
- Madhesh, D.; Kalaiselvam, S. Experimental analysis of hybrid nanofluid as a coolant. Procedia Eng. 2014, 97, 1667–1675. [Google Scholar]
- Tahat, M.S.; Benim, A.C. Experimental analysis on thermophysical properties of Al2O3/CuO hybrid nanofluid with its effects on flat plate solar collector. Defect Diffus. Forum 2017, 374, 148–156. [Google Scholar]
- Labib, M.N.; Nine, M.J.; Afrianto, H.; Chung, H.; Jeong, H. Numerical investigation on effect of base fluids and hybrid nanofluid in forced convective heat transfer. Int. J. Therm. Sci. 2013, 71, 163–171. [Google Scholar]
- Moghadassi, A.; Ghomi, E.; Parvizian, F. A numerical study of water-based Al2O3 and Al2O3–Cu hybrid nanofluid effect on forced convective heat transfer. Int. J. Therm. Sci. 2015, 92, 50–57. [Google Scholar]
- Devi, S.U.; Devi, S.P.A. Heat transfer enhancement of Cu–Al2O3/water hybrid nanofluid flow over a stretching sheet. J. Niger. Math. Soc. 2017, 36, 419–433. [Google Scholar]
- Takabi, B.; Salehi, S. Augmentation of the heat transfer performance of a sinusoidal corrugated enclosure by employing hybrid nanofluid. Adv. Mech. Eng. 2014, 6, 147059. [Google Scholar]
- Aladdin, N.A.L.; Bachok, N.; Pop, I. Cu–Al2O3/water hybrid nanofluid flow over a permeable moving surface in presence of hydromagnetic and suction effects. Alex. Eng. J. 2020, 59, 657–666. [Google Scholar]
- Plant, R.D.; Hodgson, G.K.; Impellizzeri, S.; Saghir, M.Z. Experimental and numerical investigation of heat enhancement using a hybrid nanofluid of copper oxide/alumina nanoparticles in water. J. Therm. Anal. Calorim. 2020, 141, 1951–1968. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Sherif, E.S.M. Dual solutions and stability analysis of a hybrid nanofluid over a stretching/shrinking sheet executing MHD flow. Symmetry 2020, 12, 276. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Roşca, N.C.; Roşca, A.V.; Pop, I. Mixed convection and stability analysis of stagnation-point boundary layer flow and heat transfer of hybrid nanofluids over a vertical plate. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 3737–3754. [Google Scholar] [CrossRef]
- Wang, C.Y. Stagnation flow towards a shrinking sheet. Int. J. Non-Linear Mech. 2008, 43, 377–382. [Google Scholar] [CrossRef]
- Dzulkifli, N.F.; Bachok, N.; Yacob, N.A.; Arifin, N.M.; Rosali, H. Unsteady stagnation-point flow and heat transfer over a permeable exponential stretching/shrinking sheet in nanofluid with slip velocity effect: A stability analysis. Appl. Sci. 2018, 8, 2172. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar]
- Merkin, J.H. Natural-convection boundary-layer flow on a vertical surface with Newtonian heating. Int. J. Heat Fluid Flow 1994, 15, 392–398. [Google Scholar]
- Merrill, K.; Beauchesne, M.; Previte, J.; Paullet, J.; Weidman, P. Final steady flow near a stagnation point on a vertical surface in a porous medium. Int. J. Heat Mass Transf. 2006, 49, 4681–4686. [Google Scholar]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Suresh, S.; Venkitaraj, K.P.; Selvakumar, P. Synthesis, characterisation of Al2O3–Cu nanocomposite powder and water-based nanofluids. Adv. Mater. Res. 2011, 328, 1560–1567. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I.; Nazar, R.; Hafidzuddin, E.H.; Wahi, N. Three-dimensional hybrid nanofluid flow and heat transfer past a permeable stretching/shrinking sheet with velocity slip and convective condition. Chin. J. Phys. 2020, 66, 157–171. [Google Scholar] [CrossRef]
- Ismail, N.S.; Arifin, N.M.; Nazar, R.; Bachok, N. Stability analysis of unsteady MHD stagnation point flow and heat transfer over a shrinking sheet in the presence of viscous dissipation. Chin. J. Phys. 2019, 57, 116–126. [Google Scholar] [CrossRef]
- Jusoh, R.; Nazar, R.; Pop, I. Flow and heat transfer of magnetohydrodynamic three-dimensional Maxwell nanofluid over a permeable stretching/shrinking surface with convective boundary conditions. Int. J. Mech. Sci. 2017, 124, 166–173. [Google Scholar] [CrossRef]












| Properties | ||||
|---|---|---|---|---|
| Cu | 400 | 8933 | 385 | 1.67 |
| Al2O3 | 40 | 3970 | 765 | 0.85 |
| H2O | 0.613 | 997.1 | 4179 | 21 |
| Properties | Hybrid Nanofluid |
|---|---|
| Dynamic viscosity | |
| Density | |
| Thermal capacity | |
| Thermal conductivity |
| Present Result | Mahapatra and Nandy [34] | Wang [58] | ||||
|---|---|---|---|---|---|---|
| First Solution | Second Solution | First Solution | Second Solution | First Solution | Second Solution | |
| −0.25 | 1.402241 | - | 1.402242 | - | 1.4022404 | - |
| −0.50 | 1.495670 | - | 1.495672 | - | 1.4956704 | - |
| −0.75 | 1.489298 | - | 1.489296 | - | 1.4893004 | - |
| −1.00 | 1.328817 | 0.000000 | 1.328819 | 0.000000 | 1.3288204 | 0.000000 |
| −1.10 | 1.186680 | 0.049229 | 1.186680 | 0.049229 | - | - |
| −1.15 | 1.082231 | 0.116702 | 1.082232 | 0.116702 | 1.082230 | 0.116702 |
| −1.20 | 0.932473 | 0.233650 | 0.932470 | 0.233648 | - | - |
| −1.246 | 0.609826 | 0.529035 | 0.584374 | 0.554215 | 0.5543004 | - |
First Solution | Second Solution | ||
|---|---|---|---|
| 0.1 | −1.30 | 0.7646 | −0.7093 |
| −1.380 | 0.1015 | −0.1398 | |
| −1.3820 | 0.0095 | −0.0500 | |
| 0.2 | −1.40 | 0.6870 | −0.6316 |
| −1.460 | 0.2387 | −0.2435 | |
| −1.4690 | 0.0088 | −0.0225 | |
| 0.4 | −1.68 | 0.1822 | −0.1576 |
| −1.684 | 0.0912 | −0.0696 | |
| −1.6851 | 0.0276 | −0.0067 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Unsteady Stagnation Point Flow of Hybrid Nanofluid Past a Convectively Heated Stretching/Shrinking Sheet with Velocity Slip. Mathematics 2020, 8, 1649. https://doi.org/10.3390/math8101649
Zainal NA, Nazar R, Naganthran K, Pop I. Unsteady Stagnation Point Flow of Hybrid Nanofluid Past a Convectively Heated Stretching/Shrinking Sheet with Velocity Slip. Mathematics. 2020; 8(10):1649. https://doi.org/10.3390/math8101649
Chicago/Turabian StyleZainal, Nurul Amira, Roslinda Nazar, Kohilavani Naganthran, and Ioan Pop. 2020. "Unsteady Stagnation Point Flow of Hybrid Nanofluid Past a Convectively Heated Stretching/Shrinking Sheet with Velocity Slip" Mathematics 8, no. 10: 1649. https://doi.org/10.3390/math8101649
APA StyleZainal, N. A., Nazar, R., Naganthran, K., & Pop, I. (2020). Unsteady Stagnation Point Flow of Hybrid Nanofluid Past a Convectively Heated Stretching/Shrinking Sheet with Velocity Slip. Mathematics, 8(10), 1649. https://doi.org/10.3390/math8101649






