Abstract
Unsteady stagnation point flow in hybrid nanofluid (Al2O3-Cu/H2O) past a convectively heated stretching/shrinking sheet is examined. Apart from the conventional surface of the no-slip condition, the velocity slip condition is considered in this study. By incorporating verified similarity transformations, the differential equations together with their partial derivatives are changed into ordinary differential equations. Throughout the MATLAB operating system, the simplified mathematical model is clarified by employing the bvp4c procedure. The above-proposed approach is capable of producing non-uniqueness solutions when adequate initial assumptions are provided. The findings revealed that the skin friction coefficient intensifies in conjunction with the local Nusselt number by adding up the nanoparticles volume fraction. The occurrence of velocity slip at the boundary reduces the coefficient of skin friction; however, an upward trend is exemplified in the rate of heat transfer. The results also signified that, unlike the parameter of velocity slip, the increment in the unsteady parameter conclusively increases the coefficient of skin friction, and an upsurge attribution in the heat transfer rate is observed resulting from the increment of Biot number. The findings are evidenced to have dual solutions, which inevitably contribute to stability analysis, hence validating the feasibility of the first solution.
1. Introduction
The most common problem in boundary layer flow that had been treated so far is much focused on those for steady flows. Even though it is the steady flows that seem to have the utmost significance in real-world demands, some cases of time-varying in the boundary layer which is unsteady indicate an important role in several engineering problems. Some of the examples are start-up processes where the motions in rest are transits from a steady flow to another, and periodic motions of the working fluid [1]. The behavior of unsteady boundary layer flow describes an unusual pattern compared to the steady flow owing to the additional time-dependent terms in the governing equations, which exaggerated the separation of boundary layer and the fluid motion arrangement [2,3]. The thermal and mechanical properties of such an unsteady mechanism in the boundary layer approximation have been studied both analytically and numerically. Elbashbeshy and Bazid [4] presented the numerical investigation towards the unsteady stretching surface with heat transfer analysis. At the same time, Bhattacharya [5] managed to prove the existence of dual solutions in unsteady stagnation point flow towards a shrinking sheet by employing the shooting method approach coupled with a Runge–Kutta integration scheme. Bachok et al. [6] concluded that inclusion of the unsteadiness parameter offers a significant impact towards the boundary layer flow in nanofluid and Fan et al. [7] presented analytical solutions using the homotopy analysis method (HAM) and managed to advertise a highly precise analytical estimation which is in excellent agreement with the numerical results offered by the Keller box scheme. It is worth mentioning that a considerable amount of reviews on the unsteady stagnation point flow due to a stretching/shrinking surface have been accomplished by numerous researchers, including [8,9,10,11].
The stagnation point flow is one of the important topics in mechanics of fluid, in the way that stagnation point generally occurs in both engineering and science flow fields. The stagnation point flow could be identified in the extrusion process, polymer industry, and plane counter jet [12,13]. The ground-breaking research in this topic was first initiated by Hiemenz [14] who exposed an analytical explanation of two-dimensional stagnation point flow, and soon after, Homann [15] conducted a classical study of stagnation point in three-dimensional flow with regard to an axisymmetric case; whereas Howarth [16] tackled the problem of non-axisymmetric flow close to the stagnation area in three-dimensional analysis. Recently, Khashi’ie et al. [17,18], Fang and Wang [19], Waini et al. [20], and Zainal et al. [21] have scrutinized the stagnation point flow problems in diverse aspects with no-slip boundary conditions. Nevertheless, in numerous engineering occasions, the slip effect should be comprised, such as flow over lubricated or coated surfaces, rough or striated surfaces [22] and internal rare field gas flow [23]. Examples of industrial applications involving the slip boundary conditions are fluid flow on multiple interfaces, rare field fluid problems, and also the reacting flow in reactors [24,25]. Navier [26] and Maxwell [27] were the primary researchers who pioneered the study of linear slip boundary conditions, while Wang [28] has well reflected a comprehensive theoretical analysis considering the no-slip boundaries concentrating on the stagnation point flow. Rao and Rajagopal [29] have conducted an extensive evaluation and argument between the slip and no-slip condition, and Jusoh et al. [30] deliberated a modified nanofluid model towards a stretching/shrinking surface by considering a velocity slip parameter in three-dimensional flow. The study revealed that an increase in the velocity slip magnitude contributed to the intensification of skin friction coefficients.
In certain cases, the velocity slip or the non-adherence of the fluid to a solid boundary phenomenon was witnessed, for instance, in the micro-scale devices [31]. Fluids promoting slip are critical in technical applications such as polishing artificial heart valves and internal cavities [32]. The flow behavior and the shear stress in the fluid are rather distinctive with a slip at the wall boundary compared to those with no-slip condition. Besides that, the velocity slip effect does influence the heat transfer rate and was confirmed by Mukhopadhyay [33], who had investigated the slip impact of the unsteady mixed convective flow towards a porous stretching surface with heat transfer. The analysis found that the heat transfer rate declines with the velocity slip parameter, while it upsurges with the unsteadiness parameter. Mahapatra and Nandy [34] conducted a numerical study of the unsteady stagnation point flow past a shrinking sheet and heat transfer with the presence of slip effects in a viscous fluid. The results conveyed that with the increase of the velocity slip and unsteady parameter, the heat transfer rate is reported to escalate. Meanwhile, in nanofluid flow, Majumder et al. [35] specified that exertion of the partial velocity slip against the sheet surface is common. By relying on the finding in [35], Noghrehabadi et al. [36] then examined the impact of partial velocity slip on the nanofluid boundary layer flow and heat transfer past a stretching sheet. The work in [36] reported that an increment in the velocity slip effect decreases the momentum boundary layer thickness. Van Gorder et al. [37], who examined the nanofluid boundary layer flow over a stretching surface, also conveyed a similar result as [36] and further explained that no-slip condition is not applicable for fluid flows at nanoscales. Besides that, Dinarvand and Rostami [38] studied the rotating nanofluid flow and heat transfer with the presence of internal heating, velocity slip, and different shapes of nanoparticles. They showed that an increment in the velocity slip effect reduces the skin friction coefficient significantly. Researchers also tend to analyze the effect of velocity slip in the unsteady nanofluid flow as unsteady flow problems are more relatable to real-world applications. For instance, Seth et al. [39] studied the unsteady hydromagnetic nanofluid flow and heat transfer past a non-linearly stretching surface with Navier’s velocity slip and presented the analysis of entropy generation. Other valuable references regarding unsteady nanofluid flow with the velocity slip effect can be found in [40,41,42].
Ever since the outstanding inventions achieved by Choi and Eastman [43], who originated the brilliant idea of demonstrating the nanoparticle suspension in a base fluid and came out with the nanofluid term, a better type of working fluid is still being pursued. Acknowledging the sufficient improvement in the thermal conductivity of the conventional fluid is crucial, an advanced nanofluid form known as hybrid nanofluid is introduced, which intends to have highly developed heat conductivity. This modern type of fluid agent has fascinated numerous researchers owing to its reputation in the emergence and improvement of thermal characteristics in realistic applications, including micro-channel, heat pipes, heat exchangers, air conditioning systems, and mini-channel heat sink [44,45]. Gupta et al. [46] and Xian et al. [47] have reviewed the preparation method of hybrid nanoparticles along with the stabilization and its significance in industrial sectors. One of the critical elements in establishing a sustainable hybrid nanofluid suspension is selecting an appropriate combination of nanoparticles. The most widely used nanoparticles for the formation of hybrid nanofluid suspension are carbon materials (graphite, MWCNTs, CNTs), metals (Cu, Ag), metal oxides (Al2O3, CuO, Fe2O3), metal carbide, and a metal nitride. Madhesh and Kalaiselvam [48] conducted an experimental study to examine the features of hybrid nanofluid as a coolant agent, Tahat and Benim [49] examined the efficiency of hybrid nanofluid on flat plate solar collector, and they verified that the viscosity, thermal conductivity, and density of the working fluid had increased together with the concentration of Al2O3/CuO concentration, thus enhancing the solar collector proficiency. Some early research on hybrid nanofluid that employed the numerical method was done by Labib et al. [50], who investigated the impact of base fluids and hybrid nanofluid using a two-phase mixture model in forced convective heat transfer. Moghadassi et al. [51] revealed that the heat transfer performance is enhanced by adding the nanoparticles of Al2O3-Cu hybrid nanofluid while creating a small pressure drop in the system regime, Devi and Devi [52] focused on the mathematical inspection towards a stretching sheet. In contrast, the evaluation of heat transfers in the natural convection of Al2O3/water nanofluid and Al2O3-Cu/water hybrid nanofluid with a discrete heat source was explored by Takabi and Salehi [53]. Additional details on this topic are well described in the literatures [54,55,56].
To the best of the authors’ knowledge, the existing literature does not consider the unsteady stagnation point flow of hybrid nanofluids with the presence of velocity slip parameter and stability analysis in their models. Thus, the addressed issues above have inspired the authors to perform a numerical study in unsteady stagnation point flow towards a convectively heated stretching/shrinking sheet in alumina–copper/water (Al2O3-Cu/H2O) with the impact of velocity slip on heat transfer. The hybrid nanofluid is recognized by dispersing Al2O3 nanoparticles into H2O, followed by Cu with different volume fractions and the thermophysical properties of the hybrid nanofluid are adopted from Ghalambaz et al. [57] and Takabi and Salehi [53], which were based on the feasible physical assumptions and are in agreement with the conservation of mass and energy. The present work also utilized the bvp4c approach, which can be accessed in the MATLAB programming system towards solving the formulated problem. The existence of more than one solution is predictable; thus, an analysis of solution stability is completed to confirm the steadiness of the solutions which has an actual physical interpretation. The explanation of the results and the convergence of the obtained solutions are deliberated on in detail. Particular cases of current findings are evaluated in accordance with those of Mahapatra and Nandy [34] and Wang [58]. Furthermore, the consensus between previous and current findings is outstanding, and the agreement is excellent.
2. Mathematical Model
The unsteady two-dimensional stagnation-point flow of a hybrid Al2O3-Cu/H2O nanofluid over a convectively heated stretching/shrinking sheet with the influence of velocity slip is considered in this research work, as illustrated in Figure 1 (see Dzulkifli et al. [59]). The stretching/shrinking velocity is denoted by where denotes a constant corresponds to stretching and shrinking cases while signifies the unsteadiness problem and is the velocity of the free stream where represents the strength of the stagnation flow. The ambient temperature and the reference temperature are and , respectively. Now, we let the bottom of the sheet be heated by convection from a hot fluid at a specific temperature which supplies a coefficient of heat transfer, expressed by From all of the assumptions above; the governing boundary layer equations can be acknowledged as [34].
where denotes the component of velocity in axis, is the velocity component in axis, is the Al2O3-Cu/H2O dynamic viscosity, the density of Al2O3-Cu/H2O, is the Al2O3-Cu/H2O temperature, is the thermal/heat conductivity of Al2O3-Cu/H2O and is the Al2O3-Cu/H2O heat capacity. The boundary conditions, together with the partial slip for velocity, are set to
where is the velocity slip factor, in which refers to the initial value of the velocity slip factor. The copper (Cu) thermophysical properties, along with aluminum oxide (Al2O3) and water (H2O) nanoparticles, are provided in Table 1, as demonstrated by [60]. In the meantime, Table 2 issued the thermophysical properties hybrid nanofluid as established by [53,57]. The nanoparticles solid volume fraction is represented by , indicates the H2O density, and is the density of the hybrid nanoparticle, is the constant pressure of heat capacity, while denotes the thermal conductivity of H2O and is the hybrid nanoparticles thermal conductivity.
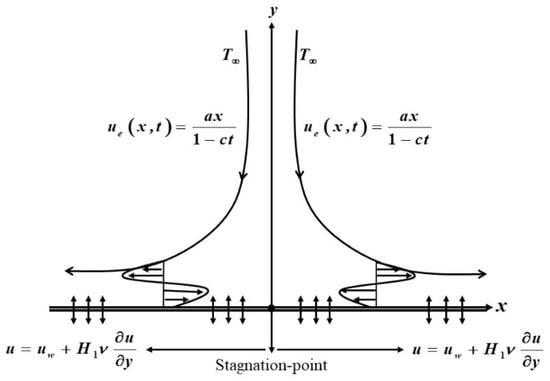
Figure 1.
The schematic of problem flow (Dzulkifli et al. [59]).

Table 1.
Cu thermophysical properties along with Al2O3 and H2O (Oztop and Abu Nada [60]).

Table 2.
Hybrid Al2O3-Cu/H2O nanofluids thermophysical properties (Takabi and Salehi [53], Ghalambaz et al. [57]).
In order to express the governing Equations (1)–(3) concerning the boundary conditions (4) in a much simpler form, the subsequent similarity transformations are presented [34]
where is the stream function that can be specified as and is the similarity variable. Thus, we attain
In view of the above relations, by employing the similarity variables (5) and (6), Equations (2) and (3) reduce to the following set of nonlinear similarity differential equations
Here, measures the unsteadiness parameter with , Pr represents the Prandtl number where Next, the initial and boundary conditions (4) now transform into
From Equation (9), symbolises as the ratio of velocity parameter, and Bi are the dimensionless velocity slip parameter and Biot number, respectively, which are described as
Next, we define the skin friction coefficient and the local Nusselt number as
The shear stress along the direction is represented by , while signifies the surface heat flux that accentuated by
By applying (5) and (12) into (11), we acquire
provided that is the local Reynolds number in x- axis.
3. Analysis of Solution Stability
By obeying the efforts of Merkin [61] and Merill et al. [62] from their outstanding discoveries of stability analysis scheme, the unsteady equations need to be deliberated in order to ultimately identify the reliable and stable solution since we notice the appearance of non-uniqueness solutions in the boundary value problem (7)–(9). Now, in accordance with the unsteady-state problem, a new similarity conversion is proposed
Employing the similarity variables of Equation (14) to Equations (7) and (8), we now obtain the following converted differential equations
with respect to
In accordance with Weidman et al. [63], to test the stability of the steady flow and which fulfil the boundary value problem and boundary conditions (refer to (7)–(9)), we write
by which is the eigenvalue of unidentified variables, while functions and are relatively small to and . The eigenvalue problems (15) and (16) result in an infinite group of eigenvalues that detect an early decay when is positive, while an early growth of disruptions is observed when is negative, which exposes the unstable flow. Substituting (18) into (15)–(17), we develop
and the boundary conditions are
The heat transfer stability and steady-state flow solutions and was implemented via , therefore and in (19)–(21). As a consequence, an early growth of Equation (18) is detected, and the subsequent generalized eigenvalue problem is recognized
subject to
The range of possible eigenvalues can be calculated by resting a boundary condition [64] of the present problem. In this study, we choose to repose , and the linear eigenvalue problems (22)–(24) are disclosed as for a fixed value of . It is worth mentioning that the values of are proficient in measuring the stability of the corresponding solutions and .
4. Results and Discussion
The mathematical computations of this research work were achieved by employing the bvp4c function in the MATLAB programming system subject to the governing ordinary differential Equations (7) and (8) together with the boundary conditions (9). A bvp4c method is a notable tool for solving the boundary value problem that has been extensively established by various researchers to clarify the boundary value concern. In order to ensure the obtainment of desired solutions, early estimation of the primary mesh point and variations step size is crucial. Also, a reasonable assumption of the thickness of the boundary layer along with effective preliminary approximation is essential for defining the non-uniqueness solutions. The consistency of the results generated in the present study is evaluated with those in [34,58], as accessible in Table 3, which is in excellent agreement.

Table 3.
Evaluation values of when by certain values of .
In this study, we recognized the hybrid Al2O3-Cu/H2O nanofluid by dispersing the first nanoparticle (alumina) into the base fluid (water) followed by the second nanoparticle (copper) with various amounts of volume fractions. It is important to declare that the dispersion of discrete nanoparticle Al2O3/Cu is capable of developing Al2O3-Cu/H2O and Cu-H2O nanofluids. Apart from that, the Prandtl number is set to be fixed at corresponds to water as the reference-based fluid, while as for the hybrid Al2O3-Cu/H2O nanofluid, the size of the nanoparticles is assumed to be standardized, and the thermophysical properties effect of nanoparticles agglomeration is ignored. The main purpose of the present study is to examine the influence of the control parameter such as the nanoparticles volume fraction , the unsteadiness parameter , the velocity slip parameter , and the Biot number towards the coefficients of skin friction variations and the heat transfer rate . The alumina and copper nanoparticles volume fraction in the present work is chosen within the range of which motivated by the experimental work done by Suresh et al. [65] who conducted the synthesis, characterization of nanocomposite powder for different volume concentrations 0.1%, 0.33%, 0.75%, 1%, and 2%. In their valuable study, the stability of the prepared nanofluids was determined by measuring the pH of nanofluids, and the nanofluid stability was found to diminish with increasing volume concentration. On another note, various values of the controlling parameter that has been used, are set within the following extent; and to ensure the certainty of the obtained solutions. The present study also interested in witnessing the non-uniqueness solutions that appear in the ordinary governing differential of the ensuing problem, hence confirm the real and valid solutions through the stability analysis by utilizing the bvp4c approach in MATLAB operating system (MATLAB R2019b, MathWorks, Natick, MA, USA).
The generated results of Equations (7) and (8) perceive the non-uniqueness (dual) solutions together with the boundary conditions (9) to a specific scope of where manifests the non-uniqueness solutions meeting point, and this too is regarded as a critical point. There is a single solution at a critical point, and that is the distinct line. The flow separation happens to occur after the critical point, and the flow is no longer laminar and does not obey the principle of boundary layer theory. According to the numerical results attained in this research work, it is proven that a non-uniqueness solutions appear, namely first and second solutions, as depicted in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15. The existence of the non-uniqueness solutions contributes to the analysis of solution stability so that one may be able to verify the theoretically relevant solution. The first solution, however, is predicted to be reliable and fundamentally exist in practice. The smallest eigenvalues for some values of when and with are tabulated in Table 4. The values of is noted approaching zero in the first and second solutions for in selected cases of Hence, the authors may assure that the stability formulation and practices of the current problem are accurate and reliable. The flow is measured unstable if is negative because it implies an early development of disruptions that leads to flow separation. The smallest eigenvalue with positive value implies the flow is practically attainable and sustainable, which elucidates the solution stabilizing property to overwhelm the allowing disruptions. Also, it denotes an initial deterioration of disruptions that appear. The positive value of describes the stable mode of the flow as in the first solution. The significance of dual solutions that contribute to stability analysis is in revealing the other possibilities of flow behavior, which may be useful for future references in the extrusion process. For example, in the present study, we have presented that the second solutions are unstable solutions with negative eigenvalues. These unstable solutions with the negative eigenvalues infer the growth of the disturbance in the solutions, especially at some range of the stretching/shrinking parameter When the shrinking rate increases, it limits other external forces’ effect at the sheet and eventually showed the opposite behavior of the transport phenomena than the first solutions in the same range of as the respective parameter varies. Moreover, any boundary value problem can generate more than one solution because of the nonlinearity in the boundary value problem; for example, see the mathematical model (7)–(9). Also, changes in the governing parameter values cause bifurcations in solutions that yield the existence of dual solutions [1]. Therefore, the mathematical model (7)–(9), which obeyed the boundary layer assumptions, managed to exhibit the variety in the fluid flow and heat transfer behavior through the uniqueness and existence of the solutions.
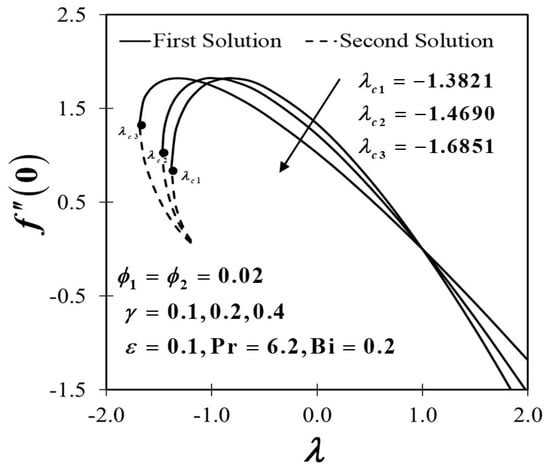
Figure 2.
Variants of towards with .
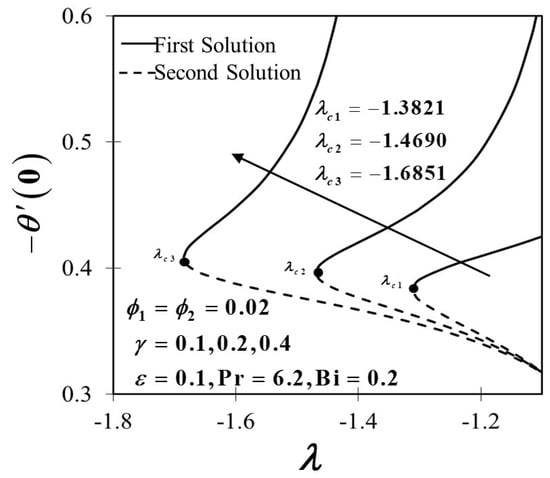
Figure 3.
Variants of towards with .
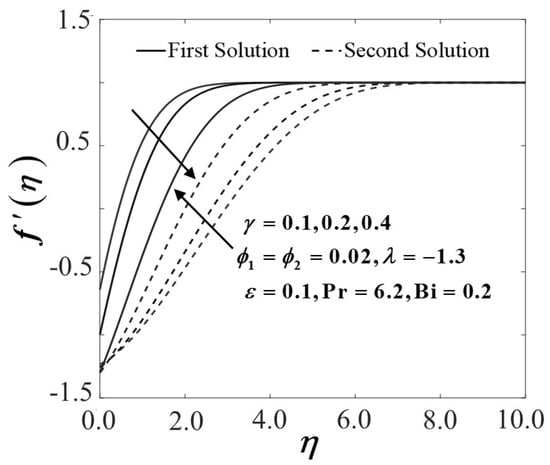
Figure 4.
Velocity profiles of with (shrinking case).
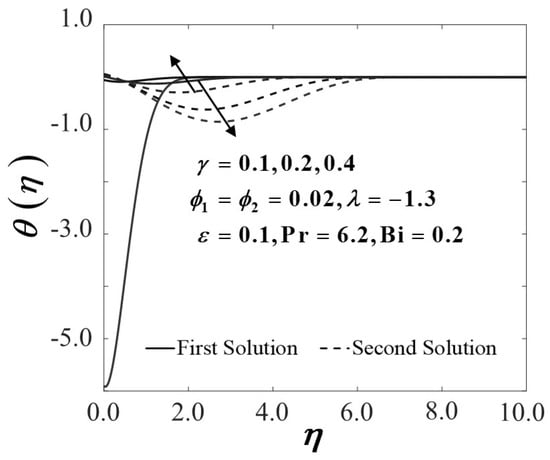
Figure 5.
Temperature profiles of with (shrinking case).
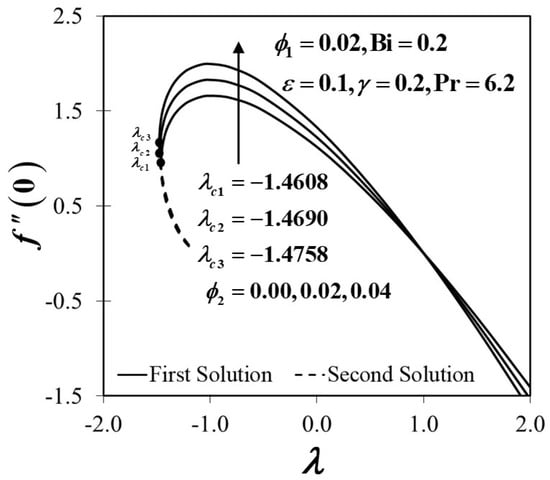
Figure 6.
Variants of towards with .
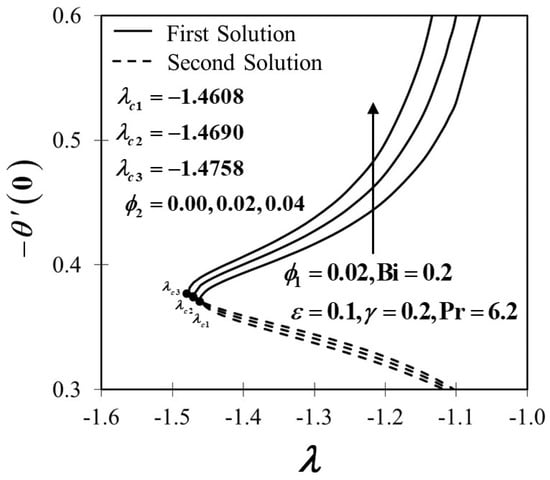
Figure 7.
Variants of towards with .
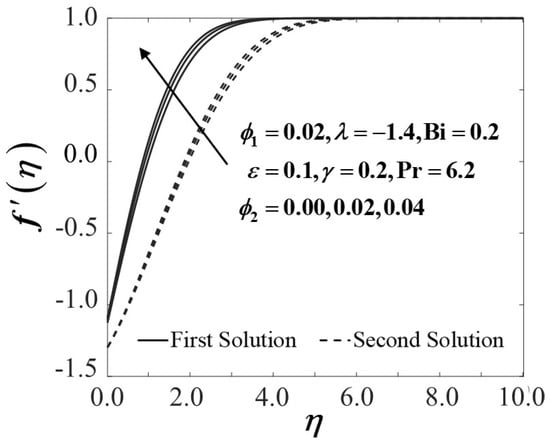
Figure 8.
Velocity profiles of with (shrinking case).
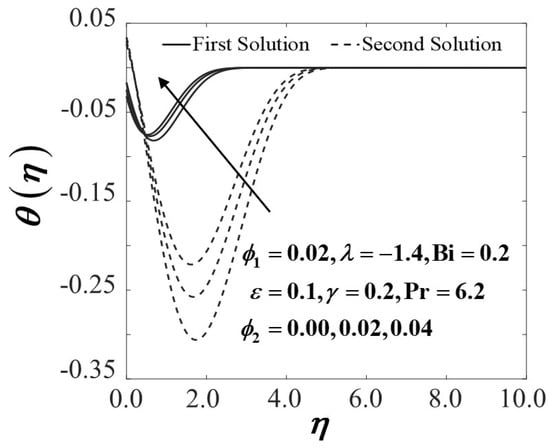
Figure 9.
Temperature profiles of with (shrinking case).
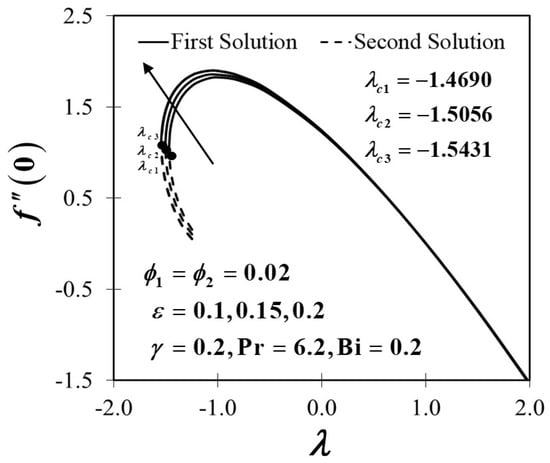
Figure 10.
Variants of towards with .
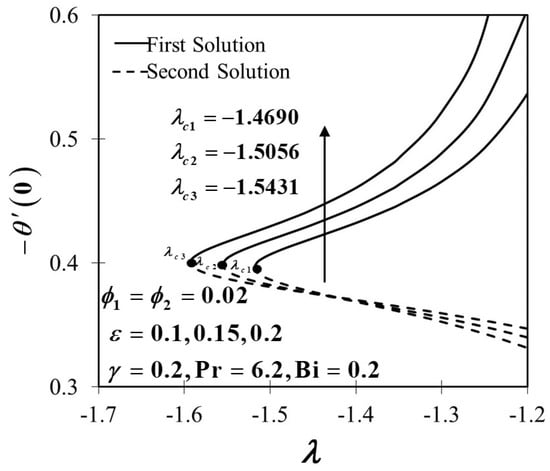
Figure 11.
Variants of towards with .
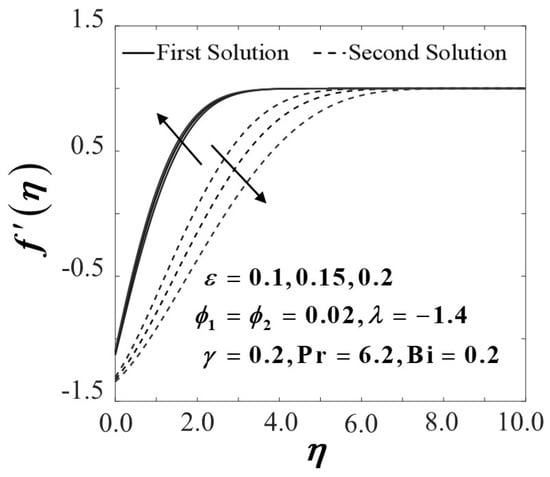
Figure 12.
Velocity profiles of with .
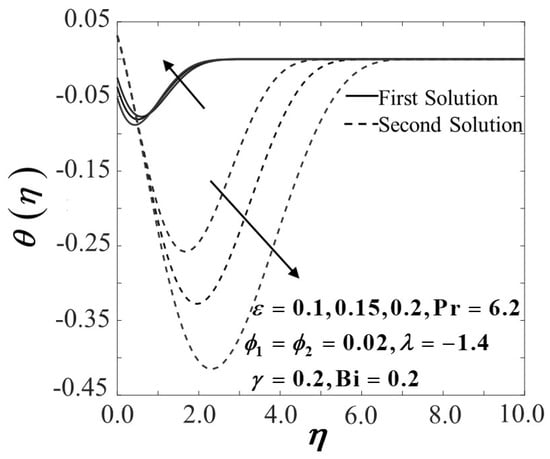
Figure 13.
Temperature profiles of with .
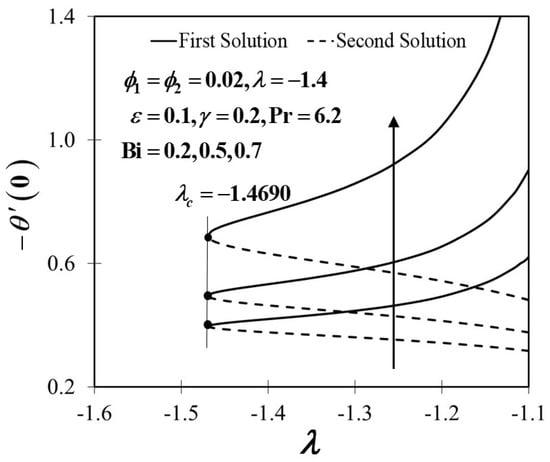
Figure 14.
Variants of towards with .
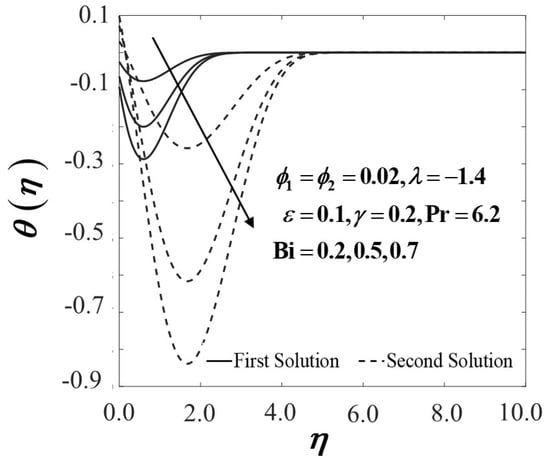
Figure 15.
Temperature profiles of with .

Table 4.
Smallest eigenvalues for some values of when .
The influence of velocity slip on the skin friction coefficient and the local Nusselt number past a convectively heated stretching/shrinking sheet of hybrid Al2O3-Cu/H2O nanofluid are displayed in Figure 2, Figure 3, Figure 4 and Figure 5. Figure 2 presents the coefficient of skin friction towards the stretching/shrinking parameter , which revealed a decline of with the occurrence of velocity slip effect at the boundary. The same results are obtained in the previous literature, as reported by Dzulkifli et al. [59]. Based on a physical perspective, an improvement in the slip parameter reflects the fact that the vorticity produced by the stretching/shrinking velocity is gradually decreased, thus the vorticity stays restricted within the boundary layer for greater stretching/shrinking velocity with the same straining velocity of the stagnation flow, and subsequently, the steady solution is achievable for some broad values of , as stated by Mahapatra and Nandy [34]. Figure 2 emphasizes that the solution for a certain value of persist prior to a critical value at which the boundary layer splits from the convectively heated stretching/shrinking sheet and the solution on the basis of the boundary layer approximations is not feasible. In short, no solution exists for . Moreover, the expansion of results in the increment of suggesting that the velocity slip parameter is efficiently influenced by raising the range of dual solutions. Thus, it is proven that the existence of a slip velocity impact may prolong the separation of the boundary layer. Figure 2 also highlights as the sheet is stretching at the rate of the value of which describes no frictional drag exerted at the convectively heated stretching/shrinking sheet.
Figure 3 exposes an upward trend in when the velocity slip parameter arises on the convectively heated stretching/shrinking sheet, which is proportionate to the heat transfer rate. Those findings are in line with the remarkable work reviewed by Mahapatra and Nandy [34] and Khashi’ie et al. [66]. Evidently, in the case of the first solution, the rate of heat transfer presents an ascendant trend with an increase of while the second solution permits a top-down direction when the velocity slip enlarges. From the existing and current findings, the authors can conclude that the velocity slip contributes to the improvement of the heat transfer rate significantly, prior to this case study. However, the authors would also like to declare that such results may vary if different control parameters are taken into consideration. The distribution of velocity and temperature profiles over several values of in the case of a convectively heated shrinking sheet is certified in Figure 4 and Figure 5. As demonstrated in Figure 4, it is confirmed that as increases, is subsequently decreased in the first solution and revealed an upward trend in the velocity profile in the second solution with the presence of velocity slip condition. As the slip occurs, the velocity flow near the sheet in no longer equal to stretching velocity. This is due to the slip condition where the pulling force of the stretching sheet is partly shifted to the fluid, resulting in the decrement of the velocity profiles in the first solution. In short, the slip condition reduces the momentum transfer from the sheet to the fluid. A contradict results are obtained in as the velocity slip effect is exaggerated, as shown in Figure 5. The first solution in the temperature profile distribution increases as intensifies, while it diminishes in the second solution. This may occur due to the appearance of slip boundary conditions on the wall, which triggers the hybrid nanofluid to retain the velocity on the walls, and such slip may prevent from total heat exchange of the hybrid nanofluid. It is therefore noticed when the slip coefficient is applied, the difference in temperature rate is increased. Additionally, the effect of convective heating progress that has been reflected in the present study, which controls the temperature of the stretching/shrinking surface also might contribute to this phenomenon. As a matter of fact, greater convection leads to increased surface temperatures, which permit the thermal impact to penetrate deeper within the hybrid Al2O3-Cu/H2O nanofluid.
Figure 6 and Figure 7 expose the coefficient of skin friction and the rate of heat transfer of a conventional nanofluid and hybrid nanofluid past a convectively heated stretching/shrinking sheet when varies from 0.00 to 0.02 where and . Figure 6 manifests that addition in which indicates the transformation of the conventional Al2O3-H2O fluid to the hybrid Al2O3-Cu/H2O nanofluid, upsurges the values of once the sheet is shrinking. The viscosity of hybrid Al2O3-Cu/H2O nanofluid rises when increases, which eventually improves the fluid velocity over the convectively heated shrinking sheet, as proven in Figure 8. The velocity profile in Figure 8 clarifies that the momentum boundary layer thickness was diminished in response to the rise of thereby raising the velocity of the fluid and boosting the gradient of velocity. In fact, the thinner momentum boundary layer continues to evolve the wall shear stress as well as the convectively heated shrinking sheet, leading to an enhancement of As increases, the result implies the increase of the frictional drag exerted on the convectively heated shrinking surface, which may delay the boundary layer flow separation. Besides, Figure 6 also highlights when the sheet is stretching at the rate of , the value of which explains no frictional drag exerted at the sheet surface. Meanwhile, Figure 7 illustrates an increasing trend of the heat transfer characteristic or when the values of past a convectively heated shrinking sheet, and this trend holds true to the first solution but is in dispute with the results in the second solution. In essence, as the conventional Al2O3-H2O nanofluid becomes the hybrid Al2O3-Cu/H2O nanofluid, the heat transfer efficiency improves. This finding upholds the assumption of the convective heat transfer system can be improved by optimizing the nanoparticle concentration when increased. The results obtained in Figure 6 and Figure 7 are consistent with Waini et al. [20] and Zainal et al. [21], whereby adding the concentrations of hybrid nanoparticles may contribute to the improvement of the heat transfer rate, accordingly. The temperature profile in Figure 9 describes the temperature variations when the conventional Al2O3-H2O nanofluid becomes the hybrid Al2O3-Cu/H2O nanofluid in both first and second solutions. The incline in the temperature of hybrid nanofluid proliferates the thermal conductivity, which may be triggered by the extra energy dispersed through the increment of the nanoparticles volume fraction over the state of convectively heated stretching/shrinking sheet.
Figure 10, Figure 11, Figure 12 and Figure 13 show the impact of the unsteadiness parameter towards a convectively heated stretching/shrinking sheet when shifts from 0.1 to 0.2. The hybrid Al2O3-Cu/H2O nanofluid characteristic with regard to the coefficient of skin friction is depicted as in Figure 10. Figure 10 captures that when the sheet shrinks, the increment in conclusively increases the trend of in the first solution. An increment in the unsteadiness parameter results in the reduction of the boundary layer thickness, as depicted in Figure 12 and consequently upsurge the velocity gradient on the convectively heated stretching/shrinking sheet, thus improves. Furthermore, the existence of nanoparticle volume fraction in the working fluid (Al2O3-Cu/H2O) might also trigger the increment of owing to an uplift of the hybrid nanofluid viscosity. This result is aligned with the study done by Ismail et al. [67]. Figure 11 presents the unsteadiness parameter effect towards the rate of heat transfer . According to the generated results, the heat transfer rate increases when increases when the convectively heated sheet is shrinking. The forced convective heat transfer is indeed proportional to the effectiveness of nanofluid heat conductivity, hence raising the reduced local Nusselt number notably. The dimensionless velocity profiles with a different value of are depicted in Figure 12, where the presence of dual velocity profiles is also observed. As illustrated in Figure 12, the first solution increases proportionally to the increment of values while the second solution displayed contradict results of the first solution, possibly because of the enhancement in the unsteadiness of the flow. Meanwhile, the same trend of the solution in Figure 12 also reflected the graph of temperature distribution in the convectively heated stretching/shrinking sheet with the existence of unsteadiness parameter, as portrayed in Figure 13. Apart from that, it is proven that the second solution in both profiles, i.e., velocity and temperature distribution showed larger boundary layer thickness in each solution of the unsteady cases than those of the first solution.
Figure 14 and Figure 15 depict the variants of heat transfer rate and temperature distribution profile with a different value of the Biot number towards the convectively heated stretching/shrinking sheet. In Figure 14, the heat transfer rate shows an upsurge trend in the dual solutions along with the augmentation of Bi values. The Biot number signifies the conduction resistance ratio within the sheet to convection resistance at the sheet. The critical values of the different usage of Biot numbers suggest no substantial impact on the magnitude of , as highlighted by Jusoh et al. [68]. An increment in the Biot number related to the improvement of convective heating is observed to decrease the fluid temperature proficiently in the first and second solutions, as displayed in Figure 15. This result is in contrast with the idea of a large Biot number representing larger internal thermal resistance of the sheet compare to the boundary layer thermal resistance since the temperature distribution profile spike as the value of Bi increases. However, note that the Biot number is specifically correlated to the coefficient of heat transfer ; therefore, it is conversely related to the thermal resistance of the current problem. Consequently, the heat resistance decreases as the Biot number increases, thereby increasing the heat transfer rate at the stretching/shrinking sheet and decreasing the temperature distribution (see Figure 15).
5. Conclusions
An analysis of the unsteady stagnation point flow of hybrid nanofluid over a convectively heated stretching/shrinking sheet incorporating the velocity slip impact on heat transfer was verified in this study. The results were generated by employing the bvp4c features in the MATLAB programming platform. The effect of diverse controlling parameters—namely, the nanoparticle volume fraction, the velocity slip, the Biot number, and the unsteadiness parameter—were reviewed. Our discoveries happen to determine that the presence of non-uniqueness solutions (first and second solutions) is verifiable within the hybrid Al2O3-Cu/H2O nanofluid for a specific range of control parameters, and the stability analysis authorizes the reliability of our first solution. The nanoparticle volume fraction increment improved both the skin friction coefficient and local Nusselt number in the hybrid nanofluid (Al2O3-Cu/H2O). From this, it is proven that the heat transfer rate improves when the ordinary Al2O3-H2O nanofluid becomes the hybrid nanofluid (Al2O3-Cu/H2O) by expanding the nanoparticles concentration. The recent addition of the velocity slip parameter at the boundary had encouraged a reduction in the skin friction coefficient and velocity profile. However, it increased the rate of heat transfer significantly. The temperature profiles escalate as the magnitude of velocity slip upsurge because of such slip may prevent from exchange of total heat in the hybrid nanofluid. An increase in the unsteadiness parameter consequently raises the velocity gradient on the convectively heated stretching/shrinking sheet, thus improving the skin friction coefficient. Besides, an upsurge in the Biot number intensity boosts the heat transfer rate since the Biot number is directly associated with the heat transfer rate coefficient. Thus, it is conversely interrelated to the thermal resistance of the designated problem. Apart from that, the critical values of the different practices of the Biot number imply no significant outcome towards the magnitude of the heat transfer coefficient.
Author Contributions
Research design, N.A.Z., R.N., K.N., and I.P.; Formulation and methodology, N.A.Z.; Result analysis, N.A.Z.; Validation, R.N. and K.N.; Article preparation, N.A.Z.; Review and editing, N.A.Z., R.N., K.N., and I.P. All authors have read and agreed to the published version of the manuscript.
Funding
The present work is endorsed by the research award (DIP-2017-009) from UKM.
Acknowledgments
All authors value the productive feedbacks by the competent reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Roman letters | |
| constant | |
| Bi | Biot number |
| skin friction coefficient | |
| specific heat at constant pressure | |
| velocity slip factor | |
| heat transfer coefficient | |
| dimensionless stream function | |
| thermal conductivity of the fluid | |
| local Nusselt number | |
| heat capacitance of the fluid | |
| Prandtl number | |
| local Reynolds number in axis | |
| time | |
| fluid temperature | |
| reference temperature | |
| ambient temperature | |
| velocities component in the and directions, respectively | |
| velocities of the free stream in | |
| velocities of the stretching/shrinking surface | |
| x, y | rtesian coordinates |
| Greek symbols | |
| stream function | |
| similarity variable | |
| dimensionless temperature | |
| unsteadiness parameter | |
| ratio of the velocity parameter | |
| velocity slip parameter | |
| dynamic viscosity of the fluid | |
| kinematic viscosity of the fluid () | |
| density of the fluid | |
| dimensionless time variable | |
| wall shear stress | |
| nanoparticle volume fractions for Al2O3 (alumina) | |
| nanoparticle volume fractions for Cu (copper) | |
| eigenvalue | |
| smallest eigenvalue | |
| Subscripts | |
| base fluid | |
| nanofluid | |
| hybrid nanofluid | |
| solid component for Al2O3 (alumina) | |
| solid component for Cu (copper) | |
| Superscript | |
| differentiation with respect to | |
References
- Schlichting, H.; Gersten, K. Boundary Layer Theory; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Smith, F.T. Steady and unsteady boundary layer separation. Annu. Rev. Fluid Mech. 1986, 18, 197–220. [Google Scholar] [CrossRef]
- White, F.M. Viscous Fluid Flow; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Elbashbeshy, E.M.A.; Bazid, M.A.A. Heat transfer over an unsteady stretching surface. Heat Mass Transf. 2004, 41, 1–4. [Google Scholar] [CrossRef]
- Bhattacharyya, K. Dual solutions in unsteady stagnation-point flow over a shrinking sheet. Chin. Phys. Lett. 2011, 28, 084702. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. The boundary layers of an unsteady stagnation-point flow in a nanofluid. Int. J. Heat Mass Transf. 2012, 55, 6499–6505. [Google Scholar] [CrossRef]
- Fan, T.; Xu, H.; Pop, I. Unsteady stagnation flow and heat transfer towards a shrinking sheet. Int. Commun. Heat Mass Transf. 2010, 37, 1440–1446. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Unsteady three-dimensional MHD non-axisymmetric Homann stagnation point flow of a hybrid nanofluid with stability analysis. Mathematics 2020, 8, 784. [Google Scholar] [CrossRef]
- Kamal, F.; Zaimi, K.; Ishak, A.; Pop, I. Stability analysis on the stagnation-point flow and heat transfer over a permeable stretching/shrinking sheet with heat source effect. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 2650–2663. [Google Scholar] [CrossRef]
- Basir, F.; Hafidzuddin, E.H.; Naganthran, K.; Chaharborj, S.S.; Kasihmuddin, M.S.M.; Nazar, R. Stability analysis of unsteady stagnation-point gyrotactic bioconvection flow and heat transfer towards the moving sheet in a nanofluid. Chin. J. Phys. 2020, 65, 538–553. [Google Scholar] [CrossRef]
- Jusoh, R.; Nazar, R.; Pop, I. Impact of heat generation/absorption on the unsteady magnetohydrodynamic stagnation point flow and heat transfer of nanofluids. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 557–574. [Google Scholar] [CrossRef]
- Zheng, Y.; Ahmed, N.A.; Zhang, W. Heat dissipation using minimum counter-flow jet ejection during spacecraft re-entry. Procedia Eng. 2012, 49, 271–279. [Google Scholar] [CrossRef][Green Version]
- Fisher, E.G. Extrusion of Plastics; Wiley: New York, NY, USA, 1976. [Google Scholar]
- Hiemenz, K. Die Grenzschicht an einem in den gleichförmigen Flüssigkeitsstrom eingetauchten geraden Kreiszylinder. Dinglers Polytech. J. 1911, 326, 321–324. [Google Scholar]
- Homann, F. Der Einfluss grosser Zähigkeit bei der Strömung um den Zylinder und um die Kugel. Z. Angew. Math. Mech. 1936, 16, 153–164. [Google Scholar]
- Howarth, L. CXLIV. The boundary layer in three-dimensional flow—Part II. The flow near a stagnation point. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1951, 42, 1433–1440. [Google Scholar]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I. Mixed convective stagnation point flow towards a vertical Riga plate in hybrid Cu–Al2O3/water nanofluid. Mathematics 2020, 8, 912. [Google Scholar]
- Khashi’ie, N.S.; Hafidzuddin, E.H.; Ariffin, N.M.; Wahi, N. Stagnation point flow of hybrid nanofluid over a permeable vertical stretching/shrinking cylinder with thermal stratification effect. CFD Lett. 2020, 12, 80–94. [Google Scholar]
- Fang, T.G.; Wang, F.J. Momentum and heat transfer of a special case of the unsteady stagnation-point flow. Appl. Math. Mech. Engl. 2020, 41, 51–82. [Google Scholar]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow towards a stagnation point on a stretching/shrinking cylinder. Sci. Rep. 2020, 10, 1–12. [Google Scholar]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. MHD mixed convection stagnation point flow of a hybrid nanofluid past a vertical flat plate with convective boundary condition. Chin. J. Phys. 2020, 66, 630–644. [Google Scholar]
- Wang, C.Y. Flow over a surface with parallel grooves. Phys. Fluids. 2003, 15, 1114–1121. [Google Scholar]
- Sharipov, F.; Seleznev, V. Data on internal rarefied gas flows. J. Phys. Chem. Ref. Data 1998, 27, 657–706. [Google Scholar]
- Hafidzuddin, E.H.; Nazar, R.; Arifin, N.M.; Pop, I. Effects of anisotropic slip-on three-dimensional stagnation-point flow past a permeable moving surface. Eur. J. Mech. B Fluids. 2017, 65, 515–521. [Google Scholar] [CrossRef]
- Pavlišič, A.; Huš, M.; Prašnikar, A.; Likozar, B. Multiscale modelling of CO2 reduction to methanol over industrial Cu/ZnO/Al2O3 heterogeneous catalyst: Linking ab initio surface reaction kinetics with reactor fluid dynamics. J. Clean. Prod. 2020, 275, 122958. [Google Scholar] [CrossRef]
- Navier, C.L. Memorie sur les lois du lois du mouvement des fluides. Mem. Acad. Sci. Inst. France 1827, 6, 298–440. [Google Scholar]
- Maxwell, J. On stresses in rarefied gases arising from inequalities of temperature. Philos. Trans. R. Soc. Lond. 1879, 27, 231–256. [Google Scholar]
- Wang, C.Y. Stagnation flows with slip: Exact solutions of the Navier-Stokes equations. Z. Fur Angew. Math. Und Phys. 2003, 54, 184–189. [Google Scholar] [CrossRef]
- Rao, I.J.; Rajagopal, K.R. Effect of the slip boundary condition on the flow of fluids in a channel. Acta Mech. 1999, 135, 113–126. [Google Scholar] [CrossRef]
- Jusoh, R.; Nazar, R.; Pop, I. Three-dimensional flow of a nanofluid over a permeable stretching/shrinking surface with velocity slip: A revised model. Phys. Fluids 2018, 30, 033604. [Google Scholar] [CrossRef]
- Yoshimura, A.; Prud’homme, R.K. Wall slip corrections for couette and parallel disk viscometers. J. Rheol. 1988, 32, 53–67. [Google Scholar] [CrossRef]
- Vajravelu, K.; Mukhopadhyay, S. Fluid Flow, Heat and Mass Transfer at Bodies of Different Shapes: Numerical Solutions; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Mukhopadhyay, S. Effects of slip-on unsteady mixed convective flow and heat transfer past a porous stretching surface. Nucl. Eng. Des. 2011, 241, 2660–2665. [Google Scholar] [CrossRef]
- Mahapatra, R.T.; Nandy, S.K. Slip effects on unsteady stagnation-point flow and heat transfer over a shrinking sheet. Meccanica 2013, 48, 1599–1606. [Google Scholar] [CrossRef]
- Majumder, M.; Chopra, N.; Andrews, R.; Hinds, B.J. Nanoscale hydrodynamics: Enhanced flow in carbon nanotubes. Nature 2005, 438, 930. [Google Scholar] [CrossRef]
- Noghrehabadi, A.; Pourrajab, R.; Ghalambaz, M. Effect of partial slip boundary condition on the flow and heat transfer of nanofluids past stretching sheet prescribed constant wall temperature. Int. J. Therm. Sci. 2012, 54, 253–261. [Google Scholar] [CrossRef]
- Van Gorder, R.A.; Sweet, E.; Vajravelu, K. Nano boundary layers over stretching surfaces. Commun. Nonlinear Sci. Numer. Simulat. 2010, 15, 1494–1500. [Google Scholar] [CrossRef]
- Dinarvand, S.; Rostami, M.N. Rotating Al2O3-H2O nanofluid flow and heat transfer with internal heating, velocity slip and different shapes of nanoparticles. Multidiscip. Model. Mater. Struct. 2020. Available online: https://doi.org/10.1108/MMMS-01-2020-0017 (accessed on 17 August 2020). [CrossRef]
- Seth, G.S.; Bhattacharyya, A.; Kumar, R.; Chamkha, A.J. Entropy generation in hydromagnetic nanofluid flow over a non-linear stretching sheet with Navier’s velocity slip and convective heat transfer. Phys. Fluids 2018, 30, 122003. [Google Scholar] [CrossRef]
- Rahman, J.U.; Khan, U.; Ahmad, S.; Ramzan, M.; Suleman, M.; Lu, D.; Inam, S. Numerical Simulation of Darcy–Forchheimer 3D Unsteady Nanofluid Flow Comprising Carbon Nanotubes with Cattaneo–Christov Heat Flux and Velocity and Thermal Slip Conditions. Processes 2019, 7, 687. [Google Scholar] [CrossRef]
- Reddy, R.C.S.; Reddy, P.S. A comparative analysis of unsteady and steady Buongiorno’s Williamson nanoliquid flow over a wedge with slip effects. Chin. J. Chem. Eng. 2020, 28, 1767–1777. [Google Scholar] [CrossRef]
- Reddy, J.V.R.; Sugunamma, V.; Sandeep, N. Thermophoresis and Brownian motion effects on unsteady MHD nanofluid flow over a slendering stretching surface with slip effects. Alex. Eng. J. 2018, 57, 2465–2473. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J. Enhancing thermal conductivity of fluids with nanoparticles. ASME Publ. Fed. 1995, 231, 99–103. [Google Scholar]
- Shah, T.R.; Ali, H.M. Applications of hybrid nanofluids in solar energy, practical limitations and challenges: A critical review. Sol. Energy 2019, 183, 173–203. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Hybrid nanofluids for heat transfer applications—A state-of-the-art review. Int. J. Heat Mass Transf. 2018, 125, 82–103. [Google Scholar]
- Gupta, M.; Singh, V.; Kumar, S.; Kumar, S.; Dilbaghi, N. Up to date review on the synthesis and thermophysical properties of hybrid nanofluids. J. Clean. Prod. 2018, 190, 169–192. [Google Scholar]
- Xian, H.W.; Azwadi, N.; Sidik, C.; Aid, S.R.; Ken, T.L.; Asako, Y. Review on preparation techniques, properties and performance of hybrid nanofluid in recent engineering applications. J. Adv. Res. Fluid Mech. Therm. Sci. 2018, 45, 1–13. [Google Scholar]
- Madhesh, D.; Kalaiselvam, S. Experimental analysis of hybrid nanofluid as a coolant. Procedia Eng. 2014, 97, 1667–1675. [Google Scholar]
- Tahat, M.S.; Benim, A.C. Experimental analysis on thermophysical properties of Al2O3/CuO hybrid nanofluid with its effects on flat plate solar collector. Defect Diffus. Forum 2017, 374, 148–156. [Google Scholar]
- Labib, M.N.; Nine, M.J.; Afrianto, H.; Chung, H.; Jeong, H. Numerical investigation on effect of base fluids and hybrid nanofluid in forced convective heat transfer. Int. J. Therm. Sci. 2013, 71, 163–171. [Google Scholar]
- Moghadassi, A.; Ghomi, E.; Parvizian, F. A numerical study of water-based Al2O3 and Al2O3–Cu hybrid nanofluid effect on forced convective heat transfer. Int. J. Therm. Sci. 2015, 92, 50–57. [Google Scholar]
- Devi, S.U.; Devi, S.P.A. Heat transfer enhancement of Cu–Al2O3/water hybrid nanofluid flow over a stretching sheet. J. Niger. Math. Soc. 2017, 36, 419–433. [Google Scholar]
- Takabi, B.; Salehi, S. Augmentation of the heat transfer performance of a sinusoidal corrugated enclosure by employing hybrid nanofluid. Adv. Mech. Eng. 2014, 6, 147059. [Google Scholar]
- Aladdin, N.A.L.; Bachok, N.; Pop, I. Cu–Al2O3/water hybrid nanofluid flow over a permeable moving surface in presence of hydromagnetic and suction effects. Alex. Eng. J. 2020, 59, 657–666. [Google Scholar]
- Plant, R.D.; Hodgson, G.K.; Impellizzeri, S.; Saghir, M.Z. Experimental and numerical investigation of heat enhancement using a hybrid nanofluid of copper oxide/alumina nanoparticles in water. J. Therm. Anal. Calorim. 2020, 141, 1951–1968. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Sherif, E.S.M. Dual solutions and stability analysis of a hybrid nanofluid over a stretching/shrinking sheet executing MHD flow. Symmetry 2020, 12, 276. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Roşca, N.C.; Roşca, A.V.; Pop, I. Mixed convection and stability analysis of stagnation-point boundary layer flow and heat transfer of hybrid nanofluids over a vertical plate. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 3737–3754. [Google Scholar] [CrossRef]
- Wang, C.Y. Stagnation flow towards a shrinking sheet. Int. J. Non-Linear Mech. 2008, 43, 377–382. [Google Scholar] [CrossRef]
- Dzulkifli, N.F.; Bachok, N.; Yacob, N.A.; Arifin, N.M.; Rosali, H. Unsteady stagnation-point flow and heat transfer over a permeable exponential stretching/shrinking sheet in nanofluid with slip velocity effect: A stability analysis. Appl. Sci. 2018, 8, 2172. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar]
- Merkin, J.H. Natural-convection boundary-layer flow on a vertical surface with Newtonian heating. Int. J. Heat Fluid Flow 1994, 15, 392–398. [Google Scholar]
- Merrill, K.; Beauchesne, M.; Previte, J.; Paullet, J.; Weidman, P. Final steady flow near a stagnation point on a vertical surface in a porous medium. Int. J. Heat Mass Transf. 2006, 49, 4681–4686. [Google Scholar]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Suresh, S.; Venkitaraj, K.P.; Selvakumar, P. Synthesis, characterisation of Al2O3–Cu nanocomposite powder and water-based nanofluids. Adv. Mater. Res. 2011, 328, 1560–1567. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I.; Nazar, R.; Hafidzuddin, E.H.; Wahi, N. Three-dimensional hybrid nanofluid flow and heat transfer past a permeable stretching/shrinking sheet with velocity slip and convective condition. Chin. J. Phys. 2020, 66, 157–171. [Google Scholar] [CrossRef]
- Ismail, N.S.; Arifin, N.M.; Nazar, R.; Bachok, N. Stability analysis of unsteady MHD stagnation point flow and heat transfer over a shrinking sheet in the presence of viscous dissipation. Chin. J. Phys. 2019, 57, 116–126. [Google Scholar] [CrossRef]
- Jusoh, R.; Nazar, R.; Pop, I. Flow and heat transfer of magnetohydrodynamic three-dimensional Maxwell nanofluid over a permeable stretching/shrinking surface with convective boundary conditions. Int. J. Mech. Sci. 2017, 124, 166–173. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).