1. Introduction
Generally, univariate and multivariate control charts are applied to identify anomalies in the industry and control the quality of products and services. However, the specific characteristics of data obtained by continuous monitoring (which has become the main trend due to advancements in sensoring and communications in the framework of Industry 4.0), require the use of increasingly sophisticated tools that take into account the presence of autocorrelation in critical to quality (CTQ) variables for the process under study.
Recently, diverse solutions have been provided that propose the modification and application of exponentially weighted moving average chart (EWMA) control charts [
1]; control charts based on the fitting of autoregressive integrated moving average (ARIMA) models [
2]; and the use of control charts for profiles, which is understood as the control of the parameters that define the relationship between two different CTQ variables [
3,
4,
5,
6]. Additionally, there are solutions that propose the use of techniques based on the control chart concept for anomaly detection such as machine learning techniques (neural networks and support vector machines, among others) and time series [
7,
8,
9,
10,
11,
12,
13,
14]. The increasingly common use of these tools is attributed to the fact that they adapt very well to the new paradigm of data (in the framework of Industry 4.0) defined by the continuous monitoring of numerous variables. Traditional control charts cannot be applied to many of the new cases due to their non-compliance with their starting hypotheses. In the domain of statistical quality control, the use of the concept of latent variables along with multivariate control charts is one of the most popular and useful alternatives to solve the problem of process control in the Industry 4.0. domain [
15,
16,
17].
Many of these new data, usually curves, can be studied as functional data. This is the case of data in the fields of energy consumption, indoor and machine temperatures, relative humidity, amount of CO
, among other variables, measured in all types of buildings. These new data, which currently characterize industrial processes, require innovative solutions, developed by researchers in the field of statistical quality control, based on the application of functional data analysis (FDA) techniques. Until now, few works have been published (in relation to the importance of the topic and the frequent monitoring of this type of data) on controlling the quality of processes when the data to be monitored are functional CTQ variables. Among the most outstanding research in this context, Reference [
18] compared the performances of different control charts used for monitoring functional data; these charts are often identified as profiles in the statistical quality control literature. According to References [
19,
20], in the case of the monitoring of profiles, a set of statistical techniques (usually multivariate) is applied for controlling processes when they are defined by the functional relationship between two variables. However, a control chart for monitoring functional data, which is based on bootstrap resampling, is also proposed in Reference [
21], whereas, in References [
22,
23], two complete monographs are proposed in which the concepts of control charts for profiles are adapted to the context of the functional data. Moreover, recently, new alternatives for outlier detection based on interlaboratory studies and those with application in industrial anomaly detection have been performed in the FDA framework [
24,
25,
26].
This study intends to provide an alternative solution to the detection of out-of-control anomalies or states in the area of energy efficiency in buildings, specifically in commercial areas such as different stores of textile companies. Therefore, an important aim of this work is to solve the problem of such companies, specifically the ones providing lighting facilities; office automation; and heating, ventilation and air conditioning (HVAC). One such company is Fridama SL. The group comprises Fridama’s facilities, qus (web platforms for big data management) and Nerxus (statistical consultancy for data analysis in the energy sector); the solution to the problem raised by this company is defined by continuously monitored data over time that can be treated as profiles or functional data. Based on this need, the present study proposes methodologies to build control charts that allow us to control the aforementioned processes. in order to test the applied statistical methodologies for anomaly detection properly, these companies have provided a database on a real HVAC installation, whose anomalies and assignable causes are identified by its maintenance personnel.
These energy efficiency data are non-Gaussian and autocorrelated, as the main component of continuously monitored data in the Industry 4.0 framework. Thus, the present proposal provides alternative control charts for Phases I and II of the statistical process control that can deal with non-Gaussian and autocorrelated data. As is well-known, using control charts, the process can be controlled in the following two phases: Phase I involves the stabilization or the calibration of the process and Phase II focuses on process monitoring. For Phase I, a control chart is proposed based on the depth measurement of a functional datum and the idea of atypical detection; in Phase II, a nonparametric range control chart is proposed, based on the calculation of the functional data depth, to monitor the process of interest. The procedure of building control charts corresponding to Phases I and II are explained in the next section; it also shows the results of their performance through a simulation study including diverse scenarios. The proposed methodology has been developed and programmed in R through different functions integrated in the “Quality Control Review” package, qcr, which can be freely and easily accessed by the practitioners.
Additionally, it provides a way to visualize the control charts for functional data, including the original data and the curves corresponding to the estimated control limits. This visual tool allows users and maintenance managers to relate each anomaly to an intuitively assignable cause. The results of the simulation study and its application to the real data show the usefulness of this control chart methodology in detecting anomalies when the process is defined by functional data, specifically the daily curves of energy consumption in commercial areas.
1.1. Alternatives of the Statistical Quality Control When the Basic Assumptions of the Control Charts Are Not Met
This control chart approximation for functional data is based on nonparametric multivariate control charts, which are useful when the assumptions of Gaussianity are not met. Therefore, a brief introduction of nonparametric control charts and statistical tools for dealing with autocorrelated data are presented in the following section.
Recently, analyses of the robustness of different control charts against the non-compliance of Gaussianity hypothesis have been developed. Particularly, several nonparametric control charts have been proposed. In this domain, we should highlight the works of Regina Liu [
27,
28,
29], who has developed the
r,
Q and
S control charts based on the data depth and rank concepts and the rank or ranges. In this regard, it is important to highlight the strong influence of Liu’s works; it must be noted that several nonparametric alternatives for control charts are based on the concepts of data depth and rank. Moreover, it should be emphasized that one of the most important lines of research of the SQC, the profiles’ control charts, are based, in many cases, on the application of nonparametric or semiparametric regression models [
3,
4]. Additionally, it is also important to highlight the use of resampling techniques for calculating natural control limits for different types of control charts [
30,
31]. The work in Reference [
32] constitutes a complete monograph on the current trends for the development of control charts.
Despite their important advantages (no assumptions on the probability distribution of CTQ variables), nonparametric control charts are not predominantly used in the industrial and business framework. As noted in Reference [
20], this can be attributed to several factors such as the lack of specific software, both commercial and free; the lack of general training in nonparametric statistics that generates insecurity and distrust in users and the lack of contrasted reference texts for the application of nonparametric methods in SQC. However, the research activity in this field is growing, as illustrated by the work in Reference [
33].
Another starting hypothesis of control charts is the independence of the observations. The data continuously monitored over time by different sensors usually show a variable level of autocorrelation (the greater the correlation the closer the observations are in time). The application of standard techniques in the case of the violation of the independence hypothesis often results in the detection of an unacceptable number of false alarms [
34]. Therefore, the development and analysis of techniques that remove the sample autocorrelation is fully justified. Within these techniques, the most widespread is the application of time series models (e.g., autoregressive moving average (ARMA) and ARIMA) to remove the correlation between observations and the subsequent monitoring of the error variable (difference between actual values and those estimated by the model) using control charts [
34,
35,
36]. Moreover, References [
37,
38] propose the combination of control charts with adjustment algorithms. Finally, the monographs of [
39,
40] describe the most relevant lines of research for controlling and monitoring autocorrelated data.
It is important to note that this type of data is related to the control charts for functional data. The use of FDA techniques allows us to consider the autocorrelation of the data as well as, by means of resampling techniques, to circumvent parametric assumptions about the trend and dependence.
1.2. Control Charts for Phases I and II
The studied process is stabilized in the framework of the Phase I control charts, that is, the process is left under control [
41]. This implies that there are no other assignable causes in the process, except for those present due to randomness itself (non assignable causes). This is equivalent to stating that the process remains stable—the parameters of the probability distribution of the CTQ characteristic remain unchanged. This allows us to estimate the natural control limits for the variable that describes the quality of the process. The natural control limits are estimated using a preliminary or calibration sample. Thus, in this stage, the main assignable causes of variation are identified and rectified through corrective actions. After the variations are removed, we estimate the natural control limits of the CTQ variable corresponding to the process under control. While most of the literature in the field has referred to Phase II control charts, within the new data paradigm for Industry 4.0, it would be essential to develop methodologies for Phase I [
19]. In this regard, Reference [
42] presents an overview of the recent contributions to the development of Phase I control charts. Among the latest proposals for control charts, the work of Grasso et al. [
43] is especially interesting taking into account that is a Phase I control chart proposal for profiles based on the use of functional data depth concept (as well as the case of the present proposal). In fact, they proposed a Phase I control chart methodology for profiles belonging to the “multi-modelling framework”, that includes the following stages: (1) a classification stage of new profiles into different operating modes or profile patterns using functional classification techniques from functional data depth measures (maximum depth approach based on Mode depth); (2) even the identification of a novel operation mode is included; (3) Once the operation mode corresponding to a new profile is identified, this is assigned to the corresponding control chart and consequently a suitable control charting method is applied to determine if the process remained in control over the period of time where those data were collected.
In this study, the atypical detection procedure presented in Reference [
44] is adapted to develop a control chart for Phase I; this approach allows us to obtain a calibration sample from an under-control process that can be monitored through new measurements using a Phase II rank control chart. In fact, in Phase II, it is assumed that the process is under control [
45]; additionally, in each new sample (monitored sample), the statistical rank is obtained and it is represented in the control chart with the estimated lower control limit.
2. Methodology
In this section, methodologies of control charts for functional random variables, , which take values in a functional space , with , are developed.
Based on observations of the functional variable , we obtain a sample each of calibration and monitoring; they are functional datasets of sizes n and m, respectively, which allow us to build control charts for Phase I (in the case of the calibration sample) and Phase II (from the monitoring sample).
In the case of designing the control charts, any unstable or out-of-control process is refereed to the assignable causes of variation emerging from unusual and avoidable events that interrupt the process, that is, when they cause a change in the parameters of the underlying model of the profile or functional data [
46]; these variations can be eliminated from the data by identifying and acting on the cause; this approach will avoid such variations in the future [
46].
Concerning a method for building quality control charts, the probability of process instability (level of significance) presents a measure of its performance. This probability, provided that it is within the
, allows the derivation of at least one measure (observed value of the statistic) outside the control limits [
18]. Phase I involves the development of a method and the estimation of the level of significance; however, in the case of Phase II, is the process is assumed to be under control, that is, the level of significance is fixed.
2.1. Procedure for Building a Control Chart for Phase I (Stabilization)
As mentioned above, in Phase I, the retrospective data corresponding to a calibration sample of size
n is analyzed for evaluating the stability of the process whose quality is ascertained over time and for estimating the parameters of the control chart [
18].
In Phase I, a control chart is used to test the hypothesis that there is no change in the distribution of observations of the variable ordered with respect to time .
These changes can be punctual (freaks or bunches) or they can be related to a change in process that is evaluated (observable through patterns of sudden or gradual change in the mean of the process). Concerning isolated changes, it refers to the occurrence of at least one observation of the observed variable that deviates from the distribution of the other observations [
47]. The hypothesis tested in Phase I is:
The stabilization phase of a process consists of applying an iterative method that allows the detection and elimination of those observations (in this context curves) that have a deviation with respect to the shape or magnitude of most of the observed curves. In other words, a curve is an atypical value if it has been generated by a different stochastic process or there is a change in the trend or variability of the stochastic process with respect to that corresponding to the remaining data [
48]. The quantity of outliers is assumed to be unknown, although small.
In this study, the proposed control charts for Phase I are based on the adaptation of outlier detection methodologies from functional data, based on the data depth calculations [
44].
The method of the detection of outliers for functional data [
44] considers an atypical curve if its depth is less than a specific quantile of the distribution of depths estimated by bootstrap. In other words, an atypical curve will have a significantly low depth.
This procedure can be used with different types of functional depths. In the library
fda.usc [
49], the following alternatives are offered: Fraiman and Muniz (FM) [
50,
51], mode depth [
52] and random projections depth (RP) [
52,
53]. In this work, the outlier detection procedure proposed by Febrero et al.
fda.usc has been adapted to estimate a specific quantile of the depth distribution that plays the role of the lower control limit (LCL) for a Phase I control chart.
The control chart proposed for Phase I is estimated and plotted from a depth measurement (FM, RP or mode) and only the lower control limit (LCL) is considered to detect if the process is out-of-control (the depth of a curve is less than the LCL). In addition to this representation, an additional chart showing the original curves is proposed to provide an intuitive idea about the cause behind the identified anomaly (by checking its shape or magnitude) and thus to identify assignable causes. For instance, in the case of the HVAC energy consumption in buildings, anomalies may include stopping air handler, failure of the counter or sensor, a change in the regulation of the machines and adverse weather conditions.
In Phase I, we consider the functional random variable , from which a random sample is drawn—. These data are used to formulate the following steps to build the control chart for Phase I:
Calculate the depth corresponding to each observation of the dataset, and make a control chart based on the depth of each datum with respect to time.
Choose the parameter LCL according to the significance level of the control chart, that is, the percentage of false alarms (observations under control but erroneously detected as out-of-control) is small (for example, 1%). The following procedures are used to estimate the LCL.
If there is any curve such that for a given LCL, then it would be considered atypical and the process would be out-of-control.
Additionally, a control chart including the original curves and the functional envelope obtained from 99% of the deeper bootstrap replicas is also developed.
Moreover, once the atypical curves are detected, they are removed and the procedure is repeated until the process becomes stable (under control), namely, defined by a total absence of atypical data.
2.2. Procedure for Building a Control Chart for Process Monitoring (Phase II)
Phase II deals with process monitoring; it involves quick detection of changes from the calibrated sample stabilized in Phase I [
48]. For the scalar and multivariate cases, the process is monitored by taking the estimated control limits in Phase I [
46] as a reference. In this phase, the average run length (ARL) is used to evaluate the performance of the control charts [
35].
In this context, we test if there are deviations between the data obtained in Phase II, also called monitoring sample, and the reference data or calibration sample, taking into account its distribution.
In Phase II, in the univariate case, an
F distribution for the under-control process is estimated from a calibration sample or reference data. It is assumed that
F is the distribution of the CTQ variable of an under-control process (Phase I). This distribution is used to establish control limits that will be used to monitor the process in Phase II. The limits comprise an interval that will cover new observations of the process with a high probability, assuming that the process is under control. In Phase II, a sample of the
G distribution is monitored. Therefore, in this stage, the methods for constructing control charts are based on contrasting the hypothesis:
In the FDA context, we do not have a density function for a functional random variable
that allows us to perform different tests corresponding to Phases I and II. Alternatively, we can estimate the distribution of the depth corresponding to the curves that belong to a sample of functional data. Thus, for Phase II, the use of the rank control charts [
27] is proposed in an FDA context. The calculation of depths for functional data is proposed, which facilitate the calculation of ranks. These form the basis for developing
r control charts, called rank charts.
The adaptation of r control charts involves the calculation of the rank statistic from functional depth measurements. The r chart plots the rank statistic as a function of time. The central control line CL = 0.5 serves as a reference point for observing possible patterns or trends. The lower limit is LCL = , where is the false alarm rate.
For the practical application of this proposal, the
qcr [
54] and
fda.usc [
49]
R packages are used. The
fda.usc package provides tools for the calculation of functional data depth, while the rank control chart, among other nonparametric charts proposed in Reference [
27], is applied using the
qcr package, which was developed by the authors.
As mentioned above, in Phase II, the curves corresponding to the calibration sample of Phase I, , are used for detecting changes or deviations with respect to the behavior of the process described in Phase I. The curves of the monitoring sample, , are collected; additionally, we test the hypothesis of each new curve belonging to the same distribution that corresponds to the calibration sample.
The procedure for estimating control charts for Phase II follows the same scheme presented in Reference [
27]. Particularly, we assume that the rank statistic follows a uniform asymptotic distribution. This result is applicable to the functional case because of the way the rank corresponding to each observation is calculated (percentage of less deep curves than the observed ones). This fact provides a computational advantage in the monitoring of continuous processes since it eliminates the need to estimate the LCL. However, it is set as the quantile of a uniform distribution at a significance level
.
The procedure to develop the rank control chart for the functional univariate case (process defined by one functional variable) is detailed below, which can be easily generalized to the functional multivariate case (process defined by more than one functional variable).
From the reference sample , get the depths of the dataset, and the depths of the curves that make up the monitoring sample, . The depth of each curve corresponding to the monitoring sample is calculated from the n curves of the calibration sample, that is, with respect to cases.
The rank statistic is calculated for each curve of the monitoring sample,
, considering the calibration sample
as sample of reference.
The values of the rank statistic, the lower control limit LCL = and central line CL = 0.5 (the expected value of the rank statistic) are plotted, thereby generating the control chart.
Proceed to monitor the process. If at least the rank of a curve, , is such that LCL, then the process is considered out-of-control.
A functional control chart is developed. This is a graphical tool that allows us to identify the possible assignable causes of the out-of-control states. The original curves are included, those correspond to the reference and monitoring samples, in addition to the functional envelope obtained from ()% of the deepest curves of the calibration sample.
4. Application to Real Data
This section shows the usefulness and performance of the new graphical methodology for quality control using functional data, which is evaluated in the case study on the detection of energy efficiency anomalies of an HVAC installation. Specifically, the case study considers a commercial area of a well-known Galician apparel brand located in the Panama City. In this controlled case study, the anomalies and their assignable causes were detected by the maintenance personnel.
The following section shows the need to develop and apply FDA methodologies for control charts, considering the observations of the data of the present case study, particularly those corresponding to August. As mentioned above, in August, no event destabilized the process due to assignable causes. However, by using a methodology for scalar data (ignoring the autocorrelation between the variables), an unacceptable number of false alarms could be detected.
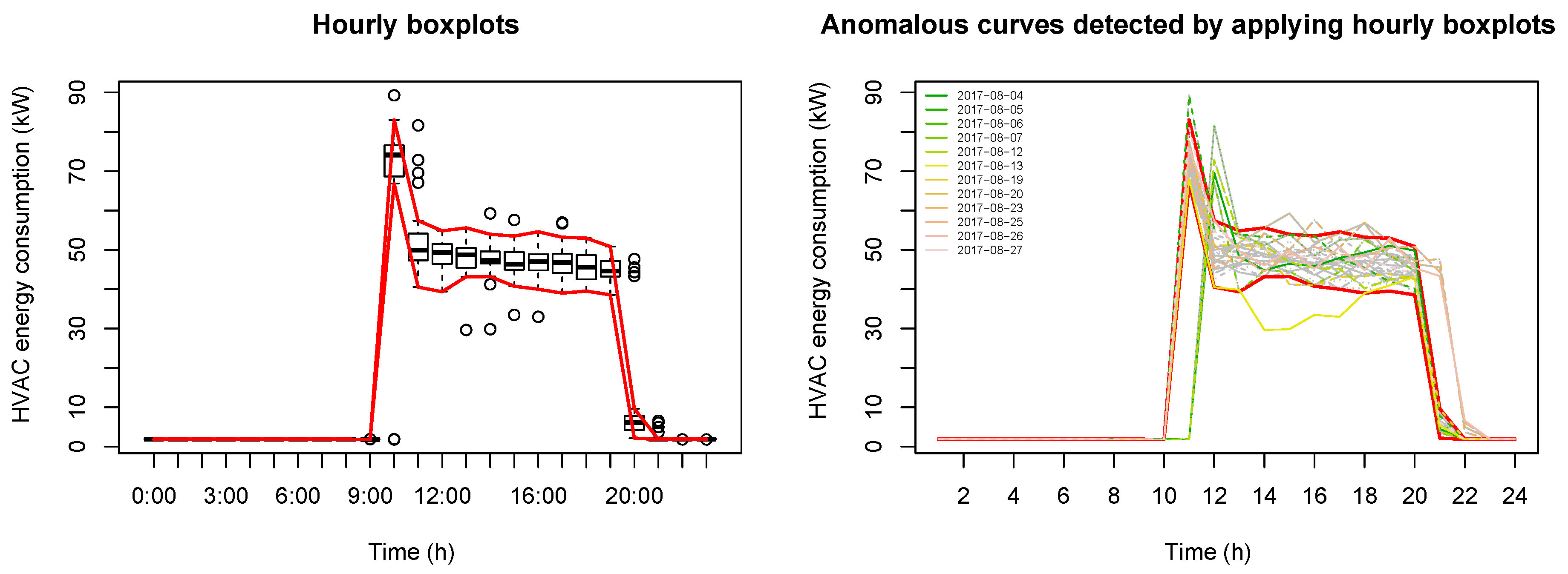
In the scalar case, boxplot [
55] is commonly used to detect anomalous or atypical data.
Figure 2 shows a traditional scalar approach for detecting outliers using boxplot. The left panel shows the boxplot for each variable of energy consumption in HVAC systems per hour, while the right panel shows the curves of daily energy consumption in HVAC systems, highlighting curves detected as outliers by the descriptive procedure based on the application of boxplots to each hourly consumption. In the usual procedure, atypical curves are those in which at least one point has been detected as an outlier in some boxplot; however, the drawback of this approach is that it increases the probability of type I error. It detects 12 daily energy consumption curves as outliers.
Based on the information described in the previous section, first, we apply the data depth control chart for Phase I and, subsequently, the rank control chart to monitor the process during Phase II. The application of these two statistical techniques, together with the contribution of an intuitive graphic tool (to facilitate the detection of assignable causes for the anomalies), constitutes the new proposed procedure of control charts for functional data. Generally, the procedure can be summarized as follows:
The energy consumption curves in HVAC during August and September accounts for the calibration sample. A broad temporal range has been taken to estimate the natural control limits of energy consumption in HVAC accurately.
For Phase I, the reference or calibration sample is stabilized by using the control chart developed from the depth measures of the curves. Particularly, curves detected as atypical by FDA outlier data detection methods are removed from the calculations to estimate the natural control limits.
Data corresponding to October and November are monitored to confirm that there is no deviation in the HVAC processes. If there is a change, that is, there are days with out-of-control HVAC energy consumption, then it was recommended that the possible assignable causes should be sought, which, when detected, should be removed in order to remove the corresponding process variations.
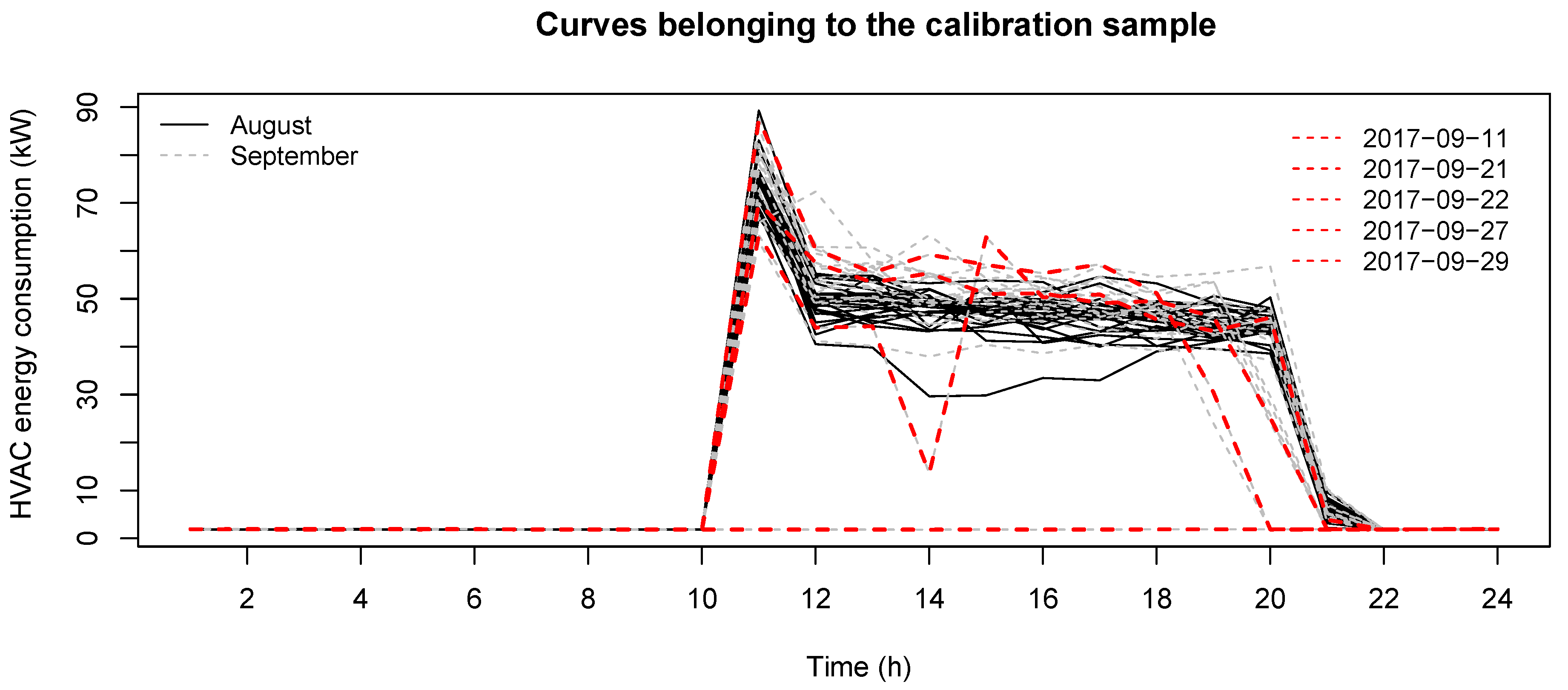
In
Figure 3, the black curves correspond to August (23 curves), whereas the gray curves account for the HVAC energy consumption in September (21 curves). The days from Monday to Friday are used in this study, taking into account that the work schedule is different on Saturday and Sunday. In September, the actual anomalies were detected (see
Figure 3, curves in red) using the Phase I control chart based on the functional data depth outlier detection methods. Particularly, the anomalies corresponding to 11, 21, 22, 27 and 29 September were identified (refer to
Section 3 for more information on the assignable causes of these anomalies).
From this reference sample and based on the simulation study corresponding to the control chart based on the functional depths (see
Section 5), the mode functional depth and the weighed method for outlier detection are used. Additionally, a significance level of
0.025 is used for the estimation of the LCL from
bootstrap resamples, a smoothing coefficient
0.8, and a percentage of Trimming
0.05, which allows obtaining an envelope of 95% of the deepest curves. The advantage of this procedure of detecting atypical curves in the Phase I control chart based on functional data is its flexibility to adapt to a wide variety of real problems, by regulating its parameters (
and
).
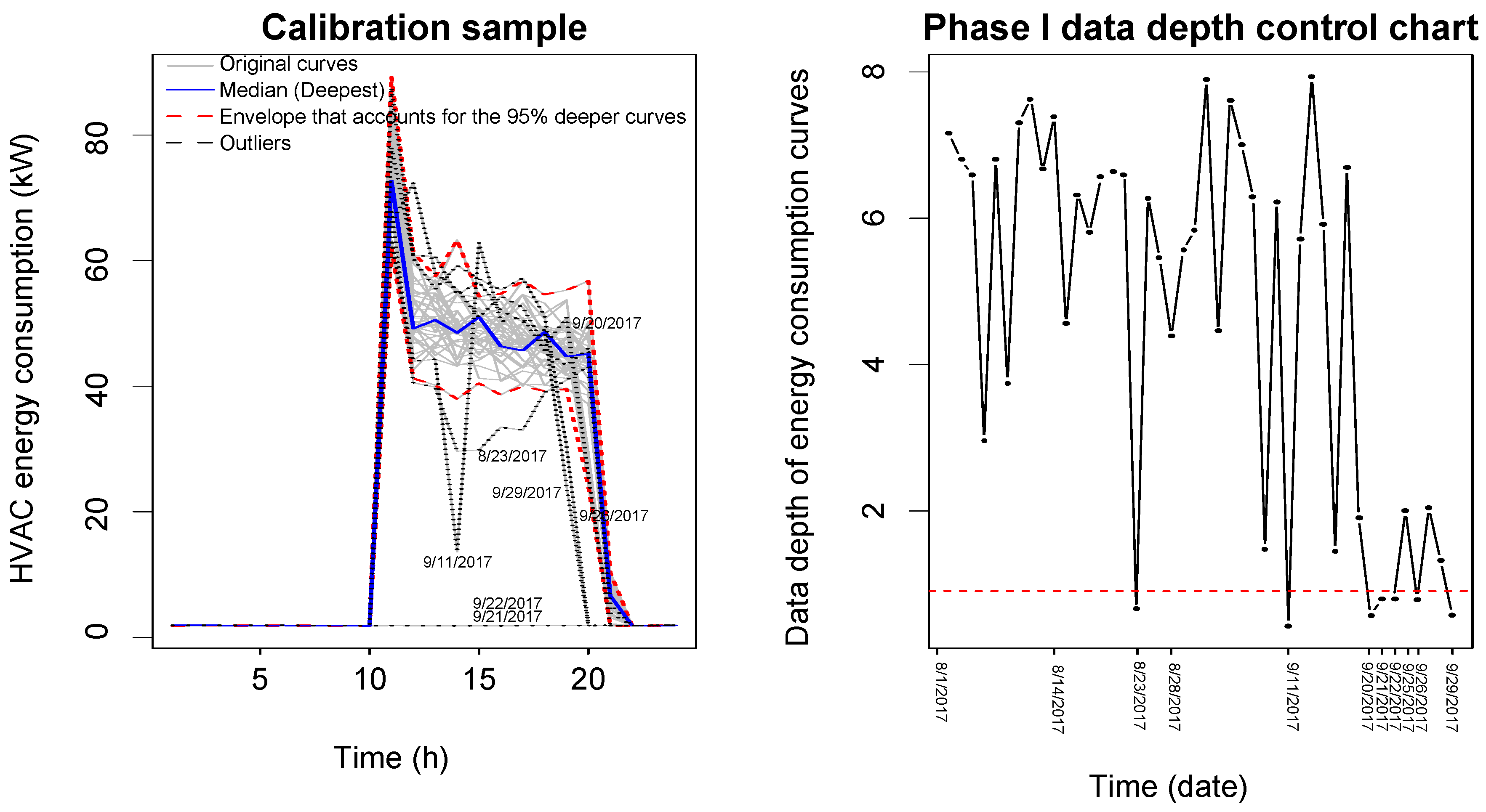
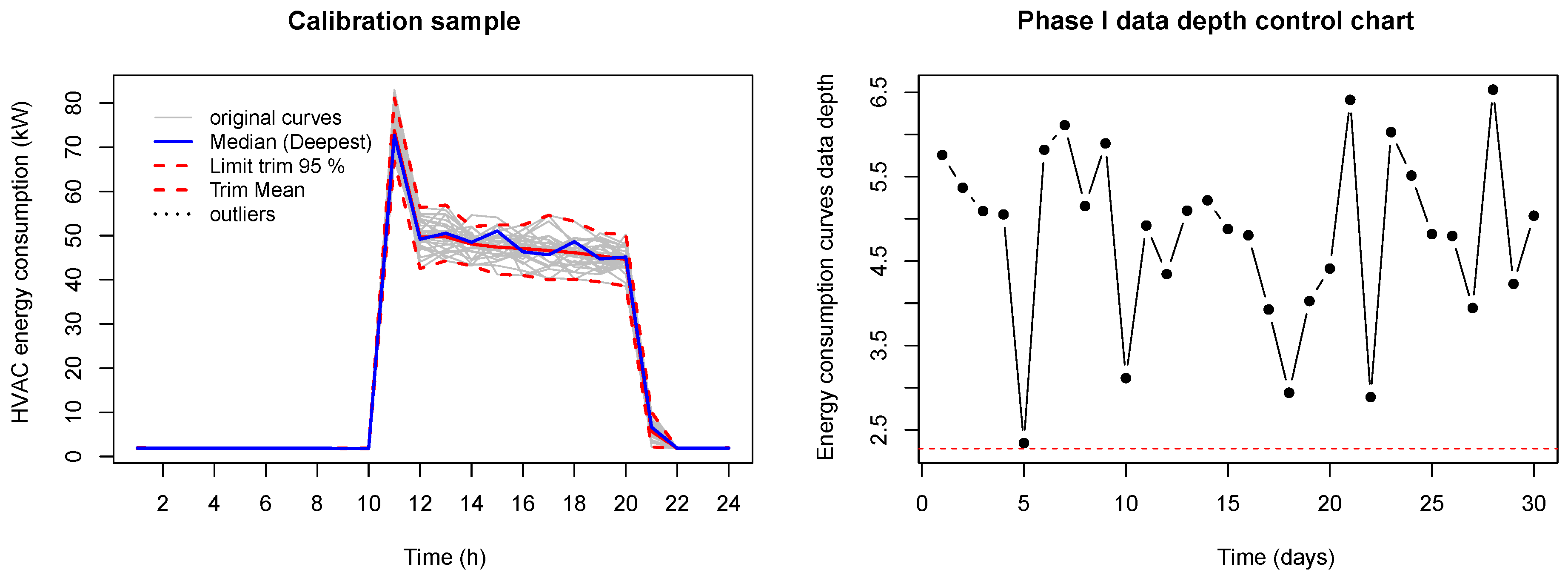
The left panel of the
Figure 4 shows the original gray curves, the estimate of the median (blue curve), the functional trimmed mean (red curve) and the envelope corresponding to the 95% of the deepest curves, which is plotted in red. The curves detected as anomalous are shown in gray and dotted in black. After the mentioned atypical energy consumption curves are identified, they are removed from any calculation related to the estimation of the natural control limits, given that their assignable causes have been identified (causes apart from the randomness of the data). Subsequently, the process is repeated according to an iterative scheme until atypical curves associated with assignable causes are not identified.
Figure 4 shows the functional approximation of the rank control chart, where each datum or point accounts for a daily curve of energy consumption in HVAC. The first 23 points represent the HVAC energy consumption curves for August, whereas the next 21 points represent the energy consumption curves of September.
In this first iteration, the previously identified curves are detected as anomalous. Their structure corresponds to an assignable cause of variation (see
Section 3). They correspond to 11, 21, 22 and 29 September. However, in this iteration, the anomalous curve corresponding to 27 September has been not detected. Additionally, the curves corresponding to 23 August, 20 and 26 September are detected. Moreover, the data depth corresponding to the curves from 19 September are very small—they are outside the lower control limit and thus they are identified as out-of-control states. The assignable cause corresponding to this behavior is that the air conditioning was being shut off half an hour earlier than usual.
In the next iteration, the following daily consumption curves are detected as out-of-control or anomalous: 4 August, 15, 19, 25 and 27 September. In this iteration, the HVAC energy consumption curve of 27 September and those corresponding to the last days of September are identified; the timing of HVAC shutdown was changed for the latter part of September. Finally, energy consumption curves are not detected as anomalous after the second iteration (see
Figure 5).
The process began with 44 curves, of which 9 (in the first iteration) and 5 (in the second iteration) curves were identified as anomalous. Of these 14 energy consumption curves, 2 and 12 curves correspond to August and September, respectively. Hence, the calibration sample comprises days in August and September, until 18 September. The current performance of energy efficiency of HVAC installation has been characterized through this reference or calibration sample. The next step is to detect changes (from the reference HVAC performance) in the HVAC system. This task belongs to Phase II control charts.
After Phase I, the Phase II control charts based on functional data, also called monitoring phase, is performed. Therefore, the sample to be monitored comprises days corresponding to October in which the HVAC facilities of the apparel store were operated at regular times. This is in consideration of the fact that a leak in the air conditioning circuit was recorded in mid-October, especially after the HVAC consumption began to rise. This behavior can be observed in
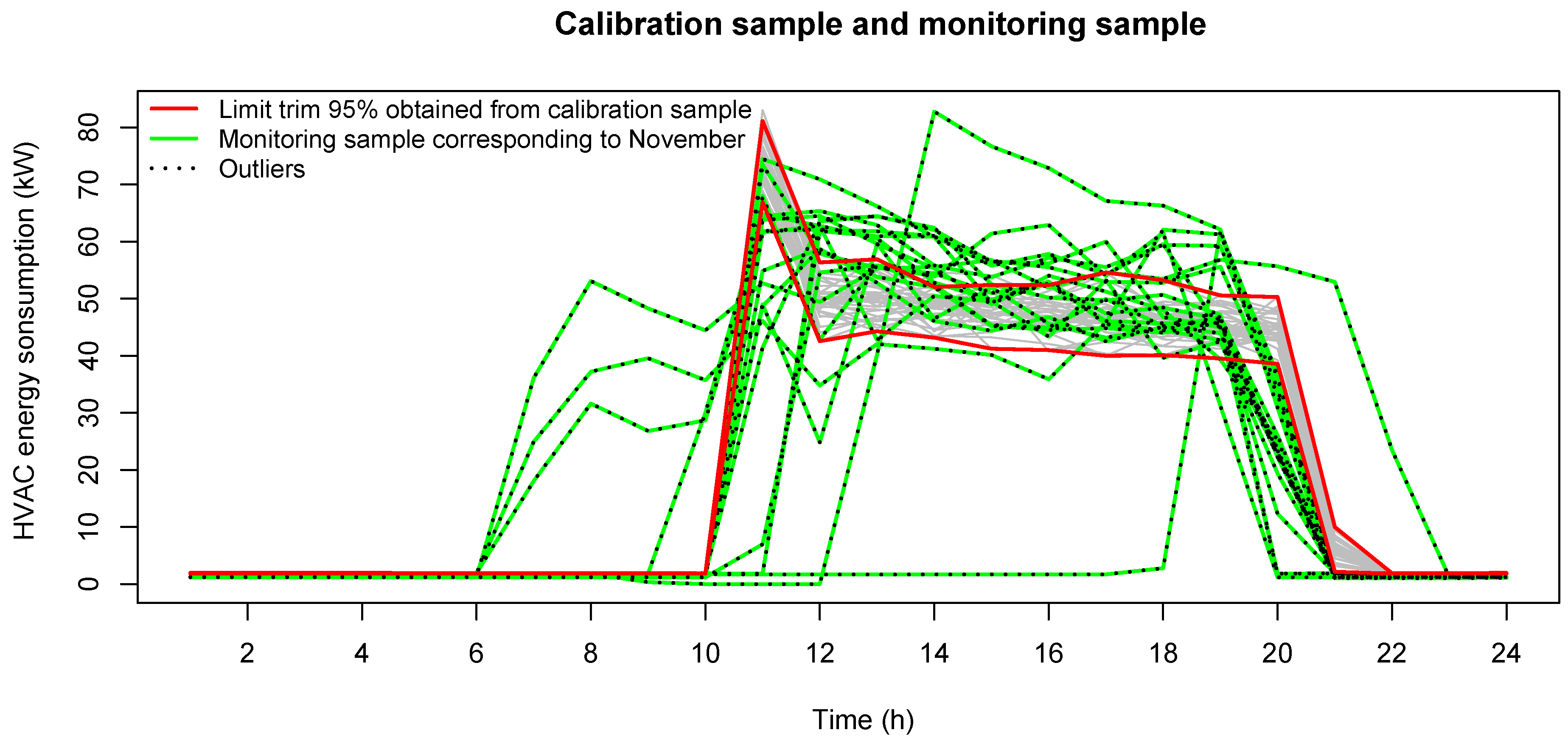
Figure 6; it plots the monitored sample as well as the curves of the calibration sample and their 95% envelope, which is estimated in Phase I.
Figure 6 shows that the HVAC energy consumption, the CTQ variable for the energy efficiency of HVAC installations, is out of control. The assignable cause is the leak in the air conditioning system. In order to rectify the anomalous operation of the HVAC installations, on 1 November, a provisional repair was performed. These actions produced a decrease in the HVAC energy consumption and attenuated peak energy consumption corresponding to the start-up (see the energy consumption curves before 11:00). Consequently, the consumption of the HVAC facilities in November is slightly different from that of August and September, which account for the calibration sample. However, this energy consumption resumes its rise between 17 and 20 October.
These changes can be observed in
Figure 7 wherein it is observed that the HVAC energy consumption corresponding to the monitored sample is characterized by a greater variability than that corresponding to the calibration or reference sample. The results of the application of the rank control chart show that the process is out-of-control both for the monitoring samples of October and November. In October, the assignable cause is the fault in HVAC facilities, whereas the assignable cause in November is the change in the process due to repair activities that deals on a decreasing in HVAC energy consumption.
Given that the process has changed, a new reference sample should be obtained and studied. The stabilization and monitoring process should begin for the next year, starting December.
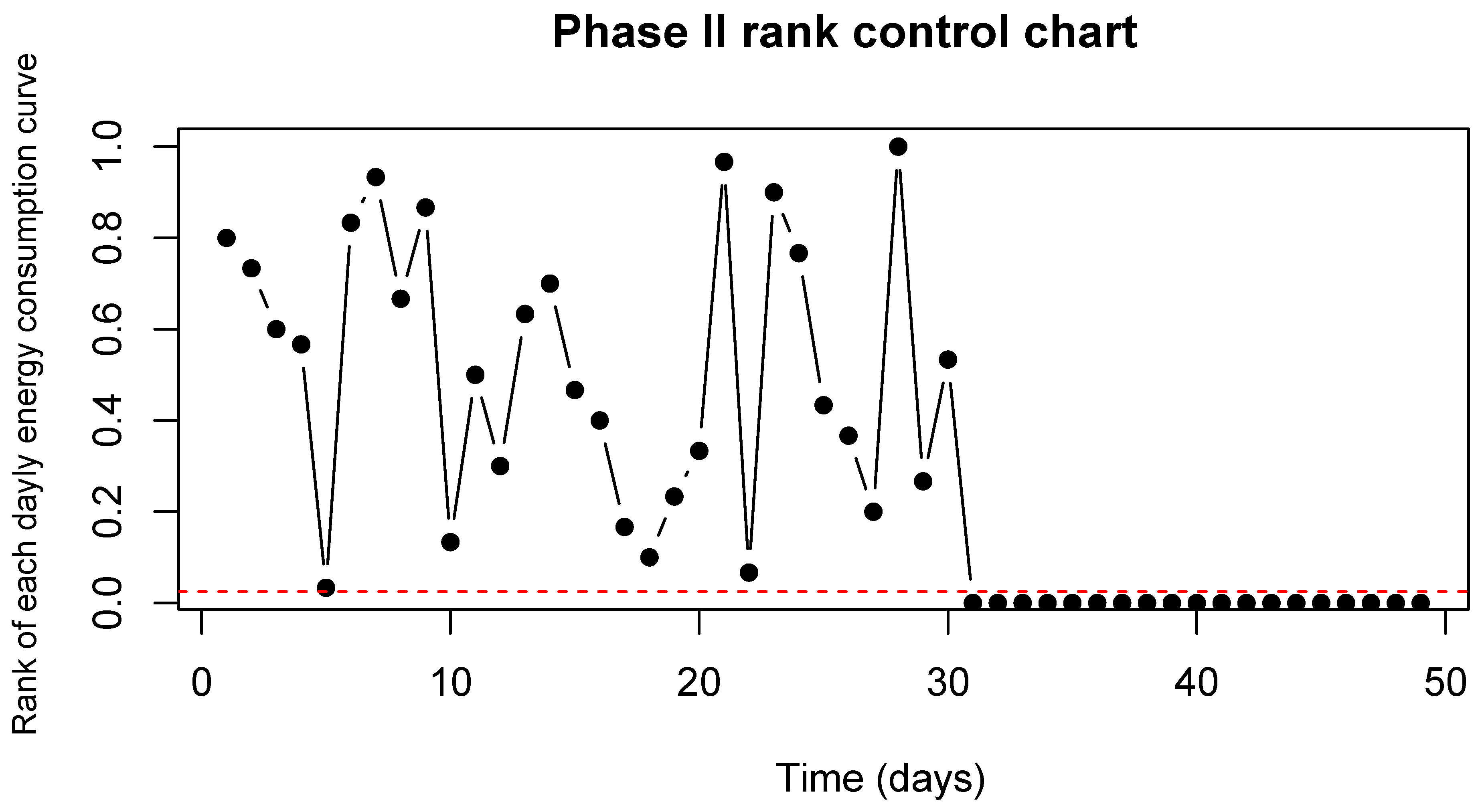
Figure 8 shows the rank control chart for the calibration (August and September) and monitoring samples of November. In practice, monitoring can be efficiently performed using the proposed control charts because you do not need to estimate the LCL through resampling procedures. Additionally, the rank control chart can be adapted for monitoring multivariate functional data, that is, when there are different types of curves that define the quality of a specific system or process simultaneously. For example, a direct case of application considers their first derivative along with the original curves.
The application of rank control charts also allows us to monitor the process by studying more than one functional variable. Particularly, it not only allows us to study the energy consumption curves but also the curves of daily temperature, daily relative humidity, daily CO concentration, among others; they completely characterize the energy efficiency of the facilities and their thermal comfort and ambient air quality. Precisely, this procedure would allow us to perform a functional multivariate monitoring.
5. Simulation Study
The control chart performance is many times measured by observing its power
. It is defined as the probability of identifying an out-of-control state when the process state is actually out-of-control [
35]. Moreover, assuming that the process is actually under control, the type I error (
) or false alarm rate will be defined as the probability of detecting an out-of-control signal [
35].
In the case of the process is under control, the probability of identifying an out-of-control observation should be small enough to prevent an unacceptable number of false alarms. Otherwise, if the process is effectively out of control, the power should be high enough to detect the process change as quickly as possible [
35].
Another common index for measuring the performance of a control chart is Average Run Length (ARL), which is defined as the average number of observations plotted before a signal is out-of-control. The ARL is equal to
(if we can assume that the signals are independent, that the run length distribution is geometric), where
p is the probability of having an out-of-control signal [
35].
To evaluate the performance of a control chart in Phase II, the
and
are often used, which are the average number of observations until the first out of control is detected, in cases where the process is really under control (
) or actually is not (
) [
35]. The
should be at its lowest to increase the probability of quickly identifying events
, power of a test that lead to the process being out-of-control [
35].
Given that the F distribution is not known, a Monte Carlo simulation is designed to calculate the control charts power. The simulated scenarios allow us to estimate and compare the power of the control charts for different data depth measurements and for the case of independent and dependent functional data.
In this section, the performance of the control graphics proposed for Phases I and II will be evaluated. First, the simulation scheme designed in Febrero et al. [
44] will be used to evaluate the performance of the control chart proposal for Phase I. Realizations of a Gaussian stochastic process have been proposed following the expression below [
44,
48]:
whereby
0.5 and
whereas
is a Gaussian process
with
0 mean and variance-covariance matrix equal to
Additionally, Reference [
44] developed an alternative model to generate atypical curves,
. In
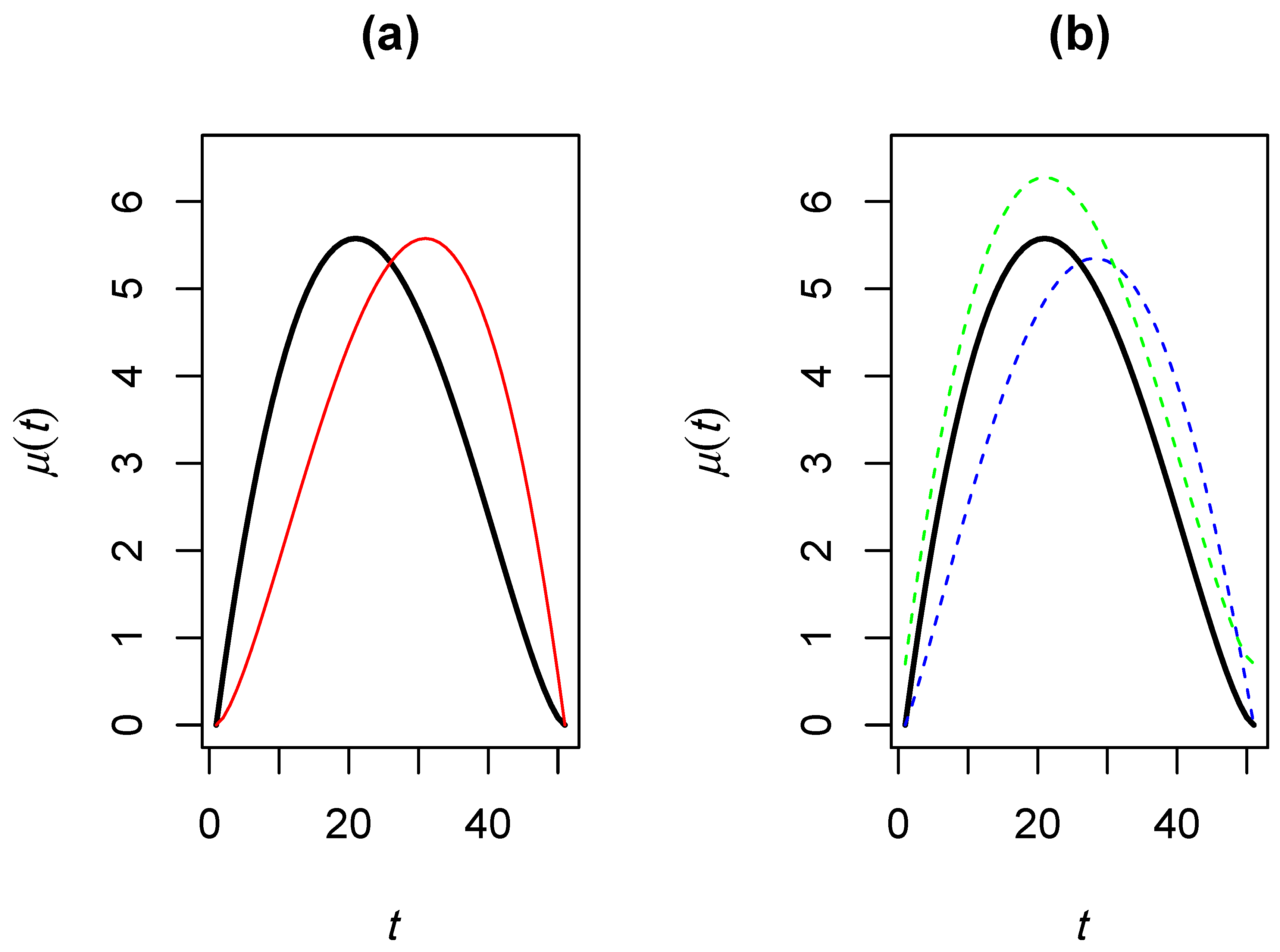
Figure 9a, the two functional means are presented. The black curve accounts for the process mean without atypical curves, while the red curve is the mean of the process that generates the atypical curves.
The control charts proposed in this work have been designed to monitor the functional mean to detect two events—change in the mean of the process in terms of the magnitude and shape—which reveal that the process is not under control. For designing control charts for Phase II, it is assumed that the process is under control, that is, outliers are not detected. To generate simulation scenarios for each of these events, the following functional means have been considered:
Mean of the model with a change in the magnitude:
by which
denotes the change that goes from 0.4 to 2 in steps of 0.4.
Mean of the model with a change in form:
where
is the change from 0.2 to 1 in steps of 0.2.
In
Figure 9b, the green curve accounts for the functional mean of a process when there is a change in the magnitude (
0.7), while the curve of blue denotes the mean of a process when there is a change in the shape (
0.3).
In Febrero et al. [
44], the functional data
denote realizations of a stochastic process
, assuming continuous trajectories in the
period and independence between the curves. However, simulation scenarios in which the simulated curves are defined by a variable degree of dependence have also been considered. This is because several practical applications of this type of chart are related to continuously monitored data with respect to time, forming functional time series, such as the curves of daily energy consumption in commercial areas. In this way, dependent curves are generated from the model
, with
, where
is the correlation measure between curves and
and both
and
are Gaussian processes [
48].
In order to compare the results of the simulations in the scenarios defined by independence and dependence between the curves, the variance of is rescaled (we define the variance of the error to be one). Specifically, considering , you have .
In
Figure 10, different scenarios are presented considering the changes in the functional mean of the process, in the shape and magnitude, in the cases of independence and dependence between curves. The gray curves show the realizations of the process when it is under control (whose mean is the Equation (
4)). However, the red curve in each graph accounts for the scenarios in which the presence of events that destabilize the process is considered, that is, the process is not under control. In
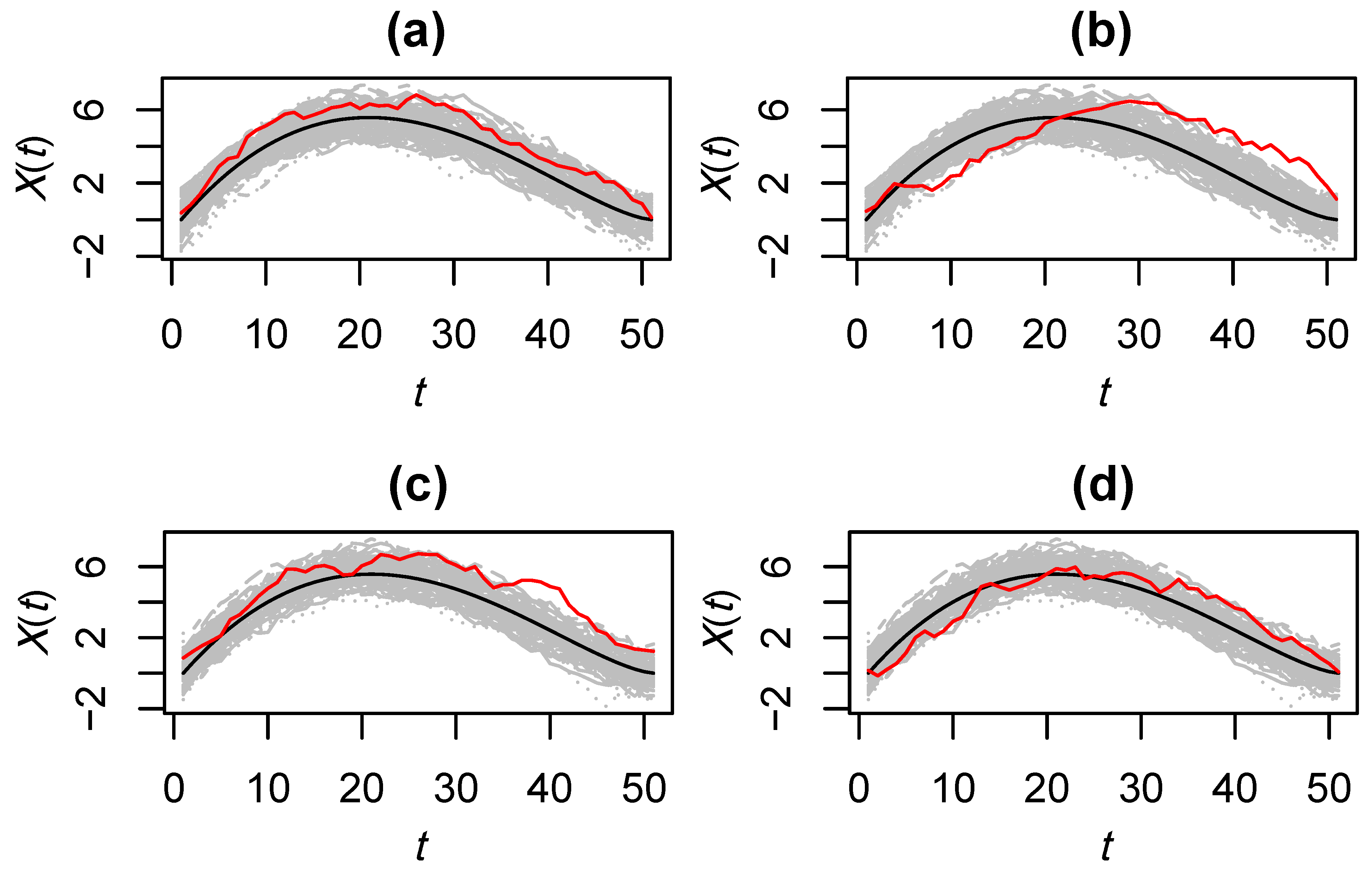
Figure 10a,b, the cases of independence between curves and the presence of events defined by changes in the functional mean in terms of the magnitude and in shape, respectively, are shown. However,
Figure 10c,d show two cases defined by the presence of dependence between curves, including changes in the magnitude of the mean (panel c), with respect to its shape (panel d).
In the building energy efficiency domain, the out of control signals of energy consumption, temperature, CO
proportion and humidity, among others, can be defined by a change of shape and/or magnitude with respect to the under control signals analogous to those analyzed in the simulation study. The change in magnitude is related with a change in the scale of the studied process, for example, the increasing of energy consumption, temperature, humidity or concentration of CO
in all the hours corresponding of a specific day with respect to the otherwise normal pattern. This type of change is accounted by the addition of the
term to the Equation (
4) in order to obtain the Equation (
5). Thus, the amount of that change is controlled by
parameter. The green curve of
Figure 9 accounts for an example of magnitude change. If we compare with the black one, we could realize that the two curves have the same shape and the only difference is the scale. On the other hand, changes in the shape of the curves are introduced by modifying the Equation (
4) by the
parameter resulting in the Equation (
6). In the energy efficiency domain, this type of change can be related to a change in the HVAC facilities programing (changes in temperature regulation, changes in the time schedule), in a failure of the HVAC in just one interval of the day, an extremely high or low level of occupation in a building and extreme changes in the weather, among other causes. The proposed simulation study has performed taking into account the specific domain where the FDA control chart approach is applied, namely energy efficiency in buildings. Thus, the shape of these types of profiles is similar to that corresponding to CO
, temperature, energy consumption and humidity curves in buildings. In order to measure the performance of the proposed control charts for very different types of profiles, new studies may be necessary.
In the following section, a simulation study is performed to determine conditions under which it can be verified that the smooth bootstrap procedure works when there is independence and dependence between curves.
5.1. Measurement and Comparison of the Performance of the Control Chart Proposed for Phase I
The performance of the control chart is estimated and compared from the generation of calibrated samples of size 50 and 100 (curves). For each sample, different functional depth measurements described in
Section 2 are calculated and the outlier detection robust procedures (weighted and trimmed) are applied for the estimation of type I error when the process is under control and the power of the test when the process is out-of-control. For the estimation of type I error, each scenario is replicated 1000 times (
50, 100, assuming independence and dependence between curves). When the power of the test is estimated, in each scenario (assuming independence and dependence), a curve within the alternative hypothesis is generated; this procedure is also repeated 1000 times.
Following the scheme described in Reference [
44], curves observed at equidistant points are considered; the number of points that define each curve is 51 in the interval
. From 1000 resamples (
) and with a 2.5% trimming procedure (removing less deep curves), a smoothing bootstrap procedure defined by a smoothing factor
0.05 is applied to estimate the
0.01 quantile representing the LCL.
First, a simulation study is performed to estimate and compare the type I error ( 0.01 is fixed) of the proposed control chart, assuming scenarios with independence and dependence between curves. Subsequently, a similar study is carried out to estimate and evaluate the power of the control chart to detect out-of-control signals in different situations (independence, dependence, different sample size and a change in the shape or magnitude).
In
Table 1, the results of the estimation of the false alarm rate (type I error) in the independence scenario are shown. The average of the percentage of false out-of-control signals (type I error) detected by the procedure shown above are very close to the nominal 1% for the two considered sample sizes. Furthermore, it can be observed that, when
n increases, the type I error percentages are closer to the nominal level. In general, for a sample of size
, the results of applying the weighted method are closer to
, especially when using the mode depth measurement. The results obtained in the simulations are similar to those presented in Reference [
44].
In any process, type I error increases the production cost. Hence, it is essential not to overestimate this error rate when managing the quality.
Table 2 shows the results of the simulation to evaluate the ability of the control chart to detect a change in the shape or magnitude of the functional mean of the process through the estimation of its power (
). The percentage of out-of-control signals (outliers) correctly detect when the population defined by the Equation (
4) is contaminated with curves belonging to the
model (Equation (
5)) and
model (Equation (
6)); it is denoted by
; however, the percentage of false alarms (false states out of control) is
. These parameters have been estimated, in all the scenarios assuming the independence of curves, using the average of the corresponding empirical values,
and
.
Table 2 shows that a better performance is achieved when the curves of model
(where changes in the magnitude of the proposed control chart are simulated) are studied. Precisely,
and
are closer to the nominal
and
. When identifying changes in the shape of the process average,
, the mode depth provides the highest percentages of correctly detected out-of-control signals. However, in the case of the
model, the use of RP depth provides percentages of the detection of the true out-of-control states lower than those corresponding to the use of FM and mode depths. With respect to a robust method for outlier detection, the performance is similar in all the scenarios. However, an exception is the case wherein the RP depth is used; it reveals the low performance of the control chart in detecting observations corresponding to actual out-of-control states.
Briefly, the detection rate of false out-of-control signals for the independence scenario is close to 1%. However, when using the trimmed method, the detection rate of false out-of-control signals is overestimated but this percentage decreases when the sample size increases.
The results of the false alarm rate (type I error) for scenarios defined by dependence between curves are shown in
Table 3. It is important to note that, for different values of
, very similar results with respect to the independence scenarios have been obtained. Precisely, the average of the percentages of false out-of-control signals are close to the nominal 1% in the two studied sample sizes. Additionally, when
n increases, the type I error percentages are closer to the nominal level. However, some differences are observed when the RP data depth measure is used to develop the control chart. In this case, there is an overestimation of the percentage of false out-of-control signals.
Table 4,
Table 5 and
Table 6 show the results of the empirical estimation of
and
, assuming different values of
(from 0.3 to 0.7). The power (estimated by
) of the control chart proposed for the model
(Equation (
5)) performs better when the weighted method is applied and if the sample size is increased. It is also observed that the performance of the control chart tends to be the same, independent of the type of data depth measurement used. Certainly, the performance of control charts in detecting real changes in the process, related to differences in the shape and mean, is better when the mode depth is used.
With respect to the false out-of-control rate , in the scenarios corresponding to the use of model, when the trimmed method is also used, a lower rate is obtained. In the case of the model, there are similar results on the scenarios defined by independence between curves, that is, the is lower when the trimmed method for outlier detection is used.
In Reference [
56], new methods for the detection of outliers were proposed for the case in which there is dependence between curves. From the simulation studies carried out in this study, at different degrees of dependence, we can say that the outlier detection method proposed in Reference [
44] was relatively robust against the presence of dependence between curves. The simulation study performed in this section supports the results obtained in the work in Reference [
56] and, in conclusion, justifies the use of this method within the new control charts proposed for Phase I, even in scenarios with dependence between curves.
Although the application of the weighed outlier detection method to Mode data depth has generally provided Phase I control charts with best performance, if the false alarm rate of
Table 1 and
Table 3 are observed, the use of trimmed outlier detection method tends to provide values of
slightly closer to
(with respect to the weighted method) when the process is actually under control, the curves are independent and the sample is relatively small (
). In addition, if the process is out of control, the curves are independent and the outliers are generated by the Equation (
5) (changes in magnitude), the trimmed method applied to FM data depth provide a
close to
and the highest
, as shown in
Table 2. In all the remaining scenarios, the use of weighed method applied to Mode data depth tends to provide the closest to
and the highest
(see
Table 3,
Table 4,
Table 5 and
Table 6).
5.2. Measurement and Comparison of the Performance of the Control Chart Proposed for Phase II
For Phase II, the monitoring stage, the use of the rank control chart has been proposed. The application of the rank control chart allows simultaneous monitoring of changes in the mean and variability of a process. In the functional case, in order to calculate the rank statistic, the functional FM, RP and mode depths are used.
An (the monitoring sample is assumed under control) is assumed to evaluate the performance of the control chart. The power of the control chart is estimated and compared for an under-control process, based on the generation of a calibration sample of size by a Monte Carlo procedure.
Following the simulation scheme of Phase I, curves observed at equidistant points are assumed; they are composed of 51 points at interval. A smoothed bootstrap with a smoothing factor 0.05, 1000 resamples (), using a 2.5% trimmed procedure (removing the shallowest curves), is applied to estimate and compare the power of the control chart to detect out-of-control signals when a significance level of is assumed. Additionally, in the same way as in Phase I, the simulation of scenarios with independence and dependence between curves are assumed.
Table 7 shows the estimates of the power (%) of the control charts for the scenario of independence between curves, whereas
Table 8 shows power of the control chart for the scenario with dependence. In both cases, the ability of the control chart to detect a change in the magnitude of the functional mean of the process is evaluated by the estimation of its power (
).
From the results of the
Table 7, any depth measure can be used to detect a shift in the process mean, since the same performance, in terms of power, is obtained.
The results of the detection of a shift in the process mean are shown in
Table 8. A similar performance is observed when using any depth measure for different values of
. Apparently, the control chart for Phase II is robust against the existence of dependence between curves.
As observed in the simulation study and in the analysis of the case study with real data, the present proposal of control charts for functional data, including Phase I and II control charts, can be useful to detect anomalies in diverse scenarios. In the case of its application to real data, the set of proposed techniques is being examined for implementation in the web platform qus and for its use by the company Nerxus for detecting false alarms in facilities in commercial areas. The present control chart methodology can be used for control tasks, monitoring, anomaly detection and continuous improvement in diverse industrial processes, monitoring of environmental variables, chemical industry and, in general, any process involving continuous monitoring of functional data over time.
Regarding the use of our methodology in more complex case studies defined by different operation modes, the application of the multi-modelling framework methodology in combination with our proposal could be useful. Indeed, in the building energy efficiency domain, there are many different operation modes of installations, each one defined by a specific operation pattern. Namely, the HVAC installations can be operated in heating or ventilation modes (there are even different modes within ventilation or heating). The automatic classification of each profile in the corresponding profile pattern could be very useful in the building energy efficiency field and previously to the application of our control chart proposal for Phase I and Phase II. With respect to the work of Grasso et al. [
43], it is also interesting to mention that the proposed profile monitoring control charting scheme is that based on functional PCA and described in Colosimo and Pacella [
57].
6. Conclusions
A new alternative of control charts has been proposed when CTQ variables of the process are functional. The proposal includes alternatives to develop the the Phase I and II control charts for stabilizing and monitoring the processes, respectively. In order to develop Phase I control charts based on functional data, outlier detection methods are used based on a method of smooth bootstrap resampling and the depth calculation of functional data is proposed. However, in order to implement Phase II, the use of rank-type nonparametric control charts based on the concept of functional data depth is proposed. This Phase II control chart is directly estimated assuming that the asymptotic distribution of the rank statistic is a uniform distribution. The application of the control charts to the two-process control phases and the development of a new graphic tool for visualizing functional data (including an envelope with 95% of the deepest curves that facilitate the identification of the assignable cause of each anomaly) give rise to the proposed methodology. It has been successfully applied in real case studies belonging to the framework of anomaly detection in building energy efficiency. Additionally, a simulation study is conducted to measure the performance (as the percentage of rejection when the null hypothesis is not met) of the control charts, depending on the functional data depth used, the sample size, the presence of dependence between curves and the use of different FDA procedures for outlier detection.
In the simulation study, the use of different types of functional depths has been compared to develop Phase II of the proposed control chart. In case of the univariate functional data (single type of curves), for the three scenarios, a better performance is obtained with the mode depth measurement combined with the weighted outlier detection method and moderately large samples. Additionally, one of the final observations of the simulation study is that the control chart methodology is robust against the presence of dependence between curves. Thus, this alternative tool can be applied to the framework of continuously monitored data streams.
Generally, the authors recommend using the weighed method and the Mode functional data depth for the case of Phase I taking into account the values of
and
. Thus, when the Phase I control chart is evaluated, both weighted method and Mode data depth are generally the best options in those scenarios defined by under control assumption and even in those where out of control curves are simulated. In the latter, when the change in magnitude or shape is very small, the corresponding
tends to be not higher to those obtained by the use of other combinations of data depth measure and outlier detection method. Nevertheless, when the change in magnitude (
) or shape (
) increases, the power of the combination of weighted method and Mode depth tends to be higher than those corresponding to the other combinations. Moreover, regarding the Phase II control chart and taking into account the higher values of power estimates included in
Table 7 and
Table 8, we also recommend the use of Mode data depth for Phase II control charts.
The present proposal has been verified by its application in a real case study dealing with the detection of energy efficiency anomalies in buildings. Specifically, all the previously identified real anomalies (by the maintenance personnel) have also been successfully identified by the application of this functional approximation of control charts for Phases I and II of process control. Additionally, the proposed graphical tool helps to intuitively identify the assignable causes corresponding to each anomaly.
This procedure can be used in different industrial and scientific domains in which the control procedures are defined by functional CTQ variables.