Dynamic Modelling of Interactions between Microglia and Endogenous Neural Stem Cells in the Brain during a Stroke
Abstract
1. Introduction
2. Mathematical Models
2.1. Modelling of the Effect of Microglia on the Brain in a Stroke Onset (SMD)
2.1.1. Equilibrium Points for the SMD Model
2.1.2. Stability of Equilibrium Points
- Stability analysis of equilibrium point, :Theorem 1.Suppose that the function where Γ is a domain in , and suppose that is an equilibrium point at which at least one eigenvalue of the Jacobian matrix has a positive real part. Then, is an unstable equilibrium point of f.Proof.The Jacobian at equilibrium point is calculated as follows:where,The characteristic equation for the Jacobian is given byWe assume that , .Then, the eigenvalues of Jacobian matrix are given by:The eigenvalues , …, are negative, but is positive. Therefore, is an unstable equilibrium point. □
- Stability Analysis of Equilibrium point, :Theorem 2.Suppose that the function where Γ is a domain in , and suppose that is an equilibrium point at which at least one eigenvalue of the Jacobian matrix has a positive real part and , . Then, is an unstable equilibrium point of f.Proof.The Jacobian , at calculated as:where,From the Jacobian , the characteristic equation is given bywhere,By Proposition 1 one of the eigenvalues is positive. So, has one at least positive root, which indicates that the equilibrium point is unstable [44]. □
- Stability analysis of equilibrium point, :Theorem 3.Suppose that the function where Γ is a domain in , and suppose that is an equilibrium point where all the eigenvalues of the Jacobian matrix have negative real parts at the equilibrium point and , . Then, is a stable equilibrium point of f.Proof.The Jacobian at is calculated as follows:where,The characteristic equation is given byThus, we can find the first two eigenvalues directly:Here, we can apply the Routh–Hurwitz Criterion if and only if [45]:
- ,
- ,
- .
whereSince from Proposition 1,Then, and ,Now, we apply the Routh–Hurwitz theorem for , givingwhere,thus,Since all the coefficients in the first column have positive signs; the Equation has no roots with positive real parts and two of the eigenvalues are negative; thus, the equilibrium point is stable. Activated microglia are capable of cleaning dead cells; however, they produce free radicals from brain cells, which increases the damage in brain cells during a stroke. This lead to further death of brain cells [17,32]. □
- As a result of Theorem 1 and Definition 1, the damage, D, can invade the SMD system if .
- As a result of Theorem 2 and Definition 2, this means that the damage, , invades C.
- As a result of Theorem 3 and Definition 3, this means that the damage, , causes the death of C.
- The SMD model is stable when the brain cells are affected by the proinflammatory cytokines of microglia; however, when the rate of production of proinflammatory cytokines leads to an increase in damage, the possibility of death of the brain cells is introduced.
2.2. Modeling the Interaction between Microglia and Neural Stem Cells and Impact on the Brain in Stroke (SMNR)
2.2.1. Equilibrium Points
- .
2.2.2. Stability of Equilibrium Points for SMNR Model
- Stability analysis of equilibrium point, :Theorem 4.Suppose that the function where Γ is a domain in , and suppose that is an equilibrium point at which at least one eigenvalue of the Jacobian matrix has a positive real part. Then, is an unstable equilibrium point of f.Proof.The Jacobian corresponding to the equilibrium point is given bywhere,From the Jacobian matrix , the characteristic equation is given byThen, the eigenvalues corresponding to are given byOne of the eigenvalues, , then is an unstable point. □
- Stability analysis of equilibrium point, :Theorem 5.Suppose that the function where Γ is a domain in , and suppose that is an equilibrium point at which at least one eigenvalue of the Jacobian matrix has a positive real part and . Then, is an unstable equilibrium point of f.Proof. The Jacobian matrix corresponding to the equilibrium point is given by:where,From the Jacobian , the characteristic equation is given bywhere,In Equation , the eigenvalue is distinctly positive, by Proposition 2. Thus, has at least one positive root. Thus, the equilibrium point is unstable [44].
- Stability analysis of equilibrium point, :Theorem 6.Suppose that the function where Γ is a domain in , and suppose that is an equilibrium point at which at least one eigenvalue of the Jacobian matrix has a positive real part and , . Then, is an unstable equilibrium point of f.Proof.We now study the stability of the equilibrium point , calculated as:The Jacobian matrix estimated at iswhereFrom the Jacobian , the characteristic equation is given byIn Equation , the eigenvalue is distinctly positive, by Proposition 2. Thus, has at least one positive root and, so, the equilibrium point is unstable [44]. □
- As a result of Theorem 4 and Definition 4, the neural stem cells, Nsc, can invade the SMNR system if .
- As a result of Theorem 5 and Definition 5, this means that the neural stem cells, , can invade C and D.
- As a result of Theorem 6 and Definition 6, this means that the neural stem cells, , can eliminate the damage D.
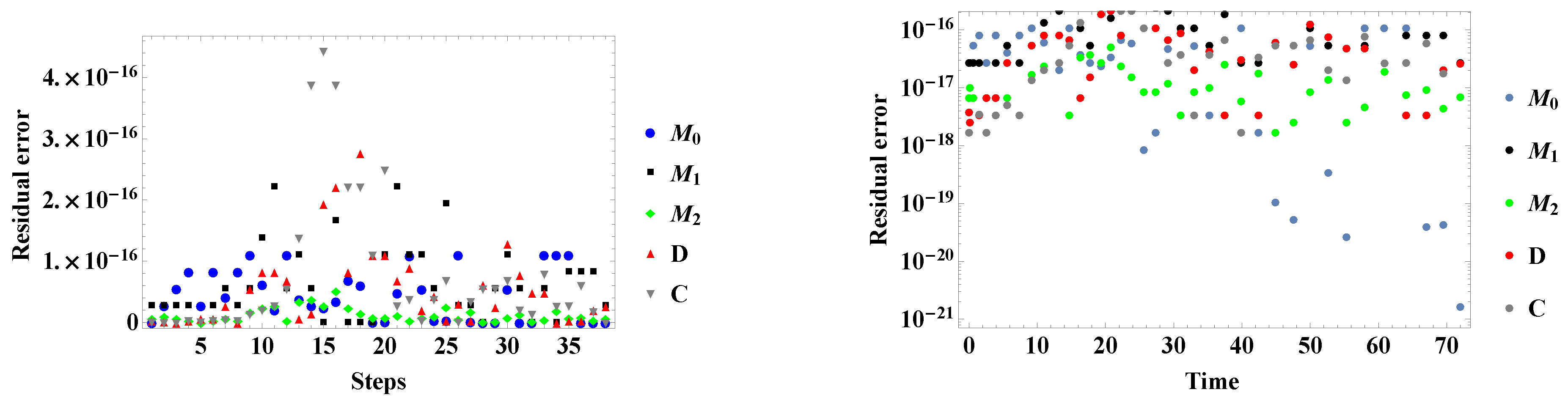
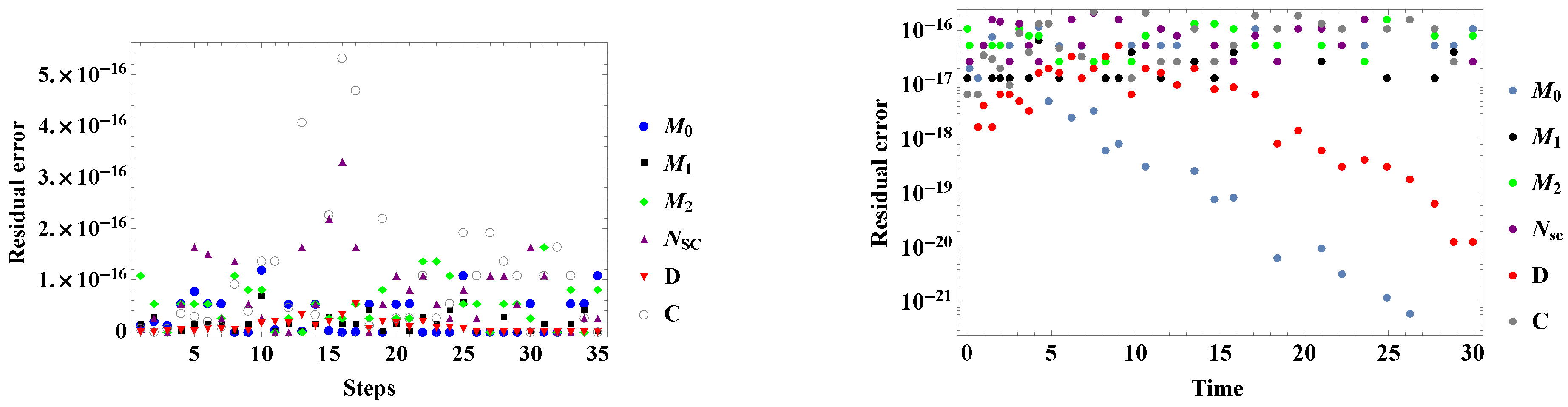
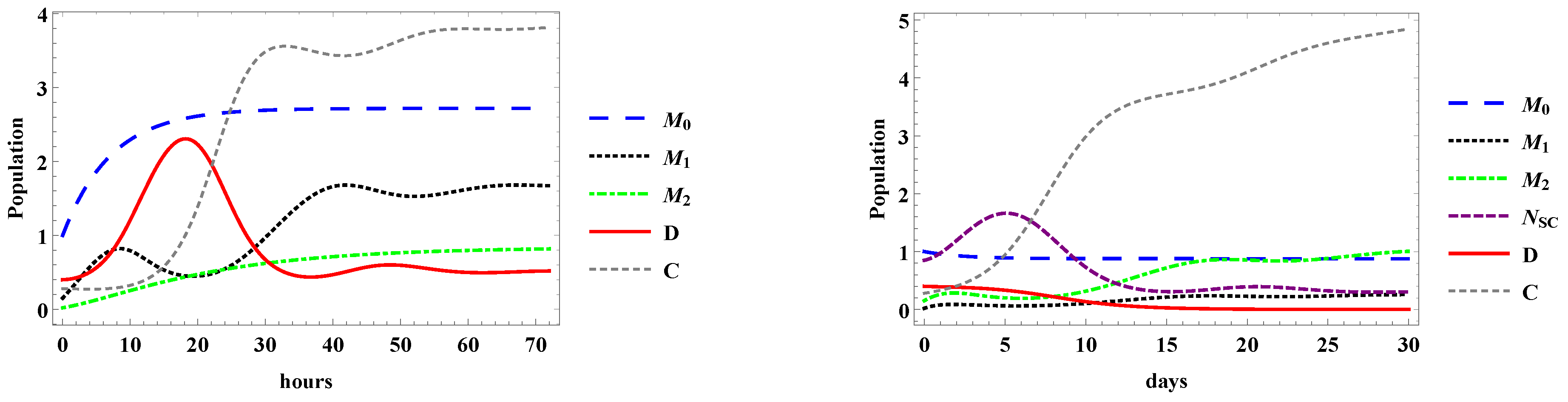
3. Numerical Experiments
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Di Russo, C. A mathematical model of inflammation during ischemic stroke. Math. Model. Med. 2010, 30, 15–33. [Google Scholar] [CrossRef]
- Guruswamy, R.; ElAli, A. Complex roles of microglial cells in ischemic stroke pathobiology: New insights and future directions. Int. J. Mol. Sci. 2017, 18, 496. [Google Scholar] [CrossRef]
- Tobin, M.K.; Bonds, J.A.; Minshall, R.D.; Pelligrino, D.A.; Testai, F.D.; Lazarov, O. Neurogenesis and inflammation after ischemic stroke: What is known and where we go from here. J. Cereb. Blood Flow Metab. 2014, 10, 1573–1584. [Google Scholar] [CrossRef] [PubMed]
- Radak, D.; Katsiki, N.; Resanovic, I.; Jovanovic, A.; Sudar-Milovanovic, E.; Zafirovic, S.; Mousad, S.A.; Isenovic, E.R. Apoptosis and acute brain ischemia in ischemic stroke. Curr. Vasc. Pharmacol. 2017, 15, 115–122. [Google Scholar] [CrossRef] [PubMed]
- Anttila, J.E.; Whitaker, K.W.; Wires, E.S.; Harvey, B.K.; Airavaara, M. Role of microglia in ischemic focal stroke and recovery: Focus on toll-like receptors. Neuro-Psychopharmacol. Biol. Psychiatry 2016, 79, 3–14. [Google Scholar] [CrossRef] [PubMed]
- Stonesifer, C.; Corey, S.; Ghanekar, S.; Diamandis, Z.; Acosta, S.A.; Borlongan, C.V. Stem cell therapy for abrogating stroke-induced neuroinflammation and relevant secondary cell death mechanisms. Prog. Neurobiol. Prog. Neurobiol. 2017, 158, 94–131. [Google Scholar] [CrossRef]
- Banjara, M.; Ghosh, C. Sterile neuroinflammation and strategies for therapeutic intervention. Int. J. Inflamm. 2017, 10, 8385961. [Google Scholar] [CrossRef]
- Rajab, N.F.; Musa, S.M.; Ahmad Munawar, M.; Leong, L.M.; Heng, K.Y.; Ibrahim, F.W.; Chan, K.M. Antineuroinflammatory effects of hibiscus sabdariffa Linn.(Roselle) on Lipopolysaccharides-induced Microglia and Neuroblastoma Cells. Malays. J. Health Sci. 2016, 14, 111–117. [Google Scholar]
- Rune, L.; Martin, W.; Daniel, G.; Christina, F.; Lasse, D.; Ishar, D.; Bente, F. Microglial cell population dynamics in the injured adult central nervous system. Brain Res. Rev. 2005, 48, 196–206. [Google Scholar]
- Galloway, D.A.; Phillips, A.E.; Owen, D.R.; Moore, C.S. Phagocytosis in the Brain: Homeostasis and Disease. Front. Immunol. 2019, 10, 790. [Google Scholar] [CrossRef]
- Pham-Huy, L.A.; He, H.; Pham-Huy, C. Free radicals, antioxidants in disease and health. Int. J. Biomed. Sci. IJBS 2008, 4, 89–96. [Google Scholar] [PubMed]
- Di Meo, S.; Reed, T.T.; Venditti, P.; Victor, V.M. Role of ROS and RNS Sources in Physiological and Pathological Conditions. Oxid. Med. Cell. Longev. 2016, 2016, 1245049. [Google Scholar] [CrossRef]
- Fresta, C.G.; Chakraborty, A.; Wijesinghe, M.B.; Amorini, A.M.; Lazzarino, G.; Lazzarino, G.; Tavazzi, B.; Lunte, S.M.; Caraci, F.; Dhar, G.; et al. Non-toxic engineered carbon nanodiamond concentrations induce oxidative/nitrosative stress, imbalance of energy metabolism, and mitochondrial dysfunction in microglial and alveolar basal epithelial cells. Cell Death Dis. 2018, 9, 245. [Google Scholar] [CrossRef] [PubMed]
- Vay, S.U.; Flitsch, L.J.; Rabenstein, M.; Rogall, R.; Blaschke, S.; Kleinhaus, J.; Bach, A.; Fink, G.R.; Schroeter, M.; Rueger, A.M. The plasticity of primary microglia and their multifaceted effects on endogenous neural stem cells in vitro and in vivo. J. Neuroinflamm. 2018, 15, 226. [Google Scholar] [CrossRef]
- Hui-Yin, Y.; Ahmad, N.; Azmi, N.; Makmor-Bakry, M. Curcumin: The molecular mechanisms of action in inflammation and cell death during kainate-induced epileptogenesis. Indian J. Pharm. Edu. Res. 2018, 52, 32–41. [Google Scholar] [CrossRef]
- Hake, I.; Schönenberger, S.; Neumann, J.; Franke, K.; Paulsen-Merker, K.; Reymann, K.; Ismail, G.; Bin Din, L.; Said, I.M.; Latiff, A.; et al. Neuroprotection and enhanced neurogenesis by extract from the tropical plant Knema laurina after inflammatory damage in living brain tissue. J. Neuroimmunol. 2009, 206, 91–99. [Google Scholar] [CrossRef]
- Cherry, J.D.; Olschowka, J.A.; O’Banion, M.K. Neuroinflammation and M2 microglia: The good, the bad, and the inflamed. J. Neuroinflamm. 2014, 11, 98. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, J.; Wang, Y.; Yang, G.Y. The biphasic function of microglia in ischemic stroke. Prog. Neurobiol. 2016, 157, 247–272. [Google Scholar] [CrossRef]
- Choi, J.Y.; Kim, J.Y.; Kim, J.Y.; Park, J.; Lee, W.T.; Lee, J.E. M2 phenotype microglia-derived cytokine stimulates proliferation and neuronal differentiation of endogenous stem cells in ischemic brain. Exp. Neurobiol. 2017, 26, 33–41. [Google Scholar] [CrossRef]
- Ahn, S.; Joyner, A. In vivo analysis of quiescent adult neural stem cells responding to Sonic hedgehog. Nature 2005, 437, 894–897. [Google Scholar] [CrossRef]
- Bauer, S. Cytokine control of adult neural stem cells. Ann. N. Y. Acad. Sci. 2009, 1153, 48–56. [Google Scholar] [CrossRef] [PubMed]
- Vieira, M.S.; Santos, A.K.; Vasconcellos, R.; Goulart, V.A.; Parreira, R.C.; Kihara, A.H.; Ulrich, H.; Resende, R.R. Neural stem cell differentiation into mature neurons: Mechanisms of regulation and biotechnological applications. Biotechnol. Adv. 2018, 7, 1946–1970. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Garza, D.M.; Cantú-Rodríguez, O.G.; Jaime-Pérez, J.C.; Gutiérrez-Aguirre, C.H.; Góngora-Rivera, J.F.; Gómez-Almaguer, D. Current state and perspectives of stem cell therapy for stroke. Med. Univ. 2016, 72, 169–180. [Google Scholar] [CrossRef]
- Matarredona, E.R.; Talaveron, R.; Pastor, A.M. Interactions between neural progenitor cells and microglia in the subventricular zone: Physiological implications in the neurogenic niche and after implantation in the injured brain. Front. Cell. Neurosci. 2018, 12, 268. [Google Scholar] [CrossRef]
- Zhang, Z.; Chopp, M. Neural stem cells and ischemic brain. J. Stroke 2016, 18, 267–272. [Google Scholar] [CrossRef] [PubMed]
- Faiz, M.; Sachewsky, N.; Gascón, S.; Bang, K.A.; Morshead, C.M.; Nagy, A. Adult neural stem cells from the subventricular zone give rise to reactive astrocytes in the cortex after stroke. Cell Stem Cell 2015, 17, 624–634. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.S.; Lee, M.Y.; Sung, K.W.; Jeong, S.W.; Choi, J.S.; Park, H.J.; Kim, O.N.; Lee, S.B.; Kim, S.Y. Regional differences in enhanced neurogenesis in the dentate gyrus of adult rats after transient forebrain ischemia. Mol. Cells 2003, 16, 232–238. [Google Scholar]
- Barkho, B.Z.; Zhao, X. Adult neural stem cells: Response to stroke injury and potential for therapeutic applications. Curr. Stem Cell Res. Ther. 2011, 6, 327–338. [Google Scholar] [CrossRef]
- Ariffin, S.H.Z.; Wahab, R.M.A.; Ismail, I.; Mahadi, N.M.; Ariffin, Z.Z. Stem cells, cytokines and their receptors. Asia-Pac. J. Mol. Biol. Biotechnol. 2005, 13, 1–13. [Google Scholar]
- Lira-Diaz, E.; Gonzalez-Perez, O. Emerging roles of microglia cells in the regulation of adult neural stem cells. Neuroimmunol. Neuroinflamm. 2008, 3, 204–206. [Google Scholar]
- Boese, A.C.; Le, Q.S.E.; Pham, D.; Hamblin, M.H.; Lee, J.P. Neural stem cell therapy for subacute and chronic ischemic stroke. Stem Cell Res. Ther. 2018, 9. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, A.; Rubin, J.; Clermont, G.; Day, J.; Vodovotz, Y.; Bard Ermentrout, G. A reduced mathematical model of the acute inflammatory response: I. derivation of model and analysis of anti-inflammation. J. Theor. Biol. 2006, 242, 220–236. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.; Clermont, G.; Vodovotz, Y.; Chow, C.C. The dynamics of acute inflammation. J. Theor. Biol. 2004, 230, 145–155. [Google Scholar] [CrossRef] [PubMed]
- Alharbi, S.; Rambely, A. A dynamic simulation of the immune system response to inhibit and eliminate abnormal cells. Symmetry 2019, 11, 572. [Google Scholar] [CrossRef]
- Hao, W.; Friedman, A. Mathematical model on Alzheimer’sdisease. BMC Syst. Biol. 2016, 10, 108. [Google Scholar] [CrossRef]
- Nakata, Y.; Getto, P.; Marciniak-Czochra, A.; Alarcón, T. Stability analysis of multi-compartment models for cell production systems. J. Biol. Dyn. 2012, 6, 2–18. [Google Scholar] [CrossRef]
- Ziebell, F.; Martin-Villalba, A.; Marciniak-Czochra, A. Mathematical modelling of adult hippocampal neurogenesis: Effects of altered stem cell dynamics on cell counts and bromodeoxyuridine-labelled cells. J. R. Soc. Interface 2014, 11, 20140144. [Google Scholar] [CrossRef]
- Cacao, E.; Cucinotta, F.A. Modeling impaired hippocampal neurogenesis after radiation exposure. Radiat. Res 2016, 185, 319–331. [Google Scholar] [CrossRef]
- Huang, L.; Zhang, L. Neural stem cell therapies and hypoxic-ischemic brain injury. Prog. Neurobiol. 2018, 173. [Google Scholar] [CrossRef]
- Leah, E.V.; Prerna, R.R.; Raj, G.K.; Amy, K.; Jonathan, E.R. A mathematical model of neuroinflammation in severe clinical traumatic brain injury. J. Neuroinflamm. 2018, 15, 345. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, J. Cellular Therapy for Stroke and CNS Injuries; Springer Series in Translational Stroke Research; Springer: Berlin, Germany, 2015; pp. 34–39. [Google Scholar]
- Loane, D.J.; Kumar, A. Microglia in the TBI brain: The good, the bad, and the dysregulated. Exp. Neurol. 2016, 275, 316–327. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.Y.; Kim, N.; Yenari, M.A. Mechanisms and potential therapeutic applications of microglial activation after brain injury. CNS Neurosci. Ther. 2015, 21, 309–319. [Google Scholar] [CrossRef] [PubMed]
- Saha Ray, S.; Sahoo, S. Generalized Fractional Order Differential Equations Arising in Physical Models; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Gantmacher, F.R. The Theory of Matrices; American Mathematical Society: Providence, RI, USA, 1959; Volume 2. [Google Scholar]
| The SMD Model | |||
|---|---|---|---|
| Parameters | Values | Meaning | Sources |
| 0.38 | Source of resting microglia | [1] | |
| 0.12 | Rate the activation of resting microglia into | [1] | |
| 0.017 | Rate the activation of resting microglia into | [35] | |
| 0.2854 | Rate of the damage produced by | [1] | |
| 0.1 | Rate of effect the damage on | [1] | |
| 0.05 | Rate of dying C through stroke | [1] | |
| 0.003 | Death rate of | simulation | |
| 0.05 | Death rate of | simulation | |
| 0.06 | Death rate of | simulation | |
| 0.05 | Damage clearance by | [1] | |
| 0.0125 | Damage clearance by | [1] |
| The SMNR Model | |||
|---|---|---|---|
| Parameters | Values | Biological Meaning | Sources |
| 0.38 | Source of resting microglia | [1] | |
| 0.12 | Rate the activation of resting microglia into | [1] | |
| 0. 26 | Rate the activation of resting microglia into | estimated | |
| 0.11 | The transition rate of | simulation | |
| 0.91 | Rate of interaction between and | simulation | |
| 0.75 | Rate of interaction between and | simulation | |
| 0.2854 | Rate of the damage produced by | [1] | |
| 0.1 | Rate of effect the damage on | [1] | |
| 0.2 | Rate of effect on | simulation | |
| 0.05 | Rate of dying C through stroke | [1] | |
| 0.053 | Death rate of | simulation | |
| 0.015 | Death rate of | [35] | |
| 0.015 | Death rate of | [35] | |
| 0.015 | Death rate of | [38] | |
| 0.05 | Damage clearance by | [1] | |
| 0.0125 | Damage clearance by | [1] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alqarni, A.J.; Rambely, A.S.; Hashim, I. Dynamic Modelling of Interactions between Microglia and Endogenous Neural Stem Cells in the Brain during a Stroke. Mathematics 2020, 8, 132. https://doi.org/10.3390/math8010132
Alqarni AJ, Rambely AS, Hashim I. Dynamic Modelling of Interactions between Microglia and Endogenous Neural Stem Cells in the Brain during a Stroke. Mathematics. 2020; 8(1):132. https://doi.org/10.3390/math8010132
Chicago/Turabian StyleAlqarni, Awatif Jahman, Azmin Sham Rambely, and Ishak Hashim. 2020. "Dynamic Modelling of Interactions between Microglia and Endogenous Neural Stem Cells in the Brain during a Stroke" Mathematics 8, no. 1: 132. https://doi.org/10.3390/math8010132
APA StyleAlqarni, A. J., Rambely, A. S., & Hashim, I. (2020). Dynamic Modelling of Interactions between Microglia and Endogenous Neural Stem Cells in the Brain during a Stroke. Mathematics, 8(1), 132. https://doi.org/10.3390/math8010132






