Bayesian Derivative Order Estimation for a Fractional Logistic Model
Abstract
1. Introduction
2. The Model
- A fractional differential equation given bywhere is the state variable of the system at the time t, is the initial condition, a is a positive constant and N represents a sort of “ideal” population or “carrying capacity”. Here is the integral operator defined bywhere is known as the Caputo fractional derivative for , and is the Gamma function,
- A statistical model given bywhere is a Gaussian error, correspond to the i-th observed value under uncertainty from a solution of Equation (1) at the discrete time ; g is the observation function.
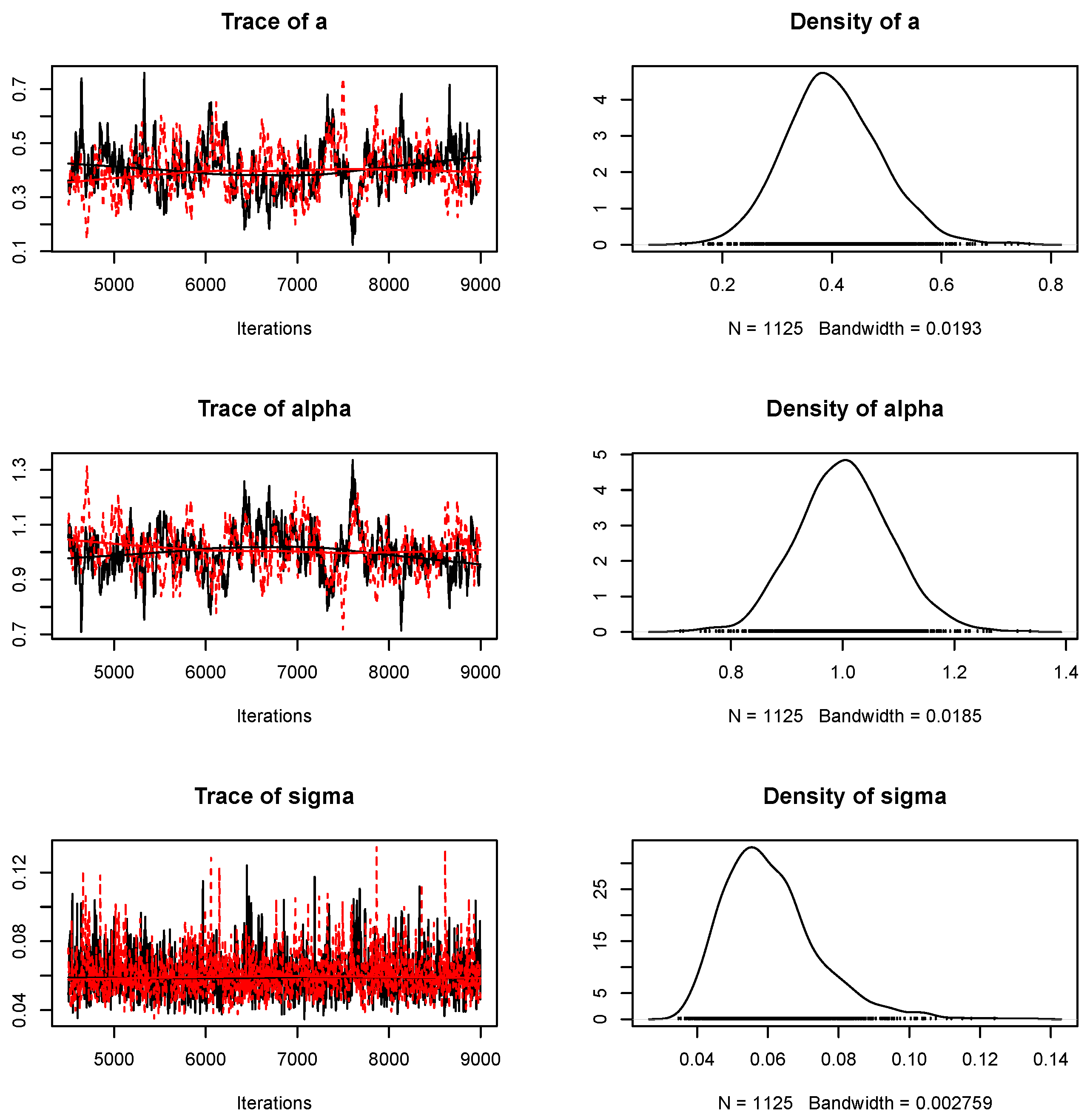
3. Bayesian Estimation
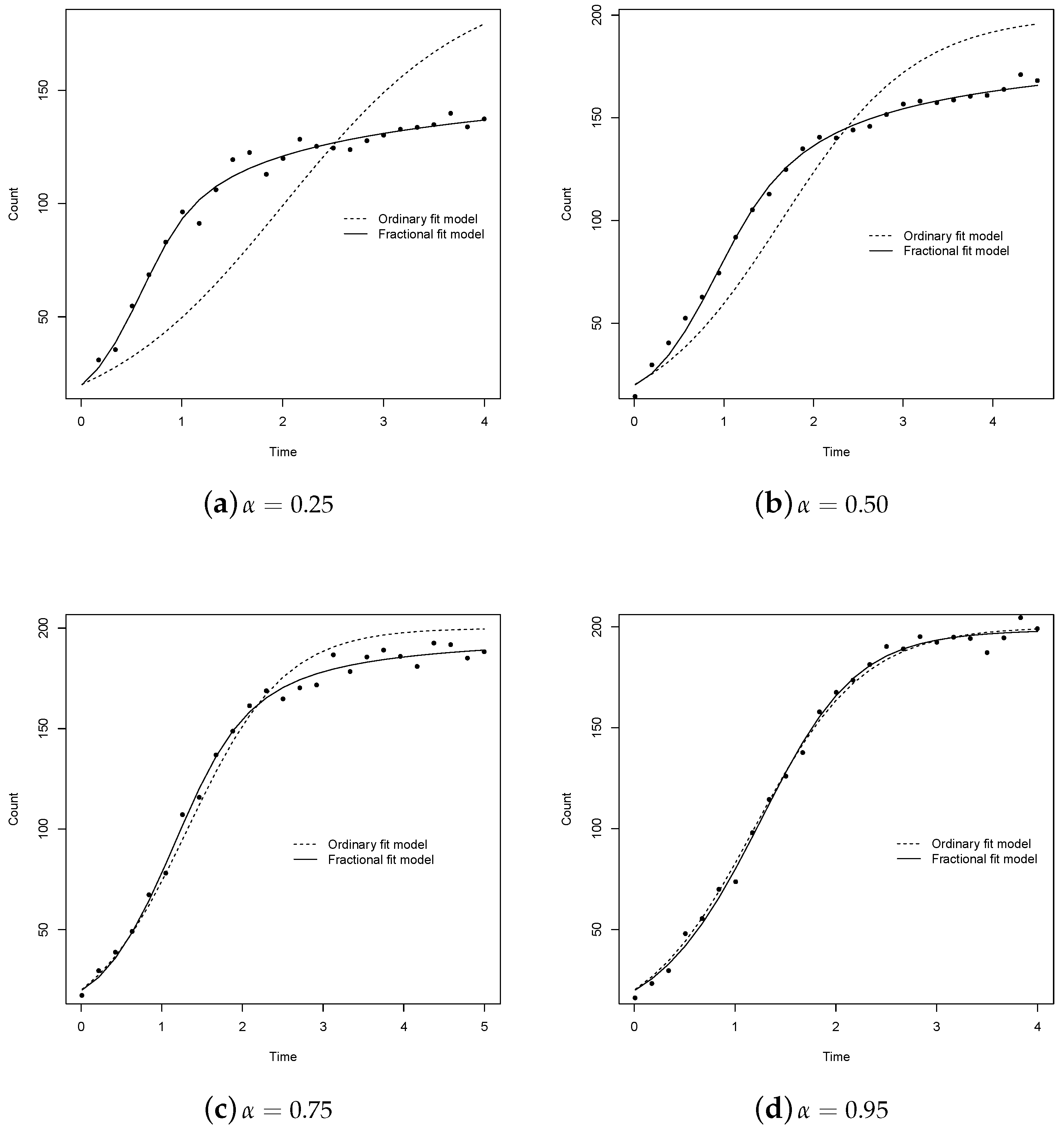
4. Simulation
- We calculated the MAP estimators of the parameters for the models and . To make inference, we use a total of 2000 iterations for each parameter of interest, with two chains of length 10,000 each one. We propose the following weakly informative prior distributions [24],
- From the 1000 samples, we obtained measures of the bias and mean-squared error of the estimators.
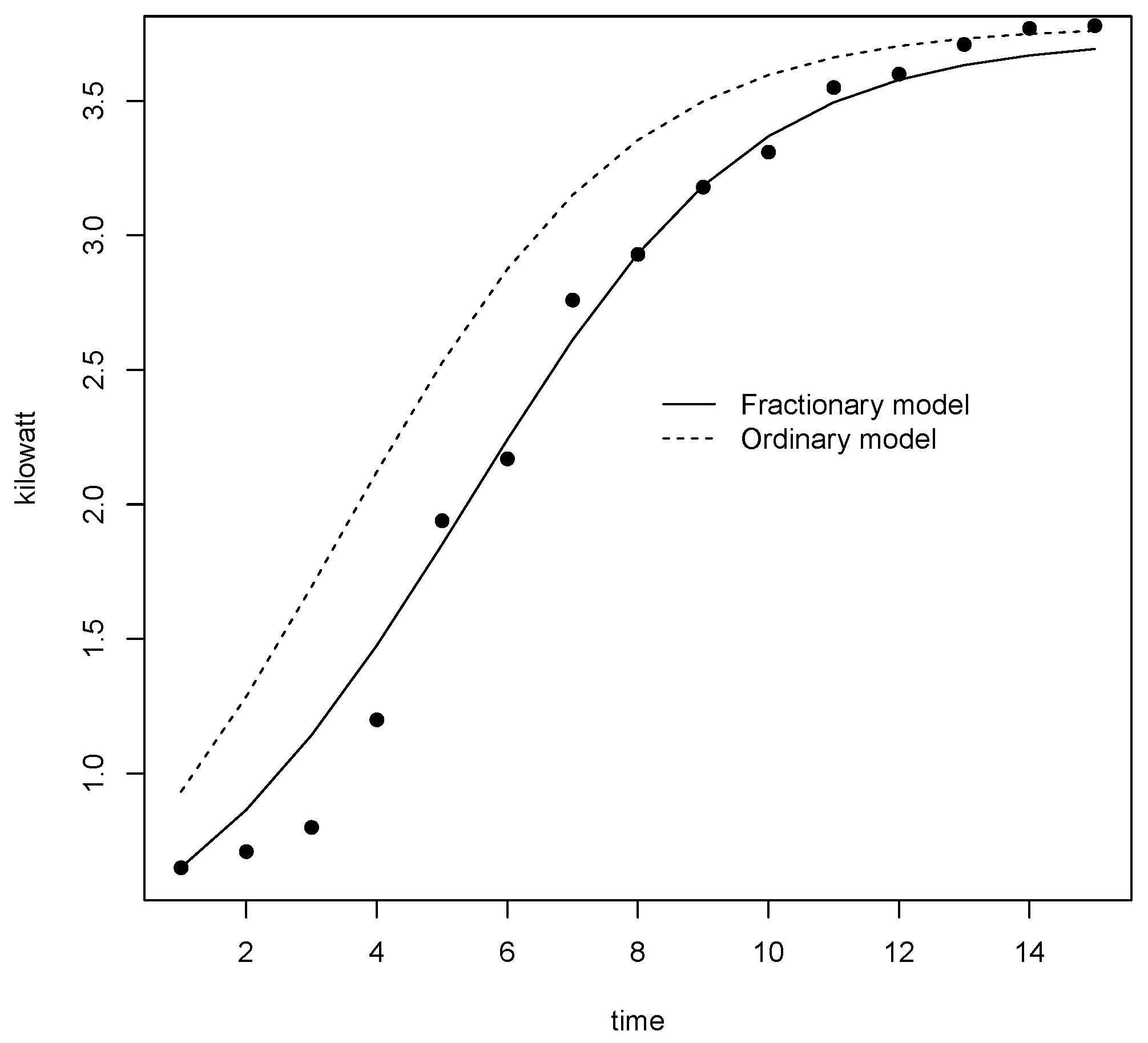
5. Illustrative Example
6. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Vazquez, L.; Trujillo, J.J.; Velasco, M.P. Fractional heat equation and the second law of thermodynamics. Fract. Calc. Appl. Anal. 2011, 14, 334–342. [Google Scholar] [CrossRef]
- Area, I.; Batarfi, H.; Losada, J.; Nieto, J.J.; Shammakh, W.; Torres, A. On a fractional order Ebola epidemic model. Adv. Differ. Equ. 2015, 2015, 278. [Google Scholar] [CrossRef]
- Jin, B.; Rundell, W. A tutorial on inverse problems for anomalous diffusion processes. Inverse Probl. 2015, 31, 035003. [Google Scholar] [CrossRef]
- Ariza-Hernandez, F.J.; Sanchez-Ortiz, J.; Arciga-Alejandre, M.P.; Vivas-Cruz, L.X. Bayesian Analysis for a Fractional Population Growth Model. J. Appl. Math. 2017, 2017, 9654506. [Google Scholar] [CrossRef]
- Mitkowski, W.; Obraczka, A. Simple identification of fractional differential equation. Solid State Phenom. 2012, 180, 331–338. [Google Scholar] [CrossRef]
- Obraczka, A.; Mitkowski, W. The comparison of parameter identification methods for fractional, partial differential equation. Solid State Phenom. 2014, 210, 265–270. [Google Scholar] [CrossRef]
- Kaipio, J.; Somersalo, E. Statistical and Computational Inverse Problems; Springer: Berlin/Heidelberg, Germany, 2006; Volume 160. [Google Scholar]
- Heydary, M.H.; Hooshmandasl, M.R.; Cattani, C.; Li, M. Legendre Wavelets Method for Solving Fractional Population Growth Model in a Closed System. Math. Probl. Eng. 2013, 2013, 161030. [Google Scholar] [CrossRef]
- Andrés Christen, J.; Capistrán, M.A.; Ángel Moreles, M. Numerical posterior distribution error control and expected Bayes Factors in the bayesian Uncertainty Quantification of Inverse Problems. arXiv 2016, arXiv:1607.02194. [Google Scholar]
- Banks, H.T.; Hu, S.; Thompson, W.C. Modeling and Inverse Problems in the Presence of Uncertainty; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; SIAM: Philadelphia, PA, USA, 2005. [Google Scholar]
- Capistrán, M.A.; Christen, J.A.; Donnet, S. Bayesian Analysis of ODE’s: Solver Optimal Accuracy and Bayes factors. SIAM/ASA J. Uncertain. Quantif. 2016, 4, 829–849. [Google Scholar] [CrossRef][Green Version]
- Bhaumik, P. Bayesian two-step estimation in differential equation models. Electron. J. Stat. 2015, 9, 3124–3154. [Google Scholar] [CrossRef]
- Calvetti, D.; Kaipio, J.P.; Somersalo, E. Inverse problems in Bayesian framework. Inverse Probl. 2014, 30, 110301. [Google Scholar] [CrossRef]
- Scherer, R.; Kalla, S.L.; Tang, Y.; Huang, J. The Grunwald- Letnikov method for fractional differential equations. Comput. Math. Appl. 2011, 62, 902–917. [Google Scholar] [CrossRef]
- Fan, W.; Jiang, X.; Chen, S. Parameter estimation for the fractional fractal diffusion model based on its numerical solution. Comput. Math. Appl. 2016, 71, 641–651. [Google Scholar] [CrossRef]
- Fan, W.; Jiang, X.; Qi, H. Parameter estimation for the generalized fractional element network Zener model based on the Bayesian method. Physica A 2015, 427, 40–49. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
- Plummer, M. JAGS Version 4.3.0 User Manual; International Agency for Research on Cancer: Lyon, France, 2017. [Google Scholar]
- Su, Y.S.; Yajima, M. R2jags: Using R to Run ‘JAGS’. R Package Version 0.5-7. Available online: https://CRAN.R-project.org/package=R2jags (accessed on 1 December 2019).
- Plummer, M. rjags: Bayesian Graphical Models Using MCMC. R Package Version 4-6. Available online: https://CRAN.R-project.org/package=rjags (accessed on 1 December 2019).
- Neal, R.M. Slice Sampling. Ann. Stat. 2003, 31, 705–767. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vethari, A.; Rubin, D.B. Bayesian Data Analysis, 3rd ed.; Taylor & Francis: Milton Park, UK, 2014. [Google Scholar]
| Sample Size | Parameter | ||||
|---|---|---|---|---|---|
| Bias | MSE | Bias | MSE | ||
| a | −0.00048 | 0.00004 | 0.446 | 0.199 | |
| −0.00088 | 0.00005 | — | — | ||
| −0.01410 | 0.00021 | −0.288 | 0.081 | ||
| a | 0.00042 | 0.00006 | 0.283 | 0.082 | |
| −0.00037 | 0.00001 | — | — | ||
| −0.01350 | 0.00019 | −0.190 | 0.037 | ||
| a | 0.00083 | 0.00007 | 0.145 | 0.022 | |
| −0.00097 | 0.00014 | — | — | ||
| −0.01330 | 0.00019 | −0.086 | 0.008 | ||
| a | −0.00014 | 0.00002 | 0.433 | 0.188 | |
| −0.00004 | 0.00003 | — | — | ||
| −0.00710 | 0.00006 | −0.310 | 0.095 | ||
| a | 0.00049 | 0.00002 | 0.294 | 0.087 | |
| −0.00022 | 0.00005 | — | — | ||
| −0.00640 | 0.00005 | −0.178 | 0.032 | ||
| a | 0.00074 | 0.000035 | 0.178 | 0.032 | |
| −0.00052 | 0.00830 | — | — | ||
| −0.00650 | 0.00005 | −0.069 | 0.005 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ariza-Hernandez, F.J.; Arciga-Alejandre, M.P.; Sanchez-Ortiz, J.; Fleitas-Imbert, A. Bayesian Derivative Order Estimation for a Fractional Logistic Model. Mathematics 2020, 8, 109. https://doi.org/10.3390/math8010109
Ariza-Hernandez FJ, Arciga-Alejandre MP, Sanchez-Ortiz J, Fleitas-Imbert A. Bayesian Derivative Order Estimation for a Fractional Logistic Model. Mathematics. 2020; 8(1):109. https://doi.org/10.3390/math8010109
Chicago/Turabian StyleAriza-Hernandez, Francisco J., Martin P. Arciga-Alejandre, Jorge Sanchez-Ortiz, and Alberto Fleitas-Imbert. 2020. "Bayesian Derivative Order Estimation for a Fractional Logistic Model" Mathematics 8, no. 1: 109. https://doi.org/10.3390/math8010109
APA StyleAriza-Hernandez, F. J., Arciga-Alejandre, M. P., Sanchez-Ortiz, J., & Fleitas-Imbert, A. (2020). Bayesian Derivative Order Estimation for a Fractional Logistic Model. Mathematics, 8(1), 109. https://doi.org/10.3390/math8010109