A Fractional Equation with Left-Sided Fractional Bessel Derivatives of Gerasimov–Caputo Type

Abstract

In this article we propose and study a method to solve ordinary differential equations with left-sided fractional Bessel derivatives on semi-axes of Gerasimov–Caputo type. We derive explicit solutions to equations with fractional powers of the Bessel operator using the Meijer integral transform.

1. Introduction

In this article we study differential equations with the fractional powers of the differential Bessel operator of the form

$$B_{\gamma }=\frac{d^2}{d{x}^2}+\frac{\gamma }{x}\frac{d}{dx},\gamma \ge 0.$$

(1)

The first explicit formulas for fractional powers of the Bessel operator on a segment in terms of the Gauss hypergeometric functions appeared in [1]. For more detailed discussion of the fractional powers of (1) on a segment and semi-axes we refer to [2,3,4]. Fractional powers of the hyper-Bessel differential operator

$${\mathbf{B}}_{{\alpha }_0,{\alpha }_1,\cdots ,{\alpha }_m}=x^{{\alpha }_0}\frac{d}{dx}{x}^{{\alpha }_1}\frac{d}{dx}\dots x^{{\alpha }_{m-1}}\frac{d}{dx}{x}^{{\alpha }_m}$$

with real parameters ${\alpha }_0,\cdots ,{\alpha }_m$ was studied in the paper [5] and continued in [6,7,8,9]. The Bessel operator (1) corresponds to ${\mathbf{B}}_{{\alpha }_0,{\alpha }_1,\cdots ,{\alpha }_m}$ when

$$m=2,{\alpha }_0=-1,{\alpha }_1=2-\gamma ,{\alpha }_2=\gamma -1,$$

or, equivalently,

$$m=2,{\alpha }_0=-\gamma ,{\alpha }_1=\gamma ,{\alpha }_2=0.$$

For other integral operators connected with the Bessel operator see [10,11,12].

Equations with fractional Bessel derivatives have not been studied before due to the lack of suitable tools for their study. The first aim of this article is to present one such tool, namely, the Meijer integral transform. This transform plays the same role for the left-sided Bessel fractional derivative on semi-axes as the Laplace transform plays for the left-sided Gerasimov–Caputo fractional derivative on semi-axes. Another aim is to show that power functions multiplied by the Fox–Wright functions are the fundamental system of solutions to the left-sided Bessel fractional derivative of Gerasimov–Caputo type on semi-axes. Equations with fractional Bessel derivatives are extremely interesting from a theoretical point of view, but also arise in applications such as problems of the random walk of a particle [13,14].

In ([15], p. 312), the Laplace transform method was applied to derive an explicit solution to a homogeneous equation of the form

$$\left({}^C{D}_{0+}^{\alpha }f\right)\left(x\right)=\lambda f\left(x\right),x>0,l-1<\alpha \le l,l\in \mathbb{N},\lambda \in \mathbb{R},$$

(2)

where for non-integer $\alpha >0$

$$\left({}^C{D}_{0+}^{\alpha }f\right)\left(x\right)=\frac{1}{\mathsf{\Gamma }(n-\alpha )}\underset{0}{\overset{x}{\int }}\frac{f^{\left(n\right)}\left(t\right)dt}{{(x-t)}^{\alpha +1-n}},x\in [0,\infty )$$

(3)

is the left-sided Gerasimov–Caputo fractional derivative on semi-axes ([15,16], p. 97, Formula 2.4.47) and for $\alpha =n=0,1,2,\cdots$

$$\left({}^C{D}_{0+}^{n}f\right)\left(x\right)=f^{\left(n\right)}\left(x\right).$$

Gerasimov [16] derived and solved fractional-order partial differential equations with the derivative (3) for applied mechanical problems in 1948.

The conditions

$$f^k(0+)=d_k,k=0,1,\cdots ,l-1,d_k\in \mathbb{R}$$

(4)

were added to Equation (2). The solution to the problem (2)–(4) is (see [15], p. 312)

$$f\left(x\right)=\sum _{k=0}^{l-1}{d}_k{x}^k{E}_{\alpha ,k+1}\left(\lambda x^{\alpha }\right),$$

(5)

where $E_{\alpha ,\beta }$ is the Mittag–Leffler function (15).

In this article we apply the Meijer transform to derive explicit solutions f to homogeneous equations of the form

$$\left({\mathcal{B}}_{\gamma ,0+}^{\alpha }f\right)\left(x\right)=\lambda f\left(x\right),$$

where the positive real power of (1) is defined by (26).

2. Basic Definitions

2.1. Special Functions

First, we give definitions of some special functions which we will use.

The modified Bessel functions (or occasionally the hyperbolic Bessel functions) of the first and second kind $I_{\alpha }\left(x\right)$ and $K_{\alpha }\left(x\right)$ are defined as (see [17,18,19,20]; for the generalization, see [21])

$$I_{\alpha }\left(x\right)=i^{-\alpha }{J}_{\alpha }\left(ix\right)=\sum _{m=0}^{\infty }\frac{1}{m!\mathsf{\Gamma }(m+\alpha +1)}{\left(\frac{x}{2}\right)}^{2m+\alpha },$$

(6)

$$K_{\alpha }\left(x\right)=\frac{\pi }{2}\frac{I_{-\alpha }\left(x\right)-I_{\alpha }\left(x\right)}{sin\left(\alpha \pi \right)},$$

(7)

where $\alpha$ is a non-integer. For integer $\alpha$, the limit is used. It is obvious that $K_{\alpha }\left(x\right)=K_{-\alpha }\left(x\right)$. For small arguments $0<\left|r\right|\ll \sqrt{\nu +1}$, we have

$$K_{\nu }\left(r\right)\sim \left\{\begin{array}{c}-ln\left({\displaystyle \frac{r}{2}}\right)-\vartheta \mathrm{if}\nu =0,\hfill \\ \frac{\mathsf{\Gamma }\left(\nu \right)}{2^{1-\nu }}{r}^{-\nu }\mathrm{if}\nu >0,\hfill \end{array}\right.$$

(8)

where

$$\vartheta =\underset{n\to \infty }{lim}\left(-lnn+\sum _{k=1}^n\frac{1}{k}\right)=\underset{1}{\overset{\infty }{\int }}\left(-\frac{1}{x}+\frac{1}{\lfloor x\rfloor }\right)dx$$

is the Euler–Mascheroni constant [22].

The kernel of the Meijer transform is the normalized modified Bessel function of the second kind $k_{\nu }$ defined by the formula

$$k_{\nu }\left(x\right)=\frac{2^{\nu }\mathsf{\Gamma }(\nu +1)}{x^{\nu }}{K}_{\nu }\left(x\right),$$

(9)

where $K_{\nu }$ is modified Bessel function of the second kind (7).

The normalized modified Bessel function of the second kind has the following properties:

$$\underset{x\to 0}{lim}{k}_{\nu }\left(x\right)=\frac{\mathsf{\Gamma }(-\nu )}{2^{2\nu +1}\mathsf{\Gamma }(1+\nu )},\nu <0,-\nu \notin \mathbb{N},$$

(10)

$$\underset{x\to 0}{lim}{x}^{\alpha }{k}_0\left(x\right)=0,\alpha >0,\underset{x\to 0}{lim}\frac{1}{lnx}{k}_0\left(x\right)=-1,$$

(11)

$$\underset{x\to 0}{lim}{x}^{2\nu }{k}_{\nu }\left(x\right)=\frac{1}{2\nu },\nu >0,$$

(12)

$$\underset{x\to 0}{lim}{x}^{2\nu +1}\frac{d{k}_{\nu }\left(x\right)}{dx}=-1,\nu >-1.$$

(13)

The kernel of the left-sided Bessel fractional derivative on semi-axes is the hypergeometric Gauss function which is inside the circle $\left|z\right|<1$ determined as the sum of the hypergeometric series (see [22], p. 373, formula 15.3.1)

$${}_2{F}_1(a,b;c;z)=F(a,b,c;z)=\sum _{k=0}^{\infty }\frac{{\left(a\right)}_k{\left(b\right)}_k}{{\left(c\right)}_k}\frac{z^k}{k!},$$

(14)

and for $\left|z\right|\ge 1$ it is obtained by analytic continuation of this series. In (14) parameters $a,b,c$ and variable z can be complex, and $c\ne 0,-1,-2,\cdots$. Multiplier ${\left(a\right)}_k$ is the Pohgammer symbol ${\left(z\right)}_n=z(z+1)\cdots (z+n-1),$ $n=1,2,\cdots ,$${\left(z\right)}_0\equiv 1$.

The Mittag–Leffler function $E_{\alpha ,\beta }\left(z\right)$ is an entire function of order $1/\alpha$ defined by the following series when the real part of $\alpha$ is strictly positive:

$$E_{\alpha ,\beta }\left(z\right)=\sum _{n=0}^{\infty }\frac{z^n}{\mathsf{\Gamma }(\alpha n+\beta )},z\in \mathbb{C},\alpha ,\beta \in \mathbb{C},\mathrm{Re}\alpha >0,\mathrm{Re}\beta >0.$$

(15)

The function (15) was introduced by Gösta Mittag–Leffler in 1903 for $\alpha =1$ and A. Wiman in 1905 in the general case. The first applications of these functions by Mittag–Leffler and Wiman were applications in complex analysis (non-trivial examples of entire functions with non-integer orders of growth and generalized summation methods). In the USSR, these functions became popularly known after the publication of the famous monograph by M. M. Dzhrbashyan [23] (see also his later monograph [24]). The most famous application of the Mittag–Leffler functions in the theory of integro-differential equations and fractional calculus is the fact that through them the resolvent of the Riemann–Liouville fractional integral is explicitly expressed in accordance with the famous Hille–Tamarkin–Dzhrbashyan formula [25]. In view of the numerous applications to the solution of fractional differential equations, this function was deservedly named in [26] the “Royal function of fractional calculus”.

The Fox–Wright function ${}_p{\mathsf{\Psi }}_q\left(z\right)$ is defined for $z\in \mathbb{C}$, $a_l,b_j\in \mathbb{C}$, ${\alpha }_l,{\beta }_j\in \mathbb{R}$, $l=1,\cdots ,p;$$j=1,\cdots ,q$ by the series (see [27,28])

$${}_p{\mathsf{\Psi }}_q\left(z\right)={}_p{\mathsf{\Psi }}_q\left[\left.\begin{array}{c}{(a_l,{\alpha }_l)}_{1,p}\\ {(b_j,{\beta }_j)}_{1,q}\end{array}\right|z\right]=\sum _{k=0}^{\infty }\frac{{\displaystyle \prod _{l=1}^p}\mathsf{\Gamma }(a_l+{\alpha }_{l}k)}{{\displaystyle \prod _{j=1}^q}\mathsf{\Gamma }(b_j+{\beta }_{j}k)}\frac{z^k}{k!}.$$

(16)

If the condition

$$\sum _{j=1}^q{\beta }_j-\sum _{l=1}^p{\alpha }_l>-1$$

is satisfied, the series in (16) is convergent for any $z\in \mathbb{C}$. Let

$$\delta =\prod _{l=1}^p|{\alpha }_l{|}^{-{\alpha }_l}\prod _{j=1}^q{\left|{\beta }_j\right|}^{{\beta }_j},$$

$$\mu =\sum _{j=1}^q{b}_j-\sum _{l=1}^p{a}_l+\frac{p-q}{2}.$$

If

$$\sum _{j=1}^q{\beta }_j-\sum _{l=1}^p{\alpha }_l=-1,$$

then the series in (16) is absolutely convergent for $\left|z\right|<\delta$ and for $\left|z\right|=\delta$ and $\mathrm{Re}\mu >\frac{1}{2}$. The same role the Mittag–Leffler function plays for ordinary fractional calculus is played by the Fox–Wright function for fractional powers of the Bessel operator.

Using the Fox–Wright function (16), we can write

$$E_{\alpha ,\beta }\left(z\right)={}_1{\mathsf{\Psi }}_1\left[\left.\begin{array}{c}(1,1)\\ (\beta ,\alpha )\end{array}\right|z\right].$$

(17)

2.2. Integral Transforms and Transmutation Poisson Operator

In this subsection we present Laplace and Meijer integral transforms and their connection by applying the transmutation Poisson operator.

The Laplace transform of a function $f\left(t\right)$, defined for all real numbers $t>0$, is the function $F\left(s\right)$, which is a unilateral transform defined by

$$\mathcal{L}\left[f\right]\left(s\right)=F\left(s\right)=\underset{0}{\overset{\infty }{\int }}f\left(t\right)e^{-st}dt,$$

(18)

where s is a complex number frequency parameter $s=\sigma +i\omega$, with real numbers $\sigma$ and $\omega$.

Let $E_a$, $a\in \mathbb{R}$ be the space of functions $f:\mathbb{R}\to \mathbb{C}$, $f\in L_1^{loc}\left(\mathbb{R}\right)$ such that $\underset{0}{\overset{\infty }{\int }}\left|f\left(t\right)\right|e^{-at}dt<\infty$ and $f\left(t\right)$ vanishes if $t<0$.

Let $f\in E_a$. Then, the Laplace integral (18) is absolutely and uniformly convergent on ${\overline{H}}_a=\{p:p\in \mathbb{C},\mathrm{Re}p\ge a\}$. The Laplace transform of function $f\in E_a$ is bounded on ${\overline{H}}_a$ and it is an analytic function on $H_a=\{p:p\in \mathbb{C},\mathrm{Re}p>a\}$ (see [29], p. 28).

Let $f\in E_a$ be smooth on every interval $(a,b)\in {\mathbb{R}}_{+}$. Then in points t of continuity the complex inversion formula

$${\mathcal{L}}^{-1}\left[F\right]\left(t\right)=f\left(t\right)=\frac{1}{2\pi i}\underset{c-i\infty }{\overset{c+i\infty }{\int }}F\left(s\right)e^{ts}ds,c>a.$$

holds (see [29], p. 37).

The Laplace transform of the Mittag–Leffler function multiplied by a power function is (see [15], p. 47, Formula 1.9.13, where $\rho =1$):

$$\mathcal{L}\left[x^{\beta -1}{E}_{\alpha ,\beta }\left(\lambda x^{\alpha }\right)\right]\left(s\right)=\frac{s^{\alpha -\beta }}{s^{\alpha }-\lambda }.$$

(19)

For functions f, the integral transforms involving the Bessel function $k_{\frac{\gamma -1}{2}}$, $\gamma \ge 1$ as kernel is the Meijer transform defined by

$${\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)=F\left(\xi \right)=\underset{0}{\overset{\infty }{\int }}{k}_{\frac{\gamma -1}{2}}\left(x\xi \right)f\left(x\right)x^{\gamma }dx.$$

(20)

The transform (20) is the modification of K-transform from ([29] p. 93, formula 1.8.48), and has the same properties but with the other asymptotic behavior of the functions (see also [30]). In [31], an integral transform enfolding kernels of a Meijer G type function is considered.

Let $f\in L_1^{loc}\left({\mathbb{R}}_{+}\right)$ and $f\left(t\right)=o\left(t^{\beta -\frac{\gamma }{2}}\right)$ as $t\to +0$, where $\beta >\frac{\gamma }{2}-2$ if $\gamma >1$, and $\beta >-1$ if $\gamma =1$. Furthermore, let $f\left(t\right)=0\left(e^{at}\right)$ as $t\to +\infty$. Then, its Meijer transform exists a.e. for $\mathrm{Re}\xi >a$ (see [29], p. 94).

If $0<\gamma <2$ and $F\left(\xi \right)$ is analytic on the half-plane $H_a=\{p\in \mathbb{C}:\mathrm{Re}p\ge a\}$, $a\le 0$ and $s^{\frac{\gamma }{2}-1}F\left(\xi \right)\to 0$, $\left|\xi \right|\to +\infty$, uniformly with respect to $\arg s$ then for any number c, $c>a$ the inverse transform ${\mathcal{K}}_{\gamma }^{-1}$ is (see [29], p. 94)

$${\mathcal{K}}_{\gamma }^{-1}\left[\widehat{f}\right]\left(x\right)=f\left(x\right)=\frac{1}{\pi i}\underset{c-i\infty }{\overset{c+i\infty }{\int }}\widehat{f}\left(\xi \right)i_{\frac{\gamma -1}{2}}\left(x\xi \right){\xi }^{\gamma }d\xi .$$

(21)

The inversion formula (21) is not convenient for calculations and has the condition $0<\gamma <2$. Here we present another inversion formula using a transmutation Poisson operator.

Let $\gamma >0$. The one-dimensional Poisson operator is defined for the integrable function f by the equality

$${\mathcal{P}}_x^{\gamma }f\left(x\right)=\frac{2C\left(\gamma \right)}{x^{\gamma -1}}\underset{0}{\overset{x}{\int }}{\left(x^2-t^2\right)}^{\frac{\gamma }{2}-1}f\left(t\right)dt,C\left(\gamma \right)=\frac{\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{\sqrt{\pi }\mathsf{\Gamma }\left(\frac{\gamma }{2}\right)}.$$

(22)

The constant $C\left(\gamma \right)$ is chosen so that ${\mathcal{P}}_x^{\gamma }\left[1\right]=1$ (see [2]).

The left inverse operator for (22) for $\gamma >0$ for any summable function $H\left(x\right)$ is defined by

$${\left({\mathcal{P}}_x^{\gamma }\right)}^{-1}H\left(x\right)=\frac{2\sqrt{\pi }x}{\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)\mathsf{\Gamma }\left(n-\frac{\gamma }{2}\right)}{\left(\frac{d}{2xdx}\right)}^n\underset{0}{\overset{x}{\int }}H\left(z\right){(x^2-z^2)}^{n-\frac{\gamma }{2}-1}{z}^{\gamma }dz,$$

(23)

where $n=\left[\frac{\gamma }{2}\right]+1.$

In order to find $f\left(x\right)$ from the equality

$${\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)=\left(\mathcal{L}F\left(z\right)\right)\left(\xi \right)=g\left(\xi \right),$$

apply to the kernel of (20) the formula

$$K_{\alpha }\left(x\xi \right)=\frac{\mathsf{\Gamma }\left(\frac{1}{2}\right)}{\mathsf{\Gamma }\left(\alpha +\frac{1}{2}\right)}{\left(\frac{x\xi }{2}\right)}^{\alpha }\underset{1}{\overset{\infty }{\int }}{e}^{-x\xi t}{(t^2-1)}^{\alpha -\frac{1}{2}}dt=\{xt=z\}$$

$$=\frac{\sqrt{\pi }}{\mathsf{\Gamma }\left(\alpha +\frac{1}{2}\right)}{\left(\frac{\xi }{2x}\right)}^{\alpha }\underset{x}{\overset{\infty }{\int }}{e}^{-\xi z}{(z^2-x^2)}^{\alpha -\frac{1}{2}}dz$$

from ([17], p. 190, formula (4)). Then,

$$k_{\frac{\gamma -1}{2}}\left(x\xi \right)=\frac{2^{\frac{1-\gamma }{2}}}{\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right){\left(x\xi \right)}^{\frac{\gamma -1}{2}}}{K}_{\frac{\gamma -1}{2}}\left(x\xi \right)$$

$$=\frac{2^{\frac{1-\gamma }{2}}}{\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right){\left(x\xi \right)}^{\frac{\gamma -1}{2}}}\frac{\sqrt{\pi }}{\mathsf{\Gamma }\left(\frac{\gamma }{2}\right)}{\left(\frac{\xi }{2x}\right)}^{\frac{\gamma -1}{2}}\underset{x}{\overset{\infty }{\int }}{e}^{-\xi z}{(z^2-x^2)}^{\frac{\gamma }{2}-1}dz$$

$$=\frac{2^{1-\gamma }\sqrt{\pi }}{x^{\gamma -1}\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)\mathsf{\Gamma }\left(\frac{\gamma }{2}\right)}\underset{x}{\overset{\infty }{\int }}{e}^{-\xi z}{(z^2-x^2)}^{\frac{\gamma }{2}-1}dz.$$

Therefore

$${\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)=\widehat{f}\left(\xi \right)=\underset{0}{\overset{\infty }{\int }}{k}_{\frac{\gamma -1}{2}}\left(x\xi \right)f\left(x\right)x^{\gamma }dx$$

$$=\frac{2^{1-\gamma }\sqrt{\pi }}{\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)\mathsf{\Gamma }\left(\frac{\gamma }{2}\right)}\underset{0}{\overset{\infty }{\int }}f\left(x\right)xdx\underset{x}{\overset{\infty }{\int }}{e}^{-\xi z}{(z^2-x^2)}^{\frac{\gamma }{2}-1}dz$$

$$=\frac{2^{1-\gamma }\sqrt{\pi }}{\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)\mathsf{\Gamma }\left(\frac{\gamma }{2}\right)}\underset{0}{\overset{\infty }{\int }}{e}^{-\xi z}dz\underset{0}{\overset{z}{\int }}f\left(x\right){(z^2-x^2)}^{\frac{\gamma }{2}-1}xdx.$$

Using the Poisson operator (22) and Laplace transform (18) we get

$${\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)=\underset{0}{\overset{\infty }{\int }}{e}^{-\xi z}F\left(z\right)dz=\left(\mathcal{L}F\left(z\right)\right)\left(\xi \right),$$

where

$$F\left(z\right)=A_{\gamma }{z}^{\gamma -1}{\mathcal{P}}_z^{\gamma }zf\left(z\right),A_{\gamma }=\frac{\pi }{2^{\gamma }{\mathsf{\Gamma }}^2\left(\frac{\gamma +1}{2}\right)}.$$

So, in order to find $f\left(x\right)$ from the equality

$${\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)=\left(\mathcal{L}{A}_{\gamma }{z}^{\gamma -1}{\mathcal{P}}_z^{\gamma }zf\left(z\right)\right)\left(\xi \right)=g\left(\xi \right),$$

we should first do an inverse Laplace transform and then we should apply the inverse Poisson operator. So, the inverse formula for functions g such that $\left({\mathcal{L}}^{-1}g\right)\left(x\right)$ exists and $x^{1-\gamma }\left({\mathcal{L}}^{-1}g\right)\left(x\right)$ is summable is

$$f\left(x\right)={\mathcal{K}}_{\gamma }^{-1}\left[g\right]\left(x\right)=\frac{1}{A_{\gamma }x}{\left({\mathcal{P}}_x^{\gamma }\right)}^{-1}{x}^{1-\gamma }\left({\mathcal{L}}^{-1}g\right)\left(x\right),g={\mathcal{K}}_{\gamma }\left[f\right].$$

(24)

3. Left-Sided Fractional Bessel Integral and Derivative on Semi-Axes

3.1. Definitions of Left-Sided Fractional Bessel Integral and Derivative on Semi-Axes

In this subsection we introduce the so-called left-sided fractional Bessel integral and derivative on semi-axes.

Let $\alpha >0$, $\gamma >0$. The left-sided fractional Bessel integral on semi-axes $B_{\gamma ,0+}^{-\alpha }$ for $f\in L[0,\infty )$ is defined by the formula

$$\left(B_{\gamma ,0+}^{-\alpha }f\right)\left(x\right)=\left(I{B}_{\gamma ,0+}^{\alpha }f\right)\left(x\right)$$

$$=\frac{1}{\mathsf{\Gamma }\left(2\alpha \right)}\underset{0}{\overset{x}{\int }}{\left(\frac{y}{x}\right)}^{\gamma }{\left(\frac{x^2-y^2}{2x}\right)}^{2\alpha -1}{}_2{F}_1\left(\alpha +\frac{\gamma -1}{2},\alpha ;2\alpha ;1-\frac{y^2}{x^2}\right)f\left(y\right)dy.$$

(25)

For $\alpha <0$, formula (25) can be continued analytically and $\left(B_{\gamma ,0+}^{0}f\right)\left(x\right)=f\left(x\right)$.

In [5], spaces adapted to work with operators of the form $B_{\gamma ,0+}^{\alpha }$, $\alpha \in \mathbb{R}$ were introduced:

$$F_p=\left\{\phi \in C^{\infty }(0,\infty ):x^k\frac{d^k\phi }{d{x}^k}\in L^p(0,\infty )\mathrm{for}k=0,1,2,\cdots \right\},1\le p<\infty ,$$

$$F_{\infty }=\left\{\phi \in C^{\infty }(0,\infty ):x^k\frac{d^k\phi }{d{x}^k}\to 0\mathrm{as}x\to 0+\mathrm{and}\mathrm{as}x\to \infty \mathrm{for}k=0,1,2,\cdots \right\}$$

and

$$F_{p,\mu }=\left\{\phi :x^{-\mu }\phi \left(x\right)\in F_p\right\},1\le p\le \infty ,\mu \in \mathbb{C}.$$

We present here theorems that are special cases of theorems from [5].

Theorem 1.

Let $\alpha \in \mathbb{R}$. For all $p,\mu$ and $\gamma >0$ such that $\mu \ne \frac{1}{p}-2m$, $\gamma \ne \frac{1}{p}-\mu -2m+1$, $m=1,2\cdots$, the operator $B_{\gamma ,0+}^{\alpha }$ is a continuous linear mapping from $F_p,\mu$ into $F_{p,\mu -2\alpha }$. If also $2\alpha \ne \mu -\frac{1}{p}+2m$ and $\gamma -2\alpha \ne \frac{1}{p}-\mu -2m+1$, $m=1,2\dots$, then $B_{\gamma ,0+}^{\alpha }$ is a homeomorphism from $F_p,\mu$ onto $F_{p,\mu -2\alpha }$ with inverse $B_{\gamma ,0+}^{-\alpha }$.

Let us compare the fractional Bessel integral $B_{\gamma ,0+}^{-\alpha }$ with the well-known Riemann–Liouville fractional integral $I_{0+}^{2\alpha }$. For this purpose, let us put $\gamma =0$:

$$\left(B_{0,0+}^{-\alpha }f\right)\left(x\right)=\frac{1}{\mathsf{\Gamma }\left(2\alpha \right)}\underset{a}{\overset{x}{\int }}{\left(\frac{x^2-y^2}{2x}\right)}^{2\alpha -1}{}_2{F}_1\left(\alpha -\frac{1}{2},\alpha ;2\alpha ;1-\frac{y^2}{x^2}\right)f\left(y\right)dy$$

$$=\frac{1}{\mathsf{\Gamma }\left(2\alpha \right)}\underset{0}{\overset{x}{\int }}{\left(\frac{x^2-y^2}{2x}\right)}^{2\alpha -1}{\left[\frac{2x}{x+y}\right]}^{2\alpha -1}f\left(y\right)dy$$

$$=\frac{1}{\mathsf{\Gamma }\left(2\alpha \right)}\underset{0}{\overset{x}{\int }}{(x-y)}^{2\alpha -1}f\left(y\right)dy=\left(I_{0+}^{2\alpha }f\right)\left(x\right).$$

Now, we would like to have the explicit formula for $B_{\gamma }^{\alpha }$ when $\alpha >0$. For applications, it is better to use the generalization of the Gerasimov–Caputo fractional derivative (3).

Let $n=\left[\alpha \right]+1$, $f\in L[0,\infty )$, $I{B}_{\gamma ,b-}^{n-\alpha }f,I{B}_{\gamma ,b-}^{n-\alpha }f\in C_{ev}^{2n}(0,\infty )$. The left-sided fractional Bessel derivatives on semi-axes of Gerasimov–Caputo type are defined by the equality

$$\left({\mathcal{B}}_{\gamma ,0+}^{\alpha }f\right)\left(x\right)=\left(I{B}_{\gamma ,0+}^{n-\alpha }{B}_{\gamma }^{n}f\right)\left(x\right).$$

(26)

It is easy to see that

$$\left({\mathcal{B}}_{0,0+}^{\alpha }f\right)\left(x\right)=\left({}^C{D}_{0+}^{2\alpha }f\right)\left(x\right),$$

where $\left({}^C{D}_{0+}^{2\alpha }f\right)\left(x\right)$ is defined by (3).

Following [1,5] we present the following results. Let $\mathrm{Re}(2\eta +\mu )+2>1/p$, and $\phi \in F_{p,\mu }$. For $\mathrm{Re}\alpha >0$, we define $I_2^{\eta ,\alpha }\phi$ by the formula

$$I_2^{\eta ,\alpha }\phi \left(x\right)=\frac{2}{\mathsf{\Gamma }\left(\alpha \right)}{x}^{-2\eta -2\alpha }\underset{0}{\overset{x}{\int }}{(x^2-u^2)}^{\alpha -1}{u}^{2\eta +1}\phi \left(u\right)du.$$

(27)

The definition of $I_2^{\eta ,\alpha }$ is extended to $\mathrm{Re}\alpha \le 0$ by means of the formula

$$I_2^{\eta ,\alpha }\phi =(\eta +\alpha +1)I_2^{\eta ,\alpha +1}\phi +\frac{1}{2}{I}_2^{\eta ,\alpha +1}x\frac{d\phi }{dx}.$$

(28)

Theorem 2.

The following factorization of (25) is valid:

$$\left(B_{\gamma ,0+}^{-\alpha }\phi \right)\left(x\right)={\left(\frac{x}{2}\right)}^{2\alpha }{I}_2^{\frac{\gamma -1}{2},\alpha }{I}_2^{0,\alpha }\phi ,$$

(29)

where

$$I_2^{0,\alpha }\phi \left(x\right)=\frac{2}{\mathsf{\Gamma }\left(\alpha \right)}{x}^{-2\alpha }\underset{0}{\overset{x}{\int }}{(x^2-u^2)}^{\alpha -1}u\phi \left(u\right)du,$$

$$I_2^{\frac{\gamma -1}{2},\alpha }\phi \left(x\right)=\frac{2}{\mathsf{\Gamma }\left(\alpha \right)}{x}^{1-\gamma -2\alpha }\underset{0}{\overset{x}{\int }}{(x^2-u^2)}^{\alpha -1}{u}^{\gamma }\phi \left(u\right)du.$$

Proof. 

We have

$$\left(B_{\gamma ,0+}^{-\alpha }\phi \right)\left(x\right)$$

$$=\frac{1}{\mathsf{\Gamma }\left(2\alpha \right)}\underset{0}{\overset{x}{\int }}{\left(\frac{u}{x}\right)}^{\gamma }{\left(\frac{x^2-u^2}{2x}\right)}^{2\alpha -1}{}_2{F}_1\left(\alpha +\frac{\gamma -1}{2},\alpha ;2\alpha ;1-\frac{u^2}{x^2}\right)\phi \left(u\right)du$$

$$=2^{-2\alpha }{x}^{2\alpha }{I}_2^{\frac{\gamma -1}{2},\alpha }{I}_2^{0,\alpha }\phi$$

$$=\frac{2^{1-2\alpha }{x}^{2\alpha }}{\mathsf{\Gamma }\left(\alpha \right)}{I}_2^{\frac{\gamma -1}{2},\alpha }{y}^{-2\alpha }\underset{0}{\overset{y}{\int }}{(y^2-u^2)}^{\alpha -1}u\phi \left(u\right)du$$

$$=\frac{2^{2-2\alpha }{x}^{2\alpha }}{{\mathsf{\Gamma }}^2\left(\alpha \right)}{x}^{-\gamma +1-2\alpha }\underset{0}{\overset{x}{\int }}{(x^2-y^2)}^{\alpha -1}{y}^{\gamma -2\alpha }dy\underset{0}{\overset{y}{\int }}{(y^2-u^2)}^{\alpha -1}u\phi \left(u\right)du$$

$$=\frac{2^{2-2\alpha }}{{\mathsf{\Gamma }}^2\left(\alpha \right)}{x}^{1-\gamma }\underset{0}{\overset{x}{\int }}u\phi \left(u\right)du\underset{u}{\overset{x}{\int }}{(y^2-u^2)}^{\alpha -1}{(x^2-y^2)}^{\alpha -1}{y}^{\gamma -2\alpha }dy.$$

Find

$$\underset{u}{\overset{x}{\int }}{(y^2-u^2)}^{\alpha -1}{(x^2-y^2)}^{\alpha -1}{y}^{\gamma -2\alpha }dy=\{y^2=t\}=\frac{1}{2}\underset{u^2}{\overset{x^2}{\int }}{(t-u^2)}^{\alpha -1}{(x^2-t)}^{\alpha -1}{t}^{\frac{\gamma -1}{2}-\alpha }dt$$

$$=\frac{\sqrt{\pi }\mathsf{\Gamma }\left(\alpha \right)}{2^{2\alpha }\mathsf{\Gamma }\left(\alpha +\frac{1}{2}\right)}{\left(x^2-u^2\right)}^{2\alpha -1}{u}^{-2\alpha +\gamma -1}{}_2{F}_1\left(\alpha +\frac{1-\gamma }{2},\alpha ;2\alpha ;1-\frac{x^2}{u^2}\right).$$

Using formula (see [22])

$${}_2{F}_1(a,b;c;z)={(1-z)}^{-a}{}_2{F}_1\left(a,c-b;c;\frac{z}{z-1}\right)$$

we obtain

$${}_2{F}_1\left(\alpha +\frac{1-\gamma }{2},\alpha ;2\alpha ;1-\frac{x^2}{u^2}\right){}_2{F}_1\left(\alpha ,\alpha +\frac{1-\gamma }{2};2\alpha ;1-\frac{x^2}{u^2}\right)$$

$$={\left(\frac{x^2}{u^2}\right)}^{-\alpha }{}_2{F}_1\left(\alpha ,\alpha +\frac{\gamma -1}{2};2\alpha ;1-\frac{u^2}{x^2}\right)$$

$$={\left(\frac{x^2}{u^2}\right)}^{-\alpha }{}_2{F}_1\left(\alpha +\frac{\gamma -1}{2},\alpha ;2\alpha ;1-\frac{u^2}{x^2}\right),$$

and

$$\underset{u}{\overset{x}{\int }}{(y^2-u^2)}^{\alpha -1}{(x^2-y^2)}^{\alpha -1}{y}^{\gamma -2\alpha }dy=\frac{\sqrt{\pi }\mathsf{\Gamma }\left(\alpha \right)}{2^{2\alpha }\mathsf{\Gamma }\left(\alpha +\frac{1}{2}\right)}$$

$$\times {\left(x^2-u^2\right)}^{2\alpha -1}{u}^{-2\alpha +\gamma -1}{\left(\frac{x^2}{u^2}\right)}^{-\alpha }{}_2{F}_1\left(\alpha ,\alpha +\frac{\gamma -1}{2};2\alpha ;1-\frac{u^2}{x^2}\right)$$

$$=\frac{\sqrt{\pi }\mathsf{\Gamma }\left(\alpha \right)}{2^{2\alpha }\mathsf{\Gamma }\left(\alpha +\frac{1}{2}\right)}{\left(x^2-u^2\right)}^{2\alpha -1}{u}^{\gamma -1}{x}^{-2\alpha }{}_2{F}_1\left(\alpha ,\alpha +\frac{\gamma -1}{2};2\alpha ;1-\frac{u^2}{x^2}\right).$$

Finally

$$\left(B_{\gamma ,0+}^{-\alpha }\phi \right)\left(x\right)=\frac{2^{2(1-2\alpha )}\sqrt{\pi }}{\mathsf{\Gamma }\left(\alpha \right)\mathsf{\Gamma }\left(\alpha +\frac{1}{2}\right)}{x}^{1-\gamma -2\alpha }$$

$$\times \underset{0}{\overset{x}{\int }}{\left(x^2-u^2\right)}^{2\alpha -1}{u}^{\gamma }{}_2{F}_1\left(\alpha +\frac{\gamma -1}{2},\alpha ;2\alpha ;1-\frac{u^2}{x^2}\right)\phi \left(u\right)du.$$

Applying the duplication formula

$$\mathsf{\Gamma }\left(\alpha \right)\mathsf{\Gamma }\left(\alpha +\frac{1}{2}\right)=2^{1-2\alpha }\sqrt{\pi }\mathsf{\Gamma }\left(2\alpha \right)$$

we obtain

$$\left(B_{\gamma ,0+}^{-\alpha }\phi \right)\left(x\right)=\frac{2^{1-2\alpha }}{\mathsf{\Gamma }\left(2\alpha \right)}{x}^{1-\gamma -2\alpha }$$

$$\times \underset{0}{\overset{x}{\int }}{\left(x^2-u^2\right)}^{2\alpha -1}{u}^{\gamma }{}_2{F}_1\left(\alpha +\frac{\gamma -1}{2},\alpha ;2\alpha ;1-\frac{u^2}{x^2}\right)\phi \left(u\right)du$$

$$=\frac{1}{\mathsf{\Gamma }\left(2\alpha \right)}\underset{0}{\overset{x}{\int }}{\left(\frac{x^2-u^2}{2x}\right)}^{2\alpha -1}{\left(\frac{u}{x}\right)}^{\gamma }{}_2{F}_1\left(\alpha +\frac{\gamma -1}{2},\alpha ;2\alpha ;1-\frac{u^2}{x^2}\right)\phi \left(u\right)du.$$

This gives (29). The proof is complete. ☐

3.2. Meijer Transform of Left-Sided Fractional Bessel Integral and Derivative on Semi-Axes

In this subsection we apply the Meijer transform to the left-sided fractional Bessel integral and derivative on semi-axes and then in Section 4 we use these results to construct explicit solutions of linear differential equations involving the left-sided fractional Bessel derivatives on semi-axes of Gerasimov–Caputo type with constant coefficients.

Theorem 3.

Let $\alpha >0$. The Meijer transform of $B_{\gamma ,0+}^{-\alpha }$ for proper functions is

$${\mathcal{K}}_{\gamma }\left[\left(B_{\gamma ,0+}^{-\alpha }\phi \right)\left(x\right)\right]\left(\xi \right)={\xi }^{-2\alpha }{\mathcal{K}}_{\gamma }\phi \left(\xi \right).$$

(30)

Proof. 

We start with (30). Let $g\left(x\right)=I_2^{0,\alpha }\phi \left(x\right)$. Then, using the factorization (29), we obtain

$${\mathcal{K}}_{\gamma }\left[\left(B_{\gamma ,0+}^{-\alpha }\phi \right)\left(x\right)\right]\left(\xi \right)=\underset{0}{\overset{\infty }{\int }}{k}_{\frac{\gamma -1}{2}}\left(x\xi \right)\left(B_{\gamma ,0+}^{-\alpha }\phi \right)\left(x\right)x^{\gamma }dx$$

$$=\frac{1}{2^{2\alpha }}\underset{0}{\overset{\infty }{\int }}{k}_{\frac{\gamma -1}{2}}\left(x\xi \right)I_2^{\frac{\gamma -1}{2},\alpha }{I}_2^{0,\alpha }\phi \left(x\right)x^{2\alpha +\gamma }dx$$

$$=\frac{1}{2^{2\alpha }}\underset{0}{\overset{\infty }{\int }}{k}_{\frac{\gamma -1}{2}}\left(x\xi \right)I_2^{\frac{\gamma -1}{2},\alpha }g\left(x\right)x^{2\alpha +\gamma }dx$$

$$=\frac{1}{2^{2\alpha -1}\mathsf{\Gamma }\left(\alpha \right)}\underset{0}{\overset{\infty }{\int }}{k}_{\frac{\gamma -1}{2}}\left(x\xi \right)xdx\underset{0}{\overset{x}{\int }}{(x^2-u^2)}^{\alpha -1}{u}^{\gamma }g\left(u\right)du$$

$$=\frac{1}{2^{2\alpha -1}\mathsf{\Gamma }\left(\alpha \right)}\underset{0}{\overset{\infty }{\int }}{u}^{\gamma }g\left(u\right)du\underset{u}{\overset{\infty }{\int }}{(x^2-u^2)}^{\alpha -1}{k}_{\frac{\gamma -1}{2}}\left(x\xi \right)xdx.$$

Consider the inner integral. Using formula 2.16.3.7 from [32] of the form

$$\underset{a}{\overset{\infty }{\int }}{x}^{1\pm \rho }{(x^2-a^2)}^{\beta -1}{K}_{\rho }\left(cx\right)dx=2^{\beta -1}{a}^{\beta \pm \rho }{c}^{-\beta }\mathsf{\Gamma }\left(\beta \right)K_{\rho \pm \beta }\left(ac\right),a,c,\beta >0,$$

(31)

we get

$$\underset{u}{\overset{\infty }{\int }}{(x^2-u^2)}^{\alpha -1}{k}_{\frac{\gamma -1}{2}}\left(x\xi \right)xdx=\frac{2^{\frac{\gamma -1}{2}}\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{{\xi }^{\frac{\gamma -1}{2}}}\underset{u}{\overset{\infty }{\int }}{(x^2-u^2)}^{\alpha -1}{K}_{\frac{\gamma -1}{2}}\left(x\xi \right)x^{1-\frac{\gamma -1}{2}}dx$$

$$=\frac{2^{\frac{\gamma -1}{2}}\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{{\xi }^{\frac{\gamma -1}{2}}}·2^{\alpha -1}{u}^{\alpha -\frac{\gamma -1}{2}}{\xi }^{-\alpha }\mathsf{\Gamma }\left(\alpha \right)K_{\frac{\gamma -1}{2}-\alpha }\left(u\xi \right)$$

and

$${\mathcal{K}}_{\gamma }\left[\left(B_{\gamma ,0+}^{-\alpha }\phi \right)\left(x\right)\right]\left(\xi \right)=\frac{2^{\frac{\gamma -1}{2}-\alpha }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{{\xi }^{\frac{\gamma -1}{2}+\alpha }}\underset{0}{\overset{\infty }{\int }}{u}^{\alpha +\frac{\gamma +1}{2}}{K}_{\frac{\gamma -1}{2}-\alpha }\left(u\xi \right)g\left(u\right)du$$

$$=\frac{2^{\frac{\gamma +1}{2}-\alpha }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{\mathsf{\Gamma }\left(\alpha \right){\xi }^{\frac{\gamma -1}{2}+\alpha }}\underset{0}{\overset{\infty }{\int }}{u}^{\frac{\gamma +1}{2}-\alpha }{K}_{\frac{\gamma -1}{2}-\alpha }\left(u\xi \right)du\underset{0}{\overset{u}{\int }}{(u^2-t^2)}^{\alpha -1}t\phi \left(t\right)dt$$

$$=\frac{2^{\frac{\gamma +1}{2}-\alpha }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{\mathsf{\Gamma }\left(\alpha \right){\xi }^{\frac{\gamma -1}{2}+\alpha }}\underset{0}{\overset{\infty }{\int }}t\phi \left(t\right)dt\underset{t}{\overset{\infty }{\int }}{(u^2-t^2)}^{\alpha -1}{u}^{\frac{\gamma +1}{2}-\alpha }{K}_{\frac{\gamma -1}{2}-\alpha }\left(u\xi \right)du.$$

Using again (31) we can write

$$\underset{t}{\overset{\infty }{\int }}{(u^2-t^2)}^{\alpha -1}{u}^{\frac{\gamma +1}{2}-\alpha }{K}_{\frac{\gamma -1}{2}-\alpha }\left(u\xi \right)du=2^{\alpha -1}{t}^{\frac{\gamma -1}{2}}{\xi }^{-\alpha }\mathsf{\Gamma }\left(\alpha \right)K_{\frac{\gamma -1}{2}}\left(t\xi \right)$$

and

$${\mathcal{K}}_{\gamma }\left[\left(B_{\gamma ,0+}^{-\alpha }\phi \right)\left(x\right)\right]\left(\xi \right)=\frac{2^{\frac{\gamma +1}{2}-\alpha }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{\mathsf{\Gamma }\left(\alpha \right){\xi }^{\frac{\gamma -1}{2}+\alpha }}·2^{\alpha -1}{\xi }^{-\alpha }\mathsf{\Gamma }\left(\alpha \right)\underset{0}{\overset{\infty }{\int }}\phi \left(t\right)K_{\frac{\gamma -1}{2}}\left(t\xi \right)t^{\frac{\gamma +1}{2}}dt$$

$$={\xi }^{-2\alpha }\underset{0}{\overset{\infty }{\int }}\phi \left(t\right)k_{\frac{\gamma -1}{2}}\left(t\xi \right)t^{\gamma }dt={\xi }^{-2\alpha }{\mathcal{K}}_{\gamma }\phi .$$

 ☐

Lemma 1.

Let $n\in \mathbb{N}$ and the Meijer transform of $B_{\gamma }^{n}f$ exist; then, for $0\le \gamma <1$

$${\mathcal{K}}_{\gamma }\left[B_{\gamma }^{n}f\right]\left(\xi \right)={\xi }^{2n}{\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)$$

$$-\sum _{k=1}^n{\xi }^{2k-1-\gamma }{B}_{\gamma }^{n-k}f(0+)-\frac{\mathsf{\Gamma }\left(\frac{1-\gamma }{2}\right)}{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}\underset{x\to 0+}{lim}\sum _{k=1}^n{\xi }^{2k-2}{x}^{\gamma }\frac{d}{dx}\left[B_{\gamma }^{n-k}f\left(x\right)\right];$$

(32)

for $\gamma =1$

$${\mathcal{K}}_{\gamma }\left[B_{\gamma }^{n}f\right]\left(\xi \right)={\xi }^{2n}{\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)-\sum _{k=1}^n{\xi }^{2k-1-\gamma }{B}_{\gamma }^{n-k}f(0+)+\underset{x\to 0+}{lim}\sum _{k=1}^n{\xi }^{2k-2}lnx\xi \frac{d}{dx}\left[B_{\gamma }^{n-k}f\left(x\right)\right];$$

(33)

for $1<\gamma$

$${\mathcal{K}}_{\gamma }\left[B_{\gamma }^{n}f\right]\left(\xi \right)$$

$$={\xi }^{2n}{\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)-\sum _{k=1}^n{\xi }^{2k-1-\gamma }{B}_{\gamma }^{n-k}f(0+)-\frac{1}{\gamma -1}\underset{x\to 0+}{lim}\sum _{k=1}^n{\xi }^{2k-1-\gamma }x\frac{d}{dx}\left[B_{\gamma }^{n-k}f\left(x\right)\right],$$

(34)

where

$$B_{\gamma }^{n-k}f(0+)=\underset{x\to +0}{lim}{B}_{\gamma }^{n-k}f\left(x\right).$$

Proof. 

Find ${\mathcal{K}}_{\gamma }\left[B_{\gamma }^{n}f\right]\left(\xi \right)$:

$${\mathcal{K}}_{\gamma }\left[B_{\gamma }^{n}f\right]\left(\xi \right)=\underset{0}{\overset{\infty }{\int }}{k}_{\frac{\gamma -1}{2}}\left(x\xi \right)\left[B_{\gamma }^{n}f\left(x\right)\right]x^{\gamma }dx=\underset{0}{\overset{\infty }{\int }}{k}_{\frac{\gamma -1}{2}}\left(x\xi \right)\frac{d}{dx}{x}^{\gamma }\frac{d}{dx}\left[B_{\gamma }^{n-1}f\left(x\right)\right]dx$$

$$=k_{\frac{\gamma -1}{2}}\left(x\xi \right)x^{\gamma }\frac{d}{dx}\left[B_{\gamma }^{n-1}f\left(x\right)\right]{|}_{x=0}^{\infty }-\underset{0}{\overset{\infty }{\int }}{x}^{\gamma }\frac{d}{dx}{k}_{\frac{\gamma -1}{2}}\left(x\xi \right)\frac{d}{dx}\left[B_{\gamma }^{n-1}f\left(x\right)\right]dx$$

$$=-k_{\frac{\gamma -1}{2}}\left(x\xi \right)x^{\gamma }\frac{d}{dx}\left[B_{\gamma }^{n-1}f\left(x\right)\right]{|}_{x=0}+\left(x^{\gamma }\frac{d}{dx}{k}_{\frac{\gamma -1}{2}}\left(x\xi \right)\right)\left[B_{\gamma }^{n-1}f\left(x\right)\right]{|}_{x=0}$$

$$+\underset{0}{\overset{\infty }{\int }}\left[B_{\gamma }{k}_{\frac{\gamma -1}{2}}\left(x\xi \right)\right]\left[B_{\gamma }^{n-1}f\left(x\right)\right]x^{\gamma }dx=-k_{\frac{\gamma -1}{2}}\left(x\xi \right)x^{\gamma }\frac{d}{dx}\left[B_{\gamma }^{n-1}f\left(x\right)\right]{|}_{x=0}$$

$$+\left(x^{\gamma }\frac{d}{dx}{k}_{\frac{\gamma -1}{2}}\left(x\xi \right)\right)\left[B_{\gamma }^{n-1}f\left(x\right)\right]{|}_{x=0}+{\xi }^2\underset{0}{\overset{\infty }{\int }}{k}_{\frac{\gamma -1}{2}}\left(x\xi \right)\left[B_{\gamma }^{n-1}f\left(x\right)\right]x^{\gamma }dx=$$

$$\cdots ={\xi }^{2n}\underset{0}{\overset{\infty }{\int }}{k}_{\frac{\gamma -1}{2}}\left(x\xi \right)f\left(x\right)x^{\gamma }dx$$

$$+\sum _{k=0}^{n-1}{\xi }^{2k}\left(\left(x^{\gamma }\frac{d}{dx}{k}_{\frac{\gamma -1}{2}}\left(x\xi \right)\right)\left[B_{\gamma }^{n-1-k}f\left(x\right)\right]-k_{\frac{\gamma -1}{2}}\left(x\xi \right)x^{\gamma }\frac{d}{dx}\left[B_{\gamma }^{n-1-k}f\left(x\right)\right]\right){|}_{x=0}.$$

Let $0\le \gamma <1$. Then, using (10), we get

$$\underset{x\to 0+}{lim}{k}_{\frac{\gamma -1}{2}}\left(x\xi \right)x^{\gamma }\frac{d}{dx}\left[B_{\gamma }^{n-1-k}f\left(x\right)\right]=\frac{\mathsf{\Gamma }\left(\frac{1-\gamma }{2}\right)}{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}\underset{x\to 0+}{lim}{x}^{\gamma }\frac{d}{dx}\left[B_{\gamma }^{n-1-k}f\left(x\right)\right].$$

For $\gamma =1$, using (11) we get

$$\underset{x\to 0+}{lim}{k}_0\left(x\xi \right)\frac{d}{dx}\left[B_{\gamma }^{n-1-k}f\left(x\right)\right]=-\underset{x\to 0+}{lim}lnx\xi \frac{d}{dx}\left[B_{\gamma }^{n-1-k}f\left(x\right)\right].$$

When $1<\gamma$, using (12) we obtain

$$\underset{x\to 0+}{lim}{k}_{\frac{\gamma -1}{2}}\left(x\xi \right)x^{\gamma }\frac{d}{dx}\left[B_{\gamma }^{n-1-k}f\left(x\right)\right]=\frac{1}{\gamma -1}\underset{x\to 0+}{lim}x{\xi }^{1-\gamma }\frac{d}{dx}\left[B_{\gamma }^{n-1-k}f\left(x\right)\right].$$

Next, we have

$$\frac{d}{dx}{k}_{\frac{\gamma -1}{2}}\left(x\xi \right)=-\frac{2^{\frac{1-\gamma }{2}}{\xi }^{\frac{3-\gamma }{2}}{x}^{\frac{1-\gamma }{2}}}{\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{K}_{\frac{\gamma +1}{2}}\left(x\xi \right)$$

and using (8) for small x

$$x^{\gamma }\frac{d}{dx}{k}_{\frac{\gamma -1}{2}}\left(x\xi \right)=-\frac{2^{\frac{1-\gamma }{2}}}{\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{x}^{\frac{\gamma +1}{2}}{\xi }^{\frac{3-\gamma }{2}}{K}_{\frac{\gamma +1}{2}}\left(x\xi \right)$$

$$\sim -\frac{2^{\frac{1-\gamma }{2}}}{\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{x}^{\frac{\gamma +1}{2}}{\xi }^{\frac{3-\gamma }{2}}\frac{\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{2^{1-\frac{\gamma +1}{2}}}{\left(\xi x\right)}^{-\frac{\gamma +1}{2}}=-{\xi }^{1-\gamma },x\to 0+,$$

therefore

$$\underset{x\to 0+}{lim}\left(x^{\gamma }\frac{d}{dx}{k}_{\frac{\gamma -1}{2}}\left(x\xi \right)\right)\left[B_{\gamma }^{n-1-k}f\left(x\right)\right]=-{\xi }^{1-\gamma }{B}_{\gamma }^{n-1-k}f(0+);$$

for $0\le \gamma <1$

$${\mathcal{K}}_{\gamma }\left[B_{\gamma }^{n}f\right]\left(\xi \right)={\xi }^{2n}{\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)-\sum _{k=0}^{n-1}{\xi }^{2k+1-\gamma }{B}_{\gamma }^{n-1-k}f(0+)$$

$$-\frac{\mathsf{\Gamma }\left(\frac{1-\gamma }{2}\right)}{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}\sum _{k=0}^{n-1}{\xi }^{2k}\underset{x\to 0+}{lim}{x}^{\gamma }\frac{d}{dx}\left[B_{\gamma }^{n-1-k}f\left(x\right)\right]$$

$$={\xi }^{2n}{\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)-\sum _{k=1}^n{\xi }^{2k-1-\gamma }{B}_{\gamma }^{n-k}f(0+)-\frac{\mathsf{\Gamma }\left(\frac{1-\gamma }{2}\right)}{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}\underset{x\to 0+}{lim}\sum _{k=1}^n{\xi }^{2k-2}{x}^{\gamma }\frac{d}{dx}\left[B_{\gamma }^{n-k}f\left(x\right)\right];$$

for $\gamma =1$

$${\mathcal{K}}_{\gamma }\left[B_{\gamma }^{n}f\right]\left(\xi \right)={\xi }^{2n}{\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)-\sum _{k=1}^n{\xi }^{2k-1-\gamma }{B}_{\gamma }^{n-k}f(0+)+\underset{x\to 0+}{lim}\sum _{k=1}^n{\xi }^{2k-2}lnx\xi \frac{d}{dx}\left[B_{\gamma }^{n-k}f\left(x\right)\right];$$

for $1<\gamma$

$${\mathcal{K}}_{\gamma }\left[B_{\gamma }^{n}f\right]\left(\xi \right)={\xi }^{2n}{\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)-\sum _{k=1}^n{\xi }^{2k-1-\gamma }{B}_{\gamma }^{n-k}f(0+)-\frac{1}{\gamma -1}\underset{x\to 0+}{lim}\sum _{k=1}^n{\xi }^{2k-1-\gamma }x\frac{d}{dx}\left[B_{\gamma }^{n-k}f\left(x\right)\right].$$

 ☐

Remark 1.

Let $n\in \mathbb{N}$, $\frac{d}{dx}\left[B_{\gamma }^{n-k}f\left(x\right)\right]$ be bounded, the Meijer transform of $B_{\gamma }^{n}f$ exist, and $\gamma \ne 1$; then,

$${\mathcal{K}}_{\gamma }\left[B_{\gamma }^{n}f\right]\left(\xi \right)={\xi }^{2n}{\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)-\sum _{k=1}^n{\xi }^{2k-1-\gamma }{B}_{\gamma }^{n-k}f(0+).$$

(35)

If $\frac{d}{dx}\left[B_{\gamma }^{n-k}f\left(x\right)\right]\sim x^{\beta }$, $\beta >0$ when $x\to 0+$, then (35) holds for $\gamma =1$.

Remark 2.

Since $k_{-\frac{1}{2}}\left(x\right)=e^{-x},$ then

$${\mathcal{K}}_0\left[f\right]\left(\xi \right)=\mathcal{L}\left[f\right]\left(\xi \right),$$

where $\mathcal{L}\left[f\right]$ is a Laplace transform of f. It is well known that

$$\mathcal{L}\left[f^{″}\right]\left(\xi \right)={\xi }^2\mathcal{L}\left[f\right]\left(\xi \right)-\xi f\left(0\right)-f^{\prime }\left(0\right).$$

From the other side

$$\frac{\mathsf{\Gamma }\left(\frac{1-\gamma }{2}\right)}{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{|}_{\gamma =0}=1,\sum _{k=1}^n{x}^{\gamma }\frac{d}{dx}\left[B_{\gamma }^{n-k}f\left(x\right)\right]{|}_{\gamma =0,n=1}=f^{\prime }\left(x\right)$$

and

$${\mathcal{K}}_0\left[B_{0}f\right]\left(\xi \right)=L{f}^{″}\left(\xi \right)={\xi }^2{\mathcal{K}}_0\left[f\right]\left(\xi \right)-\xi f\left(0\right)-f^{\prime }\left(0\right)=\mathcal{L}\left[f^{″}\right]\left(\xi \right).$$

The same situation is true for ${\mathcal{K}}_0\left[B_0^{n}f\right]\left(\xi \right)$.

Theorem 4.

Let $n=\left[\alpha \right]+1$ for fractional α and $n=\alpha$ for $\alpha \in \mathbb{N}$ and the Meijer transform of ${\mathcal{B}}_{\gamma ,0+}^{\alpha }f$ exists, then for $0\le \gamma <1$

$${\mathcal{K}}_{\gamma }\left[{\mathcal{B}}_{\gamma ,0+}^{\alpha }f\right]\left(\xi \right)$$

$$={\xi }^{2\alpha }{\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)-\sum _{k=0}^{n-1}{\xi }^{2\alpha -2k-1-\gamma }{B}_{\gamma }^{k}f(0+)-\frac{\mathsf{\Gamma }\left(\frac{1-\gamma }{2}\right)}{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}\underset{x\to 0+}{lim}\sum _{k=0}^{n-1}{\xi }^{2\alpha -2k-2}{x}^{\gamma }\frac{d}{dx}\left[B_{\gamma }^{k}f\left(x\right)\right];$$

(36)

for $\gamma =1$

$${\mathcal{K}}_{\gamma }\left[{\mathcal{B}}_{\gamma ,0+}^{\alpha }f\right]\left(\xi \right)$$

$$={\xi }^{2\alpha }{\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)-\sum _{k=0}^{n-1}{\xi }^{2\alpha -2k-1-\gamma }{B}_{\gamma }^{k}f(0+)+\underset{x\to 0+}{lim}\sum _{k=0}^{n-1}{\xi }^{2\alpha -2k-2}lnx\xi \frac{d}{dx}\left[B_{\gamma }^{k}f\left(x\right)\right];$$

(37)

for $1<\gamma$

$${\mathcal{K}}_{\gamma }\left[{\mathcal{B}}_{\gamma ,0+}^{\alpha }f\right]\left(\xi \right)$$

$$={\xi }^{2\alpha }{\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)-\sum _{k=0}^{n-1}{\xi }^{2\alpha -2k-1-\gamma }{B}_{\gamma }^{k}f(0+)-\frac{1}{\gamma -1}\underset{x\to 0+}{lim}\sum _{k=0}^{n-1}{\xi }^{2\alpha -2k-1-\gamma }x\frac{d}{dx}\left[B_{\gamma }^{k}f\left(x\right)\right],$$

(38)

where

$$B_{\gamma ,0+}^{\alpha -k}f(0+)=\underset{x\to +0}{lim}{B}_{\gamma ,0+}^{\alpha -k}f\left(x\right).$$

Proof. 

Using (30) and (35) for $0\le \gamma <1$ we obtain

$${\mathcal{K}}_{\gamma }\left[{\mathcal{B}}_{\gamma ,0+}^{\alpha }f\right]\left(\xi \right)={\mathcal{K}}_{\gamma }\left[\left(I{B}_{\gamma ,0+}^{n-\alpha }{B}_{\gamma }^{n}f\right)\left(x\right)\right]\left(\xi \right)={\xi }^{2\alpha -2n}{\mathcal{K}}_{\gamma }\left[B_{\gamma }^{n}f\right]\left(\xi \right)={\xi }^{2\alpha }{\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)$$

$$-\sum _{k=1}^n{\xi }^{2\alpha -2n+2k-1-\gamma }{B}_{\gamma }^{n-k}f(0+)-\frac{\mathsf{\Gamma }\left(\frac{1-\gamma }{2}\right)}{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}\underset{x\to 0+}{lim}\sum _{k=1}^n{\xi }^{2\alpha -2n+2k-2}{x}^{\gamma }\frac{d}{dx}\left[B_{\gamma }^{n-k}f\left(x\right)\right]$$

$$={\xi }^{2\alpha }{\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)-\sum _{k=0}^{n-1}{\xi }^{2\alpha -2k-1-\gamma }{B}_{\gamma }^{k}f(0+)-\frac{\mathsf{\Gamma }\left(\frac{1-\gamma }{2}\right)}{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}\underset{x\to 0+}{lim}\sum _{k=0}^{n-1}{\xi }^{2\alpha -2k-2}{x}^{\gamma }\frac{d}{dx}\left[B_{\gamma }^{k}f\left(x\right)\right],$$

where we put

$$\underset{x\to +0}{lim}{B}_{\gamma ,0+}^{k}f\left(x\right)=B_{\gamma ,0+}^{k}f(0+).$$

Similarly, for $\gamma =1$ we have

$${\mathcal{K}}_{\gamma }\left[{\mathcal{B}}_{\gamma ,0+}^{\alpha }f\right]\left(\xi \right)={\mathcal{K}}_{\gamma }\left[\left(I{B}_{\gamma ,0+}^{n-\alpha }{B}_{\gamma }^{n}f\right)\left(x\right)\right]\left(\xi \right)={\xi }^{2\alpha -2n}{\mathcal{K}}_{\gamma }\left[B_{\gamma }^{n}f\right]\left(\xi \right)={\xi }^{2\alpha }{\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)$$

$$-\sum _{k=1}^n{\xi }^{2\alpha -2n+2k-1-\gamma }{B}_{\gamma }^{n-k}f(0+)+\underset{x\to 0+}{lim}\sum _{k=1}^n{\xi }^{2\alpha -2n+2k-2}lnx\xi \frac{d}{dx}\left[B_{\gamma }^{n-k}f\left(x\right)\right]$$

$$={\xi }^{2\alpha }{\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)-\sum _{k=0}^{n-1}{\xi }^{2\alpha -2k-1-\gamma }{B}_{\gamma }^{k}f(0+)+\underset{x\to 0+}{lim}\sum _{k=0}^{n-1}{\xi }^{2\alpha -2k-2}lnx\xi \frac{d}{dx}\left[B_{\gamma }^{k}f\left(x\right)\right]$$

and for $\gamma >1$

$${\mathcal{K}}_{\gamma }\left[{\mathcal{B}}_{\gamma ,0+}^{\alpha }f\right]\left(\xi \right)={\mathcal{K}}_{\gamma }\left[\left(I{B}_{\gamma ,0+}^{n-\alpha }{B}_{\gamma }^{n}f\right)\left(x\right)\right]\left(\xi \right)={\xi }^{2\alpha -2n}{\mathcal{K}}_{\gamma }\left[B_{\gamma }^{n}f\right]\left(\xi \right)$$

$$={\xi }^{2\alpha }{\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)-\sum _{k=0}^{n-1}{\xi }^{2\alpha -2k-1-\gamma }{B}_{\gamma }^{k}f(0+)-\frac{1}{\gamma -1}\underset{x\to 0+}{lim}\sum _{k=0}^{n-1}{\xi }^{2\alpha -2k-1-\gamma }x\frac{d}{dx}\left[B_{\gamma }^{k}f\left(x\right)\right].$$

 ☐

Remark 3.

Let $k\in \mathbb{N}$, $\frac{d}{dx}\left[B_{\gamma }^{k}f\left(x\right)\right]$ be bounded, the Meijer transform of ${\mathcal{B}}_{\gamma ,0+}^{\alpha }f$ exist, and $\gamma \ne 1$, then

$${\mathcal{K}}_{\gamma }\left[{\mathcal{B}}_{\gamma ,0+}^{\alpha }f\right]\left(\xi \right)={\xi }^{2\alpha }{\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)-\sum _{k=0}^{n-1}{\xi }^{2\alpha -2k-1-\gamma }{B}_{\gamma }^{k}f(0+).$$

(39)

If $\frac{d}{dx}\left[B_{\gamma }^{k}f\left(x\right)\right]\sim x^{\beta }$, $\beta >0$ when $x\to 0+$, then (39) holds for $\gamma =1$.

4. Meijer Transform Method for Solution to Homogeneous Fractional Equation with the Left-Sided Fractional Bessel Derivatives on Semi-Axes of Gerasimov–Caputo Type

4.1. General Case

Using the Meijer transform method (for general scheme see [33,34]) we will solve the equation

$$\left({\mathcal{B}}_{\gamma ,0+}^{\alpha }f\right)\left(x\right)=\lambda f\left(x\right),\alpha >0,\lambda \in \mathbb{R}$$

(40)

with the left-sided fractional Bessel derivatives on semi-axes of Gerasimov–Caputo type with constant coefficient when $\gamma \ne 1$.

Let $\frac{m-1}{2}<\alpha \le \frac{m}{2}$, $m\in \mathbb{N}$. To Equation (40) we should add m conditions which are for $0\le \gamma <1$ of the form

$$\left(B_{\gamma ,0+}^{k}f\right)(0+)=a_{2k},\underset{x\to 0+}{lim}{x}^{\gamma }\frac{d}{dx}{B}_{\gamma ,0+}^{k}f\left(x\right)=a_{2k+1},a_{2k},a_{2k+1}\in \mathbb{R}.$$

(41)

For the case when $\gamma >1$ we should consider the conditions

$$\left(B_{\gamma ,0+}^{k}f\right)(0+)=b_{2k},\underset{x\to 0+}{lim}x\frac{d}{dx}{B}_{\gamma ,0+}^{k}f\left(x\right)=b_{2k+1},b_{2k},b_{2k+1}\in \mathbb{R},$$

(42)

where $k\in \mathbb{N}\cup \left\{0\right\}$, such that the following inequalities are true:

$$0\le 2k\le m-1,1\le 2k+1\le m-2ifmisodd,$$

and

$$1\le 2k+1\le m-1,0\le 2k\le m-2ifmiseven.$$

This means that for odd m the last condition is the $\left(B_{\gamma ,0+}^{k}f\right)(0+)=a_{m-1}$ or $\left(B_{\gamma ,0+}^{k}f\right)(0+)=b_{m-1}$ and for even m the last condition is the $\underset{x\to 0+}{lim}{x}^{\gamma }\frac{d}{dx}{B}_{\gamma ,0+}^{k}f\left(x\right)=a_{m-1}$ or $\underset{x\to 0+}{lim}x\frac{d}{dx}{B}_{\gamma ,0+}^{k}f\left(x\right)=b_{m-1}$.

Theorem 5.

When $0\le \gamma <1$ the solution to (40) and (41) is for the case when m is odd

$$f\left(x\right)=\frac{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{\sqrt{\pi }}\sum _{k=0}^{\frac{m-1}{2}}{a}_{2k}{x}^{2k}{}_2{\mathsf{\Psi }}_2\left[\left.\begin{array}{c}\left(k+1+\frac{\gamma }{2},\alpha \right),(1,1)\\ \left(k+1,\alpha \right),\left(2k+\gamma +1,2\alpha \right)\end{array}\right|\lambda x^{2\alpha }\right]$$

$$+\frac{\mathsf{\Gamma }\left(\frac{1-\gamma }{2}\right)}{\sqrt{\pi }}\sum _{k=0}^{\frac{m-3}{2}}{a}_{2k+1}{x}^{2k+1-\gamma }{}_2{\mathsf{\Psi }}_2\left[\left.\begin{array}{c}\left(k+\frac{3}{2},\alpha \right),(1,1)\\ \left(k+\frac{3-\gamma }{2},\alpha \right),\left(2k+2,2\alpha \right)\end{array}\right|\lambda x^{2\alpha }\right],$$

(43)

here the second sum vanishes if $\frac{m-3}{2}<0$, that is, when $m=1$, for the case when m is even

$$f\left(x\right)=\frac{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{\sqrt{\pi }}\sum _{k=0}^{\frac{m-2}{2}}{a}_{2k}{x}^{2k}{}_2{\mathsf{\Psi }}_2\left[\left.\begin{array}{c}\left(k+1+\frac{\gamma }{2},\alpha \right),(1,1)\\ \left(k+1,\alpha \right),\left(2k+\gamma +1,2\alpha \right)\end{array}\right|\lambda x^{2\alpha }\right]$$

$$+\frac{\mathsf{\Gamma }\left(\frac{1-\gamma }{2}\right)}{\sqrt{\pi }}\sum _{k=0}^{\frac{m-2}{2}}{a}_{2k+1}{x}^{2k+1-\gamma }{}_2{\mathsf{\Psi }}_2\left[\left.\begin{array}{c}\left(k+\frac{3}{2},\alpha \right),(1,1)\\ \left(k+\frac{3-\gamma }{2},\alpha \right),\left(2k+2,2\alpha \right)\end{array}\right|\lambda x^{2\alpha }\right].$$

(44)

When $\gamma >1$ the solution to (40)–(42) is for the case when m is odd

$$f\left(x\right)=\frac{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{\sqrt{\pi }}\sum _{k=0}^{\frac{m-1}{2}}{b}_{2k}{x}^{2k}{}_2{\mathsf{\Psi }}_2\left[\left.\begin{array}{c}\left(k+1+\frac{\gamma }{2},\alpha \right),(1,1)\\ \left(k+1,\alpha \right),\left(2k+\gamma +1,2\alpha \right)\end{array}\right|\lambda x^{2\alpha }\right]$$

$$+\frac{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{\sqrt{\pi }(\gamma -1)}\sum _{k=0}^{\frac{m-3}{2}}{b}_{2k+1}{x}^{2k}{}_2{\mathsf{\Psi }}_2\left[\left.\begin{array}{c}\left(k+1+\frac{\gamma }{2},\alpha \right),(1,1)\\ \left(k+1,\alpha \right),\left(2k+\gamma +1,2\alpha \right)\end{array}\right|\lambda x^{2\alpha }\right],$$

(45)

here the second sum vanishes if $\frac{m-3}{2}<0$, that is, when $m=1$, for the case when m is even

$$f\left(x\right)=\frac{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{\sqrt{\pi }}\sum _{k=0}^{\frac{m-2}{2}}{b}_{2k}{x}^{2k}{}_2{\mathsf{\Psi }}_2\left[\left.\begin{array}{c}\left(k+1+\frac{\gamma }{2},\alpha \right),(1,1)\\ \left(k+1,\alpha \right),\left(2k+\gamma +1,2\alpha \right)\end{array}\right|\lambda x^{2\alpha }\right]$$

$$+\frac{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{\sqrt{\pi }(\gamma -1)}\sum _{k=0}^{\frac{m-2}{2}}{b}_{2k+1}{x}^{2k}{}_2{\mathsf{\Psi }}_2\left[\left.\begin{array}{c}\left(k+1+\frac{\gamma }{2},\alpha \right),(1,1)\\ \left(k+1,\alpha \right),\left(2k+\gamma +1,2\alpha \right)\end{array}\right|\lambda x^{2\alpha }\right].$$

(46)

Here ${}_p{\mathsf{\Psi }}_q\left(z\right)$ is the Fox–Wright function (16).

Proof. 

First we consider the case when $0\le \gamma <1$. Applying the Meijer transform (20) to both parts of (40) and using (36), we obtain

$${\xi }^{2\alpha }{\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)-\sum _{k=0}^{n-1}{\xi }^{2\alpha -2k-1-\gamma }{B}_{\gamma }^{k}f(0+)-\frac{\mathsf{\Gamma }\left(\frac{1-\gamma }{2}\right)}{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}\underset{x\to 0+}{lim}\sum _{k=0}^{n-1}{\xi }^{2\alpha -2k-2}{x}^{\gamma }\frac{d}{dx}\left[B_{\gamma }^{k}f\left(x\right)\right]=\lambda {\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right),$$

where $n\in \mathbb{N}$, $n-1<\alpha \le n$. Taking into account conditions (41) we obtain for the case when m is odd

$${\xi }^{2\alpha }{\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)-\sum _{k=0}^{\frac{m-1}{2}}{a}_{2k}{\xi }^{2\alpha -2k-1-\gamma }-\frac{\mathsf{\Gamma }\left(\frac{1-\gamma }{2}\right)}{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}\sum _{k=0}^{\frac{m-3}{2}}{a}_{2k+1}{\xi }^{2\alpha -2k-2}=\lambda {\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right),$$

where the second sum vanishes if $\frac{m-3}{2}<0$, that is, when $m=1$, for the case when m is even

$${\xi }^{2\alpha }{\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)-\sum _{k=0}^{\frac{m-2}{2}}{a}_{2k}{\xi }^{2\alpha -2k-1-\gamma }-\frac{\mathsf{\Gamma }\left(\frac{1-\gamma }{2}\right)}{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}\sum _{k=0}^{\frac{m-2}{2}}{a}_{2k-1}{\xi }^{2\alpha -2k-2}=\lambda {\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right).$$

Therefore, when m is odd

$$f\left(x\right)=\sum _{k=0}^{\frac{m-1}{2}}{a}_{2k}{\mathcal{K}}_{\gamma }^{-1}\left[\frac{{\xi }^{2\alpha -2k-1-\gamma }}{{\xi }^{2\alpha }-\lambda }\right]\left(x\right)+\frac{\mathsf{\Gamma }\left(\frac{1-\gamma }{2}\right)}{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}\sum _{k=0}^{\frac{m-3}{2}}{a}_{2k+1}{\mathcal{K}}_{\gamma }^{-1}\left[\frac{{\xi }^{2\alpha -2k-2}}{{\xi }^{2\alpha }-\lambda }\right]\left(x\right),$$

and when m is even

$$f\left(x\right)=\sum _{k=0}^{\frac{m-2}{2}}{a}_{2k}{\mathcal{K}}_{\gamma }^{-1}\left[\frac{{\xi }^{2\alpha -2k-1-\gamma }}{{\xi }^{2\alpha }-\lambda }\right]\left(x\right)+\frac{\mathsf{\Gamma }\left(\frac{1-\gamma }{2}\right)}{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}\sum _{k=0}^{\frac{m-2}{2}}{a}_{2k+1}{\mathcal{K}}_{\gamma }^{-1}\left[\frac{{\xi }^{2\alpha -2k-2}}{{\xi }^{2\alpha }-\lambda }\right]\left(x\right).$$

In order to find the explicit expression for f, we use formula (24). First, find the inverse Laplace transforms taking into account formula (19):

$${\mathcal{L}}^{-1}\left[\frac{{\xi }^{2\alpha -2k-2}}{{\xi }^{2\alpha }-\lambda }\right]\left(x\right)=x^{2k+1}{E}_{2\alpha ,2k+2}\left(\lambda x^{2\alpha }\right),$$

$${\mathcal{L}}^{-1}\left[\frac{{\xi }^{2\alpha -2k-1-\gamma }}{{\xi }^{2\alpha }-\lambda }\right]\left(x\right)=x^{2k+\gamma }{E}_{2\alpha ,2k+\gamma +1}\left(\lambda x^{2\alpha }\right).$$

Now, find ${\left({\mathcal{P}}_x^{\gamma }\right)}^{-1}{x}^{\beta -\gamma }{E}_{2\alpha ,\beta }\left(\lambda x^{2\alpha }\right)$. Using (23) we can write

$${\left({\mathcal{P}}_x^{\gamma }\right)}^{-1}{x}^{\beta -\gamma }{E}_{2\alpha ,\beta }\left(\lambda x^{2\alpha }\right)=\frac{2\sqrt{\pi }x}{\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)\mathsf{\Gamma }\left(p-\frac{\gamma }{2}\right)}{\left(\frac{d}{2xdx}\right)}^p\underset{0}{\overset{x}{\int }}{z}^{\beta }{E}_{2\alpha ,\beta }\left(\lambda z^{2\alpha }\right){(x^2-z^2)}^{p-\frac{\gamma }{2}-1}dz,$$

where $p=\left[\frac{\gamma }{2}\right]+1.$ We have

$$E_{2\alpha ,\beta }\left(\lambda z^{2\alpha }\right)=\sum _{m=0}^{\infty }\frac{{\lambda }^m{z}^{2m\alpha }}{\mathsf{\Gamma }(2\alpha m+\beta )}$$

and

$$\underset{0}{\overset{x}{\int }}{z}^{\beta }{E}_{2\alpha ,\beta }\left(\lambda z^{2\alpha }\right){(x^2-z^2)}^{p-\frac{\gamma }{2}-1}dz=\sum _{m=0}^{\infty }\frac{{\lambda }^m}{\mathsf{\Gamma }(2\alpha m+\beta )}\underset{0}{\overset{x}{\int }}{z}^{2m\alpha +\beta }{(x^2-z^2)}^{p-\frac{\gamma }{2}-1}dz$$

$$=\sum _{m=0}^{\infty }\frac{{\lambda }^m}{\mathsf{\Gamma }(2\alpha m+\beta )}\frac{\mathsf{\Gamma }\left(m\alpha +\frac{\beta +1}{2}\right)\mathsf{\Gamma }\left(p-\frac{\gamma }{2}\right)}{2\mathsf{\Gamma }\left(m\alpha +p+\frac{\beta -\gamma +1}{2}\right)}{x}^{2m\alpha +2p+\beta -\gamma -1}.$$

Therefore,

$${\left({\mathcal{P}}_x^{\gamma }\right)}^{-1}{x}^{\beta -\gamma }{E}_{2\alpha ,\beta }\left(\lambda x^{2\alpha }\right)=\frac{\sqrt{\pi }x}{\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{\left(\frac{d}{2xdx}\right)}^p\sum _{m=0}^{\infty }\frac{{\lambda }^m}{\mathsf{\Gamma }(2\alpha m+\beta )}\frac{\mathsf{\Gamma }\left(m\alpha +\frac{\beta +1}{2}\right)}{\mathsf{\Gamma }\left(m\alpha +p+\frac{\beta -\gamma +1}{2}\right)}{x}^{2m\alpha +2p+\beta -\gamma -1}.$$

Using the formula

$${\left(\frac{d}{2xdx}\right)}^n{x}^{2\mu +2n}=\frac{\mathsf{\Gamma }(\mu +n+1)}{\mathsf{\Gamma }(\mu +1)}{x}^{2\mu },$$

we get

$${\left({\mathcal{P}}_x^{\gamma }\right)}^{-1}{x}^{\beta -\gamma }{E}_{2\alpha ,\beta }\left(\lambda x^{2\alpha }\right)=\frac{\sqrt{\pi }{x}^{\beta -\gamma }}{\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}\sum _{m=0}^{\infty }\frac{\mathsf{\Gamma }\left(m\alpha +\frac{\beta +1}{2}\right)}{\mathsf{\Gamma }(2\alpha m+\beta )\mathsf{\Gamma }\left(m\alpha +\frac{\beta -\gamma +1}{2}\right)}{\left(\lambda x^{2\alpha }\right)}^m.$$

Using the Fox–Wright function (16), we can write

$${\left({\mathcal{P}}_x^{\gamma }\right)}^{-1}{x}^{\beta -\gamma }{E}_{2\alpha ,\beta }\left(\lambda x^{2\alpha }\right)=\frac{\sqrt{\pi }{x}^{\beta -\gamma }}{\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{}_2{\mathsf{\Psi }}_2\left[\left.\begin{array}{c}\left(\frac{\beta +1}{2},\alpha \right),(1,1)\\ \left(\frac{\beta -\gamma +1}{2},\alpha \right),\left(\beta ,2\alpha \right)\end{array}\right|\lambda x^{2\alpha }\right].$$

So,

$${\mathcal{K}}_{\gamma }^{-1}\left[\frac{{\xi }^{2\alpha -2k-2}}{{\xi }^{2\alpha }-\lambda }\right]\left(x\right)=\frac{1}{A_{\gamma }x}{\left({\mathcal{P}}_x^{\gamma }\right)}^{-1}{x}^{1-\gamma }\left({\mathcal{L}}^{-1}\left[\frac{{\xi }^{2\alpha -2k-2}}{{\xi }^{2\alpha }-\lambda }\right]\right)\left(x\right)$$

$$=\frac{1}{A_{\gamma }x}{\left({\mathcal{P}}_x^{\gamma }\right)}^{-1}{x}^{2k+2-\gamma }{E}_{2\alpha ,2k+2}\left(\lambda x^{2\alpha }\right)$$

$$=\frac{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{\sqrt{\pi }}{x}^{2k+1-\gamma }{}_2{\mathsf{\Psi }}_2\left[\left.\begin{array}{c}\left(k+\frac{3}{2},\alpha \right),(1,1)\\ \left(k+\frac{3-\gamma }{2},\alpha \right),\left(2k+2,2\alpha \right)\end{array}\right|\lambda x^{2\alpha }\right],$$

$${\mathcal{K}}_{\gamma }^{-1}\left[\frac{{\xi }^{2\alpha -2k-1-\gamma }}{{\xi }^{2\alpha }-\lambda }\right]\left(x\right)=\frac{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{\sqrt{\pi }}{x}^{2k}{}_2{\mathsf{\Psi }}_2\left[\left.\begin{array}{c}\left(k+1+\frac{\gamma }{2},\alpha \right),(1,1)\\ \left(k+1,\alpha \right),\left(2k+\gamma +1,2\alpha \right)\end{array}\right|\lambda x^{2\alpha }\right].$$

(47)

Then, for the case when m is odd, we get (43) and for the case when m is even (44).

For $\gamma >1$ applying the Meijer transform (20) to both parts of (40) and using (38), we obtain

$${\xi }^{2\alpha }{\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right)-\sum _{k=0}^{n-1}{\xi }^{2\alpha -2k-1-\gamma }{B}_{\gamma }^{k}f(0+)-\frac{1}{\gamma -1}\underset{x\to 0+}{lim}\sum _{k=0}^{n-1}{\xi }^{2\alpha -2k-1-\gamma }x\frac{d}{dx}\left[B_{\gamma }^{k}f\left(x\right)\right]=\lambda {\mathcal{K}}_{\gamma }\left[f\right]\left(\xi \right),$$

where $n\in \mathbb{N}$, $n-1<\alpha \le n$. Taking into account conditions (42) we get, for the case when m is odd:

$$f\left(x\right)=\sum _{k=0}^{\frac{m-1}{2}}{b}_{2k}{\mathcal{K}}_{\gamma }^{-1}\left[\frac{{\xi }^{2\alpha -2k-1-\gamma }}{{\xi }^{2\alpha }-\lambda }\right]\left(x\right)+\frac{1}{\gamma -1}\sum _{k=0}^{\frac{m-3}{2}}{b}_{2k+1}{\mathcal{K}}_{\gamma }^{-1}\left[\frac{{\xi }^{2\alpha -2k-1-\gamma }}{{\xi }^{2\alpha }-\lambda }\right]\left(x\right).$$

For the case when m is even:

$$f\left(x\right)=\sum _{k=0}^{\frac{m-2}{2}}{b}_{2k}{\mathcal{K}}_{\gamma }^{-1}\left[\frac{{\xi }^{2\alpha -2k-1-\gamma }}{{\xi }^{2\alpha }-\lambda }\right]\left(x\right)+\frac{1}{\gamma -1}\sum _{k=0}^{\frac{m-2}{2}}{b}_{2k+1}{\mathcal{K}}_{\gamma }^{-1}\left[\frac{{\xi }^{2\alpha -2k-1-\gamma }}{{\xi }^{2\alpha }-\lambda }\right]\left(x\right).$$

Therefore, applying (47) we obtain (45) and (46) respectively. ☐

4.2. Particular Cases and Examples

In this subsection first we consider Equation (40) when conditions of Remark 3 are valid. Then, we give some examples.

Theorem 6.

Let $k,m\in \mathbb{N}$, $\frac{m-1}{2}<\alpha \le \frac{m}{2}$, $\frac{d}{dx}\left[B_{\gamma }^{k}f\left(x\right)\right]$ be bounded for $0<\gamma$, $\gamma \ne 1$ and $\frac{d}{dx}\left[B_{\gamma }^{k}f\left(x\right)\right]\sim x^{\beta }$, $\beta >0$ when $x\to 0+$. Then, the solution to equation

$$\left({\mathcal{B}}_{\gamma ,0+}^{\alpha }f\right)\left(x\right)=\lambda f\left(x\right),\alpha >0,\lambda \in \mathbb{R}$$

(48)

with m conditions for $0\le \gamma <1$ of the form

$$\left(B_{\gamma ,0+}^{k}f\right)(0+)=a_{2k},\underset{x\to 0+}{lim}{x}^{\gamma }\frac{d}{dx}{B}_{\gamma ,0+}^{k}f\left(x\right)=0,$$

(49)

with m conditions for $\gamma =1$ of the form

$$\left(B_{\gamma ,0+}^{k}f\right)(0+)=a_{2k},\underset{x\to 0+}{lim}lnx\xi \frac{d}{dx}\left[B_{\gamma }^{k}f\left(x\right)\right]=0,$$

(50)

with m conditions for $\gamma >1$ of the form

$$\left(B_{\gamma ,0+}^{k}f\right)(0+)=a_{2k},\underset{x\to 0+}{lim}x\frac{d}{dx}{B}_{\gamma ,0+}^{k}f\left(x\right)=0,$$

(51)

where $a_{2k}\in \mathbb{R}$, $k\in \mathbb{N}\cup \left\{0\right\}$, such that the following inequalities are true:

$$0\le 2k\le m-1,1\le 2k+1\le m-2\mathrm{if}m\mathrm{is}\mathrm{odd},$$

and

$$1\le 2k+1\le m-1,0\le 2k\le m-2\mathrm{if}m\mathrm{is}\mathrm{even}.$$

When $m=1$ it is $f\left(x\right)=0$, for the case of odd $m\ge 3$ it is

$$f\left(x\right)=\frac{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{\sqrt{\pi }}\sum _{k=0}^{\frac{m-1}{2}}{a}_{2k}{x}^{2k}{}_2{\mathsf{\Psi }}_2\left[\left.\begin{array}{c}\left(k+1+\frac{\gamma }{2},\alpha \right),(1,1)\\ \left(k+1,\alpha \right),\left(2k+\gamma +1,2\alpha \right)\end{array}\right|\lambda x^{2\alpha }\right],$$

(52)

and for the case of even m it is

$$f\left(x\right)=\frac{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{\sqrt{\pi }}\sum _{k=0}^{\frac{m-2}{2}}{a}_{2k}{x}^{2k}{}_2{\mathsf{\Psi }}_2\left[\left.\begin{array}{c}\left(k+1+\frac{\gamma }{2},\alpha \right),(1,1)\\ \left(k+1,\alpha \right),\left(2k+\gamma +1,2\alpha \right)\end{array}\right|\lambda x^{2\alpha }\right].$$

(53)

Here ${}_p{\mathsf{\Psi }}_q\left(z\right)$ is the Fox–Wright function (16).

Example 1.

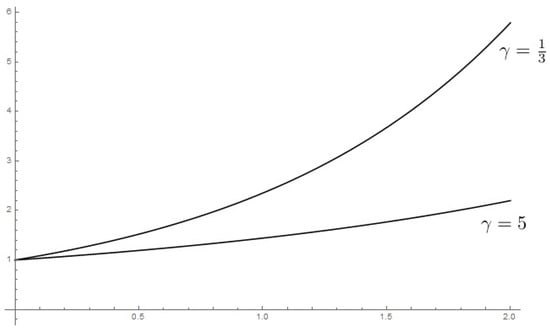
Consider the general case of the problem (40) and (41) when $0<\alpha \le \frac{1}{2}$, $0\le \gamma <1$. In this case $m=1$, $2k=0$, and using (43) we obtain that the solution to the problem

$$\left({\mathcal{B}}_{\gamma ,0+}^{\alpha }f\right)\left(x\right)=\lambda f\left(x\right),\alpha >0,\lambda \in \mathbb{R},$$

$$f(0+)=a_0,a_1\in \mathbb{R}$$

is

$$f\left(x\right)=\frac{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{\sqrt{\pi }}{a}_0{}_2{\mathsf{\Psi }}_2\left[\left.\begin{array}{c}\left(1+\frac{\gamma }{2},\alpha \right),(1,1)\\ \left(1,\alpha \right),\left(\gamma +1,2\alpha \right)\end{array}\right|\lambda x^{2\alpha }\right].$$

(54)

It is easy to see that for $\gamma >1$ the solution has the same form when $0<\alpha \le \frac{1}{2}$. In Figure 1 we present plots of f for $\gamma =\frac{1}{3}$ and for $\gamma =5$ when $\alpha =\frac{1}{2}$, $\lambda =1$.

Figure 1. Solutions (54) for $\gamma =1/3$ and $\gamma =5$.

When $\gamma =0$ we obtain

$$\left({}^C{D}_{0+}^{2\alpha }f\right)\left(x\right)=\lambda f\left(x\right),0<2\alpha \le 1,\lambda \in \mathbb{R},$$

$$f(0+)=a_1,a_1\in \mathbb{R}$$

and using (17) we obtain

$$f\left(x\right)=a_0{}_2{\mathsf{\Psi }}_2\left[\left.\begin{array}{c}\left(1,\alpha \right),(1,1)\\ \left(1,\alpha \right),\left(1,2\alpha \right)\end{array}\right|\lambda x^{2\alpha }\right]=a_0{}_1{\mathsf{\Psi }}_1\left[\left.\begin{array}{c}(1,1)\\ \left(1,2\alpha \right)\end{array}\right|\lambda x^{2\alpha }\right]=a_0{E}_{2\alpha ,1}\left(\lambda x^{2\alpha }\right),$$

which coincides with (5) if $l=1$ and $2\alpha$ is taken instead of α.

Example 2.

Consider the case presented in Theorem 6 when $\alpha =1$, $b_0=1$, $\lambda =-1$. In this case $m=2$, $2k=0$, and $2k+1=1$, which means $k=0$ and using (53) we obtain that the solution to the problem

$$B_{\gamma }f\left(x\right)=-f\left(x\right),\lambda \in \mathbb{R},$$

$$f(0+)=1,f^{\prime }(0+)=0$$

is

$$f\left(x\right)=\frac{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{\sqrt{\pi }}{}_2{\mathsf{\Psi }}_2\left[\left.\begin{array}{c}\left(1+\frac{\gamma }{2},1\right),(1,1)\\ \left(1,1\right),\left(\gamma +1,2\right)\end{array}\right|-x^2\right]=\frac{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{\sqrt{\pi }}{}_2{\mathsf{\Psi }}_2\left[\left.\begin{array}{c}\left(1+\frac{\gamma }{2},1\right)\\ \left(\gamma +1,2\right)\end{array}\right|-x^2\right]$$

$$=\frac{2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{\sqrt{\pi }}\sum _{m=0}^{\infty }\frac{{(-1)}^m\mathsf{\Gamma }\left(1+\frac{\gamma }{2}+m\right)}{\mathsf{\Gamma }\left(\gamma +1+2m\right)}\frac{x^{2m}}{m!}.$$

Using the Legendre duplication formula

$$\mathsf{\Gamma }\left(2z\right)=\frac{2^{2z-1}}{\sqrt{\pi }}\mathsf{\Gamma }\left(z\right)\mathsf{\Gamma }\left(z+\frac{1}{2}\right)$$

we obtain

$$f\left(x\right)=2^{\gamma }\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)\sum _{m=0}^{\infty }\frac{{(-1)}^m\mathsf{\Gamma }\left(1+\frac{\gamma }{2}+m\right)}{2^{\gamma +2m}\mathsf{\Gamma }\left(1+\frac{\gamma }{2}+m\right)\mathsf{\Gamma }\left(\frac{\gamma +1}{2}+m\right)}\frac{x^{2m}}{m!}$$

$$=\frac{2^{\frac{\gamma -1}{2}}\mathsf{\Gamma }\left(\frac{\gamma +1}{2}\right)}{x^{\frac{\gamma -1}{2}}}\sum _{m=0}^{\infty }\frac{{(-1)}^m}{\mathsf{\Gamma }\left(\frac{\gamma +1}{2}+m\right)}\frac{1}{m!}{\left(\frac{x}{2}\right)}^{2m+\frac{\gamma -1}{2}}=j_{\frac{\gamma -1}{2}}\left(x\right),$$

(55)

where

$$j_{\nu }\left(x\right)=\frac{2^{\nu }\mathsf{\Gamma }(\nu +1)}{x^{\nu }}{J}_{\nu }\left(x\right).$$

For $j_{\frac{\gamma -1}{2}}\left(x\right)$ we have

$$B_{\gamma }{j}_{\frac{\gamma -1}{2}}\left(\tau x\right)=-{\tau }^2{j}_{\frac{\gamma -1}{2}}\left(\tau x\right).$$

Therefore the function

$${}_2{\mathsf{\Psi }}_2\left[\left.\begin{array}{c}\left(1+\frac{\gamma }{2},\alpha \right),(1,1)\\ \left(1,\alpha \right),\left(\gamma +1,2\alpha \right)\end{array}\right|\lambda x^{2\alpha }\right]$$

can be considered as a generalization of $j_{\frac{\gamma -1}{2}}$.

5. Conclusions

In this paper, a new approach is proposed in order to solve ordinary differential equations with left-sided fractional Bessel derivatives on semi-axes of Gerasimov–Caputo type based on the Meijer integral transform method. We also presented some illustrative examples.