On the Necessary Conditions for Non-Equivalent Solutions of the Rotlet-Induced Stokes Flow in a Sphere: Towards a Minimal Model for Fluid Flow in the Kupffer’s Vesicle
Abstract
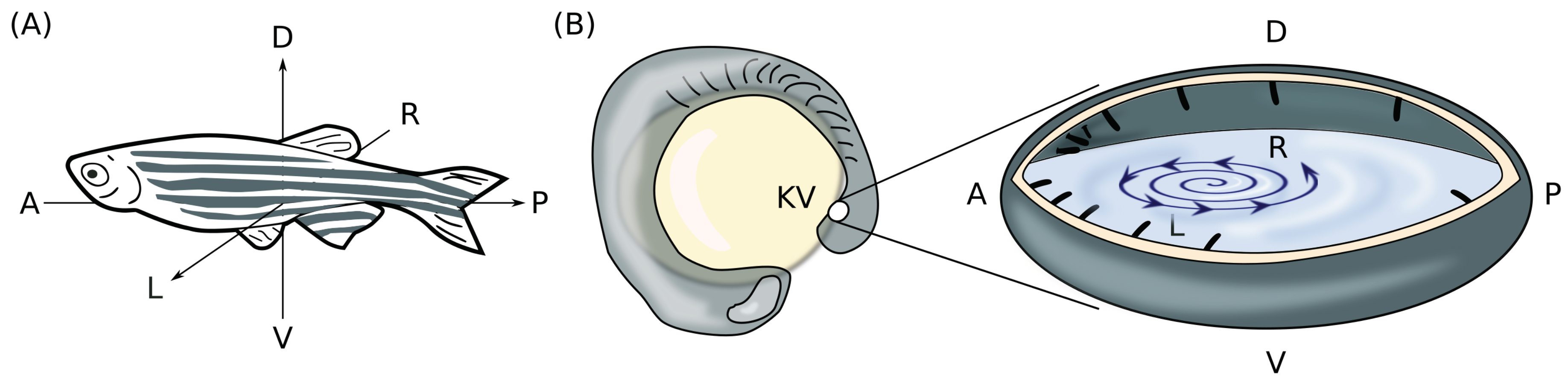
:1. Introduction
2. Results
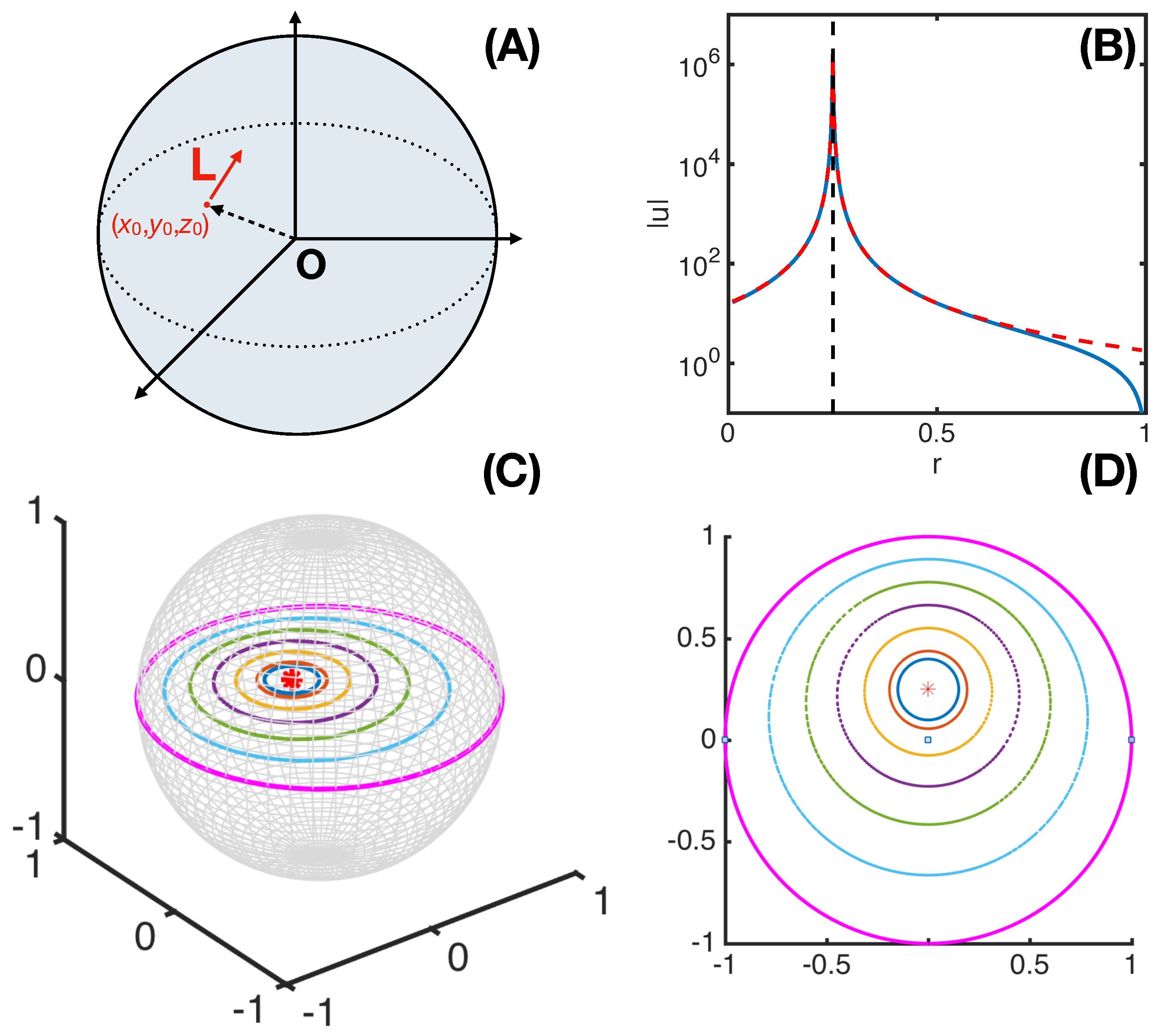
2.1. Definition of the Problem and Preliminaries
2.2. Necessary Conditions of a Three-Dimensional Rotlet with Spherically-Symmetric Boundary Conditions
2.3. On Some General Conditions
2.4. On Some Restricted Conditions
- If the condition in Equation (14) is met, we have
3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gilbert, S.F. Developmental Biology, 6th ed.; Sinauer Associates: Sunderland, MA, USA, 2000. [Google Scholar]
- Beddington, R.S.P.; Robertson, E.J. Axis development and early asymmetry in mammals. Cell 1999, 96, 195–209. [Google Scholar] [CrossRef] [Green Version]
- Hirokawa, N.; Okada, Y.; Tanaka, Y. Fluid dynamic mechanism responsible for breaking the left–right symmetry of the human body: the nodal flow. Annu. Rev. Fluid Mech. 2009, 41, 53–72. [Google Scholar] [CrossRef]
- Kartagener, M. Zur Pathogenese der Bronchiektasien. Lung 1933, 84, 73–85. [Google Scholar]
- Afzelius, B.A. A human syndrome caused by immotile cilia. Science 1976, 193, 317–319. [Google Scholar] [CrossRef]
- Nonaka, S.; Shiratori, H.; Saijoh, Y.; Hamada, H. Determination of left–right patterning of the mouse embryo by artificial nodal flow. Nature 2002, 418, 96–99. [Google Scholar] [CrossRef]
- Cartwright, J.H.E.; Piro, O.; Tuval, I. Fluid-dynamical basis of the embryonic development of left–right asymmetry in vertebrates. Proc. Natl. Acad. Sci. USA 2004, 101, 7234–7239. [Google Scholar] [CrossRef] [Green Version]
- McGrath, J.; Somlo, S.; Makova, S.; Tian, X.; Brueckner, M. Two populations of node monocilia initiate left–right asymmetry in the mouse. Cell 2003, 114, 61–73. [Google Scholar] [CrossRef] [Green Version]
- Nonaka, S.; Tanaka, Y.; Okada, Y.; Takeda, S.; Harada, A.; Kanai, Y.; Kido, M.; Hirokawa, N. Randomization of left–right asymmetry due to loss of nodal cilia generating leftward flow of extraembryonic fluid in mice lacking KIF3B motor protein. Cell 1998, 95, 829–837. [Google Scholar] [CrossRef] [Green Version]
- Okada, Y.; Takeda, S.; Tanaka, Y.; Belmonte, J.C.I.; Hirokawa, N. Mechanism of nodal flow: A conserved symmetry breaking event in left–right axis determination. Cell 2005, 121, 633–644. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nonaka, S.; Yoshiba, S.; Watanabe, D.; Ikeuchi, S.; Goto, T.; Marshall, W.F.; Hamada, H. De novo formation of left–right asymmetry by posterior tilt of nodal cilia. PLoS Biol. 2005, 3, 1467–1472. [Google Scholar] [CrossRef] [PubMed]
- Cartwright, J.H.E.; Piro, N.; Piro, O.; Tuval, I. Embryonic nodal flow and the dynamics of nodal vesicular parcels. J. R. Soc. Interface 2007, 4, 49–55. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kramer-Zucker, A.G.; Olale, F.; Haycraft, C.J.; Yoder, B.K.; Schier, A.F.; Drummond, I.A. Cilia-driven fluid flow in the zebrafish pronephros, brain and Kupffer’s vesicle is required for normal organogenesis. Development 2005, 132, 1907–1921. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Supatto, W.; Vermot, J. From cilia hydrodynamics to zebrafish embryonic development. Curr. Top. Dev. Biol. 2011, 95. [Google Scholar] [CrossRef]
- Smith, A.A.; Johnson, T.D.; Smith, D.J.; Blake, J.R. Symmetry breaking cilia-driven flow in the zebrafish embryo. J. Fluid Mech. 2012, 705, 26–45. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, R.R.; Vilfan, A.; Jülicher, F.; Supatto, W.; Vermot, J. Physical limits of flow sensing in the left–right organizer. eLife 2017, 6, e25078. [Google Scholar] [CrossRef] [Green Version]
- Supatto, W.; Fraser, S.E.; Vermot, J. An all-optical approach for probing microscopic flows in living embryos. Biophys. J. 2008, 95, 29–31. [Google Scholar] [CrossRef] [Green Version]
- Sampaio, P.; Ferreira, R.R.; Guerrero, A.; Pintado, P.; Tavares, B.; Amaro, J.; Smith, A.A.; Montenegro-Johnson, T.D.; Smith, D.J.; Lopes, S.S. Left-right organizer flow dynamics: How much cilia activity reliably yields laterality? Dev Cell. 2014, 29, 716–728. [Google Scholar] [CrossRef] [Green Version]
- Montenegro-Johnson, T.D.; Baker, D.I.; Smith, D.J.; Lopes, S.S. Three-dimensional flow in Kupffer’s Vesicle. J. Math. Biol. 2016, 73, 705–725. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Karilla, S.J. (Eds.) Microhydrodynamics: Principles and Selected Applications; Dover Publications: Mineola, NY, USA, 2005. [Google Scholar]
- Pozrikidis, C. (Ed.) Boundary Integral and Singularity Methods for Linearized Viscous Flow; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Lorentz, H.A. A general theorem concerning the motion of a viscous fluid and a few consequences derived from it. Versl. Kon. Akad. Wet. Amst. 1897, 5, 168–175. [Google Scholar]
- Oseen, C.W. Neuere Methoden und Ergebnisse in der Hydrodynamik. Leipzig Akad. Verlagsgesellschaft 1927. [Google Scholar] [CrossRef]
- Burgers, J.M. On the motion of small particles of elongated form suspended in a viscous liquid. Chap. I11 of Second Report on Viscosity and Plasticity. Kon. Ned. Akad. Wet. Verhand. 1897, 16, 113–184. [Google Scholar]
- Batchelor, G.K. The stress system in a suspension of force-free particles. J. Fluid Mech. 1970, 41, 545–570. [Google Scholar] [CrossRef] [Green Version]
- Hancock, G.J. The self-propulsion of microscopic organisms through Iiquids. Proc. R. Soc. A 1953, 217, 96–121. [Google Scholar]
- Broersma, S. Viscous force constant for a dosed cylinder. J. Chem. Phys. 1960, 32, 1632–1635. [Google Scholar] [CrossRef]
- Tuck, E.O. Some methods for flows past blunt slender bodies. J. Fluid Mech. 1964, 18, 619–635. [Google Scholar] [CrossRef]
- Tuck, E.O. Toward the calculation and minimization of Stokes drag on bodies of arbitrary shape. In Proceedings of the 3rd Australasian Conference on Hydraulics and Fluid Mechanics, Sydney, Australia, 25–29 November 1968; p. 2S32. [Google Scholar]
- Taylor, G.I. Motion of axisymmetric bodies in viscous fluids. In Problems of Hydrodynamics and Continuum Mechanics; SIAM Publications: Philadelphia, PA, USA, 1969; pp. 718–724. [Google Scholar]
- Batchelor, G.K. Slender-body theory for particles of arbitrary cross-section in Stokes flow. J. Fluid Mech. 1970, 44, 419–440. [Google Scholar] [CrossRef]
- Tillett, J.P.K. Axial and transverse Stokes flow past slender axisymmetric bodies. J. Fluid Mech. 1970, 44, 401–417. [Google Scholar] [CrossRef]
- Cox, R.G. The motion of long slender bodies in a viscous fluid. Part 1. General theory. J. Fluid Mech. 1970, 44, 791–810. [Google Scholar] [CrossRef]
- Cox, R.G. The motion of long slender bodies in a viscous fluid. Part 2. Shear flow. J. Fluid Mech. 1971, 45, 625–657. [Google Scholar] [CrossRef]
- Blake, J.R.; Chwang, A.T. Fundamental singularities of viscous flow. Part I. The image system in the vicinity of a stationary no-slip boundary. J. Eng. Math. 1974, 8, 23–29. [Google Scholar] [CrossRef]
- Hackborn, W.; O’Neill, M.E.; Ranger, K.B. The structure of an asymmetric Stokes flow. Q. J. Mech. Appl. Math. 1986, 39, 1–14. [Google Scholar] [CrossRef]
- Ranger, K.B. The Stokes drag for asymmetric flow past a spherical cap. J. Appl. Math. Phys. 1973, 24, 801–809. [Google Scholar] [CrossRef]
- Purcell, E.M. Life at low Reynolds number. Am. J. Phys. 1977, 45, 3–11. [Google Scholar] [CrossRef] [Green Version]
- Blake, J.R.; Otto, S.R. Filter Feeding, Chaotic Filtration, and a Blinking Stokeslet. Theor. Comput. Fluid Dyn. 1998, 10, 23–36. [Google Scholar] [CrossRef]
- Cartwright, J.H.E.; Piro, O.; Tuval, I. Fluid dynamics in developmental biology: Moving fluids that shape ontogeny. HFSP J. 2009, 3, 77–93. [Google Scholar] [CrossRef] [Green Version]
- Boutin, C.; Labedan, P.; Dimidschstein, J.; Richard, F.; Cremer, H.; Andre, P.; Yang, Y.; Montcouquiol, M.; Goffinet, A.M.; Tissir, F. A dual role for planar cell polarity genes in ciliated cells. Proc. Natl. Acad. Sci. USA 2014, 111, E3129–E3138. [Google Scholar] [CrossRef] [Green Version]
- Woodhouse, F.G.; Goldstein, R.E. Cytoplasmic streaming in plant cells emerges naturally by microfilament self-organization. Proc. Natl. Acad. Sci. USA 2013, 110, 14132–14137. [Google Scholar] [CrossRef] [Green Version]
- Dumortier, J.G.; Le Verge-Serandour, M.; Tortorelli, A.F.; Mielke, A.; de Plater, L.; Turlier, H.; Maitre, J.L. Hydraulic fracturing and active coarsening position the lumen of the mouse blastocyst. Science 2019, 365, 465–468. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández-Pereira, Y.; Guerrero, A.O.; Rendón-Mancha, J.M.; Tuval, I. On the Necessary Conditions for Non-Equivalent Solutions of the Rotlet-Induced Stokes Flow in a Sphere: Towards a Minimal Model for Fluid Flow in the Kupffer’s Vesicle. Mathematics 2020, 8, 1. https://doi.org/10.3390/math8010001
Hernández-Pereira Y, Guerrero AO, Rendón-Mancha JM, Tuval I. On the Necessary Conditions for Non-Equivalent Solutions of the Rotlet-Induced Stokes Flow in a Sphere: Towards a Minimal Model for Fluid Flow in the Kupffer’s Vesicle. Mathematics. 2020; 8(1):1. https://doi.org/10.3390/math8010001
Chicago/Turabian StyleHernández-Pereira, Yunay, Adán O. Guerrero, Juan Manuel Rendón-Mancha, and Idan Tuval. 2020. "On the Necessary Conditions for Non-Equivalent Solutions of the Rotlet-Induced Stokes Flow in a Sphere: Towards a Minimal Model for Fluid Flow in the Kupffer’s Vesicle" Mathematics 8, no. 1: 1. https://doi.org/10.3390/math8010001
APA StyleHernández-Pereira, Y., Guerrero, A. O., Rendón-Mancha, J. M., & Tuval, I. (2020). On the Necessary Conditions for Non-Equivalent Solutions of the Rotlet-Induced Stokes Flow in a Sphere: Towards a Minimal Model for Fluid Flow in the Kupffer’s Vesicle. Mathematics, 8(1), 1. https://doi.org/10.3390/math8010001





