Applications of Game Theory in Project Management: A Structured Review and Analysis
Abstract
1. Introduction
- We follow a comprehensive and principled method for searching and filtering relevant papers.
- We review papers across several disciplines, such as construction, ICT and education, and highlight the similarities and differences between them in their application of game theory in project management.
- We present a detailed multidimensional classification of the papers that we have reviewed.
- We present and analyse the citation network of the papers we have reviewed, highlighting their interdependency and relative impact.
- We identify gaps in the literature that point to potentially fruitful future research directions.
2. Background
2.1. Project Management
2.2. Game Theory
2.2.1. Non-Cooperative Games and Cooperative Games
2.2.2. Nash Equilibrium
2.2.3. Zero-Sum Games
2.2.4. Common Interest Games
2.2.5. Normal-Form Games and Extensive-Form Games
2.2.6. Simultaneous Games and Sequential Games
2.2.7. Subgames
2.2.8. Subgame Perfect Nash Equilibrium
2.2.9. Stackelberg Games
2.2.10. Nash Bargaining
2.2.11. Evolutionary Game Theory
- : By unilaterally changing strategy to , the player will lose out against another player who sticks with the ESS .
- & : a player, by converting to , neither gains nor loses against another player who sticks with the ESS , but playing against a player who has already “converted” to , a player is better off playing the ESS .
3. Selection Methodology
- Scopus database was searched for a number of key phrases, as elaborated below, and all papers deemed relevant in this search were downloaded. A total of 776 papers were downloaded and considered in this manner.
- A brief manual screening was conducted considering the title and abstract of the papers, selecting some papers for detailed inspection. A total of 72 papers remained at the end of this stage.
- After detailed reading of each paper, some papers were excluded from our review and classification, as described below. A total of 25 papers remained at the end of this stage.
- The reference list of each remaining paper was considered, and checked against the list of papers already excluded. If a paper was not already excluded or not in Scopus, then it went through steps 2 and 3 of the screening process, and included in our review and classification if selected. At the end of this step, 32 papers were selected for inclusion in this review.
3.1. Step 1
- ( “game theo*”) and (“project management” or “construction management” or “*contract”)
- (“decision”) and (“project management” or “construction management” or “*contract”)
- (“games”) and (“project management” or “construction management” or “*contract”)
3.2. Step 2
- Title: those papers having titles where the keywords have been used in a different context were omitted. For example, if the word “game” was used in the sense of video game, computer game or other simulated game, those papers were omitted. Similarly, papers with titles where the word “contract” was used in a context not related to project management were omitted.
- Abstract: Those papers which had abstracts that made it clear that the paper deals with ongoing operational issues, and not project management issues, were omitted.
- English language: only records written in English were further considered. Records nominally written in English where the quality of the narrative was so poor as to not make sense to a reasonable native English speaker, were also excluded. Papers which had their title and/or abstract in English, but the body of the paper in another language, were also excluded.
- Availability: Papers which were not publicly available (either freely, or for a fee) were excluded. Note, papers that were publicly available for a fee were not excluded. Only those papers which did not have the full content publicly available freely or for a fee were excluded.
- In cases where two very similar papers by the same authors were found, where one paper is an extension of the other but included all content of the previous paper, only the later (and thus the more ‘matured’) paper was considered. For example, if a conference publication was later developed into a journal paper by the inclusion of additional material, the conference paper was excluded and only the journal paper was considered.
3.3. Step 3
3.4. Step 4
4. Classification of the Selected Papers
- Classification based on the application domain
- Classification based on the players of the game
- Classification based on the type of game played
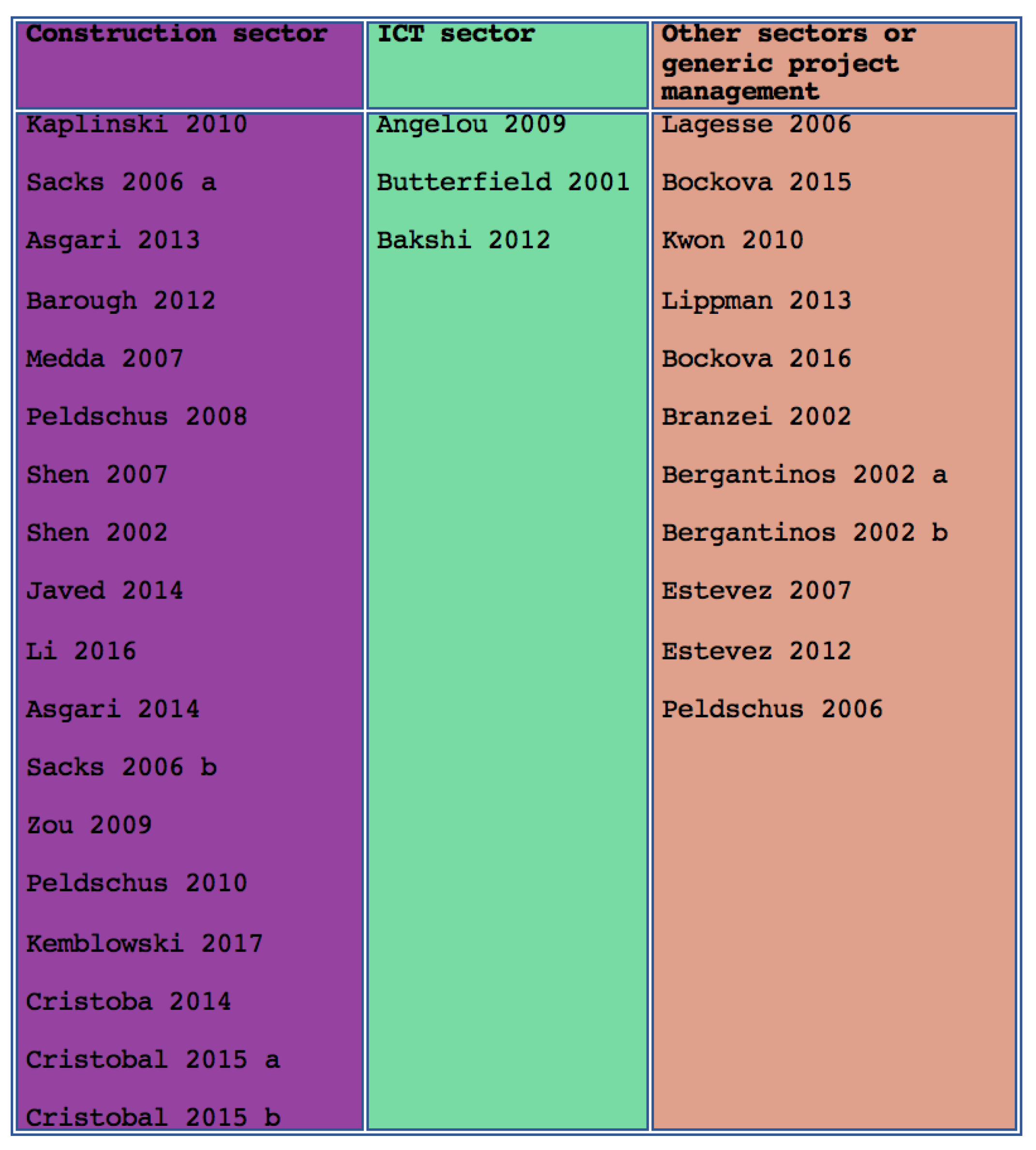
4.1. Classification Based on the Application Domain
- Papers focusing on project management in construction projects
- Papers focusing on project management in ICT (Information and Communications Technology) projects
- Papers focusing on project management in other fields or generic project management
4.2. Classification Based on Players of the Games
- Papers focusing on contractor—contractor games (including investment decision games)
- Papers focusing on contractor—subcontractor games
- Papers focusing on contractor—government games (sometimes called Public–Private Partnerships, where the phrase ‘public’ represents the government and ‘private’ represents the private company which is the contractor)
- Papers focusing on subcontractor—subcontractor games
- Papers focusing on games with other player combinations
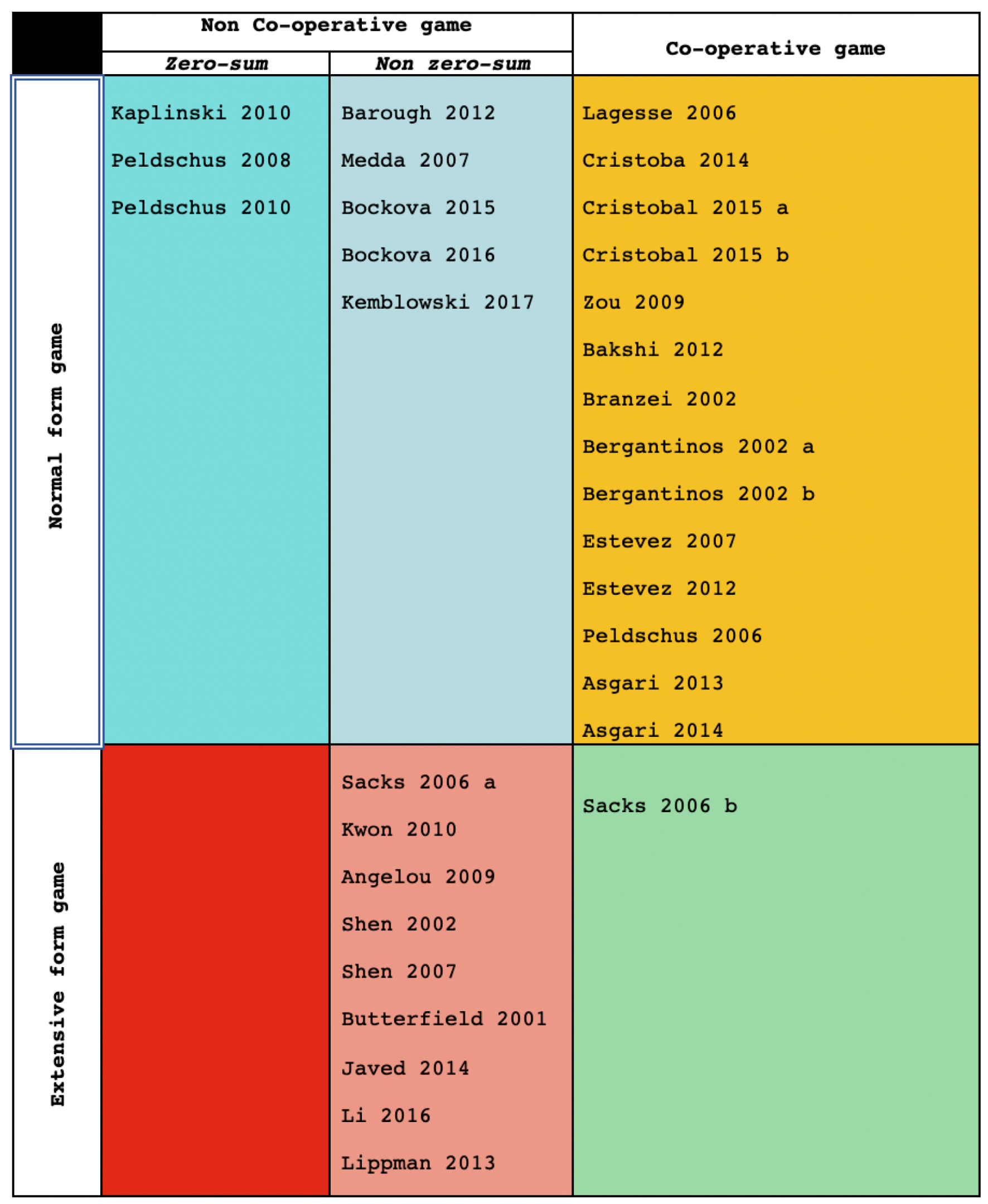
4.3. Classification Based on the type of Game Played
5. Description of the Papers Reviewed
5.1. Papers Using Normal-Form Games
5.1.1. Papers Using Normal-Form Non-Cooperative Games
5.1.2. Papers Using Normal-form Cooperative Games
5.2. Papers Using Extensive-Form Games
5.2.1. Papers Using eXtensive-Form Non-Cooperative Games
5.2.2. Papers Using Extensive-Form Cooperative Games
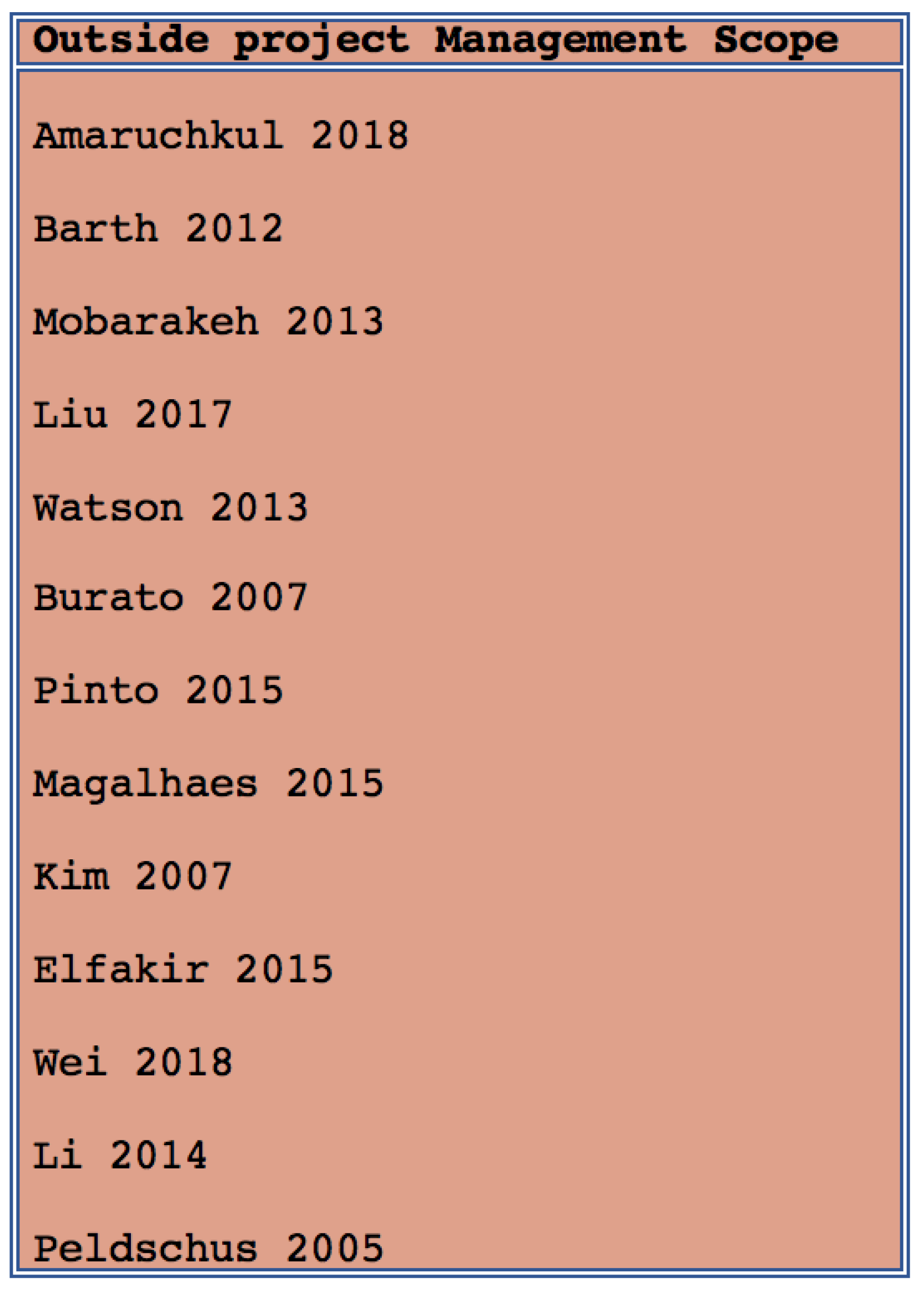
5.3. Papers Relevant to Project Management but not Explicitly Set in Project Management Context
5.4. Gaps in Literature
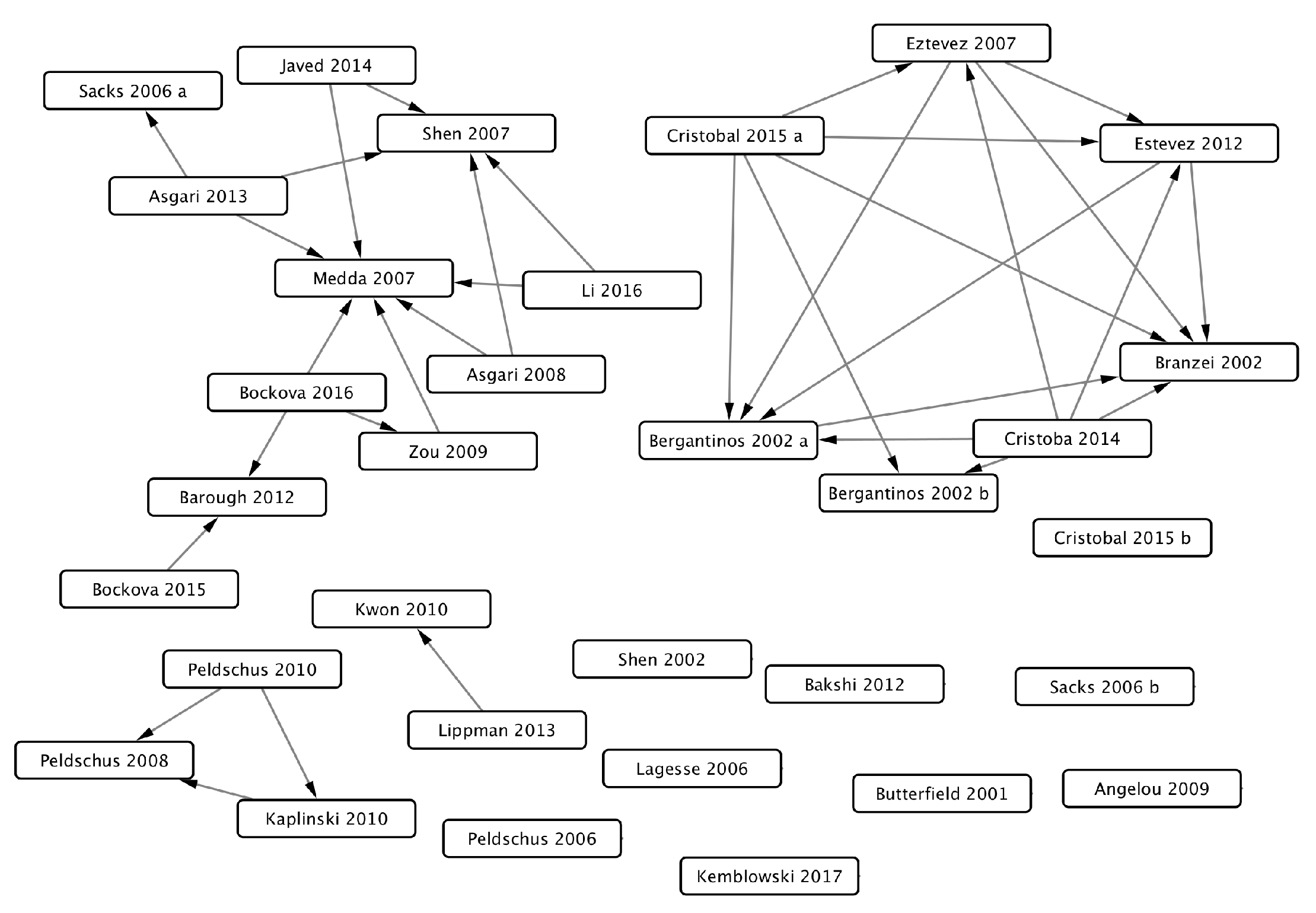
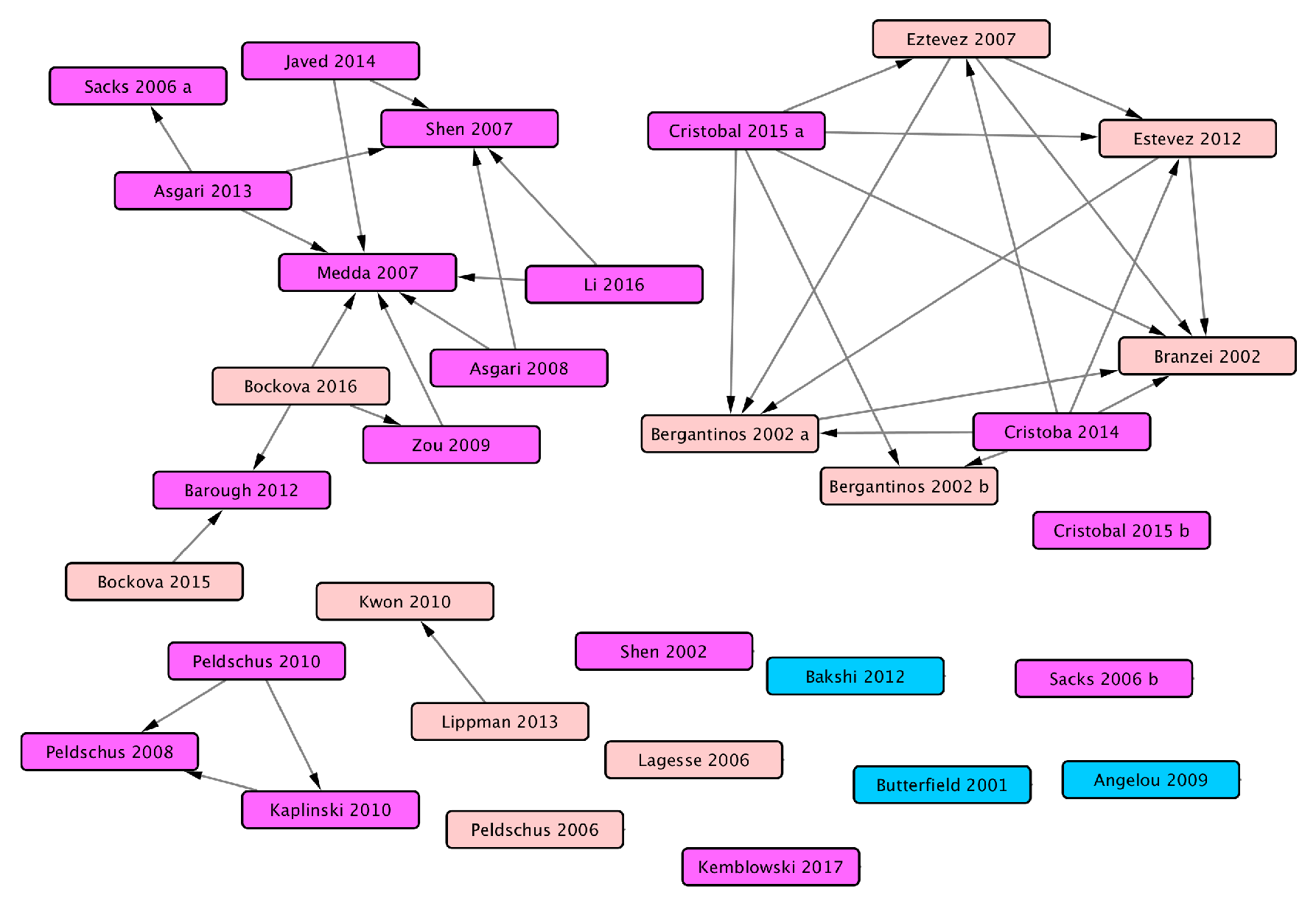
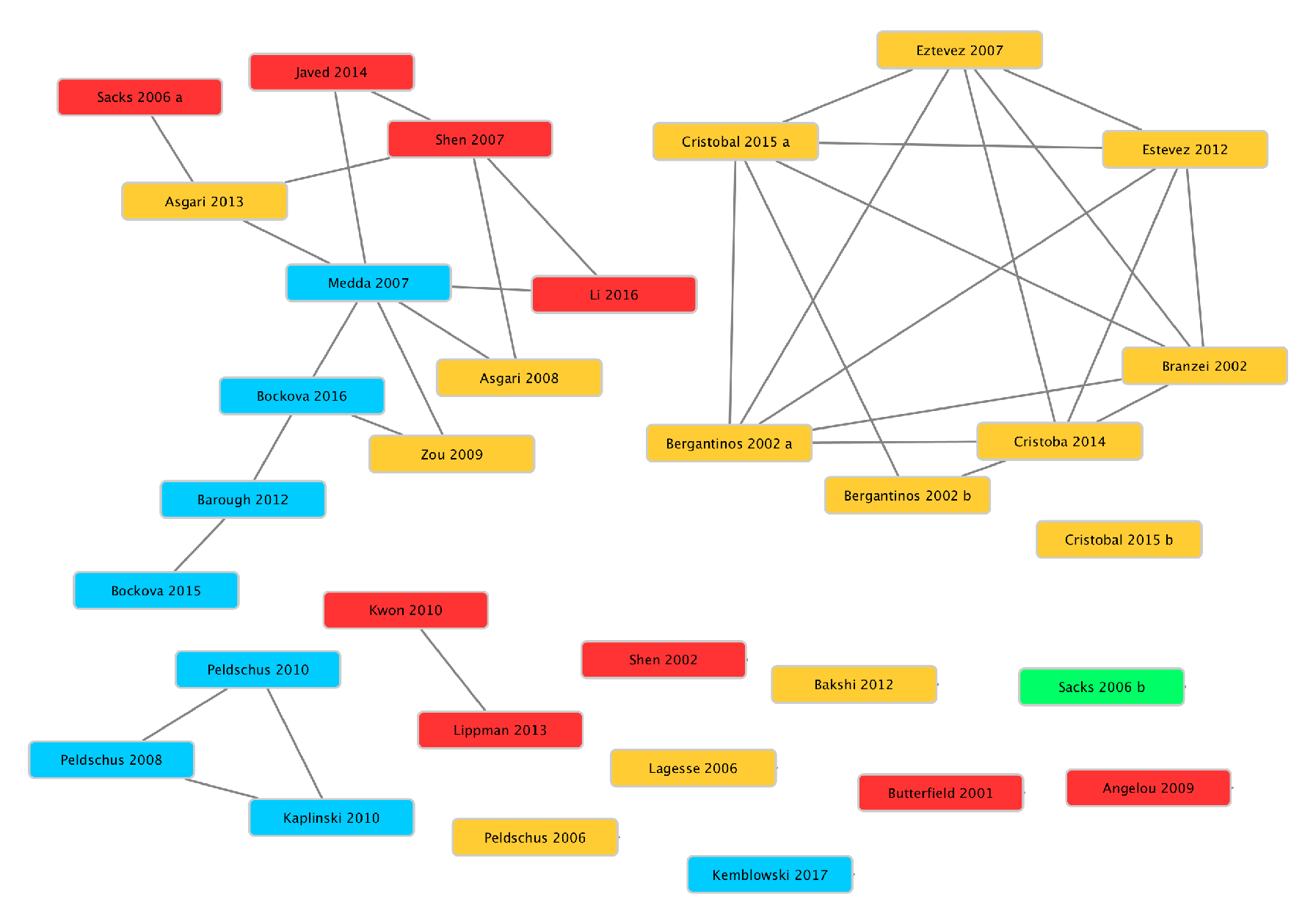
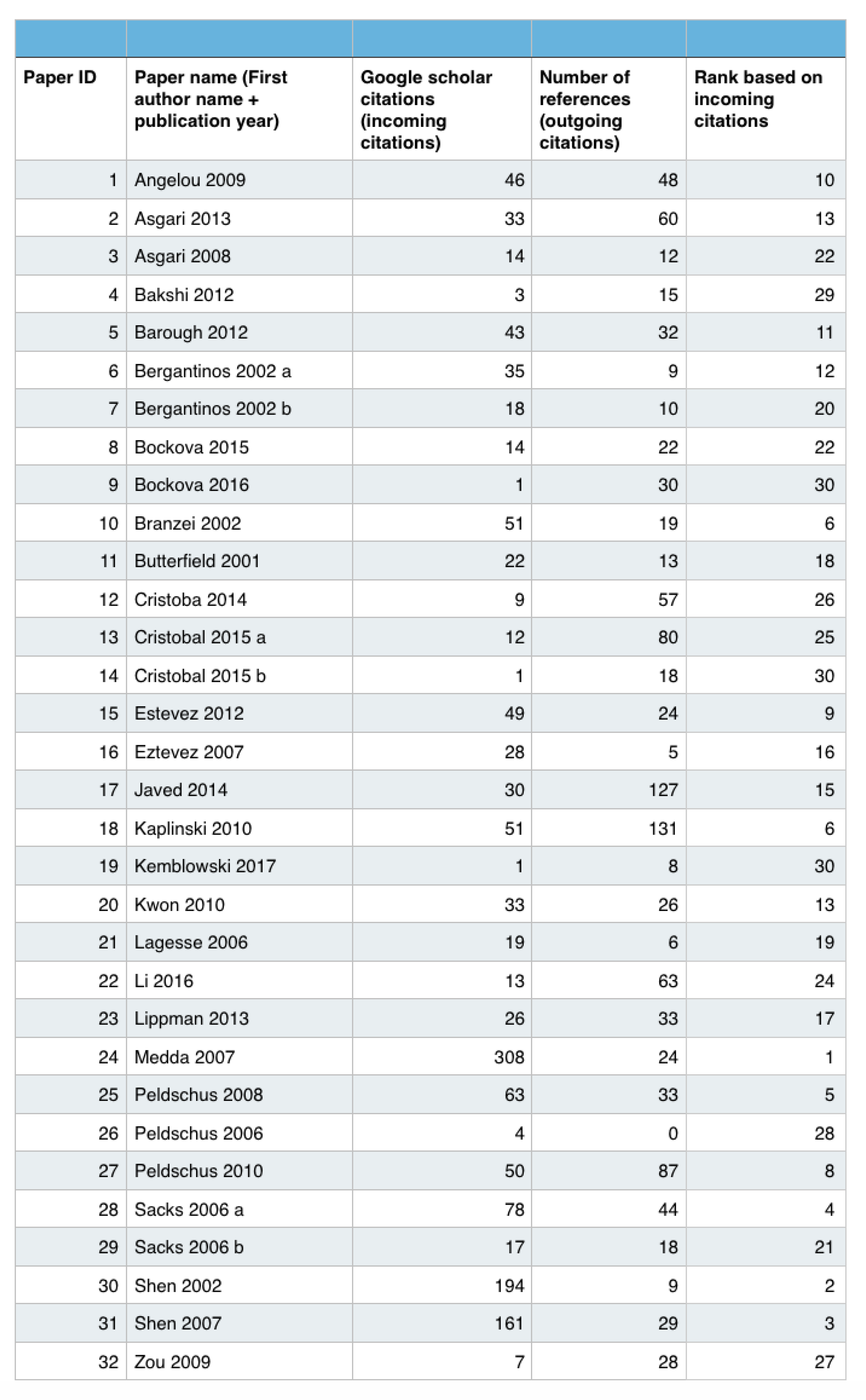
6. Citation Network of Reviewed Papers
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- A Guide to the Project Management Body of Knowledge (PMBoK Guide), 5th ed.; Project Management Institute: Pennsylvania, PA, USA, 2013.
- Rose, K.H. A Guide to the Project Management Body of Knowledge (PMBOK® Guide) Fifth Edition. Proj. Manag. J. 2013, 44, e1. [Google Scholar] [CrossRef]
- A Guide to the Project Management Body of Knowledge (PMBoK® Guide), 2000 ed.; Project Management Institute: Pennsylvania, PA, USA, 2001.
- Williams, T.M. Managing and Modelling Complex Projects; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Williams, T. The contribution of mathematical modelling to the practice of project management. IMA J. Manag. Math. 2003, 14, 3–30. [Google Scholar] [CrossRef]
- Osborne, M.J. An Introduction to Game Theory; Oxford University Press: New York, NY, USA, 2004. [Google Scholar]
- Von Neumann, J.; Morgenstern, O. Game Theory and Economic Behavior; Joh Wiley and Sons: New York, NY, USA, 1944. [Google Scholar]
- Kasthurirathna, D.; Piraveenan, M.; Harré, M. Influence of topology in the evolution of coordination in complex networks under information diffusion constraints. Eur. Phys. J. B 2014, 87, 3. [Google Scholar] [CrossRef]
- Kasthurirathna, D.; Piraveenan, M. Topological stability of evolutionarily unstable strategies. In Proceedings of the 2014 IEEE Symposium on Evolving and Autonomous Learning Systems (EALS), Orlando, FL, USA, 9–12 December 2014; pp. 35–42. [Google Scholar]
- Kasthurirathna, D.; Nguyen, H.; Piraveenan, M.; Uddin, S.; Senanayake, U. Optimisation of strategy placements for public good in complex networks. In Proceedings of the 2014 International Conference on Social Computing, Beijing, China, 4–7 August 2014; ACM: New York, NY, USA, 2014; p. 1. [Google Scholar]
- Kasthurirathna, D.; Harre, M.; Piraveenan, M. Optimising influence in social networks using bounded rationality models. Soc. Netw. Anal. Min. 2016, 6, 54. [Google Scholar] [CrossRef]
- Peldschus, F. Experience of the game theory application in construction management. Technol. Econ. Dev. Econ. 2008, 14, 531–545. [Google Scholar] [CrossRef]
- San Cristóbal, J.R. Management Science methods and methodologies for Project Management: What they model, how they model and why they model. Pmworldlibrary Net Viewed 2015, 15, 2017. [Google Scholar]
- Bilton, C.; Cummings, S. Handbook of Management and Creativity; Edward Elgar Publishing: Cheltenham, UK, 2014. [Google Scholar]
- Bočková, K.H.; Sláviková, G.; Gabrhel, J. Game Theory as a Tool of Project Management. Procedia Soc. Behav. Sci. 2015, 213, 709–715. [Google Scholar] [CrossRef]
- Kapliński, O.; Tamošaitiene, J. Game theory applications in construction engineering and management. Ukio Technol. Ekon. Vystym. 2010, 16, 348–363. [Google Scholar] [CrossRef]
- Dvir, D.; Sadeh, A.; Malach-Pines, A. Projects and project managers: The relationship between project managers’ personality, project types, and project success. Proj. Manag. J. 2006, 37, 36–48. [Google Scholar] [CrossRef]
- Cleland, D.I. The evolution of project management. IEEE Trans. Eng. Manag. 2004, 51, 396–397. [Google Scholar] [CrossRef]
- Seymour, T.; Hussein, S. The history of project management. Int. J. Manag. Inf. Syst. (Online) 2014, 18, 233. [Google Scholar] [CrossRef]
- Barough, A.S.; Shoubi, M.V.; Skardi, M.J.E. Application of Game Theory Approach in Solving the Construction Project Conflicts. Proced. Soc. Behav. Sci. 2012, 58, 1586–1593. [Google Scholar] [CrossRef]
- Rasmusen, E.; Blackwell, B. Games and Information: An Introduction to Game Theory; Blackwell Publishing: Cambridge, MA, USA, 1994; Volume 2. [Google Scholar]
- Kasthurirathna, D.; Piraveenan, M. Emergence of scale-free characteristics in socio-ecological systems with bounded rationality. Sci. Rep. 2015, 5, 10448. [Google Scholar] [CrossRef] [PubMed]
- Kasthurirathna, D.; Piraveenan, M.; Harre, M. Evolution of coordination in scale-free and small world networks under information diffusion constraints. In Proceedings of the 2013 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM 2013), Niagara Falls, ON, Canada, 25–28 August 2013; pp. 183–189. [Google Scholar]
- Thedchanamoorthy, G.; Piraveenan, M.; Uddin, S.; Senanayake, U. Influence of vaccination strategies and topology on the herd immunity of complex networks. Soc. Netw. Anal. Min. 2014, 4, 213. [Google Scholar] [CrossRef]
- Perc, M.; Jordan, J.J.; Rand, D.G.; Wang, Z.; Boccaletti, S.; Szolnoki, A. Statistical physics of human cooperation. Phys. Rep. 2017, 687, 1–51. [Google Scholar] [CrossRef]
- Bendor, J.; Swistak, P. Types of evolutionary stability and the problem of cooperation. Proc. Natl. Acad. Sci. USA 1995, 92, 3596–3600. [Google Scholar] [CrossRef] [PubMed]
- Perc, M. Phase transitions in models of human cooperation. Phys. Lett. A 2016, 380, 2803–2808. [Google Scholar] [CrossRef]
- Chen, X.; Perc, M. Optimal distribution of incentives for public cooperation in heterogeneous interaction environments. Front. Behav. Neurosci. 2014, 8, 248. [Google Scholar] [CrossRef] [PubMed]
- Capraro, V.; Perc, M.; Vilone, D. The evolution of lying in well-mixed populations. J. R. Soc. Interface 2019, 16, 20190211. [Google Scholar] [CrossRef] [PubMed]
- Helbing, D.; Brockmann, D.; Chadefaux, T.; Donnay, K.; Blanke, U.; Woolley-Meza, O.; Moussaid, M.; Johansson, A.; Krause, J.; Schutte, S.; et al. Saving human lives: What complexity science and information systems can contribute. J. Stat. Phys. 2015, 158, 735–781. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Bauch, C.T.; Bhattacharyya, S.; d’Onofrio, A.; Manfredi, P.; Perc, M.; Perra, N.; Salathe, M.; Zhao, D. Statistical physics of vaccination. Phys. Rep. 2016, 664, 1–113. [Google Scholar] [CrossRef]
- Chang, S.L.; Piraveenan, M.; Pattison, P.; Prokopenko, M. Game theoretic modelling of infectious disease dynamics and intervention methods: a mini-review. arXiv 2019, arXiv:1901.04143. [Google Scholar]
- Chang, S.L.; Piraveenan, M.; Prokopenko, M. The effects of imitation dynamics on vaccination behaviors in SIR-network model. arXiv, 2019; arXiv:1905.00734. [Google Scholar]
- Branzei, R.; Dimitrov, D.; Tijs, S. Models in Cooperative Game Theory; Springer Science & Business Media: Berlin, Germany, 2008; Volume 556. [Google Scholar]
- Brandenburger, A. Cooperative Game Theory: Characteristic Functions, Allocations, Marginal Contribution; Stern School of Business, New York University: New York, NY, USA, 2007; Volume 1, pp. 1–6. [Google Scholar]
- Bell, M.; Perera, S.; Piraveenan, M.; Bliemer, M.; Latty, T.; Reid, C. Network growth models: A behavioural basis for attachment proportional to fitness. Sci. Rep. 2017, 7, 42431. [Google Scholar] [CrossRef] [PubMed]
- Nash, J.F. Equilibrium points in n-person games. Proc. Natl. Acad. Sci. USA 1950, 36, 48–49. [Google Scholar] [CrossRef] [PubMed]
- Kasthurirathna, D.; Piraveenan, M.; Uddin, S. Evolutionary stable strategies in networked games: The influence of topology. J. Artif. Intell. Soft Comput. Res. 2015, 5, 83–95. [Google Scholar] [CrossRef][Green Version]
- Kuhn, H.; Arrow, K.; Tucker, A. Contributions to the Theory of Games; Number v. 2 in Annals of Mathematics Studies; Princeton University Press: Princeton, NJ, USA, 1953. [Google Scholar]
- Calcagno, R.; Kamada, Y.; Lovo, S.; Sugaya, T. Asynchronicity and coordination in common and opposing interest games. Theor. Econ. 2014, 9, 409–434. [Google Scholar] [CrossRef][Green Version]
- Schelling, T.C. The strategy of conflict. Prospectus for a reorientation of game theory. J. Confl. Resolut. 1958, 2, 203–264. [Google Scholar] [CrossRef]
- Schelling, T.C. The Strategy of Conflict; Harvard University Press: Cambridge, MA, USA, 1980. [Google Scholar]
- Lewis, D. Convention: A Philosophical Study; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Binmore, K. Playing for Real: A Text on Game Theory; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Hart, S. Games in extensive and strategic forms. In Handbook of Game Theory with Economic Applications; North Holland Publishing Company: Amsterdam, The Netherlands, 1992; Volume 1, pp. 19–40. [Google Scholar]
- Von Stackelberg, H. Market Structure and Equilibrium; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Nash, J.F., Jr. The bargaining problem. Econom. J. Econom. Soc. 1950, 18, 155–162. [Google Scholar] [CrossRef]
- Rubinstein, A. Perfect equilibrium in a bargaining model. Econom. J. Econom. Soc. 1982, 50, 97–109. [Google Scholar] [CrossRef]
- Smith, J.M. Evolution and the Theory of Games; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Newton, J. Evolutionary game theory: A renaissance. Games 2018, 9, 31. [Google Scholar] [CrossRef]
- Le, S.; Boyd, R. Evolutionary dynamics of the continuous iterated Prisoner’s dilemma. J. Theor. Biol. 2007, 245, 258–267. [Google Scholar] [CrossRef] [PubMed]
- Elsivier Scopus Database. Available online: www.scopus.com (accessed on 4 April 2019).
- Amaruchkul, K. Game-theoretic Analysis of Air-cargo Allotment Contract. In Proceedings of the ICORES, Funchal, Portugal, 24–26 January 2018; pp. 47–58. [Google Scholar]
- Szolnoki, A.; Wang, Z.; Perc, M. Wisdom of groups promotes cooperation in evolutionary social dilemmas. Sci. Rep. 2012, 2, 576. [Google Scholar] [CrossRef] [PubMed]
- Ladley, D.; Wilkinson, I.; Young, L. The impact of individual versus group rewards on work group performance and cooperation: A computational social science approach. J. Bus. Res. 2015, 68, 2412–2425. [Google Scholar] [CrossRef]
- Eberl, P. The development of trust and implications for organizational design: A game- and attribution- theoretical framework. Schmalenbach Bus. Rev. 2004, 56, 258–273. [Google Scholar] [CrossRef]
- Staatz, J.M. The cooperative as a coalition: a game-theoretic approach. Am. J. Agric. Econ. 1983, 65, 1084–1089. [Google Scholar] [CrossRef]
- Sexton, R.J. The formation of cooperatives: A game-theoretic approach with implications for cooperative finance, decision-making, and stability. Am. J. Agric. Econ. 1986, 68, 214–225. [Google Scholar] [CrossRef]
- Peldschus, F.; Zavadskas, E.K.; Turskis, Z.; Tamosaitiene, J. Sustainable assessment of construction site by applying game theory. Inz. Ekon.-Eng. Econ. 2010, 21, 223–237. [Google Scholar]
- Medda, F. A game theory approach for the allocation of risks in transport public private partnerships. Int. J. Proj. Manag. 2007, 25, 213–218. [Google Scholar] [CrossRef]
- Shen, L.; Bao, H.; Wu, Y.; Lu, W. Using bargaining-game theory for negotiating concession period for BOT-type contract. J. Constr. Eng. Manag. 2007, 133, 385–392. [Google Scholar] [CrossRef]
- Shen, L.; Li, H.; Li, Q. Alternative concession model for build operate transfer contract projects. J. Constr. Eng. Manag. 2002, 128, 326–330. [Google Scholar] [CrossRef]
- Javed, A.A.; Lam, P.T.; Chan, A.P. Change negotiation in public-private partnership projects through output specifications: an experimental approach based on game theory. Constr. Manag. Econ. 2014, 32, 323–348. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Wang, Y. Using bargaining game theory for risk allocation of public-private partnership projects: Insights from different alternating offer sequences of participants. J. Constr. Eng. Manag. 2016, 143, 04016102. [Google Scholar] [CrossRef]
- Kembłowski, M.W.; Grzyl, B.; Siemaszko, A. Game Theory Analysis of Bidding for A Construction Contract. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2017; Volume 245, p. 062047. [Google Scholar]
- Bockova, K.H.; Slavikova, G.; Porubcanova, D. Game theory as a tool of conflict and cooperation solution between intelligent rational decision-makers in project management. J. Econ. Manag. Perspect. 2016, 10, 147–156. [Google Scholar]
- Asgari, M.S.; Afshar, A. Modeling subcontractors cooperation in time; cooperative game theory approach. In Proceedings of the First International Conference on Construction in Developing Countries (ICCIDC-I), Karachi, Pakistan, 4–5 August 2008; pp. 312–319. [Google Scholar]
- Asgari, S.; Afshar, A.; Madani, K. Cooperative game-theoretic framework for joint resource management in construction. J. Constr. Eng. Manag. 2013, 140, 04013066. [Google Scholar] [CrossRef]
- Lagesse, B. A Game-Theoretical model for task assignment in project management. In Proceedings of the 2006 IEEE International Conference on Management of Innovation and Technology, Singapore, China, 21–23 June 2006; Volume 2, pp. 678–680. [Google Scholar]
- San Cristóba, J.R. Cost allocation between activities that have caused delays in a project using game theory. Proced. Technol. 2014, 16, 1017–1026. [Google Scholar] [CrossRef]
- San Cristóbal, J.R. The use of Game Theory to solve conflicts in the project management and construction industry. Int. J. Inf. Syst. Proj. Manag. 2015, 3, 43–58. [Google Scholar]
- Bergantiños, G.; Sánchez, E. How to distribute costs associated with a delayed project. Ann. Oper. Res. 2002, 109, 159–174. [Google Scholar] [CrossRef]
- Estévez-Fernández, A.; Borm, P.; Hamers, H. Project games. Int. J. Game Theory 2007, 36, 149–176. [Google Scholar] [CrossRef][Green Version]
- Estévez-Fernández, A. A game-theoretical approach to sharing penalties and rewards in projects. Eur. J. Oper. Res. 2012, 216, 647–657. [Google Scholar] [CrossRef]
- Brânzei, R.; Ferrari, G.; Fragnelli, V.; Tijs, S. Two approaches to the problem of sharing delay costs in joint projects. Ann. Oper. Res. 2002, 109, 359–374. [Google Scholar] [CrossRef]
- Bergantiños, G.; Sánchez, E. NTU pert games. Oper. Res. Lett. 2002, 30, 130–140. [Google Scholar] [CrossRef]
- Zou, W.; Kumaraswamy, M. Game theory based understanding of dynamic relationships between public and private sectors in PPPs. In Proceedings of the 25th Annual ARCOM Conference, Nottingham, UK, 7–9 September 2010; Association of Researchers in Construction Management: Manchester, UK, 2010. [Google Scholar]
- Bakshi, T.; Sarkar, B.; Sanyal, S.K. A new soft-computing based framework for project management using game theory. In Proceedings of the 2012 International Conference on Communications, Devices and Intelligent Systems (CODIS), Kolkata, India, 28–29 December 2012; pp. 282–285. [Google Scholar]
- Peldschus, F. Economical analysis of project management under consideration of multi-criteria decisions. Technol. Econ. Dev. Econ. 2006, 12, 169–170. [Google Scholar] [CrossRef]
- Sacks, R.; Harel, M. An economic game theory model of subcontractor resource allocation behaviour. Constr. Manag. Econ. 2006, 24, 869–881. [Google Scholar] [CrossRef]
- Angelou, G.N.; Economides, A.A. A multi-criteria game theory and real-options model for irreversible ICT investment decisions. Telecommun. Policy 2009, 33, 686–705. [Google Scholar] [CrossRef]
- Butterfield, J.; Pendegraft, N. Analyzing information system investments: a game-theoretic approach. Inf. Syst. Manag. 2001, 18, 73–82. [Google Scholar] [CrossRef]
- Lippman, S.A.; McCardle, K.F.; Tang, C.S. Using Nash bargaining to design project management contracts under cost uncertainty. Int. J. Prod. Econ. 2013, 145, 199–207. [Google Scholar] [CrossRef]
- Sacks, R.; Harel, M. How Last Planner motivates subcontractors to improve plan reliability—A game theory model. In Proceedings of the 14th Annual IGLC Conference, Santiago, Chile, 25–27 July 2006. [Google Scholar]
- de Magalhães, S.T.; Magalhães, M.J.; Sá, V.J. Establishment ofAutomatization as a Requirement for Time Management Input Modules in Project Management Information Systems for Academic Activities—A Game Theory Approach. Procedia Comput. Sci. 2015, 64, 1157–1162. [Google Scholar] [CrossRef]
- Wei, W.; Wang, J.; Chen, X.; Yang, J.; Min, X. Psychological contract model for knowledge collaboration in virtual community of practice: An analysis based on the game theory. Appl. Math. Comput. 2018, 329, 175–187. [Google Scholar] [CrossRef]
- Barth, D.; Boudaoud, B.; Mautor, T. Game theory for contracts establishment with guaranteed QoS in the interdomain network. In Proceedings of the 2012 International Conference on Communications and Information Technology (ICCIT), Hammamet, Tunisia, 26–28 June 2012; pp. 276–280. [Google Scholar]
- Mobarakeh, A.S.; Rajabi-Ghahnavieh, A.; Zahedian, A. A game-theoretic framework for DG optimal contract pricing. In Proceedings of the IEEE PES ISGT Europe 2013, Lyngby, Denmark, 6–9 October 2013; pp. 1–5. [Google Scholar]
- Pinto, T.; Vale, Z.; Praça, I.; Pires, E.; Lopes, F. Decision support for energy contracts negotiation with game theory and adaptive learning. Energies 2015, 8, 9817–9842. [Google Scholar] [CrossRef]
- Elfakir, A.; Tkiouat, M. New Projects Sharing Ratios under Musharakah Financing: A Repeated Game Theoretical Approach Using an Output versus a Proposed Effort Based Contract. Am. J. Appl. Sci. 2015, 12, 654. [Google Scholar] [CrossRef][Green Version]
- Kim, J.; Kwak, T. Game theoretic analysis of the bargaining process over a long-term replenishment contract. J. Oper. Res. Soc. 2007, 58, 769–778. [Google Scholar] [CrossRef]
- Li, X. Relational contracts, growth options, and heterogeneous beliefs: A game-theoretic perspective on information technology outsourcing. J. Manag. Inf. Syst. 2014, 31, 319–350. [Google Scholar] [CrossRef]
- Liu, X.; Wu, C.; Sun, Y.; Hu, Z.; Gaol, B.; Tang, Y. Bilateral Contract Transaction Model for Generation Companies and Large Consumers Based on Bayesian Game-Theoretic Approach. In Proceedings of the 2017 IEEE 7th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Honolulu, HI, USA, 31 July–4 August 2017; pp. 306–310. [Google Scholar]
- Watson, J. Contract and game theory: Basic concepts for settings with finite horizons. Games 2013, 4, 457–496. [Google Scholar] [CrossRef]
- Burato, E.; Cristani, M. Contract clause negotiation by game theory. In Proceedings of the 11th International Conference on Artificial Intelligence and Law, Stanford, CA, USA, 4–8 June 2007; ACM: New York, NY, USA, 2007; pp. 71–80. [Google Scholar]
- Peldschus, F.; Zavadskas, E.K. Fuzzy matrix games multi-criteria model for decision-making in engineering. Informatica 2005, 16, 107–120. [Google Scholar]
- Kasthurirathna, D.; Piraveenan, M.; Uddin, S. Modeling networked systems using the topologically distributed bounded rationality framework. Complexity 2016, 21, 123–137. [Google Scholar] [CrossRef]
- Blanc, A.; Liu, Y.K.; Vahdat, A. Designing incentives for peer-to-peer routing. In Proceedings of the 24th Annual Joint Conference of the IEEE Computer and Communications Societies (NFOCOM 2005), Miami, FL, USA, 13–17 March 2005; Volume 1, pp. 374–385. [Google Scholar]
- Christin, N.; Grossklags, J.; Chuang, J. Near rationality and competitive equilibria in networked systems. In Proceedings of the ACM SIGCOMM Workshop on Practice and Theory of Incentives in Networked Systems, Portland, OR, USA, 3 September 2014; ACM: New York, NY, USA, 2014; pp. 213–219. [Google Scholar]
- Christin, N.; Chuang, J. On the cost of participating in a peer-to-peer network. In Peer-to-Peer Systems III; Springer: Berlin/Heidelberg, Germany, 2005; pp. 22–32. [Google Scholar]
- Chun, B.G.; Fonseca, R.; Stoica, I.; Kubiatowicz, J. Characterizing selfishly constructed overlay routing networks. In Proceedings of the Twenty-third Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM 2004), Hong Kong, China, 22 November 2004; Volume 2, pp. 1329–1339. [Google Scholar]


© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piraveenan, M. Applications of Game Theory in Project Management: A Structured Review and Analysis. Mathematics 2019, 7, 858. https://doi.org/10.3390/math7090858
Piraveenan M. Applications of Game Theory in Project Management: A Structured Review and Analysis. Mathematics. 2019; 7(9):858. https://doi.org/10.3390/math7090858
Chicago/Turabian StylePiraveenan, Mahendra. 2019. "Applications of Game Theory in Project Management: A Structured Review and Analysis" Mathematics 7, no. 9: 858. https://doi.org/10.3390/math7090858
APA StylePiraveenan, M. (2019). Applications of Game Theory in Project Management: A Structured Review and Analysis. Mathematics, 7(9), 858. https://doi.org/10.3390/math7090858




