IDP-Core: Novel Cooperative Solution for Differential Games

Abstract

IDP-core is a new cooperative solution for dynamic and differential games. A novel approach of constructing solutions for dynamic and differential games was employed in which the time consistency property was used as the main axiom property for the cooperative solution. Another new and important approach used for constructing IDP-core is the IDP dominance, which allows to select undominated imputation distribution procedures and construct the cooperative solution or imputation set. This approach shows the potential of using the time consistency property as the main axiom for solutions in various fields such as Social Choice and Mechanism Design. The overall procedure for defining the cooperative solution is also new since IDP-core was constructed using imputation distribution procedures but not by using imputations directly.

1. Introduction

The theory of cooperative games examines how optimal parameters of cooperative and strategic agreements are to be determined. The main problem in the theory of cooperative games with transferable utilities is to determine the allocation procedure for total payoff in cases when all players cooperate. The rule of how to allocate cooperative payoff among the players is called the imputation. In the theory of cooperative games with non-transferable utilities, the main problem is to define agreement on strategies or a game outcome favorable to all players.

Within the framework of classical cooperative game theory with transferable utilities, numerous cooperative solutions or allocation rules were studied. One of them is the Core. The concept of Core was proposed by D. Gillis [1], which is a generalization of the contractual Edgeworth curve [2]. Edgeworth described a market with two products and two participantsp; here, the Core is defined as a part of the Pareto front. The Core is the set of undominated imputations, each of which can be used as a solution in the game.

It is important to study the non-emptiness property of a cooperative solution, which is to determine the conditions under which the cooperative solution is not empty since its applicability depends on the wideness of the class of games to which this solution can be applied. G. Scarf [3] showed that the Core is not empty for the class of convex games in characteristic function form. Characteristic function is a function of coalition or subset of players in the game, which shows the profit of coalition. Generalization of Scharf results can be found in the paper of L. Biller [4] and Shapley [5]. Necessary and sufficient conditions for the non-emptiness of Core were formulated by Bondareva [6] and Shapley [7], where the main role of proof is the concept of a balanced game. Unfortunately, based on this concept it is impossible to apply a constructive method for choosing the specific imputations from the Core.

V. Zakharov in [8] proposed the necessary and sufficient conditions for the non-emptiness of Core, which simplify the test for a single-point solution (imputation), such as the Shapley value, Banzhaf power index and others, whenever they belong to the Core. In [9,10] based on of this approach, geometric properties for several cooperative solutions were investigated. This approach implies that the non-emptiness property of Core can be formulated by a linear programming problem constructed using the values of the characteristic function.

It is also important to construct cooperative solutions for a class of dynamic and differential games. Solutions for such models can be used for modeling cooperative and strategic agreements where conditions are defined over a long time interval [11,12]. The theory of differential games was developed as a separate class of applied mathematics in the 1950s. One of the first works in the field of differential games is the work of R. Isaacs [13] in which the notions of state, controls, and the problem of aircraft interception by a guided missile were formulated, and a fundamental equation for defining the solution derived. A comprehensive description of dynamic cooperative games is presented in [14].

A natural approach for researching cooperative differential games is an attempt at transferring the results of classical static cooperative theory [15] to the theory of differential games. However, in order to use the results of classical theory, it is additionally necessary to study the time consistency and strong time consistency properties of cooperative solutions. Time consistency of cooperative solution is the property that shows that for the players it is not beneficial to deviate from the chosen cooperative solution during the game. The use of time-inconsistent cooperative solutions in the field of economics, ecology, and management makes these solutions unfeasible because players might find it profitable to reconsider the cooperative solution. The notion of the cooperative solution’s time consistency was first formulated mathematically by L.A. Petrosyan in 1977 [16]. In [17] a method was proposed to construct time-consistent cooperative solutions using a special payment scheme, called the imputation distribution procedure (IDP). The notion of strong time consistency was formulated in [18]. Recent papers [19,20,21,22] are devoted to the study of the time consistency property of cooperative solutions.

In order to solve the time inconsistency problem in a classical cooperative solution, an imputation distribution procedure should be used. However, there exists another, rather new approach that allows for constructing time-consistent cooperative solutions. This approach uses the time consistency property as a basic axiomatic property for defining the cooperative solution. This approach is the subject of this paper and carries an innovative character. It is important to notice that the further use of time consistency property for dynamic cooperative games, Social Choice, and Mechanisms Design, as an axiom, is promising. Another important property considered in this paper is the IDP dominance property. According to this property, the corresponding cooperative solution is constructed using the imputation distribution procedures, which are undominated. We say that the IDP is undominated by coalition S if there does not exist another IDP, coalition S, and time instant such that the instant payments corresponding to IDP are higher for players from coalition S at a given time instant than in the current IDP.

In the paper [23] the notion of a strong time-consistent subset of the Core was introduced. Their authors constructed a new cooperative solution using the geometric approach and proved that it was a subset of Core and possesses a strong time consistency property. Later on, this solution was called the IDP-core and it can be constructed using a system of linear constraints for imputation distribution procedures. These conditions are defined for each time instant of a differential game. From the non-emptiness of a set described by these constraints, the non-emptiness of the corresponding set of IDPs at each time instant, it follows that the IDP-core is not empty. In the paper [24] we apply the technique proposed in [8] to study the non-emptiness of IDP-core for each time instant, and if it is non-empty, we conclude that IDP-core is non-empty. Obtained results can be used for the construction of IDP-core and verification of its non-emptiness as a numerical example. Moreover, a special case of this approach is presented for 3-player differential games. It is possible to analytically construct conditions for non-emptiness of IDP-core depending on the characteristic function. Furthermore, it is possible to define an analytical formula for selectors of IDP-core, in particular, the formula for imputation distribution procedures of IDP-core selectors.

The paper is structured as follows. Section 2 contains preliminary information, including the definition of a cooperative solution and time consistency property. Section 3 is devoted to the description of IDP-dominance, to the definition of IDP-core and corresponding necessary and sufficient conditions. Section 4 is devoted to studying the non-emptiness of IDP-core using linear programming methods. Section 5 presents the differential game model of resource extraction, IDP-core for this model is constructed using the corresponding necessary and sufficient conditions, non-emptiness conditions are studied and conclusions are drawn.

2. Problem Statement and Preliminary Information

2.1. Differential Game Model

In this section, the general description of the differential game model is given. The main concepts of this model are the type of model, payoff functions of players, motion equations, and solution concept. Type of the game model reflects what we intend to do with the model, in this paper we consider the cooperative game model. Here we need to define how to allocate joint cooperative payoff among the players. Payoff functions of players define the objectives of players depending on the state of the game, strategies and are calculated on some specific time interval (in our case closed time interval). Motion equations define of how the state of the game changes according to the strategies of players. In the case of the cooperative game model solution concept defines the exact type of imputation set that will be used to allocate joint payoff among the players.

Consider an n-player differential game $\mathsf{\Gamma }(x_0,T-t_0)$ with prescribed duration $T-t_0$ and initial condition $x_0$. Game dynamics are defined by the system of differential equations:

$$\begin{array}{c}\dot{x}=f(x,u_1,\dots ,u_n),x\in R^n,u_i\in U_i\subset \mathrm{comp}{R}^k,t\in [t_0,T],i=\overline{1,n},\hfill \\ x\left(t_0\right)=x_0,\hfill \end{array}$$

(1)

for which the conditions of existence, uniqueness and continuity of solution $x\left(t\right)$ for any admissible measurable controls $u_1(·),\dots ,u_n(·)$ are satisfied. Open-loop control $u_i\left(t\right)$ satisfying the system (1) is a strategy of player i and $\mathrm{comp}{R}^k$ is the compact set in k-dimension real number space (k is integer).

Let $N=\{1,\dots ,n\}$ be the set of players. Payoff of player i is defined in the following way:

$$K_i(x_0,T-t_0;u_1,\dots ,u_n)=\underset{t_0}{\overset{T}{\int }}{h}_i(x\left(\tau \right),u_1\left(\tau \right),\dots ,u_n\left(\tau \right))d\tau ,i=\overline{1,n},$$

(2)

where $h_i(x,u_1,\dots ,u_n)\ge 0$, $i=\overline{1,n}$ and $f(x,u_1,\dots ,u_n)$ are integrable functions, $x\left(t\right)$ is the solution of system (1) with controls $u\left(t\right)=(u_1\left(t\right),\dots ,u_n\left(t\right))$ involved.

2.2. Cooperative Differential Game Model

In the cooperative differential game model with transferable utility there are two problems:

(1)

Determination of a strategy set for players which maximizes the sum of their payoffs or determination of strategies corresponding to cooperative behavior. These strategies $u^{*}=(u_1^{*},\dots ,u_n^{*})$ are called optimal, the corresponding trajectory is called the cooperative trajectory and denoted by $x^{*}\left(t\right)$.

(2)

Determination of the allocation rule for the maximum joint payoff of players corresponding to the optimal strategies $u^{*}\left(t\right)$ and determination of optimal trajectory $x^{*}\left(t\right)$. Namely, the determination of a cooperative solution as a subset of the imputation set.

Let $u^{*}=(u_1^{*},\dots ,u_n^{*})$ be the vector of optimal strategies (open-loop controls) for players; i.e., a set of controls that maximizes the joint payoff of players:

$$u^{*}=(u_1^{*},\dots ,u_n^{*})=arg\underset{u_1,\dots ,u_n}{max}\sum _{i=1}^n{K}_i(x_0,T-t_0;u_1,\dots ,u_n).$$

(3)

Suppose that the maximum in (3) is achieved on the set of admissible strategies.

In order to determine how to allocate the maximum total payoff among players, it is necessary to define the notion of the characteristic function of coalition $S\subseteq N$. The characteristic function shows the strength of a coalition and thus allows the contribution of players to each coalition to be taken into account.

Suppose that in the game $\mathsf{\Gamma }(x_0,T-t_0)$ characteristic function $V(S;x_0,T-t_0)$, $S\subseteq N$ is constructed in any relevant way (for example, as in [25]). We assume that the superadditivity conditions are satisfied:

$$\begin{array}{c}V(S_1\cup S_2;x_0,T-t_0)\ge V(S_1;x_0,T-t_0)+V(S_2;x_0,T-t_0),\hfill \\ \forall S_1,S_2\subseteq N,S_1\cap S_2=\varnothing .\hfill \end{array}$$

Denote by $L(x_0,T-t_0)$ the set of imputations [26] in the game $\mathsf{\Gamma }(x_0,T-t_0)$:

$$\begin{array}{c}L(x_0,T-t_0)=\{\xi (x_0,T-t_0)=({\xi }_1(x_0,T-t_0),\dots ,{\xi }_n(x_0,T-t_0)):\hfill \\ \sum _{i=1}^n{\xi }_i(x_0,T-t_0)=V(N;x_0,T-t_0),\\ \hfill {\xi }_i(x_0,T-t_0)\ge V(\left\{i\right\};x_0,T-t_0),i\in N\},\end{array}$$

where $V(\left\{i\right\};x_0,T-t_0)$ is a value of characteristic function $V(S;x_0,T-t_0)$ for coalition $S=\left\{i\right\}$.

By $M(x_0,T-t_0)$ denote an arbitrary cooperative solution or subset of imputation set $L(x_0,T-t_0)$:

$$M(x_0,T-t_0)\subseteq L(x_0,T-t_0).$$

Suppose that at the beginning of game $\mathsf{\Gamma }(x_0,T-t_0)$ at the instant $t_0$, players agreed to select a subset of $L(x_0,T-t_0)$ or some cooperative solution. However, suppose that at some instant $\overline{t}$ players decided to reconsider the chosen cooperative solution, or decided to reconsider the allocation rule for a cooperative payoff. In order to model their behavior, it is necessary to define the notion of subgame $\mathsf{\Gamma }(x^{*}\left(t\right),T-t)$ along the cooperative trajectory $x^{*}\left(t\right)$ starting at the instant $t\in [t_0,T]$.

For each subgame $\mathsf{\Gamma }(x^{*}\left(t\right),T-t)$, $t\in [t_0,T]$ along the trajectory $x^{*}\left(t\right)$, we define the superadditive characteristic function $V(S;x^{*}\left(t\right),T-t)$, $S\subseteq N$ in the same way as it was done for the initial game $\mathsf{\Gamma }(x_0,T-t_0)$:

$$\begin{array}{c}\forall S,A\subseteq N,S\cap A=\varnothing :\hfill \\ \hfill V(S\cup A;x^{*}\left(t\right),T-t)\ge V(S;x^{*}\left(t\right),T-t)+V(A;x^{*}\left(t\right),T-t).\end{array}$$

(4)

It is also possible to define the notion of imputation $\xi (x^{*}\left(t\right),T-t)$ for a subgame $\mathsf{\Gamma }(x^{*}\left(t\right),T-t)$ along the cooperative trajectory $x^{*}\left(t\right)$, $t\in [t_0,T]$. The set of all possible imputations in the subgame $\mathsf{\Gamma }(x^{*}\left(t\right),T-t)$ is denoted by $L(x^{*}\left(t\right),T-t)$, $t\in [t_0,T]$:

$$\begin{array}{c}L(x^{*}\left(t\right),T-t)=\{\xi (x^{*}\left(t\right),T-t)=({\xi }_1(x^{*}\left(t\right),T-t),\dots ,{\xi }_n(x^{*}\left(t\right),T-t)):\hfill \\ \sum _{i=1}^n{\xi }_i(x^{*}\left(t\right),T-t)=V(N;x^{*}\left(t\right),T-t),\\ \hfill {\xi }_i(x^{*}\left(t\right),T-t)\ge V(\left\{i\right\};x^{*}\left(t\right),T-t),i\in N\}.\end{array}$$

(5)

The superaditivity property (4) for characteristic function $V(S;x^{*}\left(t\right),T-t)$ guarantees the non-emptiness of imputation set $L(x^{*}\left(t\right),T-t)$, $t\in [t_0,T]$. The cooperative solution of subgame $\mathsf{\Gamma }(x^{*}\left(t\right),T-t)$ is denoted correspondingly by $M(x^{*}\left(t\right),T-t)$.

2.3. Core

In cooperative game theory, the main problem is “fair” allocation of the maximum joint payoff $V(N;x_0,T-t_0)$ among the players from grand coalition $N=\{1,\dots ,n\}$.

Suppose that players in the cooperative differential game $\mathsf{\Gamma }(x_0,T-t_0)$ (subgame $\mathsf{\Gamma }(x^{*}\left(t\right),T-t)$, $t\in [t_0,T]$ along the cooperative trajectory $x^{*}\left(t\right)$) made an agreement on the allocation rule $\xi (x_0,T-t_0)$ (imputation $\xi (x^{*}\left(t\right),T-t)$), where none of imputations dominates $\xi (x_0,T-t_0)$ ($\xi (x^{*}\left(t\right),T-t)$) [26]. Such an allocation rule is stable in the sense that there not exists imputation that would be better for each coalition at every time instant $t\in [t_0,T]$.

Definition 1.

We call the set of undominated imputations of cooperative differential game $\mathsf{\Gamma }(x^{*}\left(t\right),T-t)$ by the Core and denote it by $C(x^{*}\left(t\right),T-t)$, $t\in [t_0,T]$.

The following theorem holds:

Theorem 1.

Imputation $\xi (x^{*}\left(t\right),T-t)$ belongs to the Core $C(x^{*}\left(t\right),T-t)$, if and only if for all $S\subseteq N$ the following inequalities are satisfied:

$$V(S;x^{*}\left(t\right),T-t)\le \sum _{i\in S}{\xi }_i(x^{*}\left(t\right),T-t),t\in [t_0,T].$$

2.4. Non-Emptiness of Core in Static Games

These are the main results concerning the nonemptiness conditions of Core in static games. Necessary and sufficient conditions for non-emptiness of Core were formulated by O. Bondareva [6] and by L. Shapley [7]. These conditions are based on the concept of a balanced game, but the application of this approach for a specific game model is difficult.

In the paper [27] G. Owen showed that in the game $(N,v)$ exists a non-empty Core, if and only if the optimal value of the linear programming problem

$$\begin{array}{c}\sum _{i\in N}{\xi }_i⟶min\hfill \\ \sum _{i\in S}{\xi }_i\ge v\left(S\right),\forall S\subseteq N,S\ne \varnothing \hfill \end{array}$$

is equal to $v\left(N\right)$.

The papers [8,9,10] also make use of linear programming problem for Core’s non-emptiness. Consider the following linear programming problem:

$$\begin{array}{c}\sum _{i\in N}{\xi }_i⟶min\hfill \\ \sum _{i\in S}{\xi }_i\ge v\left(S\right),\forall S\subseteq N,S\ne N,\varnothing .\hfill \end{array}$$

(6)

Suppose that ${\xi }^0=({\xi }_1^0,\dots ,{\xi }_n^0)$ is some arbitrary optimal solution of the linear programming problem (6). The set of all optimal solutions of the optimization problem (6) is denoted by $X^0\left(v\right)$. In [8] it is shown that the necessary and sufficient conditions of non-emptiness of Core can be formalized in the following way:

Theorem 2.

The Core in cooperative game with transferable utility $(N,v)$ is nonempty, if and only if the following inequality is satisfied:

$$\sum _{i\in N}{\xi }_i^0\le v\left(N\right),$$

(7)

where ${\xi }^0\in X^0\left(v\right)$ is a solution of the linear programming problem (6).

2.5. Time-Consistency of Cooperative Solution and Imputation Distribution Procedure

Transferring the results of static cooperative game theory to the field of cooperative differential games brings about the problem of defining the time-consistent cooperative solution. The problem of defining the solution of the differential game with prescribed duration was studied in the papers of L.A. Petrosyan [16,17]. Time consistency of cooperative solution is the property that shows that for the players it is not beneficial to deviate from the chosen cooperative solution during the game.

The main approach for solving the problem of time inconsistency of cooperative solution in the differential game is the imputation distribution procedure, proposed in [17]. In this paper, imputation distribution procedure was defined as a vector function for a fixed imputation. In this paper, we consider another approach that generalizes the notion of IDP.

Assume IDP’s in cooperative differential game $\mathsf{\Gamma }(x_0,T-t_0)$ are integrable vector functions that constitute some imputation from the imputation set:

$$\beta \left(t\right):{\int }_{t_0}^T\beta \left(\tau \right)d\tau \in L(x_0,T-t_0)$$

(8)

or

$$\begin{array}{cc}\hfill & {\int }_{t_0}^T{\beta }_i\left(\tau \right)d\tau \ge V(\left\{i\right\};x_0,T-t_0),i\in N,\hfill \\ \hfill & \sum _{i\in N}{\int }_{t_0}^T{\beta }_i\left(\tau \right)d\tau =V(N;x_0,T-t_0).\hfill \end{array}$$

Therefore, in the above definition, IDP is not based on the imputation itself but generates it. We define also the so-called corresponding IDP, the concept of which is close to the initial definition of IDP in the paper [17].

Definition 2.

The integrable function $\beta \left(t\right)=({\beta }_1\left(t\right),\dots ,{\beta }_n\left(t\right))$, $t\in [t_0,T]$ is called a corresponding imputation distribution procedure (IDP) for $\xi (x_0,T-t_0)\in L(x_0,T-t_0)$, if the following equalities hold:

$${\xi }_i(x_0,T-t_0)={\int }_{t_0}^T{\beta }_i\left(\tau \right)d\tau ,i\in N.$$

(9)

Actually, the corresponding IDP $\beta \left(t\right)$ depends on $\xi (x_0,T-t_0)$ and is not unique for this imputation. We can represent it in the form

$$\beta \left(t\right)=\beta (t,\xi (x_0,T-t_0))$$

or

$${\beta }_i\left(t\right)={\beta }_i(t,{\xi }_i(x_0,T-t_0)),i\in N.$$

From (9) we have for $t\in [t_0,T]$, $i\in N$:

$${\xi }_i(x_0,T-t_0)={\int }_{t_0}^t{\beta }_i\left(\tau \right)d\tau +{\int }_t^T{\beta }_i\left(\tau \right)d\tau$$

or

$${\int }_t^T{\beta }_i\left(\tau \right)d\tau ={\xi }_i(x_0,T-t_0)-{\int }_{t_0}^t{\beta }_i\left(\tau \right)d\tau .$$

That is IDP shares at instant t imputations in two parts: payoffs to player i, which are received in interval $[t_0,t]$ and in interval $(t,T]$.

Definition 3.

The cooperative solution $M(x_0,T-t_0)$ in the game $\mathsf{\Gamma }(x_0,T-t_0)$ is called time-consistent, if for each imputation $\xi (x_0,T-t_0)\in M(x_0,T-t_0)$ there exists a corresponding IDP $\beta \left(t\right)=\beta (t,\xi (x_0,T-t_0))$ such that:

$${\int }_t^T\beta \left(\tau \right)d\tau \in M(x^{*}\left(t\right),T-t),t\in [t_0,T]$$

(10)

or equivalently

$$\xi (x_0,T-t_0)-{\int }_{t_0}^t\beta \left(\tau \right)d\tau \in M(x^{*}\left(t\right),T-t),t\in [t_0,T].$$

(11)

Notice that from condition (10) we have the following equality

$$\sum _{i\in N}{\int }_t^T{\beta }_i\left(\tau \right)d\tau =V(N;x^{*}\left(t\right),T-t),t\in [t_0,T].$$

(12)

It is obvious that if $M(x^{*}\left(t\right),T-t)\ne \varnothing$ for $\forall t\in [t_0,T]$, then for any differentiable by t function $\xi (x^{*}\left(t\right),T-t)\in M(x^{*}\left(t\right),T-t)$ ($\xi (x^{*}\left(t_0\right),T-t_0)=\xi (x_0,T-t_0)$) IDP $\beta \left(t\right)$ can be defined using the formula:

$$\begin{array}{cc}\hfill & \beta \left(t\right)=-{\displaystyle \frac{d}{dt}}\xi (x^{*}\left(t\right),T-t),t\in [t_0,T],i\in N,\hfill \\ \hfill & \xi (x^{*}\left(t_0\right),T-t_0)=\xi (x_0,T-t_0).\hfill \end{array}$$

(13)

Then imputation $\xi (x_0,T-t_0)$ is defined by the formula:

$$\xi (x_0,T-t_0)={\int }_{t_0}^t\beta \left(\tau \right)d\tau +\xi (x^{*}\left(t\right),T-t),t\in [t_0,T].$$

Define an imputation in the current cooperative game $\mathsf{\Gamma }(x^{*}\left(t\right),T-t)$ with characteristic function $V(S;x^{*}\left(t\right),T-t)$ which corresponds to a given IDP $\beta \left(t\right)=\beta (t,\xi (x_0,T-t_0))$ as

$$\xi (x^{*}\left(t\right),T-t)={\int }_t^T\beta \left(\tau \right)d\tau .$$

(14)

From Definition 3 we have

$$\xi (x^{*}\left(t\right),T-t)\in M(x^{*}\left(t\right),T-t).$$

(15)

We will call the imputation (14) the dynamic imputation generated by the corresponding IDP $\beta \left(t\right)=\beta (t,\xi (x_0,T-t_0))$.

3. IDP-Core and Dominance of Imputation Distribution Procedures

Consider the development of game at instant $t\in (t_0,T)$. Suppose that at instant $t_0$ players agreed to realize imputation $\xi (x_0,T-t_0)=({\xi }_1(x_0,T-t_0),\dots ,{\xi }_n(x_0,T-t_0))$. Then, according to the corresponding IDP $\beta \left(t\right)$, until the instant t, player $i\in N$ receives the payoff:

$${\int }_{t_0}^t{\beta }_i\left(\tau \right)d\tau .$$

However, for some players IDP $\beta (t,\xi (x_0,T-t_0))$ would not be beneficial if there exists another imputation distrubution procedure $\overline{\beta }(t,\xi (x_0,T-t_0))$, according to which player i at interval $[t_0,t]$ receives more payoff:

$${\int }_{t_0}^t{\overline{\beta }}_i\left(\tau \right)d\tau >{\int }_{t_0}^t{\beta }_i\left(\tau \right)d\tau .$$

(16)

In such a case IDP $\beta \left(t\right)$ may be considered as less beneficial for the player i at least in interval $[t_0,t]$. It is important to notice that the notion of IDP-dominance can be applied to imputation distribution procedures, which are not necessarily defined for a unique imputation. As IDP defines how dynamic imputation is to be constructed then it also makes sense to consider the notion of IDP-dominance not only for a fixed imputation.

3.1. Dominance of Imputation Distribution Procedures

In this section we consider the IDP $\beta \left(t\right)$ defined by the formula (8). Suppose that the function $V(S;x^{*}\left(t\right),T-t)$, $S\subseteq N$ is continuously differentiable by $t\in [t_0,T]$. Define the function $U(S;x^{*}\left(t\right),T-t)$ in the following way:

$$U(S;x^{*}\left(t\right),T-t)=-\frac{d}{dt}V(S;x^{*}\left(t\right),T-t),t\in [t_0,T],S\subseteq N.$$

(17)

Definition 4.

IDP $\beta \left(t\right)$ dominates IDP $\overline{\beta }\left(t\right)$ by coalition $S\subseteq N$ and at the instant $\overline{t}\in [t_0,T]$ (denote by $\beta \left(t\right)\stackrel{S,\overline{t}}{\succ }\overline{\beta }\left(t\right)$), if the following inequalities hold:

$$\begin{array}{c}{\beta }_i\left(\overline{t}\right)>{\overline{\beta }}_i\left(\overline{t}\right),i\in S,\hfill \\ \sum _{i\in S}{\beta }_i\left(\overline{t}\right)\le U(S;x^{*}\left(\overline{t}\right),T-\overline{t}).\hfill \end{array}$$

(18)

Definition 5.

IDP $\beta \left(t\right)$ is undominated if at any $\overline{t}\in [t_0,T]$ there does not exist $\overline{\beta }\left(t\right)$, which dominates $\beta \left(t\right)$ by coalition $S\subseteq N$:

$$\overline{\beta }\left(t\right)\stackrel{S,\overline{t}}{\neg \succ }\beta \left(t\right),\forall \overline{\beta }\left(t\right),S.$$

(19)

3.2. IDP-Core

In the paper [23] the authors first introduced and treated a subset of the imputation set in a cooperative differential game which was named subcore. This subset was designed using a set of imputation distribution procedures satisfying the system of inequalities and equalities. This approach is not classical for the theory of differential games since it uses IDP’s for imputations, not vice versa. Based on this subcore notion, we in the paper [24] redefined this notion for the dynamic case, named it IDP-core, and formulated necessary and sufficient conditions of the existence of IDP-core along the cooperative trajectory of the game. In the current paper, we define a solution concept for IDP-core by introducing the notion of IDP dominance and using the time consistency properties or axioms defined above. It is proved that IDP-core has the necessary and sufficient conditions for a dynamic imputation when defined by the system of inequalities introduced in the paper [23,28].

Suppose that players in the game $\mathsf{\Gamma }(x_0,T-t_0)$ agreed on the allocation rule for total payoff of grand coalition N (imputation $\xi (x_0,T-t_0)$) using the cooperative solution of IDP-core:

Definition 6.

By the dynamic $IDP-core(x^{*}\left(t\right),T-t)$ along the cooperative trajectory $x^{*}\left(t\right)$, $t\in [t_0,T]$ ($IDP-core(x_0,T-t_0)$), we call the solution in cooperative differential game $\mathsf{\Gamma }(x^{*}\left(t\right),T-t)$ ($\mathsf{\Gamma }(x_0,T-t_0)$), which includes all time-consistent imputations generated by undominated IDPs $\beta \left(\tau \right)$, $\tau \in [t,T]$ (8), $t\in [t_0,T]$ ($\beta \left(t\right)$, $t\in [t_0,T]$):

$$\begin{array}{cc}\hfill & IDP-core(x^{*}\left(t\right),T-t)=\{\xi (x^{*}\left(t\right),T-t)={\int }_t^T\beta \left(\tau \right)d\tau :\hfill \\ \hfill & \xi (x^{*}\left(t\right),T-t)\mathit{and}\mathit{corresponding}\beta \left(\tau \right)\mathit{satisfies}\left(10\right),\hfill \\ \hfill & \cancel{\exists }\overline{\beta }\left(t\right),S,\overline{t}:\overline{\beta }\left(t\right)\stackrel{S,\overline{t}}{\succ }\beta \left(t\right)\}.\hfill \end{array}$$

(20)

We note that $IDP-core(x^{*}\left(t\right),T-t)$ includes such imputations from the Core $C(x^{*}\left(t\right),T-t)$ of cooperative game $\mathsf{\Gamma }(x_0,T-t_0)$ for which there exists corresponding undominated IDP and this IDP generates a dynamic imputation belonging $C(x^{*}\left(t\right),T-t)$ for each $t\in [t_0,T]$.

Theorem 3.

Let $C(x^{*}\left(t\right),T-t)$ be not empty for any $t\in [t_0,T)$. Dynamic imputation $\xi (x^{*}\left(t\right),T-t)$ in cooperative differential game $\mathsf{\Gamma }(x_0,T-t_0)$ belongs to the dynamic $IDP-core(x^{*}\left(t\right),T-t)$, if and only if for corresponding $\beta \left(t\right)=\beta (t,\xi (x_0,T-t_0))$ the following conditions are satisfied $\forall t\in [t_0,T]$:

$$\begin{array}{cc}\hfill & \sum _{i\in S}^{}{\beta }_i\left(t\right)\ge U(S;x^{*}\left(t\right),T-t),\forall S\subset N,\hfill \end{array}$$

(21)

$$\begin{array}{c}\sum _{i\in N}^{}{\beta }_i\left(t\right)=U(N;x^{*}\left(t\right),T-t).\hfill \end{array}$$

(22)

Proof. 

Sufficiency. Let for corresponding IDP $\beta \left(t\right)=\beta (t,\xi (x_0,T-t_0))$ conditions (21) and (22) hold at any $t\in [t_0,T]$. By integrating (21) and (22) in interval we obtain

$$\begin{array}{c}\sum _{i\in S}^{}\xi (x^{*}\left(t\right),T-t)\ge V(S;x^{*}\left(t\right),T-t),\forall S\subset N,\hfill \\ \sum _{i\in N}^{}\xi (x^{*}\left(t\right),T-t)=V(N;x^{*}\left(t\right),T-t).\hfill \end{array}$$

(23)

This means the imputation

$$\xi (x_0,T-t_0)={\int }_{t_0}^T\beta \left(t\right)dt\in C(x^{*}\left(t_0\right),T-t_0)=C(x_0,T-t_0).$$

Let us show that $\beta \left(t\right)=\beta (t,\xi (x_0,T-t_0))$ is undominated. It is proven by contradiction. Suppose for some $\overline{S}\subset N$ there exists $\overline{t}\in [t_0,T]$ and $\overline{\beta }\left(t\right)$ such that

$$\begin{array}{c}\xi (x_0,T-t_0)={\int }_{t_0}^T\overline{\beta }\left(t\right)dt\in L(x_0,T-t_0),\hfill \\ {\overline{\beta }}_i\left(\overline{t}\right)>{\beta }_i\left(\overline{t}\right),i\in \overline{S},\hfill \\ \sum _{i\in \overline{S}}^{}{\overline{\beta }}_i\left(\overline{t}\right)\le U(\overline{S};x^{*}\left(\overline{t}\right),T-\overline{t}).\hfill \end{array}$$

(24)

Therefore

$$\sum _{i\in \overline{S}}^{}{\beta }_i\left(\overline{t}\right)<U(\overline{S};x^{*}\left(\overline{t}\right),T-\overline{t}).$$

This inequality contradicts to (21). Thus $\beta \left(t\right)=\beta (t,\xi (x_0,T-t_0))$ is undominated on the interval $[t_0,T]$. Notice that $\beta \left(t\right)$ is undominated on any subinterval $[\tau ,T]$, $\tau \in [t_0,T]$, in subgame $\mathsf{\Gamma }(x^{*}\left(\tau \right),T-\tau )$.

For $S=\left\{i\right\}$ condition (21) is represented in the form

$${\beta }_i\left(t\right)\ge U(\left\{i\right\};x^{*}\left(t\right),T-t),i\in N.$$

Integrating these inequalities and equality (22) and taking into account (9), (17) we obtain

$$\begin{array}{c}{\xi }_i(x^{*}\left(t\right),T-t)={\int }_t^T{\beta }_i\left(\tau \right)d\tau \ge V(\left\{i\right\};x^{*}\left(t\right),T-t),i\in N,\hfill \\ \sum _{i\in N}^{}{\xi }_i(x^{*}\left(t\right),T-t)=\sum _{i\in N}^{}{\int }_t^T{\beta }_i\left(\tau \right)d\tau =V(N;x^{*}\left(t\right),T-t).\hfill \end{array}$$

(25)

Thus dynamic payoff

$$\xi (x^{*}\left(t\right),T-t)={\int }_t^T\beta \left(\tau \right)d\tau$$

is the imputation in current game $\mathsf{\Gamma }(x^{*}\left(t\right),T-t)$ generated by corresponding IDP $\beta \left(t\right)=\beta (t,\xi (x_0,T-t_0))$.

Due to the non-emptiness of $C(x^{*}\left(t\right),T-t)$ for any $t\in [t_0,T]$ the IDP $\beta \left(t\right)=\beta (t,\xi (x_0,T-t_0))$ which satisfies (21) and (22) generates the payoff vector

$$\xi (x^{*}\left(t\right),T-t)={\int }_t^T\beta \left(\tau \right)d\tau ,$$

which belongs to $C(x^{*}\left(t\right),T-t)$. Thus $\xi (x^{*}\left(t\right),T-t)$ satisfies (10) and therefore imputation $\xi (x_0,T-t_0)$ is time-consistent and lies in $IDP-core(x_0,T-t_0)$.

Necessity. Let imputation $\xi (x_0,T-t_0)$ in the cooperative differential game $\mathsf{\Gamma }(x_0,T-t_0)$ belong to $IDP-core(x_0,T-t_0)$. Therefore by Definition 6 the imputation $\xi (x_0,T-t_0)$ generated by undominated IDP $\beta \left(t\right)=\beta (t,\xi (x_0,T-t_0))$ belongs to $C(x_0,T-t_0)$ and is time-consistent. Due to Definition 6 the time-consistency of imputation $\xi (x_0,T-t_0)$ means that there exists IDP $\beta \left(t\right)$ such that

$$\xi (x^{*}\left(t\right),T-t)={\int }_t^T\beta \left(\tau \right)d\tau \in C(x^{*}\left(t\right),T-t),t\in [t_0,T].$$

Let us show that this inclusion takes place for the undominated $\beta \left(t\right)=\beta (t,\xi (x_0,T-t_0))$ corresponding to imputation $\xi (x_0,T-t_0)$. Suppose this is not the fact. Then there exists coalition $\overline{S}\subset N$ and some instant $\overline{t}\in [t_0,T]$ such that the following inequality holds

$$\sum _{i\in \overline{S}}{\int }_{\overline{t}}^T\beta \left(t\right)dt<V(\overline{S};x^{*}\left(\overline{t}\right),T-\overline{t}).$$

(26)

Notice that $\beta \left(\overline{t}\right)=\beta (\overline{t},\xi (x_0,T-t_0))$ belongs to the set of undominated imputations in a cooperative game with the characteristic function $U(S;x^{*}\left(\overline{t}\right),T-\overline{t})$, $S\subseteq N$. Therefore as follows from Theorem 1 for $\overline{S}\subset N$ the following has to be fulfilled

$$\sum _{i\in \overline{S}}{\beta }_i\left(\overline{t}\right)dt\ge U(\overline{S};x^{*}\left(\overline{t}\right),T-\overline{t}).$$

(27)

Integrating this inequality in interval $[\overline{t},T]$ we receive

$$\sum _{i\in \overline{S}}{\int }_{\overline{t}}^T{\beta }_i\left(t\right)dt\ge V(\overline{S};x^{*}\left(\overline{t}\right),T-\overline{t}),$$

(28)

which contradicts (27). Thus the Theorem is proved. □

Proposition 1.

If $C(x^{*}\left(t\right),T-t)$ is empty for some $t=\overline{t}\in [t_0,T]$, then $IDP-core(x^{*}\left(t_0\right),T-t_0)$ is empty.

Proof. 

Suppose we can find the time-consistent imputation $\xi (x_0,T-t_0)\in IDP-core(x^{*}\left(t_0\right),T-t_0)$ and corresponding undominated IDP $\beta \left(t\right)$, which satisfies (21) and (22). Integrating inequalities (21) and (22) we obtain

$$\begin{array}{c}\sum _{i\in S}^{}{\int }_{\overline{t}}^T{\beta }_i\left(\tau \right)d\tau \ge V(S;x^{*}\left(\overline{t}\right),T-\overline{t}),S\subset N,\hfill \\ \sum _{i\in N}^{}{\int }_{\overline{t}}^T{\beta }_i\left(\tau \right)d\tau =V(N;x^{*}\left(\overline{t}\right),T-\overline{t}).\hfill \end{array}$$

(29)

Thus we receive

$$\xi (x^{*}\left(\overline{t}\right),T-\overline{t})={\int }_{\overline{t}}^T\beta \left(\tau \right)d\tau \in C(x^{*}\left(\overline{t}\right),T-\overline{t}).$$

(30)

It contradicts with emptiness of $C(x^{*}\left(\overline{t}\right),T-\overline{t})$. Therefore, $IDP-core(x^{*}\left(t_0\right),T-t_0)$ is empty. The Proposition is proved. □

Proposition 2.

If $C(x^{*}\left(t\right),T-t)$ is not empty for any $t\in [t_0,T]$ then $IDP-core(x^{*}\left(t_0\right),T-t_0)=C(x^{*}\left(t_0\right),T-t_0)$.

Proof. 

Consider an imputation $\xi (x_0,T-t_0)\in C(x^{*}\left(t_0\right),T-t_0)$ that does not belong to $IDP-core(x^{*}\left(t_0\right),T-t_0)$. That is $\xi (x_0,T-t_0)$ belongs to $C(x^{*}\left(t_0\right),T-t_0)$, but is time inconsistent. According to the time consistency imputation definition $\xi (x_0,T-t_0)$ is time inconsistent if there does not exist IDP $\beta \left(t\right)=\beta (t,\xi (x_0,T-t_0))$ such that at any $t\in [t_0,T]$ dynamic imputation $\xi (x^{*}\left(t\right),T-t)$ generated by this IDP belongs to core $C(x^{*}\left(t\right),T-t)$.

But as follows from Theorem 3, if the corresponding IDP $\beta \left(t\right)=\beta (t,\xi (x_0,T-t_0))$ satisfies conditions (21) and (22), then $\xi (x_0,T-t_0)$ belongs to $IDP-core(x_0,T-t_0)$. That is $\xi (x_0,T-t_0)$ is time-consistent by Definition 6, that is the following inclusion holds for any $t\in [t_0,T]$

$$\xi (x^{*}\left(t\right),T-t)={\int }_t^T\beta \left(\tau \right)d\tau \in C(x^{*}\left(t\right),T-t).$$

The Proposition is proved. □

Remark 1.

Proposition 2 states that if the Core is not empty, then IDP-core and Core coincide in the current game or equivalently imputations from the Core coincide with the imputations from the IDP-core. The system of inequalities (21) and (22) allows extracting the subset from the set of imputation distribution procedures which provides time-consistency and IDP-nondominance of imputations from the Core. For other subsets of the IDP set, this kind of result generally speaking is not true. Note also that the set of imputation distribution procedures (21) and (22) can be empty. In the next section consider the approach to check nonemptiness and construction of IDP’s from the IDP-core.

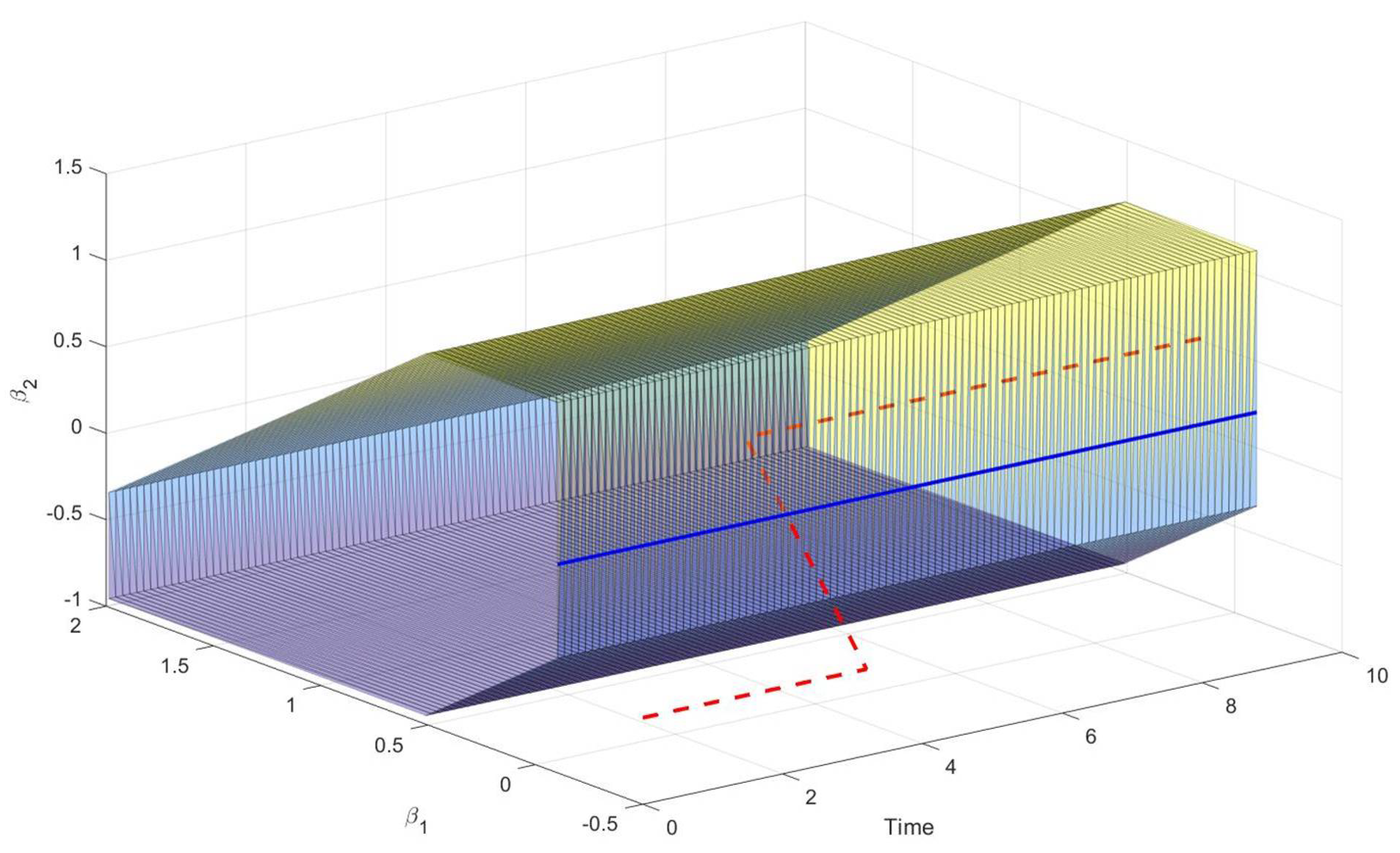
Suppose that the characteristic function $V(S;x^{*}\left(t\right),T-t)$, $t\in [t_0,T]$ is defined in some relevant way (for example, as in [25]). Suppose that it is a strictly monotonically decreasing function for any $t\in [t_0,T]$, decreasing faster than the linear law. Construct the Core $C(x_0,T-t_0)$ for the initial instant $t=t_0$. Afterwards choose imputation from the Core $\xi (x_0,T-t_0)\in C(x_0,T-t_0)$. According to the Definition 2 we choose the corresponding imputation distribution procedure $\beta \left(t\right)=\beta (t,\xi (x_0,T-t_0))$ (IDP) for $\xi (x_0,T-t_0)$ in some relevant way. As it follows from Proposition 2 for the imputations $\xi (x_0,T-t_0)\in IDP-core(x^{*}\left(t_0\right),T-t_0)=C(x^{*}\left(t_0\right),T-t_0)$ we can always find IDP ${\beta }^{\prime }\left(t\right)$ satisfying the conditions (21) and (22) such that:

$${\int }_{t_0}^T{\beta }^{\prime }\left(t\right)dt=\xi (x_0,T-t_0).$$

On the other hand $\beta \left(t\right)=\beta (t,\xi (x_0,T-t_0))$ could not satisfy conditions (21) and (22). It could be the case if $\beta \left(t\right)=\beta (t,\xi (x_0,T-t_0))$ is chosen in the following way

$$\begin{array}{c}\beta \left(t\right)=c=const,t\in [t_0,t^{\prime }),\left(t^{\prime }\in (t_0,T)\right),\hfill \\ \beta \left(t\right)=\frac{\xi (x_0,T-t_0)-c(t^{\prime }-t_0)}{T-t^{\prime }},t\in [t^{\prime },T]\hfill \end{array}$$

and the derivative of $V(S;x^{*}\left(t\right),T-t)$

$$U(S;x^{*}\left(t\right),T-t)>0,t\in [t_0,T].$$

This case will be demonstrated on the model example in Section 5.

Proposition 3.

If $C(x^{*}\left(t\right),T-t)$ is not empty for any $t\in [t_0,T]$, then all imputations of $C(x^{*}\left(t_0\right),T-t_0)$ are time-consistent.

Proof. 

Consider am imputation $\xi (x_0,T-t_0)$ from Core $C(x^{*}\left(t_0\right),T-t_0)$. According to the Proposition 2 $IDP-core(x^{*}\left(t_0\right),T-t_0)=C(x^{*}\left(t_0\right),T-t_0)$ and therefore $\xi (x_0,T-t_0)\in IDP-core(x^{*}\left(t_0\right),T-t_0)$. From the definition of the IDP-core it follows that $\xi (x_0,T-t_0)$ is time-consistent. The Proposition is proved. □

4. Application of Linear Programming Methods for Nonemptiness Properties

In this section, we consider the linear programming problem described in Section 2.4, for the non-emptiness properties of Core. IDP-core can be constructed using a system of linear constraints for the imputation distribution procedures. These constraints are defined for each instant in the game. From the nonemptiness of the set described by these constraints, it follows that the IDP-core is not empty.

Consider the following linear programming problem for a fixed t:

$$\begin{array}{c}\sum _{i\in N}{\beta }_i⟶min\hfill \\ \sum _{i\in S}{\beta }_i\ge U(S;x^{*}\left(t\right),T-t),\forall S\subseteq N,S\ne N,S\ne ⌀.\hfill \end{array}$$

(31)

Suppose that ${\beta }_i^0=({\beta }_1^0,\dots ,{\beta }_n^0)$ is an optimal solution of linear programming problem (31) with fixed t. The set of optimal solutions of problem (31) we denote by $Y^0$.

Then the following theorem is true:

Theorem 4.

The set of IDPs satisfying the conditions (25), $t\in [t_0,T)$ is not empty, if and only if $\forall t\in [t_0,T)$ the following condition is satisfied:

$$\sum _{i\in N}{\beta }_i^0\le U(N;x^{*}\left(t\right),T-t),$$

(32)

where ${\beta }^0\in Y^0$ is any solution of the linear programming problem (31).

Proof. 

Start the proof with the sufficient condition. Suppose that the condition (32) is satisfied, then according to (31) for any $t\in [t_0,T]$ there exists ${\widehat{\beta }}^0$ such that for

$${\beta }_i={\beta }_i^0+\frac{U(N;x^{*}\left(t\right),T-t)}{n}-\frac{{\sum }_{i\in N}{\beta }_i^0}{n},i\in N$$

(33)

conditions (21) and (22) are satisfied for any fixed $t\in [t_0,T]$. If it is true, then we can compose the integrable function ${\widehat{\beta }}^0\left(t\right)$ as a function of time, for which the conditions (21) and (22) will be satisfied.

Proof of the necessity condition. If the IDP-core is not empty, then there exists at least one integrable function $\beta \left(t\right)$ satisfying the conditions (21) and (22). As a result for the solution of (31) condition (32) should be satisfied. □

5. Differential Game Model of Resource Extraction

Consider a game-theoretical model of non-renewable resource extraction with asymmetric players [29,30]. The amount of resource depends on the rates of extraction which are chosen by the players. The game involves n asymmetric players, with utility functions depending on the current amount of resource and rates of extraction.

Denote by $x\left(t\right)\in R^1$ the amount of resource at instant t and by $u_i(t,x)$ resource extraction rate chosen by player i at instant t. As a class of strategies we will consider a class of feedback strategies, where the strategies are the functions of time t and state x. We assume that $\forall t$, $u_i(t,x)\ge 0$, and $x\left(t\right)=0$ implies $u_i(t,x)=0$. The amount of the resource $x\left(t\right)$ as a function of t depends in the following way on $u_i(t,x)$:

$$\begin{array}{c}\dot{x}=-\sum _{i=1}^n{a}_i{u}_i(t,x),a_i>0,i=1,\dots ,n.\\ x\left(t_0\right)=x_0.\end{array}$$

(34)

Payoff function representing the income of player i:

$$K_i(x_0,T-t_0)=\underset{t_0}{\overset{T}{\int }}log\left(u_i(\tau ,x)\right)d\tau ,i=1,\dots ,n.$$

(35)

5.1. Cooperative Strategies and Cooperative Trajectory

Consider the cooperative version of a non-renewable resource extraction game [30]. Here, players unite in a grand coalition and maximize total utility, acting as one player. The corresponding optimal control problem is formalized in the following way:

$$\sum _{i=1}^n{K}_i(x_0,T-t_0)=\sum _{i=1}^n\underset{t_0}{\overset{T}{\int }}log\left(u_i(\tau ,x)\right)d\tau \to \underset{u_i,i=\overline{1,n}}{max}$$

(36)

subject to

$$\begin{array}{cc}\hfill & \dot{x}=-\sum _{i=1}^n{a}_i{u}_i(t,x),\hfill \\ \hfill & x\left(t_0\right)=x_0>0,\hfill \\ \hfill & u(t,x)\ge 0.\hfill \end{array}$$

(37)

To solve the optimization problem (36), (37), we use the dynamic programming principle proposed by Bellman. To do this we define the Bellman function as the maximum value of the total payoff of players (35) in the subgame $\mathsf{\Gamma }(x,T-t)$ starting at the instant t in the position x:

$$W(t,x)=\underset{u_i,i=\overline{1,n}}{max}\left\{\sum _{i=1}^n{K}_i(x,T-t)\right\}=\underset{u_i,i=\overline{1,n}}{max}\left\{\sum _{i=1}^n\underset{t}{\overset{T}{\int }}logu(\tau ,x)d\tau \right\}$$

(38)

subject to Equation (37), when $x_0=x$ and $t_0=t$.

It is proved that if there exists a continuously differentiable function $W(t,x)$ that satisfies the Hamilton-Jacobi-Bellman equation

$$\begin{array}{c}-W_t(t,x)=\underset{u_i,i=\overline{1,n}}{max}\left\{\sum _{i=1}^{n}log{u}_i(t,x)-W_x(t,x)\left(\sum _{i=1}^n{a}_i{u}_i(t,x)\right)\right\},\\ \underset{t\to T-0}{lim}W(t,x)=0,\end{array}$$

(39)

then strategies $u_i^{*}(t,x)$ defined by maximizing the right hand side (39) deliver the maximum to the functional in the optimization problem (36), (37).

From the first order extremum condition of (39), we obtain:

$$u_i^{*}=\frac{1}{a_i{W}_x(t,x)},$$

then substituting to (39):

$$\begin{array}{c}{W}_t(t,x)=nlog{W}_x(t,x)+log{A}^{\left[N\right]}+n,A^{\left[N\right]}=\prod _{i=1}^n{a}_i\\ \underset{t\to T-0}{lim}W(t,x)=0.\end{array}$$

(40)

We will consider a Bellman function as a function of the form:

$$W(t,x)=A\left(t\right)logx+B\left(t\right),$$

then, by substituting in (40), we obtain:

$$\begin{array}{c}\dot{A}logx+\dot{B}=nlogA-nlogx+log{A}^{\left[N\right]}+n,\\ \underset{t\to T-0}{lim}A\left(t\right)=\underset{t\to T-0}{lim}B\left(t\right)=0.\end{array}$$

(41)

The solution of (41) are the functions:

$$\begin{array}{cc}\hfill A\left(t\right)& =n(T-t),\hfill \\ \hfill B\left(t\right)& =-(T-t)\left(log{A}^{\left[N\right]}+nlogn(T-t)\right).\hfill \end{array}$$

(42)

By substituting $A\left(t\right)$ and $B\left(t\right)$ into the Bellman function we obtain:

$$W(t,x)=n(T-t)log\frac{x}{n(T-t)}-\left(T-t\right)log{A}^{\left[N\right]},t\in [t_0,T).$$

(43)

The corresponding form of optimal control or cooperative strategy:

$$u_i^{*}(t,x)=\frac{1}{a_i{W}_x(t,x)}=\frac{x}{a_{i}n(T-t)},t\in [t_0,T).$$

(44)

Substituting the optimal control into the motion Equation (37), we obtain the differential equation for the trajectory corresponding to the optimal control:

$$\begin{array}{cc}\hfill & \dot{x}=-\frac{x}{T-t},\hfill \\ \hfill & x\left(t_0\right)=x_0.\hfill \end{array}$$

(45)

The solution has the form:

$$x^{*}\left(t\right)=x_0\frac{T-t}{T-t_0},t\in [t_0,T).$$

(46)

Trajectory $x^{*}\left(t\right)$ and strategy (control) $u^{*}(t,x)$ we will call cooperative.

In order to determine the value of players’ maximum total payoff that corresponds to the optimization problem (36), (37) in the subgame along the cooperative trajectory $x^{*}\left(t\right)$ (46), it is necessary to substitute the expression for the cooperative trajectory by the expression for the Bellman function (43):

$$W(t,x^{*}\left(t\right))=n(T-t)log\frac{x_0}{n(T-t_0)}-\left(T-t\right)log{A}^{\left[N\right]},t\in [t_0,T).$$

(47)

5.2. Characteristic Function

To construct the rule for allocating the maximum joint payoff among players, it is necessary to define the characteristic function for each coalition $S\subseteq N$:

$$V(S;x,T-t)=\left\{\begin{array}{cc}\sum _{i=1}^n{K}_i(x,T-t),\hfill & S=N\hfill \\ W_S(t,x),\hfill & S\subset N,\hfill \\ 0,\hfill & S=\varnothing ,\hfill \end{array}\right.$$

(48)

where $W_S(t,x)$ is defined as the maximum joint payoff of coalition S given that the players from coalition $N\setminus S$ use strategies from a fixed Nash equilibrium $u^{NE}=\left(u_1^{NE},\cdots ,u_n^{NE}\right)$ in the initial game.

It can be shown that in the case of a non-cooperative game, Nash equilibrium strategies are

$$u_i^{NE}(t,x)=\frac{x}{a_i(T-t)},i\in N.$$

(49)

Consider a case of coalition $S\subset N$. We introduce the Bellman function $W_S(t,x)$, as the maximum total payoff of players from coalition S in the subgame $\mathsf{\Gamma }(x,T-t)$ starting at the instant t in the position x:

$$\begin{array}{cc}\hfill W_S(t,x)& =\underset{u_i,i\in S}{max}\sum _{i\in S}\left\{{\int }_t^{T}log{u}_{i}d\tau \right\}\hfill \end{array}$$

(50)

$$\begin{array}{cc}\hfill \mathrm{subject}\mathrm{to}\dot{x}\left(\tau \right)& =-\sum _{i\in N}{a}_i{u}_i\hfill \end{array}$$

(51)

$$\begin{array}{cc}\hfill u_i& =u_i^{NE},i\in N\setminus S.\hfill \end{array}$$

(52)

The Hamilton-Jacobi-Bellman equation for this problem has the form:

$$\begin{array}{c}-\frac{\partial W_S(t,x)}{\partial t}=\underset{u_i,i\in S}{max}\left\{\sum _{i\in S}log{u}_i(t,x)-\frac{\partial W_S(t,x)}{\partial x}\left(\sum _{j=1}^n{a}_j{u}_j(t,x)\right)\right\},\\ \underset{t\to T-0}{lim}{W}_S(t,x)=0.\end{array}$$

(53)

From the first order extremum condition for (53) we obtain

$$u_i^{*}=\frac{1}{a_i\frac{\partial W_S(t,x)}{\partial x}},$$

(54)

substitute in (53):

$$\begin{array}{c}\frac{\partial W_S}{\partial t}=klog\frac{\partial W_S}{\partial x}+log{A}^{\left[S\right]}+k+\frac{\partial W_S}{\partial x}\sum _{j\in N\setminus S}\frac{x}{T-t},A^{\left[S\right]}=\prod _{i=1}^n{a}_i\\ \underset{t\to T-0}{lim}{W}_S(t,x)=0,\end{array}$$

(55)

where $k=\left|S\right|$, $n=\left|N\right|$. Consider the following form of the Bellman function:

$$W_S(t,x)=A\left(t\right)logx+B\left(t\right),$$

then by substituting in (55) we obtain:

$$\begin{array}{c}\dot{A}logx+\dot{B}=klogA-klogx+log{A}^{\left[S\right]}+k+(n-k)\frac{A}{T-t},\\ \underset{t\to T-0}{lim}A\left(t\right)=\underset{t\to T-0}{lim}B\left(t\right)=0.\end{array}$$

(56)

The solution of (56) are the functions:

$$\begin{array}{cc}\hfill A\left(t\right)& =k(T-t),\hfill \\ \hfill B\left(t\right)& =-k(T-t)\left(\frac{log{A}^{\left[S\right]}}{k}+logk(T-t)+n-k\right).\hfill \end{array}$$

(57)

Solution of the optimization problem (50):

$$W_S(t,x)=k(T-t)\left[log\frac{x}{T-t}-logk-\frac{log{A}^{\left[S\right]}}{k}-n+k\right].$$

(58)

According to the definition, we obtain the characteristic function for the coalition $S\ne N$:

$$V(S,x,T-t)=W_S(t,x).$$

In order to determine the way to allocate the maximum joint payoff of players (47) among them along the cooperative trajectory $x^{*}\left(t\right)$ (46), namely, for the subgame starting at the instant t on the cooperative trajectory $x^{*}\left(t\right)$ (46) it is necessary to define the characteristic function along the cooperative trajectory. Let us substitute the expression for $x^{*}\left(t\right)$ (46) into the expression for characteristic function $V(S,T-t,x)$, $S\subset N$ (58).

$$W_S(t,x^{*}\left(t\right))=k(T-t)\left[log\frac{x_0}{T-t_0}-logk-\frac{log{A}^{\left[S\right]}}{k}-n+k\right].$$

(59)

For the case when $S=N$, the characteristic function is calculated in accordance with (47).

5.3. IDP-Core

Suppose that all players unite in grand coalition N, then they can guarantee themselves joint payoff equal to $V(N;x^{*}\left(t\right),T-t)$. In order to determine how to allocate the maximum joint payoff among players, we use the notion of imputations $\xi (x,T-t)$. In particular, we will use IDP-core as a cooperative solution in the game. According to Theorem 3, IDP-core can be constructed using the conditions for IDP’s ${\beta }_i\left(t\right)$, $i\in N$:

$$\begin{array}{c}\sum _{i\in S}^{}{\beta }_i\left(t\right)\ge -kt\left[log\frac{x_0}{T-t_0}-logk-\frac{log{A}^{\left[S\right]}}{k}-n+k\right],\forall S\subset N,\hfill \\ \sum _{i\in N}^{}{\beta }_i\left(t\right)=-ntlog\frac{x_0}{n(T-t_0)}-\left(T-t\right)log{A}^{\left[N\right]},\forall t\in [t_0,T].\hfill \end{array}$$

(60)

5.4. Non-Emptiness of IDP-Core

In order to study non-emptiness conditions we solve the linear programming problem, as presented in the paper [24], for $t\in [t_0,T]$ with a fixed step $\Delta t$. As a result, the vector function ${\beta }^0=({\beta }_1^0,\dots ,{\beta }_n^0)$ is obtained using the numerical methods and corresponding conditions are to be verified in order for the IDP-core to be non-empty:

$$\sum _{i\in N}{\beta }_i^0\le U(N;x^{*}\left(t\right),T-t).$$

(61)

We construct IDP ${\widehat{\beta }}^0\left(t\right)$ using ${\beta }^0\left(t\right)$ and show that it satisfies the conditions (25):

$${\widehat{\beta }}_i^0\left(t\right)={\beta }_i^0\left(t\right)+\frac{U(N;x^{*}\left(t\right),T-t)-{\sum }_{i\in N}{\beta }_i^0\left(t\right)}{n}.$$

(62)

5.5. Core and IDP-Core

According to the Theorem 3, the imputation that corresponds to the IDP ${\widehat{\beta }}^0\left(t\right)$

$$\xi (x_0,T-t_0)=\underset{t_0}{\overset{T}{\int }}{\widehat{\beta }}^0\left(t\right)dt$$

(63)

belongs to the Core $C(x_0,T-t_0)$ because, for given parameters IDP ${\widehat{\beta }}^0\left(t\right)$, $t\in [t_0,T]$ satisfies conditions (21) and (22) or $\xi (x_0,T-t_0)$ belongs to $IDP-core(x_0,T-t_0)$. But if we use the Core $C(x_0,T-t_0)$ instead of $IDP-core(x_0,T-t_0)$ as a cooperative solution in the game, then we can use any IDP for the imputation (63), such as

$$\begin{array}{c}\beta \left(t\right)=c=const,t\in [t_0,t^{\prime }),\left(t^{\prime }\in (t_0,T)\right),\hfill \\ \beta \left(t\right)=\frac{\xi (x_0,T-t_0)-c(t^{\prime }-t_0)}{T-t^{\prime }},t\in [t^{\prime },T],\hfill \end{array}$$

(64)

but this does not necessarily satisfy conditions (21) and (22) at some instant and therefore it appears not to be undominated and corresponding to this IDP imputation $\xi (x_0,T-t_0)$ is time-inconsistent.

On Figure 1 the set defined by the system of constrains (25) shown, the solid line is the solution ${\beta }^0\left(t\right)$ of corresponding linear programming problem (31) as a function of time, the dashed line is IDP ${\widehat{\beta }}^0\left(t\right)$ and IDP $\beta \left(t\right)$ (64) corresponding to the imputation (63).

Function ${\widehat{\beta }}_i^0\left(t\right)$ satisfies the constrains (25). It can be seen that the IDP-core in this game model is not empty and conditions (32) of Theorem 4 are satisfied.

Using Figure 2 it is possible to verify the non-emptiness conditions (32) of Theorem 6, the solid line shows the sum of values ${\beta }_i^0\left(t\right)$, $i=\overline{1,3}$:

$$S_{{\beta }^0}\left(t\right)={\beta }_1^0\left(t\right)+{\beta }_2^0\left(t\right)+{\beta }_3^0\left(t\right),$$

(65)

the dashed line in the Figure 2 shows the value of characteristic function for a grand coalition

$$U(N;x^{*}\left(t\right),T-t)=U(\{1,2,3\};x^{*}\left(t\right),T-t),$$

where $U(\{1,2,3\};x^{*}\left(t\right),T-t)$ is defined in (17). In the Figure 2 it can be seen that

$$S_{{\beta }^0}\left(t\right)\le U(\{1,2,3\};x^{*}\left(t\right),T-t)\forall t\in [t_0,T].$$

6. Conclusions

This paper examines a new approach for defining a cooperative solution for differential games. Our approach uses the time consistency property as a basic axiom for constructing the cooperative solution. It is important to notice that the further use of the time consistency property as the axiom for the theory of dynamic cooperative games, the theory of social choice, and mechanism design is promising. The approach also defines the notion of IDP-dominance, which allows for selecting undominated imputation distribution procedures. Properties of time consistency and IDP-dominance are the key properties for constructing a new cooperative solution, namely IDP-core. The necessary and sufficient conditions for the IDP-core defining geometric properties of this solution are presented. It is also proved that the set of imputations that corresponds to the Core and to IDP-core coincides, but, as the simulation demonstrates, the IDPs that would be naturally proposed for use sometimes might not appear to be undominated and therefore lead to the time inconsistency of the corresponding imputations they generate.