Abstract
Canal surfaces are defined and divided into nine types in Minkowski 3-space , which are obtained as the envelope of a family of pseudospheres , pseudohyperbolic spheres , or lightlike cones , whose centers lie on a space curve (resp. spacelike curve, timelike curve, or null curve). This paper focuses on canal surfaces foliated by pseudohyperbolic spheres along three kinds of space curves in . The geometric properties of such surfaces are presented by classifying the linear Weingarten canal surfaces, especially the relationship between the Gaussian curvature and the mean curvature of canal surfaces. Last but not least, two examples are shown to illustrate the construction of such surfaces.
1. Introduction
The concept of canal surface is the envelope of a moving sphere whose centers lie on a space curve, and their radius varies depending on this curve in Euclidean 3-space . Canal surfaces are useful for representing long thin objects, e.g., pipes, ropes, 3D fonts, or internal body organs in solid/surface modeling. Tori and tubes are the special types of the canal surfaces. Apart from being used in pure mathematics, canal surfaces are a kind of blending surface that plays an important role in computer aided geometric design, i.e., CAGD. Most studies on canal surfaces within the CAGD context is related to such surfaces with a rational spine curve and rational radius function. For example, the authors presented that each canal surface with a rational spine curve and rational radius function is a rational Pythagorean hodograph curve in Minkowski space [1,2].
The Lorentz–Minkowski space is the basic space model of quantum physics that plays an important role in general relativity. In recent years, with the development of the theory of relativity, physicians and geometers extended the topics in classical differential geometry of Riemannian manifolds to that of Lorentzian manifolds. It is clearly demonstrated by the fact that many works in Euclidean space have found their counterparts in Minkowski space [3]. At present, the properties of canal surfaces have been researched in [4,5]. As a natural idea, we can extend canal surfaces into spaces with an indefinite metric, such as Minkowski space. Similar to the generating process of canal surfaces in , a canal surface in Minkowski 3-space can be obtained as the envelope of a family of pseudospheres , pseudohyperbolic spheres , or lightlike cones whose centers lie on a space curve (resp. spacelike curve, timelike curve, or null curve). The classification of canal surfaces was obtained by Ucum and Ilarslan in [6]. For convenience, the authors of this paper denoted the notations for all kinds of canal surfaces in . At the same time, the authors discussed canal surfaces foliated by pseudospheres along three kinds of space curves in [7]. The relationship between Gaussian curvature and mean curvature is revealed, which is an important tool for future research, such as the Weingarten canal surfaces or linear Weingarten canal surfaces. Weingarten surfaces (resp. linear Weingarten surfaces) are attractive for use in CAGD, particularly in surface design due to the advantages of using these surfaces that can mitigate curvature computations and also admit simpler, more direct shape control procedures [8].
As a follow-up work of [7], in this paper we focus on the geometric properties of canal surfaces foliated by pseudohyperbolic spheres along three kinds of space curves in . We discuss canal surfaces purely by geometric arguments, thereby avoiding a cumbersome algorithmic procedure. The paper is organized as follows. In Section 2, we review the Frenet formulas of space curves and the definitions of canal surfaces in . We recall definitions of Weingarten surface and linear Weingarten surface in . In Section 3, the geometric properties of three types of canal surfaces are discussed, respectively. For each type of canal surface, the relationships between Gaussian curvature and mean curvature are presented (Theorems 1, 5, and 9). Different kinds of linear Weingarten canal surfaces are explored, the developable, minimal and umbilical canal surfaces are discussed at the same time. The applications of these surfaces in shape control are important hopefully motivated. Finally, some common results for canal surfaces are shown (Theorems 13 and 14).
2. Preliminaries
Let be a Minkowski 3-space with natural Lorentzian metric
in terms of the natural coordinate system . It is well known that a vector ∈ is said to be spacelike if or ; timelike if ; null (lightlike) if , respectively. The norm of vector v is given by . Due to the causal character of the tangent vector of a space curve, curves in Minkowski space can be divided into a spacelike curve, timelike curve, or null curve. At the same time, a surface is called a timelike surface, spacelike surface, or lightlike surface if its normal vector is spacelike, timelike, or lightlike. In , there exist three space forms, i.e., pseudosphere , pseudohyperbolic sphere , and lightlike cones , which are complete semi-Riemannian manifolds with index 1.
Let , be vectors in . Then, their scalar product is given by
and the exterior product by
where is an orthonormal basis in .
Let be a space curve with a moving Frenet frame consisting of tangent vector T, principal normal vector N, and binormal vector B, respectively.
Case 1. Let be a spacelike curve parameterized by arc length s. Due to the causal character of the normal vector, it can be divided into the following two cases:
Case 1.1. Let , then the following Frenet equations are satisfied
where , , , . Functions and are called the curvature and torsion of , respectively. When , is called the first-kind spacelike curve, and the second-kind spacelike curve when .
Case 1.2. Let , the Frenet equations are given by
where , . Function is also called the curvature function. Such kind of spacelike curve is said to be null-type spacelike.
Case 2. Let be a timelike curve parameterized by arc length s; then, the following Frenet equations are satisfied:
where , , . The functions and are called the curvature and the torsion of , respectively.
Case 3. Let be a null curve with null arc-length parameter s, i.e., . Then, we have
where , Function is called the null curvature of .
Remark 1.
For null curves, there exist a variety of concepts where not all authors’ terminologies coincide. The null curvature here expresses the same meaning as the pseudo torsion or the pseudo curvature in articles related to null curves.
Next, we recall the definition of canal surfaces in as the following:
Definition 1.
[7] Surface in is called a canal surface that is formed as the envelope of a family of pseudohyperbolic spheres (resp. pseudospheres or lightlike cones ) whose centers lie on a space curve framed by . Then, can be parametrized by
where λ, μ and ω are differential functions of s and θ, , ( or 0). Curve is called the center curve (or spine curve), and is the radius function of .
Explicitly, if is foliated by pseudohyperbolic spheres (resp. pseudospheres or lightlike cones ), then (resp. 1 or 0) and is said to be of the type (resp. or ). Canal surfaces of type can be divided into three types. In the case that is spacelike (resp. timelike or null), it is said to be of type (resp. or ). Furthermore, can be divided into , and when is the first-kind spacelike curve, the second-kind spacelike curve, and the null-type spacelike curve, respectively. Similar to , canal surfaces (resp. ) can be divided into , and (resp. , or ). Naturally, (resp. ) can be divided into , and (resp. , or ).
Remark 2.
[9] In particular, if center curve is a straight line, then Frenet frame of can be regarded as a trivial orthogonal frame, and the canal surface is nothing but a surface of revolution. If the radius function is constant, then is a tube (or pipe) surface.
Definition 2.
[10] For curvatures K and H of a surface in , if satisfies
where W is the Jacobian determinant, then that is said to be a Weingarten surface.
Definition 3.
[10] For curvatures K and H of a surface in , if satisfies
then that is said to be a linear Weingarten surface.
Remark 3.
All surfaces we are dealing with are smooth, regular, and topologically connected unless otherwise stated.
3. Main Results
In this part, we focus on the geometric properties of different types of canal surfaces formed by the movement of pseudohyperbolic spheres along a space curve in .
3.1. Canal Surfaces of Type and
First, we assume is a canal surface formed by the movement of along a first kind spacelike curve in . i.e., . According to the definition of , through detailed calculation, we get
in Equation (1). Then, can be parameterized by
where is parameterized by arc length s. For convenience, we may assume for some smooth function . Then, canal surface can be rewritten by
Initially, we have
where
Then, quantities of the first fundamental form are given by
and
Unit normal vector field n to is given by
which point canal surface and outwards.
Furthermore, by Equation (6), we have
Quantities of the second fundamental form are obtained by
From Equations (6) and (7), we have
Proposition 1.
The quantities of the first and second fundamental forms of canal surface satisfy
and
where
Remark 4.
Due to regularity, we see that everywhere by Equation (8).
By Proposition 1, Gaussian curvature K and mean curvature H of are given by, respectively,
Second, for canal surface , according to the definition of , we get
in Equation (1). Then, can be parameterized by
where is parameterized by arc length s. Here, we may assume that for smooth function . So, canal surface can be written by
With similar calculations to those of , we have the following conclusions.
Proposition 2.
The quantities of the first and second fundamental forms of canal surface satisfy
and
where
Remark 5.
Due to regularity, we see everywhere by Equation (13).
By Proposition 2, Gaussian curvature K and mean curvature H of are given by, respectively,
Based on the Gaussian curvature and mean curvature of and , it is obvious to obtain the following results.
Theorem 1.
Gaussian curvature K and mean curvature H of canal surface are related by
Proof of Theorem 1.
Next, we study canal surface whose Gaussian curvature and mean curvature satisfy some particular conditions.
Remark 6.
In the following, we just prove the results for and omit the proof for since it can be similarly done to those of , and the results are same.
Theorem 2.
Let ()be a linear Weingarten canal surface; then, it is an open part of the following surfaces:
- a tube with radius .
Proof of Theorem 2.
Therefore, we get
Case 1: If , i.e., , then . Thus, is a surface of revolution and its radial function satisfies
Solving the above equation, we get
where .
Since , without loss of generality, we may assume the center curve is and , respectively. Then, by Equation (3), can be expressed by
where is given by Equation (19).
Case 2: If , then . Hence, is a nonzero constant. is a tube and satisfy .
Note that is a circular cylinder if . □
Corollary 1.
Let ()be a canal surface with nonzero constant Gaussian curvature. Then, it is a surface of revolution with positive constant Gaussian curvature, such as
where is given by Equation (21).
Proof of Corollary 1.
By Theorem 2 with , when has nonzero constant Gaussian curvature , from , then it is nothing but a surface of revolution with positive constant Gaussian curvature. It can be expressed by
where satisfies
□
Corollary 2.
Canal surface with nonzero constant mean curvature does not exist.
Proof of Corollary 2.
By Theorem 2 with , it must be a surface of revolution. However, from , then , it is a contradiction. □
Theorem 3.
A canal surface ()is developable iff it is congruent to a part of a circular cylinder or a circular cone.
Proof of Theorem 3.
is developable iff . By (10), we have . Then, we get
It follows that and (if , by (5), is degenerate). Then, , where are constants. Therefore, is a circular cylinder () or a circular cone () in , respectively. The converse is obvious. □
Theorem 4.
Canal surface ()is minimal iff it is a part of a surface of revolution, such as
where satisfies (22).
3.2. Canal Surfaces
Let be a canal surface formed by the movement of along a timelike curve in , i.e., . Then, by the definition of and Frenet equations, we obtain
in Equation (1). Then, can be parameterized by
where is parameterized by arc length s. Without loss of generality, we assume for some smooth function . Then, can be written by
Remark 7.
From Equation (23), tube does not exist.
Proposition 3.
The quantities of the first and second fundamental forms of canal surface satisfy
and
where
Remark 8.
Due to regularity, we see everywhere by Equation (25).
By Proposition 3, Gaussian curvature K and mean curvature H of are given by, respectively,
Theorem 5.
Gaussian curvature K and mean curvature H of canal surface are related by
Next, we study canal surface whose Gaussian curvature and mean curvature satisfy some particular conditions. We omitted the proofs for since they are similar to , .
Theorem 6.
Let be a linear Weingarten canal surface; then, it is a surface of revolution, such as
where is given by
Corollary 3.
Let be a canal surface with nonzero constant Gaussian curvature. Then, it is a surface of revolution with positive constant Gaussian curvature, such as
where is given by
Corollary 4.
Canal surface with nonzero constant mean curvature does not exist.
Theorem 7.
A canal surface is developable iff it is a circular cone.
Proof of Theorem 7.
is developable iff . By Equation (27), we have . Then, we get
Theorem 8.
A canal surface is minimal iff it is a part of a surface of revolution such as
where satisfies
3.3. Canal Surfaces of Type and
Let be a canal surface formed by the movement of along a null type spacelike curve , i.e., . By the definition of and Frenet equations, we obtain
in Equation (1). Then, can be parameterized by
where is parameterized by arc length s.
Initially, we have
where
From Equation (31), we can get
Then, the quantities of the first fundamental form are given by
Unit normal vector field n to is given by
which point canal surface and outwards.
Furthermore, by Equation (34) we have
Then, the quantities of the second fundamental form are obtained by
From Equations (34) and (35), we have
Proposition 4.
The quantities of the first and second fundamental forms of canal surfaces satisfy
and
where
Remark 9.
Due to regularity, we see everywhere by Equation (36).
By Proposition 4, Gaussian curvature K and mean curvature H of are given by, respectively,
Second, we study canal surface . By the definition of and the Frenet equations, we obtain
in Equation (1). Then, can be parameterized by
where is parameterized by null arc length s.
Remark 10.
According to Equation (39), tube does not exist.
Proposition 5.
The quantities of the first and second fundamental forms of canal surfaces satisfy
and
where
By Proposition 5, Gaussian curvature K and mean curvature H of are given by, respectively,
Based on the Gaussian curvature and mean curvature of and , it is easy to get the following results.
Theorem 9.
Gaussian curvature K and mean curvature H of canal surface can be related by
Proof of Theorem 9.
Next, we study canal surface whose Gaussian curvature and mean curvature satisfy some particular conditions.
Remark 11.
In the following, we just prove the results for and omit the proofs for , since they can be similarly done to those of and the results are similar.
Theorem 10.
Let be a linear Weingarten canal surface; then, it is a tube with radius
Proof of Theorem 10.
Therefore, we get
Assume , then . By (36), is degenerate. Thus, . Hence, is a nonzero constant. is a tube and satisfy . □
Theorem 11.
Linear Weingarten canal surface does not exist.
Proof of Theorem 11.
Similar to the proof of Theorem 10, through calculation, we obtain that is a nonzero constant. This contradicts the result of Remark 10. Thus it is completed. □
Corollary 5.
Canal surface with nonzero constant Gaussian curvature or nonzero constant mean curvature does not exist.
Proof of Corollary 5.
Similar to Corollary 5, when the Gaussian curvature or mean curvature equal to zero, by (37) and (38), the functions and , obviously. Then, we have
Theorem 12.
Canal surface is nondevelopable and nonminimal.
From the calculations above, we have the following common conclusions.
Theorem 13.
Umbilical canal surface does not exist.
Proof of Theorem 13.
Canal surface is umbilical; this means
from Propositions 1–5, we obtain . It is impossible by the regularity of those canal surfaces. □
Theorem 14.
Canal surfaces are spacelike surfaces in
Proof of Theorem 14.
The normal vector of satisfies ; it is obtained easily. □
Remark 12.
The canal surfaces obtained by pseudo spheres along a space curve, i.e., are discussed in [7]. The canal surfaces foliated by lightcones along a space curve, i.e., are degenerate surfaces by simple calculation. Here, the proof is omitted.
4. Examples
Canal surfaces are very popular in CAGD. In this section, we want to show a method to characterize geometrically via Mathematica Programme.
Example 1.
Let the timelike curve then the Frenet frame are
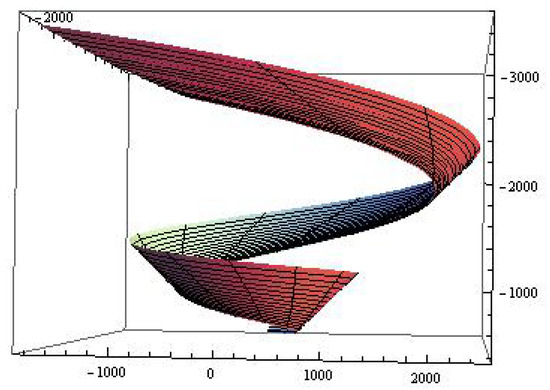
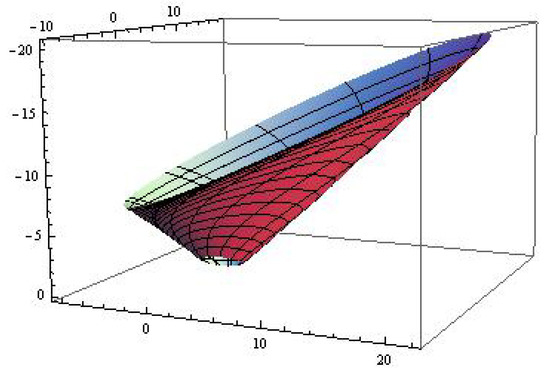
Denoting radius function , then the canal surface of type (see Figure 1) can be written by

Figure 1.
with .
Author Contributions
J.Q., M.S., and X.F. set up the problem and computed the details. S.D.J. checked and polished the draft.
Funding
The first author was supported by NSFC (No. 11801065, 11371080) and the fourth author was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIP) (NRF-2018R1A2B2002046).
Acknowledgments
We thank the referee for the careful review and the valuable comments to improve the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cho, H.C.; Choi, H.I.; Kwon, S.H.; Lee, D.S.; Wee, N.S. Clifford algebra, Lorentzian geometry, and rational parametrization of canal surfaces. Comput. Aided Geom. D 2004, 21, 327–339. [Google Scholar] [CrossRef]
- Farouki, R.T.; Sverrissor, R. Approximation of rolling-ball blends for free-form parametric surfaces. Comput. Aided Des. 1996, 28, 871–878. [Google Scholar] [CrossRef]
- Kim, Y.H.; Yoon, D.W. On non-developable ruled surface in Lorentz-Minkowski 3-spaces. Taiwan J. Math. 2007, 11, 197–214. [Google Scholar] [CrossRef]
- Kim, Y.H.; Liu, H.; Qian, J. Some characterizations of canal surfaces. Bull. Korean Math. Soc. 2016, 53, 461–477. [Google Scholar] [CrossRef]
- Xu, Z.Q.; Feng, R.Z.; Sun, J.G. Analytic and algebraic properties of canal surfaces. Appl. Math. Comput. 2016, 195, 220–228. [Google Scholar] [CrossRef]
- Ucum, A.; Ilarslan, K. New Types of Canal Surfaces in Minkowski 3-Space. Adv. Appl. Clifford Algebr. 2016, 26, 449–468. [Google Scholar] [CrossRef]
- Fu, X.; Jung, S.D.; Qian, J.; Su, M. Geometric characterizations of canal surfaces in Minkowski 3-space . Bull. Korean Math. Soc. 2019, 56, 867–883. [Google Scholar]
- Brunt, B.; Grant, K. Potential applications of Weingarten surfaces in CAGD, Part I: Weingarten surfaces and surface shape investigation. Comput. Aided Geom. D 1996, 13, 569–582. [Google Scholar] [CrossRef]
- Karacan, M.K.; Yoon, D.W.; Tuncer, Y. Tubular surface of Weingarten types in Minkowski 3-space. Gen. Math. Notes 2014, 22, 44–56. [Google Scholar]
- Lopez, R. Rotational linear Weingarten surfaces of hyperbolic type. Isr. J. Math. 2008, 167, 283–302. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).