Abstract
This paper presents a generalized targeting model that subsumes most known targeting problems. In this paper, a recurrent state is defined as a condition that requires reprocessing or rework. The generalized model can accommodate one or two specifications limits and can be used for the following quality characteristics: The nominal-the-better, the larger-the-better, and the smaller-the-better. This model can be used to find the optimal mean of a quality characteristic, as well as the optimal specification limits. In addition, the paper studies the conditions under which the solution to the proposed model can provide a global solution. The paper shows that, for some of the special cases and under very general conditions, the optimal lower limit should be zero and the optimal upper limit should be infinity. This paper proves that the expected profits improve for the case where only a lower limit on the quality characteristic is used, if a recurrent state is included by adding an optimized upper limit. A special case of the model is used to study the problem of determining a common mean for multiple products, as well as the optimal upper specification limits for each product. A solution procedure for maximizing the expected profits and obtaining the optimal solution is introduced. A numerical example is presented.
1. Introduction
Targeting models are used to find the optimal process parameters that will result in the least amount of losses, due to reworked or scrapped items, while satisfying the specification limit(s). Achieving minimum costs and high quality are prerequisites for attaining higher market shares and profit. Taguchi introduced three types of loss functions; nominal-the-better quality characteristic, N-type, smaller-the-better quality characteristic, S-type, and larger-the-better quality characteristic, L-type [1]. This paper has three main goals. The first goal is to introduce a general model for determining the optimal process parameters for targeting models, where the manufacturing process involves rework and/or scrapping of non-conforming items. The second goal is to show which of the model special cases can yield a global optimal solution. To this end, the paper investigates the strict quasi-concavity of the expected profit. The third goal is to show that adding a fictitious upper limit to a model that involves only a lower limit will result in a higher expected profits.
Over the last four decades, several papers have presented models, developed for determining the optimal process mean under various manufacturing settings. Table 1 summarizes some of the studies in the literature. The third column in Table 1 specifies which specification limits are considered in the paper, where and stand for the lower, and upper specification limits, respectively. The fourth column in the table indicates whether the mentioned paper discusses rework when non-conforming items are produced. The last column in Table 1 specifies the specification limit(s), whose violation will result in rework. In the following paragraphs, a discussion of some of the most important models in the literature is provided.

Table 1.
Summary of some of the targeting models.
To the best of the authors’ knowledge, Springer [2] was the first study that developed a targeting problem with two-sided specification limits. In that paper, a product is accepted if its quality characteristic falls within pre-defined specification limits; otherwise it is rejected. Bettes [3] presented a study for setting the optimum values for the process mean and upper specification limit. Golhar and Pollack [6] presented a model for determining the optimal process mean and upper specification limit for a process where the item is accepted if the considered quality characteristic falls between the specification limits, and is reworked if it does not. Rahim and Al-Sultan [21] studied the problem of jointly determining the optimum mean and variance of a process. Rahim and Tuffaha [29] considered a targeting problem, where the product is sold in a primary market if its quality characteristic falls within the specification limits; otherwise, it is sold in a secondary market.
In order to determine the probability distribution of the quality characteristic of the production process, a sample of data on the quality characteristic should be collected from the production line. The observations are to be tested for the best probability distribution fit. The adequacy of the fit should be assessed by goodness-of-fit tests, i.e., chi-square test. Interested readers are referred to [37]. Another technique is to apply Burr’s density function to fit the set of collected data of the quality characteristic, given the first four moments of the data of the process characteristic; i.e., the mean, standard deviation, skewness coefficient, and kurtosis coefficient, can be reasonably accurately estimated. Then, Burr distribution can be easily transferred to any normal/non-normal distribution. Interested readers are referred to [52,53].
In some cases, it would be impractical or even impossible to measure the quality characteristic. In these cases, a variable that is correlated with the quality characteristic is used to estimate the quality of the product. This correlated variable is known as a surrogate variable, and it is known to be relatively easier to measure. Many studies have investigated models with surrogate variables [9,11,15,25,35,39].
Bai and Lee [9] presented the problem of setting the optimum target value of the process mean and the lower specification limit of a cement bag-filling process. Measuring the weight of a bag is difficult, due to the high-speed packing; therefore, the milliampere reading of a load cell is used as a surrogate.
Lee and Kim [11] extended the work of Bai and Lee [9], and considered a filling process with a pre-defined lower specification limit on the quality characteristic of interest. The material in a container is inspected based on a surrogate variable. Under-filled and over-filled containers are emptied and refilled. The optimal process mean, upper and lower specification limits are determined simultaneously by maximizing the profit function.
Lee and Jang [15] considered a production process with three-class screening. They constructed two profit models; one model is based on the performance variable, while the other is based on a surrogate variable.
The preceding studies addressed the case where a single product type is considered. However, situations arise where multiple product types are produced through a common production process. Lee et al. [33] developed a targeting model for a production process with multiple products. They determined the optimal common process mean; where a product is accepted if its quality characteristic is above a predefined lower limit, otherwise it is scrapped. Park et al. [39] extended the work of Lee et al. [33] and discussed a model that contains surrogate variables. The model enabled the estimation of the common process mean and the optimum lower limit for the performance variables.
In Section 2 of this paper, a generalized targeting model, that subsumes most of the known N-type targeting models, is developed. Special cases of the model cover the S-type and the L-type. This model can be used to find the optimal mean of a quality characteristic and the optimal specification limits. Section 3 provides a discussion on the quasi-concavity of the model and its special cases. This section identifies cases where an optimal lower limit is zero and an optimal upper limit is infinity. The section also identifies those cases where the upper limit is a finite value that can be easily obtained using line search methods. In Section 4, a case for introducing an upper limit on the quality characteristic for a process targeting model, that aims to improve expected profits, is presented. Section 5 provides an application for the proposed model by considering the model presented in [33], where several products have a common quality characteristic, while holding different cost parameters. The objective is to find the optimal common mean of the quality characteristic. Each product has its own specification limits. The solution procedure of the multiple products model is presented in Section 6. An illustrative numerical example and discussion of the results are given in Section 7. Finally, Section 8 concludes the paper.
The main contributions and novel merits of the manuscript can be summarized as:
- Developing a generalized targeting model for process quality control. This generalized model subsumes most of the known N-type targeting models. Special cases of the model cover the S-type and the L-type.
- Providing a solution procedure to find the optimal mean of a quality characteristic and optimal specification limits for the generalized targeting model.
- Very useful managerial insights have been extracted from the numerical experiments.
The following notation is used throughout the paper:
| the random variable of the quality characteristic under consideration | |
| the realized value of | |
| the lower specification limit of | |
| the upper specification limit of | |
| the production cost function | |
| the net profit function for an accepted product | |
| the cost incurred when | |
| the cost incurred when | |
| TP | the total profit function |
| E(TP) | the expected total profit |
| the probability density function of with mean and variance | |
| the cumulative distribution function of |
In addition to the above notation, the following notation is used in the multiple product model:
| the random value of the quality characteristic of the ith product type, i = 1, 2, …, n | |
| the realized value of | |
| the optimal common process mean | |
| the lower specification limit of | |
| the upper specification limit of | |
| the selling price of one unit of the ith product | |
| the fixed production cost per unit | |
| the variable production cost proportional to | |
| the inspection cost per unit | |
| the scrapping cost per unit | |
| the rework cost per unit | |
| the proportion of the ith product type produced, |
2. Generalized Targeting Model
In this section, a general targeting model that incorporates most of the known targeting models is developed. This model may be used for finding the optimal mean and/or variance of a quality characteristic. It may also be used to determine the optimal “specification” limits for the quality characteristic. It is assumed that there is a single quality characteristic, x, with a probability density function . Without loss of generality, it is assumed that
The cost structure is described as follows: The production cost, is a function of the realized value of the quality characteristic. This includes raw material cost, manufacturing cost, and quality control and/or inspection costs.
It is assumed that there is a two-sided specification limit on the quality characteristic, a lower and an upper specification limit, L, and U, respectively. If the quality characteristic is less than the threshold L, i.e., , an extra cost is incurred. This could be the cost of scrapping the item, or reworking it. It is assumed that this cost is dependent on the value of the quality characteristic. This cost includes all expenses associated with scrapping or reworking the product. The expected cost in this case is defined as If the quality characteristic is between L and , then the item is accepted. In this case, revenue may be collected, but some additional costs may be incurred, such as finishing, shipping, or packaging. The notation, is used to denote the difference between the revenue and those additional costs. The expected value of this function is given by If the quality characteristic exceeds , i.e., , a cost is incurred. This could be the cost of scrapping or reworking the item. As in the case where , this cost may be dependent on x. This cost is denoted by . The expected cost in this case is given by . The functions ,, , and may also reflect any of Taguchi’s loss functions and in this case the model may have one or two limits dependent on the type of the quality characteristic.
In addition, the following assumptions are considered:
- (a)
- The quality characteristic assumes non-negative values,
- (b)
- The cost structure and parameters remain the same after rework,
- (c)
- The probability density function of the quality characteristic does not change after rework is performed, and
- (d)
- There is no limit on the number of rework attempts.
Next, the concepts of terminal and recurrent states of an item are introduced. An item is in a terminal state if it does not require any further processing, i.e., the item is scrapped or accepted. An item is in a recurrent state if it requires rework.
The literature of process targeting models discuss the case where a product is in a terminal state once it is produced. These models appear in Table 1 with “No” in the rework column. For some other models, the item is in a terminal state only if the quality characteristic is acceptable, i.e., rework is performed if , or , models in [3,6,11,16,27]. Other models assume that the terminal state is , i.e., rework is needed if , models [31,34,35,38,40,44,46,47,48]. Finally, there are models where a recurrent state is limited to the case where , models [9,19,20,25,32,36,37,42,43,49,50,51].
Before introducing the new model, let’s turn to the “specification” limits on the quality characteristic. Usually, specification limits are set by outside agents, such as downstream manufacturing processes, regulatory agencies, or clients/consumers. However, one may envision situations where this may not be the case. Consider a filling operation that has a lower specification limit on the fill volume. The lower limit is set in the interest of the consumer. However, the producer will incur a loss for overfilling. In this case, the producer may wish to introduce an upper limit for the fill volume to have a cap on lost material. A similar situation applies to coating processes, where a lower limit on the thickness of the coating is specified by standards. However, the manufacturer may want to set an upper limit on the thickness to avoid the cost of additional coating material. On the other hand, thick coating may have a significant effect on the product quality. It may result in uneven texture finish and may initiate cracking and delamination of paints, due to external forces, which will definitely affect the product life and performance. In these scenarios, the decision maker has to set a “suitable” upper limit.
Consider a quality characteristic that has to satisfy both the lower and upper limits. If the quality characteristic is outside the limits further processing is performed, i.e., a recurrent state is reached. In this case, the total profit, is given by:
The expected value of the total profit is given by:
where is the expected cost of producing a unit within the limits. One can interpret the expression in Equation (2) as the expected profit, given that the quality characteristic is within the limits. The denominator is the probability of not being in a recurrent state. Now, the following three special cases of the model shown in Equation (2) are considered:
- I.
- Consider the case where the recurrent state is reached when . In this case, the random variable, TP, will be the same as in Equation (1) above with the exception that if , then , thus:The probability of not being in a recurrent state is . Hence Equation (2) becomes,where .If there is no lower limit; i.e., , then the model shown in Equation (1) becomes,Therefore, the model shown in Equation (2) reduces to,where .This is typically the known model for S-type quality characteristic with recurrent state when .
- II.
- Similarly, if the recurrent state is reached when , then the model shown in Equation (1) reduces toHence, the model shown in Equation (2) becomes,where .For this special case, if there is no upper limit; i.e., , then the model shown in Equation (1) becomes:Hence, the model shown in Equation (2) reduces to,This represents the known model for L-type quality characteristic with recurrent state when .
- III.
- Finally, if there is no recurrent state; i.e., the item is scrapped if not accepted, then the model shown in Equation (1) becomes,Thus, the model shown in Equation (2) reduces to,where .Similar to special cases I and II, if there is only a single limit , and the acceptance condition is , then one has to substitute 0 for in any integral involving , and the model shown in Equation (5) becomes,This represents the known model for S-type quality characteristic without recurrent state.Similarly, as in special case II, if the acceptance condition is , then one has to substitute for in any integral involving , hence the model shown in Equation (5) becomes,This represents the known model for L-type quality characteristic without recurrent state.
The conclusion of this section is as follows, the model shown in Equation (2) is a general model and S-type quality characteristic and L-type quality characteristic models are special cases of the model shown in Equation (2). This general model and its special cases subsume most of the known targeting models that appear in the literature. In addition, this generalized model can be used for setting the optimum mean, variance, upper or lower limits, as will be shown in next sections.
It is important to understand whether the solution obtained is a local or global optimum. In the case of the maximizing a function, a global solution is guaranteed if the function involved is concave. However, concavity of a function is a strict condition. A less restrictive one is that the function is strictly quasi-concave. In the next section, the quasi-concavity of the models given by Equations (2)–(5) will be discussed.
3. Quasi-Concavity of the Generalized Targeting Model
Strictly quasi-concave functions have the property that a local maximum point is also global. A function, , is quasi-concave if the set is convex for any scalar and . Also, is quasi-concave if, for any and in its domain and , [54]. There is an extra method to characterize the strict quasi-concavity of a function of a single variable. A function of one variable is strictly quasi-concave if there is a point, in its domain where the function is increasing at points before , and decreasing at points after . This implies that the slope before is positive, while it becomes negative at points after . This property will be used in this paper.
The next subsections will attempt to prove the obtained results for general differentiable functions , , , , and . In some cases no result can be obtained for general functions, for those cases, this paper adopts a cost structure that is widely used in most papers in the literature, where the cost of violating the limits, and that of accepting the quality characteristic, are constants, while that of production is a linear function, i.e., , , , and .
3.1. Quasi-Concavity of Equation (2) with Respect to and
In this subsection, the quasi-concavity of the function in Equation (2) with respect to the mean, and the limits, and is studied.
Assume that the limits and are known and the mean, , is to be determined. No result can be obtained about the quasi-convexity of Equation (2) as a function of . If the above cost structure is adopted, the expected profit function given by Equation (2) becomes:
Counter-examples can be constructed to show that the function given by Equation (6) is not quasi-concave if is a normal density function.
Next, consider the case where and are known and the lower limit, , is to be determined. The partial derivative of the profit function in Equation (6) with respect to is given by:
Note that the second term in the numerator exceeds the first term, hence, the partial derivative is negative and the function achieves its maximum value at . This result is valid for any differentiable density function, .
Next, consider the case where and are known and the upper limit, , is to be determined. Assume that is differentiable. Using the same cost structure presented earlier, then the partial derivative of shown in Equation (6) with respect to is given by:
The sum of the first two terms in the numerator is negative and is a strictly decreasing function of . Eventually, this sum goes to as goes to .
Since this part of the discussion is interested in , then there are two cases:
- a.
- If the numerator at is negative then it remains negative for and the maximum of is achieved at .
- b.
- If the numerator at is positive, then as increasers, the numerator decreases and eventually becomes negative. Hence changes sign from positive to negative, and is strictly quasi-concave.
3.2. Quasi-Concavity of Equation (3) with Respect to and
Counter examples can be constructed to show that Equation (3) is not quasi-concave with respect to for the general functions and even for the special cost structure introduced at the beginning of this section.
The partial derivative of Equation (3) with respect to is given by:
Hence, the maximum of Equation (3) is achieved if is set to 0.
The partial derivative of Equation (3) with respect to , adopting the above cost-structure, is given by:
The proof in this case is similar to that in Section 3.1. If , then the maximum profit is attained when . Otherwise, the function is strictly quasi-concave function in .
3.3. Quasi-Concavity of Equation (4) with Respect to , and
Counter examples can be constructed to show that Equation (4) is not quasi-concave with respect to for the general functions and even for the special cost structure introduced at the beginning of this section. Using the same cost structure presented earlier, then Equation (4) simplifies to:
The partial derivative of Equation (7) with respect to is given by:
Note that the second term in the numerator exceeds the first term, hence the numerator is negative and the maximum of the function is achieved at .
Finally, the partial derivative of Equation (4) with respect to is given by:
Hence, the maximum is achieved by setting at its largest possible value.
3.4. Quasi-Concavity of Equation (5) with Respect to , and
If the cost structure described above is used, then Equation (5) simplifies to:
If and are known and is the density function of the normal distribution, then is concave for and is convex for . Hence, Equation (8) is a concave function in .
For the general function shown in Equation (5), it is straightforward to show that:
Hence, the maximum of the function is achieved if and if is set at the largest possible value.
Table 2 summarizes the above results. In order to show that two parameters are fixed and the third one is a decision variable, that third parameter is written as an argument of the function . For example, means that and are fixed and is a decision variable.

Table 2.
Quasi-concavity of as a function of one parameter.
4. Optimizing the Limits of a Quality Characteristic
Table 2 shows that the optimal lower limit is zero or the least acceptable value. Only the cases modeled by Equations (2) and (3) provide a chance to optimize the upper limit. Usually, specification limits are determined based on technical or contractual conditions. Hence, optimizing the upper limit does not seem natural in this case. However, there is room for improving the expected profit by including an upper limit on the quality characteristic to reduce the cost of raw material usage, as shown in the next sections. Consider a case modeled by Equation (4) with Here, the product is accepted as long as the quality characteristic exceeds the lower specification limit. If an upper limit is introduced along with an associated recurrent state, then the model described by Equation (2) is on hand. A similar case is obtained when the case is modeled by Equation (5) with . Then, introducing an upper limit and a recurrent state will result in a model given by Equation (3). In Section 5, this approach is implemented. This implementation shows that the expected profit has improved.
5. Multiple Products Model
In this section, the generalized model that is presented in Section 2 is applied and an application, where a model given by Equation (5), is modified as described in the previous section, resulting in an improvement in the objective function. Lee et al. [33] considered a facility that manufactures multiple products (these products can be considered as different grades of the same product). The products are sold at different prices. Consider a quality characteristic that is common to all of these products, where the mean of the characteristic is the same among all the products. A product is scrapped if , otherwise it is accepted. The current paper extends their work in different directions. To limit the losses of the manufacturer, an upper limit is added for the quality characteristic of each product. The upper limit assigned to each product is to be determined. If the upper limit is exceeded, a penalty is incurred. This penalty can be viewed as a rework cost. The resulting model involves the products’ selling prices, production costs, inspection costs, scrap costs, and rework costs.
Consider a case of products, and assume that the quality characteristic of product is normally distributed and given by with variance . are assumed to be independent normal random variables with a common mean . Every item is inspected for conformance to the specification limits and . The inspection operation incurs a fixed inspection cost , independent of product type. If , the item is accepted and sold at a price , i.e., . On the other hand, if , the item fails to meet the lower specification limit; thus it is scrapped at a cost , which is a fixed scrapping cost for all product types, i.e., . Moreover, if , the item is reworked where a penalty or rework cost, , is incurred, and hence, . The reworked item is inspected again and may be accepted, scrapped or reworked again. The per unit production cost is assumed to be a linear function of , hence, , where and are fixed, and variable costs per unit, respectively. The scenario described above fits the model given by Equation (3), therefore, the expected profit is given by:
where:
is the proportion of product i of the total production,
By substitution for the above equations into Equation (9), the final form of the total expected profit is given by:
where and
The problem is to maximize by determining the optimum common mean, , and the upper limits, for . Note that if , and , the model of [33] is retrieved.
6. Solution Procedure
The function is neither concave nor quasi-concave in . Hence, it may have local optima. Figure 1 shows the function behavior versus changes in .
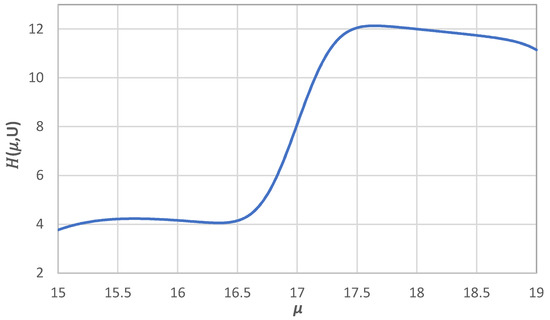
Figure 1.
An illustrative example of as a function of .
The proposed solution procedure includes an exhaustive search of . is searched in the range [, ]. For each value of , the optimum values of are obtained. Section 3 proved that the single variable function is strictly quasi-concave in . Therefore, the following solution procedure is applied:
- Set , where is a positive scalar. For normally distributed quality characteristics, it is recommended to take , this will guarantee covering more than 99.99% of the expected output of the production process. Also, set , and .
- Solve the problems for using any line search method. Let be the solution for .
- Calculate where . If , set , and Go to Step 4.
- Update the value of the process mean; set , where is a small positive scalar. If , stop; otherwise go to Step 2.
In the next section, the solution approach discussed above is implemented and a discussion of the effect of including an upper bound on the quality characteristic is presented.
7. Results and Discussion
This section presents a numerical example to find the optimum common mean for three products using the solution procedure presented in Section 6. The same data of the example presented in [33] is utilized. Subsequently, the impact on the total expected profit as a result of setting an upper limit to the quality characteristic of each product is investigated.
7.1. An Illustrative Example
This example considers a process where three types of electronic devices are processed through a common process of copper plating. The input data of the parameters are identical to the data in [33] and are shown below:
In addition to the above parameters, a rework cost is introduced; .
In the exhaustive search of , an increment , and are used.
The optimal solution is given by: , , , , and . The optimum common process mean is the same as that of [33]. However, the expected total profit is greater than that of [33] with a 9.25% enhancement. This is due to the upper limits being set.
The following section discusses the impact of the rework cost value, , on the profit improvement associated with including an upper limit on the value of the quality characteristic.
7.2. The Impact of Setting Upper Specification Limits
The following section discusses the impact of the rework cost value, , on the profit improvement associated with including an upper limit on the value of the quality characteristic.
Specification limits are considered in targeting models because quality control issues require them. However, this paper proposes including them as a stop loss measure. In the model presented in [33], a product is accepted once the quality characteristic exceeds the lower limit, regardless of how large it may be. This means that material loss could be high. It is proposed to introduce an upper limit on the quality characteristic. The introduction of the upper limit is associated with a penalty or rework cost. This subsection investigates the impact of the value of the rework cost on the improvement in the expected profit, given by Equation (10) and that of [33]. The improvement is computed using Equation (12) below, where is the maximum expected profit as obtained by the current model in Equation (10) and is the maximum profit obtained by Lee et al. [33]:
Figure 2 shows that as the rework cost, , increases, the percentage of improvement decreases. The probability of rework becomes almost nil for .
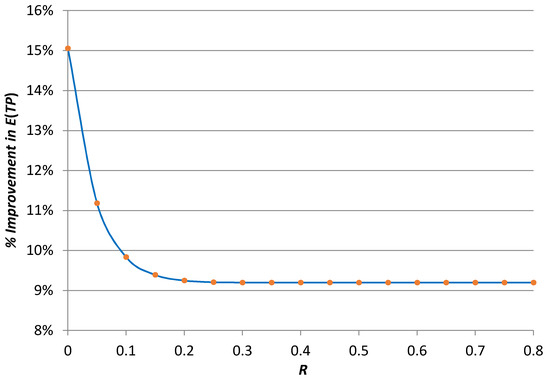
Figure 2.
The impact on by setting upper limits with different values of .
It is clear from Figure 2 that setting upper specification limits has a major impact on , and there is a significant improvement in its value. It is also worth noting that, regardless of the value of the rework cost, , there will be an improvement in . As increases, the percentage of improvement approaches 9.12%. If the model does not include rework, then it will consider the upper limits at infinity; i.e., the model described in [33], and this will result in losses from the excessive use of raw material. Therefore, rework in the analysis of the model is needed if one is interested in reducing the loss from the excess raw material.
8. Conclusions
This paper proposed a generalized targeting model that subsumes most of the known targeting models of that category. Firstly, a generalized model for the N-type targeting models is introduced. The concept of a terminal and recurrent state of an item is introduced. An item reaches a terminal state if no further processing is required; otherwise, it is in a recurrent state. A recurrent state implies further work will be performed on the item. This differentiation of states gave rise to several special cases of the general model. These special cases can be used to model L-type and S-type quality characteristics. An important issue, discussed in this paper, is the conditions under which the obtained solution can be a global solution. To accomplish this task, the strict quasi-concavity of the developed models is examined. Strict quasi-concavity implies that a local maximum is also global. It is shown that the profit function is strictly quasi-concave if one or both specification limits are to be found, assuming that the mean and the other limit are fixed. If one is interested in finding the optimal mean of the quality characteristic, while the specification limits are fixed, one will face the disappointing fact that the profit function is not quasi-concave for all cases, except for the model where there are no recurrent states. This paper used a special case of the proposed model to obtain the optimal common mean of a quality characteristic and the upper specification limits for multiple products. The quality characteristics of the products were assumed to follow independent normal distributions with known variances. A procedure for determining the optimal solution is introduced and implemented on an example having three products. The results show that, incorporating upper specification limits on the quality characteristic has a significant improvement in the value of the optimal expected profit.
A practical case that needs further research is when there is a limit on the number of times an item is allowed to be in a recurrent state. This could be due to excessive loss of material or deterioration of some physical properties. In this paper, it is assumed that the cost of rework is independent of the number of rework cycles the item goes through. This assumption may not be applicable in all cases. Finally, the assumption that the quality characteristic keeps the same probability distribution regardless of number of rework cycles may be relaxed and further research will be needed in this case.
Author Contributions
Modeling, M.A.M.A. and S.Z.S.; formal analysis, M.A.M.A. and S.Z.S.; methodology, M.A.M.A. and S.Z.S.; supervision, S.Z.S.; writing—original draft, M.A.M.A.
Funding
This research received no external funding.
Acknowledgments
The authors wish to acknowledge the support of King Fahd University of Petroleum and Minerals.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Taguchi, G. Introduction to Quality Engineering: Designing Quality into Products and Processes; Quality Resources: Tokyo, Japan, 1986. [Google Scholar]
- Springer, H.C. A method for determining the most economic position of a process mean. Ind. Qual. Control 1951, 8, 36–39. [Google Scholar]
- Bettes, D.C. Finding an Optimum Target Value in Relation to a Fixed Lower Limit and an Arbitrary Upper Limit. J. R. Stat. Soc. Ser. C Appl. Stat. 1962, 11, 202–210. [Google Scholar] [CrossRef]
- Hunter, W.G.; Kartha, C.P. Determining the Most Profitable Target Value for a Production Process. J. Qual. Technol. 1977, 9, 176–181. [Google Scholar] [CrossRef]
- Arcelus, F.J.; Banerjee, P.K. Selection of the Most Economical Production Plan in a Tool-Wear Process. Technometrics 1985, 27, 433–437. [Google Scholar] [CrossRef]
- Golhar, D.Y.; Pollock, S.M. Determination of the Optimal Process Mean and the Upper Limit for a Canning Problem. J. Qual. Technol. 1988, 20, 188–192. [Google Scholar] [CrossRef]
- Pugh, A.G. An algorithm for economically setting a uniformly-shifting process. Comput. Ind. Eng. 1988, 14, 237–240. [Google Scholar] [CrossRef]
- Rahim, M.A.; Banerjee, P.K. Optimal production run for a process with random linear drift. Omega 1988, 16, 347–351. [Google Scholar] [CrossRef]
- Bai, D.S.; Lee, M.K. Optimal target values for a filling process when inspection is based on a correlated variable. Int. J. Prod. Econ. 1993, 32, 327–334. [Google Scholar] [CrossRef]
- Dodson, B.L. Determining the Optimal Target Value for a Process with Upper and Lower Specifications. Qual. Eng. 1993, 5, 393–402. [Google Scholar] [CrossRef]
- Lee, M.K.; Kim, G.S. Determination of the optimal target values for a filling process when inspection is based on a correlated variable. Int. J. Prod. Econ. 1994, 37, 205–213. [Google Scholar] [CrossRef]
- Chen, S.L.; Chung, K.J. Determination of the optimal production run and the most profitable process mean for a production process. Int. J. Prod. Res. 1996, 34, 2051–2058. [Google Scholar] [CrossRef]
- Pulak, M.F.S.; Al-Sultan, K.S. The optimum targeting for a single filling operation with rectifying inspection. Omega 1996, 24, 727–733. [Google Scholar] [CrossRef]
- Al-Sultan, K.S.; Al-Fawzan, M.A. An extension of Rahim and Banerjee’s model for a process with upper and lower specification limits. Int. J. Prod. Econ. 1997, 53, 265–280. [Google Scholar] [CrossRef]
- Lee, K.; Jang, J.S. The optimum target values for a production process with three-class screening. Int. J. Prod. Econ. 1997, 49, 91–99. [Google Scholar] [CrossRef]
- Liu, W.; Raghavachari, M. The target mean problem for an arbitrary quality characteristic distribution. Int. J. Prod. Res. 1997, 35, 1713–1728. [Google Scholar] [CrossRef]
- Roan, J.; Gong, L.; Tang, K. Process mean determination under constant raw material supply. Eur. J. Oper. Res. 1997, 99, 353–365. [Google Scholar] [CrossRef]
- Wen, D.; Mergen, A.E. Running a Process with Poor Capability. Qual. Eng. 1999, 11, 505–509. [Google Scholar] [CrossRef]
- Kim, Y.J.; Cho, B.R.; Phillips, M.D. Determination of the Optimal Process Mean with the Consideration of Variance Reduction and Process Capability. Qual. Eng. 2000, 13, 251–260. [Google Scholar] [CrossRef]
- Lee, M.K.; Hong, S.H.; Kwon, H.M.; Kim, S.B. Optimum process mean and screening limits for a production process with three-class screening. Int. J. Reliab. Qual. Saf. Eng. 2000, 7, 179–190. [Google Scholar] [CrossRef]
- Rahim, M.A.; Al-Sultan, K.S. Joint determination of the optimum target mean and variance of a process. J. Qual. Maint. Eng. 2000, 6, 192–199. [Google Scholar] [CrossRef]
- Roan, J.; Gong, L.; Tang, K. Joint determination of process mean, production run size and material order quantity for a container-filling process. Int. J. Prod. Econ. 2000, 63, 303–317. [Google Scholar] [CrossRef]
- Williams, W.W.; Tang, K.; Gong, L. Process improvement for a container-filling process with random shifts. Int. J. Prod. Econ. 2000, 66, 23–31. [Google Scholar] [CrossRef]
- Chen, C.H.; Chou, C.Y. Determining the Optimum Process Mean of a One-Sided Specification Limit. Int. J. Adv. Manuf. Technol. 2002, 20, 439–441. [Google Scholar] [CrossRef]
- Lee, M.K.; Elsayed, E.A. Process mean and screening limits for filling processes under two-stage screening procedure. Eur. J. Oper. Res. 2002, 138, 118–126. [Google Scholar] [CrossRef]
- Duffuaa, S.O.; Siddiqui, A.W. Process targeting with multi-class screening and measurement error. Int. J. Prod. Res. 2003, 41, 1373–1391. [Google Scholar] [CrossRef]
- Bowling, S.R.; Khasawneh, M.T.; Kaewkuekool, S.; Cho, B.R. A Markovian approach to determining optimum process target levels for a multi-stage serial production system. Eur. J. Oper. Res. 2004, 159, 636–650. [Google Scholar] [CrossRef]
- Chen, C.H. Determining the Optimum Process Mean of a One-sided Specification Limit with the Linear Quality Loss Function of Product. J. Appl. Stat. 2004, 31, 693–703. [Google Scholar] [CrossRef]
- Rahim, M.A.; Tuffaha, F. Integrated model for determining the optimal initial settings of the process mean and the optimal production run assuming quadratic loss functions. Int. J. Prod. Res. 2004, 42, 3281–3300. [Google Scholar] [CrossRef]
- Chen, C.H.; Chou, C.Y. Determining the Optimum Process Mean under a Log-normal Distribution. Qual. Quant. 2005, 39, 119–124. [Google Scholar] [CrossRef]
- Chen, C.H. The Optimum Selection of Imperfect Quality Economic Manufacturing Quantity and Process Mean by Considering Quadratic Quality Loss Function. J. Chin. Inst. Ind. Eng. 2006, 23, 12–19. [Google Scholar] [CrossRef]
- Hong, S.H.; Kwon, H.-M.; Lee, M.K.; Cho, B.R. Joint optimization in process target and tolerance limit for L-type quality characteristics. Int. J. Prod. Res. 2006, 44, 3051–3060. [Google Scholar] [CrossRef]
- Lee, M.K.; Kwon, H.M.; Hong, S.H.; Kim, Y.J. Determination of the optimum target value for a production process with multiple products. Int. J. Prod. Econ. 2007, 107, 173–178. [Google Scholar] [CrossRef]
- Khasawneh, M.T.; Bowling, S.R.; Cho, B.R. A Markovian approach to determining process means with dual quality characteristics. J. Syst. Sci. Syst. Eng. 2008, 17, 66–85. [Google Scholar] [CrossRef]
- Chen, C.H.; Kao, H.S. The determination of optimum process mean and screening limits based on quality loss function. Expert Syst. Appl. 2009, 36, 7332–7335. [Google Scholar] [CrossRef]
- Darwish, M.A. Economic selection of process mean for single-vendor single-buyer supply chain. Eur. J. Oper. Res. 2009, 199, 162–169. [Google Scholar] [CrossRef]
- Duffuaa, S.O.; Al-Turki, U.M.; Kolus, A.A. A process targeting model for a product with two dependent quality characteristics using 100% inspection. Int. J. Prod. Res. 2009, 47, 1039–1053. [Google Scholar] [CrossRef]
- Chen, C.-H.; Khoo, M.B.C. Optimum Process Mean Setting for Product with Rework Process. Tamkang J. Sci. Eng. 2010, 13, 375–384. [Google Scholar]
- Park, T.; Kwon, H.M.; Hong, S.-H.; Lee, M.K. The optimum common process mean and screening limits for a production process with multiple products. Comput. Ind. Eng. 2011, 60, 158–163. [Google Scholar] [CrossRef]
- Selim, S.Z.; Al-Zu’bi, W.K. Optimal means for continuous processes in series. Eur. J. Oper. Res. 2011, 210, 618–623. [Google Scholar] [CrossRef]
- Darwish, M.A.; Abdulmalek, F.; Alkhedher, M. Optimal selection of process mean for a stochastic inventory model. Eur. J. Oper. Res. 2013, 226, 481–490. [Google Scholar] [CrossRef]
- Duffuaa, S.O.; El-Ga’aly, A. A multi-objective mathematical optimization model for process targeting using 100% inspection policy. Appl. Math. Model. 2013, 37, 1545–1552. [Google Scholar] [CrossRef]
- Duffuaa, S.O.; El-Ga’aly, A. A multi-objective optimization model for process targeting using sampling plans. Comput. Ind. Eng. 2013, 64, 309–317. [Google Scholar] [CrossRef]
- Peng, C.-Y.; Khasawneh, M.T. A Markovian approach to determining optimum process means with inspection sampling plan in serial production systems. Int. J. Adv. Manuf. Technol. 2014, 72, 1299–1323. [Google Scholar] [CrossRef]
- Chen, C.H.; Chou, C.Y.; Kan, C.C. Modified economic production and raw material model with quality loss for conforming product. J. Ind. Prod. Eng. 2015, 32, 196–203. [Google Scholar] [CrossRef]
- Chen, C.H.; Khoo, M.B.C.; Chou, C.Y.; Kan, C.C. Joint determination of process quality level and production run time for imperfect production process. J. Ind. Prod. Eng. 2015, 32, 219–224. [Google Scholar] [CrossRef]
- Chen, C.H.; Kan, C.C. Tolerance design based on specified process capability value. Int. J. Manag. Sci. Eng. Manag. 2015, 10, 210–214. [Google Scholar] [CrossRef]
- Dodd, C.; Scanlan, J.; Marsh, R.; Wiseall, S. Improving profitability of optimal mean setting with multiple feature means for dual quality characteristics. Int. J. Adv. Manuf. Technol. 2015, 81, 1767–1780. [Google Scholar] [CrossRef]
- Duffuaa, S.O.; El-Ga’aly, A. Impact of inspection errors on the formulation of a multi-objective optimization process targeting model under inspection sampling plan. Comput. Ind. Eng. 2015, 80, 254–260. [Google Scholar] [CrossRef]
- Raza, S.A.; Turiac, M. Joint optimal determination of process mean, production quantity, pricing, and market segmentation with demand leakage. Eur. J. Oper. Res. 2016, 249, 312–326. [Google Scholar] [CrossRef]
- Raza, S.A.; Abdullakutty, F.C.; Rathinam, S. Joint determination of process mean, price differentiation, and production decisions with demand leakage: A multi-objective approach. Appl. Math. Model. 2016, 40, 8446–8463. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chou, C.Y. On the design of variable sample size and sampling intervals charts under non-normality. Int. J. Prod. Econ. 2005, 96, 249–261. [Google Scholar] [CrossRef]
- Chen, C.H.; Chou, C.Y. Optimum process mean, standard deviation and specification limits settings under the Burr distribution. Eng. Comput. 2017. [Google Scholar] [CrossRef]
- Bazaraa, M.S.; Sherali, H.D.; Shetty, C.M. Nonlinear Programming: Theory and Algorithms, 3th ed.; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).