On the Rate of Convergence and Limiting Characteristics for a Nonstationary Queueing Model
Abstract
1. Introduction
2. Model Description and Basic Transformations
3. Bounds on the Rate of Convergence
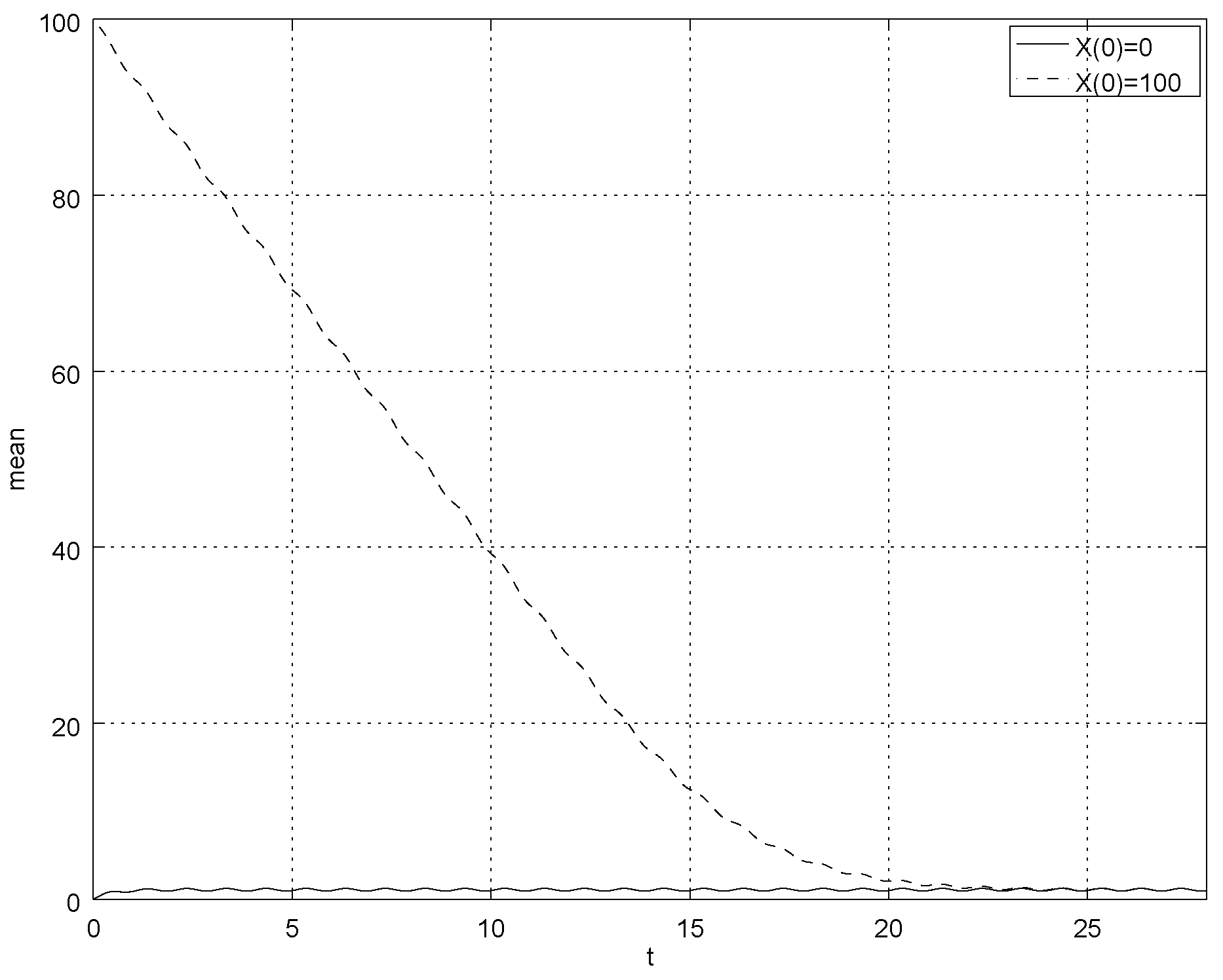
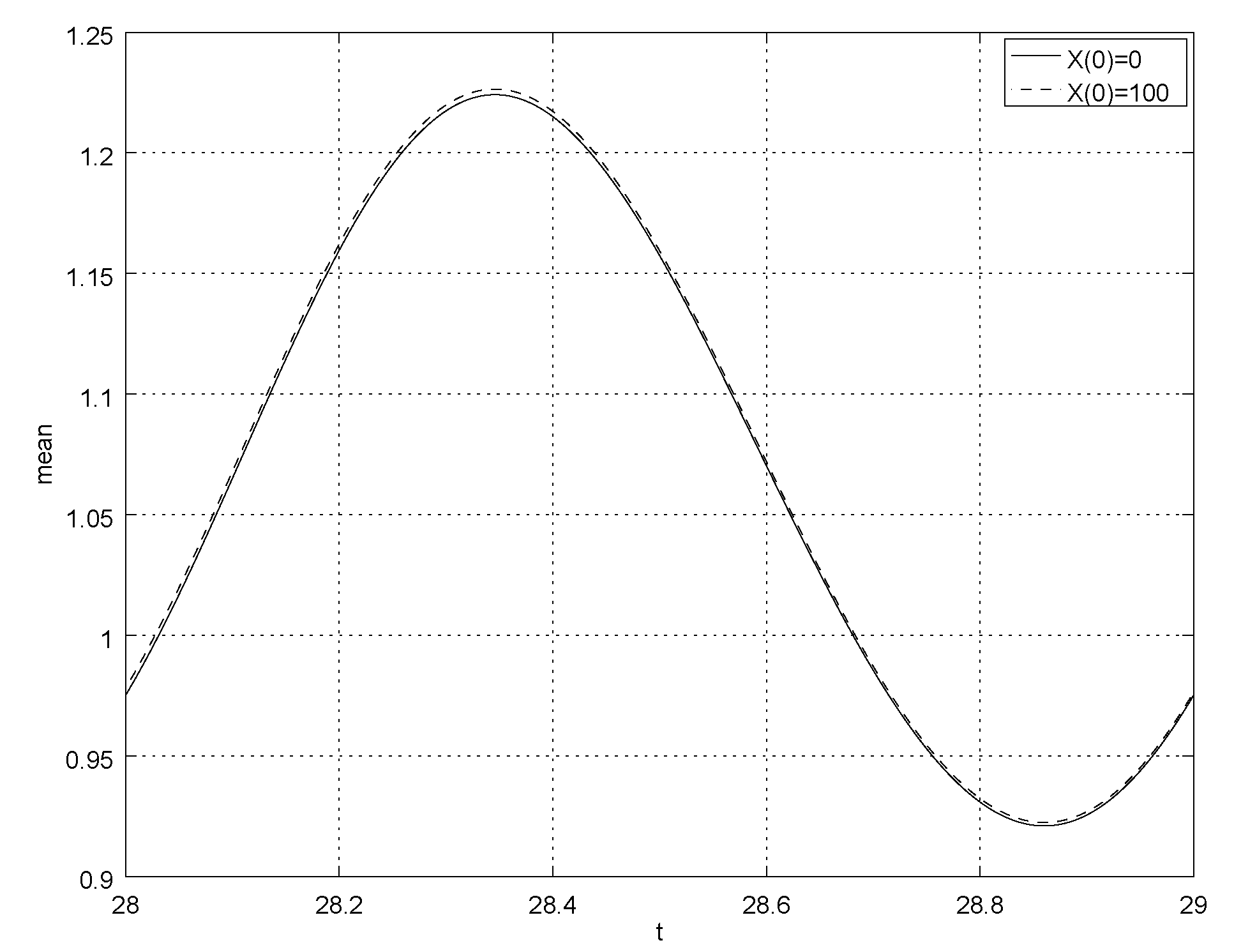
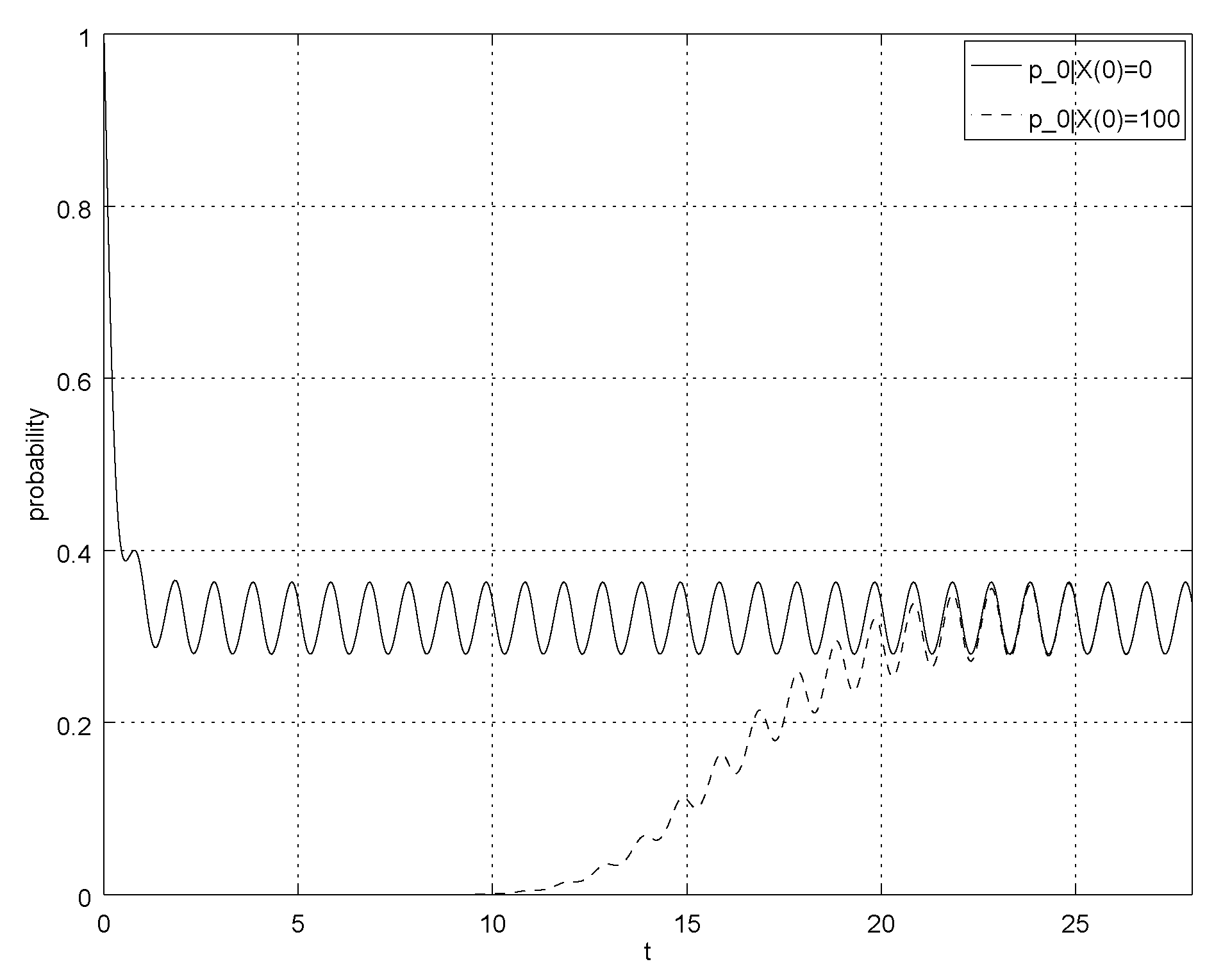
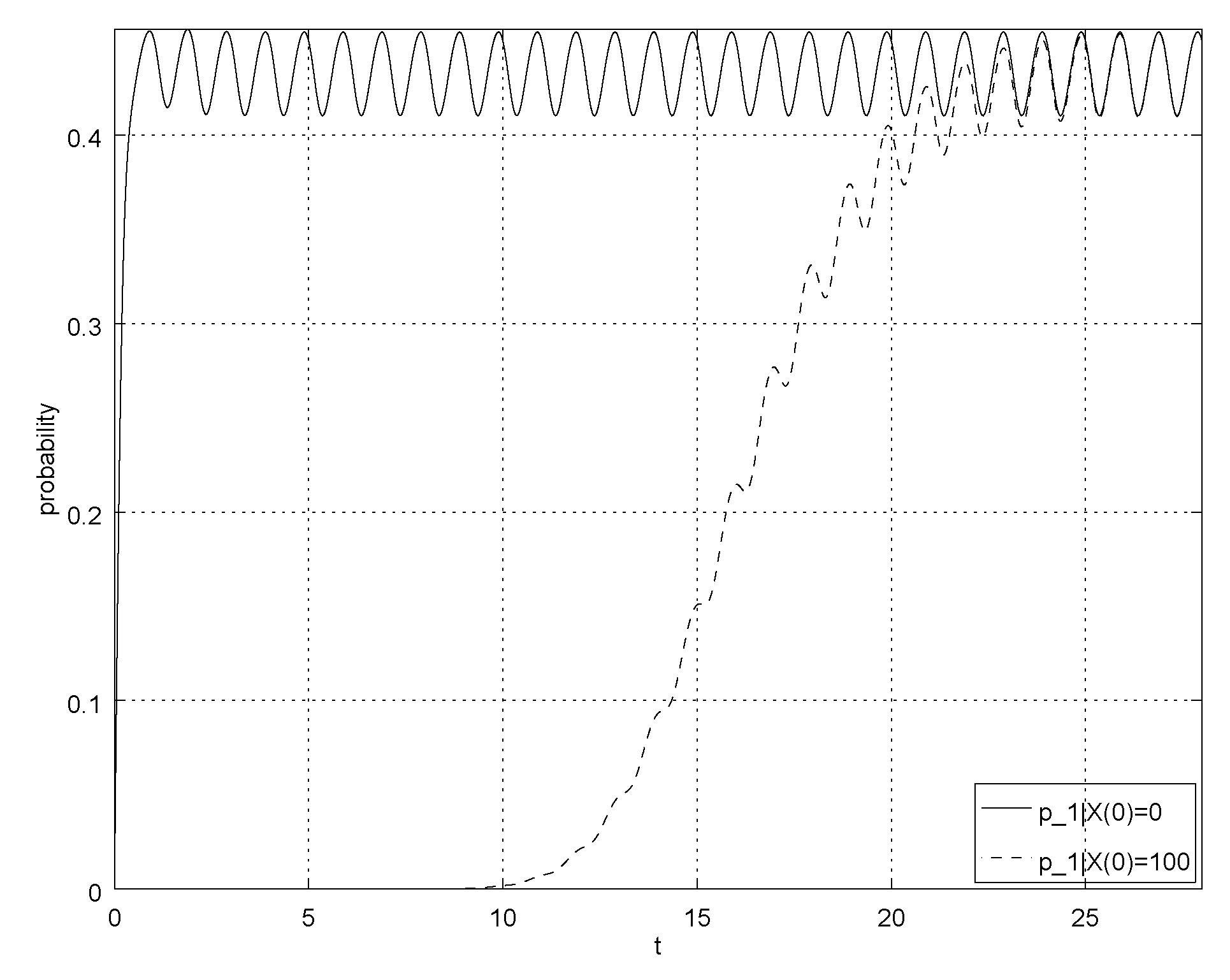
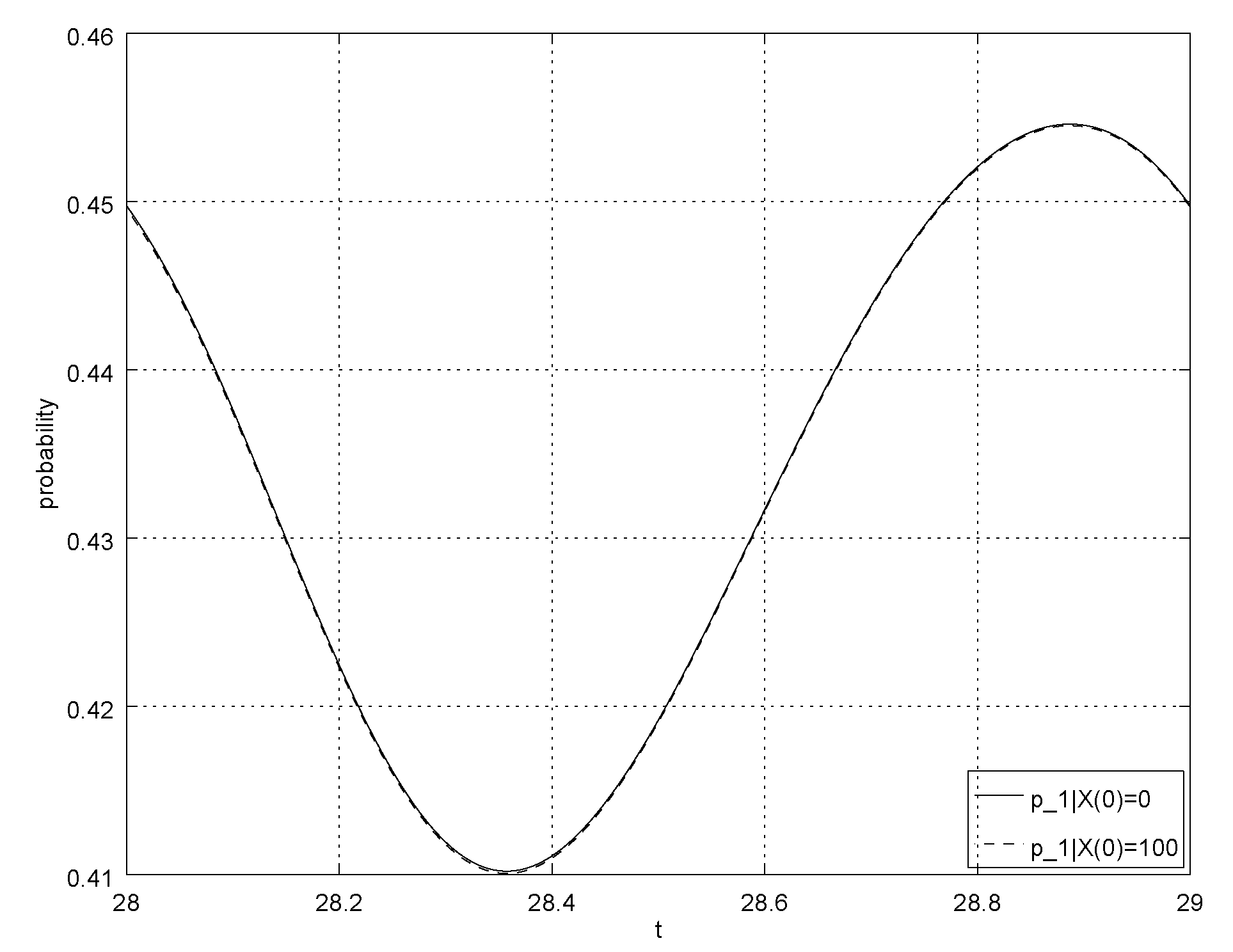
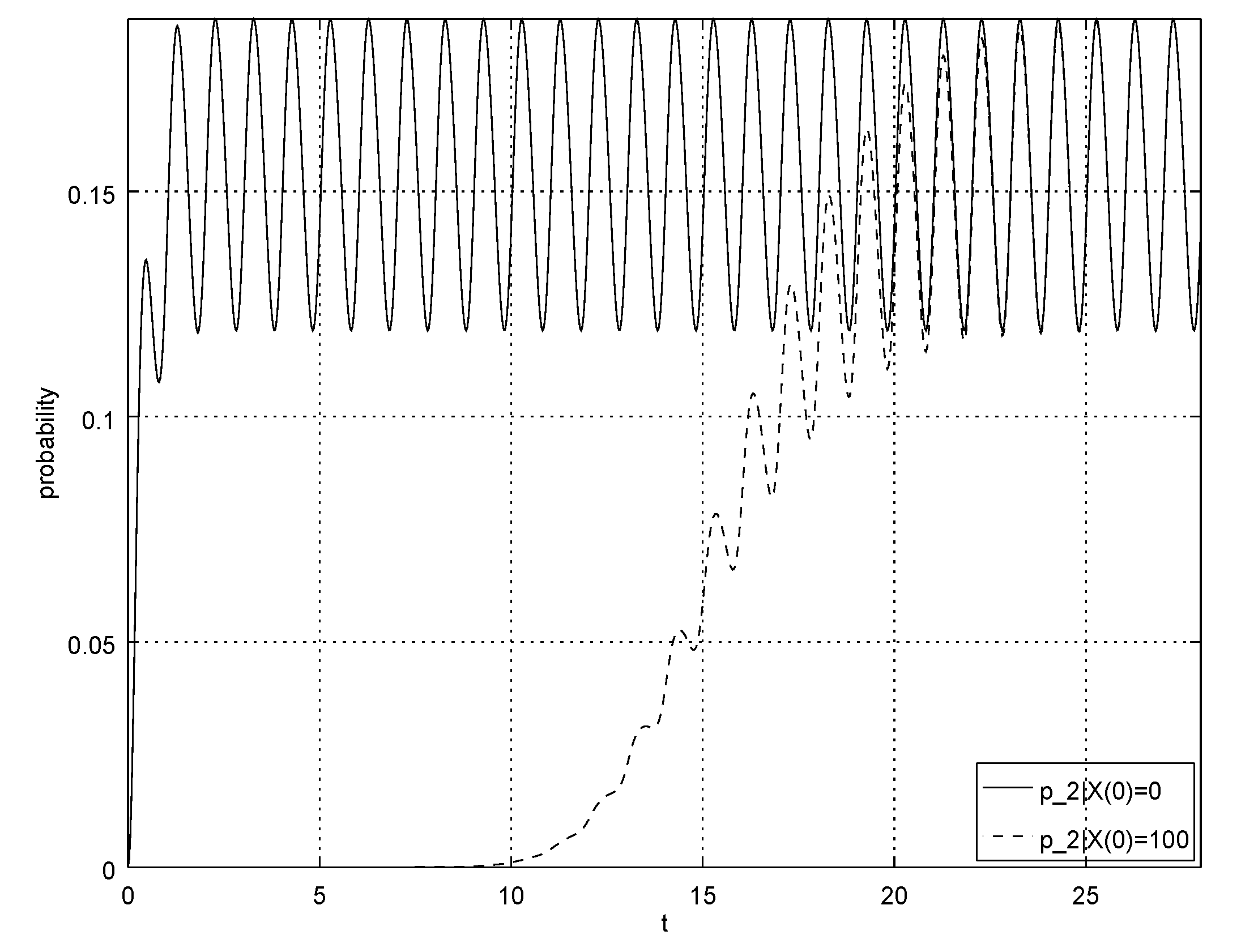
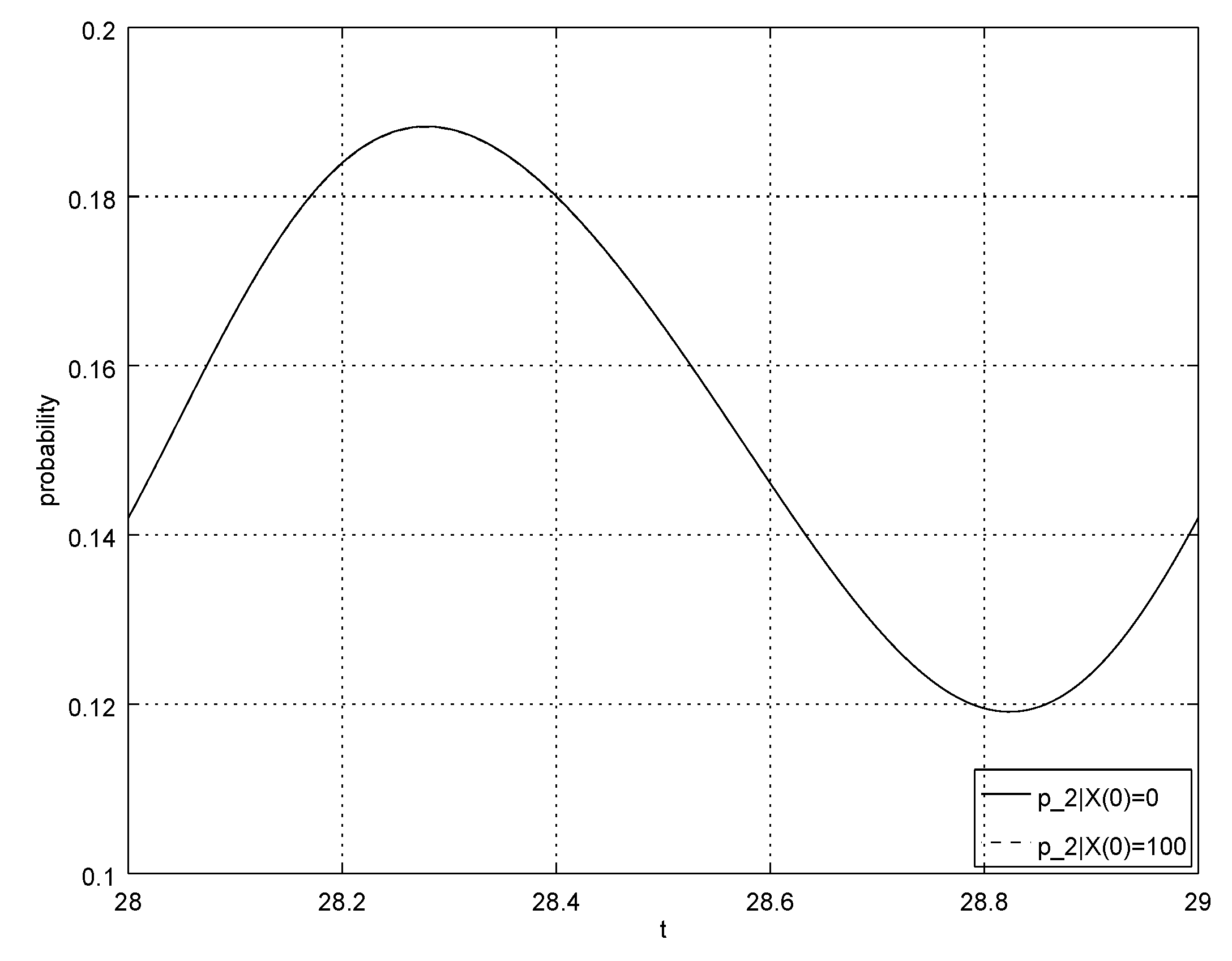
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schwarz, J.A.; Selinka, G.; Stolletz, R. Performance analysis of time-dependent queueing systems: Survey and classification. Omega 2016, 63, 170–189. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Giorno, V.; Krishna Kumar, B.; Nobile, A.G. A Time-Non-Homogeneous Double-Ended Queue with Failures and Repairs and Its Continuous Approximation. Mathematics 2018, 6, 81. [Google Scholar] [CrossRef]
- Giorno, V.; Nobile, A.G.; Spina, S. On some time non-homogeneous queueing systems with catastrophes. Appl. Math. Comp. 2014, 245, 220–234. [Google Scholar] [CrossRef]
- Ammar, S.I.; Alharbi, Y.F. Time-dependent analysis for a two-processor heterogeneous system with time-varying arrival and service rates. Appl. Math. Model. 2018, 54, 743–751. [Google Scholar] [CrossRef]
- Meyn, S.P.; Tweedie, R.L. Stability of Markovian processes III: Foster- Lyapunov criteria for continuous time processes. Adv. Appl. Probab. 1993, 25, 518–548. [Google Scholar] [CrossRef]
- Zeifman, A.; Leorato, S.; Orsingher, E.; Satin Ya Shilova, G. Some universal limits for nonhomogeneous birth and death processes. Queueing Syst. 2006, 52, 139–151. [Google Scholar] [CrossRef]
- Zeifman, A.; Razumchik, R.; Satin, Y.; Kiseleva, K.; Korotysheva, A.; Korolev, V. Bounds on the Rate of Convergence for One Class of Inhomogeneous Markovian Queueing Models with Possible Batch Arrivals and Services. Int. J. Appl. Math. Comp. Sci. 2018, 28, 141–154. [Google Scholar] [CrossRef]
- Zeifman, A.; Satin, Y.; Kiseleva, K.; Korolev, V.; Panfilova, T. On limiting characteristics for a non-stationary two-processor heterogeneous system. Appl. Math. Comput. 2019, 351, 48–65. [Google Scholar] [CrossRef]
- Kartashov, N.V. Criteria for uniform ergodicity and strong stability of Markov chains with a common phase space. Theory Probab. Appl. 1985, 30, 71–89. [Google Scholar]
- Liu, Y. Perturbation bounds for the stationary distributions of Markov chains. SIAM J. Matrix Anal. Appl. 2012, 33, 1057–1074. [Google Scholar] [CrossRef]
- Mitrophanov, A.Y. Stability and exponential convergence of continuous-time Markov chains. J. Appl. Probab. 2003, 40, 970–979. [Google Scholar] [CrossRef]
- Mitrophanov, A.Y. The spectral gap and perturbation bounds for reversible continuous-time Markov chains. J. Appl. Probab. 2004, 41, 1219–1222. [Google Scholar] [CrossRef]
- Zeifman, A.I.; Korolev, V.Y. On perturbation bounds for continuous-time Markov chains. Stat. Probab. Lett. 2014, 88, 66–72. [Google Scholar] [CrossRef]
- Mitrophanov, A.Y. Connection between the Rate of Convergence to Stationarity and Stability to Perturbations for Stochastic and Deterministic Systems. In Proceedings of the 38th International Conference Dynamics Days Europe (DDE 2018), Loughborough, UK, 3–7 September 2018; Available online: http://alexmitr.com/talk_DDE2018_Mitrophanov_FIN_post_sm.pdf (accessed on 29 June 2019).
- Rudolf, D.; Schweizer, N. Perturbation theory for Markov chains via Wasserstein distance. Bernoulli 2018, 24, 2610–2639. [Google Scholar] [CrossRef]
- Daleckij, J.L.; Krein, M.G. Stability of Solutions of Differential Equations in Banach Space; American Mathematical Society: Providence, RI, USA, 2002; Volume 43. [Google Scholar]
- Sinitcina, A.; Satin, Y.; Zeifman, A.; Shilova, G.; Sipin, A.; Kiseleva, K.; Panfilova, T.; Kryukova, A.; Gudkova, I.; Fokicheva, E. On the Bounds for a Two-Dimensional Birth-Death Process with Catastrophes. Mathematics 2018, 6, 80. [Google Scholar] [CrossRef]
- Zeifman, A.; Satin, Y.; Kiseleva, K.; Korolev, V. On the Rate of Convergence for a Characteristic of Multidimensional Birth-Death Process. Mathematics 2019, 7, 477. [Google Scholar] [CrossRef]
- Zeifman, A.; Satin, Y.; Kiseleva, K.; Kryukova, A. Applications of Differential Inequalities to Bounding the Rate of Convergence for Continuous-time Markov Chains. AIP Conf. Proc. 2019, 2116, 090009. [Google Scholar]
- Brugno, A.; D’Apice, C.; Dudin, A.; Manzo, R. Analysis of an MAP/PH/1 queue with flexible group service. Int. J. Appl. Math. Comp. Sci. 2017, 27, 119–131. [Google Scholar] [CrossRef]
- Lee, H.W.; Baek, J.W.; Jeon, J. Analysis of the MX/G/1 queue under D-policy. Stoch. Anal. Appl. 2005, 23, 785–808. [Google Scholar] [CrossRef]
- Zeifman, A.; Satin Ya Korolev, V.; Shorgin, S. On truncations for weakly ergodic inhomogeneous birth and death processes. Int. J. Appl. Math. Comp. Sci. 2014, 24, 503–518. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Satin, Y.; Zeifman, A.; Kryukova, A. On the Rate of Convergence and Limiting Characteristics for a Nonstationary Queueing Model. Mathematics 2019, 7, 678. https://doi.org/10.3390/math7080678
Satin Y, Zeifman A, Kryukova A. On the Rate of Convergence and Limiting Characteristics for a Nonstationary Queueing Model. Mathematics. 2019; 7(8):678. https://doi.org/10.3390/math7080678
Chicago/Turabian StyleSatin, Yacov, Alexander Zeifman, and Anastasia Kryukova. 2019. "On the Rate of Convergence and Limiting Characteristics for a Nonstationary Queueing Model" Mathematics 7, no. 8: 678. https://doi.org/10.3390/math7080678
APA StyleSatin, Y., Zeifman, A., & Kryukova, A. (2019). On the Rate of Convergence and Limiting Characteristics for a Nonstationary Queueing Model. Mathematics, 7(8), 678. https://doi.org/10.3390/math7080678





