Generalized Tikhonov Method and Convergence Estimate for the Cauchy Problem of Modified Helmholtz Equation with Nonhomogeneous Dirichlet and Neumann Datum
Abstract
1. Introduction
2. Conditional Stability
3. Regularization Method
3.1. Regularization Method for Problem (2)
3.2. Regularization Method for Problem (3)
4. Preparation Knowledge
5. Convergence Estimate
5.1. Convergence Estimate for the Method of Problem (2)
5.1.1. a priori Convergence Estimate
5.1.2. A Posteriori Convergence Estimate
- (a)
- The function is continuous;
- (b)
- ;
- (c)
- ;
- (d)
- For , the function is strictly monotonous increasing.
5.2. Convergence Estimate for the Method of Problem (3)
5.2.1. A Priori Convergence Estimate
5.2.2. A Posteriori Convergence Estimate
- (a)
- The function is continuous;
- (b)
- ;
- (c)
- ;
- (d)
- For , the function is strictly monotonous increasing.
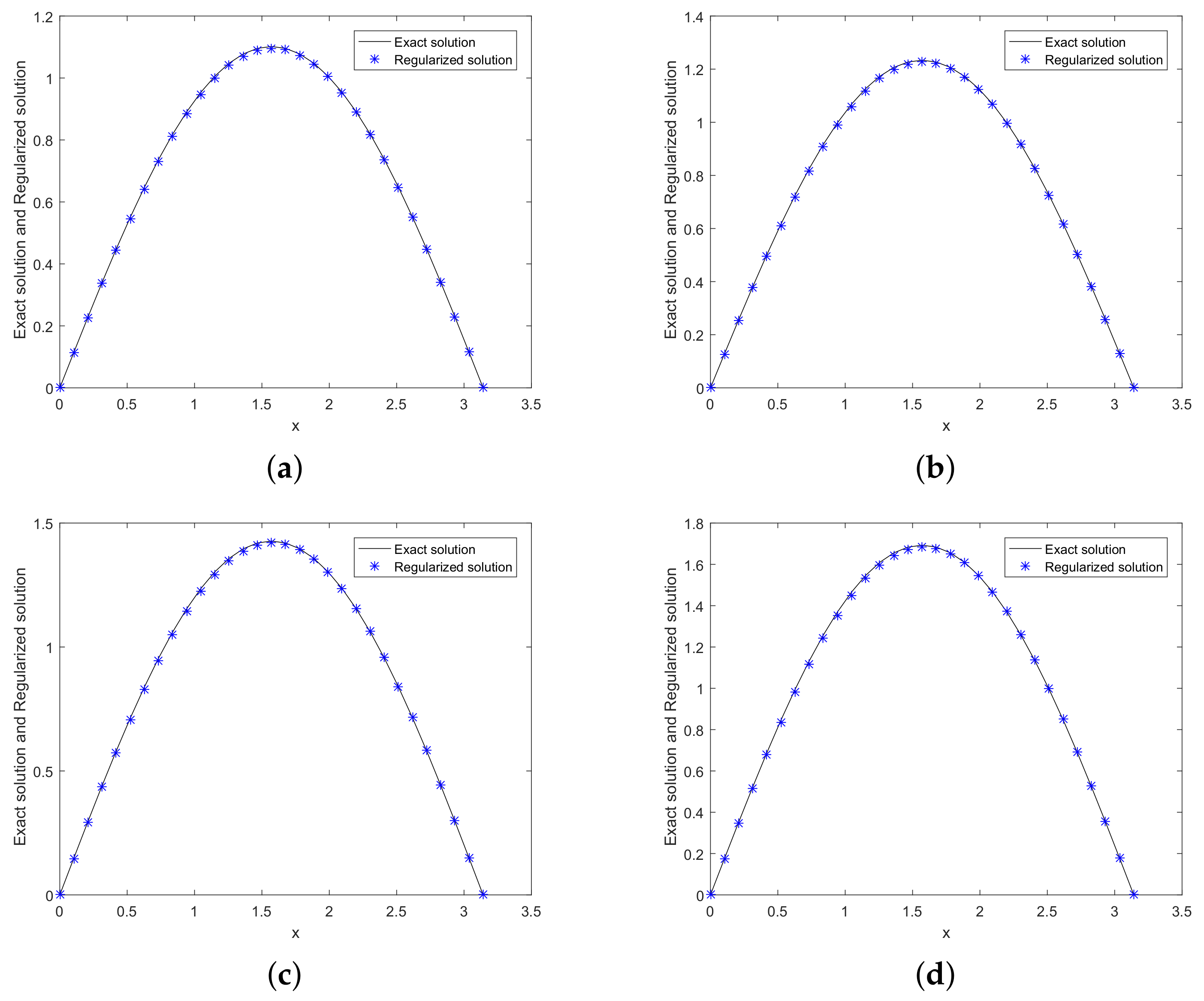
6. Numerical Experiments
7. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cheng, H.W.; Huang, J.F.; Leiterman, T.J. An adaptive fast solver for the modified Helmholtz equation in two dimensions. J. Comput. Phys. 2006, 211, 616–637. [Google Scholar] [CrossRef]
- Juffer, A.H.; Botta, E.F.F.; Van Keulen, B.A.M.; Ploeg, A.V.D.; Berendsen, H.J.C. The electric potential of a macromolecule in a solvent: A fundamental approach. J. Comput. Phys. 1991, 97, 144–171. [Google Scholar] [CrossRef]
- Liang, J.; Subramaniam, S. Computation of molecular electrostatics with boundary element methods. Biophys. J. 1997, 73, 1830–1841. [Google Scholar] [CrossRef][Green Version]
- Russel, W.B.; Saville, D.A.; Schowalter, W.R. Colloidal Dispersions; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Hadamard, J. Lectures on Cauchy Problem in Linear Partial Differential Equations; Yale University Press: New Haven, CT, USA, 1923. [Google Scholar]
- Isakov, V. Inverse Problems for Partial Differential Equations. In Applied Mathematical Sciences; Springer: New York, NY, USA, 1998; Volume 127. [Google Scholar]
- Tikhonov, A.N.; Arsenin, V.Y. Solutions of Ill-Posed Problems; V. H. Winston and Sons: Washington, DC, USA; John Wiley and Sons: New York, NY, USA, 1997. [Google Scholar]
- Engl, H.W.; Hanke, M.; Neubauer, A. Regularization of Inverse Problems. In Mathematics and Its Applications; Kluwer Academic: Dordrecht, The Netherlands, 1996; Volume 375. [Google Scholar]
- Kirsch, A. An Introduction to the Mathematical Theory of Inverse Problems. In Applied Mathematical Sciences; Springer: New York, NY, USA, 2011; Volume 120. [Google Scholar]
- Shi, R.; Wei, T.; Qin, H.H. Fourth-order modified method for the Cauchy problem of the modified Helmholtz equation. Numer. Math. Theory Methods Appl. 2009, 3, 326–340. [Google Scholar] [CrossRef]
- Qian, A.L.; Yang, X.M.; Wu, Y.S. Optimal error bound and a quasi-boundary value regularization method for a Cauchy problem of the modified helmholtz equation. Int. J. Comput. Math. 2016, 93, 2028–2041. [Google Scholar] [CrossRef]
- Qin, H.H.; Wei, T. Quasi-reversibility and truncation methods to solve a Cauchy problem for the modified Helmholtz equation. Math. Comput. Simul. 2009, 80, 352–366. [Google Scholar] [CrossRef]
- Yang, H.; Yang, Y. A quasi-reversibility regularization method for a Cauchy problem of the modified helmholtz-type equation. Bound. Value Probl. 2019, 1, 1–19. [Google Scholar] [CrossRef]
- Xiong, X.T.; Shi, W.X.; Fan, X.Y. Two numerical methods for a Cauchy problem for modified Helmholtz equation. Appl. Math. Model. 2011, 35, 4951–4964. [Google Scholar] [CrossRef]
- Cheng, H. Filtering method for the Cauchy problem of the modified Helmholtz equation. J. Lanzhou Univ. 2013, 6, 323–328. [Google Scholar]
- Cheng, H.; Zhu, P.; Gao, J. A regularization method for the Cauchy problem of the modified helmholtz equation. Math. Methods Appl. Sci. 2015, 38, 3711–3719. [Google Scholar] [CrossRef]
- He, S.Q.; Feng, X.F. A regularization method to solve a Cauchy problem for the two-Dimensional modified Helmholtz equation. Mathematics 2019, 7, 360. [Google Scholar] [CrossRef]
- He, S.Q.; Feng, X.F. A mollification method with Dirichlet kernel to solve Cauchy problem for two-dimensional Helmholtz equation. Int. J. Wavelets Multiresolut. Inf. Process. 2019. [Google Scholar] [CrossRef]
- Qian, A.; Mao, J.; Liu, L. A spectral regularization method for a Cauchy problem of the modified helmholtz equation. Bound. Value Probl. 2010, 1, 212056. [Google Scholar] [CrossRef]
- Qian, A.L.; Wu, Y.J. Optimal error bound and approximation methods for a Cauchy problem of the modified helmholtz equation. Int. J. Wavelets Multiresolut. Inf. Process. 2011, 9, 305–315. [Google Scholar] [CrossRef]
- Marin, L. A relaxation method of an alternating iterative MFS algorithm for the Cauchy problem associated with the two-dimensional modified Helmholtz equation. Numer. Methods Partial. Differ. Equ. 2012, 28, 899–925. [Google Scholar] [CrossRef]
- Johansson, B.T.; Marin, L. Relaxation of alternating iterative algorithms for the Cauchy problem associated with the modified Helmholtz equation. Comput. Mater. Contin. 2009, 13, 153–189. [Google Scholar]
- Qin, H.H.; Wen, D.W. Tikhonov type regularization method for the Cauchy problem of the modified Helmholtz equation. Appl. Math. Comput. 2008, 203, 617–628. [Google Scholar] [CrossRef]
- Sun, P.; Feng, X.L. A simple method for solving the Cauchy problem for the modified Helmholtz equation. J. Math. 2011, 31, 756–762. [Google Scholar]
- Liu, C.S.; Qu, W.; Chen, W.; Lin, J. A novel trefftz method of the inverse Cauchy problem for 3d modified helmholtz equation. Inverse Probl. Sci. Eng. 2017, 25, 1278–1298. [Google Scholar] [CrossRef]
- You, L. The weighted generalized solution Tikhonov regularization method for Cauchy problem for the modified Helmholtz equation. Adv. Inf. Technol. Educ. 2011, 201, 343–350. [Google Scholar]
- Tautenhahn, U. Optimal stable solution of Cauchy problems of elliptic equations. J. Anal. Appl. 1996, 15, 961–984. [Google Scholar] [CrossRef]
- Alessandrini, G.; Rondi, L.; Rosset, E.; Vessella, S. The stability for the Cauchy problem for elliptic equations. Inverse Prob. 2009, 25, 123004. [Google Scholar] [CrossRef]
- Cheng, J.; Yamamoto, M. One new strategy for a priori choice of regularizing parameters in Tikhonov’s regularization. Inverse Prob. 2000, 16, L31–L38. [Google Scholar] [CrossRef]
- Payne, L.E. Bounds in the Cauchy problem for the Laplace equation. Arch. Ration. Mech. Anal. 1960, 5, 35–45. [Google Scholar] [CrossRef]
- Egger, H.; Hofmann, B. Tikhonov regularization in Hilbert scales under conditional stability assumptions. Inverse Probl. 2018, 34, 115015. [Google Scholar] [CrossRef]
- Hofmann, B.; Mathe, P. Tikhonov regularization with oversmoothing penalty for non-linear ill-posed problems in Hilbert scales. Inverse Probl. 2017, 34, 015007. [Google Scholar] [CrossRef]
- Hofmann, B.; Kaltenbacher, B.; Resmerita, E. Lavrentiev’s regularization method in Hilbert spaces revisited. Inverse Probl. Imaging 2017, 10, 741–764. [Google Scholar] [CrossRef]
- Plato, R.; Mathé, P.; Hofmann, B. Optimal rates for lavrentiev regularization with adjoint source conditions. Math. Comput. 2017, 87, 1. [Google Scholar] [CrossRef]
- Chen, D.H.; Hofmann, B.; Zou, J. Regularization and convergence for ill-posed backward evolution equations in Banach spaces. J. Differ. Equ. 2018, 265, 3533–3566. [Google Scholar] [CrossRef]
- H<i>a</i>`o, D.N.; Duc, N.V.; Lesnic, D. A non-local boundary value problem method for the Cauchy problem for elliptic equations. Inverse Probl. 2009, 25, 055002. [Google Scholar]
- Morozov, V.A.; Nashed, Z.; Aries, A.B. Methods for Solving Incorrectly Posed Problems; Springer: New York, NY, USA, 1984. [Google Scholar]

| 0.001 | 0.005 | 0.01 | 0.05 | 0.1 | |
| 0.0019 | 0.0032 | ||||
| 6.4027 | 0.0030 | 0.0055 | 0.0219 | 0.0396 | |
| 8.0136 | 0.0035 | 0.0064 | 0.0233 | 0.0409 |
| 0.001 | 0.005 | 0.01 | 0.05 | 0.1 | |
| 6.3978 | 0.0032 | 0.0062 | 0.0284 | 0.0525 | |
| 7.4456 | 0.0037 | 0.0072 | 0.0316 | 0.0569 |
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 0.0064 | 0.0061 | 0.0055 | 0.0046 | 0.0039 | 0.0033 | |
| 0.0081 | 0.0075 | 0.0064 | 0.0050 | 0.0040 | 0.0034 |
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 0.0064 | 0.0063 | 0.0062 | 0.0061 | 0.0058 | 0.0055 | |
| 0.0074 | 0.0073 | 0.0072 | 0.0069 | 0.0066 | 0.0060 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Zhang, X. Generalized Tikhonov Method and Convergence Estimate for the Cauchy Problem of Modified Helmholtz Equation with Nonhomogeneous Dirichlet and Neumann Datum. Mathematics 2019, 7, 667. https://doi.org/10.3390/math7080667
Zhang H, Zhang X. Generalized Tikhonov Method and Convergence Estimate for the Cauchy Problem of Modified Helmholtz Equation with Nonhomogeneous Dirichlet and Neumann Datum. Mathematics. 2019; 7(8):667. https://doi.org/10.3390/math7080667
Chicago/Turabian StyleZhang, Hongwu, and Xiaoju Zhang. 2019. "Generalized Tikhonov Method and Convergence Estimate for the Cauchy Problem of Modified Helmholtz Equation with Nonhomogeneous Dirichlet and Neumann Datum" Mathematics 7, no. 8: 667. https://doi.org/10.3390/math7080667
APA StyleZhang, H., & Zhang, X. (2019). Generalized Tikhonov Method and Convergence Estimate for the Cauchy Problem of Modified Helmholtz Equation with Nonhomogeneous Dirichlet and Neumann Datum. Mathematics, 7(8), 667. https://doi.org/10.3390/math7080667




