A Bi-Level Programming Model for Optimal Bus Stop Spacing of a Bus Rapid Transit System
Abstract
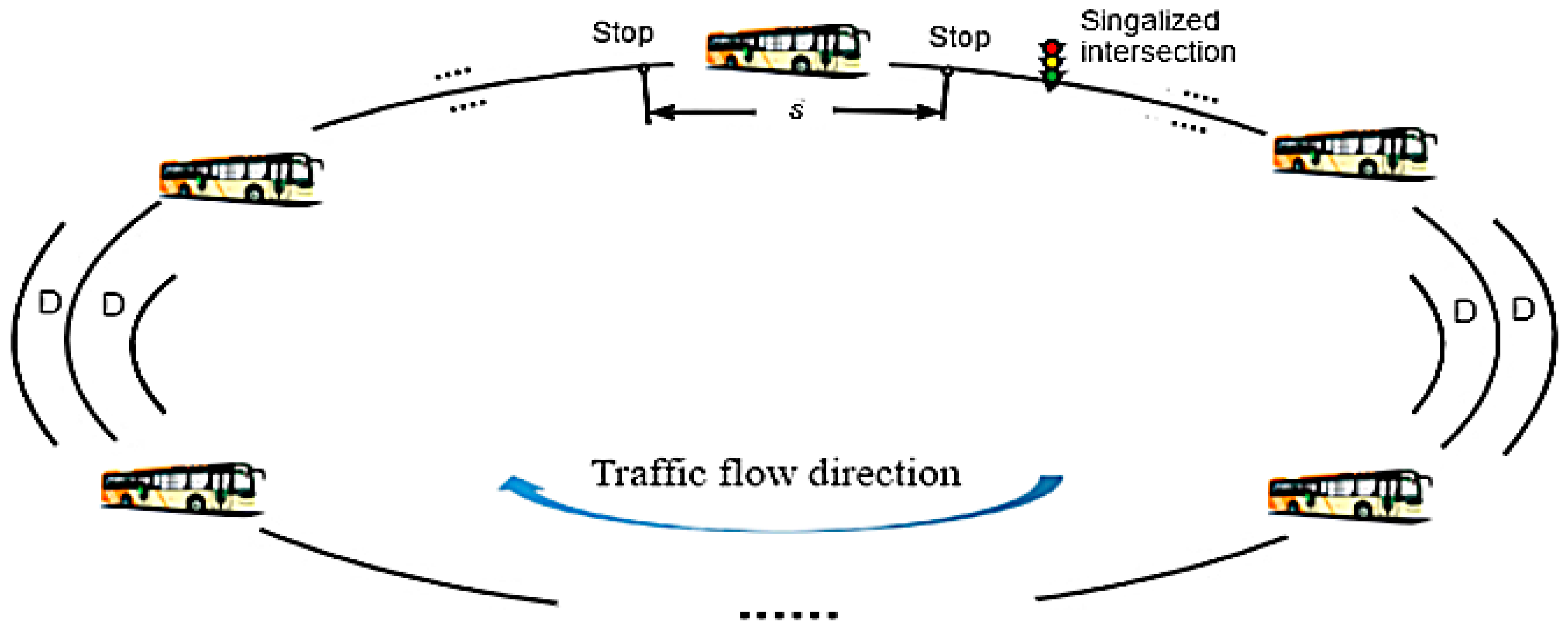
:1. Introduction
2. Overview of Solutions
3. Model Development
3.1. Top-Level Model Establishment
3.1.1. Wait Cost
3.1.2. In-Vehicle Cost
3.1.3. Walk Cost
3.1.4. Operator Cost
3.2. Construction of a Bottom-Level Model
4. Case Study
4.1. Model Verification
4.2. Sensitivity Analysis
4.2.1. Coverage Coefficient of Bus Stops
4.2.2. BRT Headway
4.2.3. Normal Speed
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Levinson, H.; Zimmerman, S.; Clinger, J.; Rutherford, G. Bus rapid transit: An overview. J. Public Transp. 2002, 5, 1–30. [Google Scholar] [CrossRef]
- Cheng, H.; Mao, C.; Madanat, S.; Horvath, A. Minimizing the total costs of urban transit systems can reduce greenhouse gas emissions: The case of San Francisco. Transp. Policy 2018, 66, 40–48. [Google Scholar] [CrossRef]
- Donaldson, R. Mass rapid rail development in South Africa’s metropolitan core: Towards a new urban form? Land Use Policy 2006, 23, 344–352. [Google Scholar] [CrossRef]
- Julsrud, T.E.; Denstadli, J.M. Smartphones, travel time-use and attitudes to public transport services. Insights from an explorative study of urban dwellers in two Norwegian cities. Int. J. Sustain. Transp. 2017, 11, 602–610. [Google Scholar] [CrossRef]
- Lin, P.Q.; Xu, J.M. Modeling, Solution and Simulation of the problem of optimizing parking line combination for BRT station group. Theory Pract. Syst. Eng. 2012, 32, 2570–2576. (In Chinese) [Google Scholar]
- Ji-Hua, H.; Cheng-Zhi, Z.; Zhi-Feng, C.; Bo, W. A research of pedestrian evacuation simulation for BRT station based on Fine Grid Method. Procedia Eng. 2013, 52, 137–144. [Google Scholar] [CrossRef]
- Xu, H.F.; Wang, D.H. Calculation method of minimum green light time for motor vehicle phase fixing at BRT priority control intersection. J. Jilin Univ. 2009, 39, 92–97. (In Chinese) [Google Scholar]
- Dessouky, M.; Hall, R.; Zhang, L.; Singh, A. Real-time control of buses for schedule coordination at a terminal. Transp. Res. Part A Policy Pract. 2003, 37, 145–164. [Google Scholar] [CrossRef]
- Furth, P.G.; Rahbee, A.B.; Information, R. Optimal bus stop spacing through dynamic programming and geographic modeling. Transp. Res. Rec. J. Transp. Res. Board 2000, 1731, 15–22. [Google Scholar] [CrossRef]
- Mylona, E.A.; Savelonas, M.A.; Maroulis, D. Effects of bus stop consolidation on passenger activity and transit operations. Transp. Res. Rec. J. Transp. Res. Board 2006, 1971, 32–41. [Google Scholar] [CrossRef]
- Vuchic, V.R.; Newell, G.F. Rapid transit interstation spacings for minimum travel time. Transp. Sci. 1968, 2, 303–339. [Google Scholar] [CrossRef]
- Tétreault, P.R.; El-Geneidy, A.M. Estimating bus run times for new limited-stop service using archived AVL and APC data. Transp. Res. Part A Policy Pract. 2010, 44, 390–402. [Google Scholar] [CrossRef]
- Ziari, H.; Keymanesh, M.R.; Khabiri, M.M. Locating stations of public transportation vehicles for improving transit accessibility. Transport 2007, 22, 99–104. [Google Scholar] [CrossRef]
- Li, H.; Bertini, R.L. Assessing a model for optimal bus stop spacing with high-resolution archived stop-level data. Transp. Res. Rec. J. Transp. Res. Board 2009, 2111, 24–32. [Google Scholar] [CrossRef]
- Tirachini, A. The economics and engineering of bus stops: Spacing, design and congestion. Transp. Res. Part A Policy Pract. 2014, 59, 37–57. [Google Scholar] [CrossRef]
- Wirasinghe, S.C.; Ghoneim, N.S. Spacing of bus-stops for many to many travel demand. Transp. Sci. 1981, 15, 210–221. [Google Scholar] [CrossRef]
- Wu, C.; Murray, A.T. Optimizing public transit quality and system access: The multiple-route, maximal covering/shortest-path problem. Environ. Plan. B Plan. Des. 2005, 32, 163–178. [Google Scholar] [CrossRef]
- Černá, A.; Cerny, J.; Přibyl, V. Bus route design in small demand areas. Transport 2011, 26, 248–254. [Google Scholar] [CrossRef]
- Otto, B.; Boysen, N. A dynamic programming based heuristic for locating stops in public transportation networks. Comput. Ind. Eng. 2014, 78, 163–174. [Google Scholar] [CrossRef]
- Zhang, X.L.; Chen, J.; Wang, W.; Jiang, D.Z. Bus stop spacing optimization method based on bus accessibility. J. Southeast Univ. 2009, 39, 384–388. (In Chinese) [Google Scholar]
- Yu, C.; Ma, W.; Lo, H.K.; Yang, X. Optimization of mid-block pedestrian crossing network with discrete demands. Transp. Res. Part B Methodol. 2015, 73, 103–121. [Google Scholar] [CrossRef]
- Mekuria, M.C.; Furth, P.G.; Melachrinoudis, E. Optimization of Spacing of Transit Stops on a Realistic Street Network. Transp. Res. Rec. J. Transp. Res. Board 2012, 2277, 29–37. [Google Scholar] [CrossRef]
- Fan, W.; Mei, Y.; Gu, W. Optimal design of intersecting bimodal transit networks in a grid city. Transp. Res. Part B Methodol. 2018, 111, 203–226. [Google Scholar] [CrossRef]
- Chien, S.; Byun, J.; Bladikas, A. Optimal stop spacing and headway of congested transit system considering realistic wait times. Transp. Plan. Technol. 2010, 33, 495–513. [Google Scholar] [CrossRef]
- Ibeas, Á.; Alonso, B.; Sainz, O.; Dell’Olio, L. Optimizing bus stop spacing in urban areas. Transp. Res. Part E Logist. Transp. Rev. 2010, 46, 446–458. [Google Scholar] [CrossRef]
- Moura, J.L.; Alonso, B.; Ibeas, Á.; Ruisánchez, F.J. A Two-Stage Urban Bus Stop Location Model. Netw. Spat. Econ. 2012, 12, 403–420. [Google Scholar] [CrossRef]
- Delmelle, E.M.; Li, S.; Murray, A.T. Identifying bus stop redundancy: A gis-based spatial optimization approach. Comput. Environ. Urban Syst. 2012, 36, 445–455. [Google Scholar] [CrossRef]
- Alonso, B.; Moura, J.L.; Dell’olio, L.; Ibeas, Á. Bus stop location under different levels of network congestion and elastic demand. Transport 2011, 26, 141–148. [Google Scholar] [CrossRef]
- Chen, J.; Wang, S.; Liu, Z. Network-level Optimization of Bus Stop Placement in Urban Areas. KSCE J. Civ. Eng. 2017, 22, 1446–1453. [Google Scholar] [CrossRef]
- Tirachini, A.; Hensher, D.A.; Rose, J.M. Multimodal pricing and optimal design of urban public transport: The interplay between traffic congestion and bus crowding. Transp. Res. Part B Methodol. 2014, 61, 33–54. [Google Scholar] [CrossRef]
- Aslan, H.; Kocaman, H. GIS Based Bus Stop Optimisation for Sakarya Public Transportation System. Sak. Univ. J. Sci. 2018, 22, 1. [Google Scholar] [CrossRef]
- Zhao, L.H.; Chien, S.I. Investigating the Impact of Stochastic Vehicle Arrivals to Optimal Stop Spacing and Headway for a Feeder Bus Route. J. Adv. Transp. Methodol. 2015, 49, 341–357. [Google Scholar] [CrossRef]
- Saka, A.A. Model for Determining Optimum Bus-Stop Spacingin Urban Areas. J. Transp. Eng. 2001, 127, 195–199. [Google Scholar] [CrossRef]
- Minocha, V.K. Discussion of “Model for Determining Optimum Bus-Stop Spacing in Urban Areas” by Anthony A. Saka. J. Transp. Eng. 2002, 128, 596. [Google Scholar] [CrossRef]
- Alshalalfah, B.W.; Shalaby, A.S. Case Study: Relationship of Walk Access Distance to Transit with Service, Travel, and Personal Characteristics. J. Urban Plan. Dev. 2007, 133, 114–118. [Google Scholar] [CrossRef]
- Krygsman, S.; Dijst, M.; Arentze, T. Multimodal public transport: An analysis of travel time elements and the interconnectivity ratio. Transp. Policy 2004, 11, 265–275. [Google Scholar] [CrossRef]





| Symbol | Definitions | Unit | Value |
|---|---|---|---|
| Equivalent cost (objective value of the top-level model) | ¥ | ||
| User cost | ¥ | ||
| Operator cost | ¥ | ||
| Wait cost | ¥ | ||
| In-vehicle cost | ¥ | ||
| Walk cost | ¥ | ||
| Value of wait time | ¥/s | 0.2 | |
| Value of in-vehicle time | ¥/s | 0.1 | |
| Value of walk time | ¥/s | 0.2 | |
| Average vehicle operating cost | ¥/(vehicle-s) | 0.5 | |
| Total wait time for all the passengers | s | ||
| Total in-vehicle time | s | ||
| Total walk time for all the passengers | s | ||
| Round-trip BRT travel time | s | ||
| tad | Time for the vehicle acceleration and deceleration | s | |
| Dwell time at the stop station | s | ||
| Dwell time caused by traffic signals | s | ||
| Unimpeded running time of vehicles | s | ||
| Total number of stops | stops | ||
| BRT passenger flow at stop | persons | ||
| Average wait time at stop | s | ||
| BRT demand attraction in relation to stop spacing | persons | ||
| BRT route length | km | 28.3 | |
| BRT stop spacing | m | ||
| Average wait time | s | ||
| BRT headway | s | ||
| Number of signalized intersections which are located at a considerable distance from stops, and the spacing is at least at a distance of 50 m | intersections | ||
| Possibility that vehicles adequately stop for red lights at intersections | 0.5 | ||
| Average cycle time of signalized intersection | s | 80 | |
| Average cycle time of signalized intersection | s | 40 | |
| Walk speed of passengers | m/s | 1.2 | |
| Average value of acceleration | m/s2 | 0.6 | |
| Average value of deceleration | m/s2 | 1 | |
| Normal speed | m/s | ||
| Speed of stops | m/s | ||
| Maximum recommended and permissible speed | m/s | 60 | |
| Distance travelled during acceleration of the BRT vehicle | m | ||
| Distance travelled during deceleration of the BRT vehicle | m | ||
| Time required per person to alight or board a bus | s | 3 | |
| Time for the opening and closing of doors | s | 3 | |
| Number of signalized intersections | intersections | 23 | |
| The coverage coefficient of bus stops caused by stop spacing | |||
| Potential bus traffic | persons | 320,000 | |
| Walking distance | m | ||
| Probability of passengers choosing a BRT | |||
| Area within 300 m from a BRT stop | m2 | ||
| Area where the distance ranges between 300 and 700 m to a stop | m2 | ||
| Probability of passengers in and choosing BRT | |||
| Actual service area of the up-run direction of the line | m2 | ||
| Ideal stop service area | m2 | ||
| Maximum value of | m2 | ||
| Maximum value of | m2 | ||
| Non-repeated service area between adjacent stops | m2 | ||
| Repeat service areas between adjacent stops in an area where stop spacing is between 0 to 300 m | m2 | ||
| Repeat service areas between adjacent stops in an area where stop spacing is between 300 to 700 m | m2 | ||
| Minimum value of stop spacing | m | ||
| Maximum value of stop spacing | m | ||
| BRT stop spacing | m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, G.; Zhao, S.; Zhang, T. A Bi-Level Programming Model for Optimal Bus Stop Spacing of a Bus Rapid Transit System. Mathematics 2019, 7, 625. https://doi.org/10.3390/math7070625
Cheng G, Zhao S, Zhang T. A Bi-Level Programming Model for Optimal Bus Stop Spacing of a Bus Rapid Transit System. Mathematics. 2019; 7(7):625. https://doi.org/10.3390/math7070625
Chicago/Turabian StyleCheng, Gang, Shuzhi Zhao, and Tao Zhang. 2019. "A Bi-Level Programming Model for Optimal Bus Stop Spacing of a Bus Rapid Transit System" Mathematics 7, no. 7: 625. https://doi.org/10.3390/math7070625
APA StyleCheng, G., Zhao, S., & Zhang, T. (2019). A Bi-Level Programming Model for Optimal Bus Stop Spacing of a Bus Rapid Transit System. Mathematics, 7(7), 625. https://doi.org/10.3390/math7070625





