A Study of Regular and Irregular Neutrosophic Graphs with Real Life Applications

Abstract

Fuzzy graph theory is a useful and well-known tool to model and solve many real-life optimization problems. Since real-life problems are often uncertain due to inconsistent and indeterminate information, it is very hard for an expert to model those problems using a fuzzy graph. A neutrosophic graph can deal with the uncertainty associated with the inconsistent and indeterminate information of any real-world problem, where fuzzy graphs may fail to reveal satisfactory results. The concepts of the regularity and degree of a node play a significant role in both the theory and application of graph theory in the neutrosophic environment. In this work, we describe the utility of the regular neutrosophic graph and bipartite neutrosophic graph to model an assignment problem, a road transport network, and a social network. For this purpose, we introduce the definitions of the regular neutrosophic graph, star neutrosophic graph, regular complete neutrosophic graph, complete bipartite neutrosophic graph, and regular strong neutrosophic graph. We define the $d_m$- and $t{d}_m$-degrees of a node in a regular neutrosophic graph. Depending on the degree of the node, this paper classifies the regularity of a neutrosophic graph into three types, namely $d_m$-regular, $t{d}_m$-regular, and m-highly irregular neutrosophic graphs. We present some theorems and properties of those regular neutrosophic graphs. The concept of an m-highly irregular neutrosophic graph on cycle and path graphs is also investigated in this paper. The definition of busy and free nodes in a regular neutrosophic graph is presented here. We introduce the idea of the $\mu$-complement and h-morphism of a regular neutrosophic graph. Some properties of complement and isomorphic regular neutrosophic graphs are presented here.

1. Introduction

Graph theory has many real-life applications for problems in computer applications, systems analysis, computer networks, transportation, operations research, and economics. A graph is basically a model of relations, and it is a used to represent the real-life problem consisting of relationships between objects. The vertices and edges of the graph are used to represent the objects and the relations between objects, respectively. In many optimization problems, the available information is inexact or imprecise for various reasons such as the loss of information, a lack of evidence, imperfect statistical data and insufficient information. Generally, the uncertainty in real-life problems may be present in the information that defines the problem.

Classical graph theory uses the basic concept of classical set theory, which was presented by Cantor. In a classical graph, for any vertex or edge, there are two possibilities: it is either in the graph or it is not in the graph. Therefore, classical graphs cannot model uncertain optimization problems. Real-life problems are often uncertain, which are hard to model using classical graphs. The fuzzy set [1] is an extended version of the classical set, where the objects have varying membership degrees. A fuzzy set gives its objects different membership degrees between zero and one. The membership degree is not the same as probability; rather, it describes membership in vaguely-defined sets. The concept of fuzziness in graph theory [2] was described by Kaufmann [3] using the fuzzy relation. Rosenfeld [4] introduced some concepts such as bridges, cycles, paths, trees, and the connectedness of the fuzzy graph and described some of the properties of the fuzzy graph. Gani and Radha [5] presented the notation of the regular fuzzy graph. Many other researchers, such as Samanta and Pal [6], Rashmanlou and Pal [7], Rashmanlou et al. [8,9], Paramik [10], Nandhini [11], Ghorai and Pal [12], Dey et. al [13], and Borzooei [14] presented much work in the domain of the fuzzy graph and its several applications in real life. Samanta and Pal [6] and Rashmanlou and Pal [15] presented the concept of the irregular and regular fuzzy graph. They also described some applications of those graphs.

Atanassov [16,17,18] presented the idea of the intuitionistic fuzzy set (IFS) as a modified version of the classical fuzzy set. The classical fuzzy set uses only the membership grade (degree), but IFS uses independent membership grade and non-membership grade for any entity, and the only requirement is that the sum of non-membership and membership degree values be no greater than one. Shannon and Atanassov [19] presented the idea of the IFS relation and the intuitionistic fuzzy graph (IFG) and discussed many theorems, proofs, and proprieties [19]. Parvathi et al. [20,21,22] presented many different operations such as the join, union, and product of two IFGs. Rashmanlou et al. [23] presented some products such as strong, direct, and lexicographic products for two IFGs. For further detailed descriptions of IFGs, please refer to [24,25,26,27]. Although the fuzzy graph and IFG have been used to model many real-word problems, uncertainties due to inconsistent and indeterminate information about a problem cannot be represented properly by the fuzzy graph or IFG. Therefore, a new idea is needed to deal with such scenarios.

Smarandache [28] introduced the idea of the neutrosophic set, by modifying the concept of the fuzzy set. The neutrosophic set can work with uncertain, indeterminate, vague, and inconsistent information of any uncertain real-life problem. It is basically a modified version of the crisp set, Type 1 fuzzy set, and IFS. It is described by the truth, indeterminate, and false membership degrees of any object. These three membership degrees are independent and always lie within ${]}^{-}0,1^{+}[$, i.e., a nonstandard unit interval. The neutrosophic graph [12] can efficiently model the inconsistent information about any real-life problem. Recently, many researchers have more actively worked on neutrosophic graph theory; for instance, Ye [29], Yang et al. [30], Naz et al. [31], Broumi [15], and Arkam [32,33,34,35].

The vertex degree is a significant way to represent the total number of relations of a vertex in a graph, and the vertex degree can be used to analyze the graph. Gani and Lathi [36] proposed the concept of irregularity, total irregularity, and total degree in a fuzzy graph. Maheswari and Sekar [37] proposed the notation of the $d_2$-vertex in a fuzzy graph and also described several properties on the $d_2$-vertex degree of a fuzzy graph. Darabian et al. [38] presented the idea of the $d_m$-regular vague graph, $t{d}_m$-regular vague graph, m-highly irregular vague graph, and m-highly total irregular vague graph, and they discussed some properties of those graphs. They described some real-life applications (e.g., fullerene molecules, wireless networks, and road networks) of regular vague graphs. Neutrosophic graphs are more effective, precise, flexible, and compatible when modeling uncertain real-life problems compared to fuzzy graphs or vague graphs. Thus, the use of the neutrosophic graph is inevitable for modeling optimization problems [29,34,39,40,41] in real-life scenarios, and it is essential to present some new properties and theories for neutrosophic graphs. This idea motivates us to introduce different types of neutrosophic graphs (regular, bipartite, isomorphic, and $\mu$ complement neutrosophic graphs) and their related theorems.

The concept of the regularity and degree of nodes has a significant role in both theories and applications (e.g., social network analysis, road transpotation network, wireless multihop network, and the assignment problem) in neutrosophic graph theory. The main contributions of this manuscript are as follows.

(i)

As far as we know, there exists no research work on the regularity of the neutrosophic graph until now. Therefore, in this manuscript, we present the definition of the regular neutrosophic graph, star neutrosophic graph, regular strong neutrosophic graph, and complete bipartite neutrosophic graph.

(ii)

We introduce the two types of degree, $d_m$ and total $d_m$-degrees, of a node in a neutrosophic graph. The definition of busy and free nodes in a regular neutrosophic graph are presented here.

(iii)

Depending on the degree of the node, we introduce the three types of regularity of a neutrosophic graph, $d_m$-regular, $t{d}_m$-regular, and m-highly-irregular neutrosophic graphs (HING), and some properties are also described. We also investigate the concept of m-HING on the cycle graph and path graph in this manuscript.

(iv)

We have presented the definition of the $\mu$-complement and h-morphism of a neutrosophic graph. Some properties of the complement and isomorphic regular neutrosophic graph are also presented here.

(v)

Some real-life applications of the regular neutrosophic graph and complete bipartite neutrosophic graph such as the road transport network, social networks, and assignment problem are described in this paper.

2. Preliminaries

In this portion, we will discuss the single-valued neutrosophic graph (SVNG), adjacent node, path, isolated node, strength of a path, strong SVNG, complement SVNG, and complete SVNG, which are efficient for the present work.

Definition 1.

Let $G=\left(N,M\right)$ be an SVNG [42,43] where N and M are represented by two neutrosophic sets on V and E, respectively, which satisfy the following.

$$\begin{array}{l}{T}_M(a,b)\le min\left(T_N\left(a\right),T_N\left(b\right)\right)\\ I_M(a,b)\ge max\left(I_N\left(a\right),I_N\left(b\right)\right)\\ F_M(a,b)\ge max\left(F_N\left(a\right),F_N\left(b\right)\right)\end{array}$$

Here, a and b are two vertices of G, and $(a,b)\in E$ is an edge of G.

Definition 2.

The two nodes a and b of an SVNG $G=\left(N,M\right)$ are defined as the adjacent nodes in G if and only if $\left(T_M(a,b),I_M(a,b),F_M(a,b)\right)>0$. The two nodes a and b are called the neighbor nodes, and $(a,b)$ is incident at a and b.

Definition 3.

Let $G=\left(N,M\right)$ be an SVNG and P be a path of G. P is a collection of different nodes, $a_0,a_1,a_2,...,a_n$ such that $\left(T_M\left(a_{i-1},a_i\right),I_M\left(a_{i-1},a_i\right),F_M\left(a_{i-1},a_i\right)\right)>0$ for $0\le i\le n$. Here, n represents the neutrosophic length of the path P. A single neutrosophic vertex, i.e., $a_i$ in G, is also assumed as a path. The path length of a single node $a_i$ is $\left(0,0,0\right)$. We define the order pair $(a_{i-1},a_i)$ as the edge of the path. P is said to be a neutrosophic cycle if $a_0=a_n$ and $n\ge 3$.

Definition 4.

A node $a_i\in V$ of an SVNG G is called the isolated node if there exists no incident arc to the vertex $a_i$.

Definition 5.

Let $G=\left(N,M\right)$ be an SVNG. If G has a path P of path length [42] k from node a to node b in G such as $P=\{a=a_1,(a_1,a_2),a_2,...,a_{k-1}(a_{k-1},a_k),a_k=b)\}$, then $T_M^k(a,b)$, $I_M^k(a,b)$, and $F_M^k(a,b)$ are described as follows.

$$\begin{array}{l}{T}_M^k(a,b)=sup\left(T_M\left(a,a_1\right)\wedge T_M\left(a_1,a_2\right)\wedge ...\wedge T_B\left(a_{k-1},a_k\right)\right)\\ I_M^k(a,b)=inf\left(I_M\left(a,a_1\right)\vee I_M\left(a_1,a_2\right)\vee ...\vee I_M\left(a_{k-1},a_k\right)\right)\\ F_M^k(a,b)=inf\left(F_M\left(a,a_1\right)\vee F_M\left(a_1,a_2\right)\vee ...\vee F_M\left(a_{k-1},a_k\right)\right)\end{array}$$

Definition 6.

Let $G=\left(N,M\right)$ be an SVNG. The strength of connection of a path P between two nodes a and b is defined by $\left(T_M^{\infty }(a,b),I_M^{\infty }(a,b),F_M^{\infty }(a,b)\right)$ where:

$$\begin{array}{l}{T}_M^{\infty }(a,b)=sup\left\{T_M^k\left(a,b\right)\right|k=1,2,...\}\\ I_M^{\infty }(a,b)=inf\left\{I_M^k\left(a,b\right)\right|k=1,2,...\}\\ F_M^{\infty }(a,b)=inf\left\{F_B^k\left(a,b\right)\right|k=1,2,...\}\end{array}$$

Definition 7.

Let $G=(N,M)$ be an SVNG. G is said to be a connected SVNG [42] if there exists no isolated node in G.

Definition 8.

Let $G=(N,M)$ be an SVNG and $a\in V$ be node of G. The degree of node a is the sum of the truth membership values, the sum of the indeterminacy membership values, and the sum of the membership values of falsity of all the arcs that are adjacent to node a. The degree of node [35] a is denoted by $d\left(a\right)=\left(d_T\left(a\right),d_I\left(a\right),d_F\left(a\right)\right)$ where:

$$d_T\left(a\right)=\sum _{\begin{array}{c}a\in V\\ a\ne b\end{array}}{T}_M\left(a,b\right),d_I\left(a\right)=\sum _{\begin{array}{c}a\in V\\ a\ne b\end{array}}{I}_M\left(a,b\right),d_F\left(a\right)=\sum _{\begin{array}{c}a\in V\\ a\ne b\end{array}}{F}_M\left(a,b\right)$$

Here, $d_T\left(a\right)$, $d_I\left(a\right)$, and $d_F\left(a\right)$ are the degree of the truth membership value, the degree of the indeterminacy membership value, and the degree falsity membership value, respectively, of vertex a.

Definition 9.

Let $G=(N,M)$ be an SVNG. Then, the order of G is denoted by $O\left(G\right)=\left(O_T\left(G\right),O_I\left(G\right),O_F\left(G\right)\right)$ where:

$$O_T\left(G\right)=\sum _{a\in V}{T}_N\left(a\right),O_I\left(G\right)=\sum _{a\in V}{I}_N\left(a\right),O_F\left(G\right)=\sum _{a\in V}{F}_N\left(a\right)$$

Here, $O_T\left(G\right)$, $O_I\left(G\right)$, and $O_F\left(G\right)$ are the order of the membership degree of the truth value, the indeterminacy value, and the falsity value of G, respectively.

Definition 10.

Let $G=(N,M)$ be an SVNG and the size graph of G be described as $S\left(G\right)=\left(S_T\left(G\right),S_I\left(G\right),S_F\left(G\right)\right)$ where:

$$S_T\left(G\right)=\sum _{\begin{array}{c}a,b\in V\\ a\ne b\end{array}}{T}_M\left(a,b\right),S_I\left(G\right)=\sum _{\begin{array}{c}a,b\in V\\ a\ne b\end{array}}{I}_M\left(a,b\right),S_F\left(G\right)=\sum _{\begin{array}{c}a,b\in V\\ a\ne b\end{array}}{F}_M\left(a,b\right)$$

Here, $S_T\left(G\right)$, $S_I\left(G\right)$, and $S_F\left(G\right)$ are respectively the order of the membership degree of the truth, indeterminacy, and falsity of G.

Definition 11.

Let $G=(N,M)$ be an SVNG. G is said to be a strong SVNG [31,35,44] if:

$$\begin{array}{l}{T}_M(a,b)=min\left(T_N\left(a\right),T_N\left(b\right)\right)\\ I_M(a,b)=max\left(I_N\left(a\right),I_N\left(b\right)\right)\\ F_M(a,b)=max\left(F_N\left(a\right),F_N\left(b\right)\right), \forall (a,b)\in E\end{array}$$

Definition 12.

Let $G=(N,M)$ be an SVNG and G be said to be a complete SVNG [31,35,44] if:

$$\begin{array}{l}{T}_M(a,b)=min\left(T_N\left(a\right),T_N\left(b\right)\right)\\ I_M(a,b)=max\left(I_N\left(a\right),I_N\left(b\right)\right)\\ F_M(a,b)=max\left(F_N\left(a\right),F_N\left(b\right)\right), \forall a,b\in V\end{array}$$

Definition 13.

Let $G=(N,M)$ be an SVNG. $G^c=(N^c,M^c)$ is the complement of an SVNG [31,35,44] if $N^c=N$ and $M^c$ is computed as below.

$$\begin{array}{l}{T}_M^c(a,b)=min\left(T_N\left(a\right),T_N\left(b\right)\right)-T_M(a,b)\\ I_M^c(a,b)=max\left(I_N\left(a\right),I_N\left(b\right)\right)-I_M(a,b)\\ F_M^c(a,b)=max\left(F_N\left(a\right),F_N\left(b\right)\right)-F_M(a,b), \forall a,b\in V\end{array}$$

Here, $T_M^c(a,b)$, $I_M^c(a,b)$, and $F_M^c(a,b)$ denote the true, intermediate, and false membership degree for edge $(a,b)$ of $G^c$.

3. Regular, $d_m$-Regular, and $t{d}_m$-Regular Neutrosophic Graphs

In this section, first we define the regular neutrosophic graph, regular strong neutrosophic graph, $d_m$-degree, and $t{d}_m$-degree of nodes in a neutrosophic graph. Then, we propose the notions of $d_m$ and $t{d}_m$-regular neutrosophic graphs and prove the necessary and sufficient conditions, for which under these conditions, $d_m$-regular with $t{d}_m$-regular neutrosophic graphs are equivalent.

Definition 14.

Let $G=(N,M)$ be an SVNG. G is a regular neutrosophic graph if it satisfies the following conditions.

$$\sum _{a\ne b}{T}_M(a,b)=\mathit{Constant},\sum _{a\ne b}{I}_M(a,b)=\mathit{Constant},\sum _{a\ne b}{F}_M(a,b)=\mathit{Constant}$$

Definition 15.

Let $G=(N,M)$ be an SVNG. G is a regular strong neutrosophic graph if it satisfies the following conditions.

$$\begin{array}{c}\hfill T_M(a,b)=min\left(T_N\left(a\right),T_N\left(b\right)\right)\mathit{and}\sum _{a\ne b}{T}_M(a,b)=\mathit{Constant}\\ \hfill I_M(a,b)=max\left(I_N\left(a\right),I_N\left(b\right)\right)\mathit{and}\sum _{a\ne b}{I}_M(a,b)=\mathit{Constant}\\ \hfill F_M(a,b)=max\left(F_N\left(a\right),F_N\left(b\right)\right)\mathit{and}\sum _{a\ne b}{F}_M(a,b)=\mathit{Constant}\end{array}$$

Definition 16.

Let $G=(N,M)$ be an SVNG and the $d_m$-degree of any node a in G be denoted as $d_m\left(a\right)$ where:

$$d_m\left(a\right)=\left(\sum _{a\ne b\in V}{T}_M^m\left(a,b\right),\sum _{a\ne b\in V}{I}_M^m\left(a,b\right),\sum _{a\ne b\in V}{F}_M^m\left(a,b\right)\right)$$

Here, the path $a,a_1,a_2,...,a_{m-1},b$ is the shortest path between the nodes u and v, and the length of this path is m.

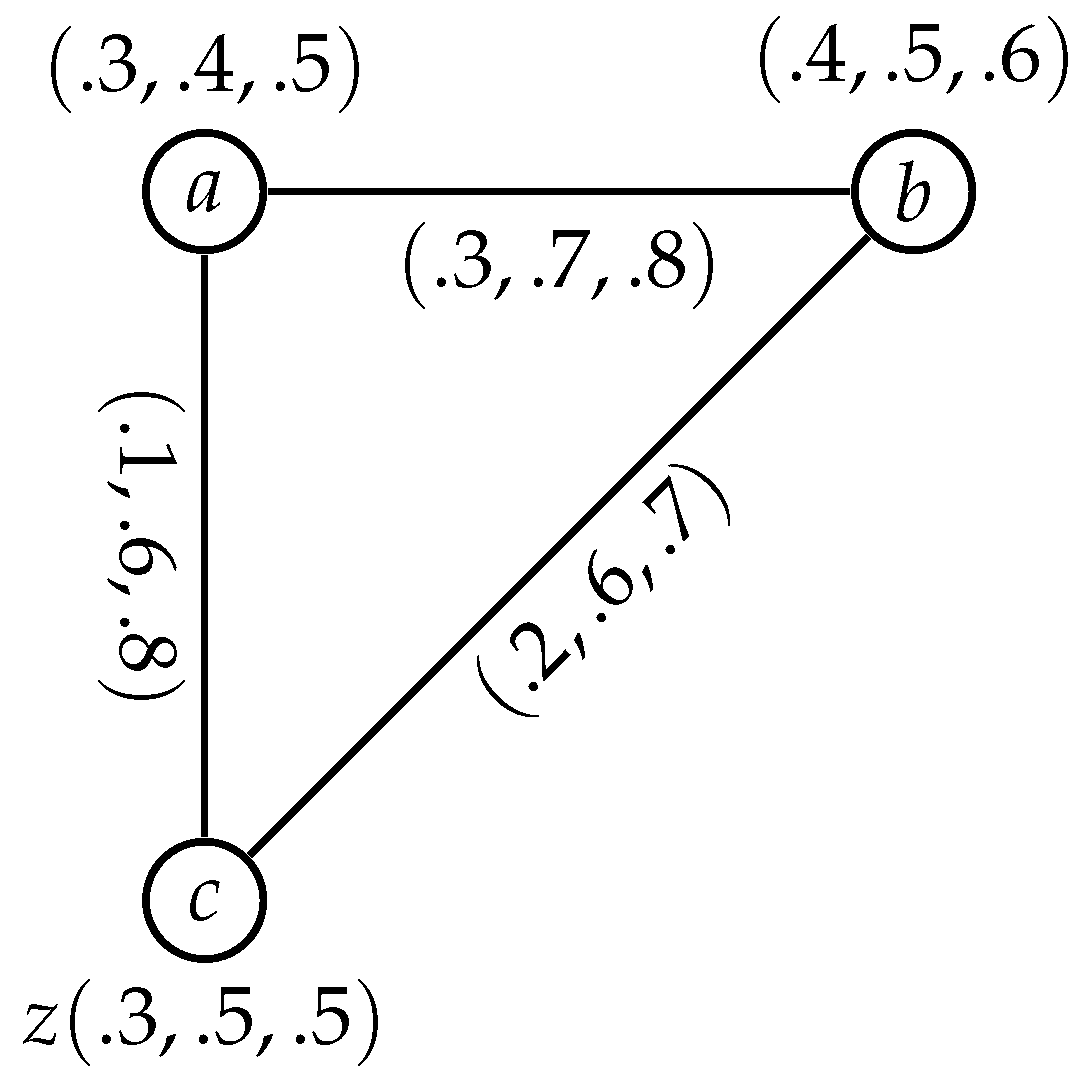
Example 1.

We have considered an example of an SVNG G, presented in Figure 1.

Then, the $d_2$-degree of the nodes in G is computed as follows.

$$\begin{array}{l}{d}_2\left(a\right)=\left(0.2+0.2,0.6+0.8,0.8+0.9\right)=\left(0.4,1.4,1.7\right)\\ d_2\left(b\right)=\left(0.2+0.2,0.8+0.8,0.9+0.9\right)=\left(0.4,1.6,1.8\right)\\ d_2\left(c\right)=\left(0.2+0.2,0.6+0.8,0.8+0.9\right)=\left(0.4,1.6,1.8\right)\end{array}$$

Definition 17.

Let $G=(N,M)$ be an SVNG and $a\in V$ be a node G. The total $d_m$-degree ($t{d}_m$-degree) of node a in G is computed as follows.

$$t{d}_m\left(a\right)=\left(\left(\sum _{a\ne b\in V}{T}_M^m\left(a,b\right)+T_N\left(a\right)\right),\left(\sum _{a\ne b\in V}{I}_M^m\left(a,b\right)+I_N\left(a\right)\right),\left(\sum _{a\ne b\in V}{F}_M^m\left(a,b\right)+F_N\left(a\right)\right)\right)$$

Here, the path $a,a_1,a_2,...,a_{m-1},b$ is the shortest path between the nodes u and v, and the length of this path is m.

Example 2.

Let us consider an example of an SVNG, shown in Figure 1. Then, the $t{d}_2$-degree of the nodes in G is as follows.

$$\begin{array}{l}t{d}_2\left(a\right)=\left(\left(\left(0.2+0.2\right)+0.3\right),\left(\left(0.6+0.8\right)+0.6\right),\left(\left(0.8+0.9\right)+0.7\right)\right)=\left(0.7,2.0,2.4\right)\\ t{d}_2\left(b\right)=\left(\left(\left(0.2+0.2\right)+0.3\right),\left(\left(0.8+0.8\right)+0.6\right),\left(\left(0.9+0.9\right)+0.6\right)\right)=\left(0.7,2.1,2.4\right)\\ t{d}_2\left(a\right)=\left(\left(\left(0.2+0.2\right)+0.4\right),\left(\left(0.8+0.8\right)+0.5\right),\left(\left(0.9+0.9\right)+0.6\right)\right)=\left(0.8,2.1,2.4\right)\end{array}$$

Definition 18.

Let $G=(N,M)$ be a neutrosophic graph. G is said to be a $\left(m,\left(d_1,d_2,d_3\right)\right)$-regular neutrosophic graph or $d_m$-regular if for all nodes $a\in V$ in G, $d_m\left(a\right)=(d_1,d_2,d_3)$.

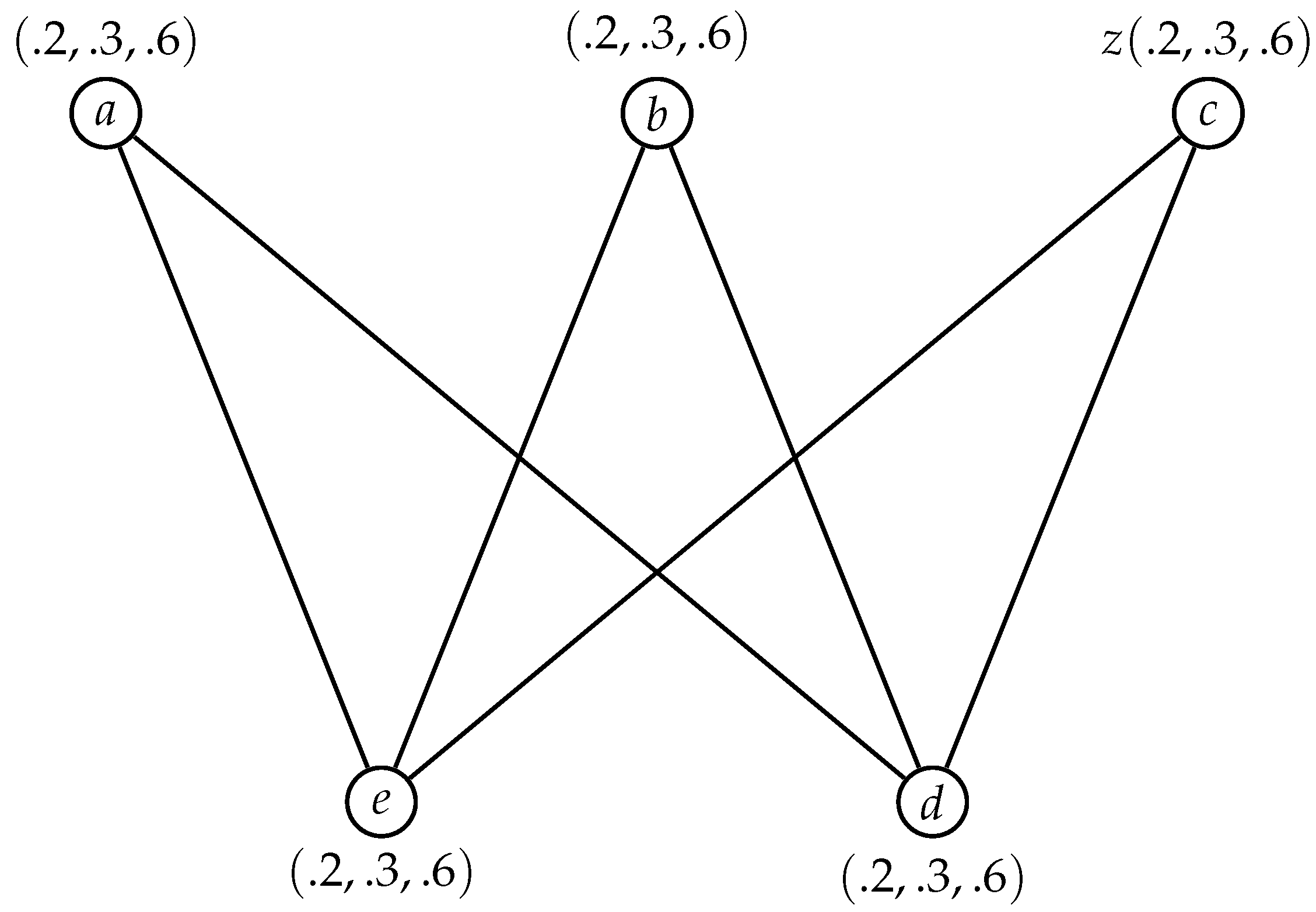
Example 3.

An example of an $\left(m,\left(d_1,d_2,d_3\right)\right)$-totally regular neutrosophic graph is pictured in Figure 2. Figure 2 is a (2, (0.1, 0.6,0.9))-regular neutrosophic graph.

$$\begin{array}{l}{d}_2\left(a\right)=\left(\left(\left(0.2+0.2\right)+0.3\right),\left(\left(0.6+0.8\right)+0.6\right),\left(\left(0.8+0.9\right)+0.7\right)\right)=\left(0.7,2.0,2.4\right)\\ t{d}_2\left(b\right)=\left(\left(\left(0.2+0.2\right)+0.3\right),\left(\left(0.8+0.8\right)+0.6\right),\left(\left(0.9+0.9\right)+0.6\right)\right)=\left(0.7,2.1,2.4\right)\\ t{d}_2\left(a\right)=\left(\left(\left(0.2+0.2\right)+0.4\right),\left(\left(0.8+0.8\right)+0.5\right),\left(\left(0.9+0.9\right)+0.6\right)\right)=\left(0.8,2.1,2.4\right)\end{array}$$

Definition 19.

Let $G=(N,M)$ is a neutrosophic graph. G is an $\left(m,\left(k_1,k_2,k_3\right)\right)$-totally regular neutrosophic graph or $t{d}_m$-regular neutrosophic graph if for all nodes $a\in V$ in G, $t{d}_m\left(a\right)=(k_1,k_2,k_3)$.

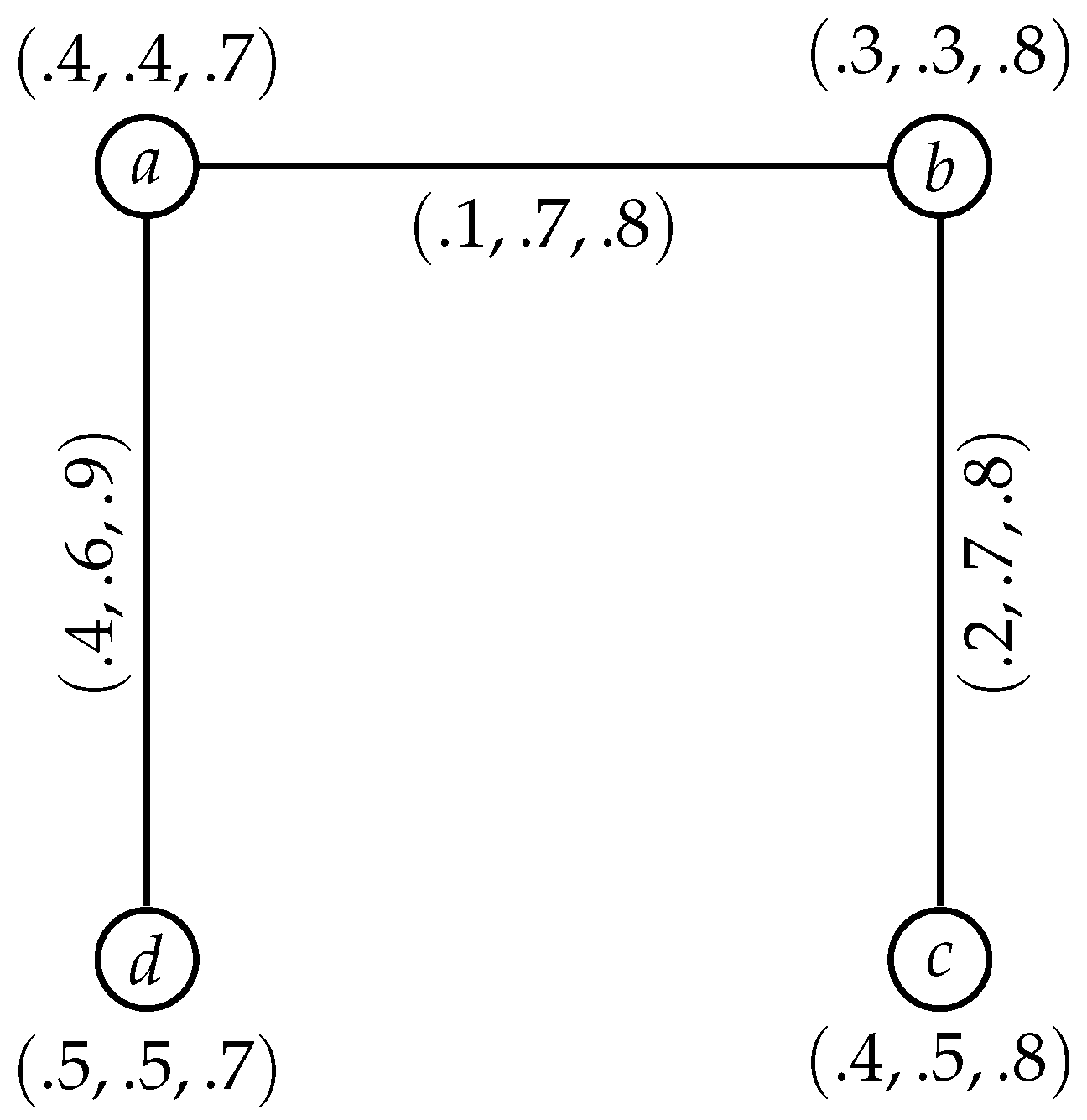
Example 4.

An example of a $\left(m,\left(k_1,k_2,k_3\right)\right)$-totally regular neutrosophic graph is shown in Figure 3. It is a (2, (0.6, 2.0,2.1))-regular neutrosophic graph.

Theorem 1.

Let $G=\left(N,M\right)$ be an SVNG. If $T_N$, $I_N$ and $F_N$ are constant functions, then G is a $d_m$-regular neutrosophic graph if G is a ${td}_m$-regular neutrosophic graph (m is a positive integer).

Proof. 

Suppose that for every node v in $G,\left(T_N\left(v\right),I_N\left(v\right),F_N\left(v\right)\right)=\left(c_1,c_2,c_3\right)$ and $d_m\left(v\right)=\left(d_1,d_2,d_3\right)$. Then:

$${td}_m\left(v\right)=d_m\left(v\right)+\left(T_N\left(v\right),I_N\left(v\right),F_N\left(v\right)\right)=\left(d_1+c_1,d_2+c_2,d_3+c_3\right);$$

hence, G is a ${td}_m$-regular neutrosophic graph. If G is a ${td}_m$-regular neutrosophic graph, then the proof is similar to the previous case. □

Theorem 2.

Let $G=\left(N,M\right)$ be an $\left(m,\left(d_1,d_2,d_3\right)\right)$-totally regular and an $\left(m,\left(k_1,k_2,k_3\right)\right)$-totally regular neutrosophic graph with n nodes. Then, $T_N,I_N$ and $F_N$ are constant functions, and $O\left(G\right)=n(k_1-d_1,k_2-d_2,k_3-d_3).$

Proof. 

If G is an $\left(m,\left(d_1,d_2,d_3\right)\right)$-regular neutrosophic graph and an $\left(m,\left(k_1,k_2,k_3\right)\right)$-totally regular neutrosophic graph respectively, then for all $v\in V$ we get,

$$d_m\left(u\right)=(d_1,d_2,d_3)\to (\sum _{u\ne v\in V}{T}_M^m\left(uv\right),\sum _{u\ne v\in V}{I}_b^m\left(uv\right),\sum _{u\ne v\in V}{F}_b^m\left(uv\right))=(d_1,d_2,d_3)$$

and:

$${td}_m\left(v\right)=(k_1,k_2,k_3)\to (\sum _{u\ne v\in V}{T}_B^m\left(uv\right),+T_N\left(v\right),\sum _{u\ne v\in V}{I}_M^m\left(uv\right),+I_N\left(v\right),\sum _{u\ne v\in V}{F}_M^m\left(uv\right),+F_N\left(v\right))=(k_1,k_2,k_3).$$

Hence, by $\left(1\right)$, $\left(d_1,d_2,d_3\right)=\left(k_1-T_N\left(v\right),k_2-I_N\left(v\right),k_3-F_N\left(v\right)\right)$ and so $\left(T_N\left(v\right),I_N\left(v\right),F_N\left(v\right)\right)=\left(k_1-d_1,k_2-d_2,k_3-d_3\right)$. Then, $T_N$,$I_N$ and $F_N$ are constant functions, and since G has n nodes, we get:

$$O\left(G\right)=(\sum _{v\in V}{T}_N\left(v\right),\sum _{v\in V}{I}_N\left(v\right),\sum _{v\in V}{F}_N\left(v\right))=n(k_1-d_1,k_2-d_2,k_3-d_3).$$

 □

Free and Busy Vertex on the Regular Neutrosophic Graph

Definition 20.

Let $G=\left(N,M\right)$ be a regular neutrosophic graph and $a\in V$ be a node of G. The neutrosophic busy value of a a is denoted by $D\left(a\right)=\left(D_T\left(a\right),D_I\left(a\right),D_F\left(a\right)\right)$, where:

$$D_T\left(a\right)=\sum min\left(T_N\left(a\right),T_N\left(a_i\right)\right),D_I\left(a\right)=\sum max\left(I_N\left(a\right),I_N\left(a_i\right)\right),D_F\left(a\right)=\sum max\left(F_N\left(a\right)\vee F_N\left(a_i\right)\right)$$

Here, $a_i$ denotes the adjacent vertex of a of G. The busy value of regular neutrosophic graph G is the sum of all busy values of all the nodes of G.

Definition 21.

Let $G=\left(N,M\right)$ be a regular neutrosophic graph and $a\in V$ be a node of G. The a of G is a busy node or vertex if:

$$T_N\left(a\right)\le d_T\left(a\right),I_N\left(a\right)\le d_I\left(a\right),F_N\left(a\right)\ge d_F\left(a\right)$$

If the vertex a is not a busy vertex, then it is said to be a free vertex.

Definition 22.

Let $G=\left(N,M\right)$ be a regular neutrosophic graph and $(a,b)\in E$ be an arc of G. $a,b$ is said to be an effective edge if:

$$T_M\left(a,b\right)=min\left(T_N\left(a\right),T_N\left(b\right)\right),I_M\left(a,b\right)=max\left(I_N\left(a\right),I_N\left(b\right)\right),F_M\left(a,b\right)=max\left(F_N\left(a\right),F_N\left(b\right)\right)$$

4. Regularity on the Complement and Isomorphic Neutrosophic Graph

Definition 23.

Let $G_1=\left(N_1,M_1\right)$ and $G_2=\left(N_2,M_2\right)$ be two regular neutrosophic graphs.

• A homomorphism h from a regular neutrosophic graph $G_1$ to another regular neutrosophic graph $G_2$ is a neutrosophic mapping function $h:$$V_1\to V_2$, which always satisfies following conditions:

  (i) 

  $\forall a_1\in V_1,a_1{b}_1\in E_1$

  (a) 

  $T_{N_1}\left(a_1\right)\le T_{N_2}\left(h\left(a_1\right)\right),I_{N_1}\left(a_1\right)\le I_{N_2}\left(h\left(a_1\right)\right),F_{N_1}\left(a_1\right)\ge F_{N_2}\left(h\left(a_1\right)\right)$

  (b) 

  $T_{B_1}\left(a_1{b}_1\right)\le T_{M_2}\left(h\left(a_1\right)h\left(a_2\right)\right),I_{M_1}\left(a_1{b}_1\right)\le I_{M_2}\left(h\left(a_1\right)h\left(a_2\right)\right),F_{M_1}\left(a_1{b}_1\right)\ge F_{B_2}\left(h\left(a_1\right)h\left(a_2\right)\right)$

• A isomorphism h from a regular neutrosophic graph $G_1$ to another regular neutrosophic graph $G_2$ is a neutrosophic bijective mapping function $h:$ $V_1\to V_2$, which always satisfies the following:

  (i) 

  $\forall a_1\in V_1,a_1{b}_1\in E_1$

  (c) 

  $T_{N_1}\left(a_1\right)=T_{N_2}\left(h\left(a_1\right)\right),I_{N_1}\left(a_1\right)=I_{N_2}\left(h\left(a_1\right)\right),F_{N_1}\left(a_1\right)=F_{N_2}\left(h\left(a_1\right)\right)$

  (d) 

  $T_{M_1}\left(a_1{b}_1\right)=T_{M_2}\left(h\left(a_1\right)h\left(a_2\right)\right),I_{M_1}\left(a_1{b}_1\right)=I_{M_2}\left(h\left(a_1\right)h\left(a_2\right)\right),F_{M_1}\left(a_1{b}_1\right)=F_{M_2}\left(h\left(a_1\right)h\left(a_2\right)\right)$

• A weak isomorphism h from a regular neutrosophic graph $G_1$ to another regular neutrosophic graph $G_2$ is a neutrosophic bijective mapping function $h:$ $V_1\to V_2$, which always satisfies the following:

  (i) 

  $\forall a_1\in V_1$

  (e) 

  h is a homomorphism.

  (f) 

  $T_{N_1}\left(a_1\right)=T_{N_2}\left(h\left(a_1\right)\right),I_{N_1}\left(a_1\right)=I_{N_2}\left(h\left(a_1\right)\right),F_{N_1}\left(a_1\right)=F_{N_2}\left(h\left(a_1\right)\right)$.

• A co-weak isomorphism h from a regular neutrosophic graph $G_1$ to another regular neutrosophic graph $G_2$ is a neutrosophic bijective mapping function $h:$ $V_1\to V_2$, which always satisfies the following:

  (i) 

  $\forall a_1{b}_1\in E_1$

  (g) 

  h is a homomorphism.

  (h) 

  $T_{N_1}\left(a_1{b}_1\right)=T_{N_2}\left(h\left(a_1{b}_1\right)\right),I_{N_1}\left(a_1{b}_1\right)=I_{N_2}\left(h\left(a_1{b}_1\right)\right),F_{N_1}\left(a_1{b}_1\right)=F_{N_2}\left(h\left(a_1{b}_1\right)\right)$.

Definition 24.

Let $G=(N,M)$ be a connected neutrosophic graph. The neutrosophic graph G is called an HING if and only if all the adjacent nodes of G are always different neutrosophic degrees.

Theorem 3.

If $G_1$ and $G_2$ are two isomorphic highly-irregular neutrosophic graphs (HING), then their size and order are always equal.

Proof. 

An isomorphism h is between two HINGs $G_1$ and $G_2$ with the underlying node set $V_1$ and $V_2$, respectively, then:

(i) 

$\forall a_1\in V_1,a_1{b}_1\in E_1$

(a) 

$T_{N_1}\left(a_1\right)=T_{N_2}\left(h\left(a_1\right)\right),I_{N_1}\left(a_1\right)=I_{N_2}\left(h\left(a_1\right)\right),F_{N_1}\left(a_1\right)=F_{N_2}\left(h\left(a_1\right)\right)$

(b) 

$T_{M_1}\left(a_1{b}_1\right)=T_{B_2}\left(h\left(a_1\right)h\left(a_2\right)\right),I_{M_1}\left(a_1{b}_1\right)=I_{M_2}\left(h\left(a_1\right)h\left(a_2\right)\right),F_{M_1}\left(a_1{b}_1\right)=F_{M_2}\left(h\left(a_1\right)h\left(a_2\right)\right)$

Therefore, we have:

$$\begin{array}{cc}\hfill S\left(G_1\right)& =\left(\sum _{a_1{b}_1\in E_1}{T}_{M_1}\left(a_1{b}_1\right),\sum _{a_1{b}_1\in E_1}{I}_{M_1}\left(a_1{b}_1\right),\sum _{a_1{b}_1\in E_1}{F}_{M_1}\left(a_1{b}_1\right)\right)\hfill \\ & =\left(\sum _{a_1,b_1\in V_1}{T}_{M_2}\left(h\left(a_1\right),h\left(b_1\right)\right),\sum _{a_1,b_1\in V_1}{I}_{M_2}\left(h\left(a_1\right),h\left(b_1\right)\right),\sum _{a_1{b}_1\in V_1}{F}_{M_2}\left(h\left(a_1\right),h\left(b_1\right)\right)\right)\hfill \\ & =\left(\sum _{a_2{b}_2\in E_2}{T}_{M_2}\left(a_2{b}_2\right),\sum _{a_2{b}_2\in E_2}{I}_{M_2}\left(a_2{b}_2\right),\sum _{a_2{b}_2\in E_2}{F}_{M_2}\left(a_2{b}_2\right)\right)=S\left(G_2\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill O\left(G_1\right)& =\left(\sum _{a_1\in V_1}{T}_{N_1}\left(a_1\right),\sum _{a_1\in V_1}{I}_{N_1}\left(a_1\right),\sum _{a_1\in V_1}{F}_{N_1}\left(a_1\right)\right)\hfill \\ & =\left(\sum _{a_1\in V_1}{T}_{N_2}\left(h\left(a_1\right)\right),\sum _{a_1\in V_1}{I}_{N_2}\left(h\left(a_1\right)\right),\sum _{a_1\in V_1}{F}_{N_2}\left(h\left(a_1\right)\right)\right)\hfill \\ & =\left(\sum _{a_2\in V_2}{T}_{N_2}\left(a_2\right),\sum _{a_2\in V_2}{I}_{N_2}\left(a_2\right),\sum _{a_2\in V_2}{F}_{N_2}\left(a_2\right)\right)=O\left(G_2\right)\hfill \end{array}$$

□

Theorem 4.

Let $G_1$ and $G_2$ be two isomorphic HINGs. Then, the degrees of nodes a and $h\left(a\right)$ of $G_1$ and $G_2$ are the same.

Proof. 

If $G_1$ and $G_2$ are two isomorphic HINGs, respectively, then $T_{M_1}\left(a\right)=T_{M_1}\left(h\left(a_1\right)h\left(b_1\right)\right)$, $I_{M_1}\left(a\right)=I_{M_1}\left(h\left(a_1\right)h\left(b_1\right)\right)$ and $F_{M_1}\left(a\right)=F_{M_1}\left(h\left(a_1\right)h\left(b_1\right)\right)$ for all $a_1,b_1\in V_1$. Therefore,

$$\begin{array}{cc}\hfill d_T\left(a_1\right)& =\sum _{a_1,b_1\in V_1}{T}_{M_1}\left(a_1{b}_1\right)=\sum _{a_1,b_1\in V_1}{T}_{M_2}\left(h\left(a_1\right)h\left(b_1\right)\right)=d_T\left(h\left(a_1\right)\right)\hfill \\ \hfill d_I\left(a_1\right)& =\sum _{a_1,b_1\in V_1}{I}_{M_1}\left(a_1{b}_1\right)=\sum _{a_1,b_1\in V_1}{I}_{M_2}\left(h\left(a_1\right)h\left(b_1\right)\right)=d_I\left(h\left(a_1\right)\right)\hfill \\ \hfill d_F\left(a_1\right)& =\sum _{a_1,b_1\in V_1}{F}_{M_1}\left(a_1{b}_1\right)=\sum _{a_1,b_1\in V_1}{F}_{M_2}\left(h\left(a_1\right)h\left(b_1\right)\right)=d_F\left(h\left(a_1\right)\right)\hfill \end{array}$$

for all $a_1\in V_1$. This proves that the degrees of nodes u and $h\left(u\right)$ of $G_1$ and $G_2$ are preserved. □

Definition 25.

Let $G=(N,M)$ be a connected neutrosophic graph. G is defined as:

1. 

A self-weak neutrosophic complementary isomorphic graph if graph G is weak isomorphic with $G^c$.

2. 

A self-complementary neutrosophic graph if $G^c\cong G$.

Theorem 5.

Let G be a self-complementary HING. Then:

$$\begin{array}{cc}\hfill \sum _{a\ne b}{T}_M(a,b)& \le \frac{1}{2}\sum _{a\ne b}min\left(T_N\left(a\right),T_N\left(b\right))\right)\hfill \\ \hfill \sum _{a\ne b}{I}_M(a,b)& \ge \frac{1}{2}\sum _{a\ne b}max\left(I_N\left(a\right),I_N\left(b\right))\right)\hfill \\ \hfill \sum _{a\ne b}{F}_M(a,b)& \ge \frac{1}{2}\sum _{a\ne b}max\left(F_N\left(a\right),F_N\left(b\right))\right)\hfill \end{array}$$

Definition 26.

Let $G=(N,M)$ be a neutrosophic graph and $G^{\mu }=(N^{\mu },M^{\mu })$ be the μ complement of G where $N=N^{\mu }$ and $M^{\mu }=\left(T_M^{\mu },I_M^{\mu },F_M^{\mu }\right)$ where:

$T_M^{\mu }=\left\{\begin{array}{c}min\left(T_N\left(a\right),T_M\left(b\right)\right)-T_M(a,b)\hfill \\ \mathit{if}{T}_M(a,b)>0\hfill \\ 0\hfill \\ \mathit{if}{T}_M(a,b)=0\hfill \end{array}\right.$

$I_M^{\mu }=\left\{\begin{array}{c}{I}_M(a,b)-max\left(T_N\left(a\right),T_M\left(b\right)\right)\hfill \\ \mathit{if}{I}_M(a,b)>0\hfill \\ 0\hfill \\ \mathit{if}{I}_M(a,b)=0\hfill \end{array}\right.$

$F_M^{\mu }=\left\{\begin{array}{c}{F}_M(a,b)-max\left(F_N\left(a\right),F_M\left(b\right)\right)\hfill \\ \mathit{if}{F}_M(a,b)>0\hfill \\ 0\hfill \\ \mathit{if}{F}_M(a,b)=0\hfill \end{array}\right.$

Theorem 6.

Let $G^{\mu }$ be the μ-complement of an HING. G need not be highly irregular.

Proof 

All the adjacent nodes of G with different neutrosophic degrees or all the other nodes of G with different neutrosophic degrees may possibly be adjacent nodes with equivalent degrees. This condition opposes the idea of HING. □

Theorem 7.

Let $G_1$ and $G_2$ be two HINGs. If $G_1$ and $G_2$ are two isomorphic neutrosophic graphs, then $G_1^{\mu }$ and $G_2^{\mu }$ are also isomorphic, and vice versa.

Proof 

Let $G_1$ and $G_2$ be two isomorphic neutrosophic graphs; there always exists a map $h:V_{1}to{V}_2$ satisfying $T_{N_1}\left(a\right)=T_{N_2}\left(h\left(a\right)\right)$, for all $a\in V_1$ and $T_{M_1}\left(ab\right)=T_{M_2}\left(h\left(a\right)h\left(b\right)\right)$, $I_{M_1}\left(ab\right)=I_{M2}\left(h\left(a\right)h\left(b\right)\right)$ and $F_{M1}\left(ab\right)=F_{M2}\left(h\left(a\right)h\left(b\right)\right)$, for all $ab\in E_1$. By the concept of the μ complement neutrosophic graph, we have $T_{M_1}^{\mu }\left(ab\right)=min\left(T_{N1}\left(a\right),T_{N1}\left(b\right)-T_{M1}\left(ab\right)=min\left(T_{N2}\left(h\left(a\right)\right),T_{N2}\left(h\left(b\right)\right)\right)\right)-T_{M2}\left(h\left(a\right)h\left(b\right)\right)$, $F_{M_1}^{\mu }\left(ab\right)=F_{M_1}^{}\left(ab\right)-max\left(F_{N1}\left(a\right),F_{N1}\left(b\right)\right)=T_{M2}\left(h\left(a\right)h\left(b\right)\right)-max\left(F_{N1}\left(h\left(a\right)\right),F_{N2}\left(h\left(b\right)\right)\right)$ for all $ab\in E_1$ ($I_{M_1}^{\mu }\left(ab\right)$ values can be calculated using the same method). Hence, $G_1^{\mu }\cong G_2^{\mu }$. The proof of the converse part is straight forward. □

5. Complete Bipartite Neutrosophic Graphs

Definition 27.

A neutrosophic graph $G=\left(N,M\right)$ is called a complete bipartite neutrosophic graph if the vertex set V can be divided into two nonempty sets, such that for every $v_1,v_2\in V_{1}or{V}_2$ and for every $u\in V_{1}andv\in V_2$:

Theorem 8.

Let $G=(N,M)$ be a complete bipartite neutrosophic graph, such that each partition of V has nodes.

(i) 

If for every $v\in V_1\setminus V_{2}orv\in V_2\setminus V_1,(t_N\left(v\right),i_N\left(v\right),f_N\left(v\right))=(c_1,c_2,c_3)$ and for the other nodes as $u,t_N\left(u\right)\ge c_1,i_N\left(u\right)\le c_2,f_N\left(u\right)\le c_3,$, then for all $1\le m\le 2k-1$, Gis a $d_m$ regular neutrosophic graph.

(ii) 

Let $W=\{v_1,v_2,...,v_k\}$ be a set of nodes, such that it contains at least one node of each partition of V.

Proof. 

Suppose that for every $v_1\in V_1\setminus V_2,(t_N\left(v\right),i_N\left(v\right),f_N\left(v\right))=(c_1,c_2,c_3)$. Therefore, in $V_1$, $t_N$ and $f_N$ are constant functions, and since for every $v_2\in V_1\setminus V_2,t_N\left(v_1\right)\le t_N\left(v_1\right),i_N\left(v_1\right)\ge i_N\left(v_2\right),f_N\left(v_1\right)\ge f_N\left(v_{21}\right)).$ Then, by the previous definition, we have that for every $uv\in E$, we get $(t_M\left(uv\right),i_M\left(uv\right),f_M\left(uv\right))=(c_1,c_2,c_3)$.

Hence, for every $v\in V$ and $1\le m\le 2k-1$, if m is odd, then $d_m\left(v\right)=k(c_1,c_2,c_3)$ and if m is even, then $d_m\left(v\right)=(k-1)(c_1,c_2,c_3)$.

Therefore, in both cases, we see that G is a $d_m$-regular neutrosophic graph. Now, if for every $v_1\in V_1\setminus V_2,(t_N\left(v\right),i_N\left(v\right),f_N\left(v\right))=(c_1,c_2,c_3)$, then the proof is similar to the proof of (i).

(ii) The proof is similar to the previous theorem only by the difference, that every $v\in Vandk+1\le m\le 2k-1$; if m is odd, then and if m is even, then $d_m\left(v\right)=(k-1)(c_1,c_2,c_3)$.

Remark 1.

If $V_1=\{v_1,v_2,...,v_n\}and{V}_1=\{u_1,u_2,...,u_m\}$ such that $n\ne m,$, then the above theorem does not hold.

Example 5.

Consider the complete bipartite neutrosophic graph $G=(N,M)$ in Figure 4 shown below.

Since G is a complete bipartite neutrosophic graph, then for every $uv\in E,(t_M\left(uv\right),i_M\left(uv\right),f_M\left(uv\right))=(0.2,0.3,0.6).$ Hence:

$$d_1\left(a\right)=(0.4,0.6,1.2),d_1\left(b\right)=(0.4,0.6,1.2),d_1\left(c\right)=(0.4,0.6,1.2),d_1\left(d\right)=(0.6,0.9,1.8),d_1\left(e\right)=(0.6,0.9,1.8)$$

$$d_2\left(a\right)=(0.4,0.6,1.2),d_2\left(b\right)=(0.4,0.6,1.2),d_2\left(c\right)=(0.4,0.6,1.2),$$

$$d_2\left(d\right)=(0.2,0.3,0.6),d_2\left(e\right)=(0.2,0.3,0.6)$$

$$d_3\left(a\right)=(0.4,0.6,1.2),d_3\left(b\right)=(0.4,0.6,1.2),d_3\left(c\right)=(0.4,0.6,1.2),$$

$$d_3\left(d\right)=(0.6,0.9,1.8),d_3\left(e\right)=(0.6,0.9,1.8)$$

$$d_4\left(a\right)=(0.4,0.6,1.2),d_4\left(b\right)=(0.4,0.6,1.2),d_4\left(c\right)=(0.4,0.6,1.2),$$

$$d_4\left(d\right)=(0,1,1),d_4\left(e\right)=(0,1,1)$$

Since $t_N,i_{N}and{f}_N$ are constant functions, we have for all $m=1,2,3,4$, G does not follow the condition of the $d_m$-regular neutrosophic graph.  □

Theorem 9.

Let $G=(N,M)$ be a regular neutrosophic graph on cycle graph $G^{*}=(V,E)$ with $k\ge 3$ nodes. If for $k-(n-1)$ arcs of G as $uv$, $(T_M\left(uv\right),I_M\left(uv\right),F_M\left(uv\right))=(c_1,c_2,c_3)$ and for arcs as $ab$, $T_M\left(ab\right)\ge c_1$, $I_M\left(ab\right)\ge c_2$, and $F_M\left(ab\right)\ge c_3$, then for any $n\le m\le k-1$, G is a $d_m$-regular neutrosophic graph.

Proof. 

Let $G=(N,M)$ be a regular neutrosophic graph on cycle graph $G^{*}$ with k nodes and for $k-(n-1)$ arcs of G as $uv$, $(T_M\left(uv\right),I_M\left(uv\right),F_M\left(uv\right))=(c_1,c_2,c_3)$.

Since $G^{*}$ is a cycle, we have for every node w in G that there exist exactly two distinct nodes $w_1$ and $w_2$ such that w and $w_1$ are connected by means of one path of length m (where $n\le m\le k-1$) and each path contains at least one arc $uv$.

Hence, for two paths,

${\lambda }_1:w_1=u_0,u_1,u_2,...u_{m-1},u_m=w$ and ${\lambda }_2:w_1=v_0,v_1,v_2,...v_{m-1},v_m=w$.

Therefore, we obtain

$T_M^m\left(w_{1}w\right)+T_M^m\left(w_{2}w\right)=T_M\left(w_1{u}_1\right)\wedge ...\wedge T_M\left(u_{m-1}w\right)+T_M\left(w_2{v}_1\right)\wedge ...\wedge T_M\left(v_{m-1}w\right)=c_1+c_1=2c_1$.

$I_M^m\left(w_{1}w\right)+I_M^m\left(w_{2}w\right)=I_M\left(w_1{u}_1\right)\vee ...\vee I_M\left(u_{m-1}w\right)+I_M\left(w_2{v}_1\right)\vee ...\vee I_M\left(v_{m-1}w\right)=c_1+c_1=2c_1$.

$F_M^m\left(w_{1}w\right)+F_M^m\left(w_{2}w\right)=F_M\left(w_1{u}_1\right)\vee ...\vee F_M\left(u_{m-1}w\right)+F_M\left(w_2{v}_1\right)\vee ...\vee F_M\left(v_{m-1}w\right)=c_1+c_1=2c_1$. □

Remark 2.

Let G be a regular neutrosophic graph on cycle graph $G^{*}$ with k nodes. If $T_M$, $I_M$, and $F_M$ are constant functions and $T_N$, $I_N$, and $F_N$ are not, then for any $1\le m\le k-1$, G is not a $t{d}_m$-regular neutrosophic graph in general.

Theorem 10.

Let $G=(N,M)$ be a neutrosophic graph on cycle graph $G^{*}=(V,E)$ with $k\ge 3$ nodes. If G is a $d_1$-regular neutrosophic graph, then $T_M$, $I_M$, and $F_M$ are constant functions.

Proof. 

Suppose that G is a $d_1$-regular neutrosophic graph and there exists $uv\in E$ such that $(T_M\left(uv\right),I_M\left(uv\right),F_M\left(uv\right))=(c_1,c_2,c_3)$, where for every $ab\in E-\left\{uv\right\}$, $(T_M\left(ab\right),I_M\left(ab\right),F_M\left(ab\right))=(c_1,c_2,c_3)$. Then, $T_M\left(uv\right)\ne c_1$, $I_M\left(uv\right)\ne c_2$, and $F_M\left(uv\right)\ne c_3$.

Case $1:$ If $T_M\left(uv\right)\ne c_1$,

${\displaystyle \sum _{u\ne z\in V}{T}_M^1\left(uz\right)=c_1+T_M\left(uv\right)}$, ${\displaystyle \sum _{v\ne z\in V}{T}_M^1\left(vz\right)=c_1+T_M\left(uv\right)}$.

Since G has $k\ge 3$ nodes, there exists $w\in V$ such that $w\ne v,u$. Hence, we get ${\displaystyle \sum _{u\ne z\in V}{T}_M^1\left(wz\right)=2c_1}$, which implies that $T_M^1\left(wz\right)\ne T_M^1\left(vz\right)$ and $T_M^1\left(wz\right)\ne T_M^1\left(uz\right)$. Therefore, $d_1\left(w\right)\ne d_1\left(u\right)$ and $d_1\left(w\right)\ne d_1\left(v\right)$; hence, G is not a $d_1$-regular neutrosophic graph, which is a contradiction.

Case $2:$ If $I_M\left(uv\right)\ne c_2$,

${\displaystyle \sum _{u\ne z\in V}{I}_M^1\left(uz\right)=c_2+I_M\left(uv\right)}$, ${\displaystyle \sum _{v\ne z\in V}{I}_M^1\left(vz\right)=c_2+I_M\left(uv\right)}$.

Since G has $k\ge 3$ nodes, there exists $w\in V$ such that $w\ne v,u$. Hence, we get ${\displaystyle \sum _{u\ne z\in V}{I}_M^1\left(wz\right)=2c_2}$, which implies that $I_M^1\left(wz\right)\ne I_M^1\left(vz\right)$ and $I_M^1\left(wz\right)\ne I_M^1\left(uz\right)$. Therefore, $d_1\left(w\right)\ne d_1\left(u\right)$ and $d_1\left(w\right)\ne d_1\left(v\right)$; hence, G is not a $d_1$-regular neutrosophic graph, which is a contradiction.

Case $3:$ If $F_M\left(uv\right)\ne c_3$,

${\displaystyle \sum _{u\ne z\in V}{F}_M^1\left(uz\right)=c_3+F_M\left(uv\right)}$, ${\displaystyle \sum _{v\ne z\in V}{F}_M^1\left(vz\right)=c_3+F_M\left(uv\right)}$.

Since G has $k\ge 3$ nodes, there exists $w\in V$ such that $w\ne v,u$. Hence, we get ${\displaystyle \sum _{u\ne z\in V}{F}_M^1\left(wz\right)=2c_3}$, which implies that $F_M^1\left(wz\right)\ne F_M^1\left(vz\right)$ and $F_M^1\left(wz\right)\ne F_M^1\left(uz\right)$. Therefore, $d_1\left(w\right)\ne d_1\left(u\right)$ and $d_1\left(w\right)\ne d_1\left(v\right)$; hence, G is not a $d_1$-regular neutrosophic graph, which is a contradiction. Hence the proof. □

Theorem 11.

Let $G=(N,M)$ be a neutrosophic graph on the path graph $G^{*}=(V,E)$ with $2m$ nodes. If for at least $m+1$ arcs of G as $uv$, $(T_M\left(uv\right),I_M\left(uv\right),F_M\left(uv\right))=(c_1,c_2,c_3)$ and for other arcs as $ab$, $T_M\ge c_1$, $I_M\le c_2$ and $F_M\le c_3$, then G is also a $d_m$-regular neutrosophic graph.

Proof. 

Suppose that $G^{*}$ is a path with $2m$ nodes and for at least $m+1$ arcs of G as $uv$, $(T_M\left(uv\right),I_M\left(uv\right),F_M\left(uv\right))=(c_1,c_2,c_3)$. Since $G^{*}$ is a path, we have for every arbitrary node w in G that there exists only one node as z such that w and z are connected by means of one path of length m and this path contains at least one $uv$. Hence, for the path $\lambda :z=z_0,z_1,z_2,...z_{m-1},z_m=w$. We get $T_M^m\left(zw\right)=T_M\left(z{z}_1\right)\wedge ...\wedge T_M\left(z_{m-1}w\right)=c_1$, $I_M^m\left(zw\right)=I_M\left(z{z}_1\right)\vee ...\vee I_M\left(z_{m-1}w\right)=c_2$, and $F_M^m\left(zw\right)=F_M\left(z{z}_1\right)\vee ...\vee F_M\left(z_{m-1}w\right)=c_3$.

Therefore, $d_m\left(w\right)=(T_M^m\left(zw\right),I_M^m\left(zw\right),F_M^m\left(zw\right))=(c_1,c_2,c_3)$, and so, G is a $(m,(c_1,c_2,c_3))$-regular neutrosophic graph. □

Remark 3.

Let $G=(N,M)$ be a neutrosophic graph on the path graph $G^{*}=(V,E)$ with $2m$ nodes. If $T_M$, $I_M$, and $F_M$ are constant functions and $T_N$, $I_N$, and $F_N$ are not, then G is not $t{d}_m$-regular.

6. m-Highly Irregular Neutrosophic Graph

In this section, we present the notation of m-HING and the m-highly totally irregular neutrosophic graph (HTING). We have proven the necessary and sufficient conditions for which the m-highly irregular and m-HTINGs are equivalent, and also, we provide m-highly irregularity on neutrosophic graph G where $G^m$ is the cycle, path, or star graph.

Definition 28.

Let $G=(N,M)$ be a regular connected neutrosophic graph, then:

(i) 

G is said to be m-HING, if each node of G is adjacent to the other nodes with the different values of the $d_m$-degree.

(ii) 

G is said to be m-HTING, if each node of G is adjacent to the other nodes with the different values of the $t{d}_m$-degree.

Theorem 12.

Let $G=(N,M)$ be a neutrosophic graph. If $T_M$, $I_M$, and $F_M$ are used to denote the three constant functions and m represents a positive integer number, then G is m-HTING if G is m-HING.

Proof. 

Suppose that G is m-HTING. Then, the value of the $t{d}_m$-degree of all the pairs of adjacent nodes are different. Let two nodes v and u be the pair of adjacent nodes with the distinct $t{d}_m$-degree. Hence, we have

${\displaystyle t{d}_m\left(u\right)=\left[\sum _{u\ne w\in V}{T}_M^m\left(uw\right)+T_N\left(u\right),\sum _{u\ne w\in V}{I}_M^m\left(uw\right)+I_N\left(u\right),\sum _{u\ne w\in V}{F}_M^m\left(uw\right)+F_N\left(u\right)\right]}$

${\displaystyle t{d}_m\left(v\right)=\left[\sum _{v\ne w\in V}{T}_M^m\left(vw\right)+T_N\left(v\right),\sum _{v\ne w\in V}{I}_M^m\left(vw\right)+I_N\left(v\right),\sum _{v\ne w\in V}{F}_M^m\left(vw\right)+F_N\left(v\right)\right]}$.

Since $t{d}_m\left(u\right)\ne t{d}_m\left(v\right)$, we have, ${\displaystyle \sum _{u\ne w\in V}{T}_M^m\left(uw\right)+T_N\left(u\right)\ne \sum _{v\ne w\in V}{T}_M^m\left(vw\right)+T_N\left(v\right)}$, ${\displaystyle \sum _{u\ne w\in V}{I}_M^m\left(uw\right)+I_N\left(u\right)\ne \sum _{v\ne w\in V}{I}_M^m\left(vw\right)+I_N\left(v\right)}$ and ${\displaystyle \sum _{u\ne w\in V}{F}_M^m\left(uw\right)+F_N\left(u\right)\ne \sum _{v\ne w\in V}{F}_M^m\left(vw\right)+F_N\left(v\right)}$.

Since $T_N\left(u\right)=T_N\left(v\right)$, $I_N\left(u\right)=I_N\left(v\right)$, and $F_N\left(u\right)=F_N\left(v\right)$, hence we get

${\displaystyle \sum _{u\ne w\in V}{T}_M^m\left(uw\right)\ne \sum _{v\ne w\in V}{T}_M^m\left(vw\right)}$, ${\displaystyle \sum _{u\ne w\in V}{I}_M^m\left(uw\right)\ne \sum _{v\ne w\in V}{I}_M^m\left(vw\right)}$, and ${\displaystyle \sum _{u\ne w\in V}{F}_M^m\left(uw\right)\ne \sum _{v\ne w\in V}{F}_M^m\left(vw\right)}$. Therefore, we have,

${\displaystyle d_m\left(u\right)=\left[\sum _{u\ne w\in V}{T}_M^m\left(uw\right),\sum _{u\ne w\in V}{I}_M^m\left(uw\right),\sum _{u\ne w\in V}{F}_M^m\left(uw\right)\right]\ne \left[\sum _{v\ne w\in V}{T}_M^m\left(vw\right),\sum _{v\ne w\in V}{I}_M^m\left(vw\right),\sum _{v\ne w\in V}{F}_M^m\left(vw\right)\right]=d_m\left(v\right)}$. Hence, any pair of adjacent nodes in G has distinct a $d_m$-degree. Then, G is m-HING.

Conversely, G is an m-HING. Then, the value of the $d_m$-degree of each and every pair of adjacent nodes such as u and v is distinct. This implies that $d_m\left(u\right)\ne d_m\left(v\right)$. Since $T_N\left(u\right)=T_N\left(v\right)$, $I_N\left(u\right)=I_N\left(v\right)$, and $F_N\left(u\right)=F_N\left(v\right)$, hence $t{d}_m\left(u\right)=d_m\left(u\right)+T_N\left(u\right)\ne i{d}_m\left(u\right)=d_m\left(u\right)+I_N\left(u\right)\ne f{d}_m\left(u\right)=d_m\left(u\right)+F_N\left(u\right)$, and so, any two adjacent nodes in G has the distinct $t{d}_m$-degree. Therefore, G is an m-HTING.

Hence the proof. □

Theorem 13.

Let $G=(N,M)$ be a neutrosophic graph on cycle graph $G^{*}=(V,E)$ with $k\ge 3$ nodes and for all $i=1,2,...,k-1$ (where $v_{k+1}=v_1$), $T_M\left(v_i{v}_{i+1}\right)<T_M\left(v_{i+1}{v}_{i+2}\right)$ or $I_M\left(v_i{v}_{i+1}\right)>I_M\left(v_{i+1}{v}_{i+2}\right)$ or $F_M\left(v_i{v}_{i+1}\right)>F_M\left(v_{i+1}{v}_{i+2}\right)$. Then, G is a $\left[1,2,3,\left[\frac{k}{2}\right]\right]$-HING.

Proof. 

Suppose that $v_1,v_2,...,v_k,v_1$ is the arcs of G, where $T_M\left(v_1{v}_2\right)<T_M\left(v_2{v}_3\right)<...<T_M\left(v_i{v}_{i+1}\right)<T_M\left(v_{i+1}{v}_{i+2}\right)<...<T_M\left(v_k{v}_1\right)$ and there exists $v_i{v}_{i+1}\in E$ such that for $1\le m\le \left[\frac{k}{2}\right]$, $d_m\left(v_i\right)=d_m\left(v_{i+1}\right)$. Therefore, we get ${\displaystyle \sum _{v_i\ne v_{i+1}\in V}{T}_M^m\left(v_i{v}_j\right)=T_M\left(v_i{v}_{i+1}\right)+T_M\left(v_j{v}_{j+1}\right)}$ and ${\displaystyle \sum _{v_{i+1}\ne v_j\in V}{T}_M^m\left(v_i{v}_j\right)=T_M\left(v_i{v}_{i+1}\right)+T_M\left(v_{j+1}{v}_{j+2}\right)}$. Since $d_m\left(v_i\right)=d_m\left(v_{i+1}\right)$, $T_M\left(v_i{v}_{i+1}\right)+T_M\left(v_j{v}_{j+1}\right)=T_M\left(v_i{v}_{i+1}\right)+T_M\left(v_{j+1}{v}_{j+2}\right)$, thus $T_M\left(v_{i}vi+1\right)=T_M\left(v_{j+1}vj+2\right)$, which is a contradiction.

Now, for every $v_1,v_2,...,v_k,v_1\in E$, also we have

$I_M\left(v_1{v}_2\right)>I_M\left(v_2{v}_3\right)>...>I_M\left(v_i{v}_{i+1}\right)>I_M\left(v_{i+1}{v}_{i+2}\right)>...>I_M\left(v_k{v}_1\right)$,

$F_M\left(v_1{v}_2\right)>F_M\left(v_2{v}_3\right)>...>F_M\left(v_i{v}_{i+1}\right)>F_M\left(v_{i+1}{v}_{i+2}\right)>...>F_M\left(v_k{v}_1\right)$.

The proof is similar to the case as true membership, and the contradiction is obtained. Therefore, G is an $\left[1,2,3,\left[\frac{k}{2}\right]\right]$-HING. □

Remark 4.

Let $G=(N,M)$ be a neutrosophic graph on cycle graph $G^{*}=(V,E)$ with $k\ge 3$ nodes and for all $i=1,2,...,k-1$ (where $v_{k+1}=v_1$), $T_M\left(v_i{v}_{i+1}\right)<T_M\left(v_{i+1}{v}_{i+2}\right)$ or $I_M\left(v_i{v}_{i+1}\right)>I_M\left(v_{i+1}{v}_{i+2}\right)$ or $F_M\left(v_i{v}_{i+1}\right)>F_M\left(v_{i+1}{v}_{i+2}\right)$. Then, G is not a $\left[1,2,3,\left[\frac{k}{2}\right]\right]$-HING in general.

Example 6.

Consider the neutrosophic graph $G=(N,M)$ on graph $G^{*}=(V,E)$ shown in the Figure 5.

We see that $T_M\left(ab\right)<T_M\left(bc\right)<T_B\left(cd\right)<T_B\left(da\right)$, and we get

$t{d}_2\left(a\right)=(0.3+0.4,0.6+0.4)=(0.7,1.0)$

$t{d}_2\left(b\right)=(0.2+0.3,0.6+0.6)=(0.5,1.2)$

$t{d}_2\left(c\right)=(0.3+0.4,0.6+0.5)=(0.7,1.1)$

$t{d}_2\left(d\right)=(0.2+0.5,0.6+0.4)=(0.7,1.0)$

Since for two vertices a and b, they are adjacent, $t{d}_2\left(a\right)=t{d}_2\left(b\right)$. Then, G is not a two-HTING.

Theorem 14.

Let $G=(N,M)$ be a neutrosophic graph on cycle graph $G^{*}=(V,E)$ with $k\ge 3$ nodes and for all $i=1,2,...,k-1$ (where $v_{k+1}=v_1$), $T_M\left(v_i{v}_{i+1}\right)<T_M\left(v_{i+1}{v}_{i+2}\right)$ or $I_M\left(v_i{v}_{i+1}\right)>I_M\left(v_{i+1}{v}_{i+2}\right)$ or $F_M\left(v_i{v}_{i+1}\right)>F_M\left(v_{i+1}{v}_{i+2}\right)$. Then, G is a $\left[1,2,3,\left[\frac{k}{2}\right]\right]$-HING.

Proof. 

Suppose that $v_1,v_2,...,v_k,v_1$ is the arcs of G, where $T_M\left(v_1{v}_2\right)<T_M\left(v_2{v}_3\right)<...<T_M\left(v_i{v}_{i+1}\right)<T_M\left(v_{i+1}{v}_{i+2}\right)<...<T_M\left(v_{k-1}{v}_k\right)$. Then, for every $1\le m\le \left[\frac{k}{2}\right]$, we get

${\displaystyle \sum _{v_i\ne v_j\in V}{T}_M^m\left(v_i{v}_j\right)=\left\{\begin{array}{c}{T}_M\left(v_i{v}_{i+1}\right),ifi=1,2,3,...,m\hfill \\ T_M\left(v_i{v}_{i+1}\right)+T_M(v_{i-m}{v}_{i-m+11},ifi=m+1,...,k-m\hfill \\ T_M(v_{i-m}{v}_{i-m+1},ifi=k-m+1,...k.\hfill \end{array}\right.}$

Hence, for every two adjacent nodes as $v_i$ and $v_{i+1}$ in G, we get $d_m\left(v_i\right)\ne d_m\left(v_{i+1}\right)$. Therefore, G is a $\left[1,2,3,\left[\frac{k}{2}-1\right]\right]$-HING. Now, suppose that $m=\left[\frac{k}{2}\right]$. If k is even, then we have

${\displaystyle \sum _{v_i\ne v_j\in V}{T}_M^m\left(v_i{v}_j\right)=\left\{\begin{array}{c}{T}_M\left(v_i{v}_{i+1}\right),ifi=1,2,3,...,m\hfill \\ T_M\left(v_{i-m}{v}_{}\right),ifi=m+1,...,k-m\hfill \end{array}\right.}$

If k is odd, then we have

${\displaystyle \sum _{v_i\ne v_j\in V}{T}_M^m\left(v_i{v}_j\right)=\left\{\begin{array}{c}{T}_M\left(v_i{v}_{i+1}\right),ifi=1,2,3,...,m\hfill \\ T_M\left(v_1{v}_2\right)+T_M(v_{i-m}{v}_{i-m+11},ifi=m+1\hfill \\ T_M(v_{i-m}{v}_{i-m+1},ifi=m+2,...k.\hfill \end{array}\right.}$

Here, in both cases, we see that for every two adjacent nodes $v_i$ and $v_{i+1}$ in G, we get $d_m\left(v_i\right)\ne d_m\left(v_{i+1}\right)$, and so, G is a $\left[\frac{k}{2}\right]$-HING. Similarly, for the indeterministic and false membership function, for each arc, it is proven.

Hence the proof. □

Example 7.

Consider the the neutrosophic graph $G=(N,M)$ on graph $G^{*}=(V,E)$ shown in Figure 6.

We see that $T_M\left(ab\right)<T_M\left(bc\right)<T_M\left(cd\right)$, and we get

$t{d}_2\left(a\right)=(0.1+0.4,0.4+0.4)=(0.5,0.8)$

$t{d}_2\left(b\right)=(0.2+0.3,0.5+0.3)=(0.5,0.8)$

$t{d}_2\left(c\right)=(0.1+0.4,0.4+0.2)=(0.5,0.6)$

$t{d}_2\left(d\right)=(0.2+0.5,0.5+0.4)=(0.7,0.9)$

Since for two adjacent nodes a and b, $t{d}_2\left(a\right)=t{d}_2\left(b\right)$. Then, we see that G is not a two-HTING.

Definition 29.

Let $G=(N,M)$ be a neutrosophic graph. The graph G is said to be a star neutrosophic graph if it is a complete bipartite neutrosophic graph such that one partition of V contains only one node.

Theorem 15.

Let $G=(N,M)$ be a star neutrosophic graph with $k\ge 4$ nodes such that the node $v_1$ is incident to the other nodes. If for all $i=1,2,...,k$, $T_M\left(v_i{v}_{i+1}\right)<T_M\left(v_{i+1}{v}_{i+2}\right)$, or $I_M\left(v_i{v}_{i+1}\right)>I_M\left(v_{i+1}{v}_{i+2}\right)$, or $F_M\left(v_i{v}_{i+1}\right)>F_M\left(v_{i+1}{v}_{i+2}\right)$. Then, G is a $\left[1,2\right]$-HING.

Proof. 

Suppose that $v_1,v_2,...,v_k,v_1$ is the arcs of G, where $T_M\left(v_1{v}_2\right)<T_M\left(v_2{v}_3\right)<...<T_M\left(v_i{v}_{i+1}\right)<T_M\left(v_{i+1}{v}_{i+2}\right)<...<T_M\left(v_k{v}_1\right)$.

Then, ${\displaystyle \sum _{v_i\ne v_j\in V}{T}_M^1\left(v_1{v}_j\right)=\sum _{j=2}^k{T}_M\left(v_1{v}_j\right)}$ and ${\displaystyle \sum _{v_i\ne v_j\in V}{T}_M^1\left(v_1{v}_j\right)=T_M\left(v_1{v}_j\right)}$; $i=2,3,...,k$.

Hence, $d_1\left(v_1\right)\ne d_1\left(v_2\right)\ne d_1\left(v_3\right)\ne ....\ne d_1\left(v_k\right)$. There, G is a one-HING. In addition, we see that $d_1\left(v_1\right)=(0,1)$ and ${\displaystyle \sum _{v_i\ne v_j\in V}{T}_M^2\left(v_1{v}_j\right)=(k-i)t_M\left(v_1{v}_i\right)+\sum _{j=2}^{i-1}{T}_M\left(v_1{v}_j\right)}$. Hence, for every $i=2,...,k,$ $d_1\left(v_i\right)\ne d_1\left(v_1\right)$, and so, G is a two-HING. Similarly, the proof is established for the indeterminacy and false membership function of each arc.

Hence the proof. □

7. Some Applications of Regular and Bipartite Neutrosophic Graphs

There are many networks that are used in real-life scenarios. Graph theory plays a vital role in the application parts of these networks. Some networks are designed for distributing commodities or services. The power grid, Internet-related issues, and road transportation networks are some examples of technological networks. There has been a phenomenal change in network research in recent years from a small graphical structure to a wide statistical analysis of large-scale networks.

Most of the real-life networks/structures are ambiguous and vague in nature and not well defined. Indeterministic information exists in almost every real-life scenario. The neutrosophic graph is more flexible and compatible to model the indeterministic information in a network when compared to the fuzzy graph or vague graph. A graph is a classical way of modeling real-life networks, which consist of relationships between entities. In a graph, the entities are expressed by nodes and relationships by arcs. If there exist uncertainties due to indeterministic or vague information about the entities, or relations, or both, then the neutrosophic graph model is very efficient to design such networks. Neutrosophic graphs are widespread and important in the area of mathematical modeling, pattern recognition, relational mapping, biological, social networks, and information systems. It can be applied to artificial intelligence with neutrosophic rules in the inference system. These graphs can be represented in different data structures in different applications internally. In those real-life applications, the basic mathematical model is that of a neutrosophic graph.

Transforming all those data-carrying networks to a neutrosophic graph using various types of information from all the possible existing levels, it is a proper multilevel method where all possible levels and ties among them are represented and analyzed mathematically at the same time. Neutrosophic graphs have more applications related to information technology and computer science such that these graphs are used to illustrate networks of communication, data optimization, machine learning, chip design, and much more.

7.1. Assignment Problem

The assignment problem is a well-known and fundamental topic of study in the field of operation research. This problem can be modeled as a bipartite neutrosophic graph. Let a neutrosophic graph $G=\left(V,E\right)$ where V denotes the nodes and E represents the arcs be represented as a neutrosophic bipartite graph, if it satisfies the condition such that $V=X\cup Y\mathrm{and}X\cap Y=\varpi$; where $\varpi$ is a null matrix, and $E\in X\times Y$. A neutrosophic bipartite graph G is described as a weighted bipartite graph if every edge (i.e., E) of it consists of a neutrosophic weight (i.e., $\varpi \left(i,j\right)$). The neutrosophic weight of one-to-one matching (i.e., M) is described by the following.

$$\omega \left(M\right)=\sum _{E\in M}\omega \left(E\right)$$

A matching (i.e., M) is called a perfect matching if each node of X is assigned to one of the Y nodes. Therefore, a linear assignment problem is defined as determining a perfect matching in G that is maximally weighted.

7.2. Road Transportation Network

A road transportation network can be modeled by a neutrosophic graph, due to its imprecise dataset, neutrosophic information for vertices as the geometric location, the grade of significance, and so on; in addition to the arcs as the width, length, quality, traffic, and so on. Therefore, we can represent a road transportation network properly by using neutrosophic graphs where the vertices and the edges represent the cities and routes between two cities, respectively. Dijkstra’s algorithm [45,46] is a popular and well-known algorithm to solve the shortest path problem (SPP). It is an algorithmic approach to find the shortest path between two cities within the road transportation network. Floyd also contributed much to the efficient route-finding algorithms, hence the famous Floyd’s algorithm to find the shortest paths in any network with weights. The SPP is very useful to model the network routing protocol. In any shortest path algorithm, we consider a node as the source node and find all the shortest paths between the source vertex and destination vertex using all other nodes in the graph. Hence, the proposed $d_m$-degree of the source node will pave a new way to find the shortest path. When its efficiency is proven, it could be considered as the best one in the road transport network.

7.3. Social Networks

Social networks are platforms on which millions of people are interconnected everywhere in the world. There are many social networks [47] like Facebook, WhatsApp, and Instagram. These networks have reached a rapid progress in recent years and have spread all over the world in several ways. There are also some security issues pointed out recently by ethical hacking teams; hence to maintain the privacy of the user and the data released by them. In the medium, messages could be tampered with easily when a user sends the information to all the other users of his/her group. However, the situation is that a user should be connected to all other users. Social networks can be modeled by a neutrosophic regular graph, since $d_m$-degree farthest vertices are assumed by paths; therefore, it is a vertex that has at most $d_m$-degrees; hence, the secrecy of this vertex is maintained, and the user information is secured. If all the vertices of a social network have the same neutrosophic $d_m$-degree, then the user’s secrecy is maintained by adding a lowest arc and producing a $d_m$-degree in these graphs. Therefore, in these ways, in social networks, the data integrity is maintained, resisting more neighborhood attacks and threats.

The concept of regularity plays an important role in modeling many real-life optimization problems (e.g., social networks, wireless networks, road networks, assignment problems), so the main focus of this study is to present the concept of regularity in neutrosophic graph theory. The degree of a vertex in a graph is a way to find the number of relations of a vertex, so to analyze a network, it is very essential to find the degree of vertices. In this study, we have described the different types of degrees ($d_m$-degree and $t{d}_m$-degree) of nodes in a neutrosophic graph. The idea of the neutrosophic degree of a node is very important from different aspects in the real-world. Here, we have presented the definition of the free vertex (node) and busy vertex (node) of a regular neutrosophic graph, which are very useful to find the solutions of many real-life problems like the traffic congestion problem. Finally, we have mentioned some real-life applications of the regular neutrosophic graph, complete bipartite neutrosophic graph, and node $d_m$-degree of a neutrosophic graph. This study will be useful when the neutrosophic graphs are extremely large. For example, we have described the utility of the regular neutrosophic graph to model a social network. In the Twenty First Century, social networks are platforms on which millions of people are interconnected everywhere in the world. Therefore, as a future study, we will have to consider some large regular neutrosophic fuzzy graphs to model the social networks in real-life scenarios, and the closeness and diameter need to be computed for the analysis of this social network. Furthermore, we will try to propose some algorithmic methods to determine the closeness and diameter of any social network in real life. Despite the demand for future work, this paper is a useful initial contribution to neutrosophic graph theory, and some problems are described under the neutrosophic environment.

8. Conclusions

The main contribution of this manuscript is to introduce the idea of regularity in neutrosophic graph theory. In this paper, we have described the notion of the $d_m$-degree and $t{d}_m$-degree of nodes in a neutrosophic graph. Some different types of neutrosophic graphs such as the regular, regular strong, $d_m$-regular, $t{d}_m$-regular, and complete bipartite neutrosophic graph were introduced here. We have also provided some sufficient criteria for which the $t{d}_m$-regular neutrosophic graph and $d_m$-regular neutrosophic graph are equivalent. We have introduced the definition of the $\mu$-complement and h-morphism of a neutrosophic graph. Some properties of the complement and isomorphic regular neutrosophic graph were also presented here. Finally, some real-life applications of the regular neutrosophic graph and complete bipartite neutrosophic graph were described for the assignment problem, road transportation network, and social networks. In the future, we will focus on the study of neutrosophic intersection graphs, neutrosophic interval graphs, neutrosophic hyper graphs, and so on. The idea of the neutrosophic graph can be used in several areas of expert systems, image processing, computer networks, and social systems.