Numeric-Analytic Solutions for Nonlinear Oscillators via the Modified Multi-Stage Decomposition Method
Abstract
1. Introduction
2. The Methodology
3. Convergence and Error Analysis
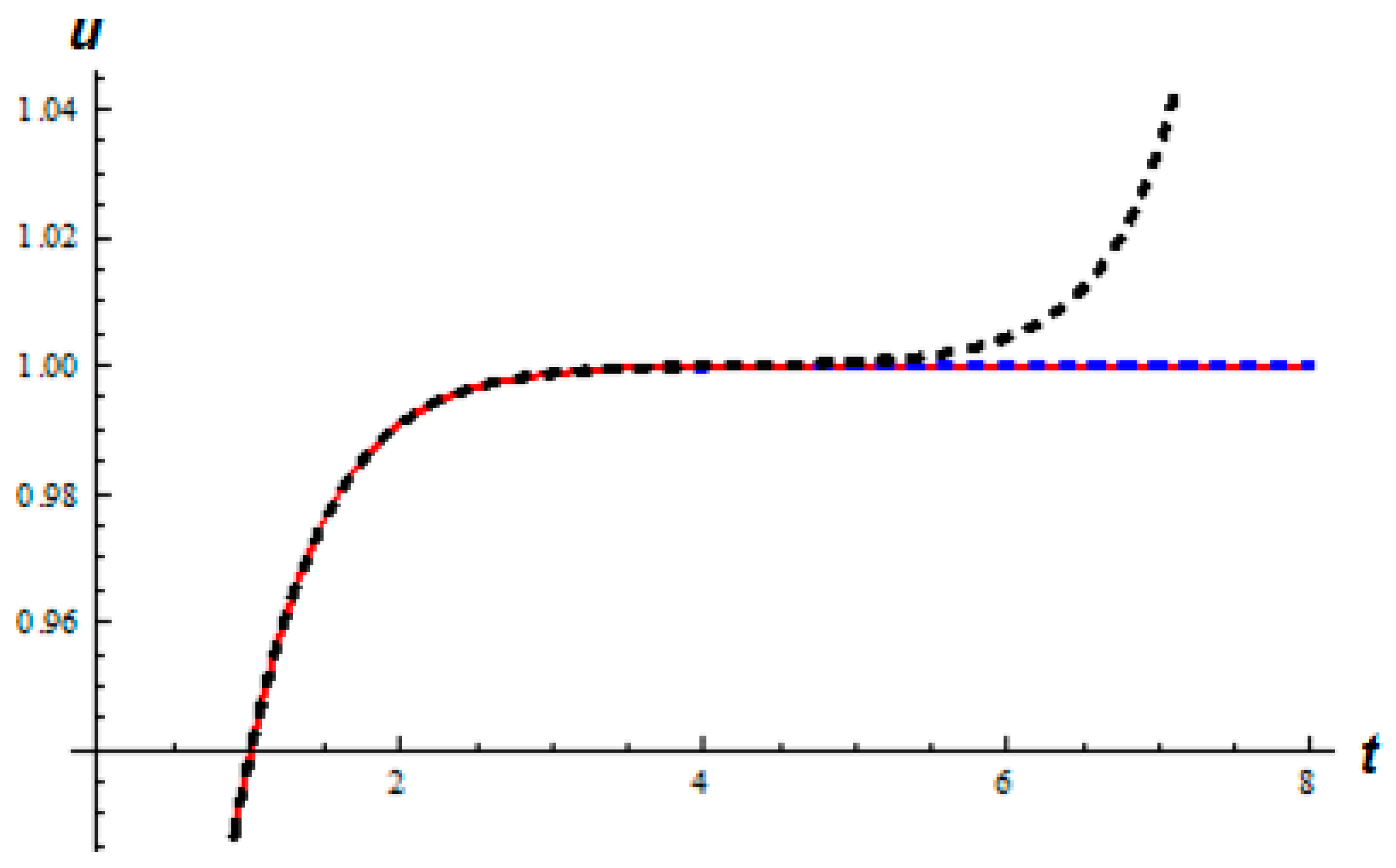
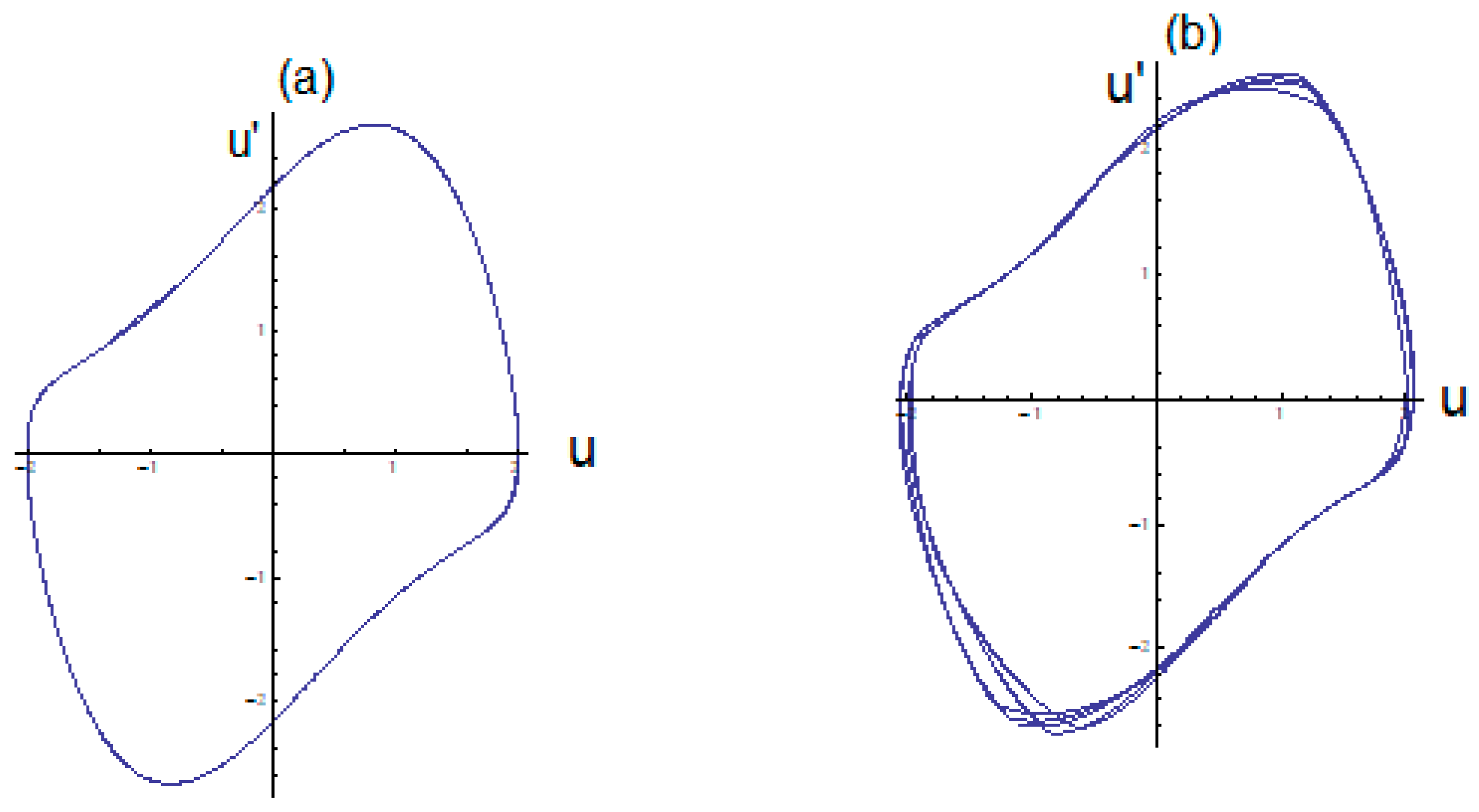
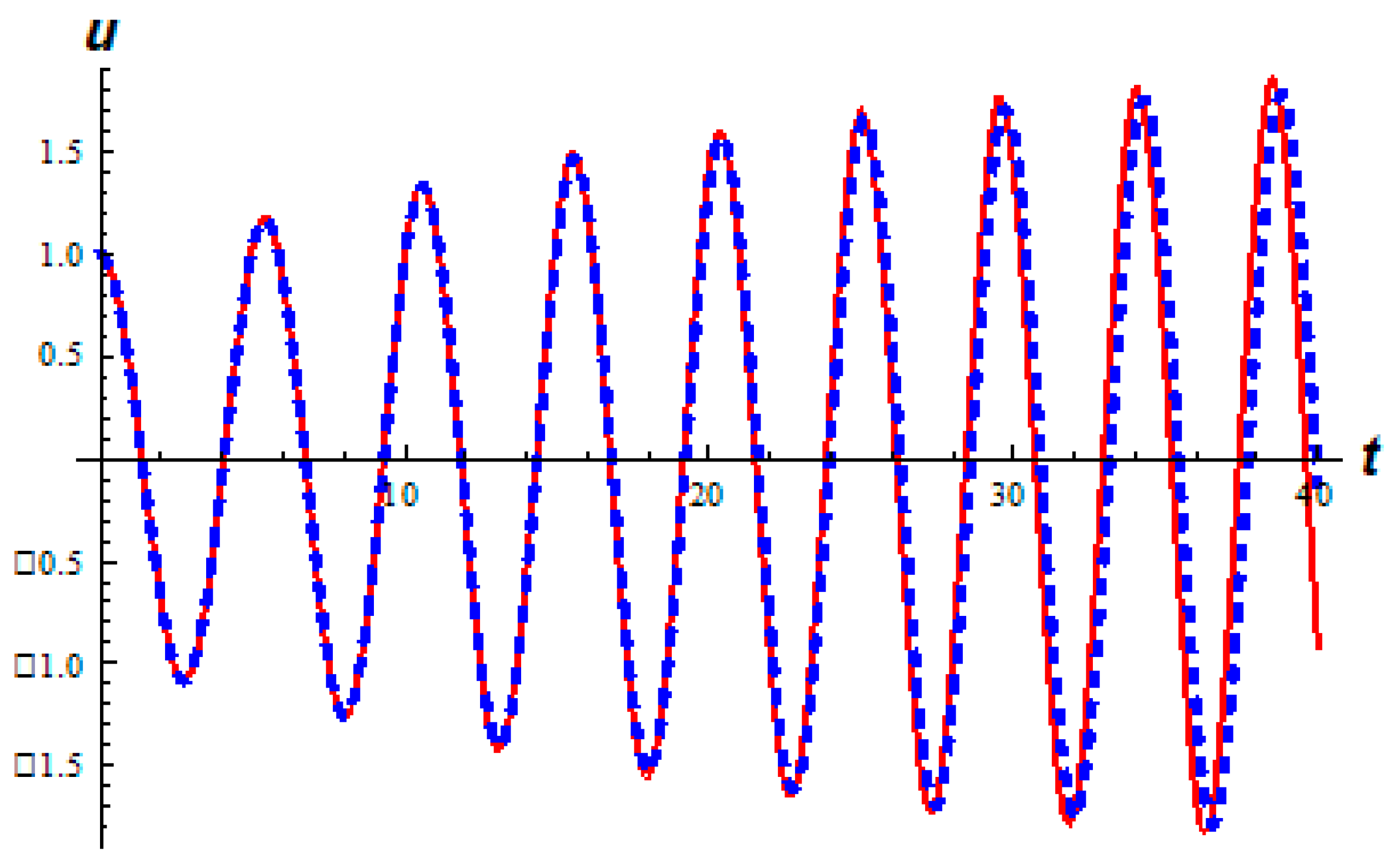
4. Numerical Applications
5. Discussions and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liénard, A. Étude des oscillations entretenues. Revue Générale L’Electricité 1928, 23, 901–912. [Google Scholar]
- Salasnich, L. On the limit cycle of an inflationary universe. Nuovo Cimento B 1997, 112, 873–880. [Google Scholar]
- Écalle, J. Introduction to Analyzable Functions and Constructive Proof of the Dulac Conjecture; Hermann: Paris, France, 1992. [Google Scholar]
- Ilyashenko, S.Y. Finiteness Theorems for Limit Cycles. Translations of Mathematical Monographs; American Mathematical Society: Providence, RI, USA, 1991; p. 94. [Google Scholar]
- Zhang, Z.; Ding, T.; Huang, W.; Dong, Z. Qualitative Theory of Differential Equations, Translations of Mathematical Monographs; American Mathematical Society: Providence, RI, USA, 1992; p. 101. [Google Scholar]
- Lefschetz, S. Existence of periodic solutions for certain differential equations. Proc. Natl. Acad. Sci. USA 1943, 29, 29–32. [Google Scholar] [CrossRef]
- Cesari, L. Asymptotic Behaviour and Stability Problems in Ordinary Differential Equations; Springer: Berlin, Germany, 1963. [Google Scholar]
- Graef, J. On the generalized Liénard equation with negative damping. J. Differ. Equ. 1972, 12, 34–62. [Google Scholar] [CrossRef][Green Version]
- Zhang, L.-H.; Wang, Y. A note on periodic solutions of a forced Linard-type equation. ANZIAM J. 2010, 51, 350–368. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; John Wiley: New York, NY, USA, 1979. [Google Scholar]
- Xu, L. He’s parameter-expanding methods for strongly nonlinear oscillators. J. Comput. Appl. Math. 2007, 207, 148–154. [Google Scholar] [CrossRef]
- Batiha, K.; Batiha, B. The variational iteration method for solving nonlinear oscillator. Appl. Math. Sci. 2012, 6, 1771–1777. [Google Scholar]
- Az-Zo’bi, E.A. On the convergence of variational iteration method for solving systems of conservation laws. Trends Appl. Sci. Res. 2015, 10, 157–165. [Google Scholar]
- He, J.H. The homotopy perturbation method for nonlinear oscillators with discontinuities. Appl. Math. Comput. 2004, 151, 287–292. [Google Scholar] [CrossRef]
- Az-Zo’bi, E.A.; Al Dawoud, K.; Marashdeh, M. Numeric-analytic solutions of mixed-type systems of balance laws. Appl. Math. Comput. 2015, 265, 133–143. [Google Scholar] [CrossRef]
- Matinfar, M.; Bahar, S.R.; Ghasemi, M. Solving the Lienard equation by differential transform method. World J. Model. Simul. 2012, 8, 142–146. [Google Scholar]
- Az-Zo’bi, E.A. On the reduced differential transform method and its application to the generalized Burgers-Huxley equation. Appl. Math. Sci. 2014, 8, 8823–8831. [Google Scholar] [CrossRef]
- Ghosh, S.; Roy, A.; Roy, D. An adaptation of Adomian decomposition for numeric-analytic integration of strongly nonlinear and chaotic oscillators. Comput. Methods Appl. Mech. Eng. 2007, 196, 1133–1153. [Google Scholar] [CrossRef]
- Az-Zo’bi, E.A. Modified Laplace decomposition method. World Appl. Sci. J. 2012, 18, 1481–1486. [Google Scholar]
- Az-Zo’bi, E.A. An approximate analytic solution for isentropic flow by an inviscid gas equations. Arch. Mech. 2014, 66, 203–212. [Google Scholar]
- Az-Zo’bi, E.A. New applications of Adomian decomposition method. Middle-East J. Sci. Res. 2015, 23, 735–740. [Google Scholar]
- Syam, M.I. A numerical solution of fractional Lienard’s equation by using the residual power series method. Mathematics 2018, 6, 1. [Google Scholar] [CrossRef]
- Az-Zo’bi, E.A. Analytic simulation for 1D Euler-like model in fluid dynamics. J. Adv. Phys. 2018, 7, 330–335. [Google Scholar] [CrossRef]
- Az-Zo’bi, E.A. Exact analytic solutions for nonlinear diffusion equations via generalized residual power series method. Int. J. Math. Comput. Sci. 2019, 14, 69–78. [Google Scholar]
- Az-Zo’bi, E.A.; Yıldırım, A.; AlZoubi, W.A. The residual power series method for the one-dimensional unsteady flow of a van der Waals gas. Physica A 2019, 517, 188–196. [Google Scholar] [CrossRef]
- Adomian, G.; Rach, R. Transformation of series. Appl. Math. Lett. 1991, 4, 69–71. [Google Scholar] [CrossRef]
- Adomian, G.; Rach, R. Nonlinear transformation of series—Part II. Comput. Math. Appl. 1992, 23, 79–83. [Google Scholar] [CrossRef]
- Az-Zo’bi, E.A.; Maysoon Qousini, M. Modified Adomian-Rach decomposition method for solving nonlinear time-dependent IVPs. Appl. Math. Sci. 2017, 11, 387–395. [Google Scholar] [CrossRef]
- Duan, J.-S.; Rach, R.; Wazwaz, A.-M. Higher order numeric solutions of the Lane-Emden-type equations derived from the multi-stage modified Adomian decomposition method. Int. J. Comput. Math. 2017, 94, 197–215. [Google Scholar] [CrossRef]
- Adomian, G.; Rach, R. Inversion of nonlinear stochastic operators. J. Math. Anal. Appl. 1983, 91, 39–46. [Google Scholar] [CrossRef]
- EL-Kalla, I.L.; El Mhlawy, A.M.; Botros, M. A continuous solution of solving a class of nonlinear two point boundary value problem using Adomian decomposition method. Ain Shams Eng. J. 2019, 10, 211–216. [Google Scholar] [CrossRef]
- Az-Zo’bi, E.A.; Al Khaled, K. A new convergence proof of the Adomian decomposition method for a mixed hyperbolic elliptic system of conservation laws. Appl. Math. Comput. 2010, 217, 4248–4256. [Google Scholar] [CrossRef]
- Az-Zo’bi, E.A. Construction of solutions for mixed hyperbolic elliptic Riemann initial value system of conservation laws. Appl. Math. Model. 2013, 37, 6018–6024. [Google Scholar] [CrossRef]
- Wazwaz, A.-M.; Rach, R.; Duan, J.-S. Steady-state concentrations of carbon dioxide absorbed into phenyl glycidal ether solutions by the Adomian decomposition method. J. Math. Chem. 2015, 53, 1054–1067. [Google Scholar]
- Rach, R.; Duan, J.-S.; Wazwaz, A.-M. Solution of higher-order, multipoint, nonlinear boundary value problems with higher-order Robin-type boundary conditions by the Adomian decomposition method. Appl. Math. Inf. Sci. 2016, 10, 1231–1242. [Google Scholar] [CrossRef]
- Cherruault, Y. Convergence of Adomian’s method. Kybernetes 1989, 18, 31–38. [Google Scholar] [CrossRef]
- Abbaoui, K.; Cherruault, Y. Convergence of Adomian’s method applied to nonlinear equations. Math. Comput. Model. 1994, 20, 60–73. [Google Scholar] [CrossRef]
- Rèpaci, A. Nonlinear dynamical systems: On the accuracy of Adomian’s decomposition method. Appl. Math. Lett. 1990, 3, 35–39. [Google Scholar] [CrossRef]
- Rach, R.; Adomian, G.; Meyers, R.E. A modified decomposition. Comput. Math. Appl. 1992, 23, 17–23. [Google Scholar] [CrossRef]
- Feng, Z. On explicit exact solutions for the Lienard equation and its applications. Phys. Lett. A 2002, 293, 50–56. [Google Scholar] [CrossRef]
- Kaya, D.; El-Sayed, S.M. A numerical implementation of the decomposition method for the Lienard equation. Appl. Math. Comput. 2005, 171, 1095–1103. [Google Scholar] [CrossRef]
- Matinfar, M.; Mahdavi, M.; Raeisy, Z. Exact and numerical solution of Lienard’s equation by the variational homotopy perturbation method. J. Inf. Comput. Sci. 2011, 6, 73–80. [Google Scholar]
- Heydari, M.H.; Hooshmandasl, M.R.; Maalek Ghain, F.M. A good approximate solution for lienard equation in a large interval using block pulse functions. J. Math. Ext. 2013, 7, 17–32. [Google Scholar]
- Wolfram Research, Inc. Mathematica, Version 9.0; Wolfram Research, Inc.: Champaign, IL, USA, 2012. [Google Scholar]
- Van der Pol, B. On relaxation-oscillations. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1927, 2, 978–992. [Google Scholar] [CrossRef]
- Ramana, P.V.; Raghu Prasad, B.K. Modified Adomian decomposition method for Van der Pol equations. Int. J. Non-Linear Mech. 2014, 65, 121–132. [Google Scholar] [CrossRef]
- Kyzioł, J.; Okniński, A. The Duffing–Van der Pol equation: metamorphoses of resonance curves. Nonlinear Dyn. Syst. Theory 2015, 15, 25–31. [Google Scholar]






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Az-Zo’bi, E.A.; Al-Khaled, K.; Darweesh, A. Numeric-Analytic Solutions for Nonlinear Oscillators via the Modified Multi-Stage Decomposition Method. Mathematics 2019, 7, 550. https://doi.org/10.3390/math7060550
Az-Zo’bi EA, Al-Khaled K, Darweesh A. Numeric-Analytic Solutions for Nonlinear Oscillators via the Modified Multi-Stage Decomposition Method. Mathematics. 2019; 7(6):550. https://doi.org/10.3390/math7060550
Chicago/Turabian StyleAz-Zo’bi, Emad A., Kamel Al-Khaled, and Amer Darweesh. 2019. "Numeric-Analytic Solutions for Nonlinear Oscillators via the Modified Multi-Stage Decomposition Method" Mathematics 7, no. 6: 550. https://doi.org/10.3390/math7060550
APA StyleAz-Zo’bi, E. A., Al-Khaled, K., & Darweesh, A. (2019). Numeric-Analytic Solutions for Nonlinear Oscillators via the Modified Multi-Stage Decomposition Method. Mathematics, 7(6), 550. https://doi.org/10.3390/math7060550





