Risk Assessment for Failure Mode and Effects Analysis Using the Bonferroni Mean and TODIM Method
Abstract
1. Introduction
2. Literature Review
2.1. Aggregation Expert Preferences
2.2. Bonferroni Mean
2.3. Failure Mode Ranking
2.4. TODIM Method
3. Preliminaries
- (1)
- ;
- (2)
- ;
- (3)
- ;
- (4)
- .
- (1)
- If, then;
- (2)
- If, then:
- (a)
- If, then;
- (b)
- If, then.
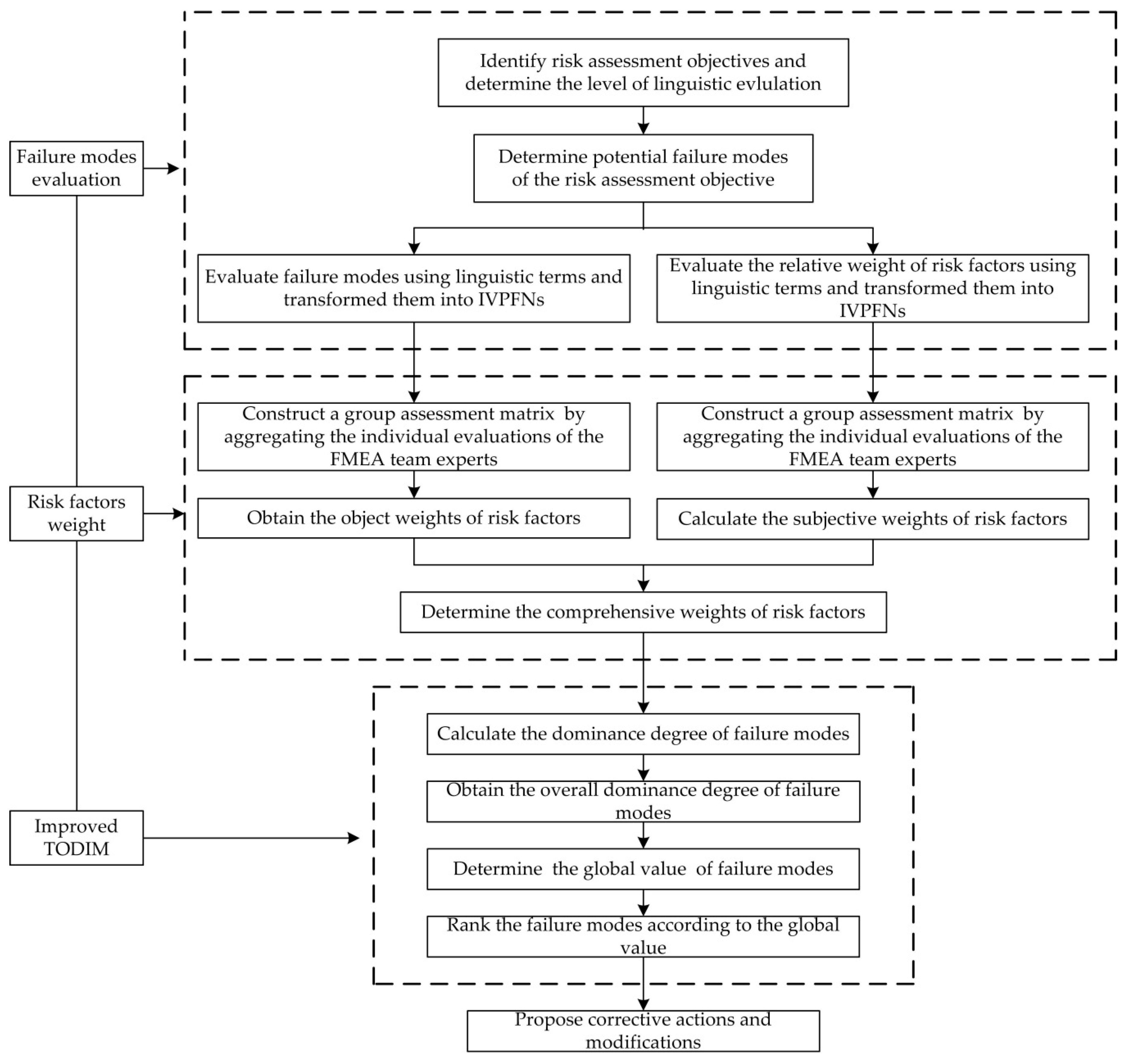
4. The Proposed FMEA Method
5. Case Illustration
5.1. Implementation of the Proposed Method
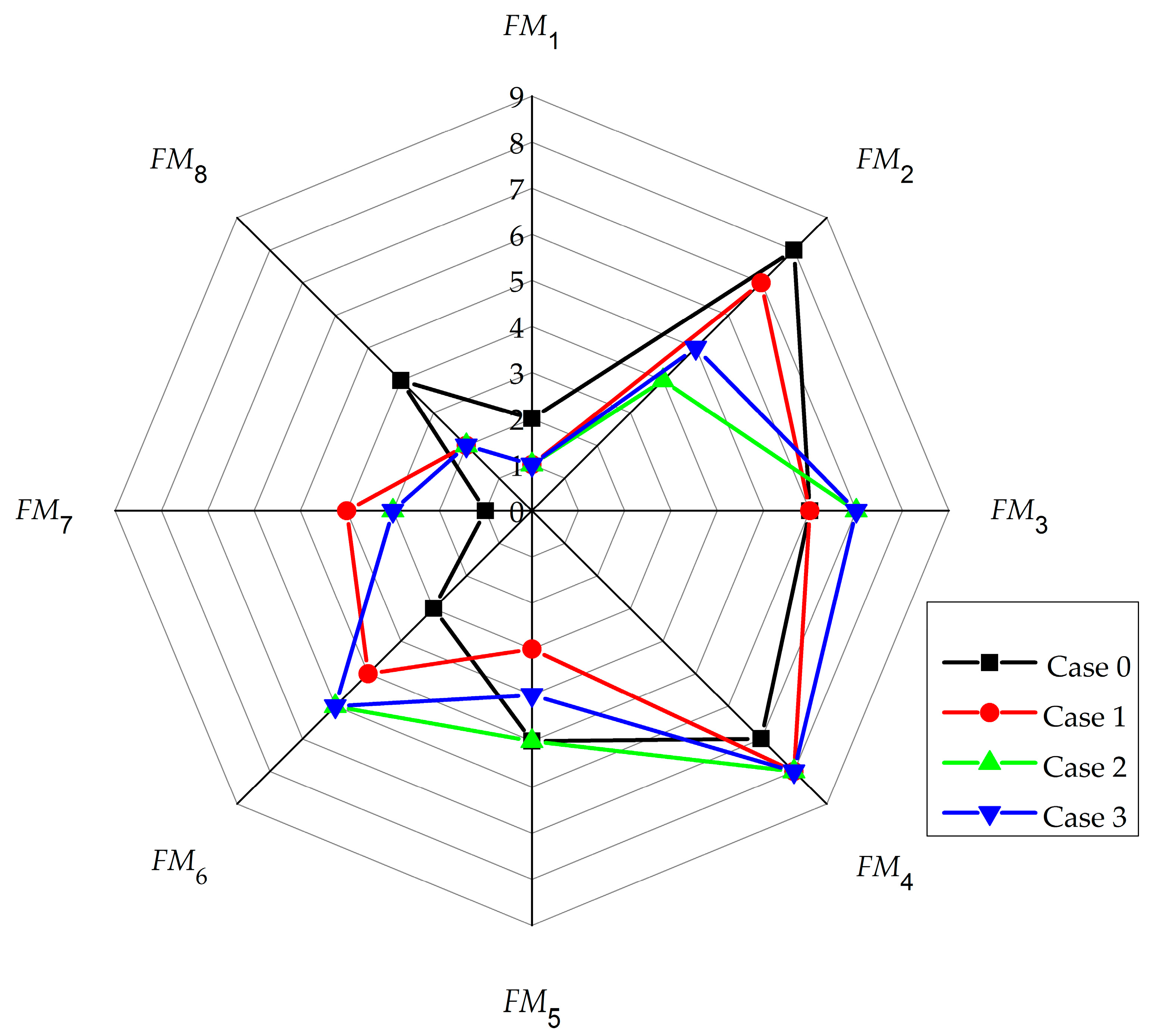
5.2. Sensitivity Analysis
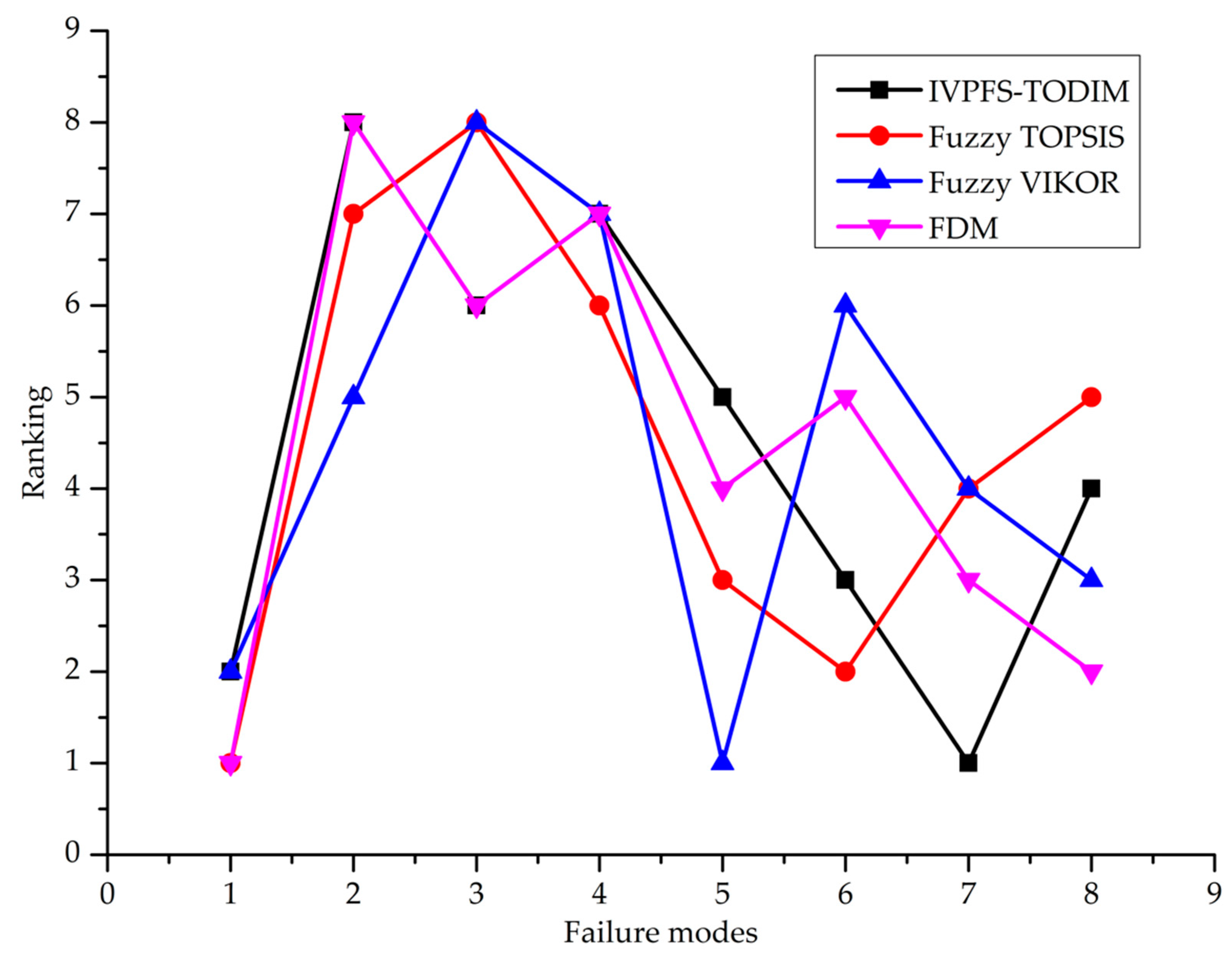
5.3. Comparisons and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Stamatis, D.H. Failure Mode and Effect Analysis: FMEA from Theory to Execution; ASQ Quality Press: Milwaukee, WI, USA, 2003. [Google Scholar]
- Bowles, J.B.; Pelaez, C.E. Fuzzy logic prioritization of failures in a system failure mode, effects and criticality analysis. Reliab. Eng. Syst. Saf. 1995, 50, 203–213. [Google Scholar] [CrossRef]
- Yeh, T.M.; Chen, L.Y. Fuzzy-based risk priority number in FMEA for semiconductor wafer processes. Int. J. Prod. Res. 2014, 52, 539–549. [Google Scholar] [CrossRef]
- Karim, M.A.; Smith, A.J.R.; Halgamuge, S. Empirical relationships between some manufacturing practices and performance. Int. J. Prod. Res. 2008, 46, 3583–3613. [Google Scholar] [CrossRef]
- Braaksma, A.J.J.; Meesters, A.J.; Klingenberg, W.; Hicks, C. A quantitative method for failure mode and effects analysis. Int. J. Prod. Res. 2012, 50, 6904–6917. [Google Scholar] [CrossRef]
- Chang, K.H.; Chang, Y.C.; Lee, Y.T. Integrating TPOSIS and dematel methods to rank the risk of failure of FMEA. Int. J. Inf. Technol. Decis. Mak. 2014, 13, 1229–1257. [Google Scholar] [CrossRef]
- Bozdag, E.; Asan, U.; Soyer, A.; Serdarasan, S. Risk prioritization in failure mode and effects analysis using interval type-2 fuzzy sets. Expert Syst. Appl. 2015, 42, 4000–4015. [Google Scholar] [CrossRef]
- Certa, A.; Hopps, F.; Inghilleri, R.; Fata, C.M.L. A Dempster-shafer theory-based approach to the failure mode, effects and criticality analysis (FMECA) under epistemic uncertainty: Application to the propulsion system of a fishing vessel. Reliab. Eng. Syst. Saf. 2017, 159, 69–79. [Google Scholar] [CrossRef]
- Braglia, M.; Frosolini, M.; Montanari, R. Fuzzy TOPSIS approach for failure mode, effects and criticality analysis. Qual. Reliab. Eng. Int. 2010, 19, 425–443. [Google Scholar] [CrossRef]
- Chin, K.S.; Wang, Y.M.; Poon, G.K.K.; Yang, J.B. Failure mode and effects analysis using a group-based evidential reasoning approach. Comput. Oper. Res. 2009, 36, 1768–1779. [Google Scholar] [CrossRef]
- Huang, J.; Li, Z.; Liu, H.C. New approach for failure mode and effect analysis using linguistic distribution assessments and TODIM method. Reliab. Eng. Syst. Saf. 2017, 167, 302–309. [Google Scholar] [CrossRef]
- Safari, H.; Faraji, Z.; Majidian, S. Identifying and evaluating enterprise architecture risks using FMEA and fuzzy vikor. J. Intell. Manuf. 2016, 27, 475–486. [Google Scholar] [CrossRef]
- Liu, H.C.; Liu, L.; Liu, N. Risk evaluation approaches in failure mode and effects analysis: A literature review. Expert Syst. Appl. 2013, 40, 828–838. [Google Scholar] [CrossRef]
- Franceschini, F.; Galetto, M. A new approach for evaluation of risk priorities of failure modes in FMEA. Int. J. Prod. Res. 2001, 39, 2991–3002. [Google Scholar] [CrossRef]
- Guo, J. A risk assessment approach for failure mode and effects analysis based on intuitionistic fuzzy sets and evidence theory. J. Intell. Fuzzy Syst. 2016, 30, 869–881. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; Chen, S.; Chen, Y.Z. An integrated failure mode and effect analysis approach for accurate risk assessment under uncertainty. Iie Trans. 2016, 48, 1027–1042. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; Duan, C.Y. An integrated approach for failure mode and effect analysis under interval-valued intuitionistic fuzzy environment. Int. J. Prod. Econ. 2017, 207, 163–172. [Google Scholar] [CrossRef]
- Wang, L.E.; Liu, H.C.; Quan, M.Y. Evaluating the risk of failure modes with a hybrid MCDM model under interval-valued intuitionistic fuzzy environment. Comput. Ind. Eng. 2016, 102, 175–185. [Google Scholar] [CrossRef]
- Zhao, H.; You, J.X.; Liu, H.C. Failure mode and effect analysis using multimoora method with continuous weighted entropy under interval-valued intuitionistic fuzzy environment. Soft Comput. 2017, 21, 5355–5367. [Google Scholar] [CrossRef]
- Kabak, Ö.; Ervural, B. Multiple attribute group decision making: A generic conceptual framework and a classification scheme. Knowl. Based Syst. 2017, 123, 13–30. [Google Scholar] [CrossRef]
- Ju, D.; Ju, Y.; Wang, A. Multi-attribute group decision making based on power generalized Heronian mean operator under hesitant fuzzy linguistic environment. Soft Comput. 2018, 23, 3823–3842. [Google Scholar] [CrossRef]
- Camerer, C. Bounded rationality in individual decision making. Exp. Econ. 1998, 1, 163–183. [Google Scholar] [CrossRef]
- Charness, G.; Rabin, M. Expressed preferences and behavior in experimental games. Games Econ. Behav. 2005, 53, 151–169. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econometrica 1979, 47, 263–291. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Z. The TODIM analysis approach based on novel measured functions under hesitant fuzzy environment. Knowl. Based Syst. 2014, 61, 48–58. [Google Scholar] [CrossRef]
- Mohsen, O.; Fereshteh, N. An extended VIKORmethod based on entropy measure for the failure modes risk assessment – a case study of the geothermal power plant (GPP). Saf. Sci. 2017, 92, 160–172. [Google Scholar] [CrossRef]
- Selim, H.; Yunusoglu, M.G.; Balaman, Ş.Y. A dynamic maintenance planning framework based on fuzzy TOPSIS and FMEA: Application in an international food company. Qual. Reliab. Eng. Int. 2016, 32, 795–804. [Google Scholar] [CrossRef]
- Song, W.; Ming, X.; Wu, Z.; Zhu, B. Failure modes and effects analysis using integrated weight-based fuzzy TOPSIS. Int. J. Comput. Integr. Manuf. 2013, 26, 1172–1186. [Google Scholar] [CrossRef]
- Bonferroni, C. Sulle medie multiple di potenze. Boll. Dell’Unione Mat. Ital. 1950, 5, 267–270. [Google Scholar]
- Liang, D.; Xu, Z.; Darko, A.P. Projection model for fusing the information of Pythagorean fuzzy multicriteria group decision making based on geometric Bonferroni mean. Int. J. Intell. Syst. 2017, 32, 966–987. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, L.; Liu, X.; Wang, P. Multi-valued neutrosophic number Bonferroni mean operators with their applications in multiple attribute group decision making. Int. J. Inf. Technol. Decis. Mak. 2016, 15, 1181–1210. [Google Scholar] [CrossRef]
- Liu, X.; Tao, Z.; Chen, H.; Zhou, L. A new interval-valued 2-tuple linguistic Bonferroni mean operator and its application to multiattribute group decision making. Int. J. Fuzzy Syst. 2017, 19, 86–108. [Google Scholar] [CrossRef]
- He, Y.; Zhen, H.; Shi, L.; Meng, S. Multiple attribute group decision making based on ivhfpbms and a new ranking method for interval-valued hesitant fuzzy information. Comput. Ind. Eng. 2016, 99, 63–77. [Google Scholar] [CrossRef]
- Fan, C.; Ye, J.; Hu, K.; Fan, E. Bonferroni mean operators of linguistic neutrosophic numbers and their multiple attribute group decision-making methods. Information 2017, 8, 107. [Google Scholar] [CrossRef]
- He, Y.; Zhen, H.; Wang, G.; Chen, H. Hesitant fuzzy power Bonferroni means and their application to multiple attribute decision making. IEEE Trans. Fuzzy Syst. 2015, 23, 1655–1668. [Google Scholar] [CrossRef]
- Liu, P.; Xi, L. Multiattribute group decision making methods based on linguistic intuitionistic fuzzy power Bonferroni mean operators. Complexity 2017, 2017, 1–15. [Google Scholar] [CrossRef]
- Lolli, F.; Ishizaka, A.; Gamberini, R.; Rimini, B.; Messori, M. Flowsort-gdss—A novel group multi-criteria decision support system for sorting problems with application to FMEA. Expert Syst. Appl. Int. J. 2015, 42, 6342–6349. [Google Scholar] [CrossRef]
- Liu, H.C.; Liu, L.; Liu, N.; Mao, L.X. Risk evaluation in failure mode and effects analysis with extended VIKOR method under fuzzy environment. Expert Syst. Appl. 2012, 39, 12926–12934. [Google Scholar] [CrossRef]
- Xu, K.; Tang, L.C.; Xie, M.; Ho, S.L.; Zhu, M.L. Fuzzy assessment of FMEA for engine systems. Reliab. Eng. Syst. Saf. 2002, 75, 17–29. [Google Scholar] [CrossRef]
- Seyed-Hosseini, S.M.; Safaei, N.; Asgharpour, M.J. Reprioritization of failures in a system failure mode and effects analysis by decision making trial and evaluation laboratory technique. Reliab. Eng. Syst. Saf. 2006, 91, 872–881. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; Lin, Q.L.; Li, H. Risk assessment in system FMEA combining fuzzy weighted average with fuzzy decision-making trial and evaluation laboratory. Int. J. Comput. Integr. Manuf. 2015, 28, 701–714. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; Ding, X.F.; Su, Q. Improving risk evaluation in FMEA with a hybrid multiple criteria decision making method. Int. J. Qual. Reliab. Manag. 2015, 32, 763–782. [Google Scholar] [CrossRef]
- Gomes, L.; Lima, M. TODIM: Basics and application to multicriteria ranking of projects with environmental impacts. Found. Comput. Decis. Sci. 1992, 16, 113–127. [Google Scholar]
- Qin, J.; Liu, X.; Pedrycz, W. An extended TODIM multi-criteria group decision making method for green supplier selection in interval type-2 fuzzy environment. Eur. J. Oper. Res. 2017, 258, 626–638. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Z. Efficiency evaluation of sustainable water management using the HF-TODIM method. Int. Trans. Oper. Res. 2019, 26, 747–764. [Google Scholar] [CrossRef]
- Ji, P.; Zhang, H.Y.; Wang, J.Q. A projection-based TODIM method under multi-valued neutrosophic environments and its application in personnel selection. Neural Comput. Appl. 2018, 29, 221–234. [Google Scholar] [CrossRef]
- Qin, Q.; Liang, F.; Li, L.; Wei, Y.M. Selection of energy performance contracting business models: A behavioral decision-making approach. Renew. Sustain. Energy Rev. 2017, 72, 422–433. [Google Scholar] [CrossRef]
- Ren, P.; Xu, Z.; Gou, X. Pythagorean fuzzy TODIM approach to multi-criteria decision making. Appl. Soft Comput. 2016, 42, 246–259. [Google Scholar] [CrossRef]
- Zhang, X. Multicriteria Pythagorean fuzzy decision analysis: A hierarchical QUALIFLEX approach with the closeness index-based ranking methods. Inf. Sci. 2016, 330, 104–124. [Google Scholar] [CrossRef]
- Peng, X.; Yang, Y. Fundamental properties of interval-valued Pythagorean fuzzy aggregation operators. Int. J. Intell. Syst. 2016, 31, 444–487. [Google Scholar] [CrossRef]
- Chen, T.Y. An interval-valued Pythagorean fuzzy outranking method with a closeness-based assignment model for multiple criteria decision making. Int. J. Intell. Syst. 2018, 33, 126–168. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, Q. A multi-criteria decision making procedure based on interval-valuedintuitionistic fuzzy Bonferroni mean. J. Syst. Sci. Syst. Eng. 2011, 20, 217–228. [Google Scholar] [CrossRef]
- Bazzazi, A.A.; Osanloo, M.; Karimi, B. Deriving preference order of open pit mines equipment through MADM methods: Application of modified vikor method. Expert Syst. Appl. 2011, 38, 2550–2556. [Google Scholar] [CrossRef]
- Wei, C.P.; Wang, P.; Zhang, Y.Z. Entropy, similarity measure of interval-valued intuitionistic fuzzy sets and their applications. Inf. Sci. 2011, 181, 4273–4286. [Google Scholar] [CrossRef]
- Wei, G. Grey relational analysis model for dynamic hybrid multiple attribute decision making. Knowl. Based Syst. 2011, 24, 672–679. [Google Scholar] [CrossRef]
- Liu, H.C.; Chen, Y.Z.; You, J.X.; Li, H. Risk evaluation in failure mode and effects analysis using fuzzy digraph and matrix approach. J. Intell. Manuf. 2016, 27, 805–816. [Google Scholar] [CrossRef]
| Linguistic Variables | Abbreviation | IVPFNs |
|---|---|---|
| Very high | VH | ([0.8000, 0.9000], [0.1000, 0.2000]) |
| High | H | ([0.7000, 0.8000], [0.2000, 0.3000]) |
| Medium high | MH | ([0.6000, 0.7000], [0.3000, 0.4000]) |
| Medium | M | ([0.5000, 0.6000], [0.4000, 0.5000]) |
| Medium low | ML | ([0.3000, 0.4000], [0.6000, 0.7000]) |
| Low | L | ([0.2000, 0.3000], [0.7000, 0.8000]) |
| Very low | VL | ([0.1000, 0.2000], [0.8000, 0.9000]) |
| Linguistic Variables | Abbreviation | IVPFNs |
|---|---|---|
| Very high | VH | ([0.8000, 0.9000], [0.1000, 0.2000]) |
| High | H | ([0.7000, 0.8000], [0.2000, 0.3000]) |
| Medium | M | ([0.5000, 0.6000], [0.4000, 0.5000]) |
| Low | L | ([0.3000, 0.4000], [0.6000, 0.7000]) |
| Very low | VL | ([0.1000, 0.2000], [0.8000, 0.9000]) |
| Risk Factors | Severity (S) | Occurrence (O) | Detection (D) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Team Experts | E1 | E2 | E3 | E4 | E1 | E2 | E3 | E4 | E1 | E2 | E3 | E4 |
| FM1 | VH | VH | VH | H | ML | ML | M | L | H | H | MH | M |
| FM2 | L | VL | VH | ML | ML | ML | M | ML | ML | M | M | ML |
| FM3 | ML | ML | L | ML | MH | MH | M | M | ML | ML | L | M |
| FM4 | MH | MH | M | M | ML | L | ML | ML | M | L | ML | ML |
| FM5 | VH | VH | MH | H | ML | ML | M | M | ML | ML | L | ML |
| FM6 | VH | VH | MH | VH | L | ML | L | ML | L | ML | ML | M |
| FM7 | MH | MH | VH | H | M | M | MH | M | ML | L | ML | ML |
| FM8 | M | M | H | MH | M | MH | M | MH | ML | M | ML | ML |
| Team Experts | E1 | E2 | E3 | E4 |
|---|---|---|---|---|
| Occurrence | L | M | M | H |
| Severity | M | H | H | VH |
| Detection | M | H | M | H |
| Risk Factors | S | O | D |
|---|---|---|---|
| FM1 | ([0.4517,0.5520], [0.6053,0.6972]) | ([0.1743,0.2292], [0.8708,0.9062]) | ([0.3416,0.4138], [0.7297,0.7875]) |
| FM2 | ([0.1943, 0.2609], [0.8627, 0.9045]) | ([0.1847, 0.2403], [0.8620, 0.8982]) | ([0.2200, 0.2770], [0.8384, 0.8772]) |
| FM3 | ([0.1357, 0.1884], [0.8936, 0.9264]) | ([0.2898, 0.3540], [0.7764, 0.8248]) | ([0.1619, 0.2163], [0.8768, 0.9123]) |
| FM4 | ([0.2898, 0.3540], [0.7764, 0.8248]) | ([0.1371, 0.1897], [0.8931, 0.9258]) | ([0.1597, 0.2136], [0.8785, 0.9136]) |
| FM5 | ([0.4077, 0.4978], [0.6539, 0.7330]) | ([0.2120, 0.2689], [0.8426, 0.8813]) | ([0.1357, 0.1884], [0.8936, 0.9264]) |
| FM6 | ([0.4264, 0.5231], [0.6286, 0.7165]) | ([0.1268, 0.1791], [0.9000, 0.9321]) | ([0.1698, 0.2243], [0.8722, 0.9077]) |
| FM7 | ([0.3818, 0.4630], [0.6928, 0.7586]) | ([0.2796, 0.3422], [0.7872, 0.8332]) | ([0.1371, 0.1897], [0.8931, 0.9258]) |
| FM8 | ([0.3141, 0.3818], [0.7586, 0.8099]) | ([0.2924, 0.3568], [0.7745, 0.8231]) | ([0.1829, 0.2385], [0.8625, 0.8988]) |
| Weights | ([0.3736, 0.4573], [0.6817, 0.7526]) | ([0.2677, 0.3366], [0.7913, 0.8386]) | ([0.3177, 0.3873], [0.7421, 0.7980]) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Shuai, B.; Wang, R.; Chin, K.-S. Risk Assessment for Failure Mode and Effects Analysis Using the Bonferroni Mean and TODIM Method. Mathematics 2019, 7, 536. https://doi.org/10.3390/math7060536
Zhu J, Shuai B, Wang R, Chin K-S. Risk Assessment for Failure Mode and Effects Analysis Using the Bonferroni Mean and TODIM Method. Mathematics. 2019; 7(6):536. https://doi.org/10.3390/math7060536
Chicago/Turabian StyleZhu, Jianghong, Bin Shuai, Rui Wang, and Kwai-Sang Chin. 2019. "Risk Assessment for Failure Mode and Effects Analysis Using the Bonferroni Mean and TODIM Method" Mathematics 7, no. 6: 536. https://doi.org/10.3390/math7060536
APA StyleZhu, J., Shuai, B., Wang, R., & Chin, K.-S. (2019). Risk Assessment for Failure Mode and Effects Analysis Using the Bonferroni Mean and TODIM Method. Mathematics, 7(6), 536. https://doi.org/10.3390/math7060536




