Impact of Fractional Calculus on Correlation Coefficient between Available Potassium and Spectrum Data in Ground Hyperspectral and Landsat 8 Image
Abstract
:1. Introduction
2. Experiment Procedure
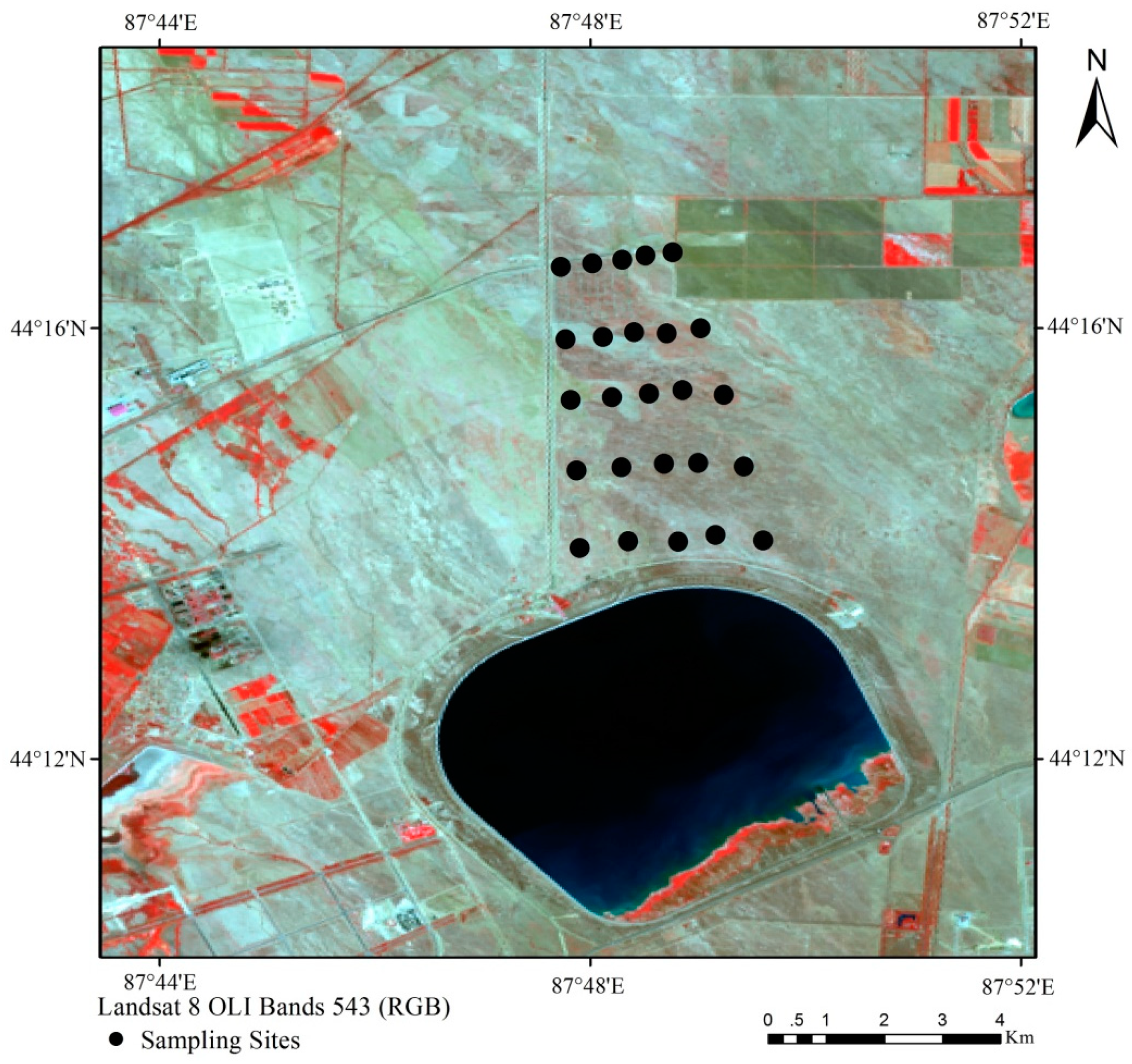
2.1. Study Area
2.2. Field Hyperspectral Data Collection
2.3. Soil Sample Collection
3. Spectral Data Preprocessing Method
3.1. Remove Interference Bands
3.2. Savitzky–Golay Convolution Smoothing
3.3. Fractional Calculus
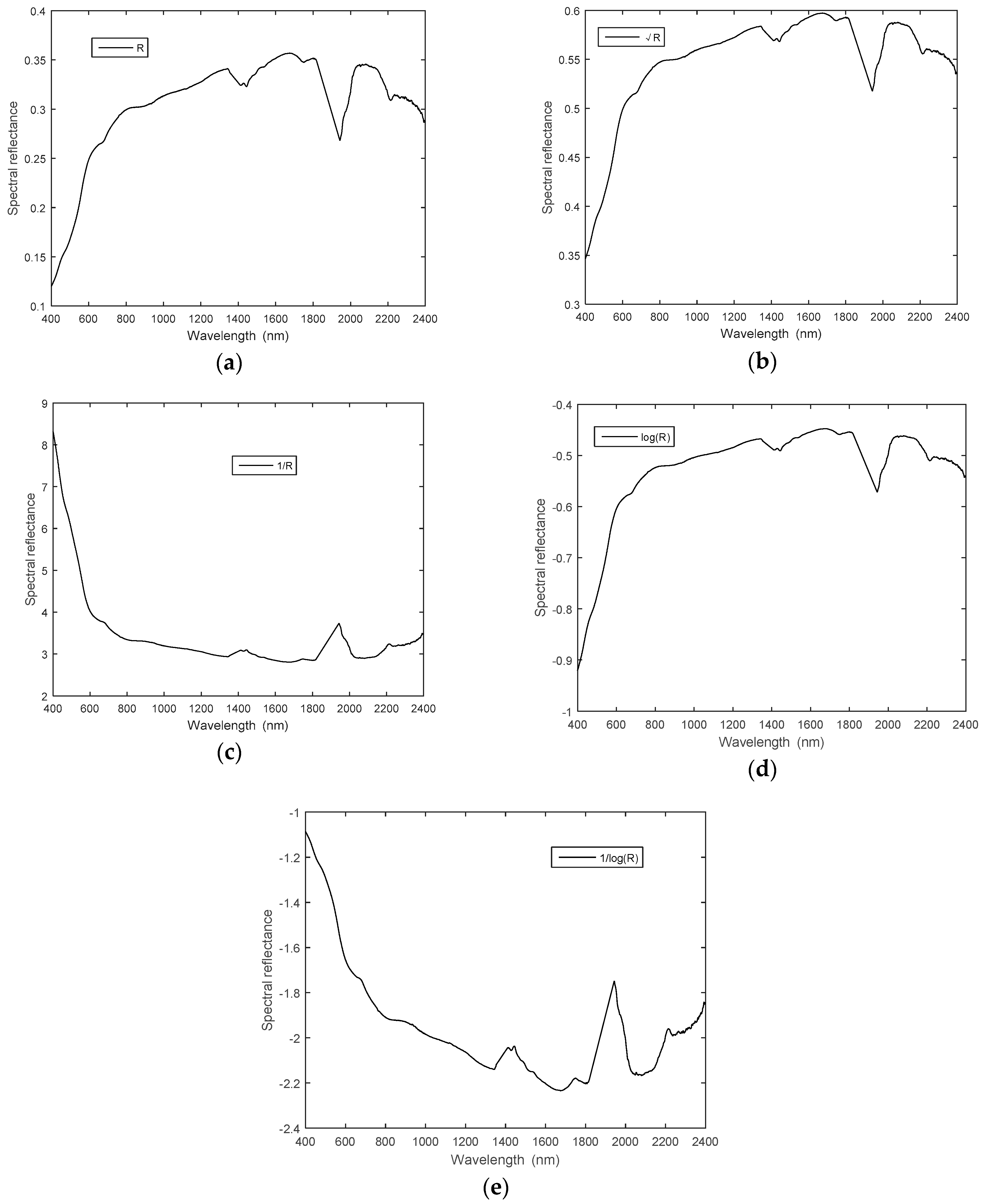
3.4. Spectral Mathematical Transformation
4. Simulation Results
4.1. Differential Calculation of Root Mean Square and Logarithm Reciprocal
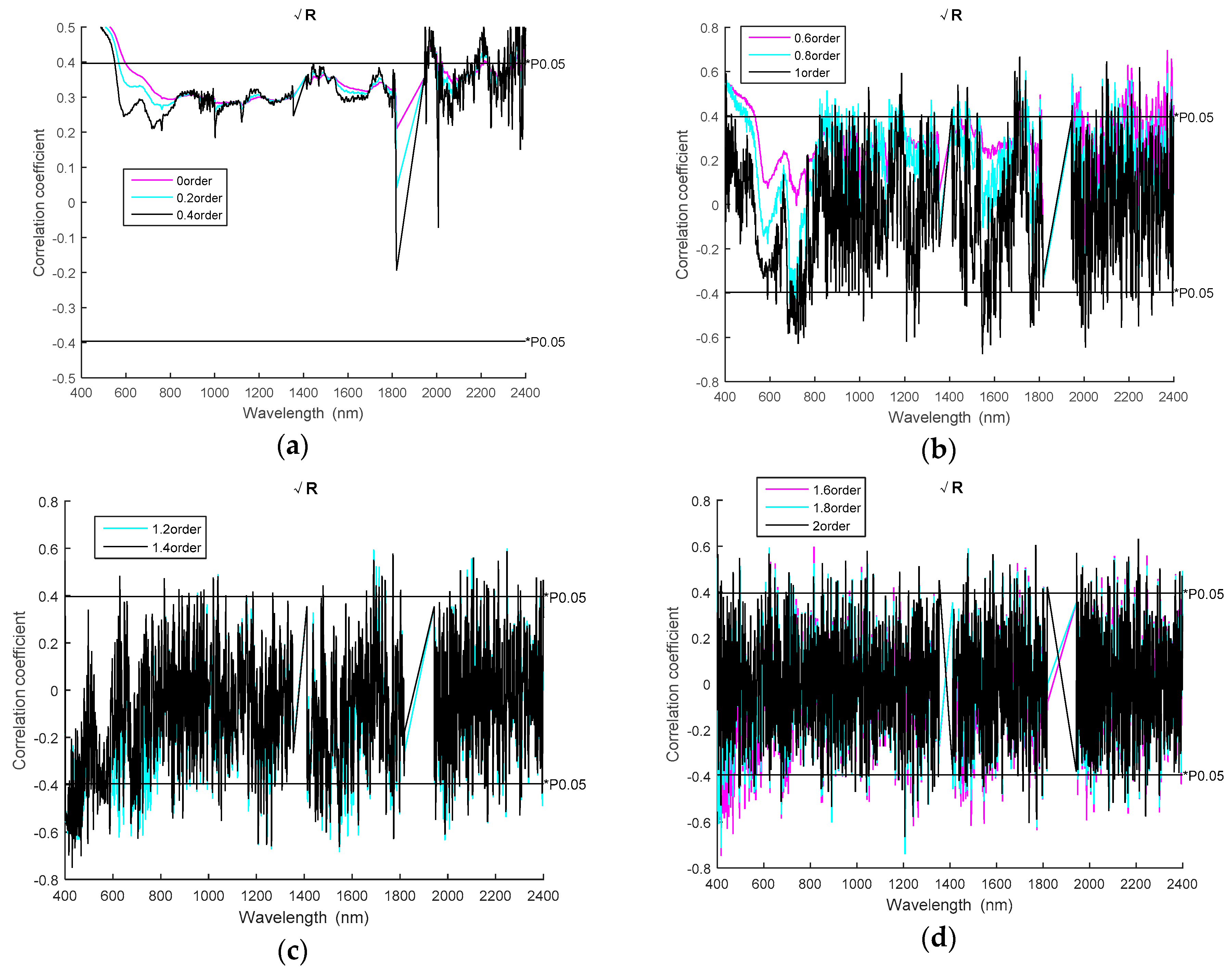
4.2. Trends of Correlation Coefficients for Root Mean Square and Logarithm Reciprocal
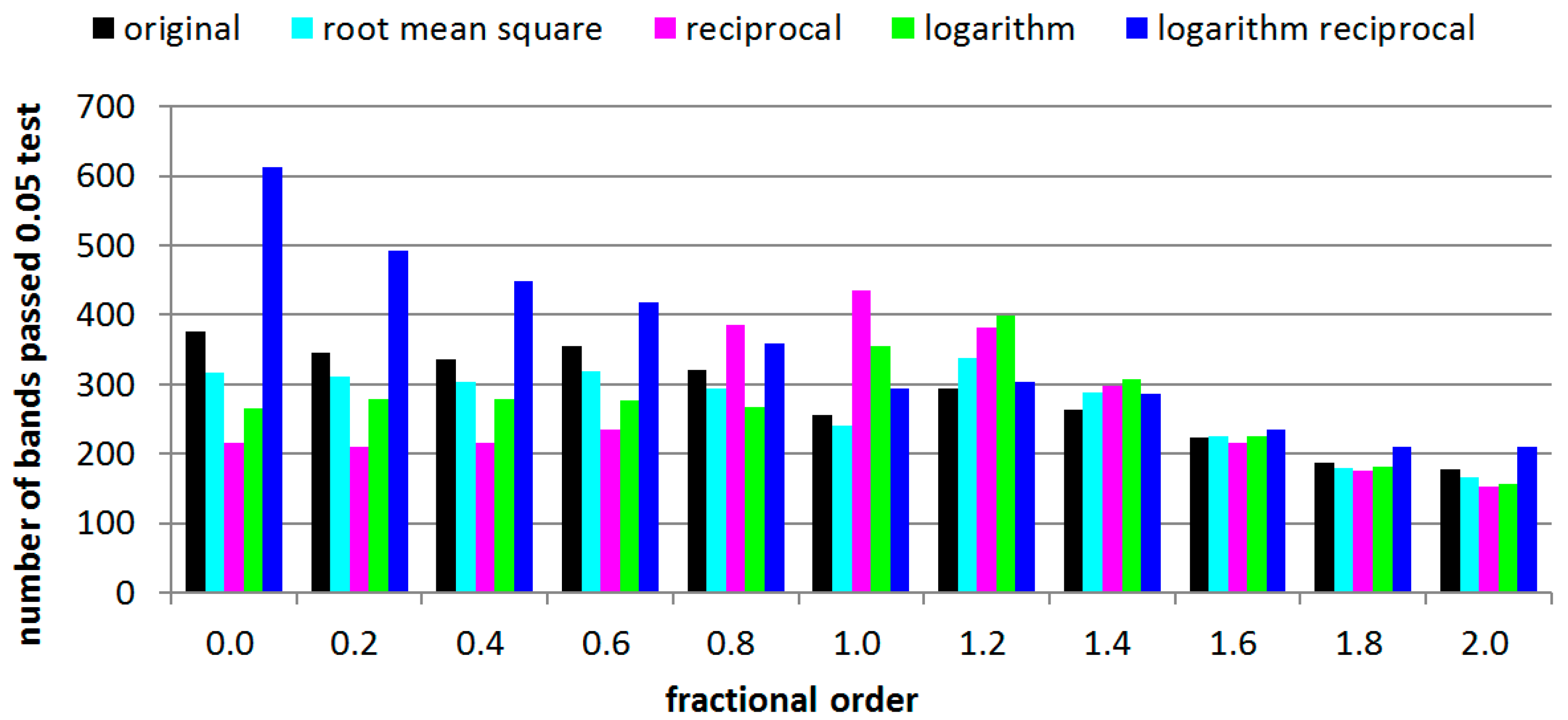
4.3. Number of Bands that Passed 0.05 Significance Level Test
4.4. Absolute Maximum Band of Correlation Coefficient under Five Spectral Transformations
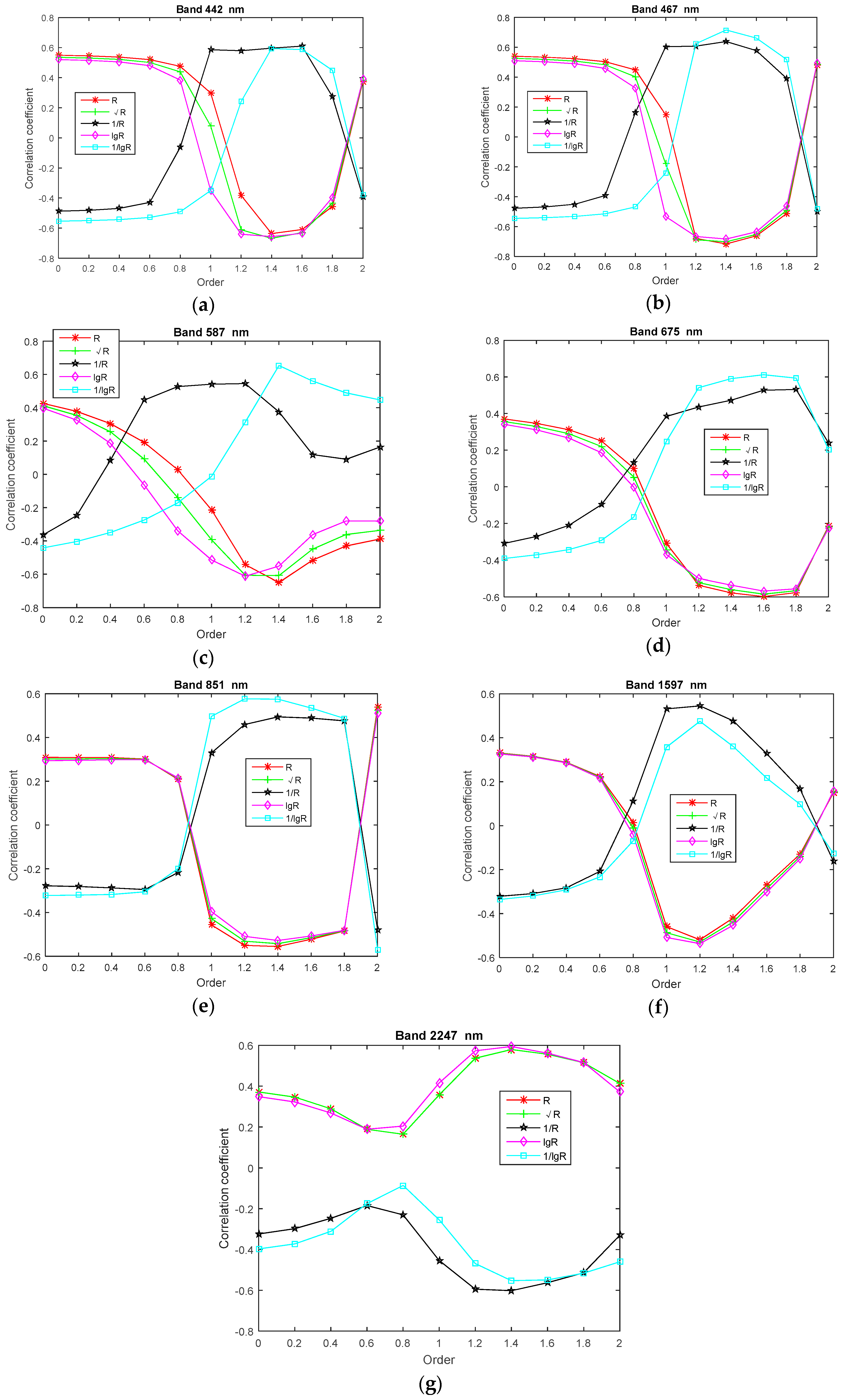
4.5. Fractional Derivative Impact on Correlation Coefficient of Landsat 8 Image Bands
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sardans, J.; Penuelas, J. Potassium: A neglected nutrient in global change. Glob. Ecol. Biogeogr. 2015, 24, 261–275. [Google Scholar] [CrossRef]
- Qiu, K.; Xie, Y.; Xu, D.; Pott, R. Ecosystem functions including soil organic carbon, total nitrogen and available potassium are crucial for vegetation recovery. Sci. Report. 2018, 8, 7607. [Google Scholar] [CrossRef] [PubMed]
- Panda, R.; Patra, S.K. Assessment of Suitable Extractants for Predicting Plant-available Potassium in Indian Coastal Soils. Commun. Soil Sci. Plant Anal. 2018, 49, 1157–1167. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Walvoort, D.J.J.; McBratney, A.B.; Janik, L.J.; Skjemstad, J.O. Visible, near infrared, mid infrared or combined diffuse reflectance spectroscopy for simultaneous assessment of various soil properties. Geoderma 2006, 131, 59–75. [Google Scholar] [CrossRef]
- Jia, S.; Yang, X.; Li, G.; Zhang, J. Quantitatively determination of available phosphorus and available potassium in soil by near infrared spectroscopy combining with recursive partial least squares. Spectro. Spectr. Anal. 2015, 35, 2516–2520. [Google Scholar]
- Sarkar, S.; Patra, S.K. Evaluation of Chemical Extraction Methods for Determining Plant-Available Potassium in Some Soils of West Bengal, India. Commun. Soil Sci. Plant Anal. 2017, 48, 1008–1019. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, M.; Ren, H.; Pu, P.; Kong, P.; Zhao, H. Comparative investigation on soil nitrate-nitrogen and available potassium measurement capability by using solid-state and PVC ISE. Comput. Electr. Agric. 2015, 112, 83–91. [Google Scholar] [CrossRef]
- O’Rourke, S.M.; Stockmann, U.; Holden, N.M.; McBratney, A.B.; Minasny, B. An assessment of model averaging to improve predictive power of portable vis-NIR and XRF for the determination of agronomic soil properties. Geoderma 2016, 279, 31–44. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Saberioo, M.; Ben-Dor, E.; Boruvka, L. Monitoring of selected soil contaminants using proximal and remote sensing techniques: Background, state-ofthe-art and future perspectives. Crit. Rev. Environ. Sci. Tech. 2018, 48, 243–278. [Google Scholar] [CrossRef]
- Lamine, S.; Petropoulos, G.P.; Brewer, P.A.; Bachari, N.E.; Srivastava, P.K.; Manevski, K.; Kalaitzidis, C.; Macklin, M.G. Heavy Metal Soil Contamination Detection Using Combined Geochemistry and Field Spectroradiometry in the United Kingdom. Sensors 2019, 19, 762. [Google Scholar] [CrossRef]
- Liu, X.; Wang, L.; Chang, Q.; Wang, X.; Shang, Y. Prediction of total nitrogen and alkali hydrolysable nitrogen content in loess using hyperspectral data based on correlation analysis and partial least squares regression. Chin. J. Appl. Ecol. 2015, 26, 2107–2114. [Google Scholar]
- Debaene, G.; Niedźwiecki, J.; Pecio, A.; Żurek, A. Effect of the number of calibration samples on the prediction of several soil propertiesat the farm-scale. Geoderma 2014, 214/215, 114–125. [Google Scholar] [CrossRef]
- Mashimbye, Z.E.; Cho, M.A.; Nell, J.P.; Declercq, W.P.D.; Niekerk, A.V.; Turner, D.P. Model-Based Integrated Methods for Quantitative Estimation of Soil Salinity from Hyperspectral Remote Sensing Data A Case Study of Selected South African Soils. Pedosphere 2012, 22, 640–649. [Google Scholar] [CrossRef]
- Yang, H.; Kuang, B.; Mouazen, A.M. Quantitative analysis of soil nitrogen and carbon at a farm scale using visible and near infrared spectroscopy coupled with wavelength reduction. Eur. J. Soil Sci. 2011, 63, 410–420. [Google Scholar] [CrossRef]
- Fu, Y.; Yang, G.; Wang, J.; Song, X.; Feng, H. Winter wheat biomass estimation based on spectral indices, band depth analysis and partial least squares regression using hyperspectral measurements. Comput. Electr. Agric. 2014, 100, 51–59. [Google Scholar] [CrossRef]
- Wu, Q.; Yang, Y.; Xu, Z.; Jin, Y.; Guo, Y.; Lao, C. Applying Local Neural Network and Visible/Near-Infrared Spectroscopy to Estimating Available Nitrogen, Phosphorus and Potassium in Soil. Spectro. Spectr. Anal. 2014, 34, 2102–2105. [Google Scholar]
- Liu, X.; Liu, J. Based on the LS-SVM Modeling Method Determination of Soil Available N and Available K by Using Near-Infrared Spectroscopy. Spectro. Spectr. Anal. 2012, 32, 3019–3023. [Google Scholar]
- Wang, J.; Tiyip, T.; Ding, J.; Zhang, D.; Liu, W.; Wang, F.; Nigara, T. Desert soil clay content estimation using reflectance spectroscopy preprocessed by fractional derivative. PLOS ONE 2017, 12, e0184836. [Google Scholar] [CrossRef]
- Wang, J.; Ding, J.; Aerzuna, A.; Cai, L. Quantitative estimation of soil salinity by means of different modeling methods and visible-near infrared (VIS-NIR) spectroscopy, Ebinur Lake Wetland, Northwest China. PeerJ 2018. [Google Scholar] [CrossRef]
- Kaslik, E.; Sivasundaram, S. Non-Existence of Periodic Solutions in Fractional-Order Dynamical Systems and a Remarkable Difference Between Integer and Fractional-Order Derivatives of Periodic Functions. Nonlinear Anal. Real World Appl. 2012, 13, 1489–1497. [Google Scholar] [CrossRef]
- Mbouna, G.S.; Woafo, P. Dynamics and Synchronization Analysis of Coupled Fractional-Order Nonlinear Electromechanical Systems. Mech. Res. Commun. 2012, 46, 20–25. [Google Scholar]
- Wu, L.; Liu, S.; Yao, L.; Yan, S.; Liu, D. Grey System Model with the Fractional Order Accumulation. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 1775–1785. [Google Scholar] [CrossRef]
- Galeone, L.; Garrappa, R. Explicit Methods for Fractional Differential Equations and Their Stability Properties. J. Comput. Appl. Math. 2009, 228, 548–560. [Google Scholar] [CrossRef]
- Schmitt, J.M. Fractional Derivative Analysis of Diffuse Reflectance Spectra. Appl. Spectro. 1998, 52, 840–846. [Google Scholar] [CrossRef]
- Zheng, K.; Zhang, X.; Tong, P.; Yao, Y.; Du, Y. Pretreating near infrared spectra with fractional order Savitzky–Golay differentiation (FOSGD). Chin. Chem. Letters 2015, 26, 293–296. [Google Scholar] [CrossRef]
- Zhang, D.; Tiyip, T.; Ding, J.; Zhang, F.; Nurmemet, I.; Kelimu, A.; Wang, J. Quantitative Estimating Salt Content of Saline Soil Using Laboratory Hyperspectral Data Treated by Fractional Derivative. J. Spectro. 2016. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Chen, Y.; Zhang, Y.; Shi, T.; Wang, J.; Hong, Y.; Fei, T.; Zhang, Y. The Influence of Spectral Pretreatment on the Selection of Representative Calibration Samples for Soil Organic Matter Estimation Using Vis-NIR Reflectance Spectroscopy. Remote Sens. 2019, 11, 450. [Google Scholar] [CrossRef]
- Zhang, K.; Dong, X.; Liu, Z.; Gao, W.; Hu, Z.; Wu, G. Mapping Tidal Flats with Landsat 8 Images and Google Earth Engine: A Case Study of the China’s Eastern Coastal Zone circa 2015. Remote Sens. 2019, 11, 924. [Google Scholar] [CrossRef]
- Lima, T.A.; Beuchle, R.; Langner, A.; Grecchi, R.; Griess, V.C.; Frédéric, A. Comparing Sentinel-2 MSI and Landsat 8 OLI Imagery for Monitoring Selective Logging in the Brazilian Amazon. Remote Sens. 2019, 11, 961. [Google Scholar] [CrossRef]
- Nawar, S.; Buddenbaum, H.; Hill, J.; Kozak, J.; Mouazen, A.M. Estimating the soil clay content and organic matter by means of different calibration methods of VIS–NIR diffuse reflectance spectroscopy. Soil Tillage Res. 2016, 155, 510–522. [Google Scholar] [CrossRef]
- Srivastava, R.; Sarkar, D.; Mukhopadhayay, S.S.; Sood, A.; Singh, M.; Nasre, R.A.; Dhale, S.A. Development of hyperspectral model for rapid monitoring of soil organic carbon under precision farming in the Indo-Gangetic Plains of Punjab, India. J. Indian Soc. Remote Sens. 2015, 43, 751–759. [Google Scholar] [CrossRef]
- Xia, N.; Tiyip, T.; Kelimu, A.; Nurmemet, I.; Ding, J.; Zhang, F.; Zhang, D. Influence of Fractional Differential on Correlation Coefficient between EC1:5 and Reflectance Spectra of Saline Soil. J. Spectro. 2017. [Google Scholar] [CrossRef]
- Hong, Y.; Chen, Y.; Yu, L.; Liu, Y.; Liu, Y.; Zhang, Y.; Liu, Y.; Cheng, H. Combining Fractional Order Derivative and Spectral Variable Selection for Organic Matter Estimation of Homogeneous Soil Samples by VIS–NIR Spectroscopy. Remote Sens. 2018, 10, 479. [Google Scholar] [CrossRef]
- Wang, J.; Tiyip, T.; Zhang, D. Spectral Detection of Chrominum Content in Desert Soil Based on Fractional Differential. Trans. Chin. Soc. Agric. Mach. 2017, 48, 152–158. [Google Scholar]
- Wang, X.; Zhang, F.; Kung, H.; Johnson, V.C. New methods for improving the remote sensing estimation of soil organic matter content (SOMC) in the Ebinur Lake Wetland National Nature Reserve (ELWNNR) in northwest China. Remote Sens. Environ. 2018, 218, 104–118. [Google Scholar] [CrossRef]
- Chen, K.; Li, C.; Tang, R. Estimation of the nitrogen concentration of rubber tree using fractional calculus augmented NIR spectra. Ind. Crops Product. 2017, 108, 831–839. [Google Scholar] [CrossRef]
- Tong, P.; Du, Y.; Zheng, K.; Wu, T.; Wang, J. Improvement of NIR model by fractional order Savitzky–Golay derivation (FOSGD) coupled with wavelength selection. Chemom. Intell. Lab. Syst. 2015, 143, 40–48. [Google Scholar] [CrossRef]


| Order | R | 1/R | lgR | 1/lgR | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Largest Absolute | Band | Largest Absolute | Band | Largest Absolute | Band | Largest Absolute | Band | Largest Absolute | Band | |
| 0 | 0.560973 | 405 | 0.547695 | 405 | 0.499854 | 400 | 0.532827 | 405 | 0.562356 | 405 |
| 0.2 | 0.570438 | 2391 | 0.559709 | 2391 | 0.521992 | 2392 | 0.547824 | 2392 | 0.586224 | 2391 |
| 0.4 | 0.700301 | 2390 | 0.690903 | 2391 | 0.655011 | 2391 | 0.680045 | 2391 | 0.719717 | 2390 |
| 0.6 | 0.712129 | 2371 | 0.697076 | 2371 | 0.645772 | 2390 | 0.680265 | 2371 | 0.734104 | 2371 |
| 0.8 | 0.632373 | 2100 | 0.62877 | 2100 | 0.663153 | 2006 | 0.623198 | 2100 | 0.645372 | 2371 |
| 1 | 0.668786 | 1547 | 0.675601 | 1547 | 0.674436 | 2006 | 0.674577 | 1547 | 0.67265 | 404 |
| 1.2 | 0.707065 | 416 | 0.746563 | 430 | 0.674899 | 495 | 0.747359 | 495 | 0.705747 | 416 |
| 1.4 | 0.722362 | 416 | 0.750124 | 430 | 0.741574 | 494 | 0.739563 | 430 | 0.730641 | 497 |
| 1.6 | 0.763605 | 416 | 0.746466 | 416 | 0.689794 | 1207 | 0.725154 | 416 | 0.762187 | 416 |
| 1.8 | 0.74986 | 1207 | 0.739655 | 1207 | 0.701802 | 416 | 0.726421 | 1207 | 0.75847 | 1207 |
| 2 | 0.678462 | 1206 | 0.664644 | 1206 | 0.621093 | 1740 | 0.648568 | 1206 | 0.69792 | 1206 |
| Band name | Band range (nm) |
|---|---|
| Band 1 Coastal | 433–453 |
| Band 2 Blue | 450–515 |
| Band 3 Green | 525–600 |
| Band 4 Red | 630–680 |
| Band 5 NIR | 845–885 |
| Band 6 SWIR1 | 1560–1660 |
| Band 7 SWIR2 | 2100–2300 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, C.; Gan, S.; Yuan, X.; Xiong, H.; Tian, A. Impact of Fractional Calculus on Correlation Coefficient between Available Potassium and Spectrum Data in Ground Hyperspectral and Landsat 8 Image. Mathematics 2019, 7, 488. https://doi.org/10.3390/math7060488
Fu C, Gan S, Yuan X, Xiong H, Tian A. Impact of Fractional Calculus on Correlation Coefficient between Available Potassium and Spectrum Data in Ground Hyperspectral and Landsat 8 Image. Mathematics. 2019; 7(6):488. https://doi.org/10.3390/math7060488
Chicago/Turabian StyleFu, Chengbiao, Shu Gan, Xiping Yuan, Heigang Xiong, and Anhong Tian. 2019. "Impact of Fractional Calculus on Correlation Coefficient between Available Potassium and Spectrum Data in Ground Hyperspectral and Landsat 8 Image" Mathematics 7, no. 6: 488. https://doi.org/10.3390/math7060488
APA StyleFu, C., Gan, S., Yuan, X., Xiong, H., & Tian, A. (2019). Impact of Fractional Calculus on Correlation Coefficient between Available Potassium and Spectrum Data in Ground Hyperspectral and Landsat 8 Image. Mathematics, 7(6), 488. https://doi.org/10.3390/math7060488





