Time-Fractional Diffusion-Wave Equation with Mass Absorption in a Sphere under Harmonic Impact
Abstract
1. Introduction
2. Statement of the Problem
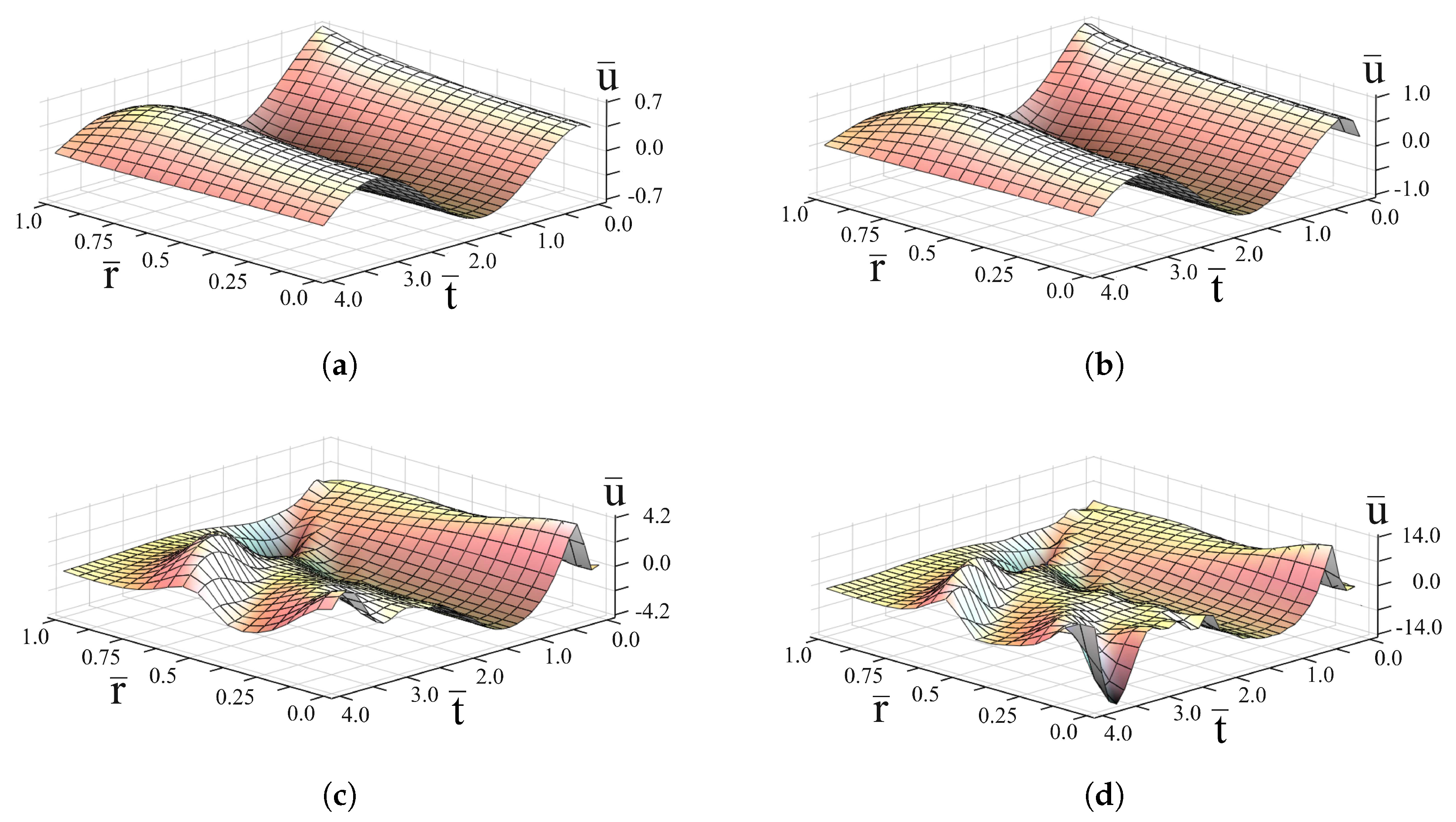
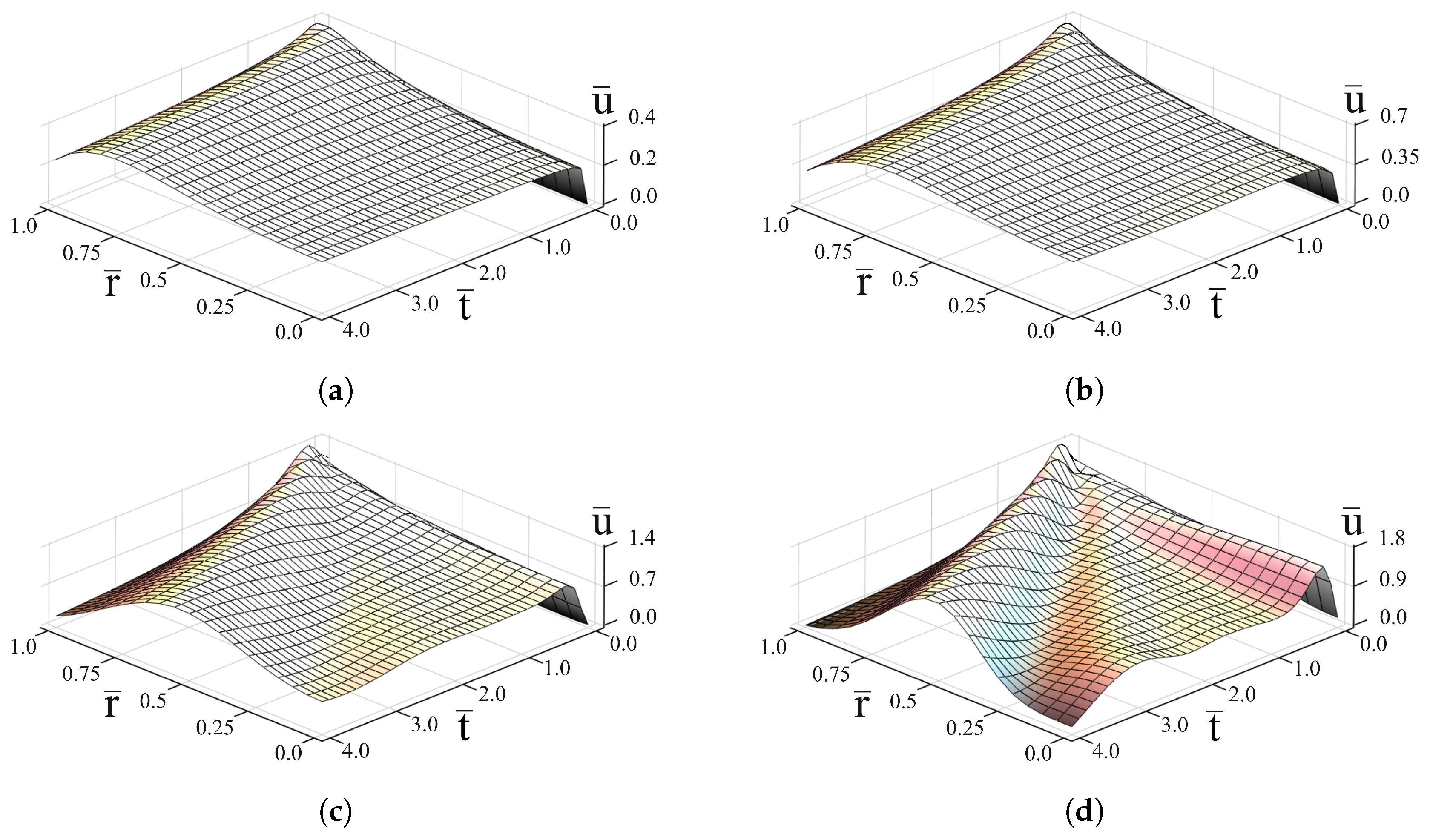
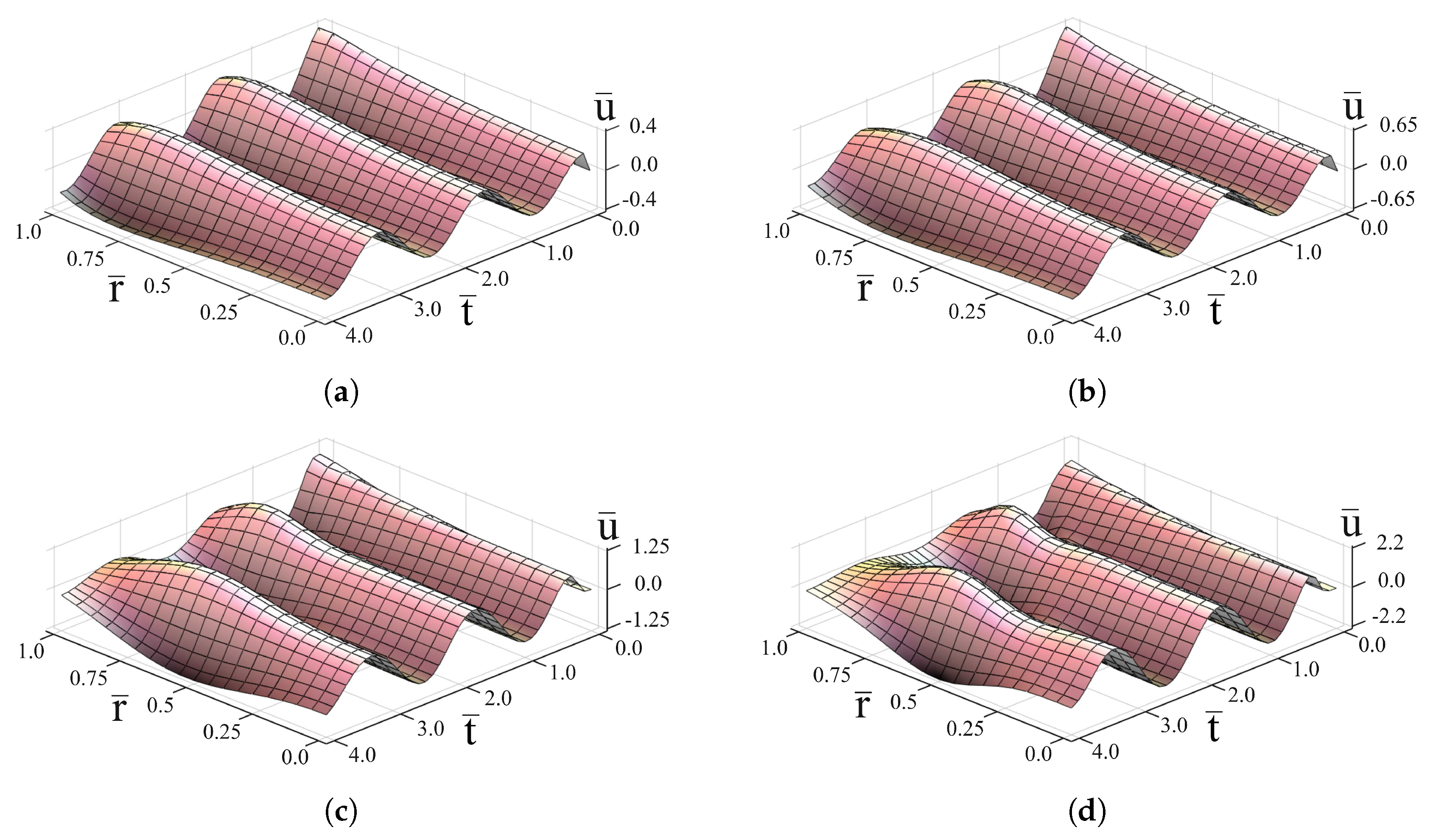
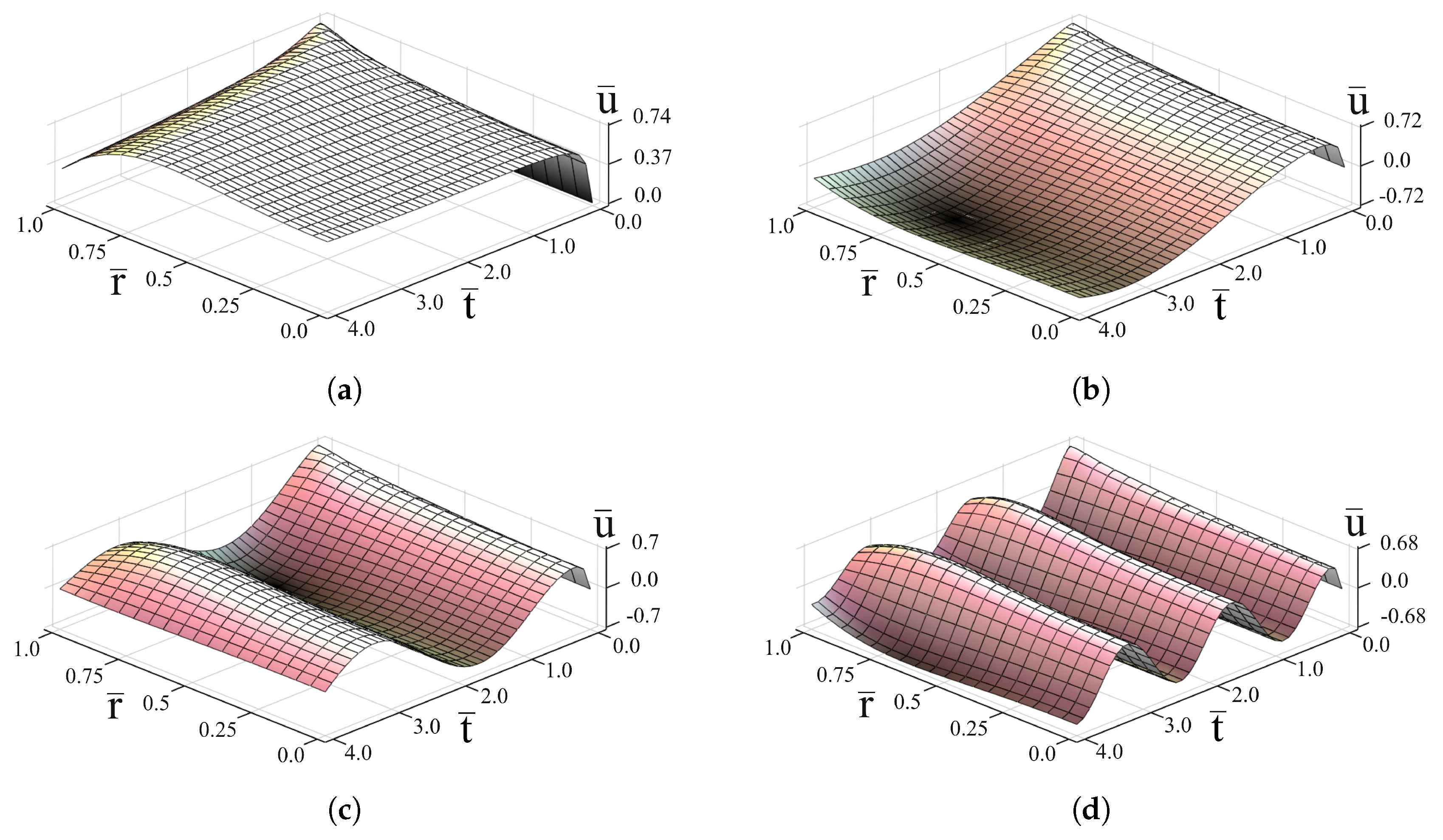
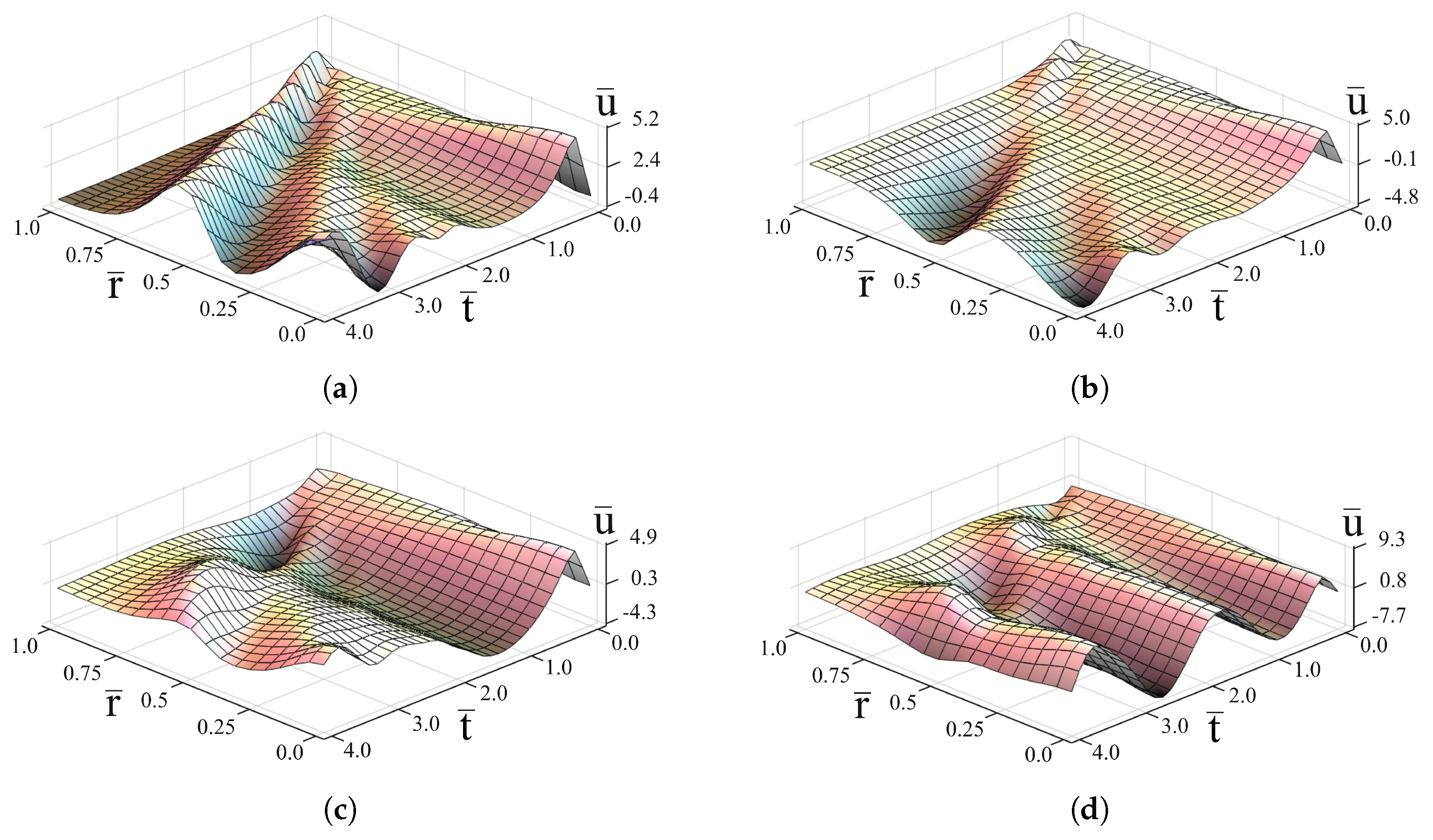
3. Analysis of the Quasi-Steady-State Oscillations
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef] [PubMed]
- Gafiychuk, V.V.; Lubashevsky, I.A.; Datsko, B.Y. Fast heat propagation in living tissue caused by branching artery network. Phys. Rev. E 2005, 72, 051920. [Google Scholar] [CrossRef]
- Datsko, B.Y.; Gafiychuk, V.V.; Lubashevsky, I.A.; Priezzhev, A.V. Self-localization of laser-induced tumor coagulation limited by heat diffusion through active tissue. J. Med. Eng. Technol. 2006, 30, 390–396. [Google Scholar] [CrossRef]
- Polyanin, A.D. Handbook of Linear Partial Differential Equations for Engineers and Scientists; Chapman & Hall/CRC: Boca Raton, FL, USA, 2002. [Google Scholar]
- Gravel, P.; Gauthier, C. Classical applications of the Klein-Gordon equation. Am. J. Phys. 2011, 79, 447–453. [Google Scholar] [CrossRef]
- Wazwaz, A.-M. Partial Differential Equations and Solitary Waves Theory; Higher Education Press: Beijing, China; Springer: Berlin, Germany, 2009. [Google Scholar]
- Abuteen, A.; Freihat, A.; Al-Smadi, M.; Khalil, H.; Khan, R.A. Approximate series solution of nonlinear, fractional Klein-Gordon equations using fractional reduced differential transform method. J. Math. Stat. 2016, 12, 23–33. [Google Scholar] [CrossRef]
- Damor, R.S.; Kumar, S.; Shukla, A.K. Solution of fractional bioheat equation in terms of Fox’s H-Function. SpringerPlus 2016, 5, 1–10. [Google Scholar] [CrossRef]
- Ferrás, L.L.; Ford, N.J.; Morgado, M.L.; Nóbrega, J.M.; Rebelo, M.S. Fractional Pennes’ bioheat equation: theoretical and numerical studies. Fract. Calc. Appl. Anal. 2015, 18, 1080–1106. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Golmankhaneh, A.K.; Baleanu, D. On nolinear fractional Klein-Gordon equation. Signal Process. 2011, 91, 446–451. [Google Scholar] [CrossRef]
- Kheiri, H.; Shahi, S.; Mojaver, A. Analytical solutions for the fractional Klein-Gordon equation. Comput. Meth. Diff. Equ. 2014, 2, 99–114. [Google Scholar]
- Qin, Y.; Wu, K. Numerical solution of fractional bioheat equation by quadratic spline collocation method. J. Nonlinear Sci. Appl. 2016, 9, 5061–5072. [Google Scholar] [CrossRef]
- Vitali, S.; Castellani, G.; Mainardi, F. Time fractional cable equation and applications in neurophysiology. Chaos Solitons Fractals 2017, 102, 467–472. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F. Fractional calculus: Integral and differential equations of fractional order. In Fractals and Fractional Calculus in Continuum Mechanics; Springer: Wien, Austria, 1997; pp. 223–276. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Povstenko, Y. Fractional heat conduction equation and associated thermal stresses. J. Therm. Stress. 2005, 28, 83–102. [Google Scholar] [CrossRef]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House Publishers, Inc.: Redding, CA, USA, 2006. [Google Scholar]
- Gafiychuk, V.V.; Datsko, B.Y. Spatiotemporal pattern formation in fractional reaction-diffusion systems with indices of different order. Phys. Rev. E 2008, 77, 066210. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; Imperial College Press: London, UK, 2010. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Datsko, B.; Luchko, Y.; Gafiychuk, V. Pattern formation in fractional reaction-diffusion systems with multiple homogeneous states. Int. J. Bifurcat. Chaos 2012, 22, 1250087. [Google Scholar] [CrossRef]
- Datsko, B.; Gafiychuk, V. Complex nonlinear dynamics in subdiffusive activator-inhibitor systems. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1673–1680. [Google Scholar] [CrossRef]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Springer: Berlin, Germany, 2013. [Google Scholar]
- Atanacković, T.M.; Pilipović, S.; Stanković, B.; Zorica, D. Fractional Calculus with Applications in Mechanics: Vibrations and Diffusion Processes; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists, 2nd ed.; World Scientific: Singapore, 2014. [Google Scholar]
- Povstenko, Y. Fractional Thermoelasticity; Springer: New York, NY, USA, 2015. [Google Scholar]
- Datsko, B.; Gafiychuk, V.; Podlubny, I. Solitary travelling auto-waves in fractional reaction–diffusion systems. Commun. Nonlinear Sci. Numer. Simul. 2015, 23, 378–387. [Google Scholar] [CrossRef]
- Anderson, J.; Moradi, S.; Rafiq, T. Non-linear Langevin and fractional Fokker-Planck equations for anomalous diffusion by Lévy stable processes. Entropy 2018, 20, 760. [Google Scholar] [CrossRef]
- Weiss, M.; Nilsson, T. In a mirror dimly: Tracing the movements of molecules in living cells. Trends Cell Biol. 2004, 14, 267–273. [Google Scholar] [CrossRef]
- Zelenyi, L.M.; Milovanov, A.V. Fractal topology and strange kinetics: From percolation theory to problems in cosmic electrodynamics. Phys. Uspekhi 2004, 47, 809–852. [Google Scholar] [CrossRef]
- Gafiychuk, V.; Datsko, B. Different types of instabilities and complex dynamics in reaction-diffusion systems with fractional derivatives. J. Comp. Nonlinear Dyn. 2012, 7, 031001. [Google Scholar] [CrossRef]
- Datsko, B.; Gafiychuk, V. Complex spatio-temporal solutions in fractional reaction-diffusion systems near a bifurcation point. Fract. Calc. Appl. Anal. 2018, 21, 237–253. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Mandelis, A. Diffusion waves and their uses. Phys. Today 2000, 53, 29–33. [Google Scholar] [CrossRef]
- Mandelis, A. Diffusion-Wave Fields: Mathematical Methods and Green Functions; Springer: New York, NY, USA, 2001. [Google Scholar]
- Vrentas, J.S.; Vrentas, C.M. Diffusion and Mass Transfer; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Lakhssassi, A.; Kengne, E.; Semmaoui, H. Modifed Pennes’ equation modelling bio-heat transfer in living tissues: analytical and numerical analysis. Natl. Sci. 2010, 2, 1375–1385. [Google Scholar] [CrossRef]
- Kengne, E.; Lakhssassi, A.; Vaillancourt, R. Temperature distributions for regional hypothermia based on nonlinear bioheat equation of Pennes type: Dermis and subcutaneous tissues. Appl. Math. 2012, 3, 217–224. [Google Scholar] [CrossRef]
- Fasano, A.; Sequeira, A. Hemomath. The Mathematics of Blood; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Malinen, M.; Huttunen, T.; Kaipio, J.P. Thermal dose optimization method for ultrasound surgery. Phys. Med. Biol. 2003, 48, 745–762. [Google Scholar] [CrossRef]
- Povstenko, Y. Fractional heat conduction in a space with a source varying harmonically in time and associated thermal stresses. J. Therm. Stress. 2016, 39, 1442–1450. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables; Dover: New York, NY, USA, 1972. [Google Scholar]
- Povstenko, Y.; Kyrylych, T. Time-fractional diffusion with mass absorption under harmonic impact. Fract. Calc. Appl. Anal. 2018, 21, 118–133. [Google Scholar] [CrossRef]
- Povstenko, Y.; Kyrylych, T. Time-fractional diffusion with mass absorption in a half-line domain due to boundary value of concentration varying harmonically in time. Entropy 2018, 19, 346. [Google Scholar] [CrossRef]
- Povstenko, Y. Linear Fractional Diffusion-Wave Equation for Scientists and Engineers; Birkhäuser: New York, NY, USA, 2015. [Google Scholar]
- Gorenflo, R.; Loutchko, J.; Luchko, Y. Computation of the Mittag-Leffler function and its derivatives. Fract. Calc. Appl. Anal. 2002, 5, 491–518. [Google Scholar]
- Podlubny, I. Mittag-Leffler Function; Calculates the Mittag-Leffler Function with Desired Accuracy, MATLAB Central File Exchange, File ID 8738. Available online: www.mathworks.com/matlabcentral/fileexchange/8738 (accessed on 17 April 2019).
- Erdélyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F. Tables of Integral Transforms; McGraw-Hill: New York, NY, USA, 1954; Volume 1. [Google Scholar]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series, Volume 1: Elementary Functions; Gordon and Breach Science Publishers: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Magnus, W.; Oberhettinger, F. Formeln und Sätze für die Speziellen Funkttionen der Mathematischen Physik, 2nd ed.; Springer: Berlin, Germany, 1948. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Datsko, B.; Podlubny, I.; Povstenko, Y. Time-Fractional Diffusion-Wave Equation with Mass Absorption in a Sphere under Harmonic Impact. Mathematics 2019, 7, 433. https://doi.org/10.3390/math7050433
Datsko B, Podlubny I, Povstenko Y. Time-Fractional Diffusion-Wave Equation with Mass Absorption in a Sphere under Harmonic Impact. Mathematics. 2019; 7(5):433. https://doi.org/10.3390/math7050433
Chicago/Turabian StyleDatsko, Bohdan, Igor Podlubny, and Yuriy Povstenko. 2019. "Time-Fractional Diffusion-Wave Equation with Mass Absorption in a Sphere under Harmonic Impact" Mathematics 7, no. 5: 433. https://doi.org/10.3390/math7050433
APA StyleDatsko, B., Podlubny, I., & Povstenko, Y. (2019). Time-Fractional Diffusion-Wave Equation with Mass Absorption in a Sphere under Harmonic Impact. Mathematics, 7(5), 433. https://doi.org/10.3390/math7050433