3. -Fuzzy Filters for
In this section, we define -fuzzy filters of hoops for , and we investigate some of their properties. Furthermore, we define a congruence relation on hoops by these filters and prove that the corresponding quotients are a bounded hoop.
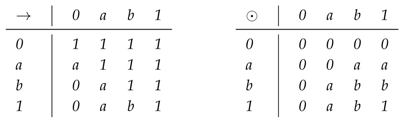
Definition 1. Let . Let λ be a fuzzy set of H. Then, λ is called an -fuzzy filter of H if the following assertions are valid. Example 1. On the set , we define two operations ⊙ and → on H by:Then, (H, ⊙, →, 1) is a hoop. Define the fuzzy set λ in H by , , and . Then, λ is an -fuzzy filter of H, and it is clear that λ is an -fuzzy filter of H. Theorem 1. A fuzzy set λ in H is an -fuzzy filter of H if and only if the following conditions hold: Proof. Let
be an
-fuzzy filter of
H and
such that
. Since
is an
-fuzzy filter of
H, by Definition 1,
. Therefore,
. Now, let
. If
and
, then
and
. Since
is an
-fuzzy filter of
H, we have
, so:
Conversely, suppose
and
. If
, then
. Since
, we have
, and so,
. Furthermore, if
and
, then by assumption,
Hence,
. Therefore,
is an
-fuzzy filter of
H. □
Proposition 2. If λ is an -fuzzy filter of H, then the following statement holds. Proof. Let
such that
. Therefore, it is clear that
. Since
is an
-fuzzy filter of
H, by Theorem 1,
and
, for any
. Then:
Hence,
. □
Theorem 2. A fuzzy set λ in H is an -fuzzy sub-hoop of H such that, for any , . Then, for any , the following statements are equivalent:
λ is an -fuzzy filter of H,
if and , then ,
if and , then .
Proof. Let
be an
-fuzzy filter of
H such that
and
. Then,
and
. By Proposition 1(vii),
. Then, by Proposition 2,
Since
, we have
. Thus, by (i),
Hence,
.
Theorem 3. Let λ be an -fuzzy filter of H, , and . Define:Then, is a congruence relation on H. Proof. It is clear that
is reflexive and symmetric. Now, we prove that
is transitive. For this, suppose
and
. Then, there exists
such that
, and also,
. By Proposition 1(vii),
, and by Proposition 2, we have:
Hence,
. In a similar way, we get that:
Hence,
. Therefore,
. Suppose that
. We show that
, for any
. Since
, for any
, we have
. Since
,
. By Proposition 1(viii),
, and so,
. Since
is an
-fuzzy filter of
H, by Proposition 2, we have:
Hence,
. In a similar way, since
, we get
. By Proposition 1(viii),
, and so,
. Since
is an
-fuzzy filter of
H, by Proposition 2, we have:
Hence,
. Therefore,
. Finally, suppose that
; we show that
, for any
. Since
, for any
, we have
. By Proposition 1(vii) and Proposition 2,
and:
Hence,
. It is easy to see that
. Therefore,
is a congruence relation on
H. □
Theorem 4. Let , and operations ⊗ and ⇝ on are defined as follows:Then, is a hoop. Proof. We have and if and only if and . Since is the congruence relation on H, then all above operations are well-defined. Thus, by routine calculation, we can see that is a hoop. □
Now, we define a relation on
by:
It is easy to see that
is a poset.
Note: According to the definition of the congruence relation, it is clear that:
Therefore, as we define a relation on quotient,
if and only if
, it is similar to writing
if and only if
.
Theorem 5. If λ is a non-zero -fuzzy filter of H, then the set:is a filter of H. Proof. Let . Since , we conclude that there exists such that . Moreover, from being an -fuzzy filter of H, by Definition 1, , then . Hence, , and so, . Now, suppose that . Then, there exist , such that and , and so, and . Thus, by Definition 1, , and so, . Hence, . Therefore, is a filter of H. □
Proposition 3. If λ is a non-zero -fuzzy filter of H, then .
Proof. Let . Since is an -fuzzy filter of H, by Theorem 1, for any , . Hence, for any , , and so, is a zero -fuzzy filter of H, which is a contradiction. Therefore, . □
Theorem 6. For any filter F of H and , there exists an -fuzzy filter λ of H such that its ∈-level set is equal to F.
Proof. Let and be defined by , for any , and , otherwise. By this definition, it is clear that . Therefore, it is enough to prove that is an -fuzzy filter of H. Let . Then, or . Since F is a filter of H and , we have , for any . Now, suppose that and . We consider the following cases:
Case 1: If and , then . Since F is a filter of H, we have , and so, . Hence, . Therefore, is an -fuzzy filter of H.
Case 2: If
and
, then it is clear that:
Hence,
. Therefore,
is an
-fuzzy filter of
H.
Case 3: If
and
, then it is clear that:
Hence,
. Therefore,
is an
-fuzzy filter of
H.
Therefore, in all cases, is an -fuzzy filter of H and . □
For any fuzzy set
in
H and
, we define three sets that are called the
∈-level set,
q-set, and
-set, respectively, as follows.
Theorem 7. Given a fuzzy set λ in H, the following statements are equivalent.
- (i)
The nonempty ∈-level set of λ is a filter of H, for all .
- (ii)
λ satisfies the following assertions.
Proof. Let
and
such that
. Then,
. Since
is a filter of
H,
. Thus,
. Moreover, since
, we have
. Hence,
. Now, suppose
and
such that
and
. Then,
. Since
is a filter of
H, we have
. Thus,
. From
, we conclude that,
Hence,
Conversely, let
. Then,
. Since
, by assumption:
Thus,
, so
. Now, suppose that
, for any
and
. Then,
and
. By assumption,
Since
, we have
, so
. Hence,
is a filter of
H. □
It is clear that every -fuzzy filter of H is an -fuzzy filter of H. However, the converse may not be true, in general.
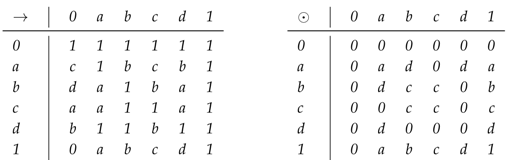
Example 2. On the set , we define two operations ⊙ and → as follows:By routine calculations, it is clear that is a bounded hoop. Define a fuzzy set λ in H as follows:It is easy to see that λ is an -fuzzy filter of hoop H, but it is not an -fuzzy filter of H; because:However, it is not an -fuzzy filter of H. Now, we investigate under which conditions any -fuzzy filter is an -fuzzy filter.
Theorem 8. If an -fuzzy filter λ of H satisfies the condition:then λ is an -fuzzy filter of H. Proof. Let , for any and . Since is an -fuzzy filter of H, by Definition 1, or . If , then the proof is clear. If , then . Since , , then . Hence, . Now, suppose that and . From is an -fuzzy filter of H, by Definition 1, or . If , then the proof is complete. However, if , then , and so, . Since , we have , and so, . Then, . Therefore, is an -fuzzy filter of H. □
Theorem 9. If λ is an -fuzzy filter of H, then the q-set is a filter of H, for all .
Proof. Let , for any and . Then, , and so, . Since is an -fuzzy filter of H, by Definition 1, we have or . If , then it is clear that . Since , we have , and so, . If , then , and so, . Thus, in both cases, . Now, suppose that , for any and . Then, and , and so, and . Since is an -fuzzy filter of H, by Definition 1, we have or . If , then , and so, . If , then , and so, . Since , we have . Hence, in both cases, . Therefore, is a filter of H, for any . □
Theorem 10. A fuzzy set λ in H is an -fuzzy filter of H if and only if the following assertion is valid. Proof. Let
, for any
and
. Since
is an
-fuzzy filter of
H, we have
or
. It means that
or
. Therefore,
. In a similar way, if
and
, for any
and
, since
is an
-fuzzy filter of
H, then we have
or
. This means that
or
. Therefore,
. Conversely, let
, for any
and
. Then, by assumption, we have
. If
, then
, and so,
. If
, then
, and so,
; thus,
. Hence,
. Now, suppose that
and
, for any
and
. Then, by assumption, we have
. If
, then:
Hence,
. If
, then:
Therefore,
. Thus,
. Hence,
. Therefore,
is an
-fuzzy filter of
H. □
Theorem 11. A fuzzy set λ in H is an -fuzzy filter of H if and only if the non-empty ∈-level set of λ is a filter of H, for all .
Proof. Let be an -fuzzy filter of H and , for any . Then, , and so, . Since is an -fuzzy filter of H, or . If , then it is clear that , and if , then . Since , , so . Thus, . Now, suppose that , then and , and so, and . Since is an -fuzzy filter of H, or . If , then it is clear that , and if , then . Since , , so . Thus, . Therefore, is a filter of H, for any .
Conversely, suppose is a filter of H and , for any and . Then, , so . Since is a filter of H, , so . Hence, , and so, . Now, let and , for any and . Then, and , and so, . Since is a filter of H, , and so, . Hence, . Therefore, . Therefore, is an -fuzzy filter of H, for any . □
Theorem 12. A fuzzy set λ in H is an -fuzzy filter of H if and only if the following assertion is valid. Proof. Assume that is an -fuzzy filter of H and . Then, by Theorem 11, is a filter of H, for any . If and , then . Thus, . If , it is clear that . Now, suppose . If and , then . Since is a filter of H, . Thus, , for . If , then .
Conversely, let
be a fuzzy set in
H that satisfies the condition (12). Since
for all
, we have
for all
. Since
for all
, we get:
for all
. It follows from Theorem 10 that
is an
-fuzzy filter of
H. □
Theorem 13. A fuzzy set λ in H is an -fuzzy filter of H if and only if is a filter of H, for all (we call an -level filter of λ).
Proof. Let be an -fuzzy filter of H and , for any and . Then, or . This means that or . Since is an -fuzzy filter of H, we have, if , then or . Furthermore, if , then or ; this means that or . Hence, in both cases, , and so, . In a similar way, let , for and . Then, or or and . Therefore, we have the following cases:
Case 1: if , then and . Since is an -fuzzy filter of H, or . Therefore, .
Case 2: if , then and . Since is an -fuzzy filter of H, or . It is equivalent to or , respectively. Therefore, .
Case 3: if and , then and . Since is an -fuzzy filter of H, , and so, it is equal to or . Thus, in both cases, .
Therefore, is a filter of H.
Conversely, let , for any and . Since is a filter of H, . Then, . Now, suppose that and , for any and . Then, it is clear that . Since is a filter of H, . Therefore, or . Hence, . Therefore, is an -fuzzy filter of H. □
Theorem 14. Let be a homomorphism of hoops. If λ and μ are -fuzzy filters of H and K, respectively, then:
- (i)
is an -fuzzy filter of H.
- (ii)
If f is onto and λ satisfies the condition:then is an -fuzzy filter of K.
Proof. Let , for any and . Then, . Since is an -fuzzy filter of H, we have . Thus, . Now, suppose and , for any and . Then, and . Since is an -fuzzy filter of H, we have . Hence, . Therefore, is an -fuzzy filter of H.
Let and be such that . Then, . By assumption, there exists such that . Then, . Since is an -fuzzy filter of H, we have . Now, , so , then or . Thus, . In a similar way, let and be such that and . Then, and . By assumption, there exist and such that and . Then, and . Since is an -fuzzy filter of H, we have . Now, , so , then or . Thus, . □
Theorem 15. Let λ be an -fuzzy filter of H such that:Then, there exist two -fuzzy filters μ and ν of H such that: - (i)
.
- (ii)
and have at least two elements.
- (iii)
μ and ν do not have the same family of -level filters.
Proof. Let
where
and
. Then, the chain of
-level filters of
is:
Define two fuzzy sets
and
in
H by:
and:
respectively, where
. Then,
and
are
-fuzzy filters of
H, and
and
. The chains of
-level filters of
and
are given by:
respectively. It is clear that
. This completes the proof.
□