Abstract
It is well-known that mathematical models are the basis for system analysis and controller design. This paper considers the parameter identification problems of stochastic systems by the controlled autoregressive model. A gradient-based iterative algorithm is derived from observation data by using the gradient search. By using the multi-innovation identification theory, we propose a multi-innovation gradient-based iterative algorithm to improve the performance of the algorithm. Finally, a numerical simulation example is given to demonstrate the effectiveness of the proposed algorithms.
1. Introduction
Parameter estimation deals with the problem of building mathematical models of systems [1,2,3,4,5] based on observation data [6,7,8] and is the basis for system identification [9,10,11]. It has widespread applications in many areas [12,13,14,15,16]. For instance, system identification is used to get the appropriate models for control system designs [17,18], simulations and predictions [19,20] in control and system modelling [21,22]. Recently, Bottegal et al. proposed a two-experiment method to identify Wiener systems by using the data acquired from two separate experiments, in which the first experiment estimates the static nonlinearity and the second experiment identifies the linear block based on the estimated nonlinearity [23]. For nonlinear errors-in-variables systems contaminated with outliers, a robust identification approach is presented by means of the expectation maximization under the framework of the maximum likelihood estimation [24,25].
The recursive identification and the iterative identification are two important types of parameter estimation methods [26,27]. In recursive identification methods, the parameter estimates can be computed recursively in real-time [28,29]. Differing from the recursive methods, the basic idea of the iterative methods is to update the parameter estimates by using batch data [30,31,32]. In recent years, a number of iterative identification methods have been proposed for all kinds of systems. A data filtering-based iterative estimation algorithm is studied for an infinite impulse response filter with colored noise [33]. For Box-Jenkins models, Liu et al. proposed a least squares-based iterative algorithm according to the auxiliary model identification idea and the iterative search [34]. Other related work includes the recursive algorithms [35,36] and the iterative algorithms [37,38,39].
The multi-innovation theory provides a new idea for system identification [40,41]. The innovation is the useful information that can improve the parameter estimation accuracy. The basic idea of the multi-innovation theory is to expand the dimension of the innovation and to enhance the data utilization. A brief review of the multi-innovation algorithms is listed as follows. An adaptive filtering based multi-innovation stochastic gradient algorithm was derived for bilinear systems with colored noise and can give small parameter estimation errors as the innovation length increases [42]. A multi-innovation gradient algorithm was developed based on the Kalman filtering to solve the joint state and parameter estimation problem for a nonlinear state space system with time-delay [43].
Identification is to fit a closest model of a practical system from observation data. The commonly used techniques are some optimization methods. These methods include linear programming and convex mixed integer nonlinear programs [44]. Some related optimization algorithms and solvers have been proposed for complete global optimization problems [45], such as the general algebraic modeling system (GAMS) and mixed-integer nonlinear programming (MINLP) solver [46] and the mixed-integer linear programming (MILP) and MINLP approaches for solving nonlinear discrete transportation problem [47]. This paper focuses on the parameter identification problems of controlled autoregressive systems by using the gradient search [48] and the multi-innovation identification theory [49]. The basic idea is to use the iterative technique for computing the parameter estimation through defining and minimizing two quadratic criterion functions. The main contributions of this paper are as follows.
- Based on the gradient search, a gradient-based iterative algorithm is presented for identifying the parameters of controlled autoregressive systems.
- A multi-innovation gradient-based iterative algorithm is derived for improving the performance of the algorithm by using the multi-innovation identification theory.
The outlines of this paper are organized as follows. Section 2 defines some definitions and derives the identification model of controlled autoregressive systems. Section 3 derives a gradient-based iterative algorithm. Section 4 proposes a multi-innovation gradient-based iterative algorithm. Section 5 offers an example to illustrate the effectiveness of the proposed algorithms. Finally, Section 6 gives some concluding remarks.
2. The System Description
Let us introduce some symbols used in this paper. The symbol denotes an identity matrix of appropriate size (); stands for an n-dimensional column vector whose elements are 1; the superscript T stands for the vector/matrix transpose; the norm of a matrix (or a column vector) is defined by .
Consider the dynamic stochastic systems described by the following controlled autoregressive (CAR) model:
where is the input sequence of the system and is the output sequence of the system, is a white noise sequence with zero mean, and are polynomials in the unit backward shift operator [, ], and defined as
Assume that and are known, and , and for .
Let , define the parameter vectors:
and the corresponding information vectors:
Through the above definitions, the system in Equation (1) can be rewritten as
This identification model for System in (1) involves two different parameter vectors and , which are merged to a new vector , and two different information vectors and , which are merged to a new vector composed of available input-output data and . The objective of this paper is by means of the gradient search and based on the multi-innovation identification theory to derive new identification algorithms for estimating the system parameter vectors from available data .
3. The Gradient-Based Iterative Algorithm
In this section, we first define a criterion function and present a gradient-based iterative algorithm by using the gradient search. In addition, a brief discussion about the choice of the iterative step-size is given in this section.
Let be an iterative variable and be the iterative estimate of at iteration k. is the largest eigenvalue of the symmetric matrix .
The observation data are basic for parameter identification algorithms. This paper uses a batch of data with the length L and is based on Model (2), we define the stacked output data vector and the stacked data matrix as
Define a static criterion function
which can be equivalently expressed as
By means of the negative gradient search, computing the partial derivative of with respect to , we can obtain the iterative relation:
where is an iterative step-size or a convergence factor. The above equation can be seen as a discrete-time system. To ensure the convergence of , all the eigenvalues of matrix must be in the unit circle, that is to say should satisfy , or , so a conservative choice of is
In order to avoid computing the complicated eigenvalues of a square matrix and to reduce computational cost, we use the trace of the matrix and take another way for selecting the step-size
Then we can obtain the gradient-based iterative (GI) algorithm for estimating the parameter vector of the CAR system in (1) [4]:
The steps of computing involved in the GI algorithm in Equations (3)–(9) are summarized in the following. The pseudo-code of implementing the gradient-based iterative algorithm is shown in Algorithm 1.
- For , all the variables are set to zero. Let , give the data length L () and set the initial values: , , and the parameter estimation accuracy .
- Collect the input and output data and , , 2, ⋯, L.
- Form the information vectors , and using Equations (8)–(9) and (7).
- Construct the stacked output vector by Equation (5) and the stacked information matrix by Equation (6), select a large according to Equation (4).
- Update the parameter vector estimate using Equation (3).
- Compare with : If , increase k by 1 and go to step 5; otherwise, obtain the iteration k and the parameter estimation vector .
| Algorithm 1 The pseudo-code of implementing the gradient-based iterative algorithm. |
|
The flowchart of computing in the GI algorithm is shown in Figure 1.
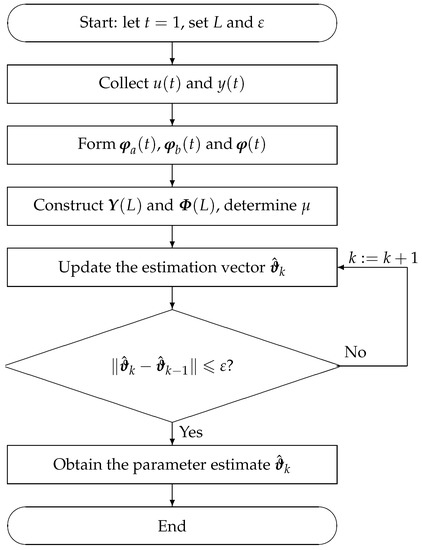
Figure 1.
The flowchart of the gradient-based iterative (GI) algorithm.
Remark 1.
The criterion function is quadratic and and a convex optimization problem. For a static optimization problem, a constant step-size is often used for simplification in parameter estimation algorithms.
Remark 2.

The computation is an important property of an algorithm, and is represented by the floating-point operation of multiplications/divisions and additions/subtractions (the flop for short). Table 1 gives the computational efficiency of the GI algorithm.

Table 1.
The computational efficiency of the gradient-based iterative (GI) algorithm.
Remark 3.
The gradient algorithm can be used to find the optimal solution for quadratic optimization problems and nonlinear optimization problems. It can handle not only the linear regression systems with the known information vector, but also the linear and nonlinear systems with the unknown information vector. However, Under the same data length L, the estimation accuracy of the GI algorithm becomes high as the iterative index k increases, and when the data length L increases, the estimation accuracy also becomes high. Thus, we choose a sufficient large data length in practice
Remark 4.
If we choose the step-size as and eliminate the intermediate variables and , the GI algorithm can be equivalently transformed into
In order to improve the performance of the GI algorithm, we introduce a forgetting factor and obtain the forgetting factor GI algorithm:
4. The Multi-Innovation Gradient-Based Iterative Algorithm
The multi-innovation identification algorithm uses the data in a moving data window to update the parameter estimates. The moving data window, which is also called the dynamical data window, moves along with t. The length of the moving data window can be variable or invariable. In this section, we derive a multi-innovation gradient-based iterative algorithm with the constant window length.
Consider the newest p data from to (p represents the data length, i.e., the length of the moving data window), and define the stacked output vector and the stacked information matrix as
According to the identification model in (2), define a dynamic data window criterion function:
Using the negative gradient search to minimize , we can obtain the following iterative relation:
where is the step-size of the time t at iteration k. Similarly, in order to guarantee the convergence of the parameter estimation vector , can be conservatively chosen as
In consideration of the computational cost of the eigenvalue calculation, by using the norm is to take as
Equations (12)–(15) and (7)–(9) form the multi-innovation gradient-based iterative (MIGI) algorithm for estimating the parameter vector [4]:
The identification steps of the MIGI algorithm in Equations (16)–(22) for computing are listed as follows.
- For , all the variables are set to zero. Let , give the data length p () and set the initial values: , , the maximum iteration and the accuracy .
- Let , collect the input and output data and .
- Form the information vectors , and using Equations (21)–(22) and (20).
- Construct the stacked output vector by Equation (18) and the stacked information matrix by Equation (19), select a large according to Equation (17).
- Update the parameter vector estimate using Equation (16).
- If , increase k by 1 and go to Step 5; otherwise, proceed with the next step.
- Compare with : If , set and increase k by 1 and go to step 2; otherwise, obtain the parameter estimation vector .
The flowchart of computing computing the parameter estimation vector is shown in Figure 2.
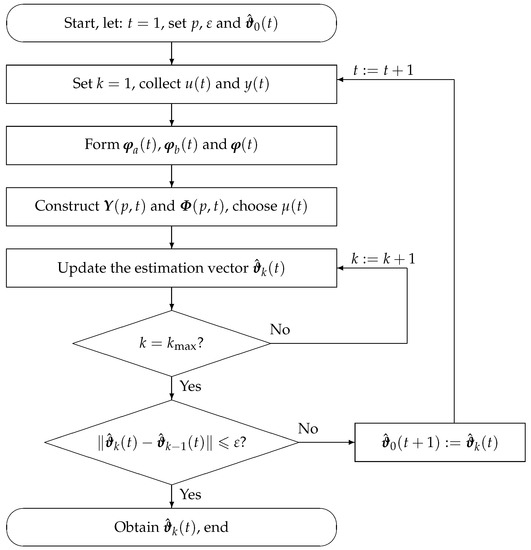
Figure 2.
The flowchart of the multi-innovation gradient-based iterative (MIGI) algorithm.
Remark 5.
The multi-innovation gradient identification method can improve the parameter estimation accuracy by expanding the dimension of the innovation and making full use of the system information. The MIGI algorithm in Equations (16)–(22) can be seen as an application of the multi-innovation theory in the iterative identification. In particular, we use the newest p data from to to do the iterative estimation. When , move the data window forward to the next moment, introduce new observation data and eliminate the oldest data to keep p data in the data window. The MISG algorithm enhances the utilization of data and improves the parameter estimation accuracy.
Remark 6.
When take , the MIGI algorithm reduces to the GI algorithm. That is the MIGI algorithm is the extension of the GI algorithm, or the GI algorithm is the special case of the MIGI algorithm.
Furthermore, the proposed approaches in the paper can combine other mathematical tools [50,51,52] and statistical strategies [53,54,55,56,57,58,59,60] to study the parameter estimation problems of linear and nonlinear systems with different disturbance noises [61,62,63,64], and can be applied to other literature [65,66,67,68] such as signal processing [69,70,71,72,73,74] and neural networks [75,76,77].
5. Example
In industrial processes, some control task can be simplified into a water tank control plant, as is shown in Figure 3 [78].
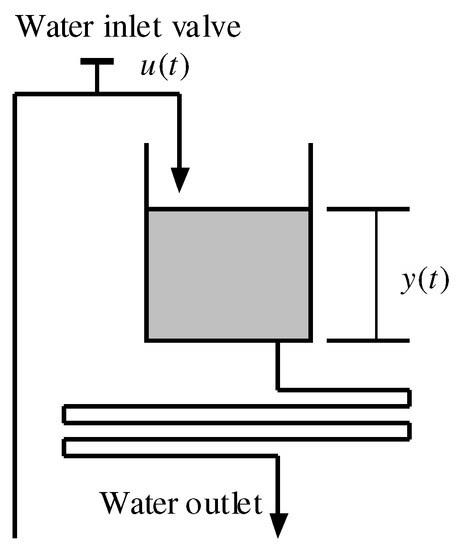
Figure 3.
A water tank plant.
In this system, the manipulated variable is the position of the inlet water valve, denoted ; the measured variable is the water level in the tank, denoted . For a two-level water tank plant, it can be described by a second-order controlled autoregressive system, we assume that its mathematical model is given by
The parameter vector to be identified is given by
In simulation, the input is taken as an uncorrelated uniform distribution random signal sequence with zero mean and unit variance, is taken as a normal distribution white noise sequence with zero mean and variance . Using the simulation model parameters and the input signal generates the output signal .
Taking the noise variances , and , respectively, the corresponding noise-to-signal ratios were , , and . Setting the data length , the convergence factor , applying the GI algorithm and the input-output data to estimate the parameters of this example system, the GI parameter estimates and errors versus with different noise variances are shown in Table 2, Table 3 and Table 4, the GI estimation errors versus k are shown in Figure 4 with , and , and the GI estimates of the parameters , , and versus k are shown in Figure 5 for .

Table 2.
The GI estimates and their errors with .

Table 3.
The GI estimates and their errors with .

Table 4.
The GI estimates and their errors with .
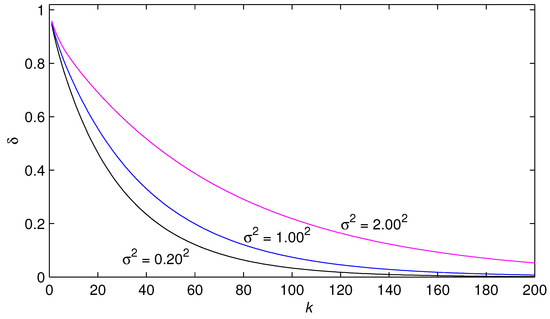
Figure 4.
The GI estimation errors versus k with , and .
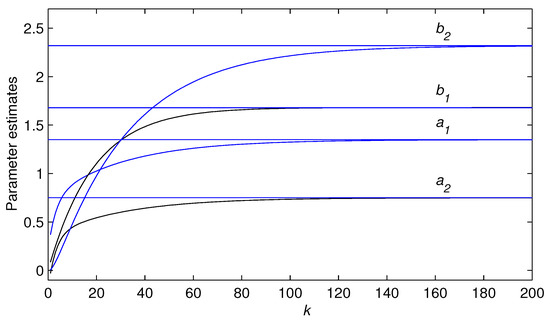
Figure 5.
The GI estimates versus k with .
- The GI parameter estimates approach to their true values for sufficiently large data length as the iteration k increases—see Figure 5.
6. Conclusions
Modeling a dynamical system is the first step for system analysis and design in control engineering. Through defining and minimizing a quadratic criterion function by using observation data, this paper studies and derives a gradient-based iterative algorithm for stochastic systems described by the controlled autoregressive model based on the gradient search. Furthermore, in order to track time-varying parameters, a multi-innovation gradient-based iterative algorithm has been proposed by means of the multi-innovation identification theory. The proposed algorithms have the following advantages.
- For a lower noise level, the gradient-based algorithm can give more accurate parameter estimates. The parameter estimation errors become smaller as the iterative index increases.
- The gradient-based iterative parameter estimates approach their true values for sufficiently large data length and iterative index.
- The multi-innovation gradient-based iterative algorithm can track time-varying parameters of dynamical systems, improving the performance of the algorithms.
- The simulation results indicate that the proposed algorithms are effective for estimating the parameters of stochastic systems.
- The proposed methods in this paper can be extended to model industrial processes and network systems [79,80,81,82,83,84] by means of some other mathematical tools and approaches [85,86,87,88,89,90].
Author Contributions
Conceptualization and methodology, F.D.; software, J.P. and F.D.; validation and analysis, A.A. and T.H.
Funding
This work was supported by the National Natural Science Foundation of China (No. 61873111) and the 111 Project (B12018).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ding, F. System Identification—New Theory and Methods; Science Press: Beijing, China, 2013; Available online: http://www.bookask.com/book/631454.html (accessed on 5 April 2019). (In Chinese)
- Ding, F. System Identification—Performances Analysis for Identification Methods; Science Press: Beijing, China, 2014; Available online: http://product.dangdang.com/23511899.html?ddclick_reco_product_alsobuy (accessed on 5 April 2019). (In Chinese)
- Ding, F. System Identification—Auxiliary Model Identification Idea and Methods; Science Press: Beijing, China, 2017; Available online: http://www.zxhsd.com/kgsm/ts/2017/07/07/3878821.shtml (accessed on 5 April 2019). (In Chinese)
- Ding, F. System Identification—Iterative Search Principle and Identification Methods; Science Press: Beijing, China, 2018; Available online: https://item.jd.com/12438606.html (accessed on 5 April 2019). (In Chinese)
- Ding, F. System Identification—Multi-Innovation Identification Theory and Methods; Science Press: Beijing, China, 2016; Available online: http://product.dangdang.com/23933240.html (accessed on 5 April 2019). (In Chinese)
- Xu, L. The damping iterative parameter identification method for dynamical systems based on the sine signal measurement. Signal Process. 2016, 120, 660–667. [Google Scholar] [CrossRef]
- Xu, L. A proportional differential control method for a time-delay system using the Taylor expansion approximation. Appl. Math. Comput. 2014, 236, 391–399. [Google Scholar] [CrossRef]
- Xu, L.; Ding, F. Parameter estimation for control systems based on impulse responses. Int. J. Control Autom. Syst. 2017, 15, 2471–2479. [Google Scholar] [CrossRef]
- Li, M.H.; Liu, X.M. The least squares based iterative algorithms for parameter estimation of a bilinear system with autoregressive noise using the data filtering technique. Signal Process. 2018, 147, 23–34. [Google Scholar] [CrossRef]
- Xu, L.; Chen, L.; Xiong, W.L. Parameter estimation and controller design for dynamic systems from the step responses based on the Newton iteration. Nonlinear Dyn. 2015, 79, 2155–2163. [Google Scholar] [CrossRef]
- Xu, L. The parameter estimation algorithms based on the dynamical response measurement data. Adv. Mech. Eng. 2017, 9, 1–12. [Google Scholar] [CrossRef]
- Tian, X.P.; Niu, H.M. A bi-objective model with sequential search algorithm for optimizing network-wide train timetables. Comput. Ind. Eng. 2019, 127, 1259–1272. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, P.; Li, X.X. The truncation method for the Cauchy problem of the inhomogeneous Helmholtz equation. Appl. Anal. 2019, 98, 991–1004. [Google Scholar] [CrossRef]
- Zhao, N.; Liu, R.; Chen, Y.; Wu, M.; Jiang, Y.; Xiong, W.; Liu, C. Contract design for relay incentive mechanism under dual asymmetric information in cooperative networks. Wirel. Netw. 2018, 24, 3029–3044. [Google Scholar] [CrossRef]
- Xu, G.H.; Shekofteh, Y.; Akgul, A.; Li, C.B.; Panahi, S. A new chaotic system with a self-excited attractor: Entropy measurement, signal encryption, and parameter estimation. Entropy 2018, 20, 86. [Google Scholar] [CrossRef]
- Li, X.Y.; Li, H.X.; Wu, B.Y. Piecewise reproducing kernel method for linear impulsive delay differential equations with piecewise constant arguments. Appl. Math. Comput. 2019, 349, 304–313. [Google Scholar] [CrossRef]
- Noshadi, A.; Shi, J.; Lee, W.S.; Shi, P.; Kalam, A. System identification and robust control of multi-input multi-output active magnetic bearing systems. IEEE Trans. Control. Syst. Technol. 2016, 24, 1227–1239. [Google Scholar] [CrossRef]
- Pan, J.; Li, W.; Zhang, H.P. Control algorithms of magnetic suspension systems based on the improved double exponential reaching law of sliding mode control. Int. J. Control Autom. Syst. 2018, 16, 2878–2887. [Google Scholar] [CrossRef]
- Zhang, X.; Ding, F.; Xu, L.; Yang, E.F. Highly computationally efficient state filter based on the delta operator. Int. J. Adapt. Control Signal Process. 2019. [Google Scholar] [CrossRef]
- Luo, X.S.; Song, Y.D. Data-driven predictive control of Hammerstein-Wiener systems based on subspace identification. Inf. Sci. 2018, 422, 447–461. [Google Scholar] [CrossRef]
- Ma, F.Y.; Yin, Y.K.; Li, M. Start-up process modelling of sediment microbial fuel cells based on data driven. Math. Probl. Eng. 2019, 2019, 7403732. [Google Scholar] [CrossRef]
- Li, M.H.; Liu, X.M. Auxiliary model based least squares iterative algorithms for parameter estimation of bilinear systems using interval-varying measurements. IEEE Access 2018, 6, 21518–21529. [Google Scholar] [CrossRef]
- Bottegal, G.; Castro-Garcia, R.; Suykens, J.A.K. A two-experiment approach to Wiener system identification. Automatica 2018, 93, 282–289. [Google Scholar] [CrossRef]
- Guo, F.; Hariprasad, K.; Huang, B.; Ding, Y.S. Robust identification for nonlinear errors-in-variables systems using the EM algorithm. J. Process. Control. 2017, 54, 129–137. [Google Scholar] [CrossRef]
- Li, M.H.; Liu, X.M.; Ding, F. Filtering-based maximum likelihood gradient iterative estimation algorithm for bilinear systems with autoregressive moving average noise. Circuits Syst. Signal Process. 2019, 37, 5023–5048. [Google Scholar] [CrossRef]
- Zhang, X.; Ding, F.; Xu, L.; Yang, E.F. State filtering-based least squares parameter estimation for bilinear systems using the hierarchical identification principle. IET Control Theory Appl. 2018, 12, 1704–1713. [Google Scholar] [CrossRef]
- Ding, F. Two-stage least squares based iterative estimation algorithm for CARARMA system modeling. Appl. Math. Model. 2013, 37, 4798–4808. [Google Scholar] [CrossRef]
- Xu, H.; Ding, F.; Yang, E.F. Modeling a nonlinear process using the exponential autoregressive time series model. Nonlinear Dyn. 2019, 95, 2079–2092. [Google Scholar] [CrossRef]
- Ding, F. Decomposition based fast least squares algorithm for output error systems. Signal Process. 2013, 93, 1235–1242. [Google Scholar] [CrossRef]
- Ge, Z.W.; Ding, F.; Xu, L.; Alsaedi, A.; Hayat, T. Gradient-based iterative identification method for multivariate equation-error autoregressive moving average systems using the decomposition technique. J. Frankl. Inst. 2019, 356, 1658–1676. [Google Scholar] [CrossRef]
- Pan, J.; Ma, H.; Jiang, X.; Ding, W.; Ding, F. Adaptive gradient-based iterative algorithm for multivariate controlled autoregressive moving average systems using the data filtering technique. Complexity 2018, 2018, 9598307. [Google Scholar] [CrossRef]
- Xu, L. Application of the Newton iteration algorithm to the parameter estimation for dynamical systems. J. Comput. Appl. Math. 2015, 288, 33–43. [Google Scholar] [CrossRef]
- Wang, Y.J.; Ding, F. Iterative estimation for a non-linear IIR filter with moving average noise by means of the data filtering technique. IMA J. Math. Control Inf. 2017, 34, 745–764. [Google Scholar] [CrossRef]
- Liu, Y.J.; Wang, D.Q.; Ding, F. Least squares based iterative algorithms for identifying Box-Jenkins models with finite measurement data. Digit. Signal Process. 2010, 20, 1458–1467. [Google Scholar] [CrossRef]
- Liu, Q.Y.; Ding, F. Auxiliary model-based recursive generalized least squares algorithm for multivariate output-error autoregressive systems using the data filtering. Circuits Syst. Signal Process. 2019, 38, 590–610. [Google Scholar] [CrossRef]
- Xu, L.; Ding, F.; Gu, Y.; Alsaedi, A.; Hayat, T. A multi-innovation state and parameter estimation algorithm for a state space system with d-step state-delay. Signal Process. 2017, 140, 97–103. [Google Scholar] [CrossRef]
- Xu, L.; Ding, F. Iterative parameter estimation for signal models based on measured data. Circuits Syst. Signal Process. 2018, 37, 3046–3069. [Google Scholar] [CrossRef]
- Xu, L.; Xiong, W.L.; Alsaedi, A.; Hayat, T. Hierarchical parameter estimation for the frequency response based on the dynamical window data. Int. J. Control Autom. Syst. 2018, 16, 1756–1764. [Google Scholar] [CrossRef]
- Ding, F.; Liu, X.P.; Liu, G. Gradient based and least-squares based iterative identification methods for OE and OEMA systems. Digit. Signal Process. 2010, 20, 664–677. [Google Scholar] [CrossRef]
- Xu, L.; Ding, F. Recursive least squares and multi-innovation stochastic gradient parameter estimation methods for signal modeling. Circuits Syst. Signal Process. 2017, 36, 1735–1753. [Google Scholar] [CrossRef]
- Pan, J.; Jiang, X.; Wan, X.K.; Ding, W. A filtering based multi-innovation extended stochastic gradient algorithm for multivariable control systems. Int. J. Control. Autom. Syst. 2017, 15, 1189–1197. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, L.; Ding, F.; Hayat, T. Combined state and parameter estimation for a bilinear state space system with moving average noise. J. Frankl. Inst. 2018, 355, 3079–3103. [Google Scholar] [CrossRef]
- Zhang, X.; Ding, F.; Alsaadi, F.E.; Hayat, T. Recursive parameter identification of the dynamical models for bilinear state space systems. Nonlinear Dyn. 2017, 89, 2415–2429. [Google Scholar] [CrossRef]
- Bonami, P.; Biegler, L.T.; Conn, A.R.; Cornuéjols, G.; Grossmann, I.E.; Lairde, C.D.; Lee, J.; Lodi, A.; Margot, F.; Sawaya, N.; et al. An algorithmic framework for convex mixed integer nonlinear programs. Discret. Optim. 2008, 5, 186–204. [Google Scholar] [CrossRef]
- Neumaier, A.; Shcherbina, O.; Huyer, W.; Vinkó, T. A comparison of complete global optimization solvers. Math. Program. 2005, 103, 335–356. [Google Scholar] [CrossRef]
- Lastusilta, T.; Bussieck, M.R.; Westerlund, T. An experimental study of the GAMS/AlphaECP MINLP solver. Ind. Eng. Chem. Res. 2009, 48, 7337–7345. [Google Scholar] [CrossRef]
- Klanšek, U. A comparison between MILP and MINLP approaches to optimal solution of nonlinear discrete transportation problem. Transport 2015, 30, 135–144. [Google Scholar] [CrossRef]
- Ding, F.; Liu, X.G.; Chu, J. Gradient-based and least-squares-based iterative algorithms for Hammerstein systems using the hierarchical identification principle. IET Control Theory Appl. 2013, 7, 176–184. [Google Scholar] [CrossRef]
- Xu, L.; Ding, F. Parameter estimation algorithms for dynamical response signals based on the multi-innovation theory and the hierarchical principle. IET Signal Process. 2017, 11, 228–237. [Google Scholar] [CrossRef]
- Wu, M.H.; Li, X.; Liu, C.; Liu, M.; Zhao, N.; Wang, J.; Wan, X.K.; Rao, Z.H.; Zhu, L. Robust global motion estimation for video security based on improved k-means clustering. J. AmbientIntell. Humaniz. Comput. 2019, 10, 439–448. [Google Scholar] [CrossRef]
- Wan, X.K.; Wu, H.; Qiao, F.; Li, F.; Li, Y.; Yan, Y.; Wei, J. Electrocardiogram baseline wander suppression based on the combination of morphological and wavelet transformation based filtering. Computat. Math. Methods Med. 2019, 201, 7196156. [Google Scholar] [CrossRef] [PubMed]
- Wen, Y.Z.; Yin, C.C. Solution of Hamilton-Jacobi-Bellman equation in optimal reinsurance strategy under dynamic VaR constraint. J. Funct. Spaces 2019, 2019, 6750892. [Google Scholar] [CrossRef]
- Yin, C.C.; Zhao, J.S. Nonexponential asymptotics for the solutions of renewal equations, with applications. J. Appl. Probab. 2006, 43, 815–824. [Google Scholar] [CrossRef]
- Yin, C.C.; Wang, C.W. The perturbed compound Poisson risk process with investment and debit interest. Methodol. Comput. Appl. Probab. 2010, 12, 391–413. [Google Scholar] [CrossRef]
- Yin, C.C.; Yuen, K.C. Optimality of the threshold dividend strategy for the compound Poisson model. Stat. Probab. Lett. 2011, 81, 1841–1846. [Google Scholar] [CrossRef]
- Yin, C.C.; Wen, Y.Z. Exit problems for jump processes with applications to dividend problems. J. Comput. Appl. Math. 2013, 245, 30–52. [Google Scholar] [CrossRef]
- Yin, C.C.; Wen, Y.Z. Optimal dividend problem with a terminal value for spectrally positive Levy processes. Insur. Math. Econ. 2013, 53, 769–773. [Google Scholar] [CrossRef]
- Yin, C.C.; Wen, Y.Z.; Zhao, Y.X. On the optimal dividend problem for a spectrally positive levy process. Astin Bull. 2014, 44, 635–651. [Google Scholar] [CrossRef]
- Yin, C.C.; Yuen, K.C. Exact joint laws associated with spectrally negative Levy processes and applications to insurance risk theory. Front. Math. China 2014, 9, 1453–1471. [Google Scholar] [CrossRef]
- Yin, C.C.; Yuen, K.C. Optimal dividend problems for a jump-diffusion model with capital injections and proportional transaction costs. J. Ind. Manag. Optim. 2015, 11, 1247–1262. [Google Scholar] [CrossRef]
- Zhang, X.; Ding, F.; Xu, L.; Alsaedi, A.; Hayat, T. A hierarchical approach for joint parameter and state estimation of a bilinear system with autoregressive noise. Mathematics 2019, 7. [Google Scholar] [CrossRef]
- Xu, L.; Ding, F.; Zhu, Q.M. Hierarchical Newton and least squares iterative estimation algorithm for dynamic systems by transfer functions based on the impulse responses. Int. J. Syst. Sci. 2019, 50, 141–151. [Google Scholar] [CrossRef]
- Wang, Y.J.; Ding, F.; Xu, L. Some new results of designing an IIR filter with colored noise for signal processing. Digit. Signal Process. 2018, 72, 44–58. [Google Scholar] [CrossRef]
- Wang, Y.J.; Ding, F.; Wu, M.H. Recursive parameter estimation algorithm for multivariate output-error systems. J. Frankl. Inst. 2018, 355, 5163–5181. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Zhang, D.; Meng, Q.; Chen, C.C. Feedback stabilization of time-delay nonlinear systems with continuous time-varying output function. Int. J. Syst. Sci. 2019, 50, 244–255. [Google Scholar] [CrossRef]
- Zhan, X.S.; Cheng, L.L.; Wu, J.; Yang, Q.S.; Han, T. Optimal modified performance of MIMO networked control systems with multi-parameter constraints. ISA Trans. 2019, 84, 111–117. [Google Scholar] [CrossRef]
- Zha, X.S.; Guan, Z.H.; Zhang, X.H.; Yuan, F.S. Optimal tracking performance and design of networked control systems with packet dropout. J. Frankl. Inst. 2013, 350, 3205–3216. [Google Scholar]
- Jiang, C.M.; Zhang, F.F.; Li, T.X. Synchronization and antisynchronization of N-coupled fractional-order complex chaotic systems with ring connection. Math. Methods Appl. Sci. 2018, 41, 2625–2638. [Google Scholar] [CrossRef]
- Wang, T.; Liu, L.; Zhang, J.; Schaeffer, E.; Wang, Y. A M-EKF fault detection strategy of insulation system for marine current turbine. Mech. Syst. Signal Process. 2019, 115, 269–280. [Google Scholar] [CrossRef]
- Cao, Y.; Lu, H.; Wen, T. A safety computer system based on multi-sensor data processing. Sensors 2019, 19, 818. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Zhang, Y.; Wen, T.; Li, P. Research on dynamic nonlinear input prediction of fault diagnosis based on fractional differential operator equation in high-speed train control system. Chaos 2019, 29, 013130. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Li, P.; Zhang, Y. Parallel processing algorithm for railway signal fault diagnosis data based on cloud computing. Future Gener. Comput. Syst. 2018, 88, 279–283. [Google Scholar] [CrossRef]
- Cao, Y.; Ma, L.C.; Xiao, S.; Zhang, X.; Xu, W. Standard analysis for transfer delay in CTCS-3. Chin. J. Electron. 2017, 26, 1057–1063. [Google Scholar] [CrossRef]
- Zhao, N.; Wu, M.H.; Chen, J.J. Android-based mobile educational platform for speech signal processing. Int. J. Electr. Eng. Edu. 2017, 54, 3–16. [Google Scholar] [CrossRef]
- Zhao, N.; Chen, Y.; Liu, R.; Wu, M.H.; Xiong, W. Monitoring strategy for relay incentive mechanism in cooperative communication networks. Comput. Electr. Eng. 2017, 60, 14–29. [Google Scholar] [CrossRef]
- Ji, Y.; Ding, F. Multiperiodicity and exponential attractivity of neural networks with mixed delays. Circuits Syst. Signal Process. 2017, 36, 2558–2573. [Google Scholar] [CrossRef]
- Ji, Y.; Liu, X.M. Unified synchronization criteria for hybrid switching-impulsive dynamical networks. Circuits Syst. Signal Process. 2015, 34, 1499–1517. [Google Scholar] [CrossRef]
- Ding, F.; Chen, T. Performance bounds of the forgetting factor least squares algorithm for time-varying systems with finite measurement data. IEEE Trans. Circuits Syst. Regul. Pap. 2005, 52, 555–566. [Google Scholar] [CrossRef]
- Li, N.; Guo, S.; Wang, Y. Weighted preliminary-summation-based principal component analysis for non-Gaussian processes. Control. Eng. Pract. 2019. [Google Scholar] [CrossRef]
- Wang, Y.; Si, Y.; Huang, B.; Lou, Z. Survey on the theoretical research and engineering applications of multivariate statistics process monitoring algorithms: 2008–2017. Can. J. Chem. 2018, 96, 2073–2085. [Google Scholar] [CrossRef]
- Feng, L.; Li, Q.X.; Li, Y.F. Imaging with 3-D aperture synthesis radiometers. IEEE Trans. Geosci. Remote. Sens. 2019, 57, 2395–2406. [Google Scholar] [CrossRef]
- Shi, W.X.; Liu, N.; Zhou, Y.M.; Cao, X.A. Effects of postannealing on the characteristics and reliability of polyfluorene organic light-emitting diodes. IEEE Trans. Electron. Devices 2019, 66, 1057–1062. [Google Scholar] [CrossRef]
- Fu, B.; Ouyang, C.X.; Li, C.S.; Wang, J.W.; Gul, E. An improved mixed integer linear programming approach based on symmetry diminishing for unit commitment of hybrid power system. Energies 2019, 12, 833. [Google Scholar] [CrossRef]
- Wu, T.Z.; Shi, X.; Liao, L.; Zhou, C.J.; Zhou, H.; Su, Y.H. A capacity configuration control strategy to alleviate power fluctuation of hybrid energy storage system based on improved particle swarm optimization. Energies 2019, 12, 642. [Google Scholar] [CrossRef]
- Liu, F.; Xue, Q.; Yabuta, K. Boundedness and continuity of maximal singular integrals and maximal functions on Triebel-Lizorkin spaces. Scie. China-Math. 2019. [Google Scholar] [CrossRef]
- Liu, F. Boundedness and continuity of maximal operators associated to polynomial compound curves on Triebel-Lizorkin spaces. Math. Inequalities Appl. 2019, 22, 25–44. [Google Scholar] [CrossRef]
- Liu, F.; Fu, Z.; Jhang, S. Boundedness and continuity of Marcinkiewicz integrals associated to homogeneous mappings on Triebel-Lizorkin spaces. Front. Math. China 2019, 14, 95–122. [Google Scholar] [CrossRef]
- Ding, J.L. The hierarchical iterative identification algorithm for multi-input-output-error systems with autoregressive noise. Complexity 2017, 2017, 1–11. [Google Scholar] [CrossRef]
- Wang, D.Q.; Yan, Y.R.; Liu, Y.J.; Ding, J.H. Model recovery for Hammerstein systems using the hierarchical orthogonal matching pursuit method. J. Computat. Appl. Math. 2019, 345, 135–145. [Google Scholar] [CrossRef]
- Wang, D.Q.; Li, L.W.; Ji, Y.; Yan, Y.R. Model recovery for Hammerstein systems using the auxiliary model based orthogonal matching pursuit method. Appl. Math. Modell. 2018, 54, 537–550. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).