An Efficient Analytical Technique, for The Solution of Fractional-Order Telegraph Equations
Abstract
:1. Introduction
2. Definitions and Preliminary Concepts
3. Idea of Fractional Laplace-Adomian Decomposition Method
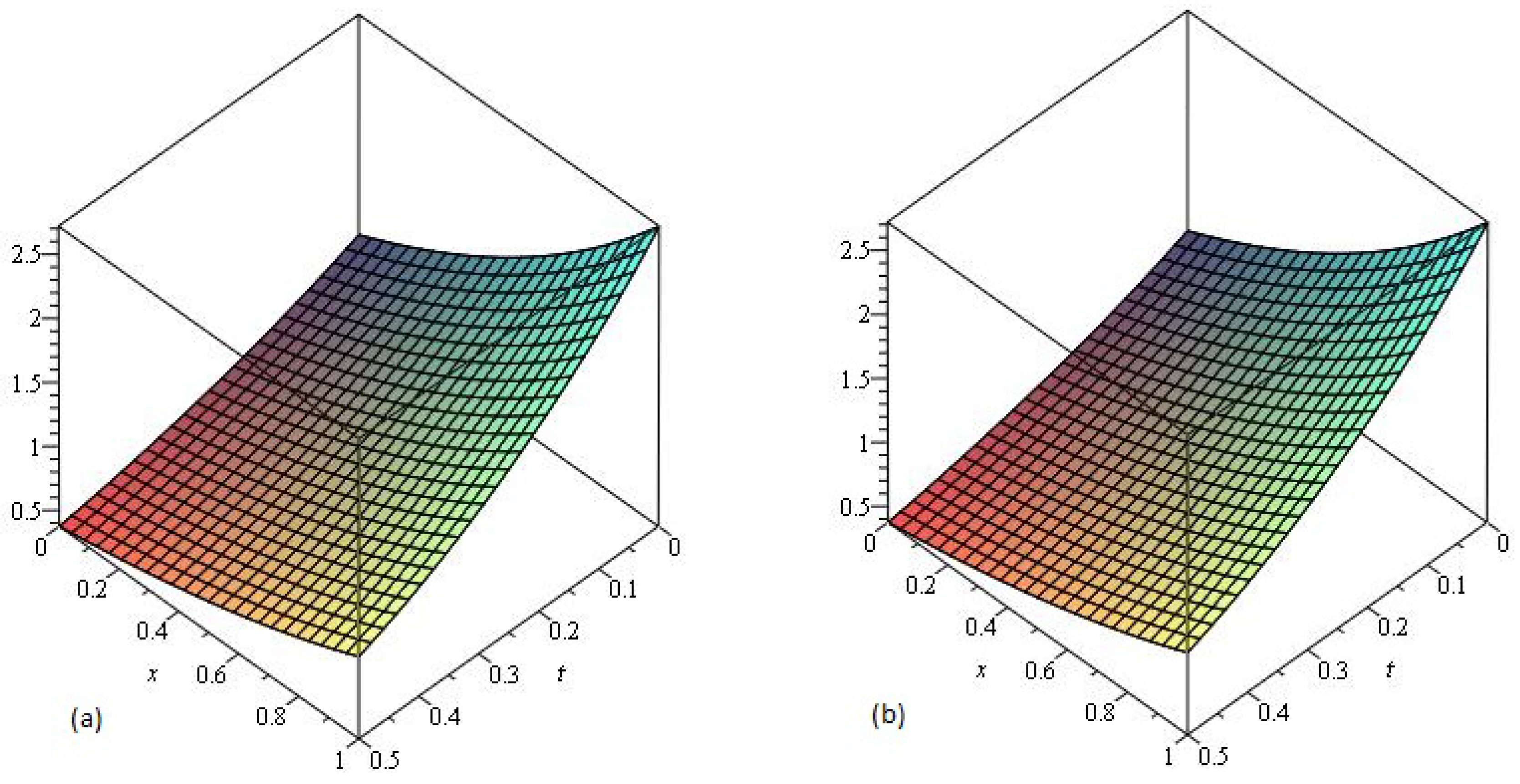
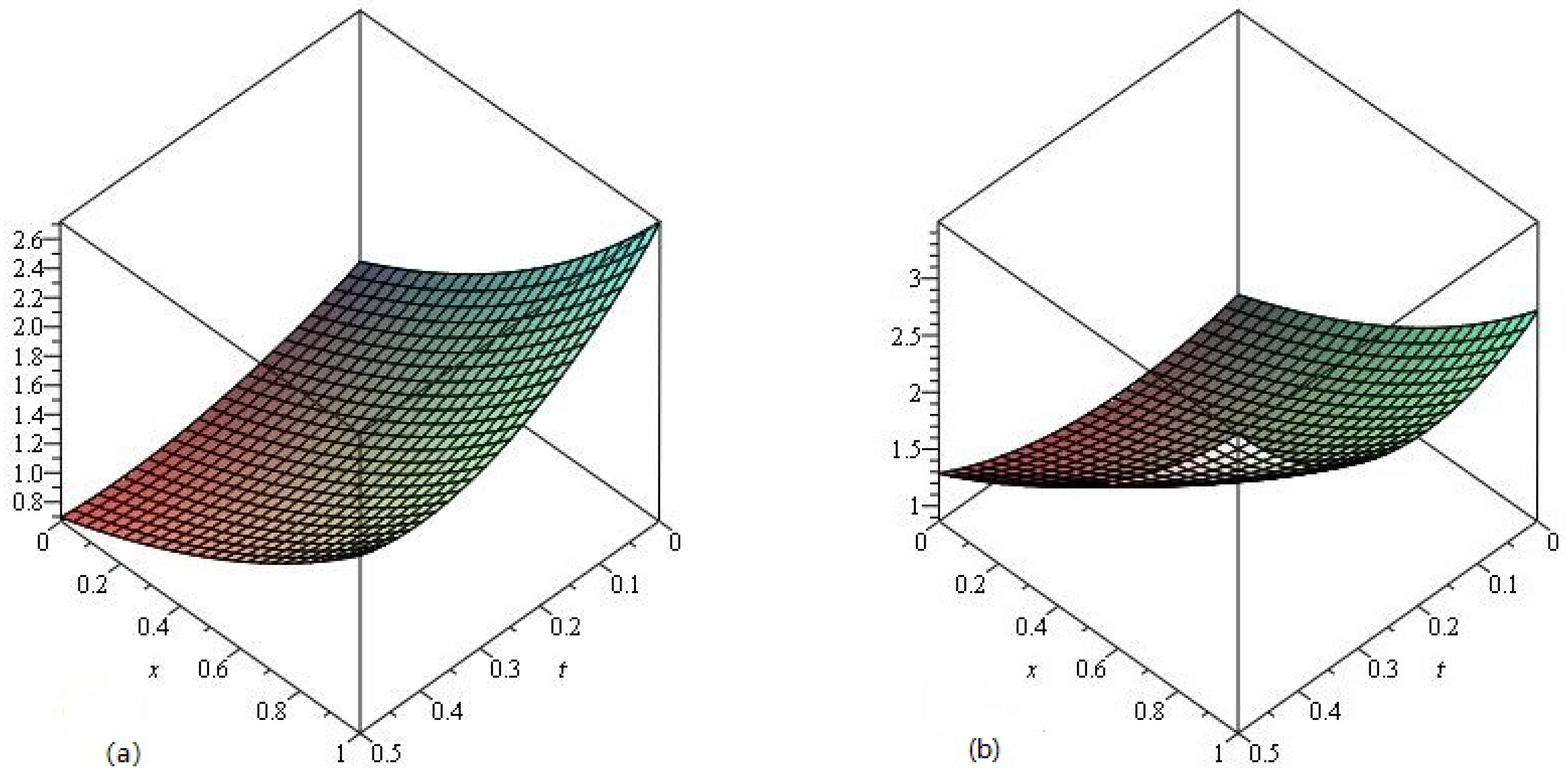
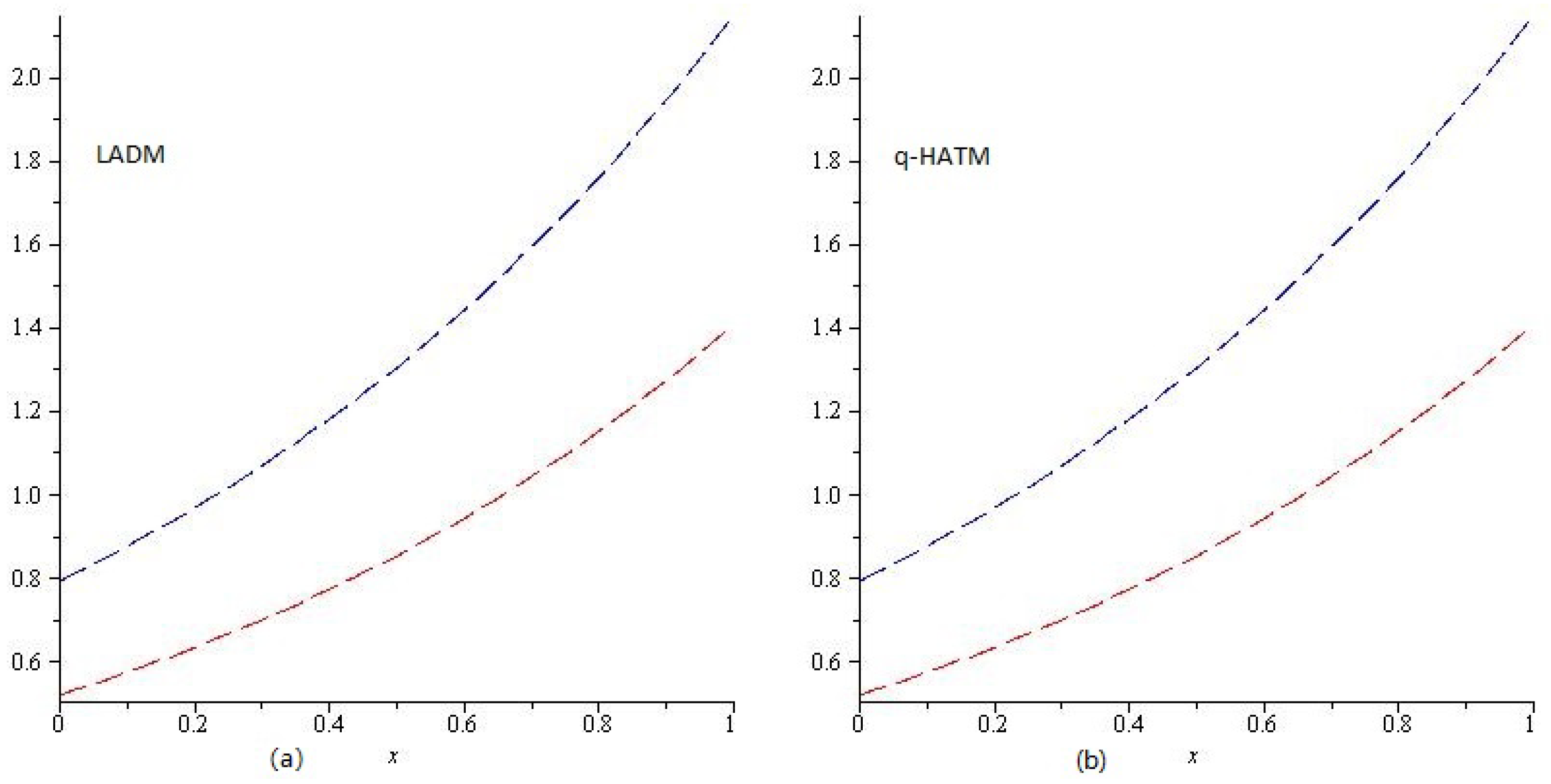
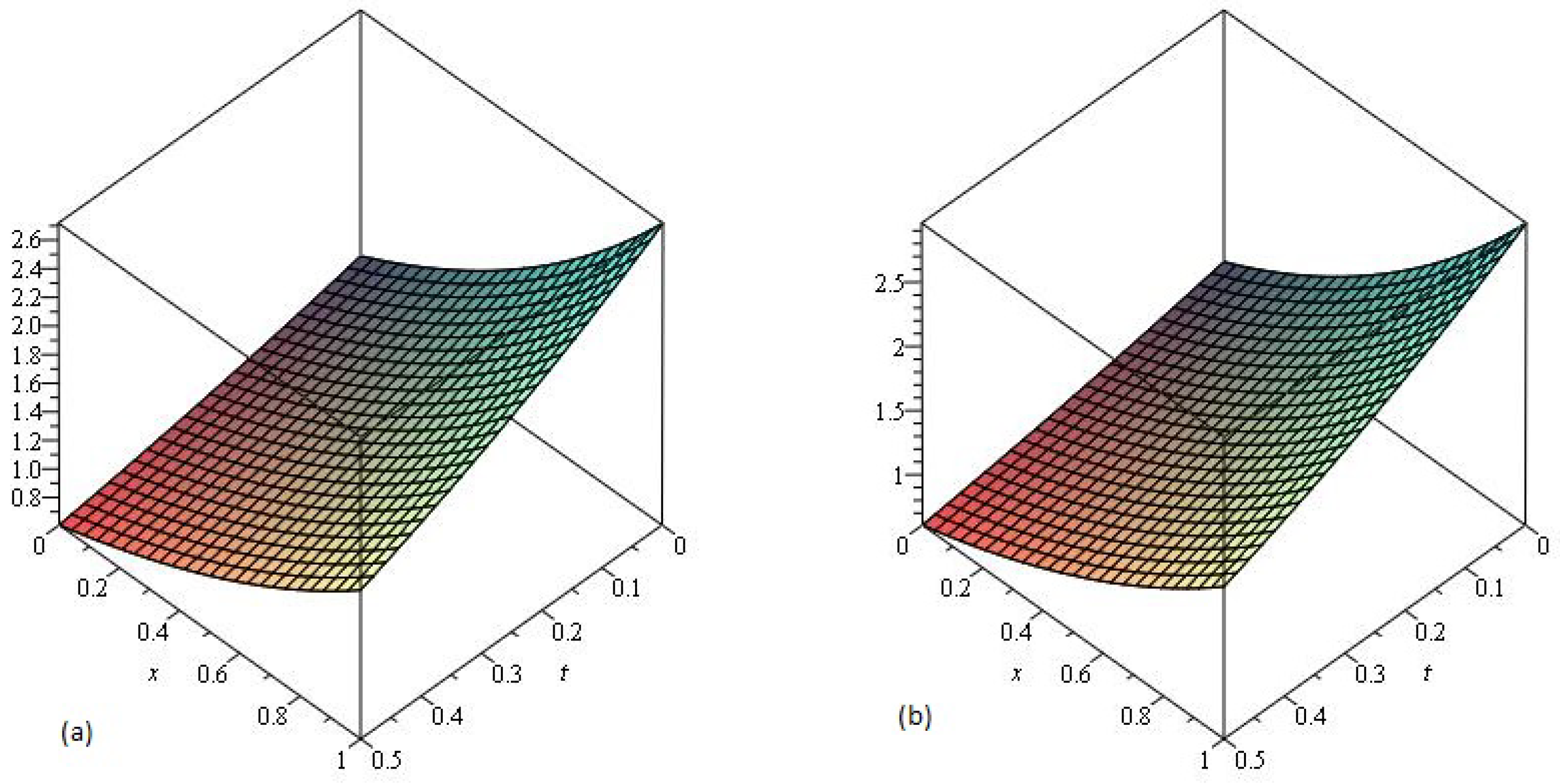
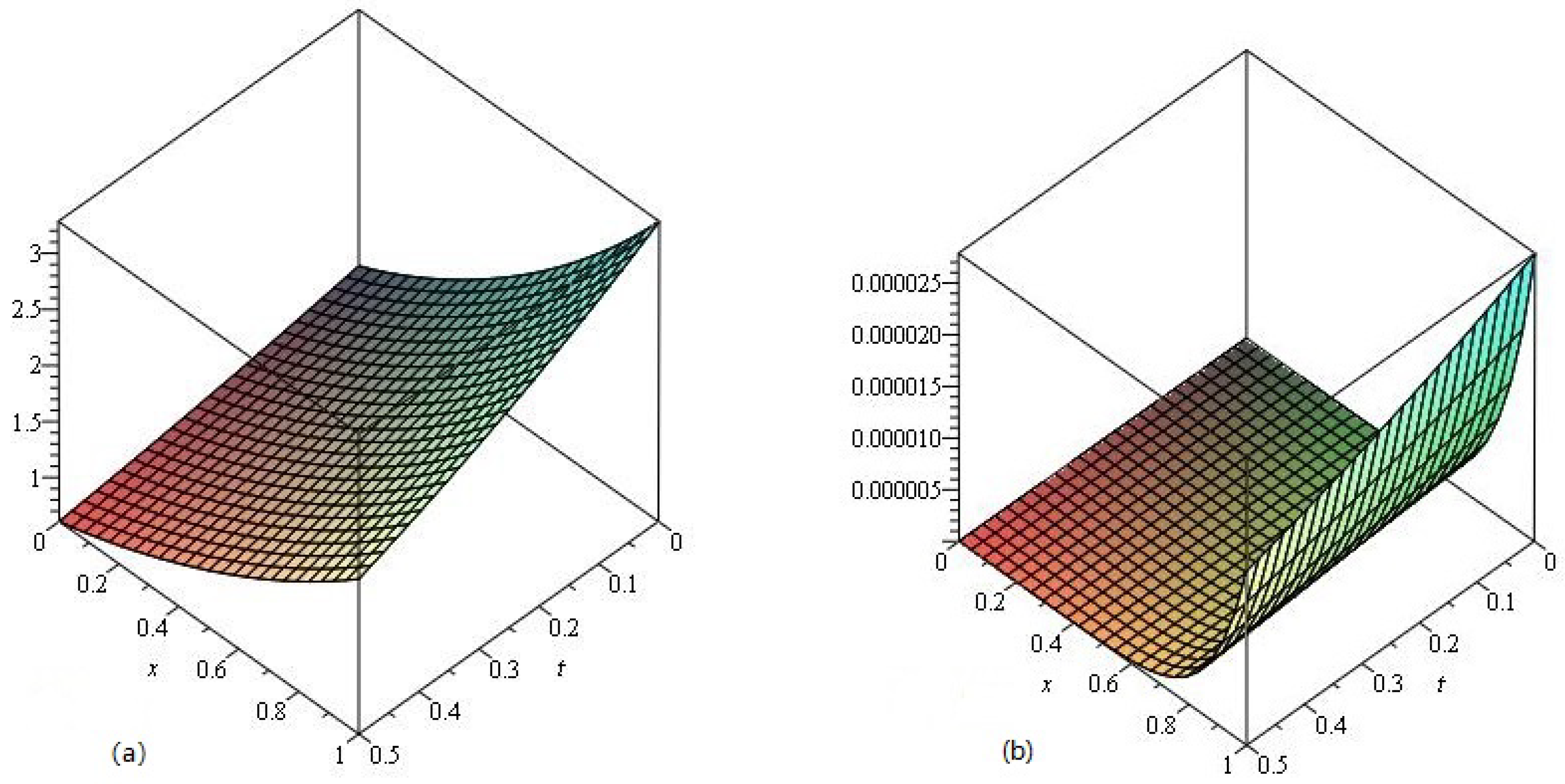
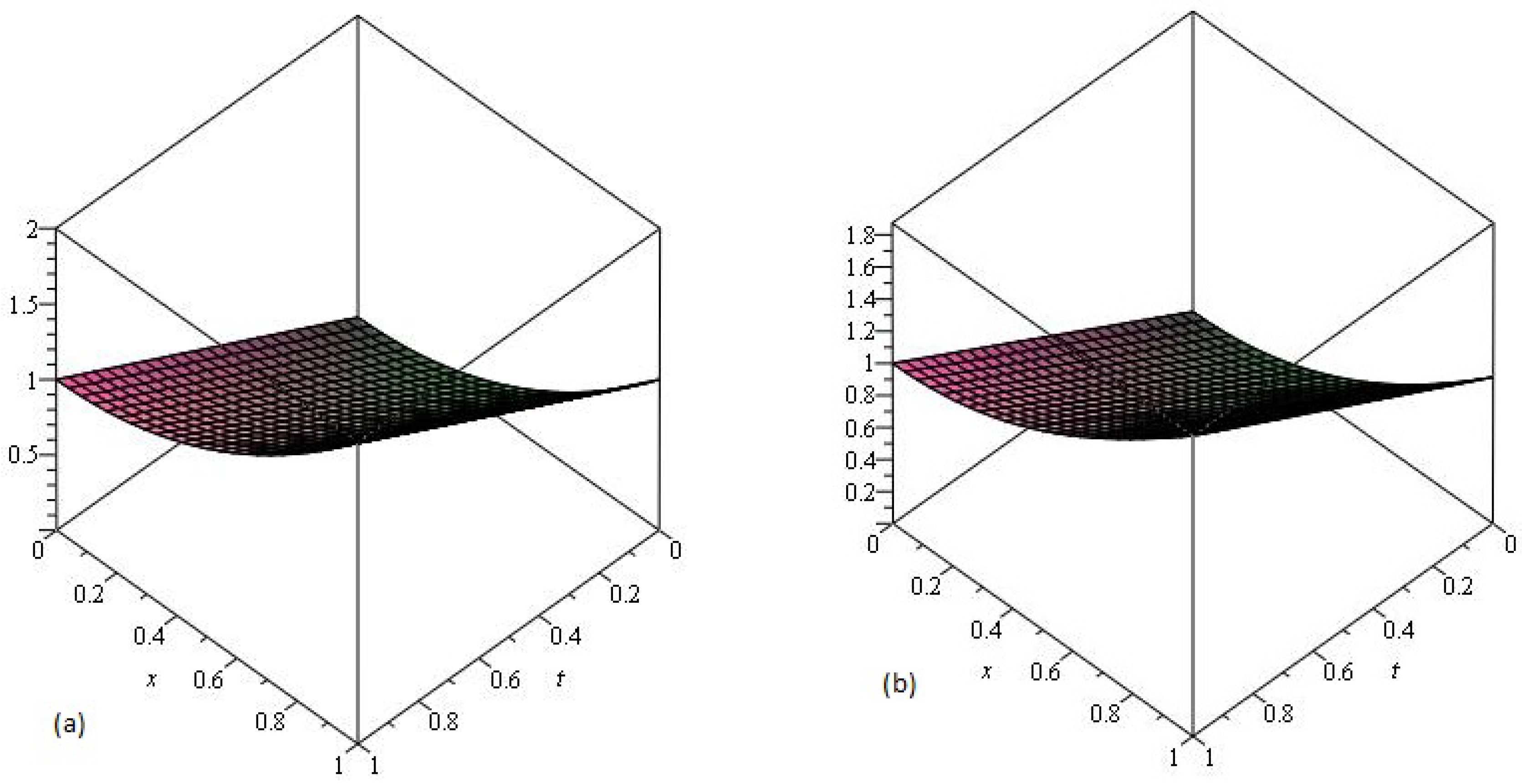
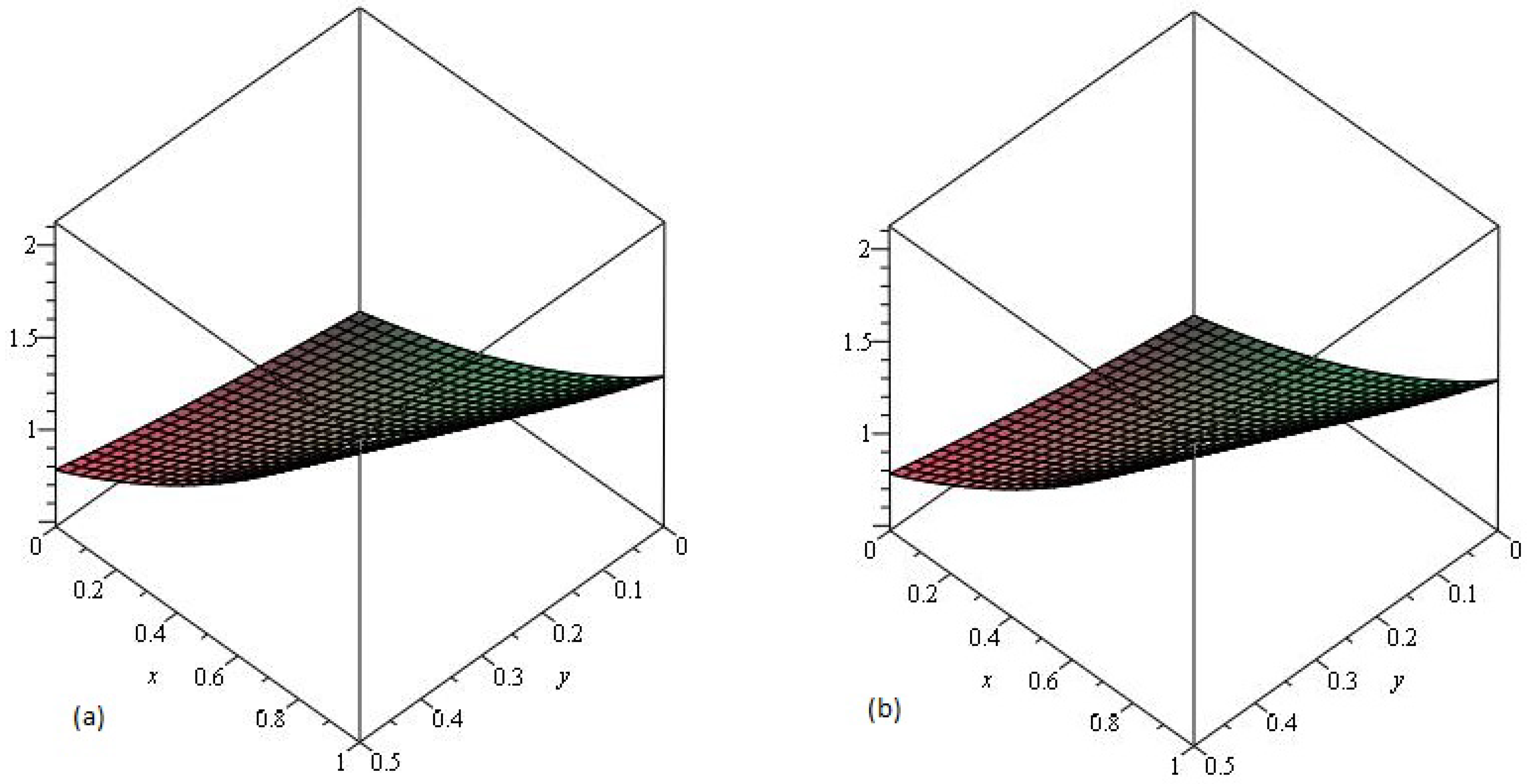
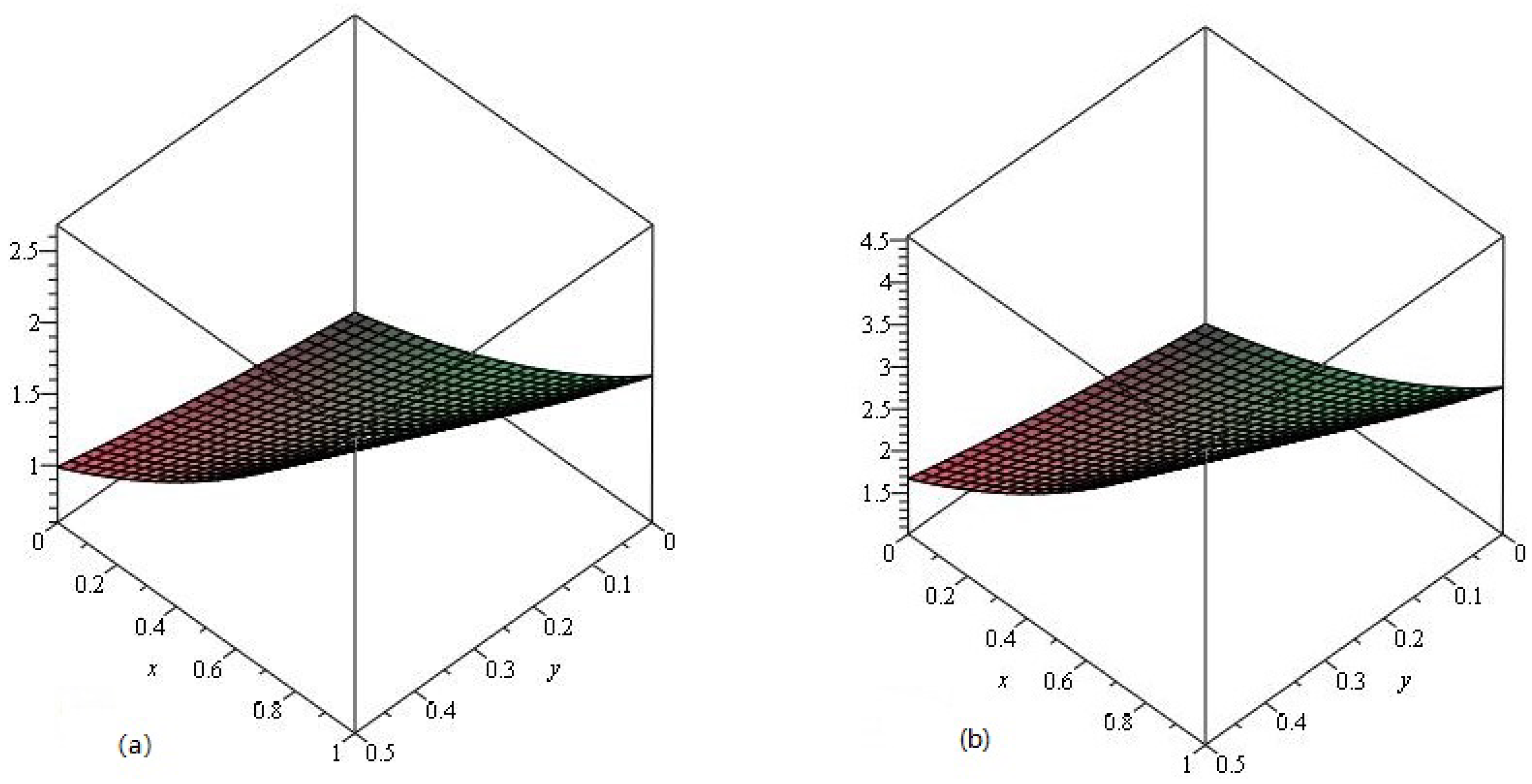
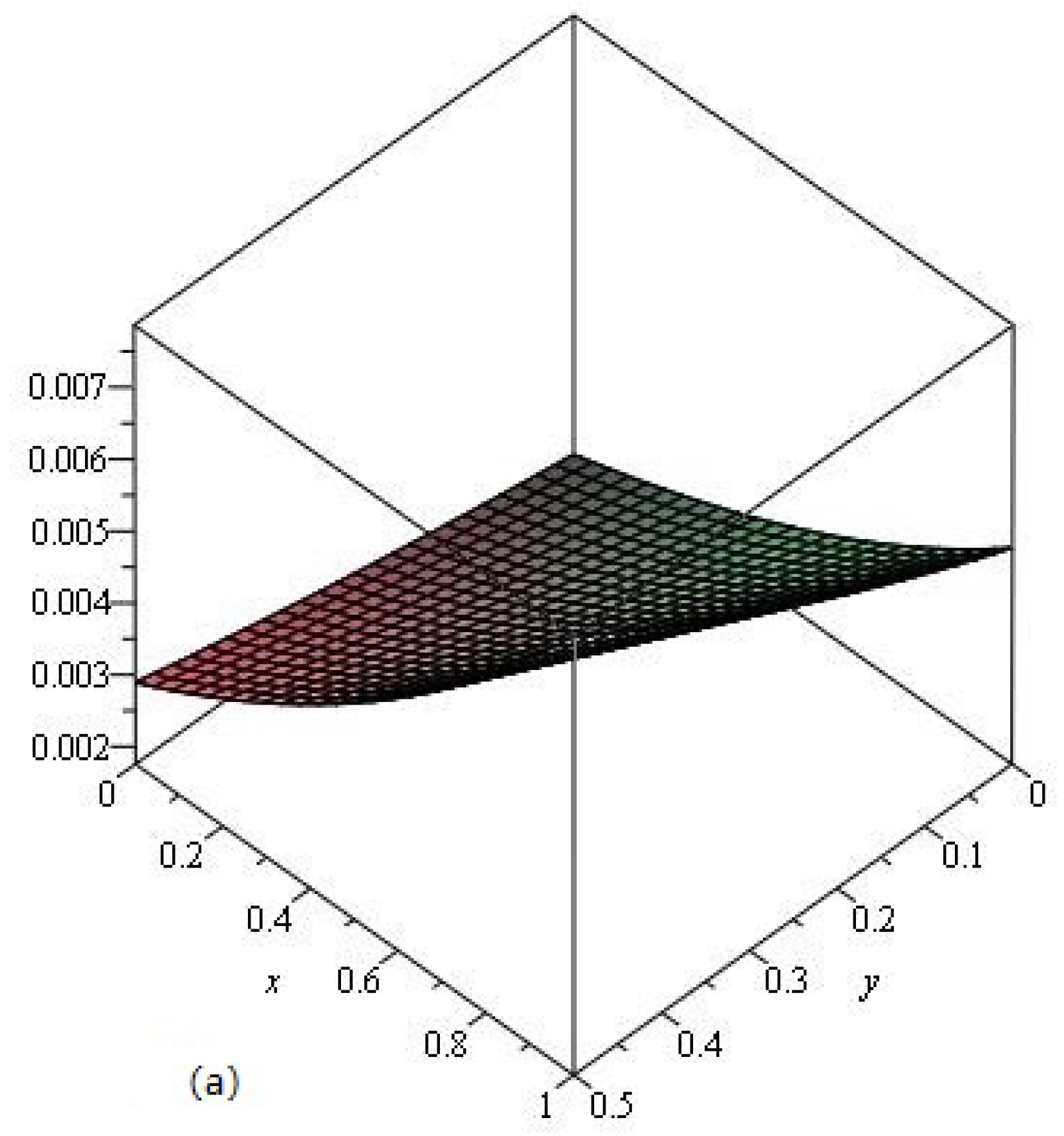
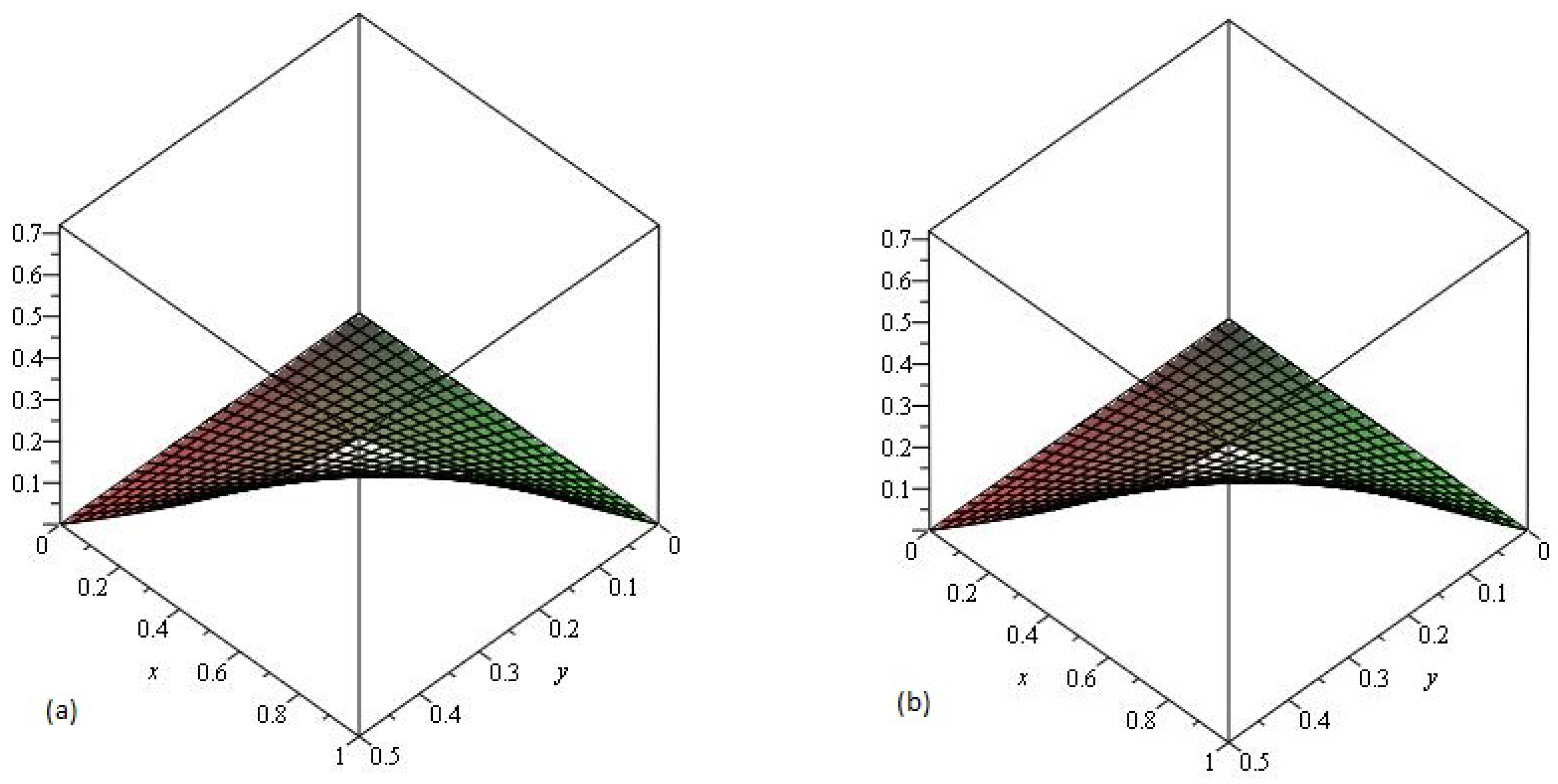
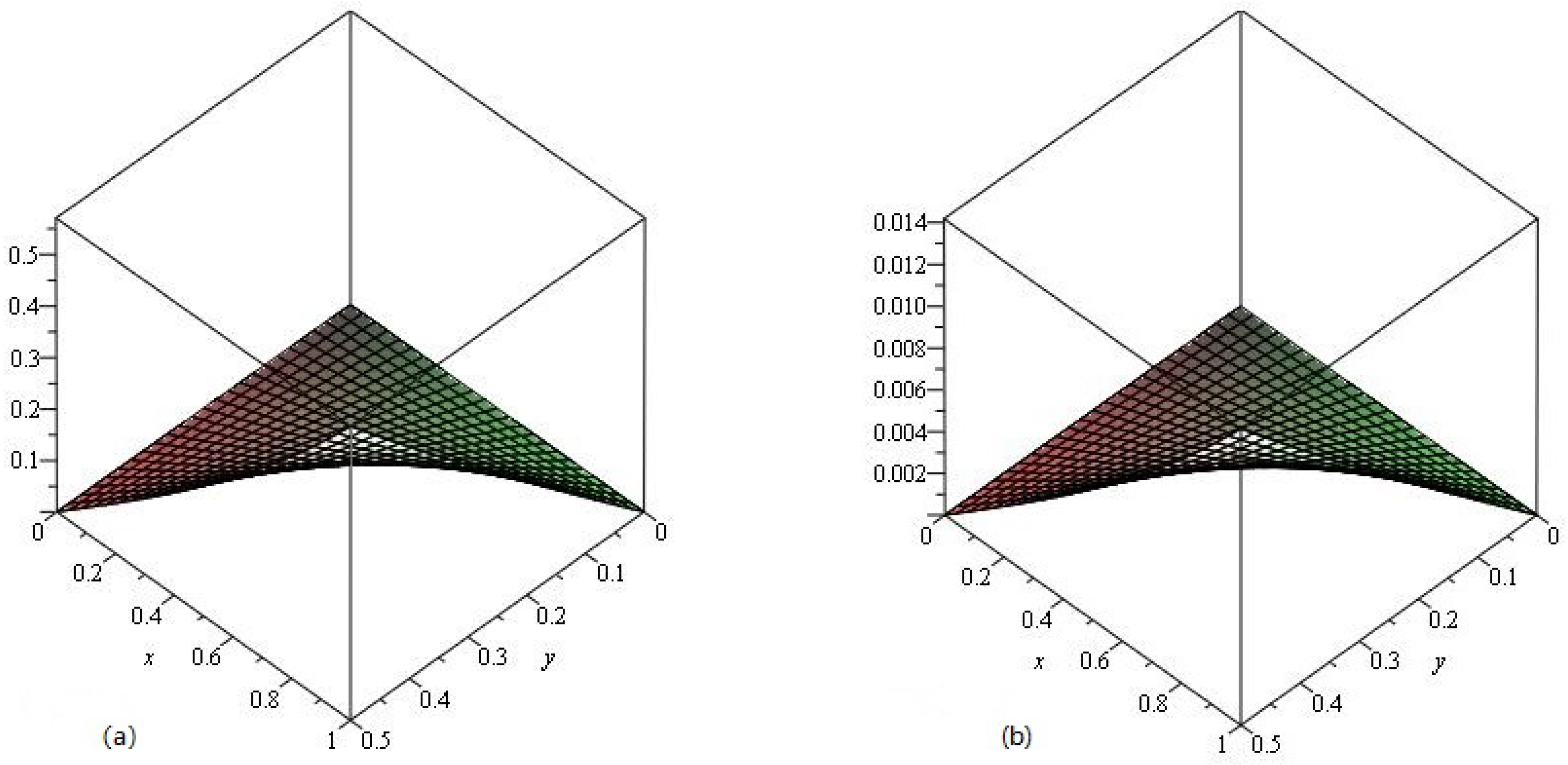
4. Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hilfer, R. Applications of Fractional Calculus in Physics; World Sci. Publishing: River Edge, NJ, USA, 2000. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998; Volume 198. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: Hoboken, NJ, USA, 1993; p. 384. [Google Scholar]
- Bildik, N.; Konuralp, A. The use of variational iteration method, differential transform method and Adomian decomposition method for solving different types of nonlinear partial differential equations. Int. J. Nonlinear Sci. Numer. Simul. 2006, 7, 65–70. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; Yépez-Martínez, H.; Torres-Jiménez, J.; Córdova-Fraga, T.; Escobar-Jiménez, R.F.; Olivares-Peregrino, V.H. Homotopy perturbation transform method for nonlinear differential equations involving to fractional operator with exponential kernel. Adv. Differ. Equations 2017, 2017, 68. [Google Scholar] [CrossRef]
- Atangana, A.; Gómez-Aguilar, J.F. Numerical approximation of Riemann-Liouville definition of fractional derivative: From Riemann-Liouville to Atangana-Baleanu. Numer. Methods Partial. Differ. Equations 2018, 34, 1502–1523. [Google Scholar] [CrossRef]
- Kilbas, A.A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier Science Limited: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Jiang, J.; Feng, Y.; Li, S. Exact Solutions to the Fractional Differential Equations with Mixed Partial Derivatives. Axioms 2018, 7, 10. [Google Scholar] [CrossRef]
- Silva, F.; Moreira, D.; Moret, M. Conformable Laplace Transform of Fractional Differential Equations. Axioms 2018, 7, 55. [Google Scholar] [CrossRef]
- Machado, J.T. Entropy analysis of integer and fractional dynamical systems. Nonlinear Dyn. 2010, 62, 371–378. [Google Scholar]
- Ball, J.M.; Chen, G.Q.G. Entropy and Convexity for Nonlinear Partial Differential Equations. Philos. Trans. A Math. Phys. Eng. Sci. 2013, 371, 2005. [Google Scholar] [CrossRef] [PubMed]
- Lopes, A.M.; Tenreiro Machado, J.A. Entropy Analysis of Soccer Dynamics. Entropy 2019, 21, 187. [Google Scholar] [CrossRef]
- Yavuz, M.; Özdemir, N. European vanilla option pricing model of fractional order without singular kernel. Fractal Fract. 2018, 2, 3. [Google Scholar] [CrossRef]
- Thabet, H.; Kendre, S.; Chalishajar, D. New analytical technique for solving a system of nonlinear fractional partial differential equations. Mathematics 2017, 5, 47. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Jafari, H. An iterative method for solving nonlinear functional equations. J. Math. Anal. Appl. 2006, 316, 753–763. [Google Scholar] [CrossRef]
- Jafari, H. Iterative Methods for Solving System of Fractional Differential Equations. Ph.D. Thesis, Pune University, Pune City, India, 2006. [Google Scholar]
- Ali, A.; Shah, K.; Khan, R.A. Numerical treatment for traveling wave solutions of fractional Whitham-Broer-Kaup equations. Alex. Eng. J. 2018, 57, 1991–1998. [Google Scholar] [CrossRef]
- Ahmed, H.F.; Bahgat, M.S.; Zaki, M. Numerical approaches to system of fractional partial differential equations. J. Egypt. Math. Soc. 2017, 25, 141–150. [Google Scholar] [CrossRef]
- Irfan, N.; Kumar, S.; Kapoor, S. Bernstein Operational Matrix Approach for Integro-Differential Equation Arising in Control theory. Nonlinear Eng. Nonlinear Eng. 2014, 3, 117–123. [Google Scholar]
- Yousef, H.M.; Ismail, A.M. Application of the Laplace Adomian decomposition method for solution system of delay differential equations with initial value problem. Aip Conf. Proc. 2018, 1974, 020038. [Google Scholar]
- Jafari, H.; Khalique, C.M.; Nazari, M. Application of the Laplace decomposition method for solving linear and nonlinear fractional diffusion–wave equations. Appl. Math. Lett. 2011, 24, 1799–1805. [Google Scholar] [CrossRef]
- Mohamed, M.Z.; Elzaki, T.M. Comparison between the Laplace Decomposition Method and Adomian Decomposition in Time-Space Fractional Nonlinear Fractional Differential Equations. Appl. Math. 2018, 9, 448–458. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Arif, M.; Kumam, P. Application of Laplace–Adomian Decomposition Method for the Analytical Solution of Third-Order Dispersive Fractional Partial Differential Equations. Entropy 2019, 21, 335. [Google Scholar] [CrossRef]
- Okubo, A. Application of the Telegraph Equation to Oceanic Diffusion: Another Mathematic Model; Chesapeake bay institute, The Johns Hopking Unversity: Baltimore, MD, USA, 1971; p. 42. [Google Scholar]
- Javidi, M.; Nyamoradi, N. Numerical solution of telegraph equation by using LT inversion technique. Int. J. Adv. Math. Sci. 2013, 1, 64–77. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G. Numerical solution for fractional model of telegraph equation by using q-HATM. arXiv 2018, arXiv:1805.03968. [Google Scholar]
- Al-badrani, H.; Saleh, S.; Bakodah, H.O.; Al-Mazmumy, M. Numerical Solution for Nonlinear Telegraph Equation by Modified Adomian Decomposition Method. Nonlinear Anal. Differ. Equations 2016, 4, 243–257. [Google Scholar] [CrossRef]
- Srivastava, V.K.; Awasthi, M.K.; Chaurasia, R.K.; Tamsir, M. The telegraph equation and its solution by reduced differential transform method. Model. Simul. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Srivastava, V.K.; Awasthi, M.K.; Tamsir, M. RDTM solution of Caputo time fractional-order hyperbolic telegraph equation. Aip Adv. 2013, 3, 032142. [Google Scholar] [CrossRef]
- Inc, M.; Akgül, A.; Kiliçman, A. Explicit solution of telegraph equation based on reproducing kernel method. J. Funct. Spaces Appl. 2012, 2012. [Google Scholar] [CrossRef]
- Biazar, J.; Ebrahimi, H.; Ayati, Z. An approximation to the solution of telegraph equation by variational iteration method. Numer. Methods Partial. Differ. Equations 2009, 25, 797–801. [Google Scholar] [CrossRef]
- Erfanian, M.; Gachpazan, M. A new method for solving of telegraph equation with Haar wavelet. Int. J. Math. Comput. Sci. 2016, 3, 6–10. [Google Scholar]
- Latifizadeh, H. The sinc-collocation method for solving the telegraph equation. J. Comput. Inform. 2013, 1, 13–17. [Google Scholar]
- Jiwari, R.; Pandit, S.; Mittal, R.C. A differential quadrature algorithm for the numerical solution of the second-order one dimensional hyperbolic telegraph equation. Int. J. Nonlinear Sci. 2012, 13, 259–266. [Google Scholar]
- Wang, Y.; Mei, L. Generalized finite difference/spectral Galerkin approximations for the time-fractional telegraph equation. Adv. Differ. Equations 2017, 2017, 281. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Kumar, S. Analytic and approximate solutions of space-time fractional telegraph equations via Laplace transform. Walailak J. Sci. Technol. 2013, 11, 711–728. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, H.; Shah, R.; Kumam, P.; Baleanu, D.; Arif, M. An Efficient Analytical Technique, for The Solution of Fractional-Order Telegraph Equations. Mathematics 2019, 7, 426. https://doi.org/10.3390/math7050426
Khan H, Shah R, Kumam P, Baleanu D, Arif M. An Efficient Analytical Technique, for The Solution of Fractional-Order Telegraph Equations. Mathematics. 2019; 7(5):426. https://doi.org/10.3390/math7050426
Chicago/Turabian StyleKhan, Hassan, Rasool Shah, Poom Kumam, Dumitru Baleanu, and Muhammad Arif. 2019. "An Efficient Analytical Technique, for The Solution of Fractional-Order Telegraph Equations" Mathematics 7, no. 5: 426. https://doi.org/10.3390/math7050426
APA StyleKhan, H., Shah, R., Kumam, P., Baleanu, D., & Arif, M. (2019). An Efficient Analytical Technique, for The Solution of Fractional-Order Telegraph Equations. Mathematics, 7(5), 426. https://doi.org/10.3390/math7050426






