Cutting Convex Polytopes by Hyperplanes

Abstract

Cutting a polytope is a very natural way to produce new classes of interesting polytopes. Moreover, it has been very enlightening to explore which algebraic and combinatorial properties of the original polytope are hereditary to its subpolytopes obtained by a cut. In this work, we devote our attention to all the separating hyperplanes for some given polytope (integral and convex) and study the existence and classification of such hyperplanes. We prove the existence of separating hyperplanes for the order and chain polytopes for any finite posets that are not a single chain, and prove there are no such hyperplanes for any Birkhoff polytopes. Moreover, we give a complete separating hyperplane classification for the unit cube and its subpolytopes obtained by one cut, together with some partial classification results for order and chain polytopes.

1. Introduction

Let $\mathcal{P}\subset {\mathbb{R}}^n$ be a convex polytope of dimension d and $\partial \mathcal{P}$ its boundary. If $\mathcal{H}\subset {\mathbb{R}}^n$ is a hyperplane, then we write ${\mathcal{H}}^{(+)}$ and ${\mathcal{H}}^{(-)}$ for the closed half-spaces of ${\mathbb{R}}^n$ with ${\mathcal{H}}^{(+)}\cap {\mathcal{H}}^{(-)}=\mathcal{H}$. We say that $\mathcal{H}$ cuts $\mathcal{P}$ if $\mathcal{H}\cap (\mathcal{P}\backslash \partial \mathcal{P})\ne ⌀$ and if each vertex of the convex polytopes $\mathcal{P}\cap {\mathcal{H}}^{(+)}$ and $\mathcal{P}\cap {\mathcal{H}}^{(-)}$ is a vertex of $\mathcal{P}$. When $\mathcal{H}\cap (\mathcal{P}\backslash \partial \mathcal{P})\ne ⌀$, it follows that $\mathcal{H}$ cuts $\mathcal{P}$ if and only if, for each edge $e=conv\left(\{v,v^{\prime }\}\right)$ of $\mathcal{P}$, where v and $v^{\prime }$ are vertices of $\mathcal{P}$, and not $e\subset \mathcal{H}$, one has $\mathcal{H}\cap e\subset \{v,v^{\prime }\}$. Cutting a polytope is a very natural way to produce new classes of interesting polytopes. For example, the hypersimplices are obtained from cutting the unit n cube by hyperplanes of the form $x_1+\cdots +x_n=k,k+1$, for some integer $0\le k<n$, which is a class of very interesting and well-studied polytopes (see for example [1,2,3]). A similar class of interesting polytopes obtained from cutting permutahedrons and in general any graphical zonotopes are studied in [4]. In general, it is a very interesting problem to explore which algebraic and combinatorial properties of $\mathcal{P}$ are hereditary to $\mathcal{P}\cap {\mathcal{H}}^{(+)}$ and $\mathcal{P}\cap {\mathcal{H}}^{(-)}$. For example, in [5] the study on separating hyperplanes of the edge polytope ${\mathcal{P}}_G$ of a finite connected simple graph G is achieved and it is shown that ${\mathcal{P}}_G$ is normal if and only if each of ${\mathcal{P}}_G\cap {\mathcal{H}}^{(+)}$ and ${\mathcal{P}}_G\cap {\mathcal{H}}^{(-)}$ is normal.

In this paper, we look at the problem from another perspective, focusing more on the hyperplane that cuts the polytope. We are interested in the existence and classification of such hyperplanes.

If $\mathcal{H}$ cuts $\mathcal{P}$, then we call $\mathcal{H}$ a separating hyperplane of $\mathcal{P}$. If $\mathcal{H}$ is a separating hyperplane of $\mathcal{P}$, then the decomposition of $\mathcal{P}$ via $\mathcal{H}$ is

$$\mathcal{P}=(\mathcal{P}\cap {\mathcal{H}}^{(+)})\cup (\mathcal{P}\cap {\mathcal{H}}^{(-)}).$$

For example, if ${[0,1]}^3\subset {\mathbb{R}}^3$ is the unit cube, then the hyperplane $\mathcal{H}\subset {\mathbb{R}}^3$ defined by the equation $x_i+x_j=1$ with $1\le i<j\le 3$ is a separating hyperplane of ${[0,1]}^3$.

Unless $n=d$, where $d=dim\mathcal{P}$, two different separating hyperplanes $\mathcal{H}$ and ${\mathcal{H}}^{\prime }$ of $\mathcal{P}$ might yield the same decomposition of $\mathcal{P}$. For example, if ${[0,1]}^2\subset {\mathbb{R}}^3$ is the square, then its separating hyperplane defined by $x_1+x_2+x_3=1$ and that defined by $x_1+x_2-x_3=1$ clearly yield the same decomposition of ${[0,1]}^2$.

An integral convex polytope is a convex polytope whose vertices have integer coordinates. Let $\mathcal{P}\subset {\mathbb{R}}^n$ be an integral convex polytope of dimension d and suppose that $\partial \mathcal{P}\cap {\mathbb{Z}}^n$ is the set of vertices of $\mathcal{P}$. It then follows that a hyperplane $\mathcal{H}\subset {\mathbb{R}}^n$ is a separating hyperplane of $\mathcal{P}$ if and only if each of the subpolytopes $\mathcal{P}\cap {\mathcal{H}}^{(+)}$ and $\mathcal{P}\cap {\mathcal{H}}^{(-)}$ is integral of dimension d.

The study of existence and classification for any general internal convex polytopes can be very hard. In the present paper, we focus our study on the following classes of polytopes: The unit cube and its subpolytopes cut by one hyperplane, order and chain polytopes, and Birkhoff polytopes. We prove the existence of separating hyperplanes for the order and chain polytopes for any finite posets that are not a single chain (Theorem 2), and prove there are no separating hyperplanes for any Birkhoff polytopes (Theorem 3). Moreover, we give a complete separating hyperplane classification for the unit cube and its subpolytopes cut by one hyperplane (Section 1), together with partial classification results for order and chain polytopes (Section 2).

2. The Unit Cube

Let ${[0,1]}^d\subset {\mathbb{R}}^d$ be the unit cube with $d\ge 2$. In the study of its separating hyperplane $\mathcal{H}$ it is assumed that $\mathcal{H}$ passes through the origin of ${\mathbb{R}}^d$. First, we discuss the question when a hyperplane $\mathcal{H}$ of ${\mathbb{R}}^d$ passing through the origin

$$\begin{array}{c}\hfill \mathcal{H}:a_1{x}_1+\cdots +a_d{x}_d=0,\end{array}$$

(1)

where each $a_i\in \mathbb{Q}$, is a separating hyperplane of ${[0,1]}^d$.

Lemma 1.

A hyperplane (1) is a separating hyperplane of ${[0,1]}^d$ if and only if there exist p and q with $a_p>0$ and $a_q<0$ and all nonzero coefficients of $\mathcal{H}$ have the same absolute value.

Proof. 

(“If”) Let e be an edge of ${[0,1]}^d$. Then there is $1\le i\le d$ with

$$e=\{(x_1,\dots ,x_d):0\le x_i\le 1\mathrm{and}{x}_j={\epsilon }_j\mathrm{for}\mathrm{all}j\ne i\},$$

where each ${\epsilon }_j$ belongs to $\{0,1\}$. Suppose that there exist p and q with $a_p>0$ and $a_q<0$ and that all nonzero coefficients of $\mathcal{H}$ have the same absolute value. By relabeling the subscripts (if necessary), we may assume that

$$\mathcal{H}:x_1+\cdots +x_s-x_{s+1}-\cdots -x_{s+t}=0,$$

where $s>0$, $t>0$ and $s+t\le d$. If $i>s+t$, then either $\mathcal{H}\cap e=e$ or $\mathcal{H}\cap e=⌀$. If $i\le s+t$, then either $\mathcal{H}\cap e=⌀$ or $\mathcal{H}\cap e$ is a vertex of ${[0,1]}^d$. Thus, each of ${[0,1]}^d\cap {\mathcal{H}}^{(+)}$ and ${[0,1]}^d\cap {\mathcal{H}}^{(-)}$ is integral. Moreover, since $s>0$ and $t>0$, it follows that $\mathcal{H}\cap {(0,1)}^d\ne ⌀$. Hence $\mathcal{H}$ is a separating hyperplane of ${[0,1]}^d$.

(“Only if”) If every coefficient $a_i$ of (1) is nonnegative, then $\mathcal{H}\cap {[0,1]}^d$ consists only of the origin. Hence $\mathcal{H}$ cannot be a separating hyperplane of ${[0,1]}^d$. Thus, there exists p and q with $a_p>0$ and $a_q<0$.

Now, suppose that there exist $i\ne j$ with $a_i\ne 0$, $a_j\ne 0$ and $|a_i|\ne |a_j|$. Let, say, $|a_i|<|a_j|$. Let e be the edge defined by $x_i=1$ and $x_k=0$ for all k with $k\notin \{i,j\}$. If $a_i{a}_j<0$, then $0<-a_i/a_j<1$ and $v=(v_1,\dots ,v_n)\in e$ with $v_j=-a_i/a_j$ belongs to $\mathcal{H}$. Thus, $\mathcal{H}$ cannot be a separating hyperplane of ${[0,1]}^d$. Hence $a_i{a}_j>0$. In particular $|a_p|=|a_q|$. Let $1\le k\le d$ with $a_k>0$. Then, since $a_k{a}_q<0$, it follows that $|a_k|=|a_q|$. Similarly, if $a_k<0$, then $|a_k|=|a_p|$. Consequently, $|a_k|=|a_p\left|\right(=|a_p\left|\right)$ for all k with $a_k\ne 0$, as desired. □

By virtue of Lemma 1, it follows that up to permuting the coordinates, a separating hyperplane of ${[0,1]}^d$ passing through the origin is of the form

$$\begin{array}{c}\hfill x_1+\cdots +x_s-x_{s+1}-\cdots -x_{s+t}=0\end{array}$$

(2)

with $s>0$, $t>0$ and $s+t\le d$. Moreover, in (2), by replacing $x_{s+i}$ with $1-x_{s+i}$ for $1\le i\le t$, we can work with a separating hyperplane of ${[0,1]}^d$ of the form

$$\begin{array}{c}\hfill x_1+\cdots +x_s+x_{s+1}+\cdots +x_{s+t}=t.\end{array}$$

(3)

Finally, Equation (3) can be rewritten as

$$\begin{array}{c}\hfill x_1+\cdots +x_k=\ell ,2\le k\le d,1\le \ell <k.\end{array}$$

(4)

If ${\mathcal{H}}_{k,\ell }$ is a separating hyperplane defined by (4) of ${[0,1]}^d$, then

$${[0,1]}^d\cap {\mathcal{H}}_{k,\ell }^{(+)}=\{(x_1,\cdots ,x_d)\in {[0,1]}^d:x_1+\cdots +x_k\le \ell \},$$

$${[0,1]}^d\cap {\mathcal{H}}_{k,\ell }^{(-)}=\{(x_1,\cdots ,x_d)\in {[0,1]}^d:x_1+\cdots +x_k\ge \ell \}.$$

In ${[0,1]}^d\cap {\mathcal{H}}_{k,\ell }^{(-)}$, again, by replacing $x_i$ with $1-x_i$ for $1\le i\le k$, it follows that since $0<k-\ell <k$, each of the subpolytopes ${[0,1]}^d\cap {\mathcal{H}}_{k,\ell }^{(\pm )}$ is, up to unimodular equivalence, of the form

$${\mathcal{Q}}_{k,\ell }=\{(x_1,\dots ,x_d)\in {[0,1]}^d:x_1+\cdots +x_k\le \ell \},2\le k\le d,1\le \ell <k.$$

(5)

It follows easily that when $(k,\ell )\ne (k^{\prime },{\ell }^{\prime })$, two subpolytopes ${\mathcal{Q}}_{k,\ell }$ and ${\mathcal{Q}}_{k^{\prime },{\ell }^{\prime }}$ cannot be unimodularly equivalent. Hence

Corollary 1.

The number of convex polytopes of the form ${[0,1]}^d\cap {\mathcal{H}}^{(\pm )}$, where $\mathcal{H}$ is a separating hyperplane of ${[0,1]}^d$ is, up to unimodular equivalence, $d(d-1)/2$.

We now turn to the problem of finding separating hyperplanes of the subpolytope ${\mathcal{Q}}_{k,\ell }$ of ${[0,1]}^d$. We say that a separating hyperplane of ${\mathcal{Q}}_{k,\ell }$ (of the form (5)) is a second separating hyperplane of ${[0,1]}^d$ following the hyperplane ${\mathcal{H}}_{k,\ell }$.

Lemma 2.

Each of the separating hyperplanes of ${[0,1]}^d$ is of the form

$$\sum _{i\in I}{x}_i-\sum _{j\in J}{x}_j=h,$$

where $⌀\ne I\subset \left[d\right]$, $⌀\ne J\subset \left[d\right]$, $I\cap J=⌀$ and where $h\ge 0$ is an integer with $0\le h<♯\left(I\right)$.

Proof. 

Let $v=(v_1,\dots ,v_d)$ be a vertex of ${[0,1]}^d$. Let $I\subset \left[d\right]$ and $J\subset \left[d\right]$ with $I\cup J=\left[d\right]$ and $I\cap J=⌀$ such that $v_i=0$ if $i\in I$ and $v_j=1$ if $j\in J$. Let

$$\begin{array}{c}\hfill \mathcal{H}:a_1{x}_1+\cdots +a_d{x}_d=\sum _{j\in J}{a}_j,\end{array}$$

(6)

with each $a_i\in \mathbb{Q}$, be a separating hyperplane of ${[0,1]}^d$ passing through v. In (6) replace $x_j$ with $1-x_j$ for $j\in J$, and the hyperplane

$$\begin{array}{c}\hfill {\mathcal{H}}^{\prime }:\sum _{i\in I}{a}_i{x}_i+\sum _{j\in J}(-a_j)x_j=0\end{array}$$

(7)

is a separating hyperplane of ${[0,1]}^d$ passing through the origin. It then follows from Lemma 1 that all nonzero coefficients of (7) have the same absolute value. Thus, each of $a_i$’s and $a_j$’ belongs to $\{0,\pm 1\}$.

It turns out that Equation (6) is

$$\mathcal{H}:\sum _{p\in I^{\prime }}{x}_p-\sum _{q\in J^{\prime }}{x}_q=h,$$

where $⌀\ne I^{\prime }\subset \left[d\right]$, $⌀\ne J^{\prime }\subset \left[d\right]$, $I\cap J=⌀$ and where $h\ge 0$ is an integer. If $h\ge ♯\left(I^{\prime }\right)$, then ${[0,1]}^d\subset {\mathcal{H}}^{(+)}$ or ${[0,1]}^d\subset {\mathcal{H}}^{(-)}$. Hence $0\le h<♯\left(I^{\prime }\right)$. If $0\le h<♯\left(I^{\prime }\right)$, then

$$({\mathcal{H}}^{(+)}\backslash \mathcal{H})\cap {[0,1]}^d\ne ⌀,({\mathcal{H}}^{(-)}\backslash \mathcal{H})\cap {[0,1]}^d\ne ⌀.$$

Thus, $\mathcal{H}$ is, in fact, a separating hyperplane of ${[0,1]}^d$. □

Let ${\mathcal{H}}^{\prime }\subset {\mathbb{R}}^d$ be a second separating hyperplane of ${[0,1]}^d$ following (4). Clearly ${\mathcal{H}}^{\prime }$ is a separating hyperplane of ${[0,1]}^d$. It then follows from Theorem 2 that

$$\begin{array}{c}\hfill {\mathcal{H}}^{\prime }:\sum _{i\in I}{x}_i-\sum _{j\in J}{x}_j=h,\end{array}$$

(8)

where $⌀\ne I\subset \left[d\right]$, $⌀\ne J\subset \left[d\right]$, $I\cap J=⌀$ and where $h\ge 0$ is an integer with $0\le h<♯\left(I\right)$.

Theorem 1.

A hyperplane ${\mathcal{H}}^{\prime }$ of (8) is a second separating hyperplane of ${[0,1]}^d$ following (4) if and only if one of the following conditions is satisfied:

• $♯\left(J\right)+h+k-♯\left(X\right)\le \ell$;
• $♯\left(I\right)-h+k-♯\left(Y\right)\le \ell$,

where $X=I\cap \left[k\right]$ and $Y=J\cap \left[k\right]$.

Proof. 

Let $\mathcal{P}\subset {\mathbb{R}}^d$ denote the subpolytope (5) of ${[0,1]}^d$. Then a hyperplane ${\mathcal{H}}^{\prime }$ of (8) is a second separating hyperplane of ${[0,1]}^d$ following (4) if and only if one has ${\mathcal{H}}^{\prime }\cap {[0,1]}^d\subset \mathcal{P}$.

(“If”) Let $v=(v_1,\dots ,v_d)\in {[0,1]}^d$ belong to ${\mathcal{H}}^{\prime }$, i.e., ${\sum }_{i\in I}{v}_i-{\sum }_{j\in J}{v}_j=h$. If $♯\left(J\right)+h+k-♯\left(X\right)\le \ell$, then

$$\begin{array}{ccc}\hfill v_1+\cdots +v_k& =& \sum _{i\in X}{v}_i+\sum _{i\in \left[k\right]\backslash X}{v}_i\hfill \\ \hfill \hspace{1em}& \le & \sum _{i\in I}{v}_i+\sum _{i\in \left[k\right]\backslash X}{v}_i\hfill \\ \hfill \hspace{1em}& =& h+\sum _{j\in J}{v}_j+\sum _{i\in \left[k\right]\backslash X}{v}_i\hfill \\ \hfill \hspace{1em}& \le & h+♯\left(J\right)+k-♯\left(X\right)\le \ell .\hfill \end{array}$$

Hence $v\in \mathcal{P}$. If $♯\left(I\right)-h+k-♯\left(Y\right)\le \ell$, then

$$\begin{array}{ccc}\hfill v_1+\cdots +v_k& =& \sum _{i\in Y}{v}_i+\sum _{i\in \left[k\right]\backslash Y}{v}_i\hfill \\ \hfill \hspace{1em}& \le & \sum _{i\in J}{v}_i+\sum _{i\in \left[k\right]\backslash Y}{v}_i\hfill \\ \hfill \hspace{1em}& =& -h+\sum _{j\in I}{v}_j+\sum _{i\in \left[k\right]\backslash Y}{v}_i\hfill \\ \hfill \hspace{1em}& \le & -h+♯\left(I\right)+k-♯\left(Y\right)\le \ell .\hfill \end{array}$$

Hence $v\in \mathcal{P}$.

(“Only if”) Let $♯\left(J\right)+h+k-♯\left(X\right)>\ell$ and $♯\left(I\right)-h+k-♯\left(Y\right)>\ell$. We claim the existence of $v=(v_1,\dots ,v_d)\in {[0,1]}^d$ with $v\in {\mathcal{H}}^{\prime }$ such that $v_1+\cdots +v_k>\ell$.

Let $♯\left(I\right)\le ♯\left(J\right)+h$. Then $0\le h<♯\left(I\right)\le ♯\left(J\right)+h$. Thus, there is $v\in {[0,1]}^d$ belonging to ${\mathcal{H}}^{\prime }$ with $v_i=1$ for all $i\in I$ such that if $j\in Y$ and $j^{\prime }\in J\backslash Y$ then $v_j\ge v_{j^{\prime }}$. Such $v\in {\mathcal{H}}^{\prime }\cap {[0,1]}^d$ can be chosen with $v_i=1$ for all $\left[k\right]\backslash (X\cup Y)$. Then

$$\begin{array}{ccc}\hfill v_1+\cdots +v_k& \ge & ♯\left(X\right)+min\{♯(I)-h,♯(Y\left)\right\}+♯\left(\right[k]\backslash (X\cup Y\left)\right)\hfill \\ \hfill \hspace{1em}& =& ♯\left(X\right)+min\{♯(I)-h,♯(Y\left)\right\}+k-♯\left(X\right)-♯\left(Y\right)\hfill \\ \hfill \hspace{1em}& =& min\{♯(I)-h,♯(Y\left)\right\}+k-♯\left(Y\right)\hfill \\ \hfill \hspace{1em}& =& min\{♯(I)-h+k-♯(Y),k\}.\hfill \end{array}$$

Since $♯\left(I\right)-h+k-♯\left(Y\right)>\ell$ and $k>\ell$, it follows that $v_1+\cdots +v_k>\ell$.

Let $♯\left(I\right)>♯\left(J\right)+h$. Then there is $v\in {[0,1]}^d$ belonging to ${\mathcal{H}}^{\prime }$ with $v_j=1$ for all $j\in J$ such that if $i\in X$ and $i^{\prime }\in I\backslash X$ then $v_i\ge v_{i^{\prime }}$. Such $v\in {\mathcal{H}}^{\prime }\cap {[0,1]}^d$ can be chosen with $v_i=1$ for all $\left[k\right]\backslash (X\cup Y)$. Then

$$\begin{array}{ccc}\hfill v_1+\cdots +v_k& \ge & ♯\left(Y\right)+min\{♯(J)+h,♯(X\left)\right\}+♯\left(\right[k]\backslash (X\cup Y\left)\right)\hfill \\ \hfill \hspace{1em}& =& ♯\left(Y\right)+min\{♯(J)+h,♯(X\left)\right\}+k-♯\left(X\right)-♯\left(Y\right)\hfill \\ \hfill \hspace{1em}& =& min\{♯(J)+h,♯(X\left)\right\}+k-♯\left(X\right)\hfill \\ \hfill \hspace{1em}& =& min\{♯(J)+h+k-♯(X),k\}.\hfill \end{array}$$

Since $♯\left(J\right)+h+k-♯\left(X\right)>\ell$ and $k>\ell$, it follows that $v_1+\cdots +v_k>\ell$. □

Corollary 2.

Let

$$\begin{array}{c}\hfill x_1+\cdots +x_d=\ell ,1\le \ell <d\end{array}$$

(9)

be a separating hyperplane of ${[0,1]}^d$. Then a hyperplane

$$x_1+\cdots +x_s=x_{s+1}+\cdots +x_{s+t}+h,0\le h<s$$

is a second separating hyperplane of ${[0,1]}^d$ following (9) if and only if one of the following conditions is satisfied:

• $d-\ell \le s-(t+h)$;
• $d-\ell \le (t+h)-s$.

3. Order and Chain Polytopes

Let $P=\{{\xi }_1,\dots ,{\xi }_d\}$ be a finite partially ordered set ( poset for short). To each subset $W\subset P$, we associate $\rho \left(W\right)={\sum }_{{\xi }_i\in W}{\mathit{e}}_i\in {\mathbb{R}}^d$, where ${\mathit{e}}_1,\dots ,{\mathit{e}}_d$ are the unit coordinate vectors of ${\mathbb{R}}^d$. In particular $\rho (⌀)$ is the origin of ${\mathbb{R}}^d$. A poset ideal of P is a subset I of P such that for all ${\xi }_i$ and ${\xi }_j$ with ${\xi }_i\in I$ and ${\xi }_j\le {\xi }_i$, one has ${\xi }_j\in I$. An antichain of P is a subset A of P such that ${\xi }_i$ and ${\xi }_j$ belonging to A with $i\ne j$ are incomparable. We say that ${\xi }_j$covers${\xi }_i$ if ${\xi }_i<{\xi }_j$ and ${\xi }_i<{\xi }_k<{\xi }_j$ for no ${\xi }_k\in P$. A chain ${\xi }_{j_1}<{\xi }_{j_2}<\cdots <{\xi }_{j_{\ell }}$ of P is called saturated if ${\xi }_{j_q}$ covers ${\xi }_{j_{q-1}}$ for $1<q\le \ell$. A maximal chain is a saturated chain such that ${\xi }_{j_1}$ is a minimal element and ${\xi }_{j_{\ell }}$ is a maximal element of the poset.

The order polytope of P is the convex polytope $\mathcal{O}\left(P\right)\subset {\mathbb{R}}^d$ which consists of those $(x_1,\dots ,x_d)\in {\mathbb{R}}^d$ such that $0\le x_i\le 1$ for every $1\le i\le d$ together with

$$x_i\ge x_j$$

if ${\xi }_i\le {\xi }_j$ in P.

The chain polytope of P is the convex polytope $\mathcal{C}\left(P\right)\subset {\mathbb{R}}^d$ which consists of those $(x_1,\dots ,x_d)\in {\mathbb{R}}^d$ such that $x_i\ge 0$ for every $1\le i\le d$ together with

$$x_{i_1}+x_{i_2}+\cdots +x_{i_k}\le 1$$

for every maximal chain ${\xi }_{i_1}<{\xi }_{i_2}<\cdots <{\xi }_{i_k}$ of P.

One has $dim\mathcal{O}\left(P\right)=dim\mathcal{C}\left(P\right)=d$. The number of vertices of $\mathcal{O}\left(P\right)$ is equal to that of $\mathcal{C}\left(P\right)$. Moreover, the volume of $\mathcal{O}\left(P\right)$ and that of $\mathcal{C}\left(P\right)$ are equal to $e\left(P\right)/d!$, where $e\left(P\right)$ is the number of linear extensions of P ([6] (Corollary 4.2)). It also follows from [6] that the facets of $\mathcal{O}\left(P\right)$ are the following:

• $x_i=0$, where ${\xi }_i\in P$ is maximal;
• $x_j=1$, where ${\xi }_j\in P$ is minimal;
• $x_i=x_j$, where ${\xi }_j$ covers ${\xi }_i$.

And that the facets of $\mathcal{C}\left(P\right)$ are the following:

• $x_i=0$ for all ${\xi }_i\in P$;
• $x_{i_1}+\cdots +x_{i_k}=1$, where ${\xi }_{i_1}<\cdots <{\xi }_{i_k}$ is a maximal chain of P.

Moreover, we have the following descriptions for vertices, which will be used frequently in this section.

Lemma 3 ([6]).

(1) 

Each vertex of the order polytope $\mathcal{O}\left(P\right)$ is of the form $\rho \left(I\right)$, where I is a poset ideal of P.

(2) 

Each vertex of the chain polytope $\mathcal{C}\left(P\right)$ is of the form $\rho \left(A\right)$, where A is an antichain of P.

Please note that in [6], “dual poset ideals” are employed instead of poset ideals. However, no essential difference arises.

3.1. Existence of Separating Hyperplanes for Order and Chain Polytopes

In this subsection, we study the existence of separating hyperplanes of order polytopes and chain polytopes (Theorem 2). First we need an explicit description of edges in terms of vertices.

Recall that the comparability graph $\mathrm{Com}\left(P\right)$ of P is the finite simple graph on the vertex set $\{{\xi }_1,\dots ,{\xi }_d\}$ whose edges are those $\{{\xi }_i,{\xi }_j\}$ with $i\ne j$ for which ${\xi }_i$ and ${\xi }_j$ are comparable in P. In general, we say that a nonempty subset $Q=\{{\xi }_{k_1},\dots ,{\xi }_{k_q}\}$ of P is connected inP if the induced subgraph of $\mathrm{Com}\left(P\right)$ on $\{{\xi }_{k_1},\dots ,{\xi }_{k_q}\}$ is connected.

Lemma 4.

Let I and J be poset ideals of P with $I\ne J$. Then $conv\left(\right\{\rho \left(I\right),\rho \left(J\right)\left\}\right)$ forms an edge of $\mathcal{O}\left(P\right)$ if and only if $I\subset J$ and $J\backslash I$ is connected in P.

Proof. 

If there exists a maximal element ${\xi }_i$ of P not belonging to $I\cup J$, then $conv\left(\right\{\rho \left(I\right),\rho \left(J\right)\left\}\right)$ lies in the facet $x_i=0$. If there exists a minimal element ${\xi }_j$ of P belonging to $I\cap J$, then $conv\left(\right\{\rho \left(I\right),\rho \left(J\right)\left\}\right)$ lies in the facet $x_j=1$. Hence, working with induction on d, we may assume that $I\cup J=P$ and $I\cap J=⌀$.

Let neither $I=⌀$ nor $J=⌀$. Then P is the disjoint union of I and J. Now, suppose that $conv\left(\right\{\rho \left(I\right),\rho \left(J\right)\left\}\right)$ is an edge of $\mathcal{O}\left(P\right)$. Then there exists a supporting hyperplane $\mathcal{H}$ of $\mathcal{O}\left(P\right)$ defined by the equation $h\left(x\right)={\sum }_{i=1}^d{a}_i{x}_i=1$ with each $a_i\in \mathbb{Q}$ such that $\mathcal{H}\cap \mathcal{O}\left(P\right)=conv\left(\right\{\rho \left(I\right),\rho \left(J\right)\left\}\right)$. Since ${\sum }_{x_i\in I}{a}_i={\sum }_{x_j\in J}{a}_j=1$, one has ${\sum }_{i=1}^d{a}_i=2$. In particular $h\left(\rho \right(P\left)\right)>1$ and $h(⌀)<1$. Thus, $\mathcal{H}$ cannot be a supporting hyperplane of P. In other words, $conv\left(\right\{\rho \left(I\right),\rho \left(J\right)\left\}\right)$ cannot be an edge of P.Hence, if $conv\left(\right\{\rho \left(I\right),\rho \left(J\right)\left\}\right)$ is an edge of P, then either $I=⌀$ or $J=⌀$. Let $I=⌀$ and $J=P$. Suppose that P is disconnected and that $conv\left(\right\{\rho (⌀),\rho \left(P\right)\left\}\right)$ is an edge of P. Again, there exists a supporting hyperplane $\mathcal{H}$ of $\mathcal{O}\left(P\right)$ defined by the equation $h\left(x\right)={\sum }_{i=1}^d{a}_i{x}_i=0$ with each $a_i\in \mathbb{Q}$ such that $\mathcal{H}\cap \mathcal{O}\left(P\right)=conv\left(\right\{\rho (⌀),\rho \left(P\right)\left\}\right)$. Let, say, $h\left(\rho \right(I\left)\right)>0$ for those poset ideals I with $I\ne ⌀$ and $I\ne P$. Since P is disconnected, there exist poset ideals $I^{\prime }$ and $J^{\prime }$ with $I^{\prime }\cap J^{\prime }=⌀$ and $I^{\prime }\cup J^{\prime }=P$. Since $h\left(\rho \left(I^{\prime }\right)\right)>0$ and $h\left(\rho \left(J^{\prime }\right)\right)>0$, it follows that $h\left(\rho \left(P\right)\right)=h\left(\rho \left(I^{\prime }\right)\right)+h\left(\rho \left(J^{\prime }\right)\right)>0$, a contradiction. Thus, P must be connected.

Conversely, suppose that $I=⌀$ and $J=P$ and that P is connected. Let ${\xi }_{i_1},\dots ,{\xi }_{i_q}$ be the maximal elements of P and ${\mathcal{A}}_{i_j}$ the set of those elements $y\in P$ with $y<{\xi }_{i_j}$. Let $k\notin \{i_1,\dots ,i_q\}$. Then we write $b_k$ for the number of $i_j$’s with ${\xi }_k\in {\mathcal{A}}_{i_j}$. Let $b_{i_j}=-♯\left({\mathcal{A}}_{i_j}\right)$. We then claim that the hyperplane $\mathcal{H}$ of ${\mathbb{R}}^d$ defined by the equation $h\left(x\right)={\sum }_{i=1}^d{b}_i{x}_i=0$ is a supporting hyperplane of $\mathcal{O}\left(P\right)$ with $\mathcal{H}\cap \mathcal{O}\left(P\right)=conv\left(\right\{\rho (⌀),\rho \left(P\right)\left\}\right)$. Clearly $h\left(\rho \right(P\left)\right)=h\left(\rho \right(⌀\left)\right)=0$. Let I be a poset ideal of P with $I\ne ⌀$ and $I\ne P$. What we must prove is $h\left(\rho \right(I\left)\right)>0$. To simplify the notation, suppose that $I\cap \{{\xi }_{i_1},\dots ,{\xi }_{i_q}\}=\{{\xi }_{i_1},\dots ,{\xi }_{i_r}\}$, where $0\le r<q$. If $r=0$, then $h\left(\rho \right(I\left)\right)>0$. Let $1\le r<q$ and $J={\cup }_{j=1}^r({\mathcal{A}}_{i_j}\cup {\xi }_{i_j})$. Then J is a poset ideal of P and $h\left(\rho \right(J\left)\right)\le h\left(\rho \right(I\left)\right)$. We claim $h\left(\rho \right(J\left)\right)>0$. One has $h\left(\rho \right(J\left)\right)\ge 0$. Moreover, $h\left(\rho \right(J\left)\right)=0$ if and only if no $z\in J$ belongs to ${\mathcal{A}}_{i_{r+1}}\cup \cdots \cup {\mathcal{A}}_{i_q}$. Now, since P is connected, if follows that there exists $z\in J$ with $z\in {\mathcal{A}}_{i_{r+1}}\cup \cdots \cup {\mathcal{A}}_{i_q}$. Hence $h\left(\rho \right(J\left)\right)>0$. Thus, $h\left(\rho \right(I\left)\right)>0$, as desired. □

Lemma 5.

Let A and B be antichains of Pwith $A\ne B$. Then $conv\left(\right\{\rho \left(A\right),\rho \left(B\right)\left\}\right)$ forms an edge of $\mathcal{C}\left(P\right)$ if and only if $(A\backslash B)\cup (B\backslash A)$ is connected in P.

Proof. 

If $A\cup B\ne P$ and if ${\xi }_i\notin A\cup B$, then $conv\left(\right\{\rho \left(A\right),\rho \left(B\right)\left\}\right)$ lies in the facet $x_i=0$. Furthermore, if $A\cup B=P$ and $A\cap B\ne ⌀$, then ${\xi }_j\in A\cap B$ is isolated in P and ${\xi }_j$ itself is a maximal chain of P. Thus, $conv\left(\right\{\rho \left(A\right),\rho \left(B\right)\left\}\right)$ lies in the facet $x_j=1$. Now, suppose that $A\cup B=P$ and $A\cap B=⌀$. Then $(A\backslash B)\cup (B\backslash A)=A\cup B=P$.

Let $conv\left(\right\{\rho \left(A\right),\rho \left(B\right)\left\}\right)$ be an edge of $\mathcal{C}\left(P\right)$ and $\mathcal{H}$ a supporting hyperplane of $\mathcal{C}\left(P\right)$ defined by $h\left(x\right)={\sum }_{i=1}^d{a}_i{x}_i=1$, where each $a_i\in \mathbb{Q}$, with $\mathcal{H}\cap \mathcal{C}\left(P\right)=conv\left(\right\{\rho \left(A\right),\rho \left(B\right)\left\}\right)$ and $\mathcal{C}\left(P\right)\subset {\mathcal{H}}^{(+)}$. If P is disconnected and if $A_1\cup B_1$ and $A_2\cup B_2$ are antichains of P, where A is the disjoint union of $A_1\cup A_2$ and B is the disjoint union of $B_1\cup B_2$, then $h\left(\rho (A_1\cup B_1)\right)<1$ and $h\left(\rho (A_2\cup B_2)\right)<1$. Hence $h\left(\rho \right(A\cup B)<2$. However, since $h\left(\rho \right(A\left)\right)=1$ and $h\left(\rho \right(B\left)\right)=1$, one has $h\left(\rho \right(A\cup B\left)\right)=2$, a contradiction. Thus, $conv\left(\right\{\rho \left(A\right),\rho \left(B\right)\left\}\right)$ cannot be an edge of $\mathcal{C}\left(P\right)$. Hence P must be connected if $conv\left(\right\{\rho \left(A\right),\rho \left(B\right)\left\}\right)$ is an edge of $\mathcal{C}\left(P\right)$.

Now, suppose that P is connected. If there exist $x,x^{\prime }\in A$ and $y,y^{\prime }\in B$ with $x<y$ and $y^{\prime }<x^{\prime }$, then P cannot be connected. We assume $y<x$ if $x\in A$ and $y\in B$ are comparable. For each ${\xi }_i\in A$ we write $a_i$ for the number of elements $y\in B$ with $y<{\xi }_i$. For each ${\xi }_j\in B$ we write $b_j$ for the number of elements $z\in A$ with ${\xi }_j<z$. Clearly ${\sum }_{{\xi }_i\in A}{a}_i={\sum }_{{\xi }_j\in B}{b}_j=q$, where q is the number of pairs $(x,y)$ with $x\in A$, $y\in B$ and $x<y$. Let $h\left(x\right)={\sum }_{{\xi }_i\in A}{a}_i{x}_i+{\sum }_{{\xi }_j\in B}{b}_j{x}_j$ and $\mathcal{H}$ the hyperplane of ${\mathbb{R}}^d$ defined by $h\left(x\right)=d$. Then $h\left(\rho \right(A\left)\right)=h\left(\rho \right(B\left)\right)=q$. We claim that for any antichain C of P with $C\ne A$ and $C\ne B$, one has $h\left(\rho \right(C\left)\right)<q$. Let $C=A^{\prime }\cup B^{\prime }$ with $A^{\prime }\subset A$ and $B^{\prime }\subset B$. Since $P=A\cup B$ is connected and since C is an antichain of P, it follows that ${\sum }_{{\xi }_i\in A^{\prime }}{a}_i+{\sum }_{{\xi }_j\in B^{\prime }}{b}_j<q$. Thus, $h\left(\rho \right(C\left)\right)<q$, as desired. □

Now we ask the question whether there exists a separating hyperplane of an order polytope as well as that of a chain polytope.

Lemma 6.

Let ${\xi }_i,{\xi }_j\in P$ with ${\xi }_i\ne {\xi }_j$ and ${\mathcal{H}}_{i,j}$ the hyperplane of ${\mathbb{R}}^d$ defined by the equation $x_i=x_j$. Then the following conditions are equivalent:

(i)

${\mathcal{H}}_{i,j}$ is a separating hyperplane of $\mathcal{O}\left(P\right)$;

(ii)

${\mathcal{H}}_{i,j}$ intersects the interior of $\mathcal{O}\left(P\right)$;

(iii)

${\xi }_i$ and ${\xi }_j$ are incomparable in P.

Proof. 

The implication (i) ⇒ (ii) is obvious. Suppose (ii). Then there exist poset ideals I and J of P with $\rho \left(I\right)\in {\mathcal{H}}_{i,j}^{(+)}\backslash {\mathcal{H}}_{i,j}$ and $\rho \left(J\right)\in {\mathcal{H}}_{i,j}^{(-)}\backslash {\mathcal{H}}_{i,j}$. In other words, there exist poset ideals I and J of P with ${\xi }_i\in I\backslash J$ and ${\xi }_j\in J\backslash I$. Thus, in particular ${\xi }_i$ and ${\xi }_j$ are incomparable in P. Hence (ii) ⇒ (iii) follows.

Suppose (iii). Let I be the poset ideal of P consisting of those $y\in P$ with $y\le {\xi }_i$ and J the poset ideal of P consisting of those $y\in P$ with $y\le {\xi }_j$. Since ${\xi }_i$ and ${\xi }_j$ are incomparable in P, it follows that ${\xi }_i\notin J$ and ${\xi }_j\notin I$. Thus $\rho \left(I\right)\in {\mathcal{H}}_{i,j}^{(+)}\backslash {\mathcal{H}}_{i,j}$ and $\rho \left(J\right)\in {\mathcal{H}}_{i,j}^{(-)}\backslash {\mathcal{H}}_{i,j}$. Hence ${\mathcal{H}}_{i,j}$ intersects the interior of $\mathcal{O}\left(P\right)$. Let, in general, $I^{\prime }$ and $J^{\prime }$ be poset ideals of P with $\rho \left(I^{\prime }\right)\in {\mathcal{H}}_{i,j}^{(+)}\backslash \mathcal{H}$ and $\rho \left(J^{\prime }\right)\in {\mathcal{H}}_{i,j}^{(-)}\backslash \mathcal{H}$. In other words, ${\xi }_i\in I\backslash J$ and ${\xi }_j\in J\backslash I$. Hence $I\neg \subset J$ and $J\neg \subset I$. Lemma 4 then guarantees that $conv\left(\right\{\rho \left(I\right),\rho \left(J\right)\left\}\right)$ cannot be an edge of $\mathcal{O}\left(P\right)$. Hence ${\mathcal{H}}_{i,j}$ is a separating hyperplane of $\mathcal{O}\left(P\right)$, as desired. □

Lemma 7.

Let $\mathcal{H}$ be the hyperplane of ${\mathbb{R}}^d$ defined by the equation ${\sum }_{i=1}^d{x}_i-1=0$. Then the following conditions are equivalent:

(i)

$\mathcal{H}$ is a separating hyperplane of $\mathcal{C}\left(P\right)$;

(ii)

$\mathcal{H}$ intersects the interior of $\mathcal{C}\left(P\right)$;

(iii)

P is not a chain.

Proof. 

The implication (i) ⇒ (ii) is obvious. Suppose (ii). Since the origin $\rho (⌀)$ of ${\mathbb{R}}^d$ belongs to ${\mathcal{H}}^{(-)}\backslash \mathcal{H}$, there is an antichain A of P with $\rho \left(A\right)\in {\mathcal{H}}^{(+)}\backslash \mathcal{H}$. Then $♯\left(A\right)\ge 2$. Thus, P cannot be a chain. Hence (ii) ⇒ (iii) follows.

Suppose (iii). One has an antichain A of P with $♯\left(A\right)\ge 2$. Then $\rho \left(A\right)\in {\mathcal{H}}^{(+)}\backslash \mathcal{H}$ and $\rho (⌀)\in {\mathcal{H}}^{(-)}\backslash \mathcal{H}$. Hence $\mathcal{H}$ intersects the interior of $\mathcal{C}\left(P\right)$. Clearly $\rho (⌀)$ is a unique vertex of $\mathcal{C}\left(P\right)$ belonging to ${\mathcal{H}}^{(-)}\backslash \mathcal{H}$. Let B be an antichain of P with $\rho \left(B\right)\in {\mathcal{H}}^{(+)}\backslash \mathcal{H}$. Thus, $♯\left(B\right)\ge 2$. Since $B=(⌀\backslash B)\cup (B\backslash ⌀)$ is disconnected in P, Lemma 5 says that $conv\left(\right\{\rho (⌀),\rho \left(B\right)\left\}\right)$ cannot be an edge. Hence $\mathcal{H}$ is a separating hyperplane of $\mathcal{C}\left(P\right)$, as desired. □

By virtue of Lemmas 6 and 7, it follows immediately that

Theorem 2.

Let P be a finite poset, but not a chain. Then each of the order polytope $\mathcal{O}\left(P\right)$ and the chain polytope $\mathcal{C}\left(P\right)$ possesses a separating hyperplane.

3.2. Description of Separating Hyperplanes for Order and Chain Polytopes

In this subsection, we study the necessary and sufficient conditions for the hyperplane $\mathcal{H}$ defined by

$$h\left(x\right)=c_1{x}_1+c_2{x}_2+\cdots +c_d{x}_d=0$$

to become a separating hyperplane for certain order polytopes and for certain chain polytopes. This study can be very difficult for general posets. Therefore, we focus on the following three basic posets: Disjoint chains; binary trees (assume connected); and zigzag posets (assume connected, a zigzag poset is a poset where its graph looks like a zigzag path, see examples of zigzag posets in Proposition 3). Notice that there are no “X” shape in all the three classes of posets, therefore their chain polytopes and order polytopes are unimodular equivalent ([7]). In this subsection, we will focus on order polytopes, and all results are also true for chain polytopes.

First, by the definition of separating hyperplanes, together with Lemmas 3 and 4 about the descriptions of the vertices and edges for order polytopes, we have the following description.

Lemma 8.

$\mathcal{H}$ is a separating hyperplane for $\mathcal{O}\left(P\right)$ if and only if the following two properties are satisfied:

1.

there exist two poset ideals I and J such that $h\left(\rho \right(I\left)\right)>0$ and $h\left(\rho \right(J\left)\right)<0$ (getting two nontrivial subpolytopes);

2.

$h\left(\rho \right(I\left)\right)h\left(\rho \right(J\left)\right)\ge 0$, for each pair of poset ideals I and J such that $(I\backslash J)\cup (J\backslash I)$ is connected in P.

We call a pair of poset ideals I and J that does not satisfy the second property in Lemma 8 a bad pair for h, i.e., $h\left(\rho \right(I\left)\right)h\left(\rho \right(J\left)\right)<0$ and $(I\backslash J)\cup (J\backslash I)$ is connected in P. In the rest of this subsection, we will prove most necessary conditions for being a separating hyperplane by constructing bad pairs. We are looking for posets which have the following property.

Consider the following three properties of the hyperplane $\mathcal{H}$ defined by $h\left(x\right)=0$.

Property 1.

1.

There exist two minimal elements ${\xi }_i$ and ${\xi }_j$ such that $c_i>0$ and $c_j<0$;

2.

All nonzero coefficients have the same absolute value, i.e., $c_i\in \{0,1,-1\}$ after rescaling, for all $i=1,2,\cdots ,d$;

3.

All the coefficients $c_i$, where ${\xi }_i$ is minimal element of P, uniquely determine the other coefficients.

In what follows, we discuss whether Property 1 can be a necessary and sufficient condition for $\mathcal{H}$ to be a separating hyperplane of the order polytope $\mathcal{O}\left(P\right)$.

Note that once Property 1 is a necessary and sufficient condition for $\mathcal{H}$ to be a separating hyperplane of $\mathcal{O}\left(P\right)$, we can easily check whether a given hyperplane is a separating hyperplane of $\mathcal{O}\left(P\right)$. Moreover, assume all coefficients for minimal elements are not zero, then the total number of separating hyperplanes of $\mathcal{O}\left(P\right)$ will be $2^{\#\left\{\mathrm{of}\min \mathrm{elements}\mathrm{in}P\right\}}$, since each minimal element can only choose to be positive or negative, and then all other coefficients are uniquely determined by the minimal elements. Among the three classes of posets we mentioned: disjoint chains, connected binary trees and connected zigzag posets, only disjoint chains satisfy Property 1. We will provide counter examples for the other two posets and give the best possible results under certain conditions.

Proposition 1.

For the order polytope $\mathcal{O}\left(P\right)$, where P consists of disjoint chains, Property 1 is a necessary and sufficient condition for $\mathcal{H}$ to be a separating hyperplane.

Proof. 

We first prove that all three conditions listed in Property 1 are necessary for $\mathcal{H}$ to be a separating hyperplane.

• By Lemma 8 (1), there exists one order ideal I of $\mathcal{P}$, such that $h\left(\rho \right(I\left)\right)>0$. We assume I is connected, otherwise we look at the chain decomposition of $P=C_1\cup \cdots \cup C_r$ and consider $I\cap C_i$, for $i=1,\cdots ,r$. At least one of the intersections is nonempty and satisfies $h\left(\rho (I\cap C_i)\right)>0$. Now back to the case when I is connected. Since I is a chain, there exists a unique minimal element i in I. We claim that $c_i\ge 0$, where $c_i$ is the coefficient of $x_i$ in $\mathcal{H}$. In fact, if $c_i<0$, I and $J=\left\{i\right\}$ is a bad pair. Actually, here we can assume $c_i>0$, since in the case $c_i=0$, we can simply throw this element away from the poset and look at the new minimal element in the subposet $\mathcal{P}\backslash \left\{i\right\}$. Since the whole I cannot have all coefficients zero, we will just assume $c_i\ne 0$. Similarly, we also have another minimal element j with $c_j<0$.
• We first prove that nonzero coefficients of the minimal elements need to have the same absolute value. For example, consider the following poset.

  Without loss of generality, pick $c_a>0$, $c_b<0$. Suppose $|c_b|>|c_a|$. Let $I=\left\{a\right\}$, $J=\{b,a\}$. Then $(I,J)$ is a bad pair. So, we need $|c_b|=|c_a|$. Considering all pairs of minimal elements with opposite signs, it follows that their coefficients have the same absolute value.
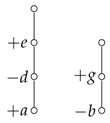  Now consider the pair $I=\left\{a\right\}$, $J=\{a,d\}$, to make $(I,J)$ not bad, we need $c_d\ge -c_a=c_b$. Consider the pair $I=\left\{b\right\}$, $J=\{b,a,d\}$, we have $c_d\le 0$. Then consider the pair $I=\{a,d\}$, $J=\{b,a,d\}$, since we want to avoid zero coefficient, assume $c_d\ne 0$, therefore we have $c_d\le -c_a$. Therefore, we need $c_d=-c_a$. For the same reason, we have $c_g=c_a$. Now consider $c_e$. Similar to above, the pairs $\left(\right\{a\},\{a,d,e\left\}\right)$, $\left(\right\{b\},\{b,a,d,e\left\}\right)$ and $\left(\right\{a,d,e\},\{b,a,d,e\left\}\right)$ provide $c_e=c_a$. Continuing this way, we can show that the signs along each chain need to alternate and their coefficients have the same absolute value.
• We have just shown in the previous part that given the coefficients of the minimal elements, there exists a unique way to extend the coefficients to other elements (assume avoiding zero coefficients), which is exactly Property 1 (3).

Now we want to show that if a hyperplane $\mathcal{H}$ satisfies the three conditions listed in Property 1, then $\mathcal{H}$ is a separating hyperplane. Condition (1) guarantees part (1) in Lemma 8. Now we want to show that there is no bad pair. For any pair of poset ideals $(I,J)$, if $J\backslash I$ is connected, then $J\backslash I$ is a segment in a chain. By the necessary conditions on the coefficients of $\mathcal{H}$, ${\sum }_{i\in J\backslash I}{c}_i\in \{-1,0,1\}$. As a result, no matter what the value of $h\left(v_I\right)$ is, we always have $h\left(v_I\right)h\left(v_J\right)\ge 0$. □

Proposition 2.

For binary trees, the following are true:

1.

Property 1 (1) is necessary.

2.

Property 1 (2) is not necessary.

3.

Assume a separating hyperplane $\mathcal{H}$ satisfying Property 1 (1) and (2), then (3) is also necessary.

4.

However, all three conditions in Property 1 together are not sufficient for a hyperplane to be a separating hyperplane.

Proof. 

• We want to show that there exist two minimal elements i and j such that $c_i>0$ and $c_j<0$. The argument in the proof for the disjoint union of chains also works here. The key point is that for any connected poset ideal I in the binary tree and one of its minimal element i, $I\backslash \left\{i\right\}$ is still connected in $\mathcal{P}$.
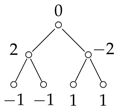
• The argument that all the minimal elements have the same absolute value still holds as in the disjoint union of chains. However, it is possible that not all elements have the same absolute value. For example, consider the hyperplane as the following labelled represented poset, where the label for an element i in P is the coefficient $c_i$ in $\mathcal{H}$. We can check that there are no bad pairs for $\mathcal{H}$, thus $\mathcal{H}$ is a separating hyperplane. However, not all coefficients in $\mathcal{H}$ have the same absolute value.
• Now assume all coefficients have the same absolute value, and thus can only take value from $\{-1,0,1\}$ after rescaling. So here we only need to talk about the sign for an element i in P (+ refers to $c_i=1$ and − refers to $c_i=-1$). Now we want to show that the sign of an element is determined by the sign of its two children. Here “the sign of the child" refers to the sign of the poset ideal generated by that child. In particular, there are exactly six local sign patterns:

  Notice that 0 appears if and only if its children have a + and a −. For two elements $a,b$ with a common parent d,

  (a)

  suppose $c_b=c_a=1$. Let e be a minimal element with $c_e=-1$. Then by the pair $(I=\{e\},J=\langle d,e\rangle )$ (J is the poset ideal generated by d and e), we have $h\left(\rho \right(J\left)\right)\ge 0$, and thus $c_d=-1$. This corresponds to the second tree above, and the same for the first tree.

  (b)

  suppose $c_b=-c_a>0$. Then by the pair $\left(\right\{b\},\{a,b,d\left\}\right)$ and $\left(\right\{a\},\{a,b,d\left\}\right)$, we have $c_d=0$, which corresponds to the third tree above.

  (c)

  suppose $c_b>0$ and $c_a=0$. This indicates that a is larger than some minimal element e with $c_e<0$. Then by the pair $\left(\right\{e\},\langle d\rangle )$ and $\left(\right\{b\},\langle d\rangle )$, we have $h\left(\rho \right(\langle d\rangle \left)\right)=0$, thus $c_d=-c_b$, which corresponds to the forth tree above. The fifth and the sixth tree can be obtained in a similar way.

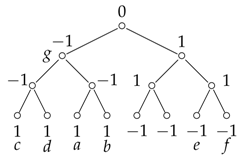
• Following the above rule will not always result in a separating hyperplane. For example, consider the hyperplane represented by the following labelled poset.

  One can easily check that the above hyperplane follows the six local rules listed above as well the other two conditions in Property 1. However, for example, $I=\langle g,e,f\rangle$ and $J=\langle a,b,c,d,e,f\rangle$ is a bad pair.

 □

Proposition 3.

For the zigzag posets, Property 1 (1) is not necessary for $\mathcal{H}$ to be a separating hyperplane. However, for any hyperplane $\mathcal{H}$ with Property 1 (1), the other two conditions listed in Property 1 are necessary and sufficient conditions for $\mathcal{H}$ to be a separating hyperplane.

Proof. 

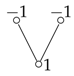
The following example is a separating hyperplane but does not satisfy Property 1 (1).

Now assume $\mathcal{H}$ is a hyperplane satisfying Property 1 (1). We first prove that if $\mathcal{H}$ is a separating hyperplane, then both Property 1 (2) and (3) are true.

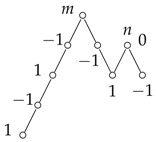
• We want to prove that all the nonzero coefficients in any separating hyperplane for a zigzag poset have the same absolute value. First notice that all the minimal elements have the same absolute value, as proved in Proposition 1. Following the same proposition, all the non-maximal elements (if nonzero) have the same absolute value. As for the maximal elements, let us have a closer look at the zigzag poset. One maximal element m covers at most two minimal elements $p,q$. For the case m only covers one minimal element, the coefficient $c_m$ needs to have the same absolute value for the same reason as disjoint chains proved in Proposition 1. Now there are two cases when m covers two minimal elements $p,q$:

  (a)

  $c_p·c_q<0$. Let $I=\langle m\rangle$ be the poset ideal generated by m. Consider the pair I and J, where $J=\left\{p\right\}$ or $\left\{q\right\}$. We have $h\left(\rho \right(I\left)\right)=0$, which implies $|c_m|\le 1$.

  (b)

  $c_p·c_q>0$. Say $c_p=c_q=1$. Let n be a maximal element adjacent to m that covers two minimal elements with different signs. For example,

  Consider the poset ideal $I=\langle m,n\rangle$. Similar to the previous case, we have $h\left(\rho \right(I\left)\right)=0$, which still implies $|c_m|\le 1$.

• Since $\mathcal{H}$ satisfies conditions (1) and (2) in Property 1, once we fix the signs of all the minimal elements, all elements except those maximal are uniquely determined the same way as the disjoint chains (Proposition 1). As for the maximal elements, they are uniquely determined by the signs of their two children the same as the binary trees (Proposition 2).

Now we want to prove that any hyperplane $h\left(x\right)=0$ satisfying the three conditions listed in Property 1 is a separating hyperplane. The condition (1) in Property 1 implies condition (1) in Lemma 8. Now we want to show that there are no bad pairs. Notice that by the rules described above, any connected component has value sum to $\{1,0,-1\}$. In the case $I\subset J$, if $h\left(\rho \right(I\left)\right)<0$, then $h\left(\rho \right(J\left)\right)=h\left(\rho \right(I\left)\right)+h\left(\rho J\backslash I\right)<1$, since $h\left(\rho \right(J\backslash I\left)\right)<1$. Now we claim that for the zigzag poset, the condition that $(I\backslash J)\cup (J\backslash I)$ is connected, implies that $I\backslash J$ or $J\backslash I$ is empty. Consider a generic connected subposet $S=(I\backslash J)\cup (J\backslash I)$. We want to show that $S\subset I$ or $S\subset J$. If S only has one maximal element, then it is clear that all the elements belong to the same order ideal as the maximal element (either I or J). If there are more than one maximal element, see the following example.

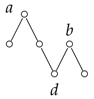
Consider two adjacent maximal elements (they are a and b in the example). These two maximal elements cover a common minimal element d, because this subposet is connected. Then d belongs to the same poset ideal as both a and b. Therefore, both a and b belong to the same poset ideal. This shows that S belongs to either I or J. □

4. Birkhoff Polytopes

The Birkhoff polytope $B_n$ is defined to be the convex hull of all $n\times n$ nonnegative real matrices with row sum and column sum equal to one. These matrices are known as the doubly stochastic matrices. Here we consider an $n\times n$ matrix as a $n^2$-vector. The Birkhoff polytope is a well-studied polytope and have many applications, in combinatorial optimization and Bayesian statistics, for example [8,9]. In this section, we look for separating hyperplanes for $B_n$ (Theorem 3).

In the rest of the section, we assume the hyperplanes have the form

$$h\left(x\right)=c_1{x}_1+\cdots +c_{n^2}{x}_{n^2}=0,$$

but actually all the results hold for general hyperplanes $h\left(x\right)=r$ for any constant r. We start with the following known properties of the Birkhoff polytope $B_n$. Here we use both the one-line notation and the cycle notation for a permutation. For example, $w=34256187$ is the one-line notation for the permutation sending $1\to 3$, $2\to 4$, $3\to 2$, $4\to 5$, $5\to 6$, $6\to 1$, $7\to 8$ and $8\to 7$. The cycle notation for w is $\left(132456\right)\left(78\right)$, thus w has two cycles.

• $dim{B}_n={(n-1)}^2$;
• $B_n$ has $n!$ vertices, which are the $n\times n$ permutation matrices;
• permutations w and u form an edge in $B_n$ if and only if $w^{-1}u$ has one cycle (excluding the fixed points), [10].

In particularly, for $n=3$, $w^{-1}u$ has one cycle for any $w,u\in S_3$ with $w\ne u$. In other words, the skeleton graph for $B_3$ is the complete graph $K_6$. Therefore, there are no separating hyperplanes for $B_3$. Moreover, we have

Lemma 9.

$B_4$ has no separating hyperplanes.

Proof. 

Suppose there exists a separating hyperplane with coefficients indicated in the following matrix:

$$\left(\begin{array}{cccc}a& b& c& d\\ e& f& g& h\\ i& j& k& \ell \\ m& n& o& p\end{array}\right).$$

We use $x_w$ to represent the vector corresponding to the permutation matrix for a permutation w. By symmetry, assume $h\left(x_{\mathrm{id}}\right)>0$. The identity permutation is connected with all other permutations except for three with two cycles $\left(12\right)\left(34\right)$, $\left(13\right)\left(24\right)$ and $\left(14\right)\left(23\right)$. Then for any permutation w that is not the above three, we have $h\left(x_w\right)\ge 0$, and the only possible u’s with $h\left(x_u\right)<0$ are among the above three. Without loss of generality, assume $h\left(x_{\left(12\right)\left(34\right)}\right)<0$. Then note that the permutation $\left(12\right)\left(34\right)$ is connected to all other permutations except for id, $\left(13\right)\left(24\right)$ and $\left(14\right)\left(23\right)$. Therefore, $h\left(x_v\right)=0$ for all permutations v with one cycle.

Now notice that $h\left(x_{\left(12\right)\left(34\right)}\right)+h\left(x_{\left(13\right)\left(24\right)}\right)=h\left(x_{2143}\right)+h\left(x_{3412}\right)=(e+b+o+\ell )+(i+n+c+h)=(e+n+c+\ell )+(i+b+o+h)=h\left(x_{2413}\right)+h\left(x_{3142}\right)=h\left(x_{\left(1243\right)}\right)+h\left(x_{\left(1342\right)}\right)=0$, therefore, $h\left(x_{\left(13\right)\left(24\right)}\right)>0$. Similarly, we can get $h\left(x_{\left(14\right)\left(23\right)}\right)>0$. However, then $0<h\left(x_{\left(13\right)\left(24\right)}\right)+h\left(x_{\left(14\right)\left(23\right)}\right)=(i+n+c+h)+(m+j+g+d)=(i+n+g+d)+(m+j+c+h)=h\left(x_{\left(1324\right)}\right)+h\left(x_{\left(1423\right)}\right)=0$, a contradiction. Therefore, there does not exist any separating hyperplane. □

Remark 1.

Even though Lemma 9 is a special case of Theorem 3, we still state it separately as a lemma, since its proof provides a good example for Theorem 3.

Theorem 3.

$B_n$ has no separating hyperplanes.

Proof. 

Assume there is a hyperplane $h\left(x\right)=0$. By symmetry, assume $h\left(x_{\mathrm{id}}\right)>0$. Since all permutations with one cycle are connected with id, we have $h\left(x_u\right)\ge 0$ for all u with one cycle. Suppose $h\left(x_v\right)<0$ for some permutation v with k cycles. Assume k is the smallest such number. In other words, $h\left(x_w\right)\ge 0$, for all w with fewer than k cycles. Notice that $k>1$. First notice that $h\left(x_{\sigma }\right)=0$, for all $\sigma$ connected with v, and have fewer cycles than v. In fact, since $\sigma$ has fewer than k cycles, we have $h\left(x_{\sigma }\right)\ge 0$. On the other hand, since $\sigma$ is connected with v, $h\left(x_{\sigma }\right)>0$ cannot happen. Therefore, $h\left(x_{\sigma }\right)=0$.

Now we apply the method in Lemma 9 to show that $h\left(x_v\right)<0$ cannot happen. Write in cycle notation $v=\left(C_1\right)\left(C_2\right)\left(C_3\right)\cdots \left(C_k\right)$, where each $C_i$ is some sequence of numbers. Without loss of generality, assume $C_1=125A$ and $C_2=34B$, where A and B are sequences of numbers. First consider the permutation ${\tau }_1=\left(325A\right)\left(14B\right)C_3\cdots C_k$. Notice that

$$h\left(x_v\right)+h\left(x_{{\tau }_1}\right)=h\left(x_{{\tau }_2}\right)+h\left(x_{{\tau }_3}\right),$$

where ${\tau }_2=\left(125A34B\right)C_3\cdots C_k$ and ${\tau }_3=\left(325A14B\right)C_3\cdots C_k$. One can check that ${\tau }_2$ and ${\tau }_3$ are both connected with v, in fact ${\tau }_2$ differs with v by $\left(13\right)$ and ${\tau }_3$ differs with v by $\left(24\right)$. Since ${\tau }_2$ and ${\tau }_3$ also have fewer than k cycles, we proved earlier that $h\left(x_{{\tau }_2}\right)=0$ and $h\left(x_{{\tau }_3}\right)=0$. Therefore, $h\left(x_{{\tau }_1}\right)>0$.

Now consider the permutation ${\sigma }_1=\left(C_3\right)\cdots \left(C_k\right)$. Since it has fewer than k cycles, we have $h\left(x_{{\sigma }_1}\right)\ge 0$. Notice that

$$h\left(x_{{\tau }_1}\right)+h\left(x_{{\sigma }_1}\right)=h\left(x_{{\sigma }_2}\right)+h\left(x_{{\sigma }_3}\right),$$

where ${\sigma }_2=\left(325A\right)C_3\cdots C_k$ and ${\sigma }_3=\left(14B\right)C_3\cdots C_k$. One can check that ${\sigma }_2$ and ${\sigma }_3$ are both connected with v. Since ${\sigma }_2$ and ${\sigma }_3$ both have fewer cycles than v, we have $h\left(x_{\left({\sigma }_2\right)}\right)=0$ and $h\left(x_{{\sigma }_3}\right)=0$. This is a contradiction, since $h\left(x_{{\tau }_1}\right)>0$ and $h\left(x_{{\sigma }_1}\right)\ge 0$. □