New Numerical Aspects of Caputo-Fabrizio Fractional Derivative Operator
Abstract
:1. Introduction
2. Mathematical Preliminaries
3. Proposed Numerical Approximation
4. Temporal Mesh for Two-Point Finite Difference
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Soontharanon, J.; Chasreechai, S.; Sitthiwirattham, T. A Coupled System of Fractional Difference Equations with Nonlocal Fractional Sum Boundary Conditions on the Discrete Half-Line. Mathematics 2019, 7, 256. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional differential equations: An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. In Mathematics in Science and Engineering; Elsevier: New York, NY, USA, 1999; Volume 198. [Google Scholar]
- Dalir, M.; Bashour, M. Applications of fractional calculus. Appl. Math. Sci. 2010, 4, 1021–1032. [Google Scholar]
- Muhammad Altaf, K.; Atangana, A. Dynamics of Ebola Disease in the Framework of Different Fractional Derivatives. Entropy 2019, 21, 303. [Google Scholar] [CrossRef]
- Mainardi, F. A note on the equivalence of fractional relaxation equations to differential equations with varying coefficients. Mathematics 2018, 6, 8. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Abdon, A. Chaotic behaviour in system of noninteger-order ordinary differential equations. Chaos Solitons Fractals 2018, 115, 362–370. [Google Scholar] [CrossRef]
- Mahmudov, N.I.; Bawaneh, S.; Al-Khateeb, A. On a Coupled System of Fractional Differential Equations with Four Point Integral Boundary Conditions. Mathematics 2019, 7, 279. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Abdon, A. Numerical simulations of chaotic and complex spatiotemporal patterns in fractional reaction–diffusion systems. Comput. Appl. Math. 2018, 37, 2166–2189. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Abdon, A. Modelling and formation of spatiotemporal patterns of fractional predation system in subdiffusion and superdiffusion scenarios. Eur. Phys. J. Plus 2018, 133, 43. [Google Scholar] [CrossRef]
- Rangaig, N.A.; Convicto, V.C. On fractional modelling of dye removal using fractional derivative with non-singular kernel. J. King Saud-Univ.-Sci. 2018. [Google Scholar] [CrossRef]
- Rangaig, N.A.; Pido, A.A.G. Finite Difference Approximation Method for Two-Dimensional Space-Time Fractional Diffusion Equation Using Nonsingular Fractional Derivative. Prog. Fract. Differ. Appl. 2019, in press. [Google Scholar]
- Veeresha, P.; Prakasha, D.G.; Baleanu, D. An Efficient Numerical Technique for the Nonlinear Fractional Kolmogorov–Petrovskii–Piskunov Equation. Mathematics 2019, 7, 265. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Abdon, A. Robustness of fractional difference schemes via the Caputo subdiffusion-reaction equations. Chaos Solitons Fractals 2018, 111, 119–127. [Google Scholar] [CrossRef]
- Sania, Q.; Yusuf, A.; Shaikh, A.A.; Mustafa, Inc.; Baleanu, D. Fractional modeling of blood ethanol concentration system with real data application. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 013143. [Google Scholar]
- Abbas, S.; Arifi, N.A.; Benchohra, M.; Zhou, Y. Random Coupled Hilfer and Hadamard Fractional Differential Systems in Generalized Banach Spaces. Mathematics 2019, 7, 285. [Google Scholar] [CrossRef]
- Yusuf, A.; Qureshi, S.; Aliyu, A.I.; Baleanu, D.; Shaikh, A.A.; Mustafa, Inc. Two-strain epidemic model involving fractional derivative with Mittag-Leffler kernel. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 123121. [Google Scholar] [CrossRef]
- Baitiche, Z.; Guerbati, K.; Benchohra, M.; Zhou, Y. Boundary Value Problems for Hybrid Caputo Fractional Differential Equations. Mathematics 2019, 7, 282. [Google Scholar] [CrossRef]
- Abro, K.A.; Memon, A.A.; Memon, A.A. Functionality of circuit via modern fractional differentiations. Analog. Integr. Circuits Signal Process. 2018. [Google Scholar] [CrossRef]
- Arqub, O.A.; Al-Smadi, M. Atangana–Baleanu fractional approach to the solutions of Bagley-Torvik and Painlevé equations in Hilbert space. Chaos Solitons Fractals 2018, 117, 161–167. [Google Scholar] [CrossRef]
- Qureshi, S.; Yusuf, A. Modeling chickenpox disease with fractional derivatives: From caputo to atangana-baleanu. Chaos Solitons Fractals 2019, 122, 111–118. [Google Scholar] [CrossRef]
- Arqub, O.A.; Maayah, B. Numerical solutions of integrodifferential equations of Fredholm operator type in the sense of the Atangana–Baleanu fractional operator. Chaos Solitons Fractals 2018, 117, 117–124. [Google Scholar] [CrossRef]
- Araci, S.; Rahman, G.; Ghaffar, A.; Azeema; Nisar, K.S. Fractional Calculus of Extended Mittag-Leffler Function and Its Applications to Statistical Distribution. Mathematics 2019, 7, 248. [Google Scholar] [CrossRef]
- Arqub, O.A. Solutions of time-fractional Tricomi and Keldysh equations of Dirichlet functions types in Hilbert space. Numer. Methods Partial. Differ. Equ. 2018, 34, 1759–1780. [Google Scholar] [CrossRef]
- Abro, K.A.; Memon, A.A.; Uqaili, M.A. A comparative mathematical analysis of RL and RC electrical circuits via Atangana-Baleanu and Caputo-Fabrizio fractional derivatives. Eur. Phys. J. Plus 2018, 133, 113. [Google Scholar] [CrossRef]
- Li, C.; Zeng, F. Numerical Methods for Fractional Calculus; Chapman and Hall/CRC: New York, NY, USA, 2015. [Google Scholar]
- Ahmad, S.N.; Ali, F.; Saqib, M.; Khan, I.; Jan, S.A.A.; Alshomrani, A.S.; Alghamdi, M.S. Comparison and analysis of the Atangana–Baleanu and Caputo–Fabrizio fractional derivatives for generalized Casson fluid model with heat generation and chemical reaction. Results Phys. 2017, 7, 789–800. [Google Scholar]
- Atangana, A.; Baleanu, D. Caputo-Fabrizio derivative applied to groundwater flow within confined aquifer. J. Eng. Mech. 2017, 143. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. Analysis of fractional differential equations. J. Math. Anal. Appl. 2002, 265, 229–248. [Google Scholar] [CrossRef]
- Hilfer, R.; Luchko, Y. Desiderata for Fractional Derivatives and Integrals. Mathematics 2019, 7, 149. [Google Scholar] [CrossRef]
- Yusuf, A.; Mustafa, Inc.; Aliyu, I.A.; Dumitru, B. Efficiency of the new fractional derivative with nonsingular Mittag-Leffler kernel to some nonlinear partial differential equations. Chaos Solitons Fractals 2018, 116, 220–226. [Google Scholar] [CrossRef]
- Mustafa, Inc.; Yusuf, A.; Aliyu, A.I.; Baleanu, D. Investigation of the logarithmic-KdV equation involving Mittag-Leffler type kernel with Atangana–Baleanu derivative. Phys. Stat. Mech. Its Appl. 2018, 506, 520–531. [Google Scholar]
- Caputo, M.; Fabrizio, M. Applications of new time and spatial fractional derivatives with exponential kernels. Prog. Fract. Differ. Appl. 2016, 2, 1–11. [Google Scholar] [CrossRef]
- Yang, X.; Srivastava, H.M.; Machado, J.T. A new fractional derivative without singular kernel. Therm. Sci. 2016, 20, 753–756. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. Detailed error analysis for a fractional Adams method. Numer. Algorithms 2004, 36, 31–52. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D.; Luchko, Y. Algorithms for the fractional calculus: A selection of numerical methods. Comput. Methods Appl. Mech. Eng. 2005, 194, 743–773. [Google Scholar] [CrossRef]
- Garrappa, R. Numerical solution of fractional differential equations: A survey and a software tutorial. Mathematics 2018, 6, 16. [Google Scholar] [CrossRef]
- Wei, Y.; Chen, Y.; Cheng, S.; Wang, Y. A note on short memory principle of fractional calculus. Fract. Calc. Appl. Anal. 2017, 20, 1382–1404. [Google Scholar] [CrossRef]
- Caputo, M.; Mauro, F. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 1–13. [Google Scholar]
- Losada, J.; Nieto, J. Properties of a new fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 87–92. [Google Scholar]
- Goufo, E.F.D. Application of the Caputo-Fabrizio Fractional Derivative without Singular Kernel to Korteweg-de Vries-Burgers Equation. Math. Model. Anal. 2016, 21, 188–198. [Google Scholar] [CrossRef]
- Ali, F.; Saqib, M.; Khan, I.; Sheikh, N.A. Application of Caputo-Fabrizio derivatives to MHD free convection flow of generalized Walters’-B fluid model. Eur. Phys. J. Plus. 2016, 131, 377. [Google Scholar] [CrossRef]
- Atangana, A. On the new fractional derivative and application to nonlinear Fisher’s reaction–diffusion equation. Appl. Math. Comput. 2016, 273, 948–956. [Google Scholar] [CrossRef]
- Atangana, A.; Alqahtani, R.T. Numerical approximation of the space-time Caputo-Fabrizio fractional derivative and application to groundwater pollution equation. Adv. Differ. Equ. 2016, 2016, 156. [Google Scholar] [CrossRef]
- Akman, T.; Yıldız, B.; Baleanu, D. New discretization of Caputo–Fabrizio derivative. Comput. Appl. Math. 2018, 37, 3307–3333. [Google Scholar] [CrossRef]
- Rangaig, N. Finite Difference Approximation for Caputo-Fabrizio Time Fractional Derivative on Non-Uniform Mesh and Some Applications. Phys. J. 2018, 1, 255–263. [Google Scholar]
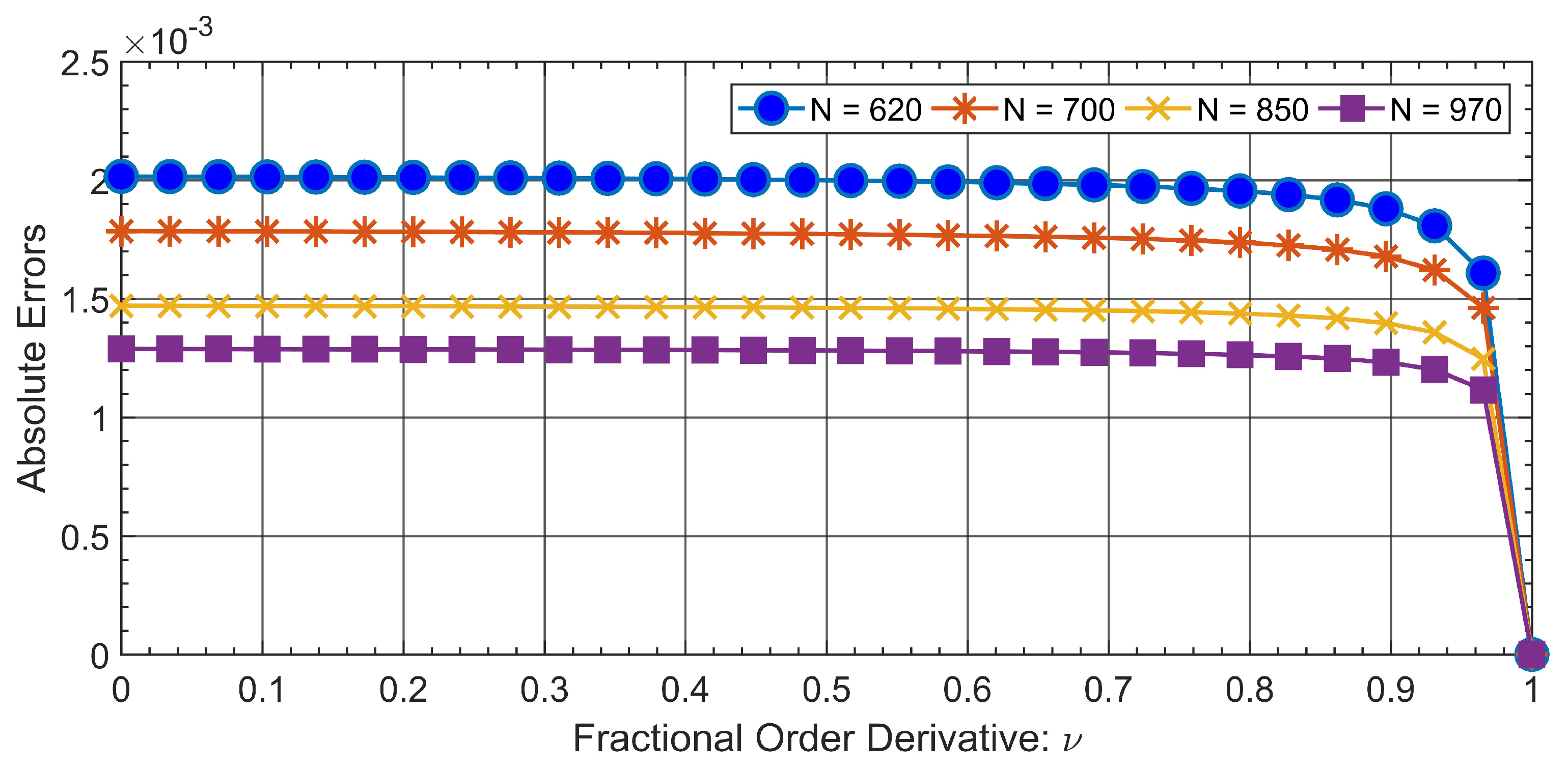
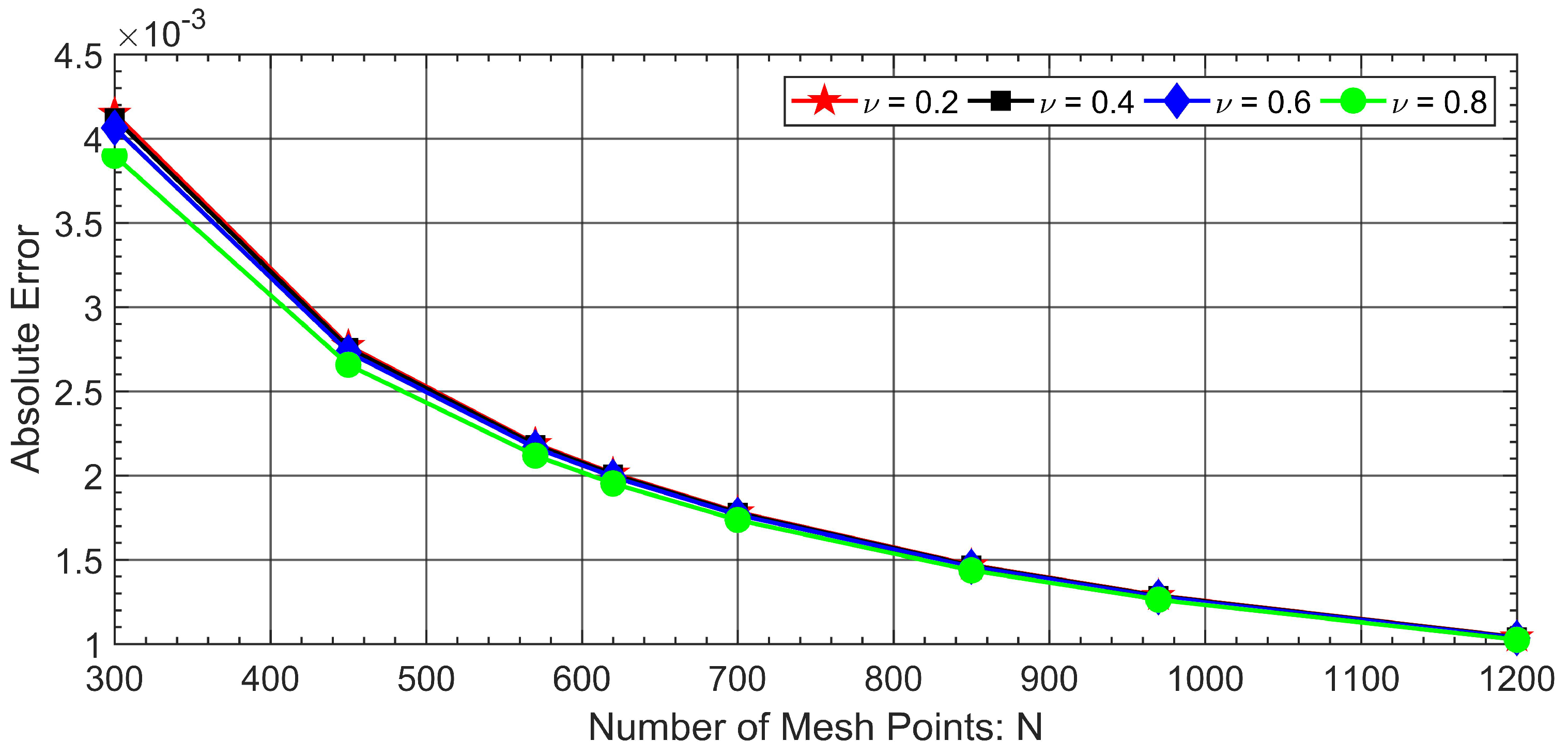
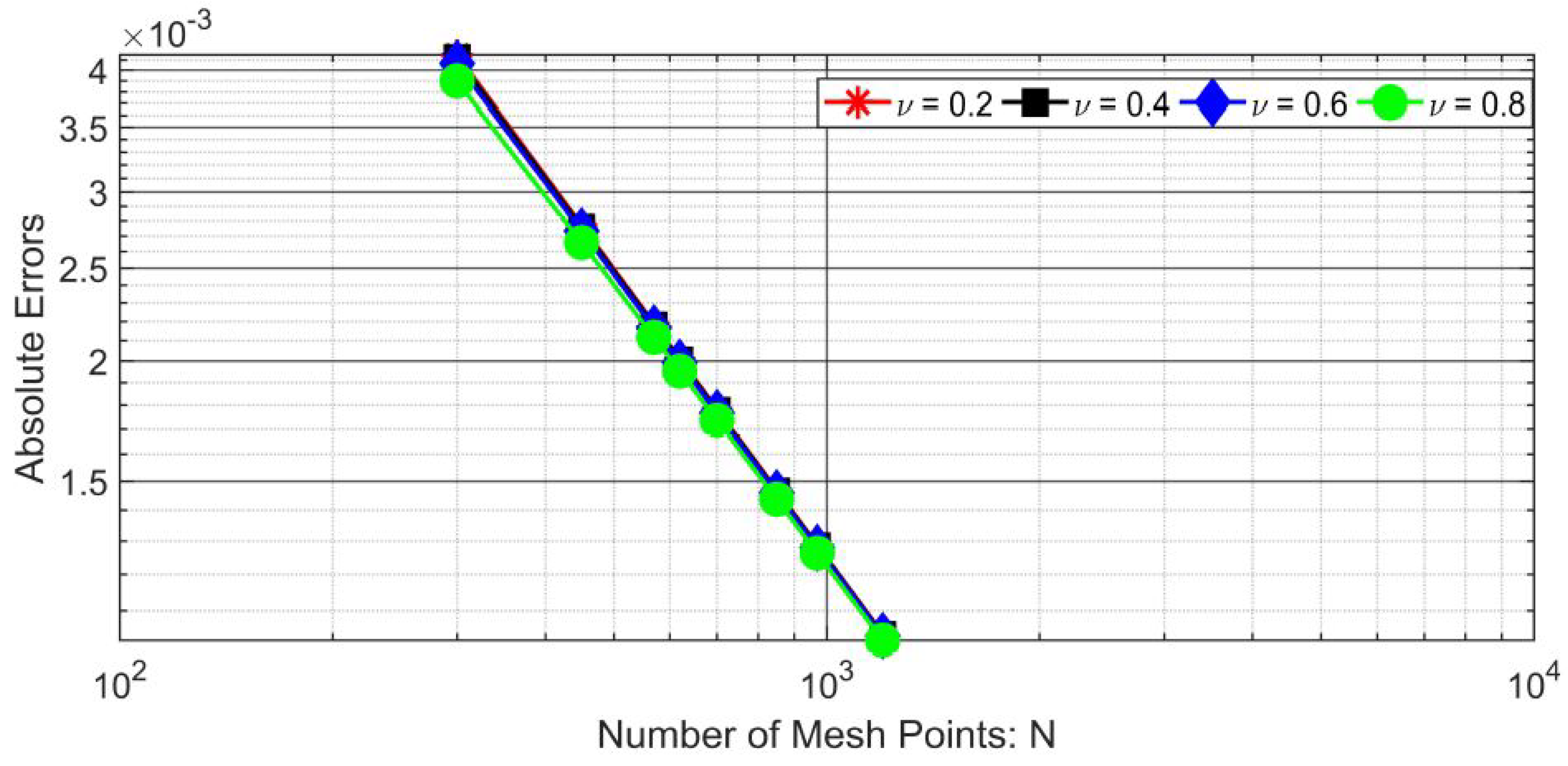
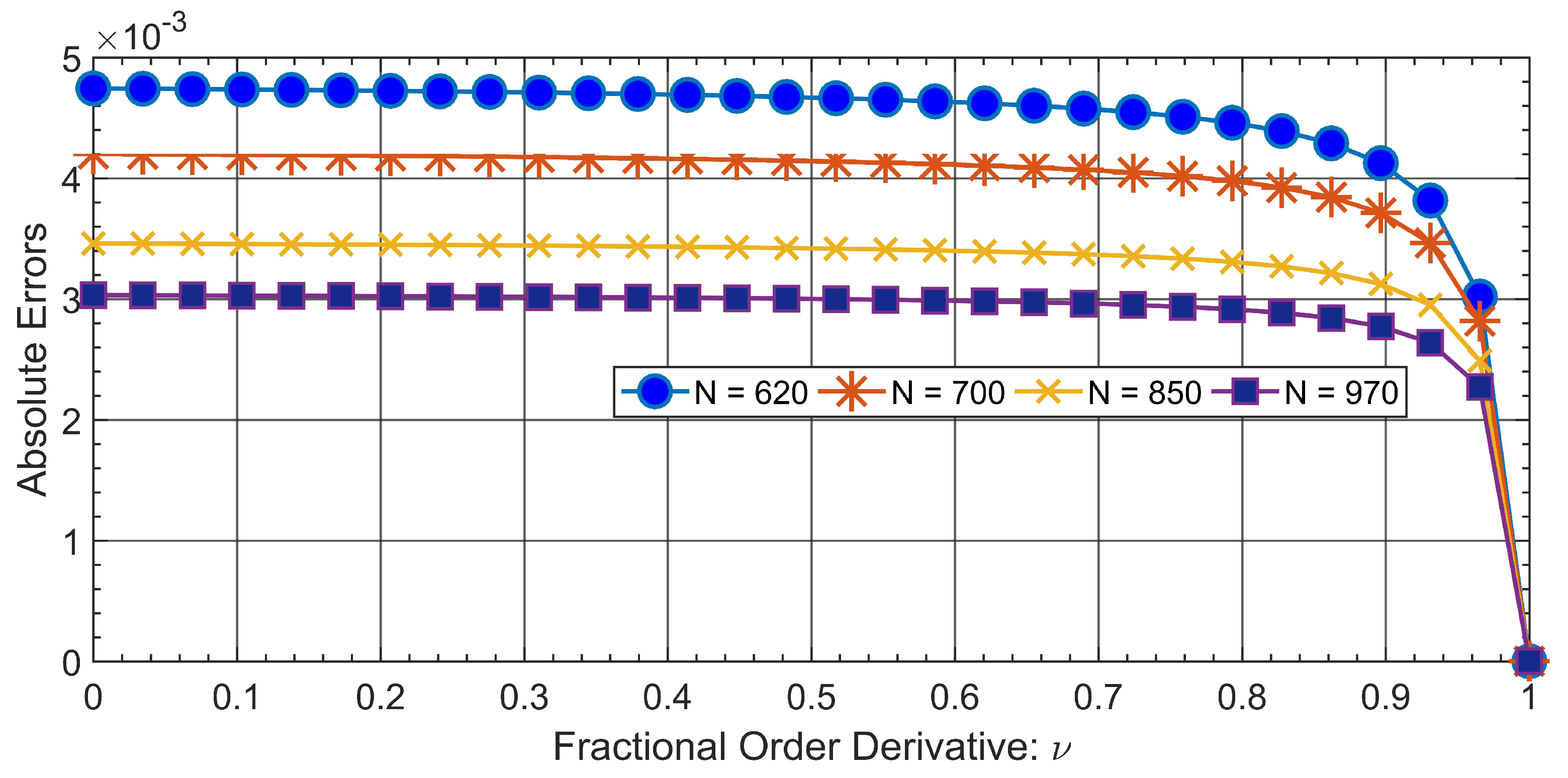
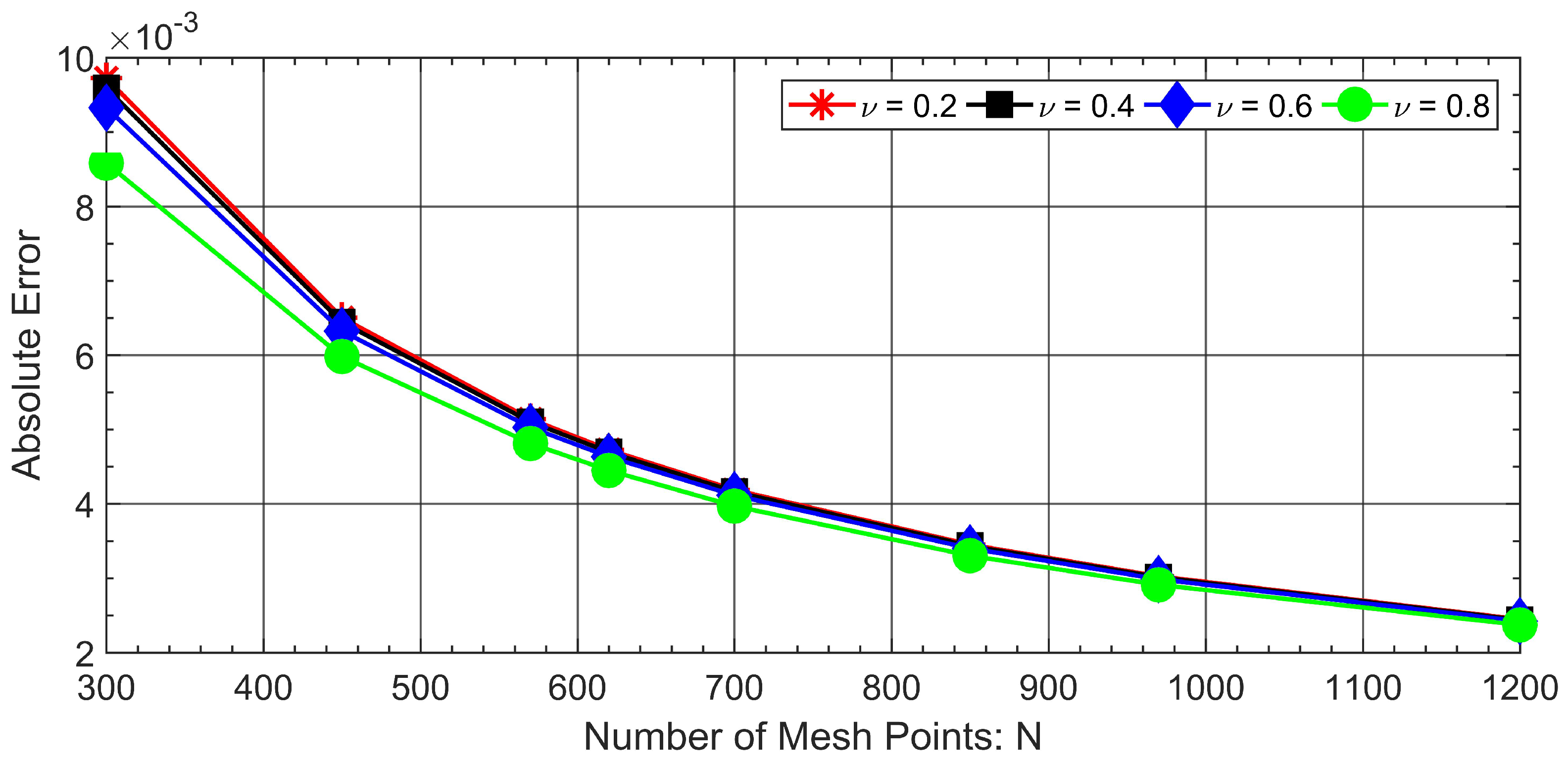
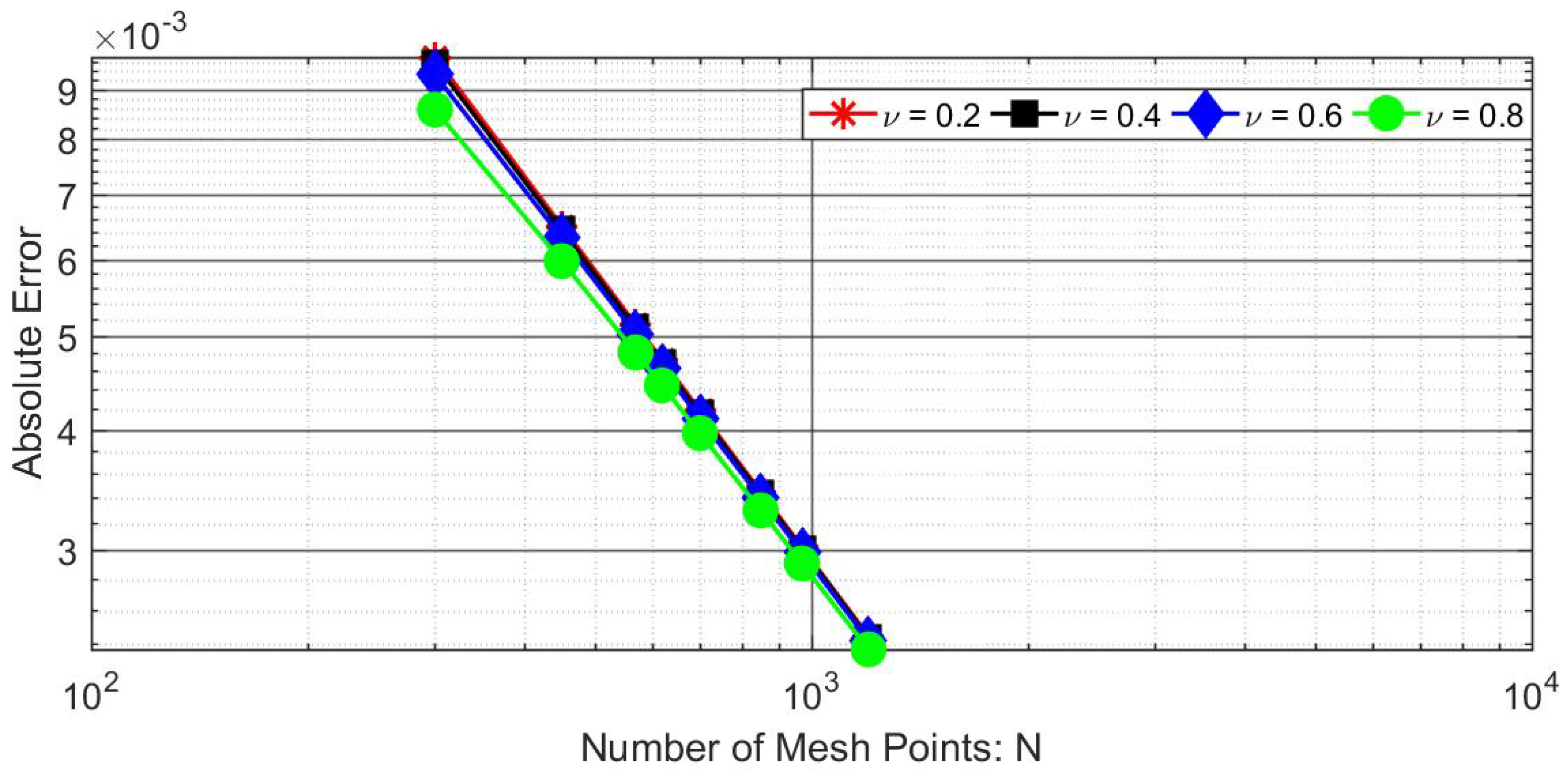
| Problem | Duration (ms) | |||
|---|---|---|---|---|
| 1 | 3.0908 × | 3.0573 × | 3.0540 × | 0.004 |
| 2 | 5.0191 × | 4.8874 × | 4.8518 × | 0.008 |
| 3 | 4.7798 × | 4.8426 × | 4.8488 × | 0.008 |
| 4 | 7.477 × | 7.5080 × | 7.5110 × | 0.005 |
| 5 | 1.9188 × | 1.9220 × | 1.9223 × | 0.008 |
| Problem | Duration (ms) | |||
|---|---|---|---|---|
| 1 | 9.5697 × | 9.5553 × | 9.5539 × | 0.006 |
| 2 | 3.0462 × | 3.0712 × | 3.0835 × | 0.008 |
| 3 | 4.1345 × | 4.0793 × | 4.0737 × | 0.006 |
| 4 | 6.1334 × | 6.1716 × | 6.1754e × | 0.005 |
| 5 | 7.0012 × | 7.0960 × | 7.1055 × | 0.008 |
| Problem | Duration (ms) | |||
|---|---|---|---|---|
| 1 | 7.3945 × | 7.3613 × | 7.3580 × | 0.006 |
| 2 | 8.9548 × | 8.0795 × | 7.7668 × | 0.007 |
| 3 | 7.4921 × | 6.7530 × | 6.6793 × | 0.007 |
| 4 | 6.9383 × | 6.9755 × | 6.9792 × | 0.006 |
| 5 | 1.2357 × | 1.2451 × | 1.2460 × | 0.006 |
| Problem | Duration (ms) | |||
|---|---|---|---|---|
| 1 | 2.0217 × | 1.9945 × | 1.9918 × | 0.007 |
| 2 | 5.3955 × | 5.2689 × | 5.2382 × | 0.007 |
| 3 | 6.0877 × | 6.1385 × | 6.1436 × | 0.005 |
| 4 | 7.5564 × | 7.5842 × | 7.5870 × | 0.005 |
| 5 | 2.0529 × | 2.0530 × | 2.0530 × | 0.006 |
| Problem | Duration (ms) | |||
|---|---|---|---|---|
| 1 | 6.6613 × | 8.8818 × | 1.3323 × | 0.006 |
| 3 | 1.1729 × | 9.1039 × | 8.4875 × | 0.008 |
| 5 | 2.5673 × | 1.9723 × | 1.8373 × | 0.007 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qureshi, S.; Rangaig, N.A.; Baleanu, D. New Numerical Aspects of Caputo-Fabrizio Fractional Derivative Operator. Mathematics 2019, 7, 374. https://doi.org/10.3390/math7040374
Qureshi S, Rangaig NA, Baleanu D. New Numerical Aspects of Caputo-Fabrizio Fractional Derivative Operator. Mathematics. 2019; 7(4):374. https://doi.org/10.3390/math7040374
Chicago/Turabian StyleQureshi, Sania, Norodin A. Rangaig, and Dumitru Baleanu. 2019. "New Numerical Aspects of Caputo-Fabrizio Fractional Derivative Operator" Mathematics 7, no. 4: 374. https://doi.org/10.3390/math7040374
APA StyleQureshi, S., Rangaig, N. A., & Baleanu, D. (2019). New Numerical Aspects of Caputo-Fabrizio Fractional Derivative Operator. Mathematics, 7(4), 374. https://doi.org/10.3390/math7040374






