Abstract
In this paper, a new definition for the fractional order operator called the Caputo-Fabrizio (CF) fractional derivative operator without singular kernel has been numerically approximated using the two-point finite forward difference formula for the classical first-order derivative of the function f (t) appearing inside the integral sign of the definition of the CF operator. Thus, a numerical differentiation formula has been proposed in the present study. The obtained numerical approximation was found to be of first-order convergence, having decreasing absolute errors with respect to a decrease in the time step size h used in the approximations. Such absolute errors are computed as the absolute difference between the results obtained through the proposed numerical approximation and the exact solution. With the aim of improved accuracy, the two-point finite forward difference formula has also been utilized for the continuous temporal mesh. Some mathematical models of varying nature, including a diffusion-wave equation, are numerically solved, whereas the first-order accuracy is not only verified by the error analysis but also experimentally tested by decreasing the time-step size by one order of magnitude, whereupon the proposed numerical approximation also shows a one-order decrease in the magnitude of its absolute errors computed at the final mesh point of the integration interval under consideration.
MSC:
65L12; 65Q10; 65G40
1. Introduction
Differential equations of arbitrary real order are used to model various physical models arising in many branches of science and engineering. Applications of such mathematical models can be seen from statistical mechanics and Brownian motion, via visco-elasticity problems, to continuum and quantum mechanics, biosciences, chemical engineering, and control theory, just to name a few; see, for example, Soontharanon et al. [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24] and the references cited therein.
The rapid rise in popularity of the field known as fractional calculus (FC) has given birth to various different ways to define fractional derivatives and fractional integrals. Unlike the Riemann-Liouville fractional integral, there are many different versions of definitions for the fractional derivative, with some of them equivalent to each other only under some restrictions imposed on the function being differentiated [25,26,27,28]. In addition to this, three new classifications of the fractional operators were debated recently in [29].
Due to increasing development of the fractional derivatives in modeling physical problems, it seems appropriate to have not only an effective and universally accepted definition for such a derivative, but also an efficient and accurate numerical approximation, which is important to deal with problems having inherited singularities and non-linearities in the systems [30,31,32,33]. However, the non-local structure of these fractional operators has provided limited options to design efficient codes, for it requires all past information to be taken into consideration while simulating. This is what we call the presence of persistent memory, which makes the computations more costly and slow [34,35,36,37]. In this regard, there are numerous short memory principles in the recent literature [38] that are widely used to reduce the computational cost and the effect of rounding-off error accumulation while using numerical techniques, thereby making the short memory principles quite useful in solving fractional initial value problems.
The definition of the fractional derivative operator called the Caputo-Fabrizio operator without singular kernel [39] is the direct consequence of the the classical Caputo derivative operator. This is because the latter involves a singular mathematical expression called the kernel in its definition, leading to a few difficulties in finding solutions to the associated differential equations, whereas the kernel of the former has no singularity at .
Various other useful properties and interesting applications of this new derivative operator, including the most celebrated one called the Laplace transform technique, can be found in [40]. Additional applications of the operator are seen in recently published works regarding the analysis of the Korteweg-de Vries-Burgers equation used in liquids and waves dynamics [41], magnetohydrodynamics (MHD) free convection flow of generalized Walters’-B fluid over a static vertical plate [42], and nonlinear Fisher’s reaction diffusion equation [43].
The present paper fundamentally aims to propose a numerical approximation for the Caputo-Fabrizio (CF) operator using a two-point finite difference formula for the term, as well as offer a discussion of error analysis associated with the proposed approximation. Thus, a numerical differentiation formula for the CF operator has been proposed in the present study. Based upon the error analysis discussed in Section 3, the current work shows that the local truncation error term of the approximation consists of a positive constant that depends upon the fractional operator , leading to the expression of the form , which proves the first-order convergence of the proposed numerical approximation. This approximation is later employed for a continuous temporal mesh with the purpose of improved accuracy, as discussed in Section 4. This is followed by some numerical experiments in Section 5 to illustrate the performance of the proposed numerical approximation.
It must be noted that the authors in [44,45] have discretized the CF operator using finite difference schemes with a different derivation approach, error analysis, and way of illustrating the numerical results. Some of the schemes in those works are explicit, and others are implicit with very promising rates of convergence. The numerical approximation presented in this paper, being simple enough with the explicit nature of first-order convergence, is computationally inexpensive with respect to machine memory storage and time consumption, as shown in the tabular data of Section 5. Next, we present some important definitions used in the present study, along with a few of the properties associated with fractional derivative operators that need to be known at this stage.
2. Mathematical Preliminaries
This section refreshes some of the basic definitions and properties considered to be useful for the present study.
Definition 1.
[2] The fractional derivative of real order for in the classical Caputo sense is defined as
where and is the singular kernel. In order to get rid of this singular kernel, a new definition was introduced in [39] that facilitates solving various natural and physical laws without being caught by the convoluted integrals.
Definition 2.
[2] The Laplace transform operation of the classical Caputo operator possesses the initial conditions to be defined at the lower terminal , for which the valid physical interpretations are easily possible. Thus, the Caputo definition is very useful for solving real life problems expressible in the form of fractional differential equations.
where , .
Definition 3.
[39] The new operator called the Caputo-Fabrizio operator for fractional derivatives of order is defined as follows:
where is the normalization function (any smooth positive function) such that , and . Furthermore, note the absence of any singular kernel in the definition above. Definition 3 forms most of the work presented in the subsequent sections.
Definition 4.
[39] The Laplace transform operation of the CF operator also carries with it the initial conditions to be defined at the lower terminal , where the physical meaning of the conditions is well defined in the literature. This once again makes the fractional derivative very useful for solving real life problems based upon fractional differential equations in CF form.
where , , and .
3. Proposed Numerical Approximation
Suppose that , and . Let h be the fixed step size with and denote . Now, we investigate the numerical approximation of the integral that appeared above in Equation (3). One of the easiest ways is to use the classical two-point finite forward difference formula for the first derivative on the interval . For and one obtains
For , and 3, we respectively get
Continuing in the same way, we obtain
One can replace k by to get the following form:
Equation (6) is the first-order time discretization of the newly developed fractional operator called the CF operator without singular kernel [39]. Thus, we have established the following theorem:
Theorem 1.
Suppose that the interval is subdivided into n sub-intervals of equal width by using the nodes for then the following relation
is the proposed numerical approximation to the CF operator without singular kernel. In addition, we have
Furthermore, if then there exists a constant that depends only upon ν in such a way that the error term has the following form:
Proof.
From the earlier steps of Section 3, we have the following:
Taking the third term of Equation (8), one obtains
where
Thus, Equation (6) is reduced to
where and
This completes the proof for the proposed numerical approximation (6) to be of first-order accuracy with the above error term. We now turn to the study of this fractional operator with the advantage of having no singular part in the main integrand for continuous temporal mesh, as discussed in the next section. □
4. Temporal Mesh for Two-Point Finite Difference
One of the interesting features of the CF operator is the absence of the singularity. In the previous section, we introduced the numerical approximation of a fractional derivative using the CF operator where two-point approximation is utilized and the truncation error of the two-point finite difference approach has been proven to have an accuracy which is dependent on the fractional order. However, in the real-world modeling of a physical system, one must consider a continuous temporal variable which gives the characteristic of the system and the improvement of accuracy is naturally considered. For any integer N, we divide the interval into N sub-intervals. We consider the time-step as where . For any temporal meshes, we present the following definition and theorem for approximating the absolute error of the interval
Definition 5.
Suppose N is a finite grid size and a sequence of mesh is finite. The mesh points are then quasi-uniform if there exists a constant such that
Definition 5 Characterize the time step and must hold. We can deduce that when , we can have the uniform mesh with . Next, we present the theorem in approximating the error for any uniform temporal meshes.
Theorem 2.
Suppose that the fractional order derivative for and let a function hold.
where the absolute error for interval is given by
Proof.
We can write the CF integral of the form
Now, using the formula integration by parts yields
and by linear interpolation of , we can get
Simplifying the second term, we obtain the following
Simplifying the above equation further gives
and the term
where
Substituting the obtained equalities into Equation (10), we have
We can easily check that the first four terms cancel each other. Thus, we obtain
and
This completes the required error approximation for a given interval . In this expression, we can directly observe that the CF operator can either be used in quasi-uniform and uniform mesh, depending on the consideration. In the context of non-uniform mesh or temporal meshes, see [46] and the results presented therein. □
In the section that follows, a few test problems have been chosen to check the performance of the above approximations.
5. Results and Discussion
Firstly, as many as five different types of mathematical functions were chosen to check the performance of the proposed numerical approximation (6) by computing the absolute errors at the last mesh point , where N is the total number of integration steps over the interval for with in the test Problems 1–5 listed below with their numerical simulations recorded in the Table 1, Table 2, Table 3 and Table 4. In addition, the choice was also tested on a few selected test problems in Table 5 to observe the behavior of the solution when goes near to 1.

Table 1.
Absolute errors at the last mesh point over with .

Table 2.
Absolute errors at the last mesh point over with .

Table 3.
Absolute errors at the last mesh point over with .

Table 4.
Absolute errors at the last mesh point over with .

Table 5.
Absolute errors at the last mesh point over with .
Secondly, Problem 6 depicts the behavior of the approximation graphically, where the absolute errors reduce with an increase in the number of mesh points. Lastly, using the approximation for the temporal mesh as discussed in the previous section, once again a decrease in the absolute errors was observed for the diffusion-wave equation presented in Problem 7. In order to carry out the numerical computations, MATLAB Ver.9.2.0.538062 (R2017a) on a personal computer equipped with a CPU Intel(R) Core(TM) i3-4005U @ 1.70 GHz running under the operating system Windows 10 was used.
Problem 1
Problem 2
Problem 3
Problem 4
Problem 5
The exact solution of Problem 2 above contains a special function that is called the error function (entire) and is defined as follows:
The absolute errors decrease with a decrease in the time-step size h, as shown in Table 1, Table 2, Table 3 and Table 4. Furthermore, note that a reduction in the time-step size h by one order of magnitude also drops the absolute error by one order of magnitude, as depicted in columns 2–4 in each of Table 1, Table 2, Table 3 and Table 4. This experimental fact can be used as a claim for the first-order accuracy of the proposed numerical approximation, as proved in the sections above. Thus, the performance of the proposed numerical approximation (6) is found to be reliable with first-order accuracy, and the same is shown by the above test problems. Furthermore, Table 5 shows a similar sort of behavior when , wherein the first test problem yields almost zero error. One of the reasons for this behavior is the test problem itself, which is linear, and besides that,
Problem 6 Given a sample function and for the interval with , we can directly obtain the exact solution as
We can numerically compute the -order derivative of on the uniform mesh. Absolute errors were plotted in Figure 1 by letting , and these errors tend to zero as the number of mesh points increases, implying that as the number of mesh points increases, the time increment decreases, as discussed in the previous section. A similar sort of behavior is depicted in Figure 2 and Figure 3.
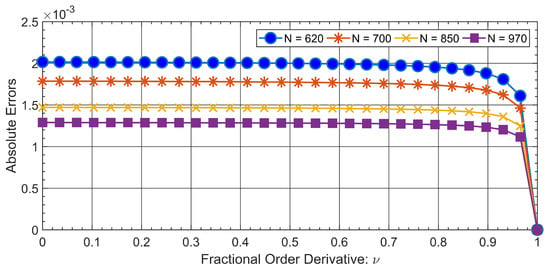
Figure 1.
Absolute errors vs. fractional order for the approximation of continuous uniform mesh for a temporal variable using the Caputo-Fabrizio operator on a given function with a varying number of mesh points.
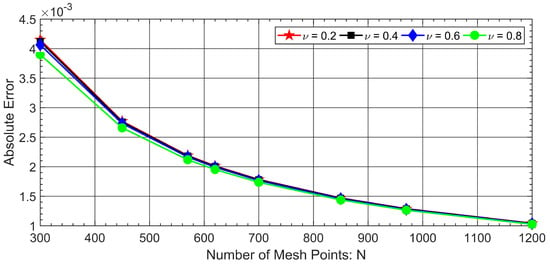
Figure 2.
Absolute errors vs. number of mesh points N for the approximation of continuous uniform mesh for a temporal variable using the Caputo-Fabrizio operator on a given function with varying fractional order .
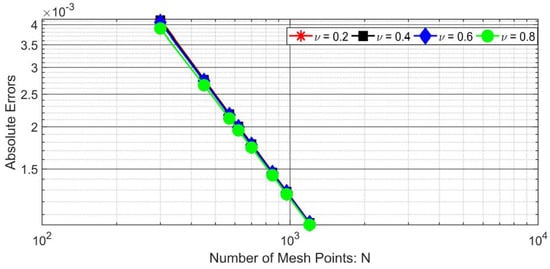
Figure 3.
Logarithmic plot of absolute errors vs. number of mesh points for Problem 6.
Problem 7 Consider a diffusion-wave equation with an exact solution
Using the approximation for temporal mesh, we can obtain the absolute errors with respect to the number of mesh points, as plotted in Figure 4. It can be seen that the absolute errors can easily be minimized. A similar sort of behavior is depicted in Figure 5 and Figure 6.
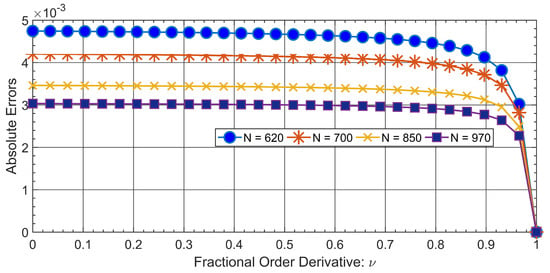
Figure 4.
Absolute errors vs. number of mesh points N for the approximation of continuous uniform mesh for a temporal variable using the Caputo-Fabrizio operator for Problem 7 with varying fractional order .
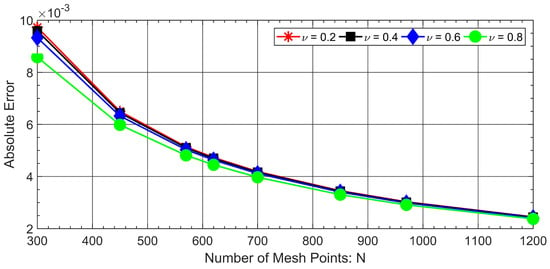
Figure 5.
Absolute errors vs. number of mesh points N for the approximation of continuous uniform mesh for a temporal variable using the Caputo-Fabrizio operator for Problem 7 with varying fractional order .
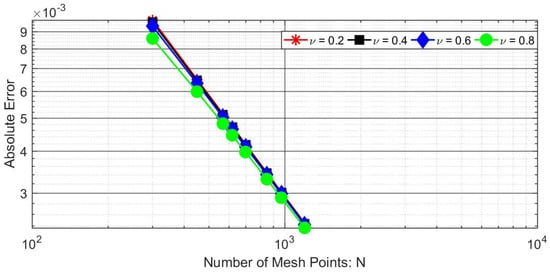
Figure 6.
Logarithmic plot of absolute errors vs. number of mesh points for Problem 7.
6. Conclusions
In this research work, a numerical approximation using the two-point finite forward difference formula of classical calculus for the first derivative of has been presented and found to be efficient with first-order accuracy for the CF operator. The error analysis presented confirms the first-order convergence of the proposed numerical approximation on the basis of getting a local truncation error term of the form , which was further extended for the continuous temporal mesh with the aim of getting better accuracy.
Test Problems 1–5 supported the claim of first-order convergence of the proposed numerical approximation with the one-order decreasing behavior of the computed absolute errors with every respective one-order drop in the magnitude of the time-step h, as demonstrated in Table 1, Table 2, Table 3 and Table 4, while consuming a considerably small CPU time in milliseconds.
Furthermore, considering the continuous uniform temporal mesh for the CF operator (3), a decrease in the amount of absolute errors with the increasing number of mesh points for the integration interval under consideration was observed once again in test Problems 6 and 7, and this experimental fact remains true if the real fractional order is allowed to vary, as shown by Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6.
Author Contributions
Each author has contributed equally towards preparing and finalizing the whole research work of the present paper.
Funding
This research received no external funding.
Acknowledgments
The first author is grateful to Muhammad Saleem Chandio and Asif Ali Shaikh, who helped to rectify a few coding issues in the present study. In addition, she is also grateful to three anonymous reviewers who critically reviewed the first and second drafts, which helped to improve the work and finally resulted in the present form of the paper.
Conflicts of Interest
The authors declare that they have no competing interests.
References
- Soontharanon, J.; Chasreechai, S.; Sitthiwirattham, T. A Coupled System of Fractional Difference Equations with Nonlocal Fractional Sum Boundary Conditions on the Discrete Half-Line. Mathematics 2019, 7, 256. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional differential equations: An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. In Mathematics in Science and Engineering; Elsevier: New York, NY, USA, 1999; Volume 198. [Google Scholar]
- Dalir, M.; Bashour, M. Applications of fractional calculus. Appl. Math. Sci. 2010, 4, 1021–1032. [Google Scholar]
- Muhammad Altaf, K.; Atangana, A. Dynamics of Ebola Disease in the Framework of Different Fractional Derivatives. Entropy 2019, 21, 303. [Google Scholar] [CrossRef]
- Mainardi, F. A note on the equivalence of fractional relaxation equations to differential equations with varying coefficients. Mathematics 2018, 6, 8. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Abdon, A. Chaotic behaviour in system of noninteger-order ordinary differential equations. Chaos Solitons Fractals 2018, 115, 362–370. [Google Scholar] [CrossRef]
- Mahmudov, N.I.; Bawaneh, S.; Al-Khateeb, A. On a Coupled System of Fractional Differential Equations with Four Point Integral Boundary Conditions. Mathematics 2019, 7, 279. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Abdon, A. Numerical simulations of chaotic and complex spatiotemporal patterns in fractional reaction–diffusion systems. Comput. Appl. Math. 2018, 37, 2166–2189. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Abdon, A. Modelling and formation of spatiotemporal patterns of fractional predation system in subdiffusion and superdiffusion scenarios. Eur. Phys. J. Plus 2018, 133, 43. [Google Scholar] [CrossRef]
- Rangaig, N.A.; Convicto, V.C. On fractional modelling of dye removal using fractional derivative with non-singular kernel. J. King Saud-Univ.-Sci. 2018. [Google Scholar] [CrossRef]
- Rangaig, N.A.; Pido, A.A.G. Finite Difference Approximation Method for Two-Dimensional Space-Time Fractional Diffusion Equation Using Nonsingular Fractional Derivative. Prog. Fract. Differ. Appl. 2019, in press. [Google Scholar]
- Veeresha, P.; Prakasha, D.G.; Baleanu, D. An Efficient Numerical Technique for the Nonlinear Fractional Kolmogorov–Petrovskii–Piskunov Equation. Mathematics 2019, 7, 265. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Abdon, A. Robustness of fractional difference schemes via the Caputo subdiffusion-reaction equations. Chaos Solitons Fractals 2018, 111, 119–127. [Google Scholar] [CrossRef]
- Sania, Q.; Yusuf, A.; Shaikh, A.A.; Mustafa, Inc.; Baleanu, D. Fractional modeling of blood ethanol concentration system with real data application. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 013143. [Google Scholar]
- Abbas, S.; Arifi, N.A.; Benchohra, M.; Zhou, Y. Random Coupled Hilfer and Hadamard Fractional Differential Systems in Generalized Banach Spaces. Mathematics 2019, 7, 285. [Google Scholar] [CrossRef]
- Yusuf, A.; Qureshi, S.; Aliyu, A.I.; Baleanu, D.; Shaikh, A.A.; Mustafa, Inc. Two-strain epidemic model involving fractional derivative with Mittag-Leffler kernel. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 123121. [Google Scholar] [CrossRef]
- Baitiche, Z.; Guerbati, K.; Benchohra, M.; Zhou, Y. Boundary Value Problems for Hybrid Caputo Fractional Differential Equations. Mathematics 2019, 7, 282. [Google Scholar] [CrossRef]
- Abro, K.A.; Memon, A.A.; Memon, A.A. Functionality of circuit via modern fractional differentiations. Analog. Integr. Circuits Signal Process. 2018. [Google Scholar] [CrossRef]
- Arqub, O.A.; Al-Smadi, M. Atangana–Baleanu fractional approach to the solutions of Bagley-Torvik and Painlevé equations in Hilbert space. Chaos Solitons Fractals 2018, 117, 161–167. [Google Scholar] [CrossRef]
- Qureshi, S.; Yusuf, A. Modeling chickenpox disease with fractional derivatives: From caputo to atangana-baleanu. Chaos Solitons Fractals 2019, 122, 111–118. [Google Scholar] [CrossRef]
- Arqub, O.A.; Maayah, B. Numerical solutions of integrodifferential equations of Fredholm operator type in the sense of the Atangana–Baleanu fractional operator. Chaos Solitons Fractals 2018, 117, 117–124. [Google Scholar] [CrossRef]
- Araci, S.; Rahman, G.; Ghaffar, A.; Azeema; Nisar, K.S. Fractional Calculus of Extended Mittag-Leffler Function and Its Applications to Statistical Distribution. Mathematics 2019, 7, 248. [Google Scholar] [CrossRef]
- Arqub, O.A. Solutions of time-fractional Tricomi and Keldysh equations of Dirichlet functions types in Hilbert space. Numer. Methods Partial. Differ. Equ. 2018, 34, 1759–1780. [Google Scholar] [CrossRef]
- Abro, K.A.; Memon, A.A.; Uqaili, M.A. A comparative mathematical analysis of RL and RC electrical circuits via Atangana-Baleanu and Caputo-Fabrizio fractional derivatives. Eur. Phys. J. Plus 2018, 133, 113. [Google Scholar] [CrossRef]
- Li, C.; Zeng, F. Numerical Methods for Fractional Calculus; Chapman and Hall/CRC: New York, NY, USA, 2015. [Google Scholar]
- Ahmad, S.N.; Ali, F.; Saqib, M.; Khan, I.; Jan, S.A.A.; Alshomrani, A.S.; Alghamdi, M.S. Comparison and analysis of the Atangana–Baleanu and Caputo–Fabrizio fractional derivatives for generalized Casson fluid model with heat generation and chemical reaction. Results Phys. 2017, 7, 789–800. [Google Scholar]
- Atangana, A.; Baleanu, D. Caputo-Fabrizio derivative applied to groundwater flow within confined aquifer. J. Eng. Mech. 2017, 143. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. Analysis of fractional differential equations. J. Math. Anal. Appl. 2002, 265, 229–248. [Google Scholar] [CrossRef]
- Hilfer, R.; Luchko, Y. Desiderata for Fractional Derivatives and Integrals. Mathematics 2019, 7, 149. [Google Scholar] [CrossRef]
- Yusuf, A.; Mustafa, Inc.; Aliyu, I.A.; Dumitru, B. Efficiency of the new fractional derivative with nonsingular Mittag-Leffler kernel to some nonlinear partial differential equations. Chaos Solitons Fractals 2018, 116, 220–226. [Google Scholar] [CrossRef]
- Mustafa, Inc.; Yusuf, A.; Aliyu, A.I.; Baleanu, D. Investigation of the logarithmic-KdV equation involving Mittag-Leffler type kernel with Atangana–Baleanu derivative. Phys. Stat. Mech. Its Appl. 2018, 506, 520–531. [Google Scholar]
- Caputo, M.; Fabrizio, M. Applications of new time and spatial fractional derivatives with exponential kernels. Prog. Fract. Differ. Appl. 2016, 2, 1–11. [Google Scholar] [CrossRef]
- Yang, X.; Srivastava, H.M.; Machado, J.T. A new fractional derivative without singular kernel. Therm. Sci. 2016, 20, 753–756. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. Detailed error analysis for a fractional Adams method. Numer. Algorithms 2004, 36, 31–52. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D.; Luchko, Y. Algorithms for the fractional calculus: A selection of numerical methods. Comput. Methods Appl. Mech. Eng. 2005, 194, 743–773. [Google Scholar] [CrossRef]
- Garrappa, R. Numerical solution of fractional differential equations: A survey and a software tutorial. Mathematics 2018, 6, 16. [Google Scholar] [CrossRef]
- Wei, Y.; Chen, Y.; Cheng, S.; Wang, Y. A note on short memory principle of fractional calculus. Fract. Calc. Appl. Anal. 2017, 20, 1382–1404. [Google Scholar] [CrossRef]
- Caputo, M.; Mauro, F. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 1–13. [Google Scholar]
- Losada, J.; Nieto, J. Properties of a new fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 87–92. [Google Scholar]
- Goufo, E.F.D. Application of the Caputo-Fabrizio Fractional Derivative without Singular Kernel to Korteweg-de Vries-Burgers Equation. Math. Model. Anal. 2016, 21, 188–198. [Google Scholar] [CrossRef]
- Ali, F.; Saqib, M.; Khan, I.; Sheikh, N.A. Application of Caputo-Fabrizio derivatives to MHD free convection flow of generalized Walters’-B fluid model. Eur. Phys. J. Plus. 2016, 131, 377. [Google Scholar] [CrossRef]
- Atangana, A. On the new fractional derivative and application to nonlinear Fisher’s reaction–diffusion equation. Appl. Math. Comput. 2016, 273, 948–956. [Google Scholar] [CrossRef]
- Atangana, A.; Alqahtani, R.T. Numerical approximation of the space-time Caputo-Fabrizio fractional derivative and application to groundwater pollution equation. Adv. Differ. Equ. 2016, 2016, 156. [Google Scholar] [CrossRef]
- Akman, T.; Yıldız, B.; Baleanu, D. New discretization of Caputo–Fabrizio derivative. Comput. Appl. Math. 2018, 37, 3307–3333. [Google Scholar] [CrossRef]
- Rangaig, N. Finite Difference Approximation for Caputo-Fabrizio Time Fractional Derivative on Non-Uniform Mesh and Some Applications. Phys. J. 2018, 1, 255–263. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).