Reformulated Zagreb Indices of Some Derived Graphs
Abstract
1. Introduction
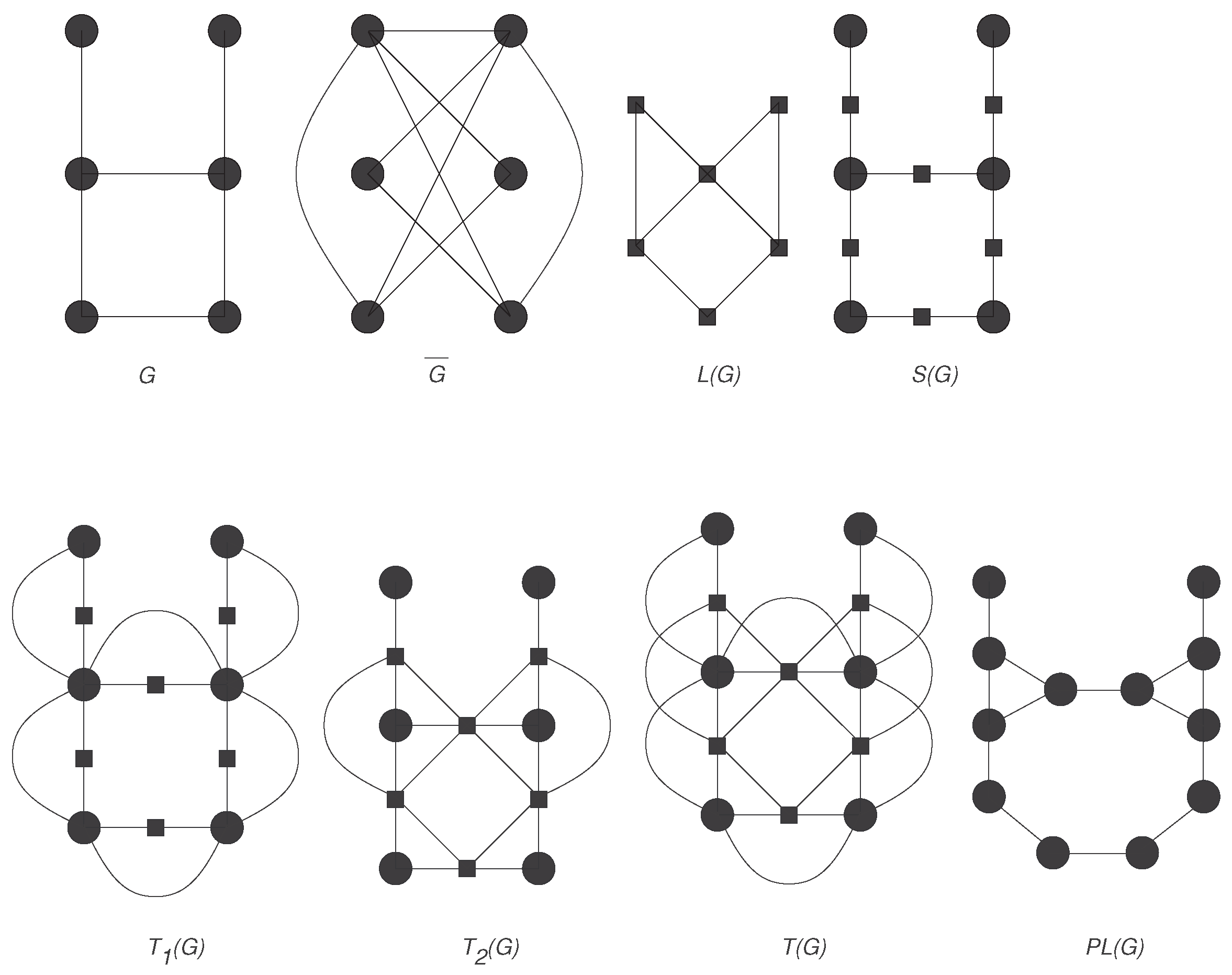
Some Derived Graphs
- Complement: The complement of G is the graph with the same set of vertices as G, but there is an edge between two vertices of if and only if there is no edge between these vertices in G. Clearly, and .
- Line graph: The line graph of G is the graph in which the vertex set is the edge set of G, and there is an edge between two vertices of L if and only if their corresponding edges are incident in G. Thus, , and by hand shaking lemma,
- Subdivision graph: A subdivision graph of a graph G can be constructed by inserting a vertex on each edge of G, which will change that edge into a path of length two. This graph is denoted as .So, and .
- Vertex-semitotal graph: A vertex-semitotal graph is constructed from G by inserting a new vertex on each edge of G and then by joining every newly-inserted vertex to the end vertices of the corresponding edge. Thus, and .
- Edge-semitotal graph: An edge-semitotal graph is made by putting a new vertex in each edge of G and then joining with edges those new vertices whose corresponding edges are incident in G. Thus, and .
- Total graph: The total graph is the union of the vertex-semitotal graph and the edge-semitotal graph. Thus, and .
- Paraline graph: The paraline graph is the line graph of the subdivision graph denoted by . Furthermore, and:
2. Reformulated First Zagreb Index of Some Derived Graphs
- -edge: an edge between two -vertices.
- -edge: an edge between two -vertices.
- -edge: an edge between a -vertex and a -vertex.
- Corresponding to every edge in G, there are two -edges and in such that:and:
- -edges are the edges corresponding to the edges of .
- Corresponding to every edge in G, there is one -edge, which is , and two -edges, which are and in T such that:and:
- -edges are the edges corresponding to the edges of .
- The edges in , where .
- Edges corresponding to edges of G. It can be seen that corresponding to every edge in G, there is an edge in of the same degree.
3. Reformulated Second Zagreb Index of Some Derived Graphs
- For any vertex , there are edges, each of degree in S, and all these edges are incident at i. Therefore, for any vertex , the total number of pairs of incident edges lying in this category is .
- Corresponding to every pair of adjacent vertices i and j in G, there is a pair of incident edges of degrees and in S.
- For any vertex , there are edges, each of degree in S, and all these edges are incident at i. Therefore, for any vertex , the total number of pairs of incident edges lying in this category is .
- Corresponding to every pair of adjacent vertices i and j in G, there is a pair of incident edges of degrees and in S.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shang, Y. Perturbation results for the Estrada index in weighted networks. J. Phys. A Math. Theor. 2011, 44, 075003. [Google Scholar] [CrossRef]
- Bondy, J.A.; Murty, U.S.R. Graph Theory; Springer: Berlin, Germany, 2008. [Google Scholar]
- Gutman, I.; Trinajstić, N. Graph theory and molecular orbitals. III. Total π-electron energy of alternate hydrocarbons. Chem. Phys. Lett. 1972, 17, 535–538. [Google Scholar] [CrossRef]
- Balaban, A.T. From Chemical Topology to Three-Dimensional Geometry; Plenum Press: New York, NY, USA, 1997. [Google Scholar]
- Devillers, J.; Balaban, A.T. (Eds.) Topological Indices and Related Descriptors in QSAR and QSPR; Gordon and Breach: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Todeschini, R.; Consonni, V. Handbook of Molecular Descriptors; Wiley-VCH: Weinheim, Germany, 2000. [Google Scholar]
- Gutman, I.; Furtula, B.; Kovijanić Vukićević, Z.; Popivoda, G. On Zagreb indices and coindices. Match Commun. Math. Comput. Chem. 2015, 74, 5–16. [Google Scholar]
- Basavanagoud, B.; Gutman, I.; Chetana, S.G. On second Zagreb index and coindex of some derived graphs. Kragujev. J. Sci. 2015, 37, 113–121. [Google Scholar]
- Miličević, A.; Nikolić, S.; Trinajstić, N. On reformulated Zagreb indices. Mol. Divers. 2004, 8, 393–399. [Google Scholar] [CrossRef] [PubMed]
- Shang, Y. On the number of spanning trees, the Laplacian eigenvalues, and the Laplacian Estrada index of subdivided-line graphs. Open Math 2016, 14, 641–648. [Google Scholar] [CrossRef]
- De, N. Some bounds of reformulated Zagreb indices. Appl. Math. Sci. 2012, 6, 5005–5012. [Google Scholar]
- Ilić, A.; Zhou, B. On reformulated Zagreb indices. Discr. Appl. Math. 2012, 160, 204–209. [Google Scholar] [CrossRef]
- Ji, S.; Li, X.; Huo, B. On reformulated Zagreb indices with respect to acyclic, unicyclic and bicyclic graphs. Match Commun. Math. Comput. Chem. 2014, 72, 723–732. [Google Scholar]
- Su, G.; Xiong, L.; Xu, L.; Ma, B. On the maximum and minimum first reformulated Zagreb index of graphs with connectivity at most k. Filomat 2011, 25, 75–83. [Google Scholar] [CrossRef]
- Zhou, B.; Trinajstić, N. Some properties of the reformulated Zagreb indices. J. Math. Chem. 2010, 48, 714–719. [Google Scholar] [CrossRef]
- Liu, J.-B.; Wang, C.; Wang, S. Zagreb indices and multiplicative Zagreb indices of Eulerian graphs. Bull. Malays. Math. Sci. Soc. 2019, 42, 67–78. [Google Scholar] [CrossRef]
- De, N.; Nayeem, S.M.A.; Pal, A. The F-coindex of some graph operations. Springer Plus 2016, 5, 221. [Google Scholar] [CrossRef] [PubMed]
- Furtula, B.; Gutman, I. A forgotten topological index. J. Math. Chem. 2015, 53, 1184–1190. [Google Scholar] [CrossRef]
- Basavanagoud, B.; Patil, S. Multiplicative Zagreb indices and coindices of some derived graphs. Opuscula Math. 2016, 36, 287–299. [Google Scholar] [CrossRef]
- Shang, Y. Vulnerability of networks: Fractional percolation on random graphs. Phys. Rev. E 2014, 89, 012813. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.-B.; Ali, B.; Malik, M.A.; Siddiqui, H.M.A.; Imran, M. Reformulated Zagreb Indices of Some Derived Graphs. Mathematics 2019, 7, 366. https://doi.org/10.3390/math7040366
Liu J-B, Ali B, Malik MA, Siddiqui HMA, Imran M. Reformulated Zagreb Indices of Some Derived Graphs. Mathematics. 2019; 7(4):366. https://doi.org/10.3390/math7040366
Chicago/Turabian StyleLiu, Jia-Bao, Bahadur Ali, Muhammad Aslam Malik, Hafiz Muhammad Afzal Siddiqui, and Muhammad Imran. 2019. "Reformulated Zagreb Indices of Some Derived Graphs" Mathematics 7, no. 4: 366. https://doi.org/10.3390/math7040366
APA StyleLiu, J.-B., Ali, B., Malik, M. A., Siddiqui, H. M. A., & Imran, M. (2019). Reformulated Zagreb Indices of Some Derived Graphs. Mathematics, 7(4), 366. https://doi.org/10.3390/math7040366






