Application of the Laplace Homotopy Perturbation Method to the Black–Scholes Model Based on a European Put Option with Two Assets
Abstract
:1. Introduction
2. The Mathematical Model
- p
- the value of put option depending on the stock prices at time t,
- ρ
- the correlation between the two underlying stock prices and ,
- wi
- the portions of underlying stock for ,
- Ki
- the strike price of the ith underlying stock for ,
- r
- the risk-free interest rate,
- σi
- the volatility of the ith underlying stock for ,
- T
- the expiration date.
3. The Basic Ideas of Homotopy Perturbation Method with Laplace Transform
4. An Analytical Solution of the Black–Scholes Model for European Put Options with Two Assets by Using LHPM
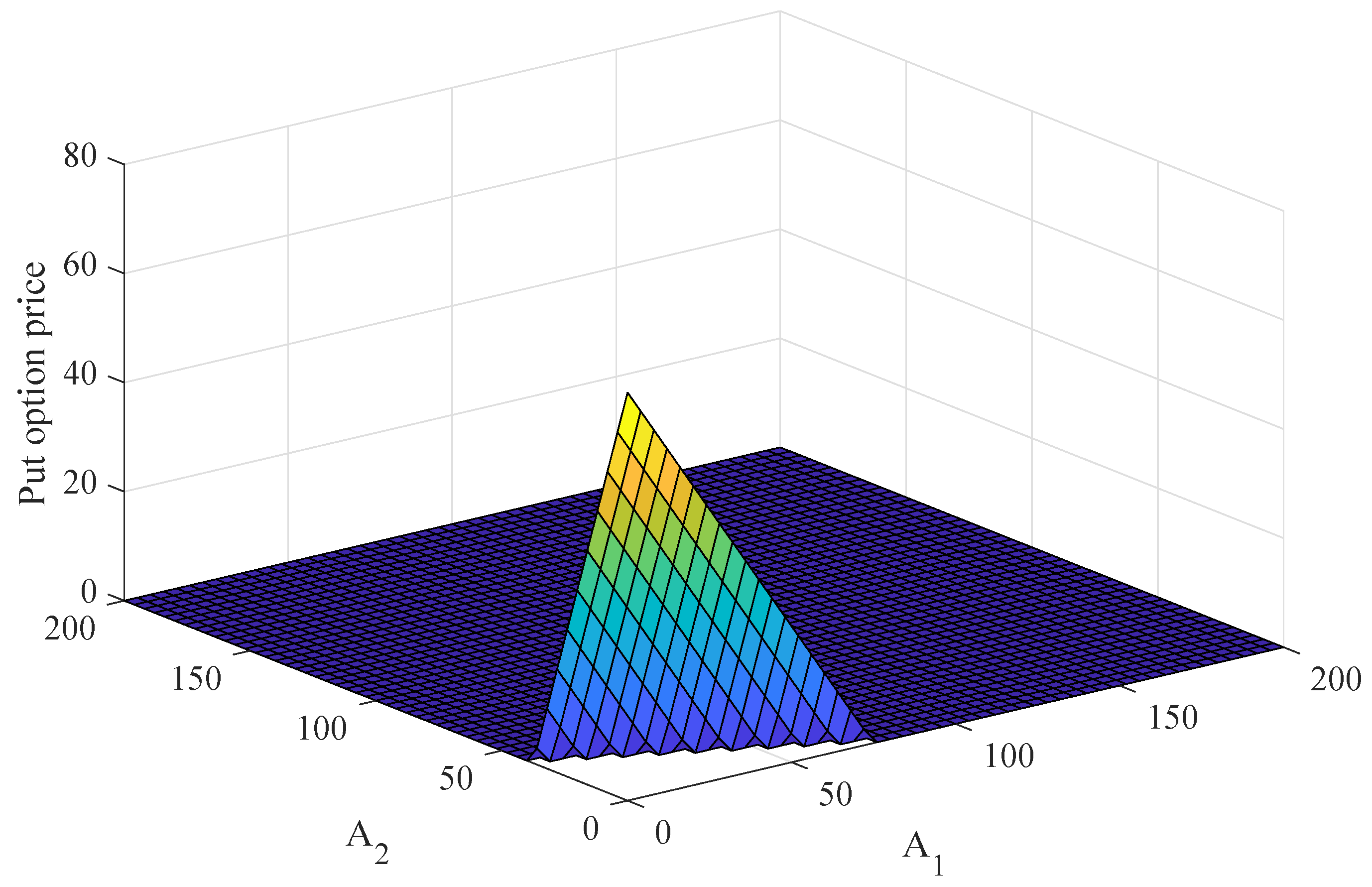
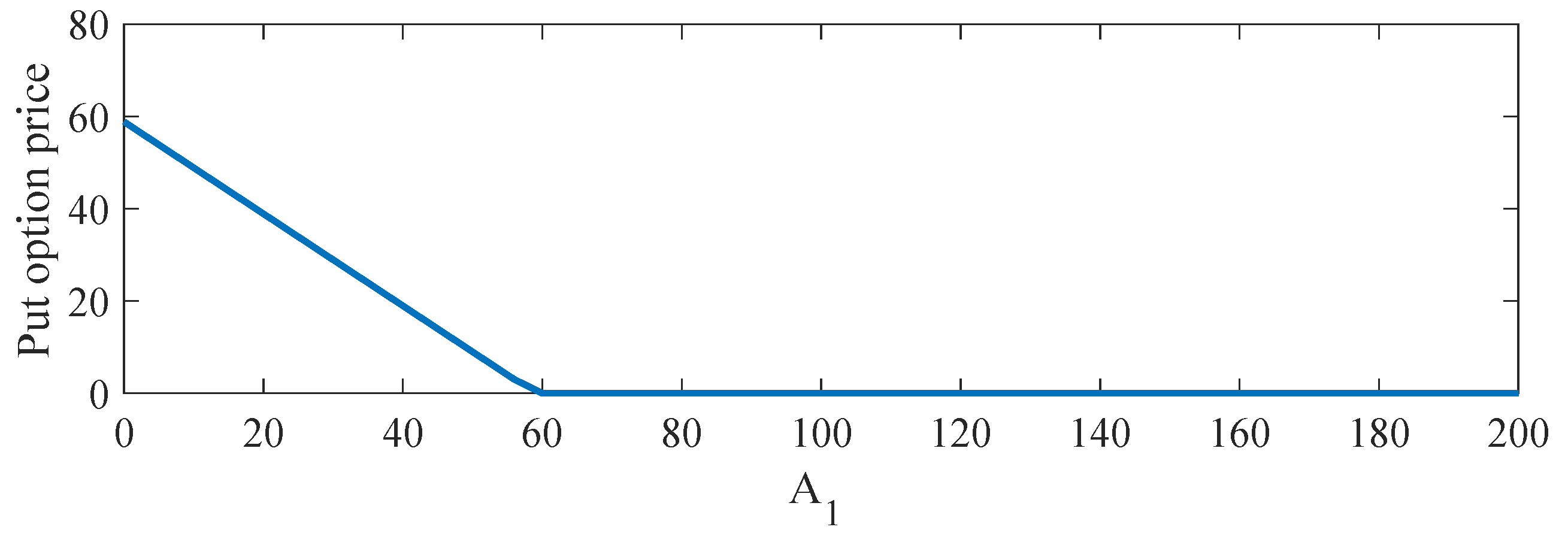
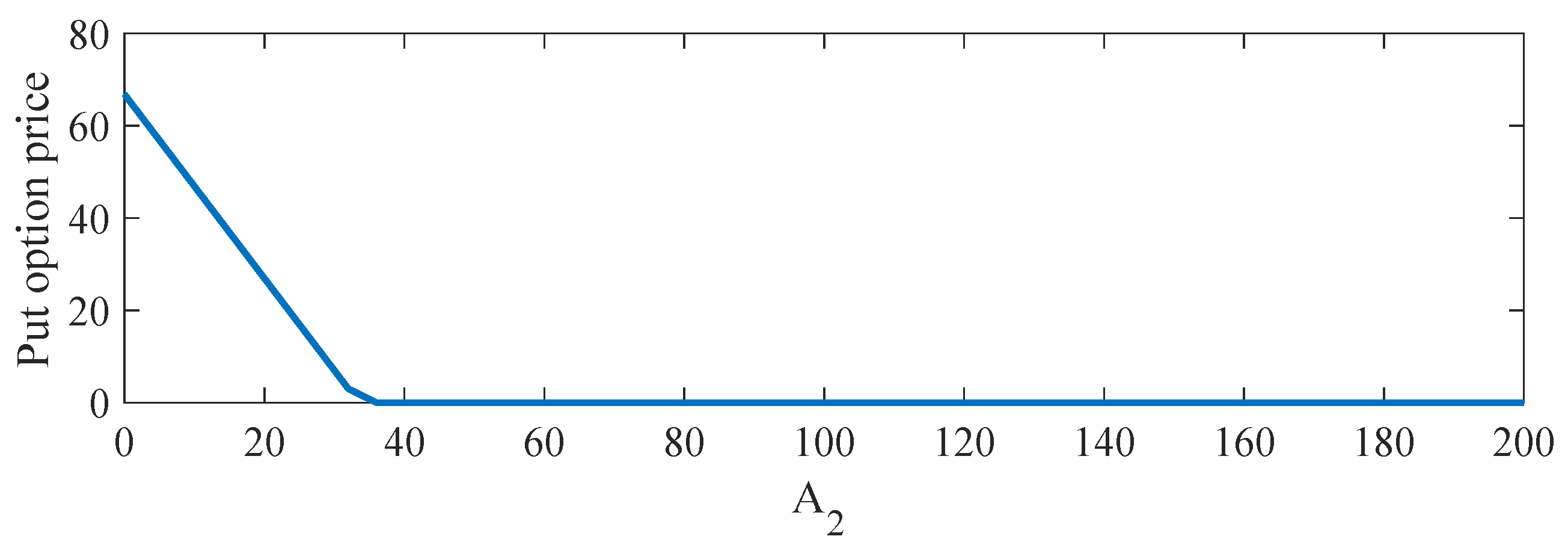
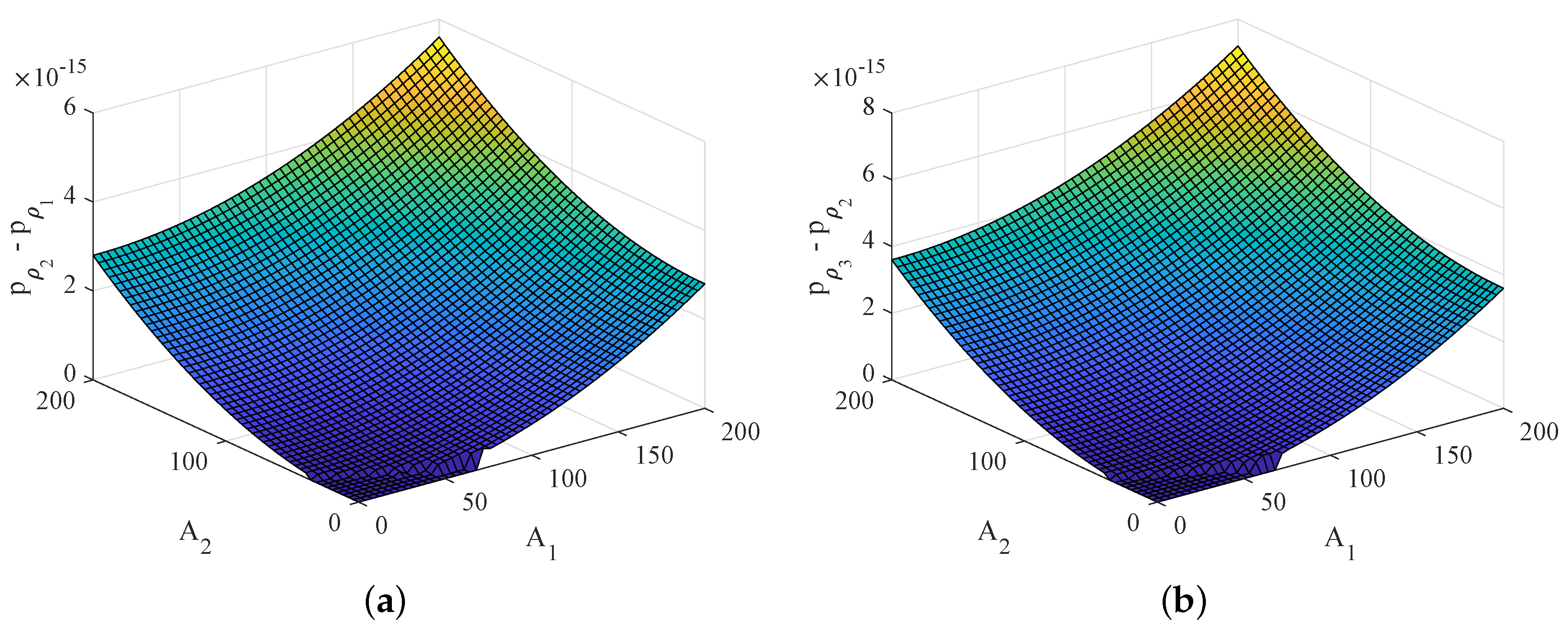
5. Solution Example
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cesare, L.D.; Sportelli, M. A dynamic IS-LM model with delayed taxation revenues. Chaos Solitons Fractals 2005, 25, 233–244. [Google Scholar] [CrossRef]
- Fanti, L.; Manfredi, P. Chaotic business cycles and fiscal policy: An IS-LM model with distributed tax collection lags. Chaos Solitons Fractals 2007, 32, 736–744. [Google Scholar] [CrossRef]
- He, X.Z.; Li, K.; Wei, J.; Zheng, M. Market stability switches in a continuous-time financial market with heterogeneous beliefs. Econ. Model. 2009, 26, 1432–1442. [Google Scholar] [CrossRef]
- Ma, J.H.; Chen, Y.S. Study for the bifurcation topological structure and the global complicated character of a kind of nonlinear finance system, I. Appl. Math. Mech. 2001, 22, 1240–1251. [Google Scholar] [CrossRef]
- Ma, J.H.; Chen, Y.S. Study for the bifurcation topological structure and the global complicated character of a kind of nonlinear finance system, II. Appl. Math. Mech. 2001, 22, 1375–1382. [Google Scholar] [CrossRef]
- He, X.Z.; Zheng, M. Dynamics of moving average rules in a continuous-time financial market model. J. Econ. Behav. Organ. 2010, 76, 615–634. [Google Scholar] [CrossRef]
- Chiarella, C.; He, X.Z.; Zheng, M. An analysis of the effect of noise in a heterogeneous agent financial market model. J. Econ. Dyn. Control 2011, 35, 148–162. [Google Scholar] [CrossRef]
- Zhou, L.; Li, Y. A generalized dynamic IS-LM model with delayed time in investment processes. Appl. Math. Comput. 2008, 196, 774–781. [Google Scholar] [CrossRef]
- Chatterjee, P.; Shukayev, M. A stochastic dynamic model of trade and growth: Convergence and diversification. J. Econ. Dyn. Control 2012, 36, 416–432. [Google Scholar] [CrossRef]
- Yang, H.; Li, L.; Wang, D. Research on the Stability of Open Financial System. Entropy 2015, 17, 1734–1754. [Google Scholar] [CrossRef]
- Prathumwan, D.; Sawangtong, W.; Wiwattanapataphee, B.; Giannini, L.M. A differential evolution algorithm for parameter optimization of an asset flow model. J. Algebra Appl. Math. 2019, 17, 33–56. [Google Scholar]
- Prathumwan, D.; Sawangtong, W.; Sawangtong, P. An Analysis on the Fractional Asset Flow Differential Equations. Mathematics 2017, 5, 33. [Google Scholar] [CrossRef]
- Cen, Z.; Le, A. A robust finite difference scheme for pricing american put options with singularity-separating method. Numer. Algorithms 2010, 53, 497–510. [Google Scholar] [CrossRef]
- Cen, Z.; Le, A. A robust and accurate finite difference method for a generalized Black–Scholes equation. J. Comput. Appl. Math. 2011, 235, 2728–2733. [Google Scholar] [CrossRef]
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Gu¨lkac, V. The homotopy pertubation method for the Black–Scholes equation. J. Stat. Comput. Simul. 2010, 80, 1349–1354. [Google Scholar] [CrossRef]
- Paliathanasis, A.; Morris, R.M.; Leach, P.G.L. Lie Symmetries of (1+2) Nonautonomous Evolution Equations in Financial Mathematics. Mathematics 2016, 4, 34. [Google Scholar] [CrossRef]
- Rigatos, G.; Siano, P. Stabilization of the multi-asset Black–Scholes PDE using differential flatness theory. IFAC-Papers OnLine 2016, 49, 180–185. [Google Scholar] [CrossRef]
- Hicks, W. PT Symmetry, Non-Gaussian Path Integrals, and the Quantum Black–Scholes Equation. Entropy 2019, 21, 105. [Google Scholar] [CrossRef]
- Cox, J.C.; Ross, S.; Rubinstein, M. Option pricing: A simplified approach. J. Financ. Econ. 1979, 7, 229–263. [Google Scholar] [CrossRef]
- Lesmana, D.C.; Wang, S. An upwind finite difference method for a nonlinear Black–Scholes equation governing European option valuation under transaction costs. J. Appl. Math. Comput. 2013, 219, 8811–8828. [Google Scholar] [CrossRef]
- Song, L.; Wang, W. Solution of the fractional Black–Scholes option pricing model by finite difference method. Abstr. Appl. Anal. 2013, 2013, 194286. [Google Scholar] [CrossRef]
- Phaochoo, P.; Luadsong, A.; Aschariyaphotha, N. The meshless local Petrov–Galerkin based on moving kriging interpolation for solving fractional Black–Scholes model. J. King Saud Univ.-Sci. 2016, 28, 111–117. [Google Scholar] [CrossRef]
- Jodar, L.; Sevilla-Peris, P.; Cortes, J.C.; Sala, R. A new direct method for solving the Black–Scholes equation. Appl. Math. Lett. 2002, 18, 29–32. [Google Scholar] [CrossRef]
- Yan, H. Adaptive Wavelet Precise Integration Method for Nonlinear Black–Scholes Model Based on Variational Iteration Method. Abstr. Appl. Anal. 2013, 2013, 735919. [Google Scholar] [CrossRef]
- Cavoretto, R.; Schneider, T.; Zulian, P. OpenCL Based Parallel Algorithm for RBF-PUM Interpolation. J. Sci. Comput. 2018, 74, 267–289. [Google Scholar] [CrossRef]
- Safdari-Vaighani, A.; Heryudono, A.; Larsson, E. A Radial Basis Function Partition of Unity Collocation Method for Convection–Diffusion Equations Arising in Financial Applications. J. Sci. Comput. 2015, 64, 341–367. [Google Scholar] [CrossRef]
- Shcherbakov, V.; Larsson, E. Radial basis function partition of unity methods for pricing vanilla basket options. Comput. Math. Appl. 2016, 71, 185–200. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method: A new nonlinear analytical technique. Appl. Math. Comput. 2003, 135, 73–79. [Google Scholar] [CrossRef]
- He, J.H. The homotopy perturbation method for nonlinear oscillations with discontinuities. Appl. Math. Comput. 2004, 151, 287–292. [Google Scholar]
- He, J.H. Homotopy perturbation method for bifurcation of nonlinear problems. Int. J. Nonlinear Sci. Numer. Simul. 2005, 6, 207–208. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- Khan, Y. A novel Laplace decomposition method for non-linear stretching sheet problem in the presence of MHD and slip condition. Int. J. Numer. Methods Heat Fluid Flow 2014, 24, 73–85. [Google Scholar] [CrossRef]
- Khan, Y.; Abdou, M.A.; Faraz, N.; Yildirim, A.; Wu, Q. Numerical Solution of MHD Flow over a Nonlinear Porous Stretching Sheet. Iran. J. Chem. Chem. Eng. 2012, 31, 125–132. [Google Scholar]
- Madani, M.; Khan, Y.; Fathizadeh, M.; Yildirim, A. Application of homotopy perturbation and numerical methods to the magneto-micropolar fluid flow in the presence of radiation. Eng. Comput. 2012, 29, 277–294. [Google Scholar] [CrossRef]
- Shateyi, S.; Motsa, S.S.; Khan, Y. A new piecewise spectral homotopy analysis of the Michaelis-Menten enzymatic reactions model. Numer. Algorithms 2014, 66, 495–510. [Google Scholar] [CrossRef]
- Baholian, E.; Azizi, A.; Saeidian, J. Some notes on using the homotopy perturbation method for solving time-dependent differential equations. Math. Comput. Model. 2009, 50, 213–224. [Google Scholar] [CrossRef]
- Khan, Y.; Wu, Q. Homotopy perturbation transform method for nonlinear equations using He’s polynomials. Comput. Math. Appl. 2011, 61, 1963–1967. [Google Scholar] [CrossRef]
- Kumar, S.; Yildirim, A.; Khan, Y.; Jafari, H.; Sayevand, K.; Wei, L. Analytical Solution of Fractional Black–Scholes European Option Pricing Equation by using Laplace Transform. J. Fract. Calc. Appl. 2012, 2, 1–9. [Google Scholar]
- Madani, M.; Fathizadeh, M.; Khan, Y.; Yildirim, A. On the coupling of the homotopy perturbation method and Laplace transformation. Math. Comput. Model. 2011, 53, 1937–1945. [Google Scholar] [CrossRef]
- Sawangtong, P.; Trachoo, K.; Sawangtong, W.; Wiwattanapataphee, B. The Analytical Solution for the Black–Scholes Equation with Two Assets in the Liouville-Caputo Fractional Derivative Sense. Mathematics 2018, 6, 129. [Google Scholar] [CrossRef]
- Trachoo, K.; Sawangtong, W.; Sawangtong, P. Laplace Transform Homotopy Perturbation Method for the Two Dimensional Black–Scholes Model with European Call Option. Math. Comput. Appl. 2017, 22, 23. [Google Scholar] [CrossRef]
- Mathai, A.M.; Haubold, H.J. Special Functions for Applied Scientists; Springer: New York, NY, USA, 2008. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prathumwan, D.; Trachoo, K. Application of the Laplace Homotopy Perturbation Method to the Black–Scholes Model Based on a European Put Option with Two Assets. Mathematics 2019, 7, 310. https://doi.org/10.3390/math7040310
Prathumwan D, Trachoo K. Application of the Laplace Homotopy Perturbation Method to the Black–Scholes Model Based on a European Put Option with Two Assets. Mathematics. 2019; 7(4):310. https://doi.org/10.3390/math7040310
Chicago/Turabian StylePrathumwan, Din, and Kamonchat Trachoo. 2019. "Application of the Laplace Homotopy Perturbation Method to the Black–Scholes Model Based on a European Put Option with Two Assets" Mathematics 7, no. 4: 310. https://doi.org/10.3390/math7040310
APA StylePrathumwan, D., & Trachoo, K. (2019). Application of the Laplace Homotopy Perturbation Method to the Black–Scholes Model Based on a European Put Option with Two Assets. Mathematics, 7(4), 310. https://doi.org/10.3390/math7040310




