3D Visualization through the Hologram for the Learning of Area and Volume Concepts
Abstract
:1. Introduction
2. Literature Review
2.1. The Teaching of Geometry in Secondary Education
2.2. The Importance of Visualization and the Use of Technologies in the Geometry Learning Process
2.3. The Use of the Hologram in Geometry
3. Methodology
3.1. Objective and Hypothesis
3.2. Sample
3.3. Research Design
3.4. Information Collection Tools
- Lateral and total areas of polyhedrons
- Lateral and total areas of bodies in revolution
- Volumes of polyhedrons
- Volumes of bodies of revolution
3.5. Procedure
3.6. Data Analysis
4. Results and Discussion
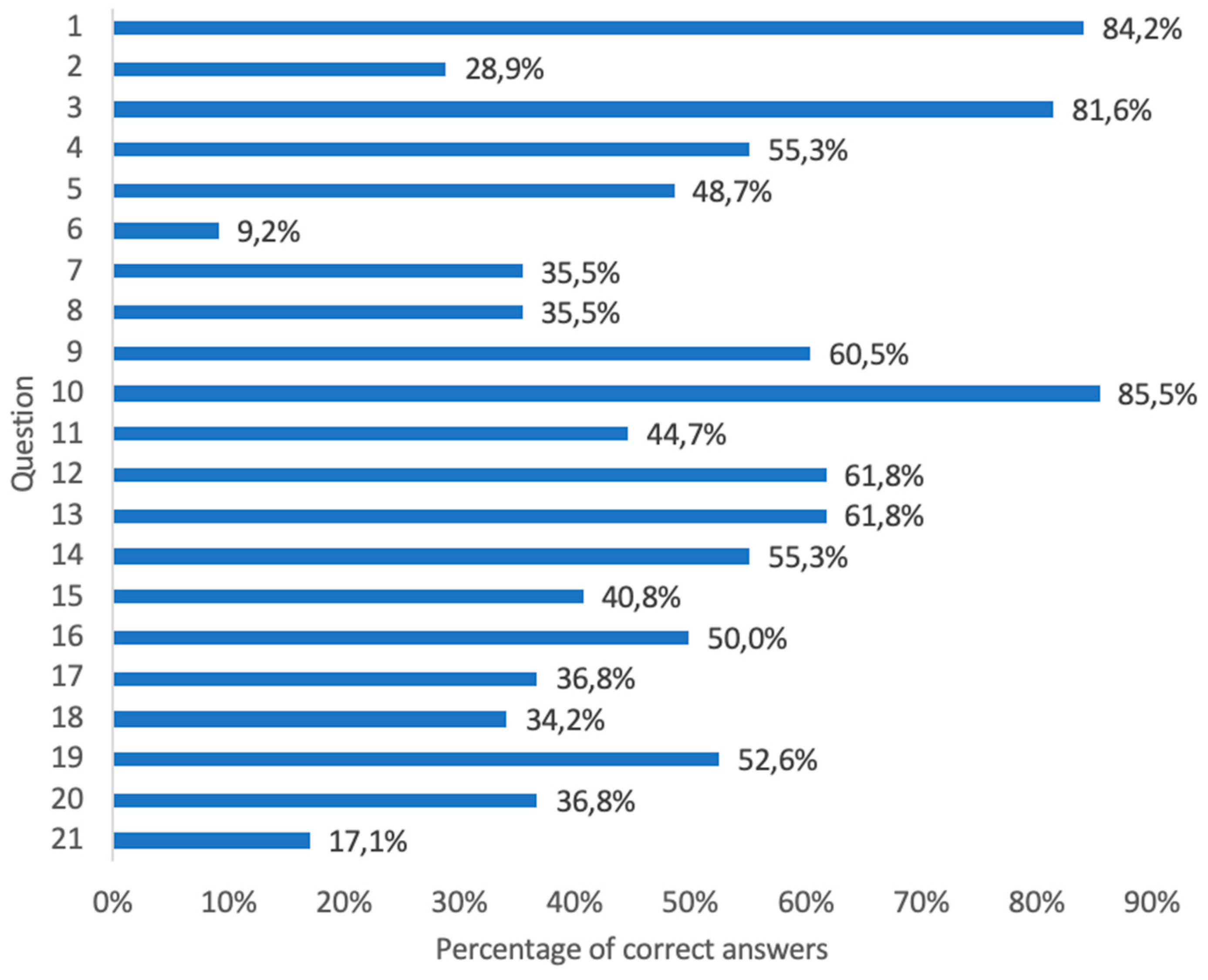
4.1. Pre-Test Results
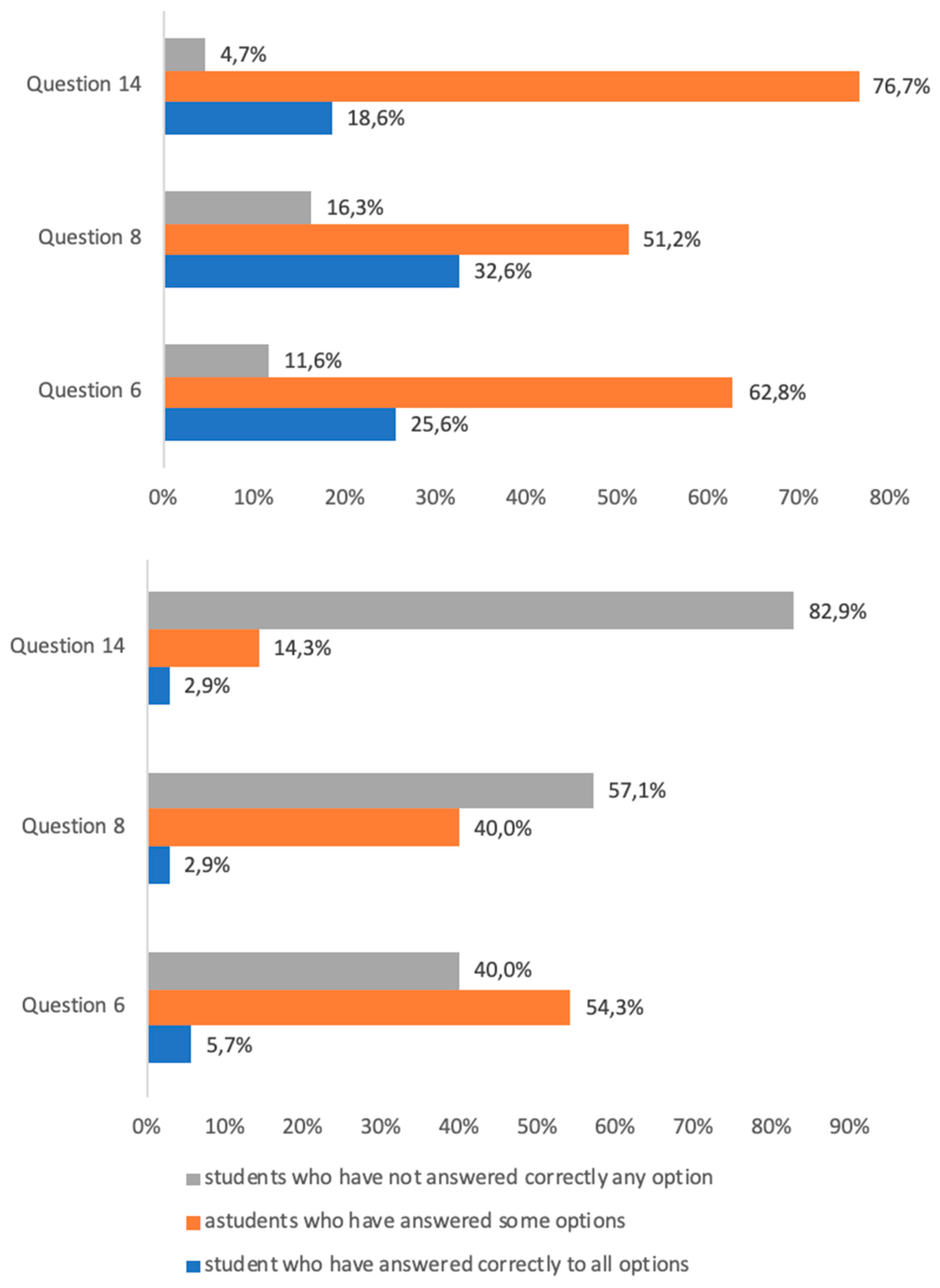
4.2. Post-Test Results
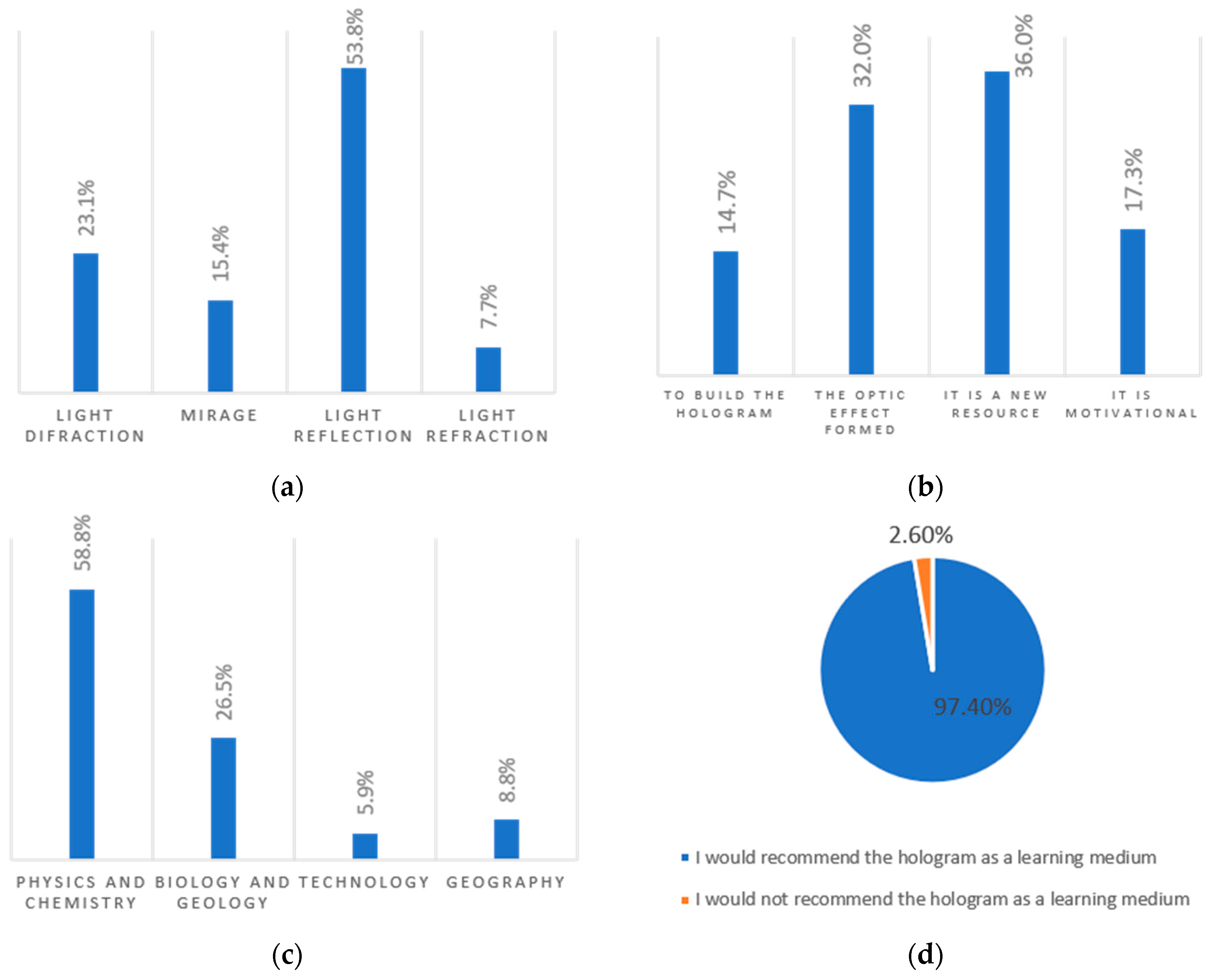
4.3. User Experience Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Pre-Test
| 1. The polygons are flat figures (T/F) |
| 2. The quadrilaterals have: |
| a. Four equal sides |
| b. Four equal sides two to two |
| c. Four equal angles |
| d. Four right angles |
| 3. A triangle with two equal sides and a different one is called: |
| a. Equilateral |
| b. Isosceles |
| c. Scalene |
| d. Acute |
| 4. In a triangle with an angle greater than 90º it is called: |
| a. Scalene |
| b. Acute |
| c. Obtuse |
| d. Rectangle |
| 5. The apothem of a regular polygon is: |
| a. The side of the polygon |
| b. The sum of the sides of the polygon |
| c. The distance from the center of the polygon to the vertex |
| d. The distance of the polygon to the middle of the side |
| 6. What is the perimeter of a flat figure: |
| a. The sum of its angles |
| b. The sum of its sides |
| c. The line that forms its outline |
| d. The space that collects |
| 7. The circumference of a circle is: |
| a. πr2 |
| b. 2πr2 |
| c. 2πr |
| d. πr |
| 8. A piece of circumference is called: |
| a. Arc |
| b. Sector |
| c. Radio |
| d. Angle |
| 9. To which flat figure corresponds the formula for calculating area axb, where a and b are the sides: |
| a. Rectangle |
| b. Quadrilateral |
| c. Triangle |
| d. Hexagon |
| 10. The formula of the area of the triangle is: |
| a. Base x height/3 |
| b. Base x height/2 |
| c. Base x height |
| d. Side by side |
| 11. How is the area of a hexagon calculated? |
| a. Decomposing in equilateral triangles |
| b. Decomposing in isosceles triangles |
| c. Decomposing in triangles |
| d. Decomposing in scalene triangles |
| 12. The area of a circle is: |
| a. πr2 |
| b. 2πr2 |
| c. 2πr |
| d. πr |
| 13. A polyhedron is: |
| a. A flat figure |
| b. A 3D figure |
| c. A 3D figure whose faces are polygons |
| d. A 3D figure whose lateral surface is curved |
| 14. A orthohedron is shaped like a shoe box (T/F) |
| 15. What is a polyhedron: |
| a. Cube |
| b. Prism |
| c. Orthopedic |
| d. pyramid |
| e. Everyone |
| 16. A body in revolution is: |
| a. A flat figure |
| b. A 3D figure |
| c. A 3D figure whose faces are polygons |
| d. A 3D figure whose lateral surface is curved |
| 17. What is a body in revolution? |
| a. Cylinder |
| b. Cone |
| c. Sphere |
| d. Everyone |
| 18. The word edge refers to: |
| a. The side of a polyhedron |
| b. The vertex of a polyhedron |
| c. The height of a polyhedron |
| d. The face of a polyhedron |
| 19. The total surface area of the polyhedrons is calculated as: |
| a. Area of the bases plus the lateral area |
| b. Area of a base by height |
| 20. The surface area of the bodies in revolution is calculated as the sum of the lateral area plus the areas of the base, except that of the sphere |
| 21. Point out the false statement: |
| a. The volume of a cube, orthohedron, prism and cylinder is calculated as the area of the base by height |
| b. The volume of a polyhedron is calculated as the area of the base by the height |
| c. The volume of a cone is one-third of the volume of the cylinder |
| d. The volume of a square base pyramid is one-third of the volume of a cube |
Appendix B. Post-Test
| 1. The surface area of a 5 cm long, 2 cm wide and 3 cm high orthohedron is: |
| a. 30 cm2 |
| b. 30 cm3 |
| c. 62 cm2 |
| d. 10 cm2 |
| 2. The total surface area of a prism with right triangle base whose legs measure 4 cm and 3 cm and the height of the prism is 6 cm is: |
| a. 72 cm2 |
| b. 84 cm2 |
| c. 78 cm2 |
| d. 36 cm2 |
| 3. The total surface area of a hexagonal prism of 7 cm high whose base is formed by a hexagon of 6 cm side and whose apothem is 4 cm is: |
| a. 396 cm2 |
| b. 66 cm2 |
| c. 276 cm2 |
| d. 324 cm2 |
| 4. The lateral area of a square-based pyramid whose faces are formed by isosceles triangles in which the equal sides have 5 cm and the other 6 cm is: |
| a. 12 cm2 |
| b. 48 cm2 |
| c. 84 cm2 |
| d. 24 cm2 |
| e. 60 cm2 |
| 5. The lateral area of a trunk squared-base pyramid in which the faces are trapezoids with a great base of 7 cm, a small base of 4 cm and an apothem of 5 cm is: |
| a. 70cm2 |
| b. 280 cm2 |
| c. 110 cm2 |
| d. 88 cm2 |
| 6. Label the correct statement/s: |
| a. A cylinder is a body of revolution obtained when rectangle or a square rotates on one of its sides so its lateral surface area is calculated by multiplying the length of the circumference it forms by the height |
| b. A cone is a body of revolution obtained when a right triangle rotates by one of its sides and the lateral surface area is obtained by multiplying the length of the circumference that it forms by the height |
| c. A truncated cone is a body of revolution obtained by cutting a cone or rotating a trapezoid on its straight side and its lateral surface area is πg (R + r) |
| d. A sphere is a body of revolution obtained when a semicircle or a circle rotates around its diameter and its surface area is the sum of the area of 4 circles. |
| 7. Label the correct statement/s: |
| a. The volume of a cube and an octohedron is always calculated as the product of the area of the base by the height |
| b. The volume of a hexagonal prism is calculated as the product of the area of its base by its height |
| c. The volume of a cylinder is calculated as the product of area of the base by height |
| d. a and b are correct |
| e. All are correct |
| 8. Point out the correct affirmation or affirmations |
| a. Three triangular-base pyramids form a cube |
| b. Three triangular-base pyramids form a tetrahedron |
| c. Three square-base pyramids form a cube |
| d. Three square-base pyramids form a tetrahedron |
| 9. If a cube has a volume of 27 cm3, what will be the volume of the three equal pyramids it can form? |
| a. 3 cm3 |
| b. 9 cm3 |
| c. 13.5 cm3 |
| d. 6.75 cm3 |
| 10. If a squared-base pyramid of side 7 cm and height 6 cm is cut at a height from the ground of 4 cm so that the side of the square of the smaller base is 2 cm, the volume of the pyramid trunk is: |
| a. 86 cm3 |
| b. 95.3 cm3 |
| c. 6 cm3 |
| d. 12 cm3 |
| 11. The volume of a cone of diameter 6 cm and height 5 cm is: |
| a. 47.1 cm3 |
| b. 141.3 cm3 |
| c. 188.4 cm3 |
| d. 70.65 cm3 |
| 12. If a cone in which the base has a radius of 3 cm and 5 cm in height is cut at a height from the base of 3 cm so that the smallest radius of the circle that forms is 1.2 cm, the volume of the trunk of the cone is: |
| a. 47.1 cm3 |
| b. 44.1 cm3 |
| c. 42.58 cm3 |
| d. 3.01 cm3 |
| 13. Label the false statement in relation to the volume of the sphere |
| a. It is calculated as one third of the product of the surface area by the radius |
| b. It can be calculated by adding the volumes of all the square-base pyramids that constitute it |
| c. A sphere can be filled with two cones if the height and diameter of the cone are equal to the diameter of the sphere |
| d. Three cylinders can be filled with two spheres if the height and diameter of the cylinder is equal to the diameter of the sphere |
| 14. Label the false statement/s |
| a. With three cones you can fill three cylinders if they have the same height and same base area |
| b. With three cones you can fill a cylinder if they have the same height and same base area |
| c. With a cone, a semi-sphere can be filled if the height and diameter of the cone are equal to the diameter of the semi-sphere |
| d. With three spheres two cylinders can be filled if the height and diameter of the cylinder are equal to the diameter of the sphere |
| e. With two spheres three cylinders can be filled if the height and diameter of the cylinder are equal to the diameter of the sphere |
Appendix C. User Experience Test
| Likert-type questions: |
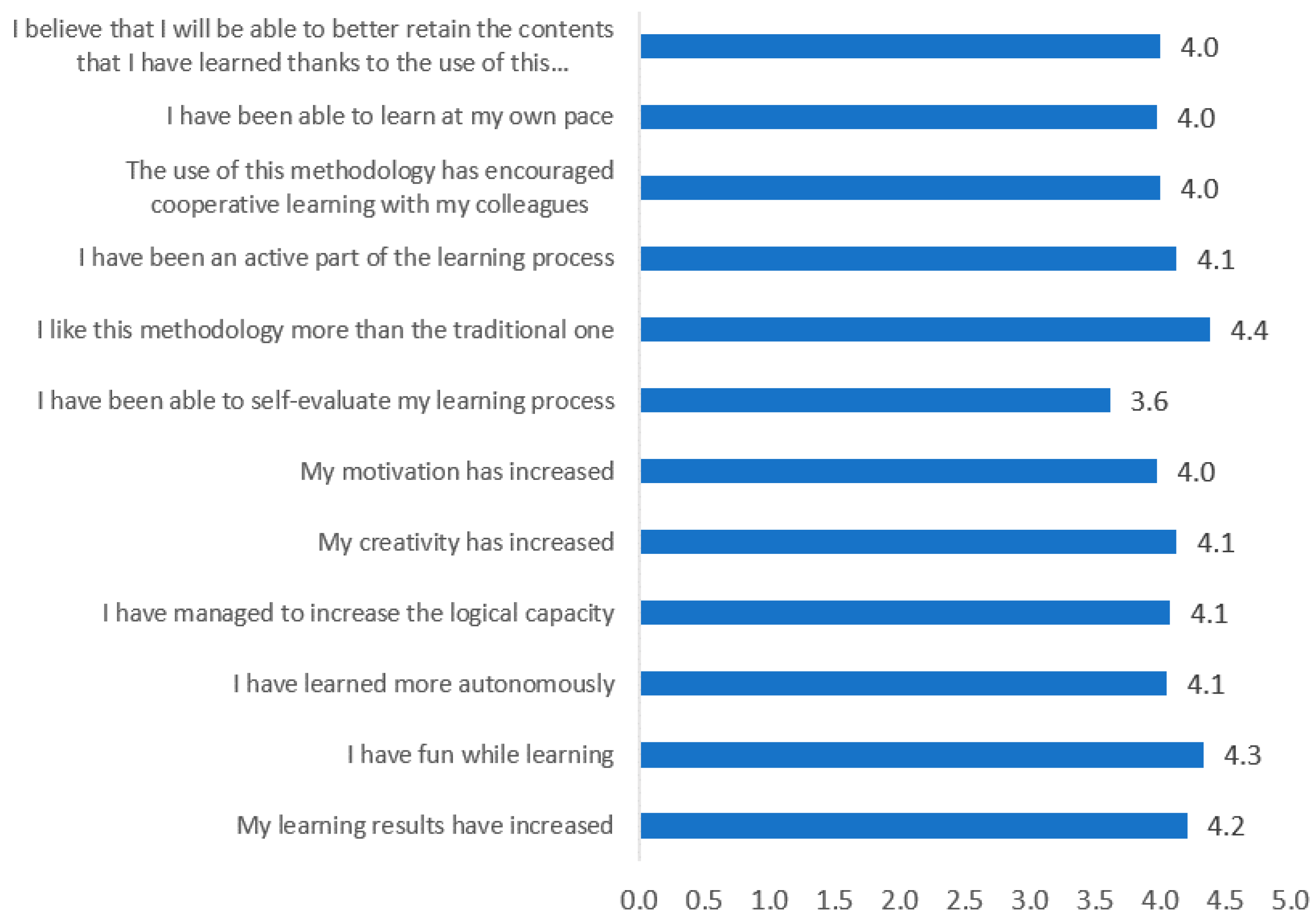
| 1. My learning results have increased |
| 2. I had fun learning |
| 3. I have learned more autonomously |
| 4. I have managed to increase the logical capacity |
| 5. My creativity has increased |
| 6. My motivation has increased |
| 7. I have been able to self-evaluate my learning process |
| 8. I liked this methodology more than the traditional one |
| 9. The learning has been more active on my part |
| 10. The use of this methodology has encouraged cooperative learning with my colleagues |
| 11. I have been able to learn at my own rhythm |
| 12. I believe that I will be able to retain better the contents that I have learned thanks to the use of this methodology |
| Open questions: |
| 1. The physical phenomenon that has taken place in the use of the hologram is: |
| 2. What I liked most about the use of hologram is: |
| 3. In what subject/s do you think it could be used in addition to mathematics? |
| 4. Would you recommend the hologram as a teaching tool? |
| 5. Is there something you want to comment? |
References
- Blanco, L.J.; Barrantes, M. Concepciones de los estudiantes para maestro en España sobre la Geometría escolar y su enseñanza-aprendizaje. Relime 2003, 6, 107–132. [Google Scholar]
- Gómez-Chacón, I.M. Matemática Emocional. Los Efectos en el Aprendizaje Matemático; Narcea: Madrid, Spain, 2000. [Google Scholar]
- Villella, J. Uno, Dos, Tres… Geometría Otra Vez; Aique: Buenos Aires, Argentina, 2001. [Google Scholar]
- Serra, R.; Vega, G.; Ferrat, Á; Lunazzi, J.J.; Magalhães, D.S.F. El holograma y su utilización como un medio de enseñanza de la física en Ingeniería. Revista Brasileira de Ensino de Física 2009, 31, 1401. [Google Scholar] [CrossRef]
- Orcos, L.; Magreñán, Á.A. The hologram as a teaching medium for the acquisition of STEM contents. Int. J. Learn. Technol. 2018, 13, 163–177. [Google Scholar] [CrossRef]
- Fabres, R. Estrategias metodológicas para la enseñanza y el aprendizaje de la Geometría, utilizadas por docentes de segundo ciclo, con la finalidad de generar una propuesta metodológica atingente a los contenidos. Estudios Pedagógicos 2016, 42, 87–105. [Google Scholar] [CrossRef]
- Fujita, T.; Jones, K. The bridge between practical and deductive geometry: Developing the geometrical eye. In Proceedings of the 26th PME International Conference, Norwich, UK, 21–26 July 2002; Cockburn, A.D., Nardi, E., Eds.; University of East Anglia: Norwich, UK, 2002; Volume 2, pp. 384–391. [Google Scholar]
- Jaramillo López, C.; Duarte, P. Enseñanza y aprendizaje de las estructuras matemáticas a partir del modelo de Van Hiele. Revista Educación y Pedagogía 2009, 18, 109–118. [Google Scholar]
- Schonberger, A.K. The relationship between visual spatial abilities and mathematical problem solving are there sex-related differences? In Proceedings of the 3rd PME International Conference, Coventry, UK, 9–14 July 1979; Volume 1, pp. 179–185. [Google Scholar]
- Gutiérrez, Á. Las representaciones planas de los cuerpos 3-dimensioanles en la enseñanza de la Geometría espacial. Rev. EMA 1998, 3, 193–220. [Google Scholar]
- Owens, K.; Outhred, L. The Complexity of learning geometry and measurement. In Handbook of Research on the Psychology of Mathematics Education: Past, Present and Future; Gutierrez, A., Boero, P., Eds.; Sense Publishers: Rotterdam, The Netherlands, 2006; pp. 83–115. [Google Scholar]
- Bishop, A.J. Spatial abilities and mathematics education—A review. Educ. Stud. Math. 1980, 11, 257–269. [Google Scholar] [CrossRef]
- Suh, J.; Seshaiyer, P. The Role of Information Technology in Engaging Elementary Students in Mathematical Modeling. In Proceedings of the Society for Information Technology & Teacher Education International Conference, Kuala Lumpur, Malaysia, 24–25 March 2016; pp. 2576–2583. [Google Scholar]
- Moyer-Packenham, P.; Suh, J. Learning mathematics with technology: The influence of virtual manipulatives on different achievement groups. J. Comput. Math. Sci. Teach. 2012, 31, 39–59. [Google Scholar]
- Clements, D.H.; Sarama, J. Effects of a preschool mathematics curriculum: Summative research on the Building Blocks project. J. Res. Math. Educ. 2007, 38, 136–163. [Google Scholar]
- Adams Becker, S.; Cummins, M.; Davis, A.; Freeman, A.; Hall Giesinger, C.; Ananthanarayanan, V. NMC Horizon Report: 2017 Higher Education Edition; The New Media Consortium: Austin, TX, USA, 2017. [Google Scholar]
- Liu, Y.Z.; Pang, X.N.; Jiang, S.; Dong, J.W. Viewing-angle enlargement in holographic augmented reality using time division and spatial tiling. Opt. Express 2013, 21, 12068–12076. [Google Scholar] [CrossRef] [PubMed]
- Gabor, D. Holography, 1948–1971. Science 1972, 177, 299–313. [Google Scholar] [CrossRef] [PubMed]
- Lee, H. 3D Holographic Technology and Its Educational Potential. Teach Trends 2013, 57, 34–39. [Google Scholar] [CrossRef]
- Walker, R.A. Holograms as teaching agents. In Journal of Physics: Conference Series; IOP Publishing: London, UK, 2013; Volume 415, p. 012076. [Google Scholar]
- Ohlmann, O.M. 3D and Education. In Journal of Physics: Conference Series; IOP Publishing: London, UK, 2013; Volume 415, p. 012066. [Google Scholar]
- Suh, J.M.; Moyer-Packenham, P.S. The application of dual coding theory in multi-representational virtual mathematics environments. In Proceedings of the 31st Conference of the International Group for the Psychology of Mathematics Education, Seoul, Korea, 8–13 July 2007; Woo, J.-H., Lew, H.-C., Park, K.-S., Seo, Y., Eds.; PME: Seoul, Korea, 2007; Volume 4, pp. 209–216. [Google Scholar]
- Moyer, P.S.; Bolyard, J.J.; Spikell, M.A. What are virtual manipulatives? Teach. Child. Math. 2002, 8, 372–377. [Google Scholar]
- Moyer-Packenham, P.S.; Lommatsch, C.W.; Litster, K.; Ashby, J.; Bullock, E.K.; Roxburgh, A.L.; Shumway, J.F.; Speed, E.; Covington, B.; Hartmann, C.; et al. How design features in digital math games support learning and mathematics connections. Comput. Hum. Behav. 2019, 91, 316–332. [Google Scholar] [CrossRef]
- Melhuish, K.; Falloon, G. Looking to the future: M-learning with the iPad. Comput. N. Z. Sch. 2010, 22, 1–16. [Google Scholar]
- Martín-Gutiérrez, J.; Saorín, J.L.; Contero, M.; Alcañiz, M.; Pérez-López, D.C.; Ortega, M. Design and Validation of an Augmented Reality for Spatial Abilities Development in Engineering Students. Comput. Graph. 2010, 34, 7–91. [Google Scholar] [CrossRef]
- Kesim, M.; Ozarsla, Y. Augmented Reality in Education: Current Technologies and the Potential for Education. Procedia Soc. Behav. Sci. 2012, 47, 297–302. [Google Scholar] [CrossRef]
- Heinrich, P. The iPad as a Tool for Education: A Study of the Introduction of iPads at Longfield Academy; The ICT Association: Nottingham, UK, 2012; Available online: http://www.naace.co.uk/publications/longfieldipadresearch (accessed on 10 December 2012).
- Clements, D.H.; Battista, M.T. Geometry and spatial reasoning. In Handbook of Research on Mathematics Teaching and Learning; Grouws, D.A., Ed.; MacMillan: New York, NY, USA, 1992; pp. 420–464. [Google Scholar]
- De la Torre, J.; Martín-Dorta, N.; Soarín, J.L.; Carbonel, C.; Contero, M. Entorno de aprendizaje ubicuo con realidad aumentada y tabletas para estimular la compresión del espacio tridimensional. Revista de Educación a Distancia 2013, 37. Available online: http://www.um.es/ead/red/37/ (accessed on 9 March 2019).
- Grouws, D.A. Handbook of Research on Mathematics Teaching and Learning. A Project of the National Council of Teachers of Mathematics; MacMillan: New York, NY, USA, 1992; pp. 420–464. [Google Scholar]
- Pozo, J.I.; Monereo, C. Introducción: La nueva cultura del aprendizaje universitario o por qué cambiar nuestras formas de enseñar y aprender. In Psicología del Aprendizaje Universitario: La Formación en Competencias; Pozo, J.I., Pérez, M.P., Eds.; Morata: Madrid, Spain, 2009; pp. 9–28. [Google Scholar]
- LeTendre, G.; McGinnis, E.; Mitra, D.; Montgomery, R.; Pendola, A. American Journal of Education: Retos y oportunidades en las ciencias translacionales y la zona gris de la publicacion academica|The American Journal of Education: Challenges and opportunities in translational science and the grey area of academic. Revista Espanola de Pedagogía 2018, 76, 413–435. [Google Scholar] [CrossRef]
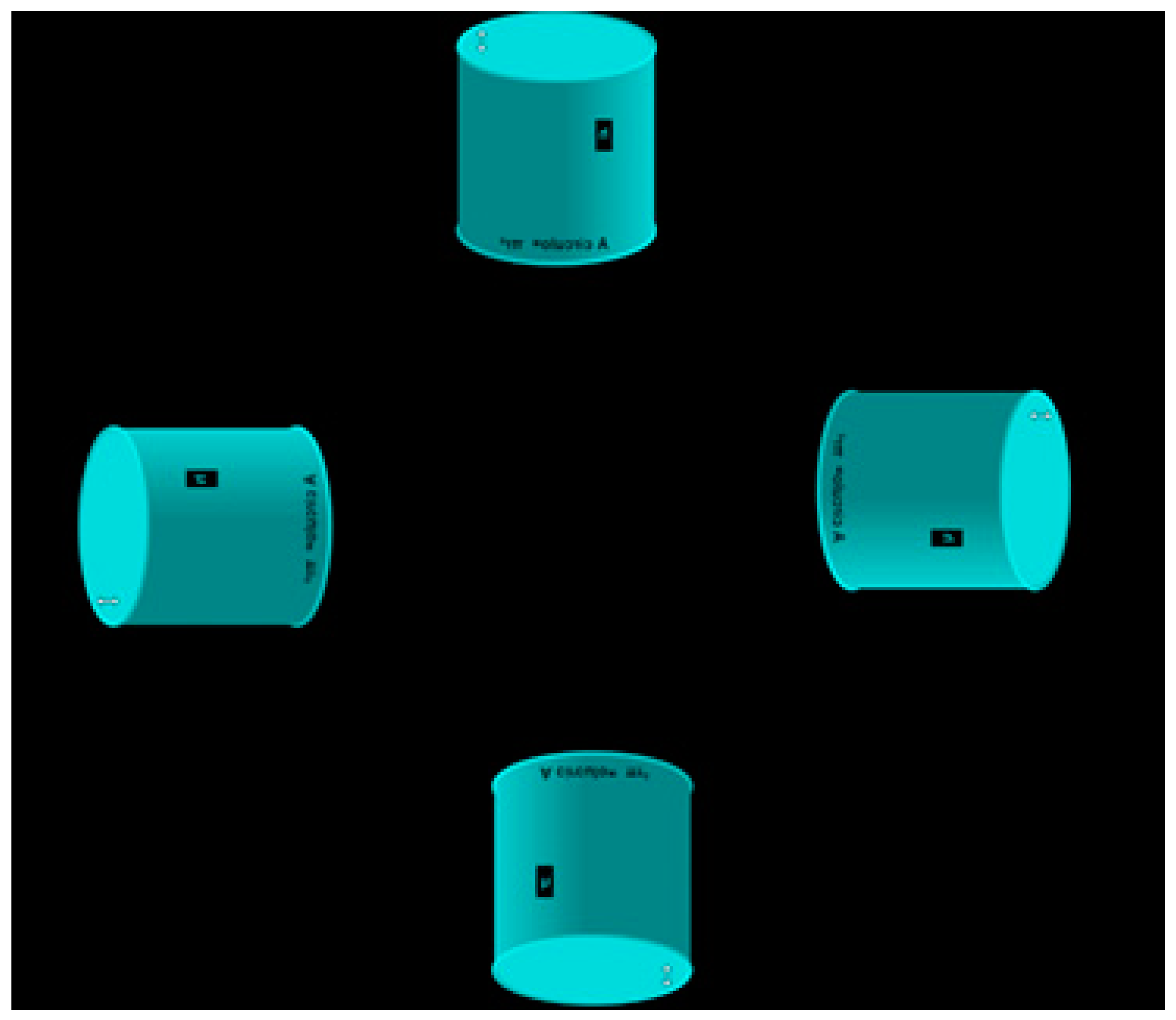



| Independent Samples Test | |||||||
|---|---|---|---|---|---|---|---|
| Levene Proof | t-Test of Equality of Means | ||||||
| F | Sig. | t-Value | gl | Sig. | Mean Differences | Standard Error Differences | |
| Assuming equal variances | 3.184 | 0.078 | −15.983 | 76 | 0.000 | −3.9021 | 0.2441 |
| Non assuming equal variances | - | - | −16.766 | 70.777 | 0.000 | −3.9021 | 0.2327 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orcos, L.; Jordán, C.; Magreñán, A. 3D Visualization through the Hologram for the Learning of Area and Volume Concepts. Mathematics 2019, 7, 247. https://doi.org/10.3390/math7030247
Orcos L, Jordán C, Magreñán A. 3D Visualization through the Hologram for the Learning of Area and Volume Concepts. Mathematics. 2019; 7(3):247. https://doi.org/10.3390/math7030247
Chicago/Turabian StyleOrcos, Lara, Cristina Jordán, and Alberto Magreñán. 2019. "3D Visualization through the Hologram for the Learning of Area and Volume Concepts" Mathematics 7, no. 3: 247. https://doi.org/10.3390/math7030247
APA StyleOrcos, L., Jordán, C., & Magreñán, A. (2019). 3D Visualization through the Hologram for the Learning of Area and Volume Concepts. Mathematics, 7(3), 247. https://doi.org/10.3390/math7030247






