The Kumon Method: Its Importance in the Improvement on the Teaching and Learning of Mathematics from the First Levels of Early Childhood and Primary Education

Abstract

The present work gathers an educational experience based on the application of the personalized Kumon Mathematics Method, carried out in the school year 2015–2016, in which 30,849 students and 230 teachers from several educational centers throughout Spain have participated. We start with a theoretical foundation of the Kumon Method and continue with a description of the research methodology used. The empirical analysis carried out has been both in descriptive and correlational terms, using Spearman’s Rho statistic, between the levels at which the students of the sample have started and the Kumon level reached. The results show that the sooner students begin to learn Mathematics with the Kumon Method, the greater the chance of reaching a level of knowledge above their school level, which helps us to demonstrate the potential of this method in the teaching and learning process of Mathematics in the educational levels of Early Childhood and Primary Education.

1. Introduction

The learning of Mathematics in the early stages of education has a great influence on the subsequent progress of the academic life of students, not only in this subject, but also in all others, mainly due to the perception of achievement that good mathematical academic results will provide. It is a fact that the more efficient the mathematical learning in these first periods, the greater the motivation of the student towards the academic world, in general, and towards Mathematics in particular. It is important to comment on what authors such as [1] point out in reference to the lack of interest of students to choose scientific and technological degrees, considering it as a factor that complicates the improvement of the quality of learning in Mathematics. In this sense, it is crucial to awaken in children, from an early stage, the interest in Science learning, so that they perceive themselves as competent and efficient in these areas, as Mathematics is the first contact they have with this field of knowledge. Stoffelsma and Spooren in [1] comment on the connection between good qualifications in Mathematics at early ages and in other subjects such as Science.

Equally, the official curriculum of Mathematics does not always fit the learning rhythm of each child, because sometimes it is above or below their level of competence (knowledge, skills, and attitudes). It is at this point where personalized education acquires greater relevance as it will allow for the adaptation to individuals according to their characteristics. The school also needs to comply with an official program that, in certain cases, does not give the chance to dedicate enough time to certain cases of the leaning process that would slow down the pace of the class itself, or to attend to other students with more capacity.

That is the reason why personalized education requires methods that allow attending and adapting learning to the rhythm of each student. It is precisely at this point where the Kumon Method—which emerged 60 years ago in Japan—is involved, with the aim of answering this question. This method aims to maximize the learning potential of each child through self-learning, the ability to concentrate, and the habit of study through a series of personalized activities that are carried out daily. The personalization of the method allows each student to go at their own pace of learning, making possible, in some cases, that children are able to study differential and integral calculus in Primary Education.

This study aims to demonstrate the influence of the early onset in the Kumon Method and the subsequent progression of the students along the different levels of mathematical learning, in which they can be ahead of the course that corresponds to them according their age. This allows self-taught learning and the development of the full potential of the individual. For this reason, in the realization of this research, a wide sample of students has been used from educational centers where the Kumon Method is taught, and the results obtained have been analyzed carefully, studying the starting points of each student, their ages, as well as their evolution along the different contents and levels of the method. A series of statistical procedures have been used to confirm, empirically, the influence of an early start initiation of the Kumon Method and the acquisition of high levels of mathematical skills.

2. Fundamental Principles of Kumon Method

Kumon is a pedagogic method of Japanese origin whose purpose is to develop the full learning potential of each individual. To this end, it relies on several aspects, such as self-learning, concentration ability, habit of study, self-confidence, and academic self-esteem of students. To achieve these goals, Kumon uses several programs, such as the Mathematics one which was the first created, and on which this research is based on, followed by Reading and English as a foreign language program. The method aims to discover the potential of learning in students by providing them with the possibility of developing self-taught learning in these disciplines.

There is extensive scientific literature and research about the Kumon Method that covers a broad spectrum within the educational field in which we can find, from research on students with specific needs, to studies that apply it in areas of social exclusion.

Then, we present some studies based on this method that give more support to our research and to the concepts about it that we will present later.

One of the most consulted works in relation to the Kumon Method is the one of Ukai in [2], which details a complete approach to the method, from its origins in Japan to its subsequent international expansion across the United States and other parts of the world.

Regarding autonomous work, the ability to concentrate, and the agility to calculate, Lluch in [3] carried out an investigation in which the Kumon Method was valued from a socio-educational point of view. In this work, he concludes that students working with the Kumon Method work in an autonomous and concentrated way, developing, from the beginning, the capacity and agility in mental calculation as a consequence, among other factors, of the daily work.

In addition, related to the ability to concentrate—another of the key points of the Kumon Method—studies such as Henríquez, Quirós, and Reumay in [4] showed that there are external agents (given by the medium or the context), and internal (personal reflection), which influence the student’s attitudes when facing the teaching–learning process of mathematics. Among these, there would be the human models which are available to him, the proper guides to exercises, and the knowledge and good use of mental reasoning and operations, among which the abstraction and imagination are highlighted and analyzed. Imaginative capacity is involved in the process, among other things, such as the capacity for concentration and forming mental pictures that can respond to the situation. These authors state that not only is it important to train this concentration capacity for learning mathematics but, also, in doing so, you will have the possibility to develop your creativity and will be able to abstract problematic situations.

Concerning another important issue of the Kumon Method, which is the habit of study, several investigations [5,6,7] in the field of education, in general, and of mathematics learning, in particular, indicate the importance of concepts, such as the habit of study, to improve students learning. Hassan, Sadaf, Aly, and Baig, in [5], insist on this idea.

Study habits are study practices that include the frequency of studying sittings, rehearsal of learned material, review of material, studying in favorable surroundings, and self-testing. The approach of students toward the act of studying are referred to as study attitudes. The learning behavior of students is the outcome of factors that are complex in nature and comprise of internal and external factors that play a critical role in education [5].

However, Luque in [7] then demonstrated that the habits of study influence the academic performance of students in the mathematical area. In the same way, he also mentions that other dimensions should be reinforced, such as the study space and environment, study time and planning, study methods, and study motivation, since he considers his influence on the academic performance of the students to be significant, see [8].

Moreover, the concept of self-learning is of great importance in the Kumon Method since the students learn by themselves from examples that help them to face new exercises and problems. Research, such as that of Renkl in [9], demonstrates the importance of self-learning as well as self-explanations that positively influence the improvement of mathematics learning. This author provides an approach on the significance of self-explanations in mathematics learning from worked-out examples. Chi et al. in [10] have shown that the extent to which learners profited from the study of worked-out examples depended on how well they explained the rationale of the presented solutions to themselves. This was called the “self-explanation effect”.

By constrast, in relation to the concepts of self-confidence and academic self-esteem, studies such as Agüero-Calvo, Calderón-Ferrey, Maza-Cascante, and Suárez-Valdés in [11] reveal “the existence of a significant linear relationship between the level of mathematical self-confidence and self-esteem”. These authors also consider that low self-esteem can affect academic performance. However, Cruz and Quiñones in [12] propose to strengthen the students’ self-esteem by pointing out that many educational intervention proposals plan an improvement of academic performance from the stimulation of self-esteem through “a complex psychological process that involves perception, image, esteem and self-concept”.

According to the learning of mathematics throughout the Kumon Method we highlight the investigation of Oakley et al. in [8] who conducted a research in Southern Michigan on how to revitalize mathematics in an inner-urban school district. They showed how “Kumon Mathematics appears to provide an ideal structured support in mathematics for at-risk children who receive little or no help at home”.

Finally, we comment on the study of Thijsse [13] related to the anxiety and achievement in mathematics, in which it is demonstrated how the Kumon Method contributes to reduce anxiety and to improve self-confidence. It also shows how students who perform the method improve in aspects such as the speed of conducting operations and the exam qualifications.

The results support the hypothesis that a structured teaching method involves a decrease in mathematics anxiety and an increase in mathematics achievement. Results also show that three learners increased their achievement on the Kumon achievement test.

2.1. The Origin of Kumon Method

The Kumon Method emerged in 1954 in Osaka, Japan, by the hand of Toru Kumon, a Mathematics teacher of a High School, who decided to take an active part in his son’s education, when he realized that he obtained low grades in Mathematics in the second year of Primary Education [14]. Therefore, the Method emerged as a way of learning at home, since Professor Toru Kumon developed some materials with a very specific purpose that was to make his son able to do differential and integral calculus before starting to study Secondary Education, allowing him to learn by himself [15]. The boy managed to master integrals in the sixth grade of Primary Education when working around 30 min per day with the method devised by his father. The improvements experienced by Professor Kumon´s son were not only limited to Mathematics, but also extended to the rest of the subjects. After having developed the Mathematic method, Toru Kumon elaborated the Reading one since he concluded that most of the outstanding students would share two qualities: they would read frequently, and they would have the ability to understand the content of the texts [3].

2.2. Aim and Skills Developed by the Kumon Method

The mission of Kumon Method is as follows: “By discovering the potential of each individual and developing his or her ability to the maximum, we aim to foster capable people and thus contribute to the global community” [16]. Therefore, the main objective of the Kumon Method is to maximize the learning potential of each child. To achieve this, it works with the three aforementioned programs, through which a series of habits and abilities are acquired that will accompany the individual during their school and adult life. The habits and capacities on which Kumon relies, to achieve its goal, are:

• Self-learning, the child learns how to learn by himself, without the need of depending of another person.
• Habit of study, which allows the child to carry out learning tasks without difficulty.
• To foster concentration, if the student is not able to focus on a specific task, it will be difficult for him to learn effectively.
• Self-confidence that allows him to face any educational challenge.
• Motivation to learn, to perceive learning as something enjoyable that will help him to grow as a person [17].

The methodological principles of Kumon: objectives, personalization, and self-learning. First of all, it is important to take into account the idea that Kumon was born as a method of home education with the purpose of developing the academic ability of the student to become a competent member of society. Then again, the method aim is that children can be independent in their study, for which it is intended that they acquire the skills of self-taught learning.

The objectives pursued by the Kumon Method are:

• To discover the learning potential of children and to develop their full potential offering them an individualized guidance.
• To provide as many students as possible the opportunity to learn with the Kumon Method, taking into account that its dissemination can contribute widely to the society.
• To help students to become more competent people by developing better guidance materials and orientation practices through continuous research and thinking process on how they learn with the Kumon Method.
• To develop students’ skills and contribute to the future applying of these methodological principles in other fields apart from education.
• To achieve a positive cycle in which instructors and support programs members work together to offer the highest number of children as possible the opportunity to learn with the Kumon Method. This will result in developing the skills of both instructors and support programs members and, at the same time, it will allow the study with Kumon to be increasingly accessible [18].

To achieve the objectives and skills outlined above, the Kumon Method develops a series of materials created with the aim of getting the best results in the shortest time possible. Therefore, it is not intended to perform a review of the official curriculum of the school. In the case of Kumon Mathematics Method, it contains the essential elements that will allow the student to be able to work and master the Mathematics of High School level easily, for which it is important to build a strong base in the previous stages. By contrast, the Kumon Reading Method aims to develop an advanced level of reading competence. Finally, the Kumon English Method (English as a foreign language) is designed for students to read original versions of texts in English [19]. All these programs are designed for the student to achieve the objectives by self-learning, and to progress naturally without over-exerting. In this sense, one of the keys of the method is the personalization of the teaching–learning process. For Kumon instructors, to orientate with the method involves adjusting the rhythm of the student’s progress individually, evaluating the level of mastery of each learning block systematically and assigning reinforcement in accordance with that evaluation.

Some of the orientation fundamentals of the method consist of the following aspects:

• Self-study of the materials: the instructor does not explain lectures or expository sessions but encourages the student to find the answers by reading the instructions of the materials carefully, so he can develop the skills and mentality of self-learning.
• Correction of mistakes: after completing the task, the instructor has to qualify them immediately, so that the student can correct them quickly while he is still concentrated.
• Daily work: the method is designed for the students to work about 30 min per program per day, so that instructor will have to customize the task that each child does daily.
• Study in the order of the method: the method is sequenced by levels and each of these levels is distributed in blocks and booklets that follow a logical order and increase in difficulty, with a clear and specific objective, so it is not possible to mix the different content blocks arbitrarily.
• Record of daily work: the instructor makes a record and a detailed study of the daily activity of each child, which will be the empirical material on which he bases the personalized guidance to each student.

The whole process is based on personalization, and the moment when the student begins with the Kumon Method is considered crucial. Before having started with the method, the student completes a diagnostic test to determine the appropriate starting point from which the new knowledge will be built, based on the student’s prior knowledge. In this sense, the Kumon Method is closely related to the Theory of Meaningful Learning and the Constructivist Theory, as it is based on the meaningful learning rather than rote. Fuller, in [20], comments that “the demand for meaningful learning instead of rote memorization, stems from the premises that Mathematics are too complex to be taught by rote”. As David said in [21], students constantly “invent” new algorithms anyway. Their discoveries race ahead of the standard algorithms of adults, giving meaning from the child’s conceptual scheme—how learning is really consolidated. However, the Constructivist Theory is related to learning by discovery and the Zone of Proximal Development stated by Vygotsky in [22], among other concepts.

All of them are concepts intimately related to the Kumon Method and the role of the instructors as elements that enable this type of learning. Learning by discovery has a long and complex history in education (Dewey in [23] and Bruner in [24]). Although it reached its apogee as a pedagogical framework in the sixties, the generality of the term allows its application to any learning environment in which the student participates actively in solving problems (Bruner, 1961), building his own learning. At its original formulation, learning by discovery focused on the learning process, with the aim of developing inquiry skills in the domain of a content, considering inquiry as a way to address the issues (Duffy and Cunningham in [25]).

Vygotsky, in [22], presented the Zone of Proximal Development (Zo-ped) as “the distance between the actual developmental level of a child as determined by independent problem solving and the level of potential development as determined through problem solving under adult guidance or in collaboration with more capable peers”. In other words, it is the form of joint cognition posed by the Constructivist Theory where the counsellor-tutor provides support or scaffolding for the child until he is able to appropriate knowledge for his own use. Progressively, the support of the counsellor will be withdrawn until the student is able to face the resolution of new problems by himself.

In this way, Kumon instructors constantly value the learning situation of their students having, as a reference, whether they are at their ideal point of study or not. Thus, observing the students completing the material, the instructors can describe concretely what the student is able to do with respect to his ideal point of understanding (what is the student able to do without help?), with respect to his ideal point of ability to study (is he able to solve the material within the standard time? How many sheets of the booklets is he able to do?) and with respect to his ideal point of attitude toward the study (how does he study the material? Does he read the headings? Does he stop to study the examples? Does he check the clues printed on the material?). In relation to the criterion from which the student can advance within the different levels of the method, it is important to mention that there is no single quantitative criterion. It is based on a compendium of decisions resulting from qualitative observation, bearing in mind how the student solves the material, and a series of quantitative criteria among which it is the “standard complexion time” (which is particular for each level and for each group of activities within each of these levels) and the number of errors committed by the student. These two criteria give very valuable information regarding the precision in the execution of the exercises, but they do not make sense without the teacher’s observation and guidance. In addition, in Kumon, there are no lectures or theoretical explanations of the teacher; it is the material itself that, through examples, allows the student to discover the theory by himself. In some sheets there are brief explanatory theoretical notes to promote student´s learning discovery.

2.3. Kumon Mathematics Contents

Kumon Mathematics is composed by 21 levels (6A, 5A, 4A, 3A, 2A, A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, X), among which, the following contents are addressed:

• Counting, writing, and number sequencing (levels 6A, 5A, 4A)
• Addition and subtraction (levels 3A, 2A, A, B)
• Multiplication and division (levels C, D)
• Fractions and decimals (levels D, E, F)
• Order of operations (level F)
• Positive and negative numbers (level G)
• Solving equations (levels G, H)
• Graphs (loves H, I, L, M)
• Algebra, from elementary to advanced (algebraic expressions, linear equations, inequalities, functions, quadratic equations) (levels J, K, L)
• Trigonometry and logarithms (levels M, N)
• Calculus (level O)
• Probability and statistics (level X)

As it can be seen, the first levels of the method are dedicated to the learning of writing numbers. Also, the Kumon Method dedicates an important part of its levels to problem reading and problem solving, a crucial issue also in the learning of Mathematics, as some authors argue: “Writing is recognized as a critical skill in science, technology, engineering, and mathematical fields, as it provides opportunities for individuals to think critically about learned information, to integrate knowledge, to communicate understanding, and to contribute new information to the field [26].

2.4. Self-Learning as a Great Goal

Taking into account that the aim of Kumon Method is the development of students’ potential, self-learning is considered as the way to achieve this goal. In the words of Vygotsky, the learning potential would be “the set of tasks that each person does not yet perform on his own, but that he can achieve with adequate support from the environment (level of potential development)” [15]. By contrast, self-learning would be the “ability of a subject to define himself, being the person who educates and is educated” [27]. In this sense, this author states that learning how to learn does not only refer to the ability to seek information and to appropriate it, but it also involves learning how to discriminate the information and, therefore, to analyze what is being learned and to seek the link or confrontation with what has already been acquired [28]. Therefore, Kumon suggests that this potential development is achieved in a self-taught way, with the instructors and the material itself standing at the level of potential development mentioned by Vygotsky. As we see, the concept of potential development has great weight in the Kumon Method, and it will be obtained through the mediation of the didactic material itself and the guidelines given by the instructors.

In that sense, the quality of mediation is decisive. Therefore, Vygotsky commented that it is necessary to differentiate what is the Real Evolutionary Level, understood as the state of development in the cognitive level of the child achieved through maturation and manifested with the activities that can develop on its own, with the Evolutionary Potential Level, which is what the person can achieve thanks to the intervention of the mediator [29].

This is the vision that arises from the Kumon Method when it is presented the concept of developing the potential of each individual: to achieve the reach of higher goals, through the mediation of materials and guidance of the instructors, that help the student to contribute to society.

3. Methodology

3.1. Hypothesis and Objective

The main hypothesis of this study is “using the Kumon Mathematics Method the students of the sample will increase the possibility of obtaining a significant improvement in the learning of the Mathematics contents established by the method”. From this premise, we will be able to deduce the suitability of the Kumon Mathematics Method for the learning of Mathematics since childhood. For this reason, the objective of the study is to demonstrate, empirically and through different techniques of statistical analysis, that the students of the sample will improve their academic results in Mathematics.

3.2. Sample

Regarding the sample data, the study is based on the detailed information of the process and learning results corresponding to the academic year 2015–2016. The students and the instructors who have participated in the study are of several educational centers that cover the entire Spanish national territory in which the Kumon Method is performed.

The sample formed by all the students who attend the mathematics program of the Kumon Method is homogeneous and representative. The students come from different socioeconomic and cultural levels.

The sample s consisted of 30,849 students from the First Elementary Education grade to the last level of High School Education. The data has been collected by 230 teachers specialized in mathematics didactics, through monthly reports in which the learning and the evaluation of the students was provided.

The study has been carried out for 9 months and the data collected has been:

• The Kumon level of students at the beginning, before having taken part in the Method.
• The Kumon level at the end of each month. It is important to mention that in order to evaluate the potential of the method, we have just taken data corresponding to the last month.
• The level at 6 months, 2 years, or 3 years, in which they are above the level they should have according to the course in which they are.

3.3. Research Design and Phases of the Study

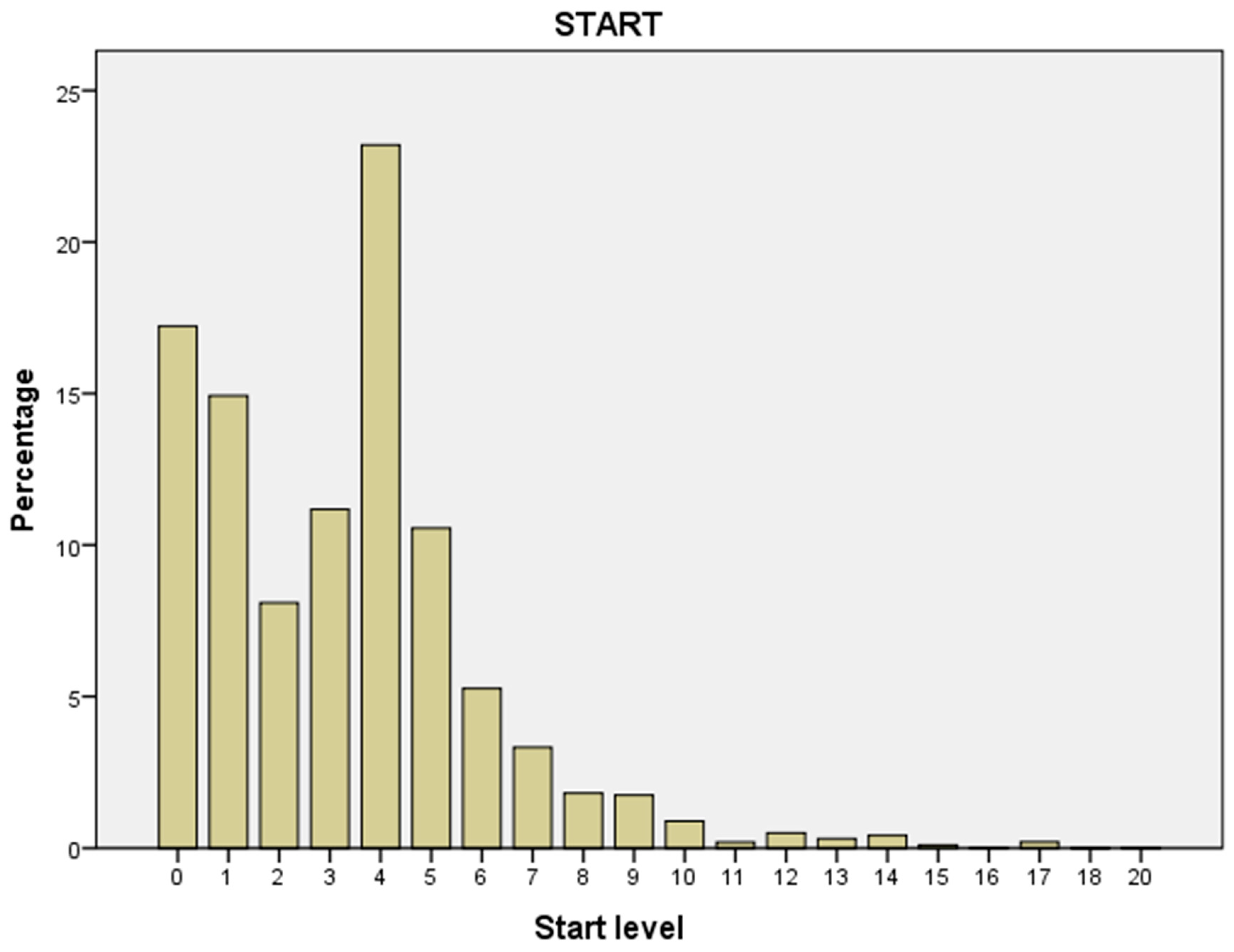
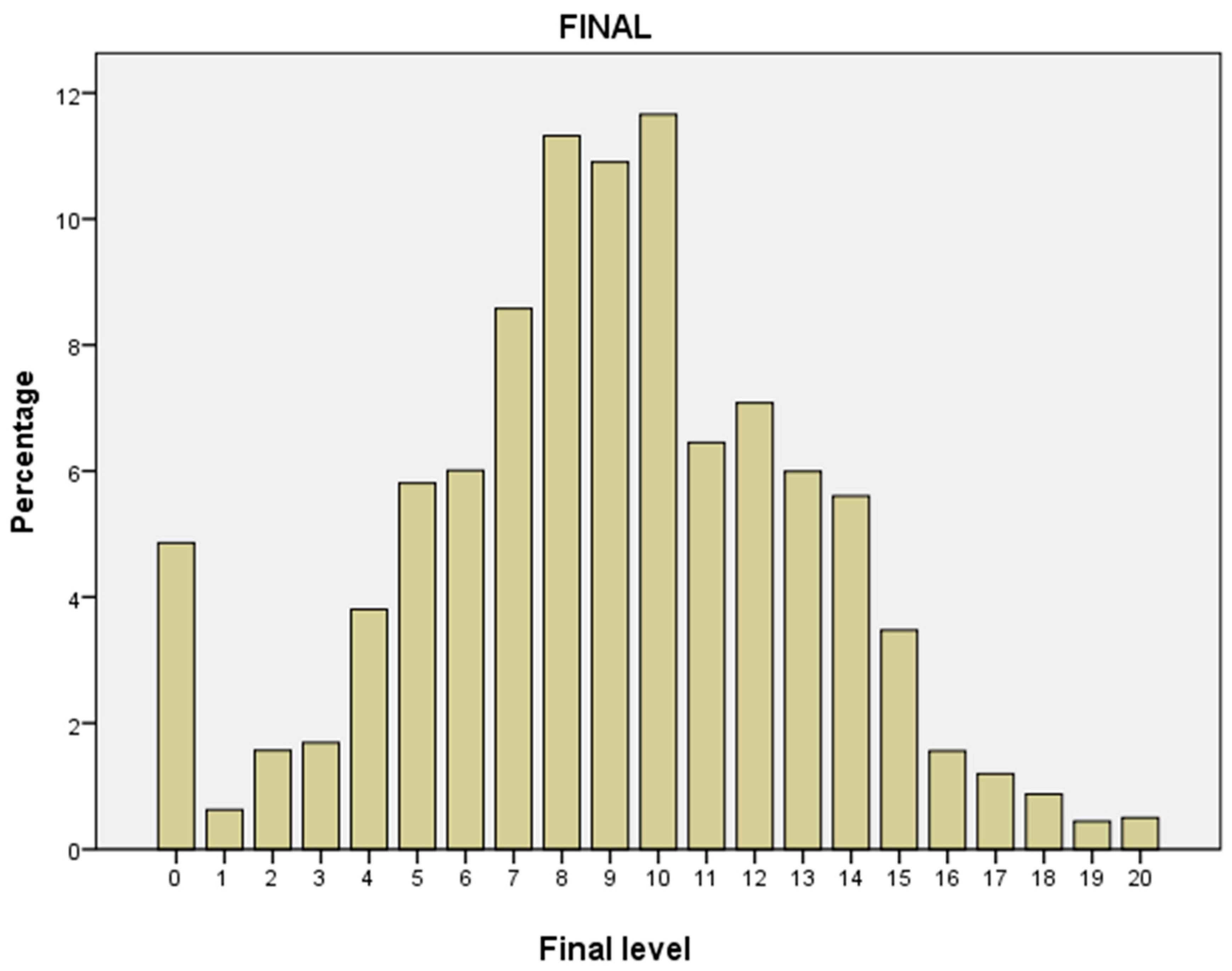
A descriptive and correlational analysis of the data obtained has been carried out, and the methodology used in this study is quantitative, since it is based on the analysis of quantifiable data according to the levels obtained after the development of the experiment. We have named the levels from level 6A as 0 to Level X as 20, in order to show the graphics and the tables in a more compact way.

The research process has been the analysis of variables through descriptive and correlative statistical techniques (which will be detailed in the data analysis section).

3.4. Information Collection Tools

With regard to data collection, it has been taken into account the considerations of [15], done through monthly reports sent by each Kumon Center to the Kumon head office. This consists of an Excel table, made from the information of the sheets, containing the following data: month of the report, name of the center, student identification, date of birth of the student, date of enrolment in the Kumon Method, starting level at the beginning of the Kumon Method, level at the beginning of the current month, level at the end of the current month, number of pages completed during current month, and situation with respect to the school level (below or advanced, 6 months, 2 years, or 3 years).

Therefore, data have been collected monthly for each student and each center through these reports.

3.5. Data Analysis

As can be seen in [30], the use of techniques and instruments is very important for the analysis of data in education, either in the classroom or in any other context. Before the analysis, both the limitations and the technical possibilities of the instruments used (sheets, s) were assessed, considering their quality and suitability.

In this study, the registry of the data has been carried out through the construction of a matrix, with one of the most used and known in social research programs, Statistical Package for Social Sciences [31]. The data analyzed includes all the students of the Kumon Method and all the information regarding their process of evolution and learning of Mathematics throughout the academic year 2015–2016.

Due to the huge amount of data, selection of the start level, the final level, and the level above the one that corresponds to these was required, due to the use of school grade as an analytical variable for study.

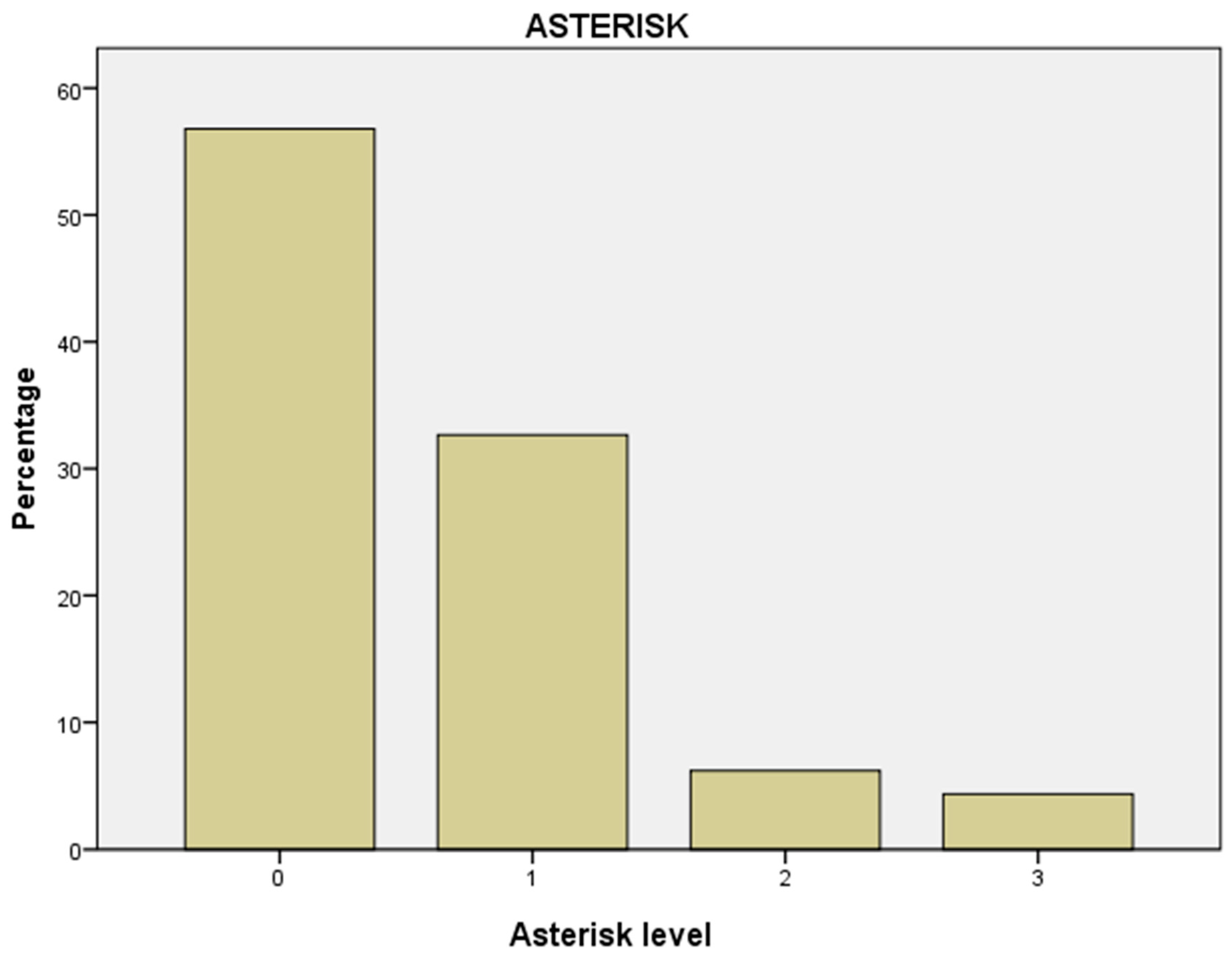
Kumon has a nomenclature that establishes three categories, called asterisk level, that alludes to the fact that the student can be six months, and two years or three years above the school level that corresponds to the student. It is a quality criterion established by Kumon Centers around the world, and which is included in the reports of the students that teachers send periodically.

The asterisk level can be as follows:

• No asterisk or level 0 means same level as the one of the school grade in which they are.
• One asterisk or level 1 means 6 months above the school grade level.
• Two asterisks or level 2 means 2 years above the school grade level.
• Three asterisks or level 3 means 3 years above the school grade level.

To simplify the analysis of this work, due to the huge amount of data, only the date related to the end of the year has been taken, that is, after nine months, leaving the temporary analysis during each month.

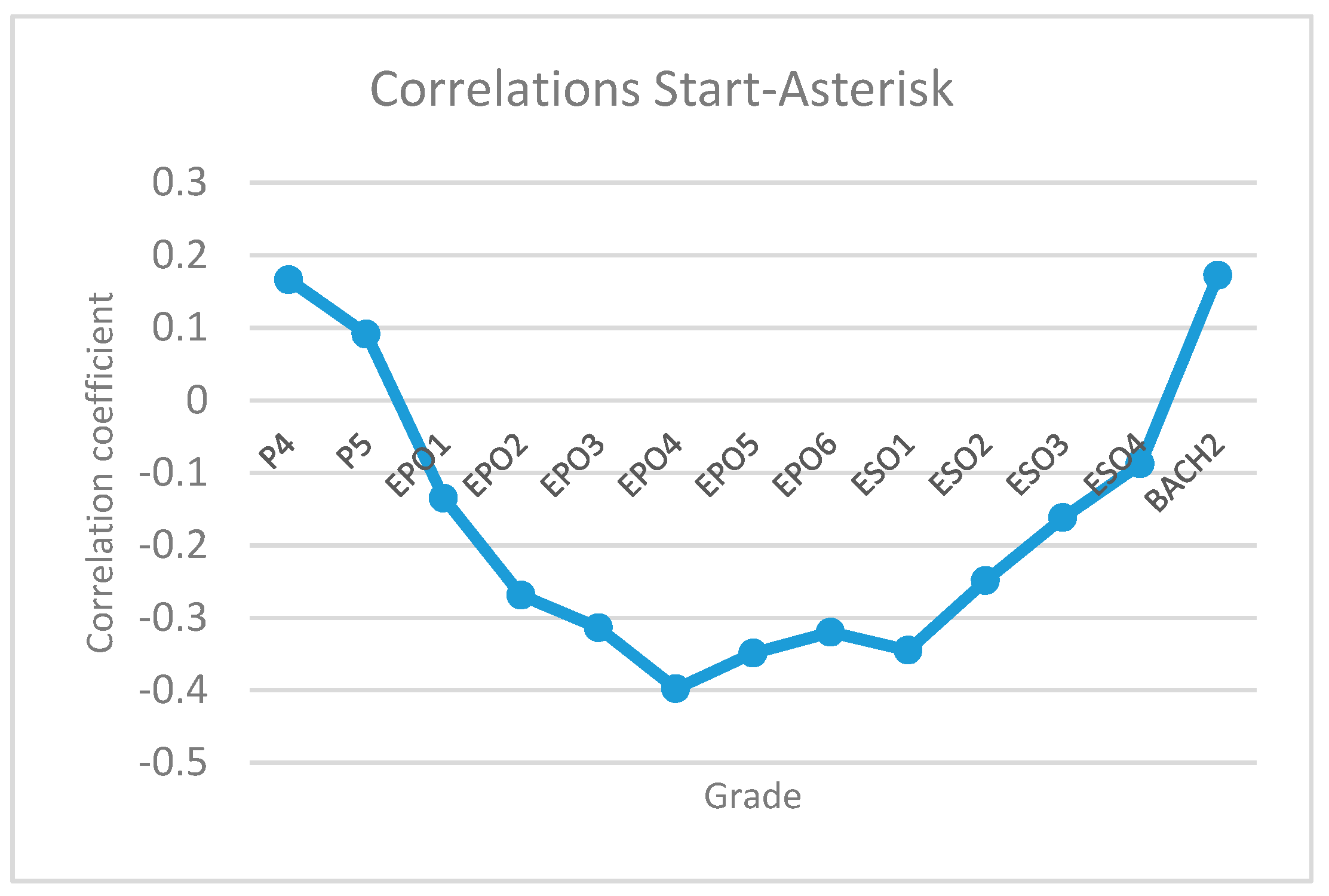
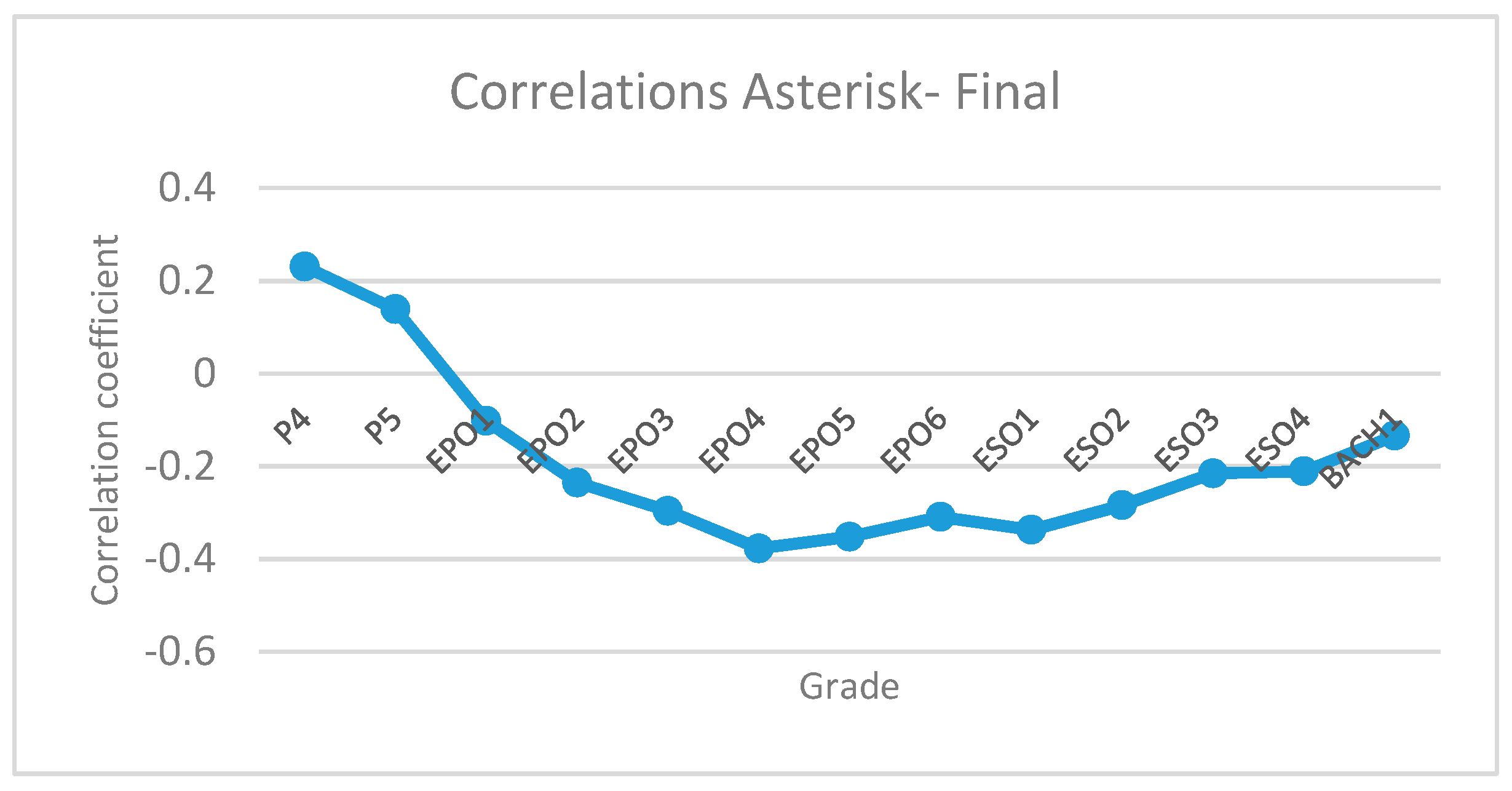
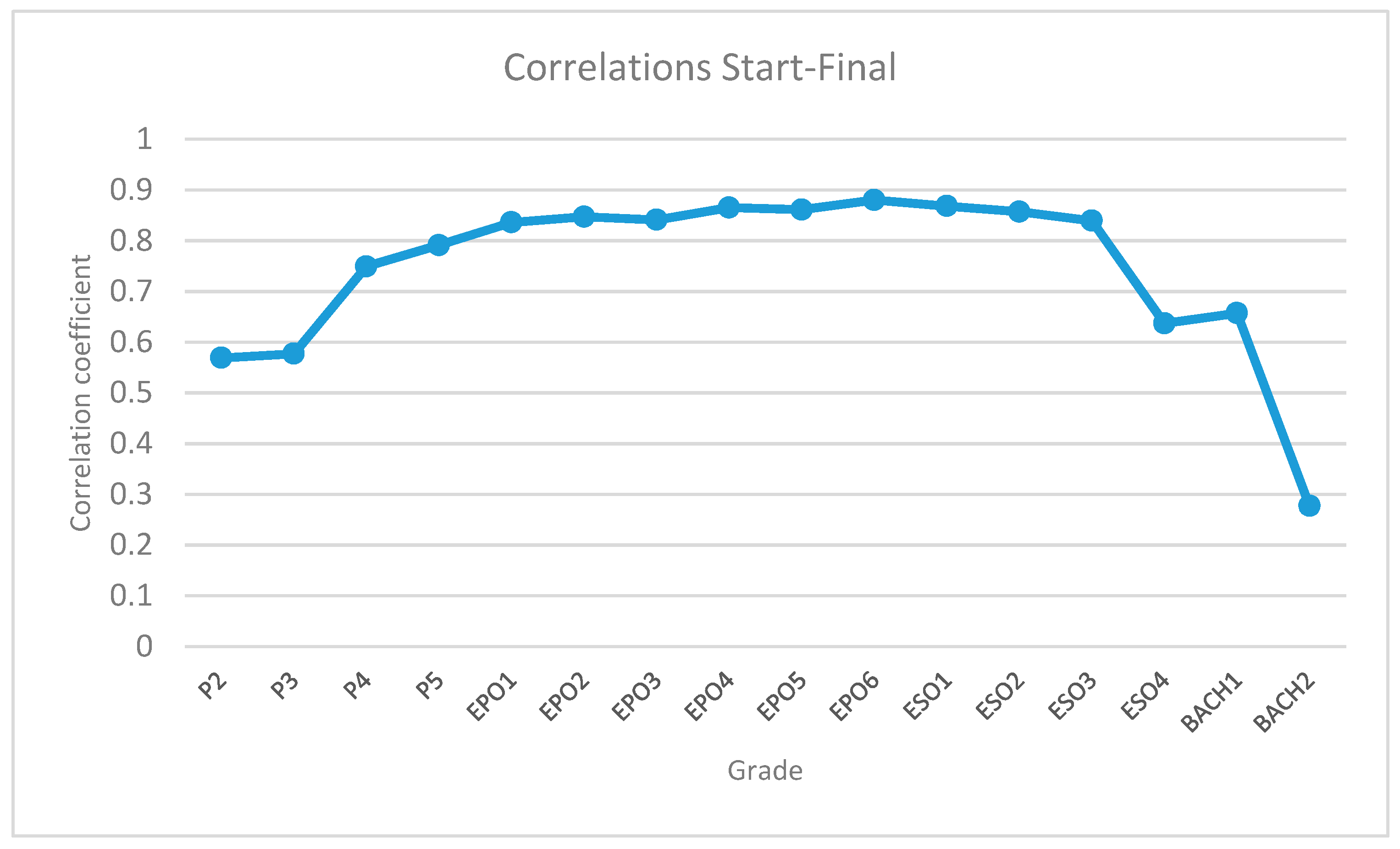
In a second phase, we proceed to the descriptive analysis of data and the analysis of correlations of pairs of variables (2-tailed analysis) that connects the levels of learning prior to the application of the Kumon Method, and the levels subsequent to the application of the method for the learning of mathematics. These are:

The correlation between the start and the final levels.

• The correlation between the start level and the level above the one that corresponds to them due to their school grade, 6 months, 1 year, or 2 years.
• The correlation between the final level and the level above the one that corresponds to them due to their school grade, 6 months, 1 year, or 2 years.

For this aim, it has been necessary to codify the Kumon levels (from 6A to X) into ordinal quantitative variables (0–18). Due to the nature of the variables, which are not continuous, the correlation statistic, under non-parametric assumptions, has been Rho of Spearman as correlation coefficient, and the hypotheses established are as follows:

• H₀, null hypothesis: there are no significant correlations between the variables.
• H₁, alternative hypothesis: there are significant correlations between the variables.

Once the data is analyzed using SPSS, if the level of significance obtained is lower than 0.05 (2-tailed), we can reject the null hypothesis and conclude that there are significant correlations between those variables.

4. Results

4.1. Global Descriptive Statistics

First, the global descriptive statistics of the data have been analyzed, in order to have a global view of the data collected in terms of the central tendency with the mean, median, and mode values for the three variables in which we are interested: start level (START), asterisk level (ASTERISK), and final level (FINAL).

Regarding to the start level (START), the results in

Table 1. Global descriptive statistics by start, asterisk, and final levels.

Global Descriptive Statistics.	START	ASTERISK	FINAL
N valid	30,849	30,849	30,849
N lost	0	0	0
Mean	3.28	0.581	8.98
Standard error of the mean	0.015	0.0045	0.023
Median	3.00	0.000	9.00
Mode	4	0	10

show an average value of 3.28, that implies that the students are between levels 4A and 3A (writing numbers up to 50, 100, and 120, adding up to +1, +2, and +3) when they start to work with Kumon Mathematics. The average value indicates that 50% of the students are below the level 4A (in the levels prior to this, the reading of numbers is worked on, gradually increasing in difficulty until the sequence of numbers reaches 50) and 50% above 3A. Then, again, the mode and the results of the percentage of students in each start level (START), shown in Figure 1, indicate that the level in which there are more students at the beginning is 3A (writing numbers up to 100 and 120, adding up to +1, +2, and +3).

In terms of the asterisk level (ASTERISK), Table 1 shows an average value of 0.58, which implies that, globally, the students are between level 0 and level 1 of asterisk after 9 months of using this method, that is, almost 6 months above the academic level they should have. Taking these data into account, as well as the information related to the percentages per asterisk level (ASTERISK), which appear in Figure 2, 43.2% of students have reached an asterisk level above 0, which is a very positive result since it means that Kumon Mathematics Method has enhanced more than 40% of the students to work at a certain level ahead of that corresponding to their actual school year.

In relation to the final level, the values in Table 1 show an average value of 8.98, that indicates that the students are in level D (multiplication, division, fractions) are almost reaching Level E (operations with fractions—addition, subtraction, multiplication, division and mixed numbers—and decimals). This result is also very important because it means that, after 9 months, students have managed to increase their level from 3A to almost E, that is, 6 levels.

Moreover, from data of Table 1 and Figure 3, it can be seen that the three most repeated levels are D, E, and F (fractions and decimals), with Level F being the most repeated one. Also, from Figure 3, it can be observed that the distribution of the final level reached by the students is similar to a Gaussian bell curve.

4.2. Descriptive Statistics per School Grade

Another aim of this work is to carry out a descriptive analysis per school grade, distinguishing them into the different asterisk levels. Figure 4 shows the results of the percentages of the levels reached per academic year. The course with the highest percentage in level 0 of the asterisk is the second course of High School Education (Bach2), which is understandable because it is the most advanced course and, therefore, there is a lower probability for students to reach a level above the level that corresponds to them, due to the difficulty of the contents. The level 3 graph shows that 71.4% of students who have started Kumon Mathematics in the first year of Elementary Education (P1) obtained a 3-year improvement in their school performance (level 3 of asterisk), which is also a very important result that shows that almost 3 out of every 4 students in P1 reached a level 3 years above the one that corresponds to them according to their school grade. Moreover, it can be seen that in the first year of Elementary Education (P1), a dichotomy exists between Level 0 and Level 3, that means that there is not an intermediate value. Considering that more than 71% of the students reach Level 3, it means that the sooner the students begin with the method, the greater is the possibility to reach a higher mathematics level. Another important result is observed from the first course of Primary Education (EPO1) to the third course of Secondary Education (ESO3) that shows that more than 40% of the students in these levels obtained improvements, highlighted in EPO2, EPO3, and EPO4 (second, third, and fourth courses of Primary Education), in which more than half of the students obtained the desired improvement.

4.3. Global Correlations

As mentioned before, when dealing with ordinal variables, it is required to make use of the Rho of Spearman correlation coefficient, in order to prove our alternative hypothesis, which is considered as follows:

H₁, alternative hypothesis: there are significant correlations between the variables

First of all, we can deduce, from the first line in

Table 2. Global correlations between variables.

Variables	Correlation Coefficient (Rho Of Spearman)	Significance Level (2-Tailed)
START-ASTERISK	−0.258	0.000
START-FINAL	0.133	0.000
ASTERISK-FINAL	0.421	0.000

, that the correlation coefficient between the start level in Kumon (START) and the level of improvement obtained (ASTERISK) which, as said before, was the most important correlation we wanted to demonstrate, is significant and negative (−0.258), so both variables are inversely related, which means that the lower the starting level in Kumon, the higher the level of improvement obtained. Therefore, the sooner the students start in Kumon, the better the results that they will have in the future. Although the coefficient is lower than 0.3, in absolute value, and the fact that the relation between those variables is low, we wanted to find out whether the relation exists, which has now been demonstrated.

Now, if we observe the second line of Table 2, it is clear that a correlation exists between the starting Kumon level (START) and final Kumon level (FINAL), which is also significant and positive (0.133), so both variables are directly related, which means that the higher the starting level in Kumon, the higher the level they finally reach. These data seem to be opposite to that obtained in the previous point, however, it is necessary to clarify that the level they reach in Kumon (FINAL) and the level of improvement (ASTERISK) are not comparable magnitudes, since one measures the level of Kumon that they reach, and the other the level of improvement with respect to the level that they should have if they did not follow the Kumon methodology. Again, the coefficient is low but the relation between the variables exists.

Finally, again from the study, the correlation between the final Kumon level (FINAL) and the level of improvement obtained (ASTERISK) was significant and positive (0.421), so both variables are directly related, which means that the higher the level they reach in Kumon (FINAL), the higher the level of improvement with respect to the level they would obtain if they did not follow the Kumon methodology (ASTERISK). This fact seems clear, but we also needed to show it.

After carrying out this study, we can conclude that the alternative hypothesis was proven since we have seen that there exist correlations between the 3 variables.

4.4. Correlation per School Grade

Another are of interest for us was to find the relations between the variables distinguishing the school grade so, according to data in

Table 3. Correlations between variables per school grade.

Grade	Start-Asterisk	Sign (2-Tailed)	Asterisk-Final	Sign (2-Tailed)	Start-Final	Sign (2-Tailed)
P1	−0.4	0.374	0.083	0.860	0.746	0.054
P2	0.107	0.319	0.174	0.104	0.569	0.000
P3	0.004	0.942	0.089	0.086	0.577	0.000
P4	0.166	0.000	0.231	0.000	0.749	0.000
P5	0.091	0.000	0.139	0.000	0.791	0.000
EPO1	−0.135	0.000	−0.102	0.000	0.836	0.000
EPO2	−0.269	0.000	−0.235	0.000	0.847	0.000
EPO3	−0.314	0.000	−0.296	0.000	0.841	0.000
EPO4	−0.398	0.000	−0.377	0.000	0.865	0.000
EPO5	−0.349	0.000	−0.352	0.000	0.861	0.000
EPO6	−0.32	0.000	−0.309	0.000	0.88	0.000
ESO1	−0.345	0.000	−0.337	0.000	0.868	0.000
ESO2	−0.249	0.000	−0.284	0.000	0.857	0.000
ESO3	−0.162	0.000	−0.215	0.000	0.839	0.000
ESO4	−0.088	0.012	−0.211	0.000	0.637	0.000
BACH1	−0.049	0.308	−0.134	0.006	0.657	0.000
BACH2	0.172	0.019	−0.106	0.151	0.277	0.000
BEYOND	-	-	-	-	−0.024	0.553

, the correlations per school grade are different, both in significance and in value. On the one hand, it is observed that the significant values obtained are lower than 0.05, which allows us to reject the null hypothesis and conclude that there are significant correlations, which was set as the alternative hypothesis. Taking this fact into account, we can conclude, from data in Table 3 and Figure 5, that there is a significant correlation between the start Kumon level (START) and the level of improvement obtained (ASTERISK), which is present from the fourth course of Elementary Education (P4) to the fourth course of Secondary Education (ESO4) and in the last grade of High School Education (BACH2). Then, it is observed that from the first course of Primary Education (EPO1) to the fourth course of secondary Education (ESO4), the correlation is negative, having its highest value in the fourth course of Primary Education (EPO4). The negative correlation led us to conclude that the lower the Kumon level in which students start, the higher the level of improvement obtained.

According to the correlation between the final Kumon level (FINAL) and the level of improvement obtained (ASTERISK), (this data can be seen in both Table 3 and Figure 6) we can state that there is a significant correlation between them from the third course of Elementary Education (P3) to the first course of High School Education (BACH1). Next, it is observed how, from the first course of Primary Education (EPO1) to the first course of High School Education (BACH1), the correlation is negative, having its highest value also in the fourth course of Primary Education (EPO4). The fact of having the negative correlation implies that the lower the final Kumon level the students start in, the higher the level of improvement they will obtain, so, in the light of the results obtained, we can state that from the first course of Primary Education (EPO1) to the first course of High School Education (BACH1), it is better to begin as soon as possible with the Kumon Method.

Finally, the last study we wanted to perform was to find the relation between the starting Kumon level and the final Kumon level obtained by students. It is easy to see (in Table 3 and in Figure 7), that the correlations between the initial Kumon level (START) and the final Kumon level (FINAL) are significant and are present from the second course of Elementary Education (P2) to the last course of the High School Education (BACH2). We see how the values of the correlations are positive and very high, therefore, the data show that the final level they reach is related to the initial one they have.

5. Conclusions

In conclusion, it can be said that the objective stated in the work, according to which it was intended to demonstrate, empirically, that the students of the study sample have improved their learning with the Kumon Method, has been fulfilled.

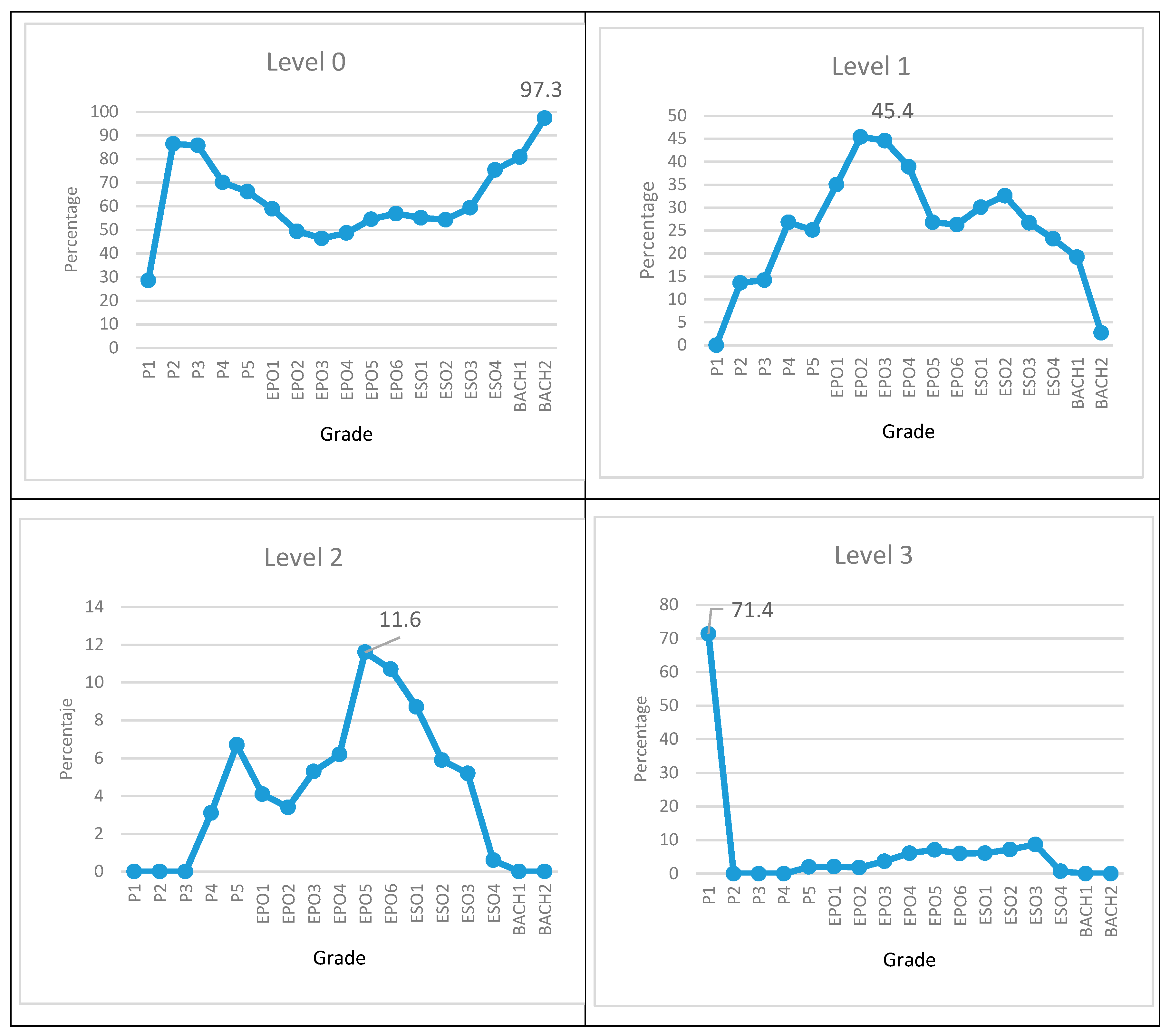
In global terms, the results show that after nine months of application of the Kumon Method, 43.2% of the students are 6 months above their school level, having advanced 6 Kumon levels. In relation to the results by academic year, it should be mentioned that 71.4% of the students who have started in the first year of Elementary Education have reached 3 years above the level they should have according to their course.

By contrast, the correlation data, both the global results and the results per academic year, give us the information that there is a significant and negative correlation between the level at which the students started and the level they reached after the nine months the experience has lasts. For this reason, it can be said that the learning of mathematics, with the Kumon Method, improves as soon as we begin to use this method. This information is evident through the use of the method itself and the analyses, as well as the assessment made of it.

The number of students and the information analyzed gives validity and reliability to the research as it has been proven throughout the work. The information gathered is extensive and reflects the fact that the study of mathematics through the Kumon Method fosters mathematical learning of a high quality, notably improving the academic results of students.

Although we do not add results in this paper, it has been possible to probe the goals established by the Kumon Method, such as self-learning, self-confidence, motivation, habit of study, and concentration. Moreover, some of the objectives of the method have also been corroborated, due to the fact that it has been possible to discover the learning potential of each student of the sample, which has been so large, with this fact also allowing us to cover the objective of the Kumon Method “to provide as many students as possible the opportunity to learn with the Kumon Method, taking into account that its dissemination can contribute widely to the society”.

All of this makes the study of Mathematics through this method highly recommended for the students and that the sooner it is applied and monitored, the better the results are obtained.

In short, the suitability, effectiveness, and efficiency of the method for learning Kumon Mathematics is objectively reflected in scientific evidence.

6. Future Work

As we have seen in this research, the early start in the study of Mathematics in general, and with the Kumon Method in particular, ostensibly improves the progression of students in the learning of this subject. In this regard, we believe that it can be considered that future research would reveal the implications at the Primary School level, during the Early Childhood Education stage, taking into account that children have been stimulated enough in the mathematical area, either through the Kumon Method or another method. Research could also be done to establish whether there is a difference between students who have been stimulated by the Kumon Method and students who have not had this opportunity. Finally, we consider it of great interest to investigate the level of satisfaction by the students and teachers involved, in terms of motivation and self-learning, among others.