Study of a High Order Family: Local Convergence and Dynamics
Abstract
1. Introduction
2. Method’s Local Convergence
- is a differentiable function.We know that exist a constant , , such that for each is fulfilled
- , .
- Let . There exist constants , such that for each
- .There exist parameters and continuous nondecreasing functions such that :
- and
- or a number greater than 0 as . For , consider the functions
- are continuous functions such that for each , and
- for some to be appointed subsequently.
- 1.
- 2.
- The results that we have seen, can also be applied for F operators that satisfy the autonomous differential equation [5,7] of the formwhere P is a known continuous operator. As we are able to use the previous results without needing to know the solution Take for example Now, we can take . However, we do not know the solution.
- 3.
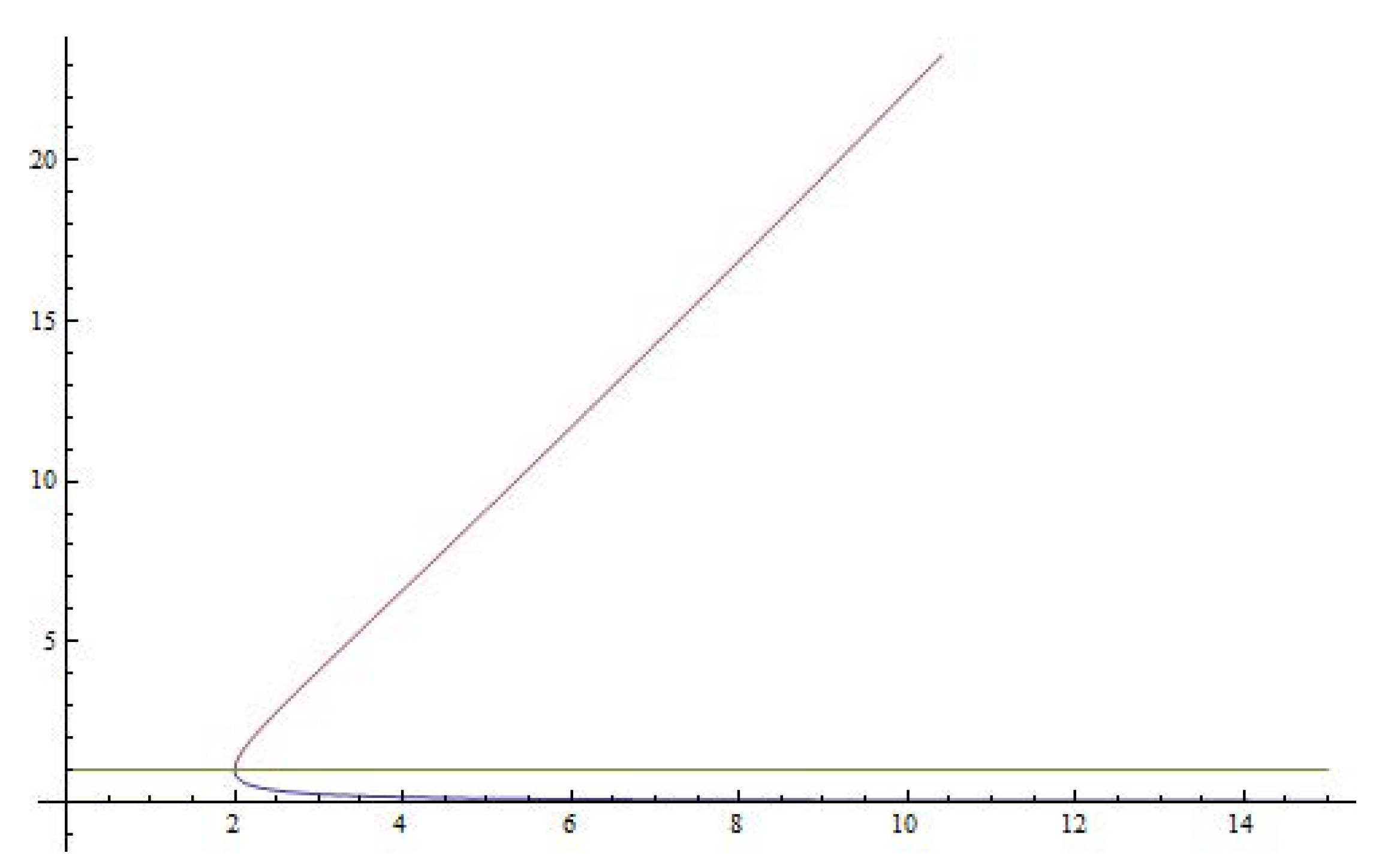
- In the articles [5,7] was shown that the radius has to be the convergence radius for Newton’s method using (10) and (11) conditions. If we apply the definition of and the estimates (8), the convergence radius r of the method (2) it can no be bigger than the convergence radius of the second order Newton’s method. The convergence ball given by Rheinboldt [8] isIn particular, for or we have thatandThat is our convergence ball which is maximum three times bigger than Rheinboldt’s. The precise amount given by Traub in [28] for .
- 4.
- We should note that family (3) stays the same if we use the conditions of Theorem 1 instead of the stronger conditions given in [15,36]. Concerning, for the error bounds in practice we can use the approximate computational order of convergence (ACOC) [36]or the computational order of convergence (COC) [40]And these order of convergence do not require higher estimates than the first Fréchet derivative used in [19,23,32,33,41].
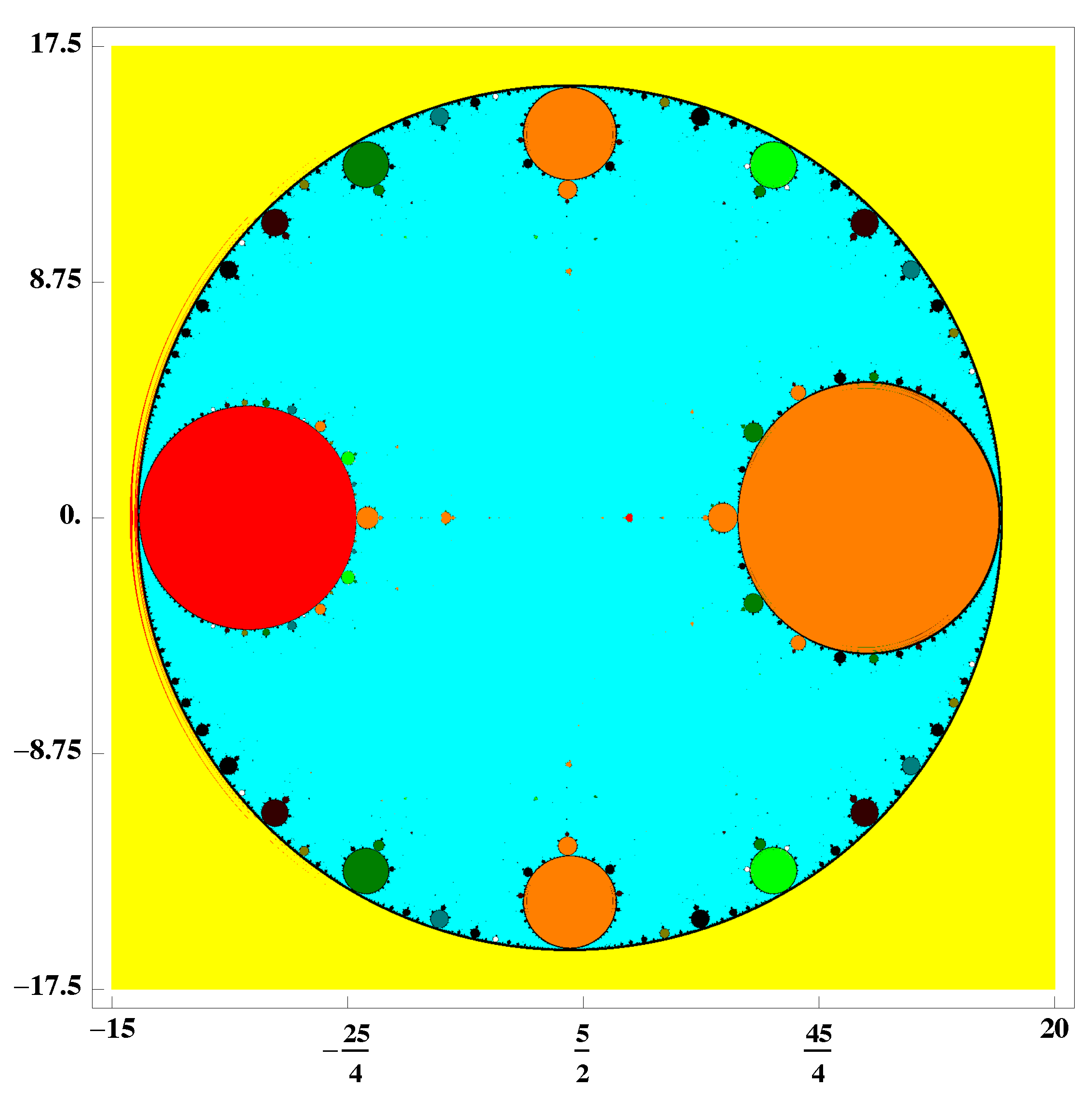
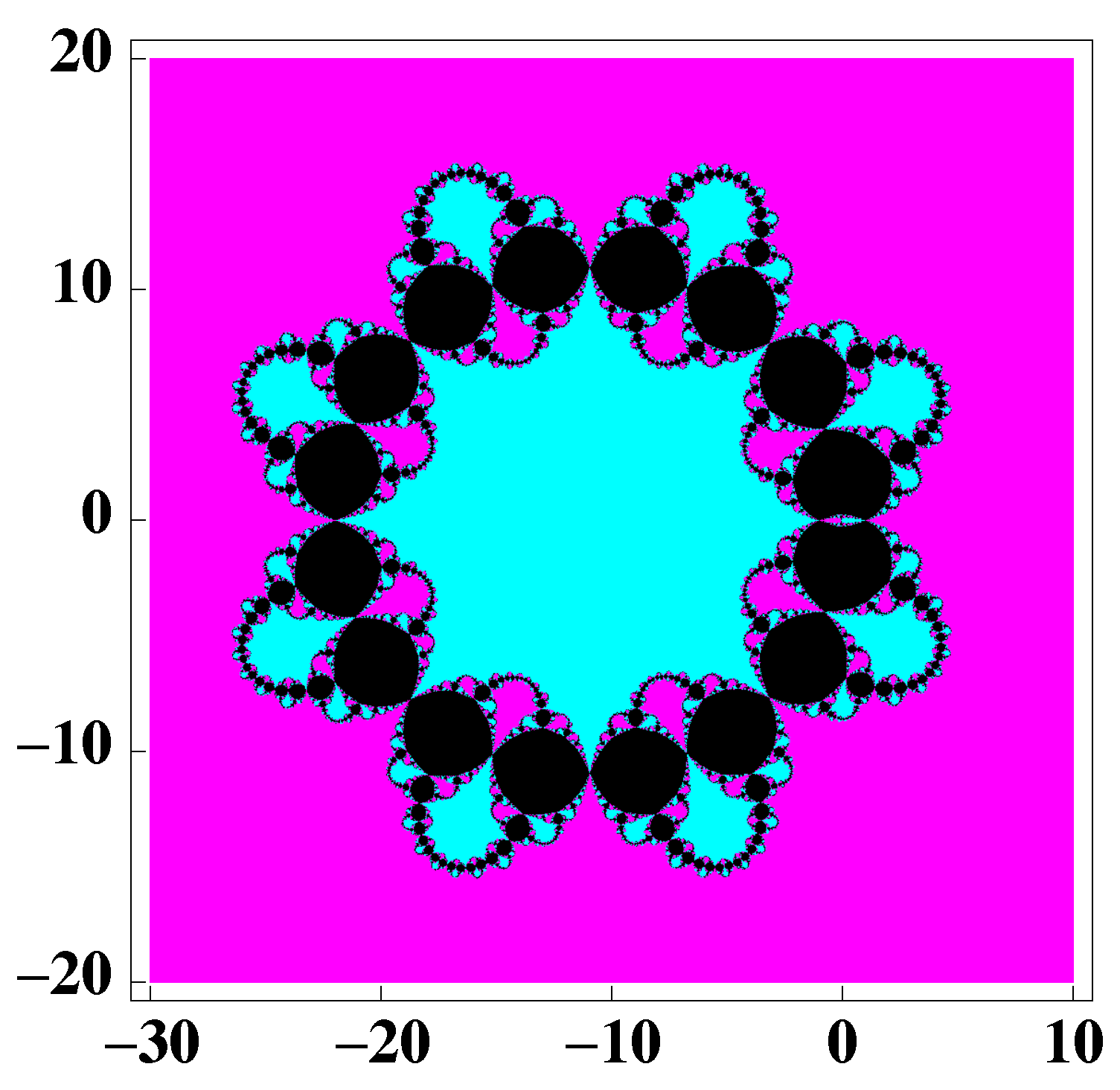
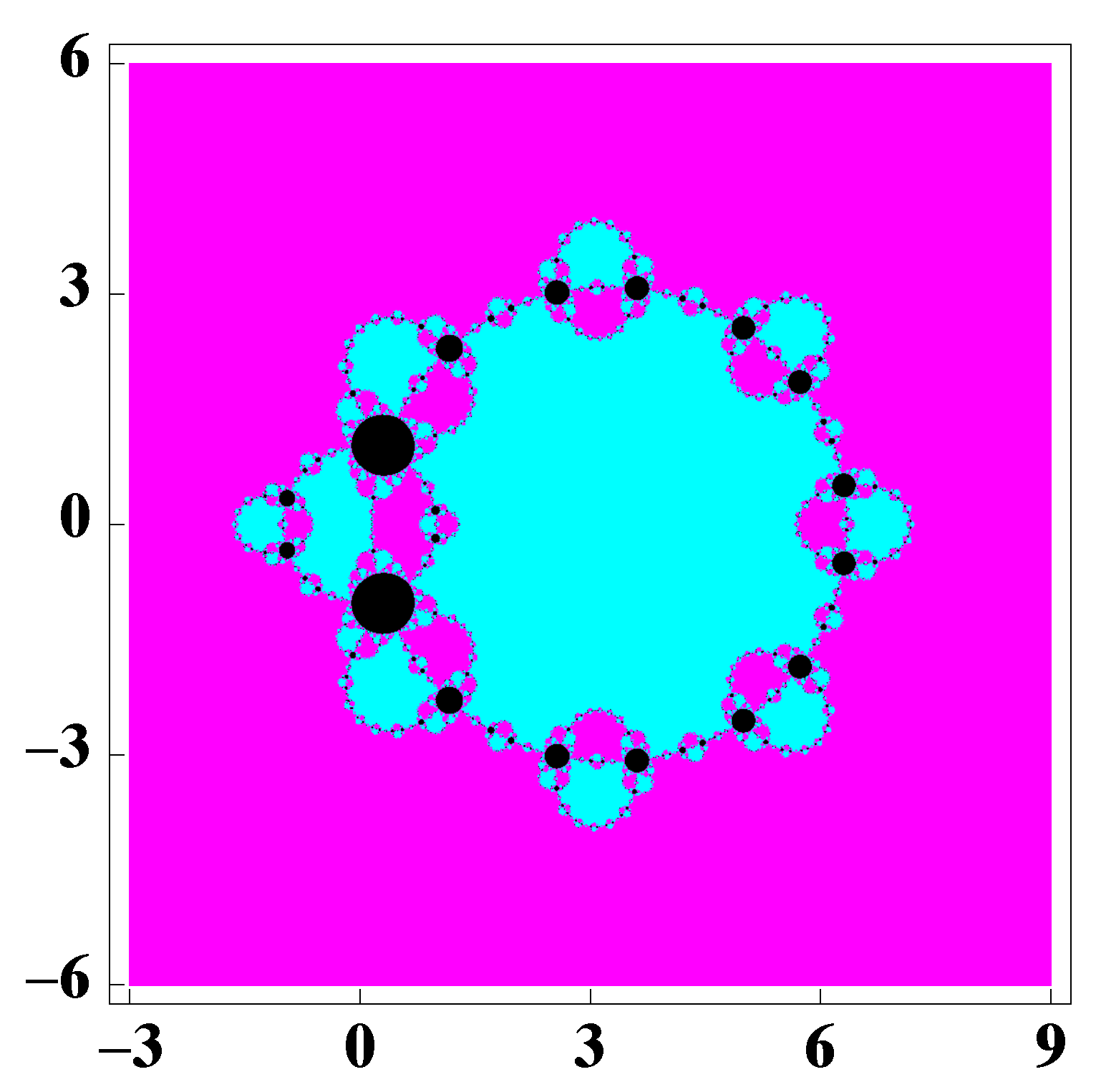
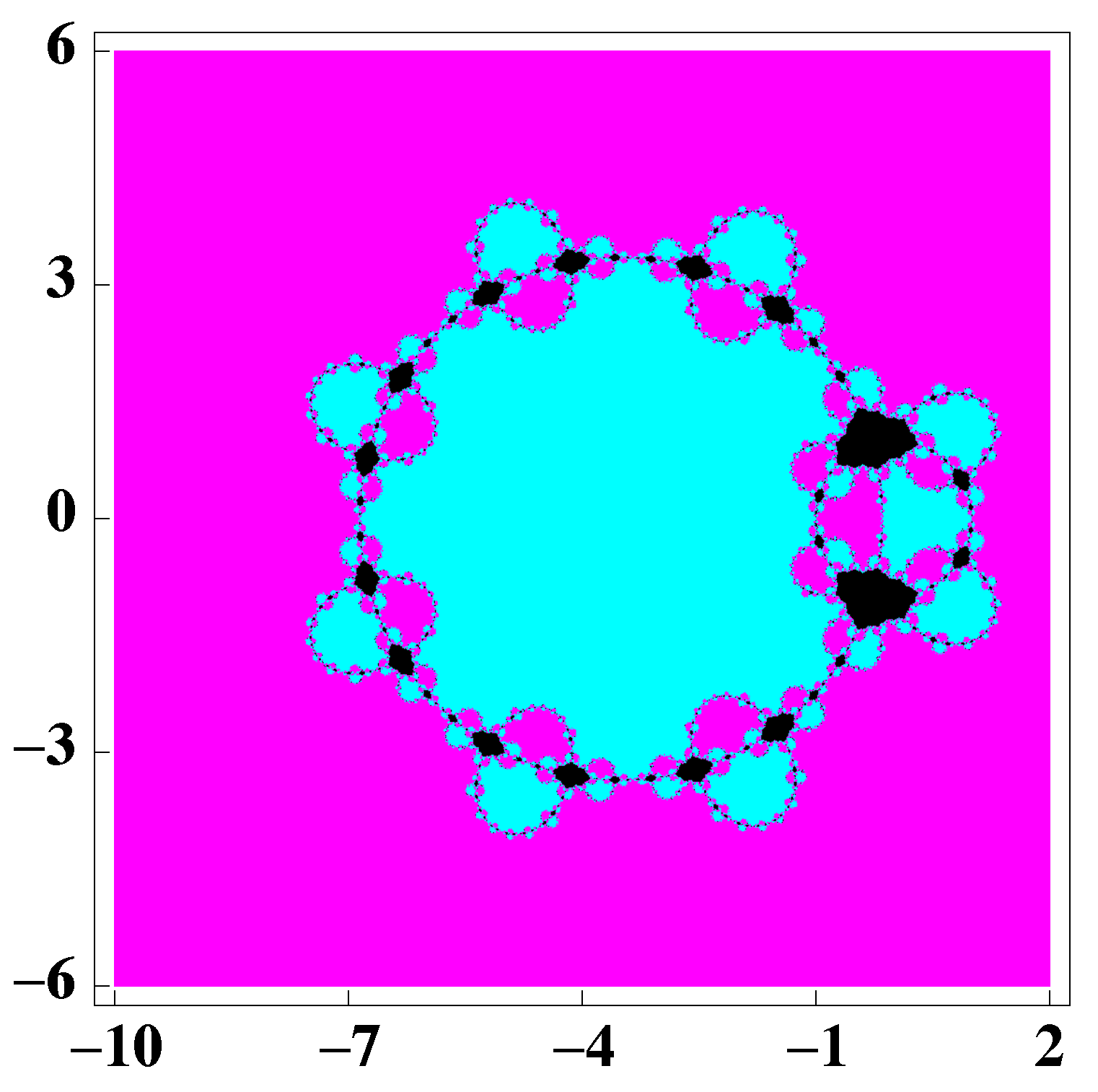
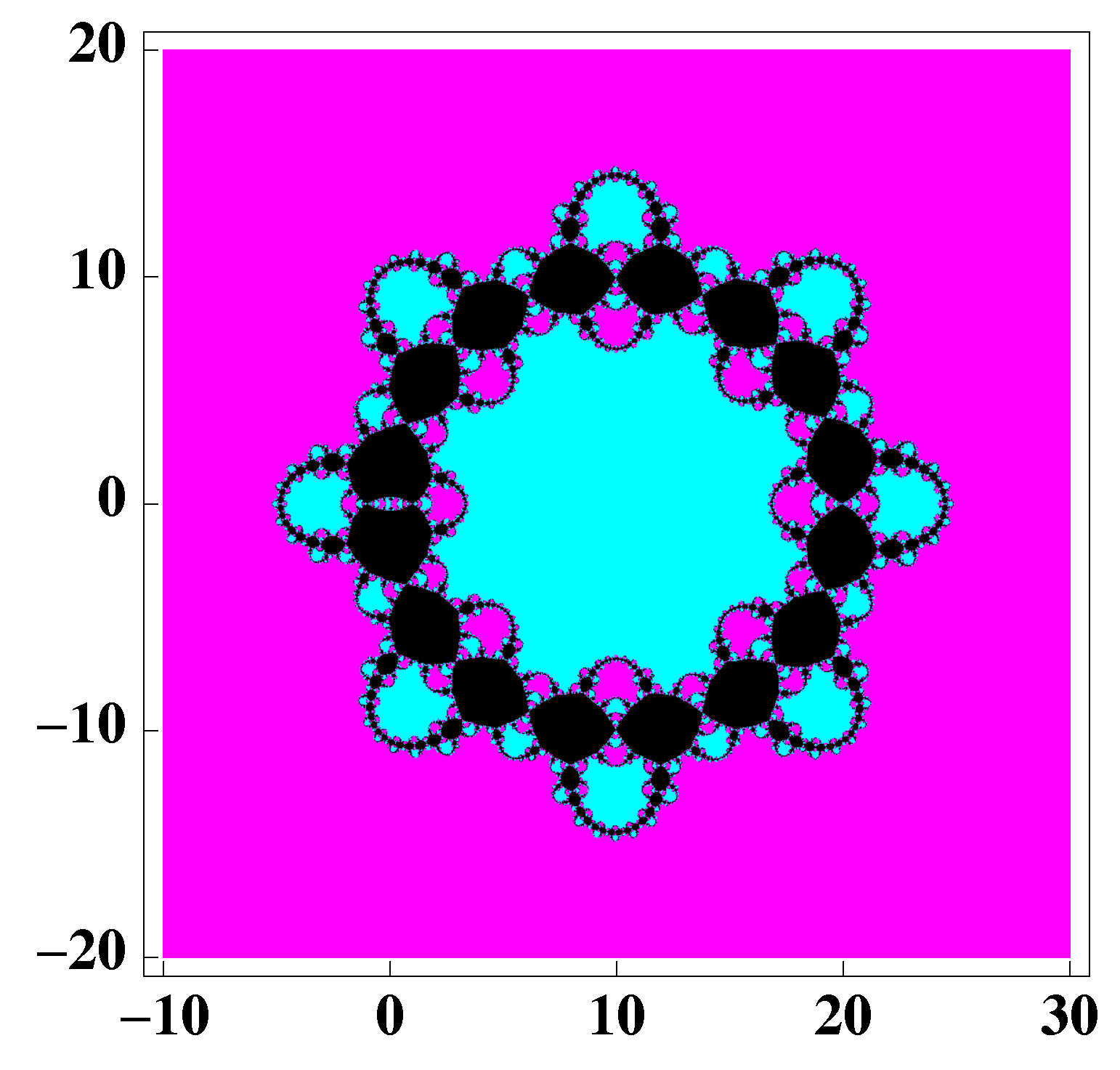
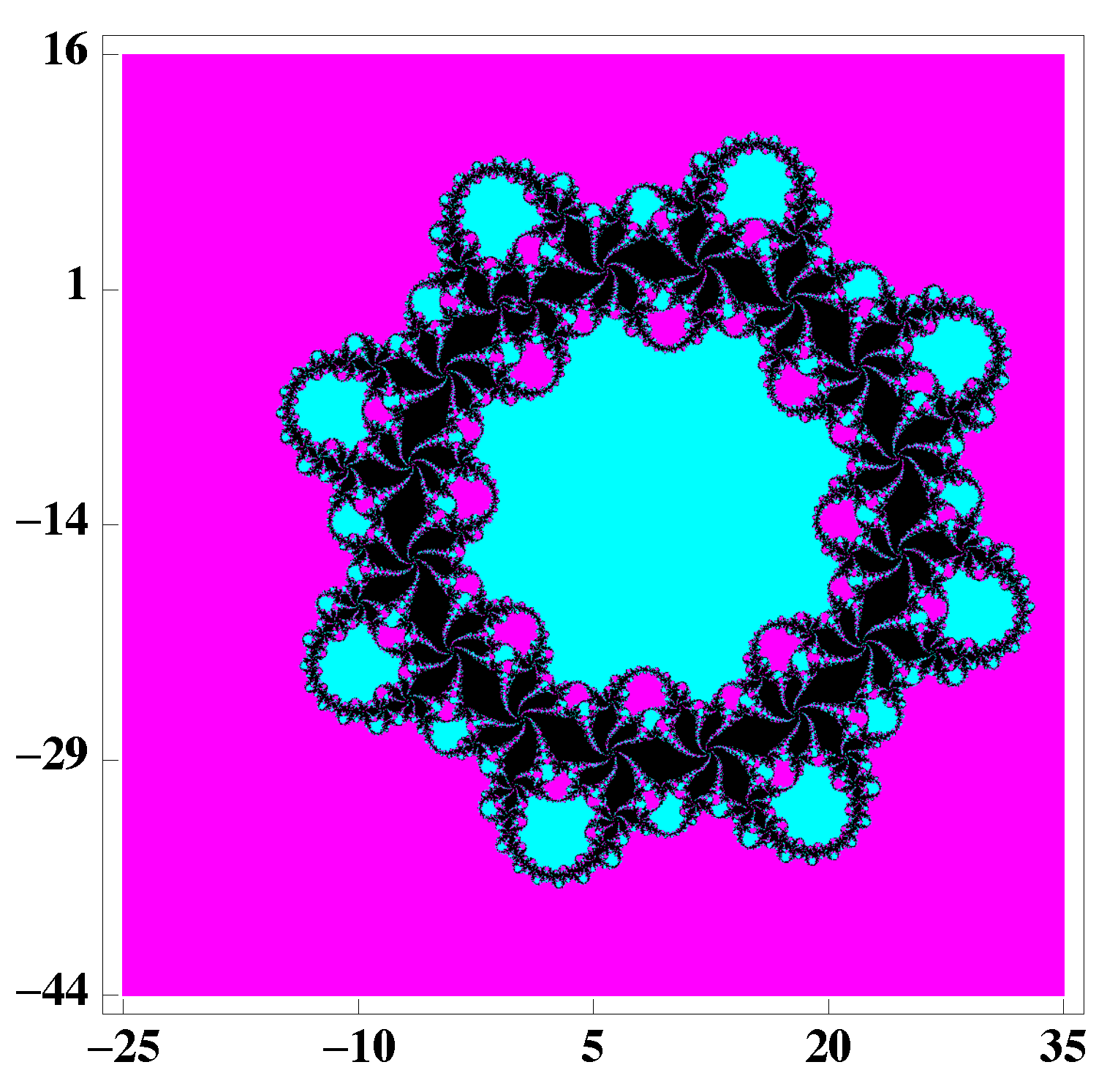
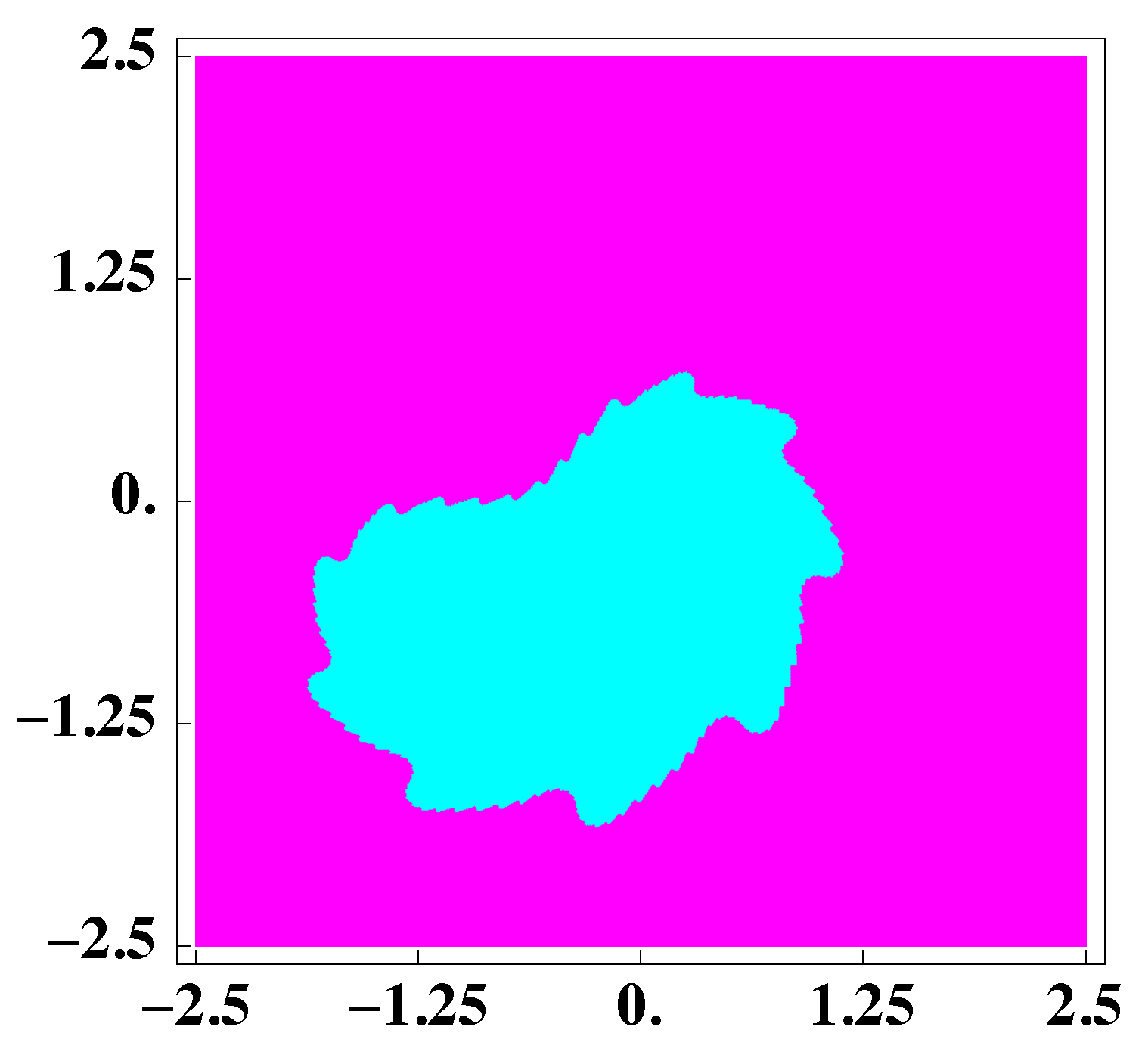
3. Dynamical Study of a Special Case of the Family (2)
- 0
- ∞
- And 15 more, which are
- -
- 1 (related to original ∞).
- -
- The roots of a 14 degree polynomial.
- (a)
- If
- (i)
- .
- (b)
- If
- (i)
- .
4. Example Applied
Author Contributions
Funding
Conflicts of Interest
References
- Tello, J.I.C.; Orcos, L.; Granados, J.J.R. Virtual forums as a learning method in Industrial Engineering Organization. IEEE Latin Am. Trans. 2016, 14, 3023–3028. [Google Scholar] [CrossRef]
- LeTendre, G.; McGinnis, E.; Mitra, D.; Montgomery, R.; Pendola, A. The American Journal of Education: Challenges and opportunities in translational science and the grey area of academic. Rev. Esp. Pedag. 2018, 76, 413–435. [Google Scholar] [CrossRef]
- Argyros, I.K.; González, D. Local convergence for an improved Jarratt–type method in Banach space. Int. J. Interact. Multimed. Artif. Intell. 2015, 3, 20–25. [Google Scholar] [CrossRef][Green Version]
- Argyros, I.K.; George, S. Ball convergence for Steffensen–type fourth-order methods. Int. J. Interact. Multimed. Artif. Intell. 2015, 3, 27–42. [Google Scholar] [CrossRef][Green Version]
- Argyros, I.K.; Magreñán, Á.A. Iterative Methods and Their Dynamics with Applications: A Contemporary Study; CRC-Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Behl, R.; Sarría, Í.; González-Crespo, R.; Magreñán, Á.A. Highly efficient family of iterative methods for solving nonlinear models. J. Comput. Appl. Math. 2019, 346, 110–132. [Google Scholar] [CrossRef]
- Magreñán, Á.A.; Argyros, I.K. A Contemporary Study of Iterative Methods: Convergence, Dynamics and Applications; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Rheinboldt, W.C. An adaptive continuation process for solving systems of nonlinear equations. Pol. Acad. Sci. 1978, 3, 129–142. [Google Scholar] [CrossRef]
- Amat, S.; Busquier, S.; Plaza, S. Dynamics of the King and Jarratt iterations. Aequ. Math. 2005, 69, 212–223. [Google Scholar] [CrossRef]
- Amat, S.; Busquier, S.; Plaza, S. Chaotic dynamics of a third-order Newton-type method. J. Math. Anal. Appl. 2010, 366, 24–32. [Google Scholar] [CrossRef]
- Amat, S.; Hernández, M.A.; Romero, N. A modified Chebyshev’s iterative method with at least sixth order of convergence. Appl. Math. Comput. 2008, 206, 164–174. [Google Scholar] [CrossRef]
- Chicharro, F.; Cordero, A.; Torregrosa, J.R. Drawing dynamical and parameters planes of iterative families and methods. Sci. World J. 2013, 2013, 780153. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez, J.M.; Hernández, M.A. Recurrence relations for the super-Halley method. Comput. Math. Appl. 1998, 36, 1–8. [Google Scholar] [CrossRef]
- Kou, J.; Li, Y. An improvement of the Jarratt method. Appl. Math. Comput. 2007, 189, 1816–1821. [Google Scholar] [CrossRef]
- Li, D.; Liu, P.; Kou, J. An improvement of the Chebyshev-Halley methods free from second derivative. Appl. Math. Comput. 2014, 235, 221–225. [Google Scholar] [CrossRef]
- Magreñán, Á.A. Different anomalies in a Jarratt family of iterative root-finding methods. Appl. Math. Comput. 2014, 233, 29–38. [Google Scholar]
- Budzko, D.; Cordero, A.; Torregrosa, J.R. A new family of iterative methods widening areas of convergence. Appl. Math. Comput. 2015, 252, 405–417. [Google Scholar] [CrossRef]
- Bruns, D.D.; Bailey, J.E. Nonlinear feedback control for operating a nonisothermal CSTR near an unstable steady state. Chem. Eng. Sci. 1977, 32, 257–264. [Google Scholar] [CrossRef]
- Candela, V.; Marquina, A. Recurrence relations for rational cubic methods I: The Halley method. Computing 1990, 44, 169–184. [Google Scholar] [CrossRef]
- Candela, V.; Marquina, A. Recurrence relations for rational cubic methods II: The Chebyshev method. Computing 1990, 45, 355–367. [Google Scholar] [CrossRef]
- Ezquerro, J.A.; Hernández, M.A. New iterations of R-order four with reduced computational cost. BIT Numer. Math. 2009, 49, 325–342. [Google Scholar] [CrossRef]
- Ezquerro, J.A.; Hernández, M.A. On the R-order of the Halley method. J. Math. Anal. Appl. 2005, 303, 591–601. [Google Scholar] [CrossRef]
- Ganesh, M.; Joshi, M.C. Numerical solvability of Hammerstein integral equations of mixed type. IMA J. Numer. Anal. 1991, 11, 21–31. [Google Scholar] [CrossRef]
- Hernández, M.A. Chebyshev’s approximation algorithms and applications. Comput. Math. Appl. 2001, 41, 433–455. [Google Scholar] [CrossRef]
- Hernández, M.A.; Salanova, M.A. Sufficient conditions for semilocal convergence of a fourth order multipoint iterative method for solving equations in Banach spaces. Southwest J. Pure Appl. Math. 1999, 1, 29–40. [Google Scholar]
- Jarratt, P. Some fourth order multipoint methods for solving equations. Math. Comput. 1966, 20, 434–437. [Google Scholar] [CrossRef]
- Ren, H.; Wu, Q.; Bi, W. New variants of Jarratt method with sixth-order convergence. Numer. Algorithms 2009, 52, 585–603. [Google Scholar] [CrossRef]
- Traub, J.F. Iterative Methods for the Solution of Equations; Prentice-Hall Series in Automatic Computation: Englewood Cliffs, NJ, USA, 1964. [Google Scholar]
- Wang, X.; Kou, J.; Gu, C. Semilocal convergence of a sixth-order Jarratt method in Banach spaces. Numer. Algorithms 2011, 57, 441–456. [Google Scholar] [CrossRef]
- Cordero, A.; Torregrosa, J.R.; Vindel, P. Dynamics of a family of Chebyshev-Halley type methods. Appl. Math. Comput. 2013, 219, 8568–8583. [Google Scholar] [CrossRef]
- Artidiello, S.; Cordero, A.; Torregrosa, J.R.; Vassileva, M.P. Optimal high order methods for solving nonlinear equations. J. Appl. Math. 2014, 2014, 591638. [Google Scholar] [CrossRef]
- Petković, M.; Neta, B.; Petković, L.; Džunić, J. Multipoint Methods for Solving Nonlinear Equations; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Zhao, L.; Wang, X.; Guo, W. New families of eighth-order methods with high efficiency index for solving nonlinear equations. Wseas Trans. Math. 2012, 11, 283–293. [Google Scholar]
- Dźunic, J.; Petković, M. A family of Three-Point methods of Ostrowski’s Type for Solving Nonlinear Equations. J. Appl. Math. 2012, 2012, 425867. [Google Scholar] [CrossRef]
- Chun, C. Some improvements of Jarratt’s method with sixth-order convergence. Appl. Math. Comput. 1990, 190, 1432–1437. [Google Scholar] [CrossRef]
- Cordero, A.; Torregrosa, J.R. Variants of Newton’s method using fifth-order quadrature formulas. Appl. Math. Comput. 2007, 190, 686–698. [Google Scholar] [CrossRef]
- Ezquerro, J.A.; Hernández, M.A. Recurrence relations for Chebyshev-type methods. Appl. Math. Optim. 2000, 41, 227–236. [Google Scholar] [CrossRef]
- Magreñán, Á.A. A new tool to study real dynamics: The convergence plane. Appl. Math. Comput. 2014, 248, 215–224. [Google Scholar] [CrossRef]
- Rall, L.B. Computational Solution of Nonlinear Operator Equations; Robert E. Krieger: New York, NY, USA, 1979. [Google Scholar]
- Weerakon, S.; Fernando, T.G.I. A variant of Newton’s method with accelerated third-order convergence. Appl. Math. Lett. 2000, 13, 87–93. [Google Scholar] [CrossRef]
- Cordero, A.; García-Maimó, J.; Torregrosa, J.R.; Vassileva, M.P.; Vindel, P. Chaos in King’s iterative family. Appl. Math. Lett. 2013, 26, 842–848. [Google Scholar] [CrossRef]
- Gopalan, V.B.; Seader, J.D. Application of interval Newton’s method to chemical engineering problems. Reliab. Comput. 1995, 1, 215–223. [Google Scholar]
- Shacham, M. An improved memory method for the solution of a nonlinear equation. Chem. Eng. Sci. 1989, 44, 1495–1501. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amorós, C.; Argyros, I.K.; González, R.; Magreñán, Á.A.; Orcos, L.; Sarría, Í. Study of a High Order Family: Local Convergence and Dynamics. Mathematics 2019, 7, 225. https://doi.org/10.3390/math7030225
Amorós C, Argyros IK, González R, Magreñán ÁA, Orcos L, Sarría Í. Study of a High Order Family: Local Convergence and Dynamics. Mathematics. 2019; 7(3):225. https://doi.org/10.3390/math7030225
Chicago/Turabian StyleAmorós, Cristina, Ioannis K. Argyros, Ruben González, Á. Alberto Magreñán, Lara Orcos, and Íñigo Sarría. 2019. "Study of a High Order Family: Local Convergence and Dynamics" Mathematics 7, no. 3: 225. https://doi.org/10.3390/math7030225
APA StyleAmorós, C., Argyros, I. K., González, R., Magreñán, Á. A., Orcos, L., & Sarría, Í. (2019). Study of a High Order Family: Local Convergence and Dynamics. Mathematics, 7(3), 225. https://doi.org/10.3390/math7030225








