More Results on the Domination Number of Cartesian Product of Two Directed Cycles

Abstract

Let $\gamma (D)$ denote the domination number of a digraph D and let $C_m\square C_n$ denote the Cartesian product of $C_m$ and $C_n$, the directed cycles of length $n\ge m\ge 3$. Liu et al. obtained the exact values of $\gamma (C_m\square C_n)$ for m up to 6 [Domination number of Cartesian products of directed cycles, Inform. Process. Lett. 111 (2010) 36–39]. Shao et al. determined the exact values of $\gamma (C_m\square C_n)$ for $m=6,7$ [On the domination number of Cartesian product of two directed cycles, Journal of Applied Mathematics, Volume 2013, Article ID 619695]. Mollard obtained the exact values of $\gamma (C_m\square C_n)$ for $m=3k+2$ [M. Mollard, On domination of Cartesian product of directed cycles: Results for certain equivalence classes of lengths, Discuss. Math. Graph Theory 33(2) (2013) 387–394.]. In this paper, we extend the current known results on $C_m\square C_n$ with m up to 21. Moreover, the exact values of $\gamma (C_n\square C_n)$ with n up to 31 are determined.

1. Introduction

In this paper, we only consider digraphs without multiple edges or loops. For a digraph $D=(V,A)$ (or $D=(V(G),A(G))$) with vertex set V, arc set A, and a vertex $v\in V$, $N_D^{+}(v)$ and $N_D^{-}(v)$ denote the set of out-neighbors and in-neighbors of v, $d_D^{+}(v)=|N_D^{+}(v)|$ and $d_D^{-}(v)=|N_D^{-}(v)|$ denote the out-degree and in-degree of v in D, respectively. For two vertices u and v in D, we say u dominates v if $u=v$ or $uv\in A$. Let $N_D^{+}\left[v\right]=N_D^{+}(v)\cup \left\{v\right\}$. A vertex v dominates all vertices in $N_D^{+}\left[v\right]$. A set $S\subseteq V$ is a dominating set of D if S dominates $V(D)$. The domination number of D, denoted by $\gamma (D)$, is the minimum cardinality of a dominating set of D. A dominating set S is called a $\gamma$-set of D if $|S|$ is the minimum cardinality over all dominating sets of D.

The Cartesian product of graphs $D_1$ and $D_2$ is the graph $D_1\square D_2$ with the vertex set $V(D_1)\times V(D_2)$, and $(a,b)(a^{\prime },b^{\prime })\in A(D_1\square D_2)$ if either $a{a}^{\prime }\in A(D_1)$ and $b=b^{\prime }$, or $b{b}^{\prime }\in A(D_2)$ and $a=a^{\prime }$. For more information on the Cartesian product of graphs [1]. It can be seen that if $D_1$ and $D_2$ are directed graphs, then $D_1\square D_2$ is also a directed graph. We denote by $C_n$ and $P_n$ the directed cycle and directed path with n vertices, respectively. Then we study the domination number of directed graphs $C_m\square C_n$ for $n\ge m\ge 3$.

Graph domination and associated concepts have been studied for many years and there are more than 200 papers to study on the subject [2,3,4]. Among them, many authors study the domination number of products of graphs [5,6], especially for cylinders [7], torus [8,9] and grids [10]. Liu et al. initiated the study of the domination number of two directed cycles, and they [11,12] determined the exact values of $\gamma (C_m\square C_n)$ for m up to 6 and showed that

Theorem 1.

$\gamma (C_m\square C_n)=\frac{mn}{3}$ if $m\equiv 0$ (mod 3) and $n\equiv 0$ (mod 3).

Shao et al. [13] extended the exact values of $\gamma (C_m\square C_n)$ for $m\in \{7,10\}$. Mollard [14] determined exact values of $\gamma (C_m\square C_n)$ for $m=3k+2$.

In this paper, we again apply the “dynamic algorithm”, used in [15], to extend the exact values of $\gamma (C_m\square C_n)$ for m up to 21. These results go much further from the previous known results. Moreover, the exact values of $\gamma (C_n\square C_n)$ with n up to 31 are determined.

2. The Approach—General Outline

The “dynamic algorithm” was proposed to compute invariants of fasciagraphs and rotagraphs [16], and thus it can be used to compute the chromatic number, independence number, domination number etc. of products of graphs. For example, Shao et al. [13] apply the “dynamic algorithm” to compute the domination number of Cartesian product of two cycles with one cycle of length 7 or 10 and in [15] authors derived some formulas for the Roman domination number of products of paths and cycles.

In [17], the approach was used to derive closed expressions for domination numbers $\gamma (P_n\square C_k)$ (for $k\le 11$, $n\in \mathbb{N}$) and domination numbers $\gamma (C_n\square P_k)$ and $\gamma (C_n\square C_k)$ (for $k\le 7$, $n\in \mathbb{N}$). We recall a brief formal description from [17].

Let $D_1,\dots ,D_n$ be arbitrary mutually disjoint (di)graphs, here called monographs, and $X_1,\dots ,X_n$ a sequence of sets of arcs. An arc of $X_i$ joins a vertex of $V(D_i)$ with a vertex of $V(D_{i+1})$ ($X_i\subseteq V(D_i)\times V(D_{i+1})$ for $i=1,\dots ,n$). Furthermore, for convenience we set $D_{n+1}=D_1$. A polygraph ${\Omega }_n={\Omega }_n(D_1,\dots D_n;X_1,\dots X_n)$ over monographs $D_1,\dots ,D_n$ is defined in the following way:

$$V({\Omega }_n)=V(D_1)\cup \dots \cup V(D_n),$$

$$A({\Omega }_n)=A(D_1)\cup X_1\cup \dots \cup A(D_n)\cup X_n.$$

For a polygraph ${\Omega }_n$ and for $i=1,\dots ,n$ we also define

$$L_i=\{u\in V(D_i)|\exists v\in D_{i+1}:uv\in X_i\},$$

$$R_i=\{u\in V(D_{i+1})|\exists v\in D_i:uv\in X_i\}.$$

In general, $R_i\cap L_{i+1}$ does not have to be empty. Special types of polygraphs are rotagraphs and fasciagraphs. If all (di)graphs $D_i$ are isomorphic to a fixed (di)graph D and all sets $X_i$ are equal to a fixed set X, we call such a graph rotagraph, ${\omega }_n(D;X)$. More precisely, in a rotagraph (1) there are isomorphisms ${\phi }_i:V(D_i)⟶V(D)$ for $i=1,\dots ,n+1$, and ${\phi }_{n+1}={\phi }_1$ and (2) all sets $X_i$ are equal to a fixed set $X\subseteq V(D)\times V(D)$ ($(u,v)\in X⟺\left({\phi }_i^{-1}(u),{\phi }_{i+1}^{-1}(v)\right)\in X_i$ for all i). Losely speaking, a fasciagraph, ${\psi }_n(D;X)$ is a rotagraph without edges between the last and the first copy of D. Formally, in a fasciagraph we have $X_n=\varnothing$ and $X_1=X,\dots ,X_{n-1}=X$. Note that in a rotagraph, all sets $L_i$ and $R_i$ are equal to fixed sets L and R (i.e., $L_i={\phi }_i^{-1}(L)$ and $R_i={\phi }_{i+1}^{-1}(R)$). This holds for fasciagraphs with one exception, namely $L_n=\varnothing$ and $R_n=\varnothing$. Clearly, the Cartesian products of paths $P_n\square P_k$ are examples of fasciagraphs and Cartesian products of cycles $C_n\square C_k$ are examples of rotagraphs. Products of a path and a cycle can be seen either as rotagraphs or as fasciagraphs. In previous work [15,17,18], this fact has been used in studies of undirected graphs to obtain a number of results regarding the products of paths and cycles.

We now recall the definition of a semiring $\mathcal{P}=(P,\oplus ,\circ ,e^{\oplus },e^{\circ })$. It is a set P together with two binary operations, ⊕ and ○ such that the following hold:

• $(P,\oplus )$ is a commutative monoid with $e^{\oplus }$ as a unit;
• $(P,\circ )$ is a monoid with $e^{\circ }$ as a unit;
• ○ is left– and right–distributive over ⊕;
• $\forall x\in P,x\circ e^{\oplus }=e^{\oplus }=e^{\oplus }\circ x$.

A path algebra is an idempotent semiring. It is well known that a semiring is a path algebra exactly when $e^{\circ }\oplus e^{\circ }=e^{\circ }$ holds for $e^{\circ }$, the unit of the monoid $(P,\circ )$. Let ${\mathbb{N}}_0$ denote the set of nonnegative integers and $\mathbb{N}$ the set of positive integers. An example of a path algebra that is important here is ${\mathcal{P}}_1=({\mathbb{N}}_0\cup \{\infty \},min,+,\infty ,0)$.

Let $\mathcal{P}=(P,\oplus ,\circ ,e^{\oplus },e^{\circ })$ be a path algebra and let ${\mathcal{M}}_n(\mathcal{P})$ be the set of all $n\times n$ matrices over P. Let $M,N\in {\mathcal{M}}_n(\mathcal{P})$ and define operations ⊕ and ○ in the usual way:

$$\begin{array}{ccc}\hfill {(M\oplus N)}_{ij}& =& M_{ij}\oplus N_{ij},\hfill \\ \hfill {(M\circ N)}_{ij}& =& \underset{k=1}{\overset{n}{⨁}}{M}_{ik}\circ N_{kj}.\hfill \end{array}$$

Note that in the case of the path algebra ${\mathcal{P}}_1=({\mathbb{N}}_0\cup \{\infty \},min,+,\infty ,0)$, the above definitions can be rewritten as:

$$\begin{array}{ccc}\hfill {(M\oplus N)}_{ij}& =& min\{M_{ij},N_{ij}\},\hfill \\ \hfill {(M\circ N)}_{ij}& =& \underset{k\in \{1,\dots ,n\}}{min}\{M_{ik}+N_{kj}\}.\hfill \end{array}$$

${\mathcal{M}}_n(\mathcal{P})$ equipped with above operations is a path algebra where the units of semiring are the zero matrix and the unit matrix. In our example, ${\mathcal{P}}_1=({\mathbb{N}}_0\cup \{\infty \},min,+,\infty ,0)$, all elements of the zero matrix are ∞, the unit of the monoid $(P,min)$, and the unit matrix is a diagonal matrix with diagonal elements equal to $e^{\circ }=0$ and all other elements equal to $e^{\oplus }=\infty$.

Let D be a labeled digraph with a labeling function ℓ which assigns to every arc of D an element of a path algebra P. Let $V(D)=\left\{v_1,v_2,\dots ,v_n\right\}$. The labeling ℓ of D can be extended to paths in the following way: For a path $Q=(v_{i_0},v_{i_1})(v_{i_1},v_{i_2})\dots (v_{i_{k-1}},v_{i_k})$ of D let

$$\ell (Q)=\ell \left(v_{i_0},v_{i_1}\right)\circ \ell \left(v_{i_1},v_{i_2}\right)\circ \dots \circ \ell \left(v_{i_{k-1}},v_{i_k}\right).$$

Let $S_{ij}^k$ be the set of all paths of order k from $v_i$ to $v_j$ in D and let $M(D)$ be the matrix defined by:

$$M{(D)}_{ij}=\left\{\begin{array}{cc}\ell \left(v_i,v_j\right);\hfill & \mathrm{if}(v_i,v_j)\mathrm{is}\mathrm{an}\mathrm{arc}\mathrm{of}D\hfill \\ e^{\oplus };\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

It is well-known [19] that

$${\left(M{(D)}^k\right)}_{ij}=\underset{Q\in S_{ij}^k}{⨁}\ell (Q).$$

Let ${\omega }_n(D;X)$ be a rotagraph and ${\psi }_n(D;X)$ a fasciagraph. Set $U_i=L_i\cup R_i$. Note that in the case of fasciagraphs or rotagraphs, all sets $L_i$ and $R_i$ are equal to fixed sets L and R, respectively. Therefore we can write $U=L\cup R$, keeping in mind that this is a disjoint union of sets L and R, where $L\subseteq D_i$ and $R\subseteq D_{i+1}$. Denote $N=2^{|U|}$. The labeled digraph $\mathcal{D}=\mathcal{D}(D;X)$ is defined as follows: (1) elements of vertex set of $\mathcal{D}$ are the subsets of U, denoted $V_i$; (2) the label (or, weight) of the arc that joins a subset $V_i$ with a subset $V_j$ is the contribution of the monograph $D_i$ to the solution, assuming the sets $V_i$ and $V_j$ are part of the solution. In general however, for example when independent domination is considered, some of the pairs of sets $V_i$ and $V_j$ do not allow any feasible solution. In such case either a very large label is given (∞), or the arc $V_i{V}_j$ is deleted from $\mathcal{D}=\mathcal{D}(D;X)$, and consequently $\mathcal{D}$ need not be a complete graph.

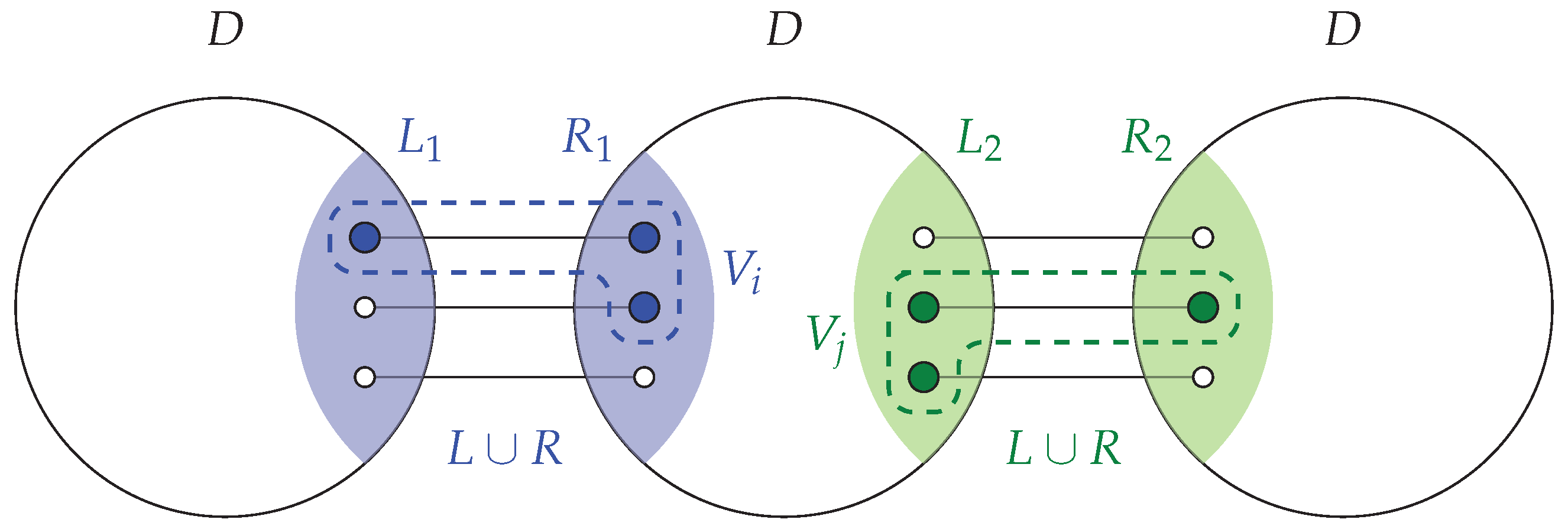
Consider for a moment ${\psi }_3(D;X)$ and let $V_i\subseteq L_1\cup R_1$ and $V_j\subseteq L_2\cup R_2$ (of course $R_1=R_2=R$ and $L_1=L_2=L$ (see Figure 1)). Let ${\gamma }_{i,j}(D;X)$ stand for the size of minimum dominating set of $D_2\setminus \left((V_i\cap R_1)\cup (L_2\cap V_j)\right)$. Then we define a labeling of $\mathcal{D}$, $\ell :A(\mathcal{D})⟶{\mathbb{N}}_0\cup \left\{\infty \right\}$, in the following way:

$$\begin{array}{cc}\hfill \ell (V_i,V_j)& =\left|V_i\cap R\right|+{\gamma }_{i,j}(D;X)+\left|L\cap V_j\right|-\left|V_i\cap R\cap L\cap V_j\right|.\hfill \end{array}$$

(1)

We now recall Algorithm 1, first proposed in [16], that computes the domination number of a fasciagraph or a rotagraph in $O(logn)$ time:

Algorithm 1 The domination number.

Step 1: Let ${\mathcal{P}}_1=({\mathbb{N}}_0\cup \{\infty \},min,+,\infty ,0)$ be a path algebra. Step 2: Label $\mathcal{D}(D;X)$ with the labeling, defined in (1). Step 3: In $\mathcal{M}({\mathcal{P}}_1)$ calculate $M{\left(\mathcal{D}\right)}^n$. Step 4: Let $\gamma \left({\psi }_n(D;X)\right)={\left(M{\left(\mathcal{D}\right)}^n\right)}_{00}$ and $\gamma \left({\omega }_n(D;X)\right)={min}_i{\left(M{\left(\mathcal{D}\right)}^n\right)}_{ii}.$

This algorithm can be considerably improved because in some cases, computing the powers of $M{\left(\mathcal{D}\right)}^n=M_n$ in $O(C)$ time is possible. For example, it is well-known that improvements using special structure of the matrices give rise to constant time algorithm for computation of the domination numbers:

Lemma 1.

([20]) Let $k=|V(\mathcal{D}(D;X))|$ and $K=|V(D)|$. Then there is an index $q\le {(2K+2)}^{k^2}$ such that $M_q=M_p+C$ for some index $p<q$ and some constant matrix C. Let $P=q-p$. Then for every $r\ge p$ and every $s\ge 0$ we have

$$M_{r+sP}=M_r+sC.$$

Note that this phenomena is not restricted to domination type problems. For example, an analogous lemma for distance based invariants was elaborated already in [21].

Hence, if we assume that the size of the monograph is a given constant (and n is a variable), the algorithm will run in constant time. But it is important to emphasize that the algorithm is useful for practical purposes only if the number of vertices of the monograph is relatively small. Namely, the matrices $\mathcal{M}{(\mathcal{D})}^k$ are of size $|V(\mathcal{D})|\times |V(\mathcal{D})|$, and manipulating such matrices implies that the time complexity is in general exponential in the number of vertices of the monograph. Therefore, a straightforward implementation of the algorithm may have prohibitively long running times.

A method that is particulary useful for fasciagraphs is the following. Observe that one may consider each row of the matrices separately. Thus, instead of using $O(|V(\mathcal{D}){|}^2)$ space, only $O(|V(\mathcal{D})|)$ is required. Furthermore, depending on the problem, it may not be necessary to compute all the rows of $\mathcal{M}{(\mathcal{D})}^n$. Instead of calculating the whole matrices $\mathcal{M}{(\mathcal{D})}^n$, the correct answer is obtained if only those rows which are important for the result are calculated and the difference of the new row against the previously stored rows is checked until a constant difference is detected. This idea was used in [15] on Roman domination problem and in [22] for pentomino exclusion problem. Formally, it is based on the following lemma

Lemma 2.

[15] Assume that the j-th row of $M^{n+P}$ and $M^n$ differ by a constant, $M_{ji}^{n+P}=M_{ji}^n+C$ for all i. Then ${\displaystyle \underset{i}{min}{M}_{ji}^{n+P}=\underset{i}{min}{M}_{ji}^n+C}$.

The idea may be even easier to explain directly in terms of graphs, avoiding the matrix notation. As we study products of cycles in this paper, we restrict attention to rotagraph type problems. Observe that a dominating set in $C_m\square C_n$ corresponds to a cycle of length n in the auxiliary graph $\mathcal{D}$. This leads to the problem of finding a cycle of length n with minimal weight. Above considerations translate into the ideas that if there is a subset of vertices of $\mathcal{D}$ that must be in any solution, then we can start the search for cycles on these vertices only.

In this paper we make use of another idea [13]. Namely, if there are vertices of $\mathcal{D}$ that can not be on any minimal cycle, then we can ignore them.

3. The Approach: Details

Below, we define the labelled auxiliary digraph $\mathcal{D}$ that can be used to solve our domination problem. Then we provide a procedure for reducing the number of vertices of the auxiliary digraph $\mathcal{D}$, similarly as in [13]. The dynamic algorithm is then applied on the reduced auxiliary graph.

Before we continue, let us denote $V(C_n)=\{0,1,\dots ,n-1\}$ and $C_m^i$ a $C_m$-layer of $C_m\square C_n$, which corresponds to vertex $i\in V(C_n).$ Similarly as in [13], the vertices v of the auxiliary digraph are represented with a “pattern”, i.e., a dominating set on two consecutive $C_m$-layers. A pattern here is a sequence of 0 s and 1 s, where 1 stands for a vertex in a dominating set of $C_m^i\cup C_m^{i+1}$ and 0 for a vertex that needs to be dominated from a neighboring vertex. The weight of a vertex v, $w(v)$, is defined to be the number of 1 s in a given pattern, i.e., $w(v)=\left|S\cap (C_m^i\cup C_m^{i+1})\right|$, where S is a dominating set of $C_m\square C_n$. Clearly, for a cycle C of length n we have $w(C)=2|S|$, since every vertex in S appears in two consecutive patterns.

The following procedure is used to provide a subset of patterns that will be the vertices of $\mathcal{D}$.

ProcedureReduceNumberOfVertices:

Step 1:

for a fixed m, find an upper bound of $\gamma (C_m\square C_n)$ in the form of $an+b$ for some $a,b\in \mathbb{Q}$;

Step 2:

establish a lower bound ${\ell }_b>0$ for the number of vertices in a minimum dominating set of $C_m^i\cup C_m^{i+1}$ for any $i\in \{0,\dots ,n-2\}.$

Step 3:

remove each vertex v in $\mathcal{D}$ such that $w(v)-{\ell }_b>2na+2b-n{\ell }_b$.

Remark 1.

Procedure ReduceNumberOfVertices can reduce the order of $\mathcal{D}$ for finding the domination number of $C_m\square C_n$.

Let S be a minimum dominating set of $C_m\square C_n$. Steps 1 and 2 of Procedure ReduceNumberOfVertices provide a, $b\in \mathbb{Q}$, and ${\ell }_b>0$, such that

$$\gamma (C_m\square C_n)\le an+b,$$

(2)

and

$$|S\cap (C_m^i\cup C_m^{i+1})|\ge {\ell }_b\mathrm{for}\mathrm{any}\mathrm{i}\in \{0,1,\cdots ,n-2\}.$$

(3)

Assume that S is such a dominating set, that for some i there is a corresponding vertex v with $w(v)-{\ell }_b>2na+2b-n{\ell }_b$ and recall that $w(v)=|S\cap (C_m^i\cup C_m^{i+1})|$.

Let ${\xi }_j=|S\cap (C_m^j\cup C_m^{j+1})|-{\ell }_b$ for each $j\in \{0,1,\dots ,n-2\}$. It is clear ${\xi }_j\ge 0$. Let

$$\xi =\sum _{j=0}^{n-1}{\xi }_j=2|S|-n{\ell }_b.$$

(4)

Since ${\xi }_j\ge 0$ for each j, we have $\xi =2|S|-n{\ell }_b\ge {\xi }_j=|S\cap (C_m^j\cup C_m^{j+1})|-{\ell }_b$. Since $|S\cap (C_m^j\cup C_m^{j+1})|-{\ell }_b>2na+2b-n{\ell }_b$, we have $|S|>na+b$, contradicting Equation (2) (and the minimality of S). Therefore, there is no vertex v of $\mathcal{D}$ with $w(v)-{\ell }_b>2na+2b-n{\ell }_b$ and those vertices can be removed from the auxiliary digraph.

In practice, the procedure ReduceNumberOfVertices reduce the vertices of auxiliary graph dramatically for almost all cases, and we give the following examples:

Example 1.

For $m=10$, let ${\ell }_b=\frac{7n}{2}$. We label the graph $P_2\square C_n$ and the constructed auxiliary digraph has 328362 vertices. By removing unnecessary vertices, the auxiliary digraph can be reduced to 16,575 vertices by letting $(w_1,w_2)\in \{(3,3),(3,4),(4,3),(4,4),(3,5),(5,3),(4,5),(5,4)\}$, where $w_1,w_2$ are the weight restricted to the first and second column of $P_2\square C_{10}$, respectively.

Example 2.

For $m=11$, let ${\ell }_b=4n$. We label the graph $P_2\square C_{11}$ and the constructed auxiliary digraph has 1,169,558 vertices. By removing unnecessary vertices, the auxiliary digraph can be reduced to 2442 vertices by letting $(w_1,w_2)\in \{(4,4),(3,5),(5,3),(3,4),(4,3),(2,4),(4,2)\}$, where $w_1,w_2$ are the weight restricted to the first and second column of $P_2\square C_{11}$, respectively.

We apply Algorithm 1 with the auxiliary graph $\mathcal{D}$ reduced by procedure ReduceNumberOfVertices, and it is carried out on a 2.6-GHz Intel(R) Core(TM) i7-5600U CPU with a memory of 20G. As a result we are able to extend the formulae for $\gamma (C_m\square C_n)$ with m up to 20.

4. Results

The formulae for $\gamma (C_m\square C_n)$ are listed below for $m\le 20$ and arbitrary $n\ge m$. For $m\le 6$ the formulae were proved by Liu, Zhang, Chen, and Meng [11,12]. Shao et al. proved the formulae for $m=7,10$. All these formulae were confirmed by the algorithm described in this paper and furthermore formulae for $m\le 21$ were determined. In particular, the domination numbers of the square torus graphs $C_n\square C_n$ with n up to 31 ($n\not\equiv 0$ (mod 3)) are presented in

Table 1. Exact values of some square torus $C_n\square C_n$.

n	19	20	22	23	25	26	28	29	31
$\gamma (C_n\square C_n)$	127	140	169	184	217	234	271	290	331

, where a dominating set with 290 vertices in $C_{29}\square C_{29}$ is presented in Figure 2 and a dominating set with 331 vertices in $C_{31}\square C_{31}$ is presented in Figure 3, the sets of black vertices stand for the corresponding dominating sets, and the direction of the cycle is top to bottom and left to right.

• $\gamma (C_3\square C_n)=\left\{\begin{array}{cc}n,\hfill & n\equiv 0(\mathrm{mod}3);\hfill \\ n+1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$
• $\gamma (C_4\square C_n)=\left\{\begin{array}{cc}\frac{3n}{2},\hfill & n\equiv 0(\mathrm{mod}8);\hfill \\ n+\lceil \frac{n+1}{2}\rceil ,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$
• $\gamma (C_5\square C_n)=2n$.
• $\gamma (C_6\square C_n)=\left\{\begin{array}{cc}2n,\hfill & n\equiv 0(\mathrm{mod}3);\hfill \\ 2n+2,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$
• $\gamma (C_7\square C_n)=\left\{\begin{array}{cc}\lfloor \frac{5n}{2}\rfloor ,\hfill & n\equiv 0(\mathrm{mod}14);\hfill \\ \lfloor \frac{5n}{2}\rfloor +1,\hfill & n\equiv 3,4,6,8,10,11(\mathrm{mod}14);\hfill \\ \lfloor \frac{5n}{2}\rfloor +2,\hfill & n\equiv 1,2,5,7,9,12,13(\mathrm{mod}14).\hfill \end{array}\right.$
• $\gamma (C_8\square C_n)=3n$.
• $\gamma (C_9\square C_n)=\left\{\begin{array}{cc}3n,\hfill & n\equiv 0(\mathrm{mod}3);\hfill \\ 3n+3,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$
• $\gamma (C_{10}\square C_n)=\left\{\begin{array}{cc}\lfloor \frac{7n}{2}\rfloor ,\hfill & n\equiv 0(\mathrm{mod}20);\hfill \\ \lfloor \frac{7n}{2}\rfloor +1,\hfill & n\equiv 3,6,14,17(\mathrm{mod}20);\hfill \\ \lfloor \frac{7n}{2}\rfloor +2,\hfill & n\equiv 4,7,8,9,10,11,12,13,16(\mathrm{mod}20);\hfill \\ \lfloor \frac{7n}{2}\rfloor +3,\hfill & n\equiv 1,2,5,15,18,19(\mathrm{mod}20).\hfill \end{array}\right.$
• $\gamma (C_{11}\square C_n)=4n$.
• $\gamma (C_{12}\square C_n)=\left\{\begin{array}{cc}4n,\hfill & n\equiv 0(\mathrm{mod}3);\hfill \\ 4n+4,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$
• $\gamma (C_{13}\square C_n)=\left\{\begin{array}{cc}\lfloor \frac{9n}{2}\rfloor ,\hfill & n\equiv 0(\mathrm{mod}26);\hfill \\ \lfloor \frac{9n}{2}\rfloor +1,\hfill & n\equiv 3,6,20,23(\mathrm{mod}26);\hfill \\ \lfloor \frac{9n}{2}\rfloor +2,\hfill & n\equiv 9,10,12,14,16,17(\mathrm{mod}26);\hfill \\ \lfloor \frac{9n}{2}\rfloor +3,\hfill & n\equiv 4,7,8,11,13,15,18,19,22(\mathrm{mod}26);\hfill \\ \lfloor \frac{9n}{2}\rfloor +4,\hfill & n\equiv 1,2,5,21,24,25(\mathrm{mod}26).\hfill \end{array}\right.$
• $\gamma (C_{14}\square C_n)=5n$.
• $\gamma (C_{15}\square C_n)=\left\{\begin{array}{cc}5n,\hfill & n\equiv 0(\mathrm{mod}3);\hfill \\ 5n+5,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$
• $\gamma (C_{16}\square C_n)=\left\{\begin{array}{cc}\lfloor \frac{11n}{2}\rfloor ,\hfill & n\equiv 0(\mathrm{mod}32);\hfill \\ \lfloor \frac{11n}{2}\rfloor +1,\hfill & n\equiv 3,6,26,29(\mathrm{mod}32);\hfill \\ \lfloor \frac{11n}{2}\rfloor +2,\hfill & n\equiv 9,12,20,23(\mathrm{mod}32);\hfill \\ \lfloor \frac{11n}{2}\rfloor +3,\hfill & n\equiv 10,13,14,15,16,17,18,19,22(\mathrm{mod}32);\hfill \\ \lfloor \frac{11n}{2}\rfloor +4,\hfill & n\equiv 4,7,8,11,21,24,25,28(\mathrm{mod}32);\hfill \\ \lfloor \frac{11n}{2}\rfloor +5,\hfill & n\equiv 1,2,5,27,30,31(\mathrm{mod}32).\hfill \end{array}\right.$
• $\gamma (C_{17}\square C_n)=6n$.
• $\gamma (C_{18}\square C_n)=\left\{\begin{array}{cc}6n,\hfill & n\equiv 0(\mathrm{mod}3);\hfill \\ 6n+6,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$
• $\gamma (C_{19}\square C_n)=\left\{\begin{array}{cc}\lfloor \frac{11n}{2}\rfloor ,\hfill & n\equiv 0(\mathrm{mod}38);\hfill \\ \lfloor \frac{11n}{2}\rfloor +1,\hfill & n\equiv 3,6,32,35(\mathrm{mod}38);\hfill \\ \lfloor \frac{11n}{2}\rfloor +2,\hfill & n\equiv 9,12,26,29(\mathrm{mod}38);\hfill \\ \lfloor \frac{11n}{2}\rfloor +3,\hfill & n\equiv 15,16,18,20,22,23(\mathrm{mod}38);\hfill \\ \lfloor \frac{11n}{2}\rfloor +4,\hfill & n\equiv 10,13,14,17,19,21,24,25,28(\mathrm{mod}38);\hfill \\ \lfloor \frac{11n}{2}\rfloor +5,\hfill & n\equiv 4,8,11,34(\mathrm{mod}38);\hfill \\ \lfloor \frac{11n}{2}\rfloor +6,\hfill & n\equiv 1,2,5,33,36,37(\mathrm{mod}38).\hfill \end{array}\right.$
• $\gamma (C_{20}\square C_n)=7n$.
• $\gamma (C_{21}\square C_n)=\left\{\begin{array}{cc}7n,\hfill & n\equiv 0(\mathrm{mod}3);\hfill \\ 7n+7,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$