Convergence Theorems for Modified Inertial Viscosity Splitting Methods in Banach Spaces

Abstract

In this article, we study a modified viscosity splitting method combined with inertial extrapolation for accretive operators in Banach spaces and then establish a strong convergence theorem for such iterations under some suitable assumptions on the sequences of parameters. As an application, we extend our main results to solve the convex minimization problem. Moreover, the numerical experiments are presented to support the feasibility and efficiency of the proposed method.

1. Introduction

Throughout this paper, we let E be a real Banach space with norm $\parallel .\parallel$ and $E^{*}$ be its dual space. The normalized duality mapping J from E into $2^{E^{*}}$ is defined by the following equation:

$$J\left(x\right)=\{f\in E^{*}:⟨x,f⟩=\parallel f\parallel \parallel x\parallel =\parallel x{\parallel }^2\}\forall x\in E.$$

we denote the generalized duality pairing between E and $E^{*}$ by $⟨.,.⟩$ and the single-valued duality mapping by j.

The inclusion problem is to find $x\in E$ such that

$$0\in (A+B)x$$

where $A:E\to E$ is an operator and $B:E\to 2^E$ is a set-valued operator. Please note that on the one hand, this problem takes into account some special cases, such as variational inequalities, convex programming, minimization problem, and split feasibility problem [1,2,3]. On the other hand, as an important branch of nonlinear functional analysis and optimization theory, it has been studied numerous times in the literature to solve the real-world problem, such as machine learning, image reconstruction, and signal processing; see [4,5,6,7] and the references therein.

In 2012, Takashashi et al. [8] studied a Halpern-type iterative method for an $\alpha$-inverse strongly monotone mapping A and a maximal monotone operator B in a Hilbert space as follows:

$$x_{n+1}={\beta }_n{x}_n+(1-{\beta }_n)({\alpha }_{n}u+(1-{\alpha }_n)J_{r_n}^B(x_n-r_{n}A{x}_n)),$$

under certain conditions, the algorithm was showed to converge strongly to a solution of $A+B$. Furthermore, Lopez et al. [9] introduced the following method for accretive operators:

$$x_{n+1}={\alpha }_{n}u+(1-{\alpha }_n)(J_{r_n}^B(x_n-r_n(A{x}_n+a_n))+b_n),$$

they studied strong convergence theorems for Halpern-type splitting methods in Banach spaces. In 2016, Pholasa et al. [10] extended the above results [8,9] and studied the modified forward-backward splitting methods in Banach spaces:

$$x_{n+1}={\beta }_n{x}_n+(1-{\beta }_n)({\alpha }_{n}u+(1-{\alpha }_n)J_{r_n}^B(x_n-r_{n}A{x}_n)),$$

it was proved that $x_n$ converges strongly to a point $z=Q\left(u\right)$ under some mild conditions, where Q is the sunny nonexpansive retraction.

Inertial extrapolation is an important technique to speed up the convergence rate [11,12,13,14]. Recently, the fast-iterative algorithms by using inertial extrapolation studied by some authors [15,16,17]. For instance, in 2003, Moudafi et al. [18] studied the following inertial proximal point algorithm of a maximal monotone operator:

$$\left\{\begin{array}{cc}\hfill y_n& =x_n+{\theta }_n(x_n-x_{n-1}),\hfill \\ \hfill x_{n+1}& ={(I+{\lambda }_{n}T)}^{-1}\left(y_n\right).\hfill \end{array}\right.$$

If ${\lambda }_n$ is non-decreasing and ${\theta }_n\in [0,1)$ is chosen such that

$$\sum _{n=1}^{\infty }{\theta }_n{\parallel x_n-x_{n-1}\parallel }^2<\infty ,$$

then $x_n$ converges to a zero point of T. In 2015, Lorenz et al. [19] applied inertial extrapolation technique to forward-backward algorithm for monotone operators in Hilbert spaces. They proved that the iterative process defined by

$$\left\{\begin{array}{cc}\hfill y_n& =x_n+{\theta }_n(x_n-x_{n-1}),\hfill \\ \hfill x_{n+1}& ={(I+r_{n}B)}^{-1}(y_n-r_{n}A{y}_n).\hfill \end{array}\right.$$

converges weakly to a solution of the inclusion $0\in (A+B)\left(x\right)$. In 2018, Cholamjiak et al. [20] proposed a Halpern-type inertial iterative method for monotone operators in Hilbert spaces and they proved the strong convergence of the algorithm.

Inspired and motivated by the above-mentioned works, we apply inertial extrapolation algorithms and viscosity approximation to give an extension, and then we study a modified splitting method for accretive operators in Banach spaces. The strong convergence theorems for such iterations are established and some applications including the numerical experiments are presented to support our main theorem.

2. Preliminaries

Recall that a Banach space E is said to be uniformly convex if for any $ϵ\in (0,2]$, there exists a $\delta ={\delta }_E\left(ϵ\right)>0$ such that $x,y\in E$ with $\parallel x\parallel =\parallel y\parallel =1$, and $\parallel x-y\parallel \ge ϵ$, then $\parallel x+y\parallel /2\le 1-\delta$. We denote the modulus of smoothness ${\rho }_E:R^{+}\to R^{+}$ of E as follows:

$${\rho }_E\left(t\right)=sup\{\frac{\parallel x+ty\parallel +\parallel x-ty\parallel }{2}-1:\parallel x\parallel =1,\parallel y\parallel =1\},$$

for $1<q\le 2$, a Banach space E is said to be q-uniformly smooth if there exists a constant $c_q>0$ such that ${\rho }_E\left(t\right)\le c_q{t}^q,t>0$. E is said to be uniformly smooth if ${lim}_{n\to \infty }{\rho }_E\left(t\right)/t=0$. It is obvious that q-uniformly smooth Banach space must be uniformly smooth and E is uniformly smooth if and only if the norm of E is uniformly Fréchet differentiable.

Let I be the identity operator. We denote by $D\left(A\right)=\{z\in E:Az\ne \varnothing \}$, $R\left(A\right)=\bigcup \{Az:z\in D(A\left)\right\}$ the domain and range of an operator $A\subset E\times E$, respectively. A is called accretive if for each $x,y\in D\left(A\right)$, there exists $j(x-y)\in J(x-y)$ such that

$$⟨u-v,j(x-y)⟩\ge 0,\forall u\in Ax,v\in Ay.$$

An accretive operator A is called $\alpha$-inverse strongly accretive, if for each $x,y\in D\left(A\right)$, there exists $j(x-y)\in J(x-y)$ such that

$$⟨u-v,j(x-y)⟩\ge {\alpha \parallel u-v\parallel }^2,\forall u\in Ax,v\in Ay.$$

It is well-known that an accretive operator A is m-accretive if $R(I+rA)=E$ for all $r>$0. If A is an accretive operator which satisfies the range condition, then, for each $r>0$, the mapping $J_r^A:R(I+rA)\to D\left(A\right)$ is defined by $J_r^A={(I+rA)}^{-1}$, which is called the resolvent operator of A.

Let C be a nonempty, closed and convex subset of E, and let D be a nonempty subset of C. A mapping $T:C\to D$ is called a retraction of C onto D, if for all $x\in D$, there is $Tx=x$. We called T is sunny if T has the following property: $T(tx+(1-t\left)Tx\right)=Tx$ for each $x\in C$ and $t\ge 0$ whenever $tx+(1-t)Tx\in C$. It is known that a sunny nonexpansive retraction is a sunny retraction which is also nonexpansive.

The following lemmas are needed to prove our results.

Lemma 1

([21]).Let E be a smooth Banach space. Then the following inequality holds:

$${\parallel x+y\parallel }^2\le {\parallel x\parallel }^2+2⟨y,j(x+y)⟩,\forall x,y\in E.$$

Lemma 2

([22]).For any $r>0$, give $0<s\le r$ and $x\in E$, if

$$T_r:=J_r^B(I-rA)={(I+rB)}^{-1}(I-rA)$$

then $Fix\left(T_r\right)={(A+B)}^{-1}\left(0\right)$. In addition, there holds the relation

$$\parallel x-T_{s}x\parallel \le 2\parallel x-T_{r}x\parallel .$$

Lemma 3

([23]).If a Banach space E is uniformly smooth, then the duality mapping J is single valued and norm-to-norm uniformly continuous on each bounded subset of E.

Lemma 4

([21]).Let E be a uniformly smooth Banach space and $T:C\to C$ be a nonexpansive mapping with a fixed point. Let $f:C\to C$ be a contraction with coefficient $\rho \in (0,1)$ and $t\in (0,1)$, the unique fixed point $x_t\in C$ of the contraction $C\ni x\mapsto tf\left(x\right)+(1-t)Tx$ converges strongly as $t\to 0$ to a fixed point of T. Define a mapping $Q:C\to D$ by $Qu=s-{lim}_{t\to 0}{x}_t$. Then Q is the unique sunny nonexpansive retract from C onto D.

Lemma 5

([24]).Assume $\left\{a_n\right\}\subset R^{+}$, $\left\{{\delta }_n\right\}\subset (0,1)$ and $\left\{b_n\right\}\subset R$ be the sequences such that

$$a_{n+1}\le (1-{\delta }_n)a_n+b_n,n\ge 0,$$

(i) If ${\mathsf{\Sigma }}_{n=0}^{\infty }{\delta }_n=\infty$; (ii) $limsu{p}_{n\to \infty }\frac{b_n}{{\delta }_n}\le 0or{\mathsf{\Sigma }}_{n=1}^{\infty }\left|b_n\right|<\infty$; then $li{m}_{n\to \infty }{a}_n=0$.

Lemma 6

([25]).Assume $\left\{s_n\right\}$ is a sequence of nonnegative real numbers such that

$$s_{n+1}\le (1-{\gamma }_n)s_n+{\gamma }_n{\tau }_n,n\ge 1,$$

$$s_{n+1}\le s_n-{\eta }_n+d_n,n\ge 1,$$

where $\left\{{\gamma }_n\right\}$ is a sequence in $(0,1)$, $\left\{{\eta }_n\right\}$ is a sequence of nonnegative real numbers and $\left\{{\tau }_n\right\}$, $\left\{d_n\right\}$ are real sequences such that

(i) 

${\mathsf{\Sigma }}_{n=0}^{\infty }{\gamma }_n=\infty$,

(ii) 

${lim}_{n\to \infty }{d}_n=0$,

(iii) 

${lim}_{k\to \infty }{\eta }_{n_k}=0$ implies ${lim\; sup}_{k\to \infty }{\tau }_{n_k}\le 0$ for any subsequence $\left\{n_k\right\}\subset \left\{n\right\}$.

Then ${lim}_{n\to \infty }{s}_n=0$.

Lemma 7

([26]).Let A be a single-valued α-isa in a real uniformly convex Banach space with Fréchet differentiable norm. Then, for all $x,y\in E$ and given $s>0$, there exists a continuous, strictly increasing and convex function $\Phi :R^{+}\to R^{+}$ with $\Phi \left(0\right)=0$ such that

$$\parallel T_{r}x-T_r{y\parallel }^2\le {\parallel x-y\parallel }^2{-r(2\alpha -rk)\parallel Ax-Ay\parallel }^2-\Phi (\parallel (I-J_r^B)(I-rA)x-(I-J_r^B)(I-rA)y\parallel )$$

where k is the uniform smoothness coefficient of E.

Lemma 8

([27]).Let E be a uniformly convex Banach space. Then, for all $x,y\in E$ and $t\in [0,1]$, there exists a convex continuous and strictly increasing function $g:[0,\infty )\to [0,\infty )$ with $g\left(0\right)=0$ such that

$${\parallel tx+(1-t)y\parallel }^2\le {t\parallel x\parallel }^2+{(1-t)\parallel y\parallel }^2-t(1-t)g(\parallel x-y\parallel ).$$

3. Main Results

Theorem 1.

Let E be a uniformly convex and uniformly smooth Banach space. Let $A:E\to E$ be an α-inverse-strongly accretive mapping and $B:E\to 2^E$ be an m-accretive operator. Assume that $\Omega ={(A+B)}^{-1}\left(0\right)\ne \varnothing$. Let $f:E\to E$ be a contraction with coefficient $\rho \in [0,1)$ and $\left\{{\beta }_n\right\}\subset (0,1)$, $\left\{{\alpha }_n\right\}$, $\left\{{\delta }_n\right\}$ be real number sequences in $[0,1)$ and $r_n\subset (0,+\infty )$. Define a sequence $\left\{x_n\right\}$ in E as follows:

$$\left\{\begin{array}{cc}\hfill w_n& =x_n+{\alpha }_n(x_n-x_{n-1}),\hfill \\ \hfill y_n& ={\delta }_n{w}_n+(1-{\delta }_n)J_{r_n}^B(w_n-r_{n}A{w}_n),\hfill \\ \hfill x_{n+1}& ={\beta }_{n}f\left(x_n\right)+(1-{\beta }_n)y_n.\hfill \end{array}\right.$$

(1)

for all $n\in N$, where $x_0,x_1\in E$ and $J_{r_n}^B={(I+r_{n}B)}^{-1}$. Assume that the following conditions hold:

$$\begin{array}{c}\left(i\right)\sum _{n=1}^{\infty }{\alpha }_n\parallel x_n-x_{n-1}\parallel <\infty ;\hfill \\ \left(ii\right)\underset{n\to \infty }{lim}{\beta }_n=0,\sum _{n=1}^{\infty }{\beta }_n=\infty ;\hfill \\ \left(iii\right)0<\underset{n\to \infty }{lim\; inf}{r}_n<\underset{n\to \infty }{lim\; sup}{r}_n<\frac{2\alpha }{k};\hfill \\ \left(iv\right)\underset{n\to \infty }{lim\; sup}{\delta }_n<1.\hfill \end{array}$$

Then the sequence $\left\{x_n\right\}$ converges strongly to $z=Q\left(f\right(z\left)\right)$, where Q is the sunny nonexpansive retraction of E onto Ω.

Proof. 

Let $T_n=J_{r_n}^B(I-r_{n}A)$, $z=Q\left(f\right)$. Then, we have

$$\begin{array}{cc}\hfill \parallel y_n-z\parallel & =\parallel {\delta }_n{w}_n+(1-{\delta }_n)T_n{w}_n-z\parallel \hfill \\ & \le {\delta }_n\parallel w_n-z\parallel +(1-{\delta }_n)\parallel T_n{w}_n-z\parallel \hfill \\ & \le {\delta }_n\parallel w_n-z\parallel +(1-{\delta }_n)\parallel w_n-z\parallel \hfill \\ & \le \parallel w_n-z\parallel \hfill \\ & \le \parallel x_n+{\alpha }_n(x_n-x_{n-1})-z\parallel \hfill \\ & \le \parallel x_n-z\parallel +{\alpha }_n\parallel (x_n-x_{n-1})\parallel .\hfill \end{array}$$

In view of Lemma 2, we have

$$\begin{array}{cc}\hfill \parallel x_{n+1}-z\parallel & =\parallel {\beta }_{n}f\left(x_n\right)+(1-{\beta }_n)y_n-z\parallel \hfill \\ & \le {\beta }_n\parallel f\left(x_n\right)-z\parallel +(1-{\beta }_n)\parallel y_n-z\parallel \hfill \\ & \le {\beta }_n\parallel f\left(x_n\right)-f\left(z\right)\parallel +{\beta }_n\parallel f\left(z\right)-z\parallel +(1-{\beta }_n)\parallel y_n-z\parallel \hfill \\ & \le {\beta }_n\rho \parallel x_n-z\parallel +{\beta }_n\parallel f\left(z\right)-z\parallel +(1-{\beta }_n)(\parallel x_n-z\parallel +{\alpha }_n\parallel (x_n-x_{n-1})\parallel )\hfill \\ & =[1-{\beta }_n(1-\rho )]\parallel x_n-z\parallel +{\beta }_n\parallel f\left(z\right)-z\parallel +(1-{\beta }_n){\alpha }_n\parallel (x_n-x_{n-1})\parallel .\hfill \end{array}$$

From the restriction and Lemma 5, we find that $\left\{x_n\right\}$ is bounded. Hence $\left\{w_n\right\}$, $\left\{y_n\right\}$ are also bounded.

Using the inequality in Lemma 1 and Lemma 8 , we find that

$$\begin{array}{cc}\hfill \parallel w_n{-z\parallel }^2& =\parallel x_n+{\alpha }_n(x_n-x_{n-1}){-z\parallel }^2\hfill \\ & \le \parallel x_n{-z\parallel }^2+2{\alpha }_n⟨x_n-x_{n-1},j(w_n-z)⟩,\hfill \end{array}$$

(2)

and

$$\begin{array}{cc}\hfill \parallel x_{n+1}{-z\parallel }^2& =\parallel {\beta }_{n}f\left(x_n\right)+(1-{\beta }_n)y_n{-z\parallel }^2\hfill \\ & =\parallel {\beta }_n(f\left(x_n\right)-f\left(z\right))+(1-{\beta }_n)(y_n-z)+{\beta }_n(f\left(z\right)-z){\parallel }^2\hfill \\ & \le \parallel {\beta }_n(f\left(x_n\right)-f\left(z\right))+(1-{\beta }_n)(y_n-z){\parallel }^2+2{\beta }_n⟨f\left(z\right)-z,j(x_{n+1}-z)⟩\hfill \\ & \le {\beta }_n\parallel f\left(x_n\right)-f\left(z\right){\parallel }^2+(1-{\beta }_n){\parallel y_n-z\parallel }^2\hfill \\ & -{\beta }_n(1-{\beta }_n)g(\parallel (f\left(x_n\right)-f\left(z\right))-(y_n-z)\parallel )+2{\beta }_n⟨f\left(z\right)-z,j(x_{n+1}-z)⟩\hfill \\ & \le {\beta }_n{\rho }^2\parallel x_n{-z\parallel }^2+(1-{\beta }_n){\parallel y_n-z\parallel }^2+2{\beta }_n⟨f\left(z\right)-z,j(x_{n+1}-z)⟩.\hfill \end{array}$$

(3)

In view of Lemmas 7 and 8, we get

$$\begin{array}{cc}\hfill \parallel y_n{-z\parallel }^2& =\parallel {\delta }_n{w}_n+(1-{\delta }_n)T_n{w}_n{-z\parallel }^2\hfill \\ & \le {\delta }_n\parallel w_n{-z\parallel }^2+(1-{\delta }_n){\parallel T_n{w}_n-z\parallel }^2\hfill \\ & \le {\delta }_n\parallel w_n{-z\parallel }^2+(1-{\delta }_n)[\parallel w_n{-z\parallel }^2\hfill \\ & -r_n(2\alpha -r_{n}k)\parallel A{w}_n{-Az\parallel }^2-\Phi (\parallel (I-J_{r_n}^B)(I-r_{n}A)w_n-(I-J_{r_n}^B)(I-r_{n}A)z\parallel \left)\right]\hfill \\ & =\parallel w_n{-z\parallel }^2-(1-{\delta }_n)r_n(2\alpha -r_{n}k){\parallel A{w}_n-Az\parallel }^2\hfill \\ & -(1-{\delta }_n)\Phi (\parallel w_n-r_{n}A{w}_n-T_n{w}_n+r_{n}Az\parallel ).\hfill \end{array}$$

(4)

Substitute (2), (4) into (3), we get

$$\begin{array}{cc}\hfill \parallel x_{n+1}{-z\parallel }^2& \le {\beta }_n{\rho }^2{\parallel x_n-z\parallel }^2+2{\beta }_n⟨f\left(z\right)-z,j(x_{n+1}-z)⟩\hfill \\ & +(1-{\beta }_n)\parallel w_n{-z\parallel }^2-(1-{\beta }_n)(1-{\delta }_n)r_n(2\alpha -r_{n}k){\parallel A{w}_n-Az\parallel }^2\hfill \\ & -(1-{\beta }_n)(1-{\delta }_n)\Phi (\parallel w_n-r_{n}A{w}_n-T_n{w}_n+r_{n}Az\parallel )\hfill \\ & \le {\beta }_n{\rho }^2\parallel x_n{-z\parallel }^2+2{\beta }_n⟨f\left(z\right)-z,j(x_{n+1}-z)⟩+(1-{\beta }_n){\parallel x_n-z\parallel }^2\hfill \\ & +2(1-{\beta }_n){\alpha }_n⟨x_n-x_{n-1},j(w_n-z)⟩-(1-{\beta }_n)(1-{\delta }_n)r_n(2\alpha -r_{n}k){\parallel A{w}_n-Az\parallel }^2\hfill \\ & -(1-{\beta }_n)(1-{\delta }_n)\Phi (\parallel w_n-r_{n}A{w}_n-T_n{w}_n+r_{n}Az\parallel )\hfill \\ & =(1-{\beta }_n(1-{\rho }^2)){\parallel x_n-z\parallel }^2+2{\beta }_n⟨f\left(z\right)-z,j(x_{n+1}-z)⟩\hfill \\ & +2(1-{\beta }_n){\alpha }_n⟨x_n-x_{n-1},j(w_n-z)⟩-(1-{\beta }_n)(1-{\delta }_n)r_n(2\alpha -r_{n}k){\parallel A{w}_n-Az\parallel }^2\hfill \\ & -(1-{\beta }_n)(1-{\delta }_n)\Phi (\parallel w_n-r_{n}A{w}_n-T_n{w}_n+r_{n}Az\parallel ).\hfill \end{array}$$

(5)

We can check that ${\beta }_n(1-{\rho }^2)$ is in $(0,1)$, by the condition $\left(iii\right)$, we can show that $(1-{\beta }_n)(1-{\delta }_n)r_n(2\alpha -r_{n}k)$ is positive. Then, we have

$$\begin{array}{cc}\hfill \parallel x_{n+1}{-z\parallel }^2& \le (1-{\beta }_n(1-{\rho }^2)){\parallel x_n-z\parallel }^2+2{\beta }_n⟨f\left(z\right)-z,j(x_{n+1}-z)⟩\hfill \\ & +2(1-{\beta }_n){\alpha }_n⟨x_n-x_{n-1},j(w_n-z)⟩,\hfill \end{array}$$

(6)

and

$$\begin{array}{cc}\hfill \parallel x_{n+1}{-z\parallel }^2& \le \parallel x_n{-z\parallel }^2-(1-{\beta }_n)(1-{\delta }_n)r_n(2\alpha -r_{n}k){\parallel A{w}_n-Az\parallel }^2\hfill \\ & -(1-{\beta }_n)(1-{\delta }_n)\Phi (\parallel w_n-r_{n}A{w}_n-T_n{w}_n+r_{n}Az\parallel )\hfill \\ & +2{\beta }_n⟨f\left(z\right)-z,j(x_{n+1}-z)⟩+2(1-{\beta }_n){\alpha }_n⟨x_n-x_{n-1},j(w_n-z)⟩.\hfill \end{array}$$

(7)

For each $n\ge 1$, let

$$\begin{array}{c}{s}_n={\parallel x_n-z\parallel }^2,{\gamma }_n={\beta }_n(1-{\rho }^2),\hfill \\ {\tau }_n=\frac{2}{1-{\rho }^2}⟨f\left(z\right)-z,j(x_{n+1}-z)⟩+\frac{2{\alpha }_n(1-{\beta }_n)}{{\beta }_n(1-{\rho }^2)}⟨x_n-x_{n-1},j(w_n-z)⟩,\hfill \\ {\eta }_n=(1-{\beta }_n)(1-{\delta }_n)r_n(2\alpha -r_{n}k){\parallel A{w}_n-Az\parallel }^2\hfill \\ +(1-{\beta }_n)(1-{\delta }_n)\Phi (\parallel w_n-r_{n}A{w}_n-T_n{w}_n+r_{n}Az\parallel ),\hfill \\ d_n=2{\beta }_n⟨f\left(z\right)-z,j(x_{n+1}-z)⟩+2(1-{\beta }_n){\alpha }_n⟨x_n-x_{n-1},j(w_n-z)⟩.\hfill \end{array}$$

(8)

we find from (6), (7) that

$$\begin{array}{c}\hfill s_{n+1}\le (1-{\gamma }_n)s_n+{\gamma }_n{\tau }_n,\end{array}$$

and also

$$\begin{array}{c}\hfill s_{n+1}\le s_n-{\eta }_n+d_n.\end{array}$$

Notice that ${\sum }_{n=1}^{\infty }{\beta }_n=\infty$, we see that ${\sum }_{n=1}^{\infty }{\gamma }_n=\infty$. By the boundedness of $\left\{w_n\right\}$, $\left\{x_n\right\}$ and the restriction ${lim}_{n\to \infty }{\beta }_n=0$, implies that ${lim}_{n\to \infty }{d}_n=0$.

On the other hand, using Lemma 6, it remains to show that ${lim}_{k\to \infty }{\eta }_{n_k}=0$ implies ${lim\; sup}_{k\to \infty }{\tau }_{n_k}\le 0$, for any subsequence $\left\{n_k\right\}\subset \left\{n\right\}$. Let ${\eta }_{n_k}$ be a subsequence of ${\eta }_n$ such that ${lim}_{k\to \infty }{\eta }_{n_k}=0$. It follows from the restrictions and the property of $\varphi$, we derive from (8) the following

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}\parallel A{w}_{n_k}-Az\parallel =0=\underset{k\to \infty }{lim}\parallel w_{n_k}-r_{n_k}A{w}_{n_k}-T_{n_k}{w}_{n_k}+r_{n_k}Az\parallel =0.\end{array}$$

By the triangle inequality, it turns out that

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}\parallel T_{n_k}{w}_{n_k}-w_{n_k}\parallel =0.\end{array}$$

and moreover, since $0<{lim\; inf}_{n\to \infty }{r}_n$, there exists $ϵ>0$, such that $r_n\ge ϵ$ for all $n>0$, in view of the inequality in Lemma 2, we have

$$\begin{array}{c}\hfill \parallel T_{ϵ}{w}_{n_k}-w_{n_k}\parallel \le 2\parallel T_{n_k}{w}_{n_k}-w_{n_k}\parallel .\end{array}$$

It turns out that

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim\; sup}\parallel T_{ϵ}{w}_{n_k}-w_{n_k}\parallel \le 0.\end{array}$$

Therefore, we can get

$$\begin{array}{c}\hfill \parallel T_{ϵ}{w}_{n_k}-w_{n_k}\parallel =0.\end{array}$$

(9)

Please note that

$$\begin{array}{cc}\hfill \parallel T_{ϵ}{w}_{n_k}-x_{n_k}\parallel & \le \parallel T_{ϵ}{w}_{n_k}-w_{n_k}\parallel +\parallel w_{n_k}-x_{n_k}\parallel \hfill \\ & \le \parallel T_{ϵ}{w}_{n_k}-w_{n_k}\parallel +{\alpha }_n\parallel x_{n_k}-x_{n_k-1}\parallel \hfill \end{array}$$

We get from condition $\left(i\right)$ and (9) that

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}\parallel T_{ϵ}{w}_{n_k}-x_{n_k}\parallel =0.\end{array}$$

(10)

Put $z_t=tf\left(z_t\right)+(1-t)T_{ϵ}{z}_t$ for any $t\in (0,1)$. Apply Lemma 4, we get $z_t\to Q\left(f\right)=z,t\to 0$. Then we have

$$\begin{array}{cc}\hfill \parallel z_t-x_{n_k}{\parallel }^2& =\parallel tf\left(z_t\right)+(1-t)T_{ϵ}{z}_t-x_{n_k}{\parallel }^2\hfill \\ & =\parallel t(f\left(z_t\right)-x_{n_k})+(1-t)(T_{ϵ}{z}_t-x_{n_k}){\parallel }^2\hfill \\ & \le {(1-t)}^2{\parallel T_{ϵ}{z}_t-x_{n_k}\parallel }^2+2t⟨f\left(z_t\right)-x_{n_k},j(z_t-x_{n_k})⟩\hfill \\ & ={(1-t)}^2{\parallel T_{ϵ}{z}_t-x_{n_k}\parallel }^2+2t⟨f\left(z_t\right)-z_t,j(z_t-x_{n_k})⟩+2t⟨z_t-x_{n_k},j(z_t-x_{n_k})⟩\hfill \\ & \le {(1-t)}^2(\parallel T_{ϵ}{z}_t-T_{ϵ}{w}_{n_k}\parallel +\parallel T_{ϵ}{w}_{n_k}-x_{n_k}{\parallel )}^2\hfill \\ & +2t⟨f\left(z_t\right)-z_t,j(z_t-x_{n_k})⟩+2t⟨z_t-x_{n_k},j(z_t-x_{n_k})⟩\hfill \\ & \le {(1-t)}^2(\parallel z_t-w_{n_k}\parallel +\parallel T_{ϵ}{w}_{n_k}-x_{n_k}{\parallel )}^2\hfill \\ & +2t⟨f\left(z_t\right)-z_t,j(z_t-x_{n_k})⟩+2t{\parallel z_t-x_{n_k}\parallel }^2\hfill \\ & \le {(1-t)}^2(\parallel z_t-x_{n_k}\parallel +{\alpha }_n\parallel x_{n_k}-x_{n_k-1}\parallel +\parallel T_{ϵ}{w}_{n_k}-x_{n_k}{\parallel )}^2\hfill \\ & +2t⟨f\left(z_t\right)-z_t,j(z_t-x_{n_k})⟩+2t{\parallel z_t-x_{n_k}\parallel }^2\hfill \end{array}$$

This implies that

$$\begin{array}{cc}\hfill ⟨z_t-f\left(z_t\right),j(z_t-x_{n_k})⟩& \le \frac{{(1-t)}^2}{2t}(\parallel z_t-x_{n_k}\parallel +{\alpha }_n\parallel x_{n_k}-x_{n_k-1}\parallel \hfill \\ & +\parallel T_{ϵ}{w}_{n_k}-x_{n_k}{\parallel )}^2+\frac{2t-1}{2t}{\parallel z_t-x_{n_k}\parallel }^2.\hfill \end{array}$$

(11)

From (10), (11) we obtain

$$\begin{array}{cc}\hfill \underset{k\to \infty }{lim\; sup}⟨z_t-f\left(z_t\right),j(z_t-x_{n_k})⟩& \le \frac{{(1-t)}^2}{2t}{M}^2++\frac{2t-1}{2t}{M}^2\hfill \\ & =\frac{t}{2}{M}^2\to 0,ast\to 0,\hfill \end{array}$$

(12)

for some $M>0$ large enough. Since the duality mapping J is norm-to-norm uniformly continuous on bounded sets of E, we see that $\parallel j(z_t-x_{n_k})-j(z-x_{n_k})\parallel \to 0,t\to 0$. Then, we have that

$$\begin{array}{c}\parallel ⟨z_t-f\left(z_t\right),j(z_t-x_{n_k})⟩-⟨z-f\left(z_t\right),j(z-x_{n_k})⟩\parallel \hfill \\ =\parallel ⟨z_t-z+z-f\left(z_t\right),j(z_t-x_{n_k})⟩-⟨z-f\left(z_t\right),j(z-x_{n_k})⟩\parallel \hfill \\ \le \parallel ⟨z_t-z,j(z_t-x_{n_k})⟩\parallel +\parallel ⟨z-f\left(z_t\right),j(z_t-x_{n_k})⟩-⟨z-f\left(z_t\right),j(z-x_{n_k})⟩\parallel \hfill \\ \le \parallel z_t-z\parallel \parallel z_t-x_{n_k}\parallel +\parallel z-f\left(z_t\right)\parallel \parallel j(z_t-x_{n_k})-j(z-x_{n_k})\parallel \hfill \end{array}$$

(13)

From (12), (13) and let $t\to 0$, we get that

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim\; sup}⟨z-f\left(z\right),j(z-x_{n_k})⟩\le 0.\end{array}$$

(14)

On the other hand, we have

$$\begin{array}{c}\parallel y_{n_k}-x_{n_k}\parallel \hfill \\ =\parallel {\delta }_{n_k}{w}_{n_k}+(1-{\delta }_{n_k})T_{n_k}{w}_{n_k}-x_{n_k}\parallel \hfill \\ \le {\delta }_{n_k}\parallel w_{n_k}-x_{n_k}\parallel +(1-{\delta }_{n_k})\parallel T_{n_k}{w}_{n_k}-x_{n_k}\parallel \hfill \\ \le {\delta }_{n_k}\parallel w_{n_k}-x_{n_k}\parallel +(1-{\delta }_{n_k})\parallel T_{n_k}{w}_{n_k}-w_{n_k}\parallel +(1-{\delta }_{n_k})\parallel w_{n_k}-x_{n_k}\parallel \hfill \\ =\parallel w_{n_k}-x_{n_k}\parallel +(1-{\delta }_{n_k})\parallel T_{n_k}{w}_{n_k}-w_{n_k}\parallel \hfill \\ \le {\alpha }_{n_k}\parallel x_{n_k}-x_{n_{k-1}}\parallel +(1-{\delta }_{n_k})\parallel T_{n_k}{w}_{n_k}-w_{n_k}\parallel \hfill \end{array}$$

$$\begin{array}{c}\parallel x_{n_k+1}-x_{n_k}\parallel \hfill \\ =\parallel {\beta }_{n_k}f\left(x_{n_k}\right)+(1-{\beta }_{n_k})y_{n_k}-x_{n_k}\parallel \hfill \\ \le {\beta }_{n_k}\parallel f\left(x_{n_k}\right)-x_{n_k}\parallel +(1-{\beta }_{n_k})\parallel y_{n_k}-x_{n_k}\parallel \hfill \\ \le {\beta }_{n_k}\parallel f\left(x_{n_k}\right)-f\left(z\right)\parallel +{\beta }_{n_k}\parallel f\left(z\right)-x_{n_k}\parallel +(1-{\beta }_{n_k})\parallel y_{n_k}-x_{n_k}\parallel \hfill \\ \le {\beta }_{n_k}\parallel f\left(x_{n_k}\right)-f\left(z\right)\parallel +{\beta }_{n_k}\parallel f\left(z\right)-x_{n_k}\parallel \hfill \\ +(1-{\beta }_{n_k}){\alpha }_{n_k}\parallel x_{n_k}-x_{n_{k-1}}\parallel +(1-{\beta }_{n_k})(1-{\delta }_{n_k})\parallel T_{n_k}{w}_{n_k}-w_{n_k}\parallel \hfill \end{array}$$

From condition $\left(i\right)$,$\left(ii\right)$ and (9), we have

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel x_{n_k+1}-x_{n_k}\parallel =0.\end{array}$$

(15)

From (14) and (15), we obtain

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim\; sup}⟨z-f\left(z\right),j(z-x_{n_k+1})⟩\le 0.\end{array}$$

This implies that ${lim\; sup}_{k\to \infty }{\tau }_{n_k}\le 0$ that means by Lemma 6, we get ${lim}_{n\to \infty }{s}_n=0$. Hence, we see that $x_n\to z,n\to \infty$. This finishes the proof. □

Corollary 1.

Let E be a uniformly convex and uniformly smooth Banach space. Let $A:E\to E$ be an α-inverse-strongly accretive mapping and $B:E\to 2^E$ be an m-accretive operator. Assume that $\Omega ={(A+B)}^{-1}\left(0\right)\ne \varnothing$. Let $\left\{{\beta }_n\right\}\subset (0,1)$, $\left\{{\alpha }_n\right\}$, $\left\{{\delta }_n\right\}$ be real number sequences in $[0,1)$ and $r_n\subset (0,+\infty )$. Define a sequence $\left\{x_n\right\}$ in E as follows:

$$\left\{\begin{array}{cc}\hfill w_n& =x_n+{\alpha }_n(x_n-x_{n-1}),\hfill \\ \hfill y_n& ={\delta }_n{w}_n+(1-{\delta }_n)J_{r_n}^B(w_n-r_{n}A{w}_n),\hfill \\ \hfill x_{n+1}& ={\beta }_{n}u+(1-{\beta }_n)y_n.\hfill \end{array}\right.$$

for all $n\in N$, where $u,x_0,x_1\in E$ and $J_{r_n}^B={(I+r_{n}B)}^{-1}$. Assume that the following conditions hold:

$$\begin{array}{c}\left(i\right)\sum _{n=1}^{\infty }{\alpha }_n\parallel x_n-x_{n-1}\parallel <\infty ;\left(ii\right)\underset{n\to \infty }{lim}{\beta }_n=0,\sum _{n=1}^{\infty }{\beta }_n=\infty ;\hfill \\ \left(iii\right)0<\underset{n\to \infty }{lim\; inf}{r}_n<\underset{n\to \infty }{lim\; sup}{r}_n<\frac{2\alpha }{k};\left(iv\right)\underset{n\to \infty }{lim\; sup}{\delta }_n<1.\hfill \end{array}$$

Then the sequence $\left\{x_n\right\}$ converges strongly to $z=Q\left(u\right)$, where Q is the sunny nonexpansive retraction of E onto Ω.

Proof. 

In this case, the map $f:E\to E$ defined by $f\left(x\right)=u$, $\forall x\in E$ is a strict contraction with constant $\rho =0$. The proof follows from Theorem 1 above. □

Corollary 2.

Let H be a uniformly convex and uniformly smooth Hilbert space. Let $A:H\to H$ be an α-inverse-strongly monotone operator and $B:H\to 2^H$ be a maximal monotone operator. Assume that $\Omega ={(A+B)}^{-1}\left(0\right)\ne \varnothing$. Let $f:H\to H$ be a contraction with coefficient $\rho \in [0,1)$ and $\left\{{\beta }_n\right\}\subset (0,1)$, $\left\{{\alpha }_n\right\}$,$\left\{{\delta }_n\right\}$ be real number sequences in $[0,1)$ and $r_n\subset (0,2\alpha )$. Define a sequence $\left\{x_n\right\}$ in E as follows:

$$\left\{\begin{array}{cc}\hfill w_n& =x_n+{\alpha }_n(x_n-x_{n-1}),\hfill \\ \hfill y_n& ={\delta }_n{w}_n+(1-{\delta }_n)J_{r_n}^B(w_n-r_{n}A{w}_n),\hfill \\ \hfill x_{n+1}& ={\beta }_{n}f\left(x_n\right)+(1-{\beta }_n)y_n.\hfill \end{array}\right.$$

for all $n\in N$, where $x_0,x_1\in E$ and $J_{r_n}^B={(I+r_{n}B)}^{-1}$. Assume that the following conditions hold:

$$\begin{array}{c}\left(i\right)\sum _{n=1}^{\infty }{\alpha }_n\parallel x_n-x_{n-1}\parallel <\infty ;\left(ii\right)\underset{n\to \infty }{lim}{\beta }_n=0,\sum _{n=1}^{\infty }{\beta }_n=\infty ;\hfill \\ \left(iii\right)0<\underset{n\to \infty }{lim\; inf}{r}_n<\underset{n\to \infty }{lim\; sup}{r}_n<\frac{2\alpha }{k};\left(iv\right)\underset{n\to \infty }{lim\; sup}{\delta }_n<1.\hfill \end{array}$$

Then the sequence $\left\{x_n\right\}$ converges strongly to $z=P\left(f\right(z\left)\right)$, where P is the metric projection of H onto Ω.

Proof. 

We only need to replace Banach space E with Hilbert space H in the proof of Theorem 1. □

Corollary 3.

(Convex minimization problem) Let H be a real Hilbert space. Let $f:H\to R$ be a convex and differentiable function with K-Lipschitz continuous gradient $\nabla f$ and $g:H\to R$ a convex and lower semi-continuous function which $f+g$ attains a minimizer. Let $\left\{{\beta }_n\right\}\subset (0,1)$, $\left\{{\alpha }_n\right\}$, $\left\{{\delta }_n\right\}$ be real number sequences in $[0,1)$ and $r_n\subset (0,2\alpha )$. Define a sequence $\left\{x_n\right\}$ in H as follows:

$$\left\{\begin{array}{cc}\hfill w_n& =x_n+{\alpha }_n(x_n-x_{n-1}),\hfill \\ \hfill y_n& ={\delta }_n{w}_n+(1-{\delta }_n)J_{r_n}^{\partial g}(w_n-r_n\nabla f\left(w_n\right)),\hfill \\ \hfill x_{n+1}& ={\beta }_{n}f\left(x_n\right)+(1-{\beta }_n)y_n.\hfill \end{array}\right.$$

for all $n\in N$, where $x_0,x_1\in E$ and $J_{r_n}^B={(I+r_{n}B)}^{-1}$. Assume that the following conditions hold:

$$\begin{array}{c}\left(i\right)\sum _{n=1}^{\infty }{\alpha }_n\parallel x_n-x_{n-1}\parallel <\infty ;\left(ii\right)\underset{n\to \infty }{lim}{\beta }_n=0,\sum _{n=1}^{\infty }{\beta }_n=\infty ;\hfill \\ \left(iii\right)0<\underset{n\to \infty }{lim\; inf}{r}_n<\underset{n\to \infty }{lim\; sup}{r}_n<2\alpha ;\left(iv\right)\underset{n\to \infty }{lim\; sup}{\delta }_n<1.\hfill \end{array}$$

Then the sequence $\left\{x_n\right\}$ converges strongly to a minimizer of $f+g$.

Proof. 

We get that gradient $\nabla f$ is K-Lipschitz continuous, then it is $\frac{1}{K}$ inverse strongly monotone, and g is a convex and lower semi-continuous function, so $\partial g$ is maximal monotone. Thus, let $A=\nabla f$ and $B=\partial g$ in Theorem 1, the conclusion of Theorem 1 still holds. □

4. Applications and Numerical Experiments

In this section, we give a concrete example of the numerical results to support the main theorem. Furthermore, we give it to compare the efficiency of our proposed algorithm with the algorithm of Pholasa et al. [10]. And we also show the algorithm presented in this paper converges more quickly. The whole codes are written by Matlab R2013b. All the results are carried out by personal computer with Intel(R) Core(TM) i7-4710MQ CPU @ 2.50GHz and RAM 8.00GB.

Example 1.

Let $l_3$ be a uniformly convex and uniformly smooth Banach space, we set $Ax=5x+(1,1,1,0,0,0...)$ and $Bx=6x$ where $x=(x_1,x_2,x_3,...)\in l_3$. We can check that $A:l_3\to l_3$ is a $\frac{1}{5}$-isa, $B:l_3\to l_3$ is an m-accretive operator and $R(I+rB)=l_3$ for all $r>0$. we take $r_n=0.02$, ${\alpha }_n=0.4$ for all $n\in N$. Let ${\beta }_n=\frac{1}{1000n+1}$, ${\delta }_n=\frac{1}{200n}$ and $f\left(x\right)=\frac{1}{3}x$ be a contraction with coefficient $\rho =\frac{1}{3}$. Starting $x_0=(1.8,3.2,9.6,...)$, $x_1=(1.4290014,2.5542525,7.6982578,...)$ and using algorithm (1) in Theorem 1, we obtain the following numerical results.

From Table 1 we see that $x_{600}=(-0.0909,-0.0909,-0.0909,0.0000,0.0000,0.0000,...)$ is an approximation of a solution with an error $1.8770214\times {10}^{-9}$. And we make the same choices for $x_1$ as reported in Table 1. In terms of the number of iterations and the errors, we provide the numerical examples to demonstrate the performance and to compare our proposed algorithm with the iterative algorithm with ${\alpha }_n=0$.

Table 1. Numerical results of Example 1 for iteration process.

n	${\mathit{x}}_{\mathit{n}}$	$\parallel {\mathit{x}}_{\mathit{n}+1}-{\mathit{x}}_{\mathit{n}}{\parallel }_{{\mathit{l}}_3}$
1	$(1.4290014,2.5542525,7.6982578,0.0000000,0.0000000,0.0000000,...)$	2.1732179
10	$(-0.0677632,-0.0506892,0.0273635,0.0000000,0.0000000,0.0000000,...)$	$8.911330\times {10}^{-2}$
20	$(-0.0908530,-0.0908328,-0.0907403,0.0000000,0.0000000,0.0000000,...)$	$1.9408448\times {10}^{-4}$
30	$(-0.0908917,-0.0908919,-0.0908926,0.0000000,0.0000000,0.0000000,...)$	$6.7808717\times {10}^{-7}$
40	$(-0.0908964,-0.0908964,-0.0908964,0.0000000,0.0000000,0.0000000,...)$	$5.1789690\times {10}^{-7}$
50	$(-0.0908991,-0.0908991,-0.0908991,0.0000000,0.0000000,0.0000000,...)$	$3.1714100\times {10}^{-7}$
60	$(-0.0909009,-0.0909009,-0.0909009,0.0000000,0.0000000,0.0000000,...)$	$2.1345961\times {10}^{-7}$
70	$(-0.0909021,-0.0909021,-0.0909021,0.0000000,0.0000000,0.0000000,...)$	$1.5346777\times {10}^{-7}$
80	$(-0.0909030,-0.0909030,-0.0909030,0.0000000,0.0000000,0.0000000,...)$	$1.1564503\times {10}^{-7}$
90	$(-0.0909037,-0.0909037,-0.0909037,0.0000000,0.0000000,0.0000000,...)$	$9.0267844\times {10}^{-8}$
100	$(-0.0909043,-0.0909043,-0.0909043,0.0000000,0.0000000,0.0000000,...)$	$7.2416422\times {10}^{-8}$
200	$(-0.0909067,-0.0909067,-0.0909067,0.0000000,0.0000000,0.0000000,...)$	$1.7357133\times {10}^{-8}$
300	$(-0.0909075,-0.0909075,-0.0909075,0.0000000,0.0000000,0.0000000,...)$	$7.6097663\times {10}^{-9}$
400	$(-0.0909079,-0.0909079,-0.0909079,0.0000000,0.0000000,0.0000000,...)$	$4.2517012\times {10}^{-9}$
500	$(-0.0909082,-0.0909082,-0.0909082,0.0000000,0.0000000,0.0000000,...)$	$2.7101525\times {10}^{-9}$
600	$(-0.0909083,-0.0909083,-0.0909083,0.0000000,0.0000000,0.0000000,...)$	$1.8770214\times {10}^{-9}$

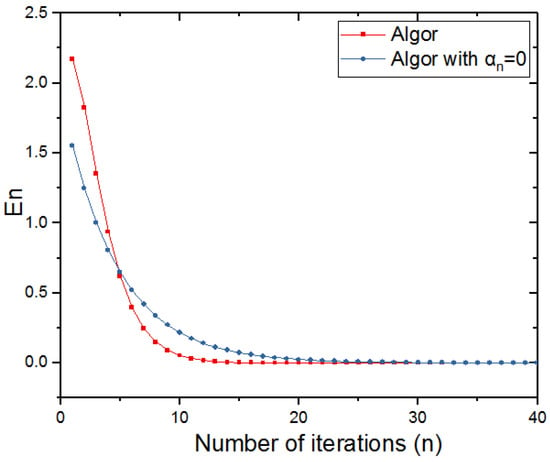
In these 600 experiments, Table 2 shows that the final approximation solution is the same as Table 1. Figure 1 shows that the number of iterations and errors of our algorithm and the algorithm with ${\alpha }_n=0$ for the above initial points. We can see that the convergence of our algorithm is faster than the algorithm of Pholasa et al. [10].

Table 2. Numerical results for iteration process Algorithm (1) with ${\alpha }_n=0$ in Example 1.

n	${\mathit{x}}_{\mathit{n}}$	$\parallel {\mathit{x}}_{\mathit{n}+1}-{\mathit{x}}_{\mathit{n}}{\parallel }_{{\mathit{l}}_3}$
1	$(1.4290014,2.5542525,7.6982578,0.0000000,0.0000000,0.0000000,...)$	1.9308196
10	$(0.1216527,0.2789583,0.9980697,0.0000000,0.0000000,0.0000000,...)$	$2.702205\times {10}^{-1}$
20	$(-0.0670158,-0.0493531,0.031391,0.0000000,0.0000000,0.0000000,...)$	$3.034530\times {10}^{-2}$
30	$(-0.0882106,-0.0862275,-0.0771619,0.0000000,0.0000000,0.0000000,...)$	$3.407800\times {10}^{-3}$
40	$(-0.0905947,-0.0903721,-0.0893543,0.0000000,0.0000000,0.0000000,...)$	$3.8297598\times {10}^{-4}$
50	$(-0.0908649,-0.0908399,-0.0907256,0.0000000,0.0000000,0.0000000,...)$	$4.3220033\times {10}^{-5}$
60	$(-0.0908968,-0.0908940,-0.0908812,0.0000000,0.0000000,0.0000000,...)$	$5.0028407\times {10}^{-6}$
70	$(-0.0909015,-0.0909012,-0.0908997,0.0000000,0.0000000,0.0000000,...)$	$6.7427458\times {10}^{-7}$
80	$(-0.0909028,-0.0909028,-0.0909026,0.0000000,0.0000000,0.0000000,...)$	$1.7183921\times {10}^{-7}$
90	$(-0.0909036,-0.0909036,-0.0909036,0.0000000,0.0000000,0.0000000,...)$	$9.9664118\times {10}^{-8}$
100	$(-0.0909042,-0.0909042,-0.0909042,0.0000000,0.0000000,0.0000000,...)$	$7.5993686\times {10}^{-8}$
200	$(-0.0909067,-0.0909067,-0.0909067,0.0000000,0.0000000,0.0000000,...)$	$1.7674516\times {10}^{-8}$
300	$(-0.0909075,-0.0909075,-0.0909075,0.0000000,0.0000000,0.0000000,...)$	$7.6990015\times {10}^{-9}$
400	$(-0.0909079,-0.0909079,-0.0909079,0.0000000,0.0000000,0.0000000,...)$	$4.2884018\times {10}^{-9}$
500	$(-0.0909082,-0.0909082,-0.0909082,0.0000000,0.0000000,0.0000000,...)$	$2.7286629\times {10}^{-9}$
600	$(-0.0909083,-0.0909083,-0.0909083,0.0000000,0.0000000,0.0000000,...)$	$1.8876276\times {10}^{-9}$

Figure 1. Error plotting of $\parallel x_{n+1}-x_n{\parallel }_{l_3}$.

5. Conclusions

In this paper, we give a modified inertial viscosity splitting algorithm for accretive operators in Banach spaces. The strong convergence theorems are established, and the numerical experiments are presented to support that the inertial extrapolation greatly improves the efficiency of the algorithm. In Theorem 1 and Corollary 1, if $f\left(x_n\right)=u$ and A is an inverse strongly monotone operator in Hilbert space, it is the main results of Cholamjiak et al. [20]. In Theorem 1, if ${\alpha }_n=0$, $f\left(x_n\right)=u$ and E is a uniformly convex and q-uniformly smooth Banach space, it is the main results of Pholasa et al. [10]. Furthermore, some other results are also improved (see [8,9,18,19,26]).

The introduction of the inertial viscosity splitting algorithms sheds new light on inclusion problem. Combined with recent research findings ([4,13,19,20]), Theorem 1 can be further applied to the fixed-point problem, the split feasibility problem and the variational inequality problem. Indeed, it is an important but unsolved problem to choose the optimal inertia parameters ${\alpha }_n$ in the acceleration algorithm. In the future, more work will be devoted to the wide application of the proposed algorithm and the improvement of its convergence rate.