Abstract
The low efficiency of using appropriate strategies to solve problems in the classroom environment is not due to the lack of knowledge of how to classify concepts, but rather due to the failure to apply this knowledge strategically. Therefore, it is necessary to find a balance between them, i.e., to let the pupils discuss the problems while supporting the teacher’s intervention. The aim of the presented study was to examine the influence of a teacher’s progressiveness on the level of metacognitive knowledge of the pupil. Altogether, 47 teachers and 278 pupils at grade 5 were participating in the study. It is shown that the approach of teachers to innovation itself has an influence on the pupil. When comparing all five groups of innovators, the difference among the categories of teachers was significant () with the low effect (. When considering only the two almost antagonistic poles of teachers, the innovators and the late majority according to Roger’s innovation diffusion theory, this influence was very strong () and with medium effect (). Our research shows that it is necessary to address the teacher’s innovativeness, affecting the level of metacognitive knowledge of the pupil as an important prediction tool determining school success.
1. Introduction
Since the development of the Internet, we have been experiencing steep increases in the volume of available information [1]. The incorporation of technology and innovation into society is not only a matter of recent years since this issue has been under investigation for more than 30 years. Innovation can be “an idea, product or activity that is incorporated into society ([2], p. 7)”. This is not the only possible definition [3,4]. These definitions (in particular, the definition of innovation) can be further characterized by a closer definition. If the particular innovation is to be considered as an innovation, then it is sufficient that it appears as a “novelty” for at least one individual receiving it [5]. Among the most well-known theories there is Rogers’ theory of Diffusion of Innovations [5], though Rogers’ concept of the innovation process is not the only one. There are many diverse models of other innovation processes that use the general knowledge of innovation diffusion theory, and these are linked to the Basel model [6]. One of the assets of Roger’s theory is that it features a very wide scope of application; it can be applied in many disciplines, such as economics, education, politics, or business [7]. Liebová [6], for example, focused on the use of Rogers’ theory in organizations, because innovations increase “the competitiveness, efficiency and performance of organizations”.
It is surprising that only a small amount of works have focused on comparing the influences of teacher’s innovativeness on their pupils during the learning processes. Thus innovation can be perceived intentionally from the point of view of education, and we could consider educational innovations categorized in the six different types at least. Innovation can be understood in the educational process as “novelty, change, certain action, process or intention” [8]. This research paper focuses on the issue of teacher’s influence and impacts, from the point of view of their innovativeness, on pupil’s metacognition, viewed upon as a multidimensional construct related to the constructs such as critical thinking [9], ability to solve problems [10,11], and other factors such as motivation and interest [12,13]. Bransford, Brown and Cocking [14] argue that learning and the development of metacognitive strategies in pupils should be the standard of every teacher’s work and, therefore, it is necessary to pay attention to this relation.
1.1. Dissemination of Innovation in Mathematics Education
Rogers [5] defines diffusion as “the process by which we spread innovation over time through various channels of communication among members of the social system”. The definition formulated in this way anticipates the reception and use of information, considering the points and rules that are commonly encountered by all recipients during the acquisition of a new piece of knowledge [15]. Diffusion of innovations is understood as a special type of communication, during which the recipients and the communicators communicate something new in order to understand each other [5,16]. This communication is growing faster, as we are now in a process of great acceleration [17]. For this reason, most of diffusion research focuses on technological innovations [7], which can be considered as an interdisciplinary problem [18], so even the influence and impacts of technologies on the school education process cannot be denied [19]. In a number of studies, a broad application of this theory has been described in detail, for example, Dooley [20] and Stuart [21] have reported using it in fields such as political science, communication, history, and economics [7]. Self-confidence in adopting an innovation can be enhanced by the fact that the individual is well informed not only about particular advantages, but also about specific disadvantages of that innovation, so that they can develop their own opinion [7].
Our research is aimed at the issue of innovation in the course of education process, simultaneously considering relationships between the teacher and their pupils in order to find out how one person is able to influence others. Implementation of this issue in the education field has already been described by Bennett and Bennett [22], Ogrezeanu and Ogrezeanu [23], Sahin [7] and Seymour [24]. A specific questionnaire designed based on Rogers’ theory of diffusion of innovation has been used [5]. This tool differentiates the five specific groups of people according to their tendency to use an innovation approach. They can be briefly described and categorized as follows: (i) “Innovators” (venturesome) who like to share information without being afraid of failing or receiving any new information; however, they are not often understood, though they are the ones who invent new theories and following, introduce them into practice; (ii) “Early adopters” (respectable) are usually much more respected than Innovators (venturesome) and therefore their key role lies in reducing uncertainty in others; they regularly “play a crucial role at virtually every stage of the innovation process, from the initiation to implementation phases, especially when distributing resources that bring innovation forward” [25]; unlike innovators, they consider applying an innovation to a greater extent and are more conservative [26]; (iii) “Early majority” (deliberate) represents those who can receive information, however, they are only very rarely leaders; (iv) “Late majority” (sceptical) receive information only as a necessity and are very sceptical to it; before receiving any new information, it is necessary to remove all their doubts; and (v) “Laggards” (traditional or conservative) almost never work with any new information and focus mainly on the past [7,27].
This classification allows investigating the innovative role of teachers in dissemination of experience using the ICT (information and communication technologies) tools in the education process if supported [28,29].
1.2. Metacognition in Mathematics Education
Metacognition is usually defined as the cognition of an individual about their own cognitive functions [30], e.g., thinking about thinking. Metacognition is a construct based on the socio-cognitive approach to the learning process as such and is closely related to the concept of self-regulating learning [31]. The basic theories of self-regulating learning cite the metacognitive component as their integral part, either implicitly [32] or with an explicit accent [33]. Although, in the context of self-regulated learning, a distinction is made between the cognitive, non-cognitive and metacognitive aspects, and therefore, we must understand this definition primarily in the context of research comprehension. Tobias and Everson [34] give a very specific operational definition. They understand metacognition as something we can describe from scales, subjective testimonies, and metacognition observation protocols, based on a collection of the most commonly used methods to collect data on metacognition, i.e., from judgments about pupils’ and students’ performance and testimonies through interviews, questionnaires and self-assessment scales (see also [35]). According to Ronzano [36], metacognition is a phenomenon that combines decision-making with memory, learning with motivation and learning with cognitive development. Thus, the original, purely cognitive view of the concept of metacognition (referred to as a ‘cool’ or ‘pure’ view described in [37,38]) is extended to other non-cognitive factors [39].
Educational science researchers do not agree on a uniform definition of metacognition. However, all available definitions agree that metacognition consists of the following two main components: (i) knowledge of cognition, and (ii) control and regulation of cognition [40,41]. Özsoy [42] found a strong relation between metacognitive knowledge and mathematical achievement while investigating 242 pupils attending grade 5 within schools reviewed in Turkey. Procedural metacognitive knowledge and the ability to predict, monitor and evaluate one’s own work are the strongest facets of metacognitive knowledge having an impact on success in mathematics. A certain relation between the self-regulation and mathematics achievement is confirmed also for students aged from 14 to 16 years attending Russian schools [43]. However, other investigated factors, such as intelligence quotient or number sense were significantly correlated with the performance of mathematical problem solving. Vo et al. [44] investigated 45 children aged from 5 to 8 years and suggested that the metacognition seems to be domain-specific and children’s number sense is related to their metacognitive skills in mathematics. To conclude, recent research studies point to the fact that both cognitive regulation and metacognitive knowledge correlate with success in mathematical problem-solving from the primary level [44,45] to the high school level [46,47].
Nowinska and Preaetorius [48] state that metacognition plays “an essential role in regulating students’ cognitive processes in problem-solving as well as in learning mathematics in general, in particular, when constructing, organising, systematising, and connecting (pieces of) knowledge.” According to Flavell [49], metacognition itself features a dual nature, consisting of both knowledge of cognitive processes (metacognitive knowledge) and knowledge that can be used to control and manage cognitive processes (metacognitive ability). This dual concept, despite the terminological disharmony, is still accepted across the scientific discourse [50]. While metacognitive abilities, according to Flavell [49], refer to the procedural (active) “online” components (setting goals, predicting, planning, strategizing, self-questioning, organizing, etc.), on the other hand, metacognitive knowledge includes such knowledge and beliefs (affective dimension) that one has about his cognitive resources (strategies, heuristics), the nature of tasks, including knowledge and beliefs about themselves and others as learners (e.g., why a certain strategy may be theoretically more effective in solving problems).
Metacognitive knowledge is, therefore, rather more a “static” component, and its activation occurs before a cognitive action (off-line) starts up. At present, the following types of knowledge are commonly used to divide the metacognitive knowledge as such: (i) declarative knowledge, relating to self-knowledge, self-abilities, skills, and characteristics of learning that affect their own cognitive processes; (ii) procedural knowledge responsible for the ways different learning strategies are implemented; (iii) conditional knowledge containing such types of knowledge on when and why it is appropriate to use a specific or certain strategy under the given circumstances [51,52]. Borkowski et al. [53,54] cited relational metacognitive knowledge as one of the three components of metacognitive knowledge relevant in the context of MAESTRA5-6+ [55] used in this study.
At present, there is a dominant, relatively stable opinion that metacognitive knowledge evolves step by step with the age of pupils and the acquisition of their experience. This assumption is supported by empirical investigations in the context of declarative [56] and contextual knowledge [57]; this is not, however, entirely clear for developing procedural knowledge. Lai in [58] and then in this context presents an indicative diagram of the development of the metacognitive components. Metacognitive knowledge is the first to be developed (around in the age of 6 years), and metacognitive abilities lead to significant improvements in planning capabilities (between the age from 10 to 14 years, observable at grade 5). The development of monitoring and evaluation functions (components of metacognitive abilities) comes very slowly, and even many adults do not reach the required level. The last to be developed are metacognitive theories allowing individuals to understand cognitive knowledge and regulate cognition as a complementary phenomenon.
The view of the presented development of metacognition is neither a linear nor hierarchical form [59], because the process of forming a metacognition is not only long-term and gradual, but it also takes different times and takes on its original form due to the individuality of each person [60]. We, however, believe that teachers should be aware of how to facilitate this process.
The importance of metacognitive knowledge is empirically documented. For example, it is demonstrated that any form of training aimed at metacognitive knowledge can increase the performance levels of pupils, regardless of their previous performance levels and interest in the area [61]. Whereas, Hidi [62] states that the area of interest has an impact on cognitive functioning. Carr [63] also emphasizes the development of declarative metacognitive knowledge for the development of conceptual knowledge, stating that the quality of this knowledge further supports procedural knowledge and strategy building. Mevarech [64] states that since the pre-school age, metacognitive knowledge has been a stronger prediction tool of mathematical performance in verbal tasks than general knowledge tests. Schneider [56] lists the studies on the predictive potential of metacognitive knowledge. The results show that this factor not only has an impact on the younger school-age children, but also determines their performance levels in mathematics (including reading comprehension) at the secondary school stage, regardless of differences in the intellectual abilities of individual pupils. Recent empirical findings confirm that regardless of whether it is a knowledge or management component of metacognition, both areas explain a significant amount of individual test score differences [41,65,66], and their predictive potential in relation to school success is higher than standard ways the level of intelligence quotient is measured [67,68].
Several factors influence the pupils’ metacognitive knowledge, e.g., their self-efficacy [69], metacognitive skills of the teacher [70], teachers’ beliefs [71], teaching quality [72] or teacher’s metacognitive awareness [73]. It is shown [74] that the warm and nurturing relationships seem to provide students with opportunities for metacognitive skill development, especially in the primary education milieu.
Gurbin [75], in detail, focuses on the issue of linking the diffusion of innovation and metacognition. Referring to [76], he claims that its involvement is important for understanding the complex learning process that facilitates the successful adoption of technology. Straub [76] also adds that technology acceptance is a source of research, both in relation to the education process and to everyday life. “As adopting a technology is closely related to learning a technology, success in technology adoption involves metacognition” ([75] p. 1578). The successful adoption of technology requires metacognitive capabilities such as an ability to track and evaluate your ideas and products to achieve a goal [77]. Metacognitive processes such as planning, strategizing, reflection, and autoregulation are needed to learn any new knowledge and skills in computer learning environments [78]. Azevedo [78] refers to a number of other authors aimed at similar issues. The link between these domains (metacognition and acceptance of innovations) can already be seen when searching for information on the Internet. For example, metacognitive skills and capabilities can help all novice students in organizing unknown online information into some hierarchies so that they can continue to explore it [79]. Tu, Shih & Tsai [80] add that they are metacognitive skills that can enable them to choose appropriate keywords that have a high impact on finding a solution to the given task.
Based on the results of research in the field of intentional intervention, we can conclude that it is possible to develop metacognitive functions and abilities via systematic rehearsals. Several authors [81,82,83,84,85] have reported that intervention has resulted in some significant positive changes of participants. Furthermore, metacognition function is developed simultaneously with other competencies [86], so it seems worth investigating the relations of development of metacognition with the development of the effort related to adoption of technologies [75]. As mentioned above, the impact of ICT tools on the school education process is undeniable [19]. In addition, Rogers himself already tested the diffusion of innovations in the school environment in a number of studies [87]. Salaway and Caruso [88] reported that, in terms of using electronic textbooks for college students, 9.5% are innovators, 25.9% early adopters, 51.4% early majority, 9.3% late majority, and 3.9% laggards. Others who have been involved in the theory in education are Shaban and Egbert [89], who have used Rogers’s theory to create a two-phase model that teacher educators can consider for developing and delivering professional development for teachers. This theory was also linked to mobile learning. According to the results of Bulun, Gulnar, & Güran, [90], approximately 65% of social science teachers are in the groups that give the most favourable response to the spread of innovation theory within mobile learning (innovators, early adopters and early majority). Outside the tertiary education segment, but still within the education system, Rogers’s theory of diffusion of innovation is used [91] in connection with education for sustainable development at primary schools. Several authors have used this theory in education recently [92,93,94,95,96]. To summarise this section, (i) metacognition can be positively developed, (ii) technology has an impact on teaching, (iii) innovation theory can be used as a basis for developing effective educational strategies, and (iv) innovation theory is already used in the school environment. Based on the described studies, the following research question is formulated: What is the impact of different teachers’ progressiveness in using digital technologies on their pupils’ metacognitive knowledge at grade 5?
2. Methodology
2.1. Aims
The main aim of this study is to investigate whether there is a relation between teachers’ tendencies to adopt an innovation, particularly digital technology tools, and the metacognitive knowledge of their pupils. As there are many factors potentially influencing this relationship, in particular, and including the age of pupils, we focus only on the pupils at the edge between the primary and lower-secondary levels of education. In the Czech Republic, pupils attending grade 5 still have only one teacher for all subjects (except special subjects), so we anticipate that the influence of the teacher is most visible at this grade. Furthermore, an equal level of knowledge is expected at grade 5, as the pupils are not differentiated yet. The hypothesis is formulated as follows: The metacognitive knowledge in mathematics of grade 5 pupils differs according to their teacher’s category of innovativeness. As the categories of teachers can be understood as ordinal variables, we expect the difference between the pupils of innovators (the most innovative) and the laggards (the least innovative) to be of the highest effect size.
2.2. Instruments and Procedure
Data collection proceeds in two phases. Firstly, teachers are approached in order to classify them based on the Rogers’ theory of diffusion of innovation, and then their pupils’ metacognitive knowledge levels are tested. Teachers are given a tool containing 25 Likert-type items, each of them responding to the following scale: I strongly agree (5), I agree (4), I do not have a clear opinion (3), I disagree (2), I strongly disagree (1) and I don’t know. These 25 items are divided into pentads, each pentad corresponding to the one group of innovators in the series: (i) Innovators (venturesome), (ii) Early adopters (respectable), (iii) Early majority (deliberate), (iv) Late majority (sceptical), and (v) Laggards (traditional or conservative). In addition, each of the five items is averaged according to the highest number obtained, so the respondent falls in the respective category. Only those teachers who fall into only one of the categories are selected for further investigation. In order to qualify for a category, any teacher has to reach a minimum of 3.8 points in the given area. “Respondents ranging from 2.3 to 3.7 are considered to have a nondescript opinion.” ([26] p. 102). A questionnaire created by Kankaanrinta [8] was first translated and piloted in the Czech Republic by Černochová et al. [97]. Adaptation of this instrument to the context has been described in more details in [26,27]. The most problematic category is the group (v) Laggards (traditional or conservative); in this case, respondents generally refuse to fill out the questionnaire because they do not want to point out their approach to innovation. For this reason, we managed to find only one teacher who was willing to cooperate. We are, however, considering such a small sample of respondents (pupils) that we put it in the data matrix as an addition and only out of interest. Therefore, in addition to the inductive analysis, we also use an effect size and then the sample size is of a lesser importance. The tool reliability is . This is a sufficiently high value for the instrument as a whole, since the coefficient values between 0.7 and 0.95 are particularly acceptable [98]. However, as several categories of innovation are evaluated (the tool is multidimensional), internal consistency is also given for each dimension (Table 1).

Table 1.
Reliability of the dimensions of the tool for categorization of teachers according to their progressiveness.
The MAESTRA 5 − 6 + tool [55] is used to map the metacognitive knowledge of pupils. This test is created based on simplifying and modifying already existing tests, such as WLST [99] or some tasks from the Program for International Student Assessment [100] and is intended for pupils at the 5th grade or at the first term of the 6th grade. The tool used is built on the Qualitative standard defined [101], defined against the Quantitative standard, which is based on recording the frequency of using strategies and achieving the highest possible score as an indicator of metacognitive knowledge level [101]. Questionnaires assessing the frequency of use of strategies often fail to predict learning performance [102]. Neuenhaus et al. [103] add that the approaches to assessing the frequency of use of strategies actually measure whether the learner recognizes the strategy (rather than detecting metacognitive knowledge). The Qualitative standard is based on the pupil’s ability to evaluate the adequacy and effectiveness of the strategy against the background of a particular task situation. It means not only considering: (1) what strategy the pupil uses (declarative knowledge), (2) in relation to other available strategies (relational strategy knowledge), but also (3) when under and what conditions (conditional knowledge) this pupil applies it in the context of understanding the characteristics of the described, and (4) task situation (declarative knowledge). A deficit in any of the above areas of metacognition may lead to an erroneous strategic evaluation. Thus, correct evaluation of strategies can be considered as a qualitative indicator enabling strategic choices through a metacognitive knowledge base that from the perspective of “the Good Strategy User Model”, is already an advanced stage of development. Although the pupil is required to have a higher degree of generalization, it relates to the context and not to the (very difficult) generalization across domains [54]. The tool is validated in the Czech education environment by Chytrý, Pešout and Říčan [104].
The tool outlines a total of five specific mathematical scenarios (learning situations) that correspond to the framework model of the four phases of cognitive activity in solving mathematical problems. Each of the five mathematical scenarios has its own five or six different strategic alternatives of different functionality and efficiency (see Appendix A Table A1). Pupils assess the effectiveness of the strategies with regard to the quality and adequacy, not only in relation to the presented task scenario, but also in relation to other offered alternatives; the assessment is done on six-point scales. As a benchmark for pupils’ judgment (projection of their own experience on strategies and their usage conditions), expert opinions are obtained within the validation of the tool’s construct (for the Czech environment see e.g., [105]). Criterion boundaries (80% match of experts) and selectivity lead to expected reduction in the number of pair comparisons: The 28 strategies are divided into five scenarios (three scenarios of six strategies and two scenarios of five strategies). By the 80% consensus, it is meant that if 4 out of 5 experts agree that strategy A is better than strategy B and the pupil decides in the same way, then the pupil is assigned a point. Therefore, it is theoretically possible to achieve different comparisons. An expert agreement of 80% is proved in 34 cases. The pupil is rated from 0 to 34 points. To complete the test, the pupil has a time limit of 20–25 min. The calculated α-coefficient according to the Cronbach test reaches a sufficient value of .
2.3. Participants
Within the data collection, a total of 200 teachers from the ordinary elementary schools were approached, who do not have an increased subsidy for teaching mathematics or other subjects. If it turned out that some teachers worked with pupils more, for example, in the form of an increased grant of mathematics lessons, he/she was excluded from the data matrix. These teachers were asked to complete a questionnaire based on the Rogers’ theory of diffusion of innovation [5] and give their contact (telephone + email) in case of their interest in further cooperation, consisting of testing pupils. Of the 200 respondents, 108 teachers filled in the questionnaire of which only 47 provided a contact address for possible further data collection and provided the written informed consent for research. Further elimination occured when it was necessary to classify the teachers into one of the five categories of innovation adopters. In order to categorize the teachers into one of the five categories, they had to achieve at least 3.8 points in the category and fall only into one category (Innovators, Early adopters, Early majority, Late majority, Laggards). Respondents with a score of 2.3 (the minimum value achieved by respondents of this study) and 3.7 were considered as having an indeterminate opinion. If teachers achieved at least 3.8 points in several categories (e.g., they would be labelled both, innovators and early adopters), they were excluded from further investigation as they would not fit any of the defined categories. These conditions naturally led to a reduction of the number of participants. It turned out that 27 teachers could not be assigned to any of the categories or, on the contrary, they fitted into more than one category as mentioned in the Methods chapter. In total, only 20 teachers could be assigned to one of the specific Rogers’ categories. Together, these teachers work with 278 pupils aged from 10 to 12 years (136 boys and 142 girls in total). The written informed consent for research was collected by the teachers from the parents of all the participating pupils. These pupils are differentiated according to it which of the above categories their teacher is assigned. For MAESTRA 5-6 +, the numbers of respondents were and .
2.4. Data Preparation
All variables are analyzed as an interval based on recommendations given [105]. Data is converted to the electronic form and then analyzed using Excel 2016 (Microsoft Office Professional 2016) for descriptive and Statistica v13 (StatSoft Inc., TIBCO Software, Palo Alto, CA, USA) for inductive analysis. In addition to statistical significance, material significance is also calculated, and there is no exaggeration based on the size of the set [106]. Nonparametric statistical methods are used, as normality is violated based on the results of the Shapiro-Wilk’s test. Due to the above-mentioned hypotheses and data abnormality, Kruskal-Wallis test is used as a non-parametric analogy of ANOVA scattering analysis followed by post-hoc analysis allowing for multiple comparisons of p values. Due to the nature of the test and the method of statistical significance testing, the effect sizes were estimated [107]. Eta squared () and [108] are used for this examination. Outlying values are tested using box-and-whisker plots. Although we work with a relatively large set, it is surprising that no outliers are identified (see [109]).
3. Results
On the basis of a descriptive analysis, it is possible to observe an interesting trend: The poorer results the teacher achieves in the Rogers’ theory of innovation diffusion [5], the poorer are the results of their pupils in terms of metacognitive knowledge. This issue is further discussed based on the inductive analysis.
Inductive Analysis
We consider Fisher’s recommendation of a significance level of 5% restriction (see for example [110]). While Fisher introduces a recommendation to use the value 0.05, it is only part of his recommendation that is uncritically accepted [111]. Fisher further claims that if the calculated level of statistical significance exceeds this value but does not exceed 0.20, the researcher should consider whether to focus on the effect in further experiments. Since the lower calculated significance level indicates a higher statistical significance, we follow the recommendation (level of significance 0.05), but if the p-level value is in the range 0.05 to 0.2, we also comment on the conclusions. In each part of the inductive analysis, the relevant level of significance is mentioned each time, and we do not incline neither towards to the extreme proponents of statistical significance [112] and neither to their opponents [111,113]. On the contrary, we analyze the data in a completely unbiased way by considering both concepts. The following hypothesis is tested: The pupil’s metacognitive knowledge is dependent on the teacher’s level according to Rogers’ theory of innovation diffusion. This hypothesis implies to formulate the relevant null hypothesis : The medians of metacognitive knowledge in mathematics are equal for the different categories of teachers according to Rogers’ innovation diffusion theory. The hypothesis can be rejected at a 5% significance level, as the Kruskal-Wallis test values are . The results are visualised in Figure 1.
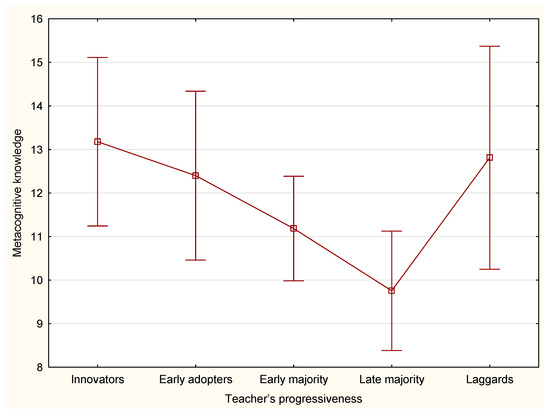
Figure 1.
Median and interquartile range of the level of pupils’ metacognitive knowledge in mathematics according to the teacher’s progressiveness in implementation of digital technologies (source: own computation).
If we do not consider the Laggards—traditional or conservative group, consisting of just a small number of respondents—then the following values will be found: and again could be rejected at a 10% significance level. The post-hoc analysis shows that in both cases a statistically significant difference is only between the innovators and the late majority. Generalization is therefore possible between the first (Innovators—venturesome) and the fourth group (Late majority—sceptical) only. In the case of effect size, the values of and are found for all five options, without consideration of Laggards (fourth option) and . In both cases, we are considering a small effect [114]. These findings do not support Moore’s conjecture [115] about the gap between the early adopters and the early majority. The results of pairwise comparison by the mean of Mann-Whitney test and their effect sizes are summarized in Table 2.

Table 2.
Results of pairwise comparison of metacognitive knowledge of pupils with teachers in different categories.
When a similar comparison of almost antagonistic positions only, i.e., Innovators (venturesome) and Late majority (sceptical), is done by the Mann-Whitney test, we reach the value (). Focusing on these two variables, it is therefore possible to reject the revised even at a 1% level of significance. In this case, the appropriate effect size would be and would have a medium effect as such. It is, therefore, obvious that the issue needs to be investigated more deeply.
4. Discussion
Inductive data analysis opens up a question related to the personality type and professional “setting” of teachers (typology of teachers based on Rogers’ theory) and their concepts of teaching (i.e., “how” they teach, including the implementation of activities aimed at developing the metacognitive potential of pupils). The formulated research hypothesis is partially confirmed. The highest difference is observed between the innovators and the late majority. The difference might be a result of more extensive implementation of ICT tools in the everyday practice of innovators and early adopters [116] and the impact of ICT tools on the metacognitive knowledge of pupils [117]. Another possible explanation of the phenomenon is that the innovativeness in the ICT field may be related to the innovativeness in other areas [118], including the pupil-centered activities where self-regulation is more required and needed and therefore more developed [86]. The design of this study does not allow us to isolate the two described sources or identify other, possibly latent, variables.
This is important in the context of both, meaning the undergraduate preparation of future teachers as well as their further postgraduate studies. Unfortunately, little is known about the teachers’ knowledge of metacognition [119]. It is rather striking that there are relatively well defined and documented ways of designing a teaching process and teaching modes leading to the development of metacognitive potential of pupils, however, there is a low number of studies on how to teach teachers to gain and achieve their metacognitively-oriented teaching [120]. This way of teaching requires from teachers not only a deep understanding of their own strategies, but also how to make their own thoughts and strategic actions accessible to pupils [121]. This is one of the central causes of why it is difficult for educators to implement such teaching modes [122]. As Anders, Hoffman and Duffy [123] state, more research is needed to help teachers in developing their day-to-day practice in the field of metacognitively-designed teaching.
The conclusions of some studies point out that even when teachers undertake some well-designed training and seminars aimed at transforming their didactic practice, their teaching mode is and remains still the same and unchanged as before the well-designed training courses [124]. Cummins, Stewart, and Block [125] carried out an 8-month survey involving 1278 pupils with their teachers, with educators receiving instructions in relation to metacognitively designed teaching modes. Although these teachers gained a higher level of confidence and subjectively perceived competence, they only possessed a superficial knowledge of metacognitive content (for example, they could name strategies, however, they did not know the purpose of using the strategies and the reason why the strategy was important). Wenglinsky [126] investigated the relationship between the teacher’s development and the performance of 7146 pupils in mathematics. In this context, data from 1996 within NAEP (National Assessment of Educational Progress) were examined. The research confirmed almost a direct proportion between the teachers participating in their high quality professional development and the higher performance of their pupils, that is, when the educators are constantly professionally developing (for example, they are able to individualize the pupils’ needs), then their pupils achieve higher performance levels. The above conclusions highlight the importance of paying attention to the professional and personal “setting” of teachers, e.g., teachers’ innovativeness, in relation to their didactic practice aimed at developing actual metacognitive potential of pupils.
Research Limitations
For the purposes of this research, schools with an equal number of lessons were selected, i.e., schools that do not provide any extra lessons (e.g., of mathematics, physical education, etc.). Each pupil included in the study was taught by the same teacher for at least 1 year. Furthermore, we conclude that nowadays many authors also draw attention to the fact that there exist only a small number of studies aimed at similar issues. As the largest limitations of the survey, we consider the absence of supplementary qualitative analysis, where maximum validity of the research would be achieved. Supplementing quantitative data by observations and interviews would allow investigating the meanings, concepts, definitions, characteristics, metaphors, symbols, and descriptions of things instead of the counts or measures. In the observations, one would observe whether the teachers really apply metacognitively designed teaching modes. From the interviews, this conclusion could be confirmed. If these conditions are met, it would be possible to consider this issue for further research, where it would also be necessary to expand the sample’s representativeness, for example, as stated by Israel [127]. Another limitation of the study is the reliability of the instrument to categorize teachers. The instrument was tested and piloted in the Czech context. However, the estimated reliability in one of the subscales (late majority) is α = 0.517, which is considered as poor. Sekaran (1992) sets the minimum acceptable reliability coefficient level at 0.60.
5. Conclusions
In the presented study, the relation between teachers’ tendency to implement technological innovations in mathematical instructions and metacognitive knowledge of their pupils at grades 5 and 6 has been assessed using a quantitative inquiry. This relation is confirmed by the means of mathematical statistics. Pupils of the teachers with higher tendencies of implementing innovation are performing better in tests focused on metacognitive knowledge aspects, as standardized and tailored to the national context by the authors. The difference between the innovators and the laggards has a really large effect size and is consistent enough to be considered as really important.
We are aware that the innovativeness of our teachers is only one aspect among various factors influencing the metacognitive knowledge aspects of pupils, and thus, their learning of mathematics and performance levels in mathematical problem solving. The interrelations between these factors are worth being studied further.
Author Contributions
Conceptualization, V.C. and J.Ř.; methodology, V.C.; software, V.C.; validation, V.C. and J.M.; data curation, V.C.; writing—original draft preparation, V.C., J.Ř. and J.M.; writing—review and editing, J.M.; visualization, J.M.; supervision, V.C.; project administration, V.C., J.Ř. and J.M.; funding acquisition, V.C. and J.Ř. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by project conducted at University of Jan Evangelista Purkyne, Usti nad Labem, Czech Republic: UJEP-SGS-2019-43-002-1 and UJEP-SGS-2019-43-011-1. This work was also supported by the Slovak Research and Development Agency under the contract No. APVV-15-0368.
Acknowledgments
Authors cordially thank to three anonymous reviewers whose comments significantly increased the quality of the presented paper.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A

Table A1.
Example of item in the test of metacognitive knowledge.
Table A1.
Example of item in the test of metacognitive knowledge.
| Task: “Problems” Solving a complex calculation within the homework activity requires usually more steps. You don’t know how to continue in one of the steps. What can help you in such a situation? | Mark | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| A | I start again from the beginning and think about it whether there is another way to solve the task. I start again from the beginning and think about other options. | □ | □ | □ | □ | □ | □ |
| B | I ask my parents, siblings or a friend from our school if any of them can help me. | □ | □ | □ | □ | □ | □ |
| C | I consider whether I made a mistake in the first step of the calculation. | □ | □ | □ | □ | □ | □ |
| D | I calculate what is easy to calculate and then I start the next task. | □ | □ | □ | □ | □ | □ |
| E | I wonder what intermediate result I need, to be able to calculate the result. | □ | □ | □ | □ | □ | □ |
| F | I skip a step I don’t know how to do to avoid losing too much time. | □ | □ | □ | □ | □ | □ |
References
- Arbesman, S. The Half-Life of Facts. Why Everything We Know Has an Expiration Date; Penguin Group: New York, NY, USA, 2013. [Google Scholar]
- Mahajan, V.; Peterson, R.A. Models for Innovation Diffusion; Sage: Thousand Oaks, CA, USA, 1985. [Google Scholar]
- Damanpour, F.; Aravind, D. Managerial Innovation: Conceptions, Processes, and Antecedents. Manag. Organ. Rev. 2011, 8, 423–454. [Google Scholar] [CrossRef]
- Walker, R.M.; Damanpour, F.; Devece, C.A. Management Innovation and Organizational Performance: The Mediating Effect of Performance Management. J. Public Adm. Res. Theory 2010, 21, 367–386. [Google Scholar] [CrossRef]
- Rogers, E.M. Diffusion of Innovations, 4th ed.; Free Press: New York, NY, USA, 1995. [Google Scholar]
- Liebová, V. Difuze Inovací v Organizaci. [Diffusion of Inovation in Organisation]. Bachelor’s Thesis, Karlova Univerzita, Prague, Czech Republic, 2014. [Google Scholar]
- Sahin, I. Detailed review of Rogers’ diffusion of innovations theory and educational technology-related studies based on Rogers’ theory. TOJET Turk Online J. Educ. Tech. 2006, 5, 14–23. [Google Scholar]
- Kankaanrinta, I.K. Finnish kindergarden student teachers’ attitudes towards modern information and communication technologies. In Media, Mediation, Time and Communication; Tella, S., Ed.; University of Helsinki: Helsinki, Finland, 2000; pp. 147–169. [Google Scholar]
- Halpern, D.F. Teaching critical thinking for transfer across domains: Disposition, skills, structure training, and metacognitive monitoring. Am. Psychol. 1998, 53, 449. [Google Scholar] [CrossRef] [PubMed]
- Rozencwajg, P. Metacognitive factors in scientific problem-solving strategies. Eur. J. Psychol. Educ. 2003, 28, 281–294. [Google Scholar] [CrossRef]
- Swanson, H.L. Influence of metacognitive knowledge and aptitude on problem solving. J. Educ. Psychol. 1990, 82, 306–314. [Google Scholar] [CrossRef]
- Zimmerman, B.J. Self-regulation involves more than metacognition: A social cognitive perspective. Educ. Psychol. 1995, 30, 217–221. [Google Scholar] [CrossRef]
- Borkowski, J.; Chan, L.; Muthukrishna, N. A Process-Oriented Model of Metacognition: Links between Motivation and Executive Functioning. Issues in the Measurement of Metacognition. 2000. Available online: http://digitalcommons.unl.edu/burosmetacognition/2 (accessed on 25 August 2019).
- Bransford, J.D.; Brown, A.L.; Cocking, R.R. How People Learn: Brain, Mind, Experience, and School; National Academy Press: Washington, DC, USA, 2000. [Google Scholar]
- Neumajer, O. Inovativní Výukové Aktivity pro Rozvoj Dovedností pro 21. Století. [Innovative Educational Activities for Development 21st Century Skills]; PF Univerzita Karlova: Prague, Czech Republic, 2014. [Google Scholar]
- Círus, L. Vliv Učitele na Formování Digitální Gramotnosti Žáků 1. Stupně Základní Školy. [Teachers’ Impact on Digital Literacy of Primary Pupils]. Ph.D. Thesis, Univerzita Hradec Králové, Hradec Králové, Czech Republic, 2017. [Google Scholar]
- Steffen, W.; Broadgate, W.; Deutsch, L.; Gaffney, O.; Ludwig, C. The trajectory of the Anthropocene: The Great Acceleration. Anthr. Rev. 2014, 2, 81–98. [Google Scholar] [CrossRef]
- Szczyrba, Z.; Klapka, P.; Kunc, J.; Tonev, P. Difúzní procesy v prostředí českého maloobchodu. Reg. Studia 2007, 1, 8–12. [Google Scholar]
- Zounek, J.; Šeďová, K. Učitelé a technologie. Mezi tradičním a moderním pojetím. Pedagogika 2009, 61, 414–418. [Google Scholar]
- Dooley, K.E. Towards a holistic model for the diffusion of educational technologies: An integrative review of educational innovation studies. Educ. Tech. Soc. 1999, 2, 35–45. [Google Scholar]
- Stuart, W.D. Influence of Sources of Communication, User Characteristics and Innovation Characteristics on Adoption of a Communication Technology. Ph.D. Thesis, The University of Kansas, Lawrence, KS, USA, 2000. [Google Scholar]
- Bennett, J.M.; Bennett, M.J. Developing intercultural sensitivity: An integrative approach to global and domestic diversity. In Handbook of Intercultural Training; Landis, D., Bennett, J., Bennett, M.J., Eds.; Sage: Thousand Oaks, CA, USA, 2003; pp. 147–165. [Google Scholar]
- Ogrezeanu, A.; Ogrezeanu, A. ICT use and attitudes among secondary education teachers in Romania. eLearn. Software Educ. 2014, 4, 458–465. [Google Scholar]
- Seymour, E. Tracking the processes of change in US undergraduate education in science, mathematics, engineering, and technology. Sci. Educ. 2002, 86, 79–105. [Google Scholar] [CrossRef]
- Light, P.C. Sustaining Innovation; Jossey-Bass: San Francisco, CA, USA, 1998. [Google Scholar]
- Zounek, J.; Sebera, M. Budoucí učitelé a inovace v oblasti informačních a komunikačních technologií [Prospective teachers and innovation in ICT area]. Studia Paedagog. 2005, 53, 95–108. [Google Scholar]
- Rusek, M.; Stárková, D.; Chytrý, V.; Bílek, M. Adoption of ICT Innovations by Secondary School Teachers and Pre-service Teachers within Education. J. Balt. Sci. Educ. 2017, 16, 510–523. [Google Scholar]
- Lamanauskas, V.; Vilkonis, R. Information and communication technologies in natural science education: Situational analysis and prospects in Baltic countries. J. Balt. Sci. Educ. 2007, 6, 35–49. [Google Scholar]
- Henriksen, D.; Henderson, M.; Čeretková, S.; Černochová, M.; Sendova, E.; Sointu, E.; Tienken, C. Creativity and Technology in Education: An International Perspective. Tech. Knowl. Learn. 2018, 23, 409–424. [Google Scholar] [CrossRef]
- Wilson, B. The relationships and impact of teachers’ metacognitive knowledge and pedagogical understandings of metacognition. Metacogn. Learn. 2010, 5, 269–288. [Google Scholar] [CrossRef]
- Bandura, A. Social Foundations of Thought and Action: A Social Cognitive Theory; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1986. [Google Scholar]
- Pintrich, P.R. The role of goal orientation in self-regulated learning. In Handbook of Self-Regulation; Boekarts, M., Pintrich, P.R., Eds.; Academic Press: San Diego, CA, USA, 2000; pp. 451–502. [Google Scholar]
- Zimmerman, B.J. Becoming a Self-Regulated Learner: An Overview. Theory Pract. 2002, 41, 64–70. [Google Scholar] [CrossRef]
- Tobias, S.; Everson, H.T. Cognition and metacognition. Issues Educ. 2000, 6, 167–173. [Google Scholar]
- Schraw, G.; Impara, J.C. Issues in the Measurement of Metacognition; Buros Institute of Mental Instruments, University of Nebraska-Lincoln: Lincoln, NE, USA, 2000. [Google Scholar]
- Ronzano, S. Effectiveness of Metacognitive Strategies for Improving Reading Comprehension in Secondary Students. Ph.D. Thesis, California State University, Long Beach, CA, USA, 2010. [Google Scholar]
- Flavell, J.H.; Wellman, H.M. Metamemory. In Proceedings of the Annual Meeting of the American Psychological Association 83rd, Chicago, IL, USA, 30 August–3 September 1975. [Google Scholar]
- Nelson, T.O.; Narens, L. A theoretical framework and new findings. In The Psychology of Learning and Motivation: Advances in Research and Theory; Bower, G., Ed.; Academic Press: New York, NY, USA, 1990; Volume 26, pp. 125–141. [Google Scholar]
- Efklides, A. Interactions of metacognition with motivation and affect in self-regulated learning: The MASRL model. Educ. Psychol. 2011, 46, 6–25. [Google Scholar] [CrossRef]
- Larkin, S. Socially mediated metacognition and learning to write. Think. Ski. Creat. 2009, 4, 149–159. [Google Scholar] [CrossRef]
- Schneider, W.; Artelt, C. Metacognition and mathematics education. ZDM Math. Educ. 2010, 42, 149–161. [Google Scholar] [CrossRef]
- Özsoy, G. An investigation of the relationship between metacognition and mathematics achievement. Asia Pac. Educ. Rev. 2011, 12, 227–235. [Google Scholar] [CrossRef]
- Morosanova, V.I.; Fomina, T.G.; Kovas, Y.; Bogdanova, O.Y. Cognitive and regulatory characteristics and mathematical performances in high school students. Personal. Individ. Differ. 2016, 90, 177–186. [Google Scholar] [CrossRef]
- Vo, V.A.; Li, R.; Kornell, N.; Pouget, A.; Cantlon, J.F. Young children bet on their numerical skills: Metacognition in the numerical domain. Psychol. Sci. 2014, 25, 1712–1721. [Google Scholar] [CrossRef] [PubMed]
- Cornoldi, C.; Carretti, B.; Drusi, S.; Tencati, C. Improving problem solving in primary school students: The effect of a training programme focusing on metacognition and working memory. Br. J. Educ. Psychol. 2015, 85, 424–439. [Google Scholar] [CrossRef]
- Van der Stel, M.; Veenman, M.V.J.; Deelen, K.; Haenen, J. The increasing role of metacognitive skills in math: A cross-sectional study from a developmental perspective. ZDM Math. Educ. 2010, 42, 219–229. [Google Scholar] [CrossRef]
- Veenman, M.V.J.; Kok, R.; Blote, A.W. The relation between intellectual and metacognitive skills in early adolescence. Instr. Sci. 2005, 33, 193–211. [Google Scholar] [CrossRef]
- Nowinska, E.; Praetorius, A. Evaluation of a Rating System for the Assessment of Metacognitive-Discursive Instructional Quality. CERME 10, February 2017. Dublin, Ireland. Available online: https://hal.archives-ouvertes.fr/hal-01949097/ (accessed on 7 September 2019).
- Flavell, J.H. Metacognition and cognitive monitoring: A new area of cognitive-developmental inquiry. Am. Psychol. 1979, 34, 906–911. [Google Scholar] [CrossRef]
- Říčan, J.; Škoda, J.; Doulík, P. Metakognice: Neujasněný konstrukt. In QUAERE; Proceedings from the Scientific Interdisciplinary Conference of Graduate Students and Junior Lecturers, 26–30 May 2014, Hradec Králové, Czech Republic; Magnanimitas: Hradec Králové, Czech Republic, 2014; Volume IV, pp. 1067–1074. [Google Scholar]
- Jacobs, J.E.; Paris, S.G. Children’s metacognition about reading: Issues in definition, measurement, and instruction. Educ. Psychol. 1987, 22, 255–278. [Google Scholar] [CrossRef]
- Veenman, M.V.J.; Van Hout-Wolters, B.H.A.M.; Affenbach, P. Metacognition and learning: Conceptual and methodological considerations. Metacogn. Learn. 2006, 1, 3–14. [Google Scholar] [CrossRef]
- Borkowski, J.G.; Milestead, M.; Hale, C. Components of childrens metamemory. In Memory Development: Universal Changes and Individual Differences; Weinert, F.E., Perlmutter, M., Eds.; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1988; pp. 73–100. [Google Scholar]
- Borkowski, J.G.; Chan, L.K.S.; Muthukrishna, N. A process-oriented model of metacognition: Links between motivation and executive functioning. In Issues in the Measurement of Metacognition; Schraw, G., Impara, J.C., Eds.; Buros Institute of Mental Measurements: Lincoln, OR, USA, 2000; pp. 1–42. [Google Scholar]
- Götz, L.; Lingel, K.; Schneider, W. Diagnostik mathematischer Kompetenzen in der Sekundarstufe I am Beispiel der Deutschen Mathematiktests für die fünften und sechsten Klassen (DEMAT 5+, DEMAT 6+) [Diagnostics of Mathematical Competencies in the Secondary Level I. Using the Example of the German Mathematical Tests for the Fifth and Sixth Grades (DEMAT 5+, DEMAT 6+)]. In Diagnostik Mathematischer Kompetenzen; (Tests und Trends, N.F. Bd. 11, 241–260); Hasselhorn, M., Heinze, A., Schneider, W., Trautwein, U., Eds.; Hogrefe Verlag: Göttingen, Germany, 2013. [Google Scholar]
- Schneider, W. The development of metacognitive knowledge in children and adolescent. Major trends and implications for education. Mind Brain Educ. 2008, 2, 114–121. [Google Scholar] [CrossRef]
- Neuenhaus, N. Metakognition und Leistung: Eine Längsschnittuntersuchung in den Bereichen Lesen und Englisch bei Schülerinnen und Schülern der Fünften und Sechsten Jahrgangsstufe [Metacognition and Performance: A Longitudinal Study in the Areas of Reading and English for 5 and 6 Grade Pupils]. Ph.D. Thesis, Universität Otto-Friedrich, Bamberg, Germany, 2011. [Google Scholar]
- Lai, R.E. Metacognition: A Literature Review. 2011. Available online: www.pearsonassessments.com (accessed on 14 January 2019).
- Azevedo, R. Theoretical, conceptual, methodological, and instructional issues in research on metacognition and self-regulated learning: A discussion. Metacogn. Learn. 2009, 4, 87–98. [Google Scholar] [CrossRef]
- Vališová, A.; Kasíková, H. Pedagogika pro Učitele. [Pedagogy for Teachers]; Grada Publishing: Prague, Czech Republic, 2007. [Google Scholar]
- Scott, M.B. Exploring the Effects of Student Perceptions of Metacognition Across Academic Domains. Ph.D. Thesis, Indiana University, Bloomington, IN, USA, 2008. [Google Scholar]
- Hidi, S. Interest and Its Contribuiton as a Mental Resource for Learning. Rev. Educ. Res. 1990, 60, 549–571. [Google Scholar] [CrossRef]
- Carr, M. The importance of metacognition for conceptual change and strategy use in mathematics. In Metacognition, Strategy Use, and Instruction; Waters, H.S., Schneider, W., Eds.; The Guilford Press: New York, NY, USA, 2010; pp. 176–197. [Google Scholar]
- Mevarech, Z.R. Metacognition, general ability, and mathematical understanding. Early Educ. Dev. 1995, 6, 155–168. [Google Scholar] [CrossRef]
- Schneider, W.; Schlagmüller, M.; Visé, M. The impact of metamemory and domain-specific knowledge on memory performance. Eur. J. Psychol. Educ. 1998, 13, 91–103. [Google Scholar] [CrossRef]
- Dunlosky, J.; Metcalfe, J. Metacognition; Sage Publications: Thousand Oaks, CA, USA, 2009. [Google Scholar]
- Wang, M.; Haertel, G.; Walberg, J.H. What influences learning? A content analysis of review literature. J. Educ. Psychol. 1990, 84, 30–43. [Google Scholar] [CrossRef]
- Veenman, M.V.J.; Spaans, M.A. Relation between intellectual and metacognitive skills: Age and task differences. Learn. Individ. Differ. 2005, 15, 159–176. [Google Scholar] [CrossRef]
- Gurat, M.G.; Medula, C. Metacognitive strategy knowledge use through mathematical problem solving amongst pre-service teachers. Am. J. Educ. Res. 2016, 4, 170–189. [Google Scholar]
- Soodla, P.; Jõgi, A.-L.; Kikas, E. Relationships between teachers’ metacognitive knowledge and students’ metacognitive knowledge and reading achievement. Eur. J. Psychol. Educ. 2017, 32, 201–218. [Google Scholar] [CrossRef]
- Handal, B.; Herrington, A. Mathematics teachers’ beliefs and curriculum reform. Math. Educ. Res. J. 2003, 15, 59–69. [Google Scholar] [CrossRef]
- Rieser, S.; Naumann, A.; Decristan, J.; Fauth, B.; Klieme, E.; Büttner, G. The connection between teaching and learning: Linking teaching quality and metacognitive strategy use in primary school. Br. J. Educ. Psychol. 2016, 86, 526–545. [Google Scholar] [CrossRef] [PubMed]
- Hart, L.C.; Memnun, D.S. The relationship between preservice elementary mathematics teachers’ beliefs and metacognitive awareness. J. Educ. Train. Stud. 2015, 3, 70–77. [Google Scholar] [CrossRef]
- Zee, M.; de Bree, E. Students’ self-regulation and achievement in basic reading and math skills: The role of student–teacher relationships in middle childhood. Eur. J. Dev. Psychol. 2017, 14, 265–280. [Google Scholar] [CrossRef]
- Gurbin, T. Metacognition and Technology Adoption: Exploring Influences. Procedia Soc. Behav. Sci. 2015, 191, 1576–1582. [Google Scholar] [CrossRef]
- Straub, E.T. Understanding technology adoption: Theory and future directions for informal learning. Rev. Educ. Res. 2009, 79, 625–649. [Google Scholar] [CrossRef]
- Schraw, G.; Dennison, R.S. Assessing Metacognitive Awareness. Contemp. Educ. Psychol. 1994, 19, 460–475. [Google Scholar] [CrossRef]
- Azevedo, R. Computer environments as metacognitive tools for enhancing learning. Educ. Psychol. 2005, 40, 193–197. [Google Scholar] [CrossRef]
- Lin, C.Y.; Hu, R.P. Students’ understanding of energy flow and matter cycling in the context of the food chain, photosynthesis, and respiration. Int. J. Sci. Educ. 2003, 25, 1529–1544. [Google Scholar] [CrossRef]
- Tu, Y.W.; Shih, M.; Tsai, C.C. Eighth graders’ web searching strategies and outcomes: The role of task types, web experiences and epistemological beliefs. Comput. Educ. 2008, 51, 1142–1153. [Google Scholar] [CrossRef]
- Kurtz, B.E.; Borkowski, J.G. Children´s metacognition: Exploring relations among knowledge, process, and motivational variables. J. Exp. Child Psychol. 1984, 37, 335–354. [Google Scholar] [CrossRef]
- Pressley, M.; Harris, K.R.; Marks, M.B. But good strategy instructors are constructivists. Educ. Psychol. Rev. 1992, 4, 3–21. [Google Scholar] [CrossRef]
- Schneider, W.; Pressley, M. Memory Development between Two and Twenty; Psychology Press: London, UK, 1997. [Google Scholar]
- Schraw, G. Promoting general metacognitive awareness. Instr. Sci. 1998, 26, 113–125. [Google Scholar] [CrossRef]
- Schleifer, D. Metacognition and performance in the accounting classroom. Issues Account. Educ. 2009, 24, 339–367. [Google Scholar] [CrossRef]
- Duchovičová, J.; Tomšik, R. Managerial Competencies of a Teacher in the Context of Learners’ Critical Thinking Development: Exploratory Factor Analysis of a Research Tool and the Results of the Research. TEM J. 2018, 7, 335–347. [Google Scholar] [CrossRef]
- Rogers, E.M. A prospective and retrospective look at the diffusion model. J. Health Commun. 2004, 9, 13–19. [Google Scholar] [CrossRef]
- Salaway, G.; Caruso, J. ECAR Study of Undergraduate Students and Information Technology. 2008. Available online: https://net.educause.edu/ir/library/pdf/ERS0808/RS/ERS0808w.pdf (accessed on 23 June 2018).
- Shaban, A.E.; Egbert, J. Diffusing education technology: A model for language teacher professional development in CALL. System 2018, 78, 234–244. [Google Scholar] [CrossRef]
- Bulun, M.; Gülnar, B.; Güran, S. Eğitimde Mobil Teknolojiler. Turk. Online J. Educ. Technol. TOJET 2004, 3, 165–169. [Google Scholar]
- Prabawani, B.; Hanika, I.M.; Pradhanawati, A.; Budiatmo, A. Primary Schools Eco-Friendly Education in the Frame of Education for Sustainable Development. Int. J. Environ. Sci. Educ. 2017, 12, 607–616. [Google Scholar]
- Abednia, A.; Crookes, G.V. Online Language Teacher Education for a Challenging Innovation: Towards Critical Language Pedagogy for Iran. In Innovation in Language Learning and Teaching. New Language Learning and Teaching Environments; Reinders, H., Coombe, C., Littlejohn, A., Tafazoli, D., Eds.; Palgrave Macmillan: Cham, Switzerland, 2019. [Google Scholar]
- Di Novi, C.; Marenzi, A. The smoking epidemic across generations, genders, and educational groups: A matter of diffusion of innovations. Econ. Hum. Biol. 2019, 33, 155–168. [Google Scholar] [CrossRef] [PubMed]
- Huang, R.; Spector, J.M.; Yang, J. Emerging Issues in Educational Technology. In Educational Technology; Springer: Singapore, 2019. [Google Scholar]
- Armstrong, E. Maximising motivators for technology-enhanced learning for further education teachers: Moving beyond the early adopters in a time of austerity. Res. Learn. Technol. 2019, 27. [Google Scholar] [CrossRef]
- Maeda, M.; Ono, Y. Diffusion of lesson study as an educational innovation. Int. J. Comp. Educ. Dev. 2019, 21, 46–60. [Google Scholar] [CrossRef]
- Černochová, M.; Siňor, S.; Kankaanrinta, I.K. Jak budoucí učitelé přijímají novinky ze světa informačních a komunikačních technologií [How prospective teachers accept news from the world of information and communication technology]. In Nové Možnosti Vzdělávání a Pedagogický Výzkum; Lukášová, H., Květoň, P., Eds.; Ostravská univerzita, Pedagogická fakulta: Ostrava, Czech Republic, 2001; pp. 330–336. [Google Scholar]
- Tavakol, M.; Dennick, R. Making sense of Cronbach’s alpha. Int. J. Med. Educ. 2011, 2011, 53–55. [Google Scholar] [CrossRef] [PubMed]
- Schlagmüller, M.; Schneider, W. WLST 7-12. Würzburger Lesestrategie-Wissenstest für die Klassen 7-12. [WLST 7-12. Würzburg Reading Strategy Knowledge Test for grades 7-12.]; Hogrefe Publishing Group: Göttingen, Germany, 2007. [Google Scholar]
- Artelt, C.; Beinicke, A.; Schlagmüller, M.; Schneider, W. Diagnose von Strategiewissen beim Text verstehen. Z. Entwickl. Pädagogische Psychol. 2009, 41, 96–103. [Google Scholar] [CrossRef]
- Wirth, J.; Leutner, D. Self-regulated learning as a competence. Z. Psychol. J. Psychol. 2008, 216, 102–110. [Google Scholar] [CrossRef]
- Lind, G.; Sandmann, A. Lernstrategien und Domänen wissen. Z. Psychol. 2003, 211, 171–192. [Google Scholar] [CrossRef]
- Neuenhaus, N.; Artelt, C.; Lingel, K.; Schneider, W. Fifth graders metacognitive knowledge: General or domain-specific? Eur. J. Psychol. Educ. 2011, 26, 163–178. [Google Scholar] [CrossRef]
- Chytrý, V.; Pešout, O.; Říčan, J. Preference Metakognitivních Strategií na Pozadí Úkolových Situací v Matematice u Žáků Druhého Stupně ZŠ. [Preference of Metacognitive Strategies on the Background of the Problem Situations in Mathematics in Lower-Secondary Pupils]; University of Jan Evangelista (UJEP): Ústí nad Labem, Czech Republic, 2014. [Google Scholar]
- Chytrý, V.; Kroufek, R. Možnosti využití Likertovy škály v pedagogickém výzkumu na příkladu analýzy vztahu člověka k přírodě [The possibilities of the use of Likert scales in educational research on the example of the analysis of a man’s relation to nature]. Sci. Educ. 2017, 8, 2–17. [Google Scholar]
- Rosenthal, R.; Rosnow, R.L.; Rubin, D.B. Contrasts and Effect Sizes in Behavioral Research: A Correlational Approach; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Fritz, C.O.; Morris, P.E.; Richler, J.J. Effect size estimates: Current use, calculations, and interpretation. J. Exp. Psychol. Gen. 2012, 141, 2–18. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Science, 2nd ed.; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1988. [Google Scholar]
- Hendl, J. Přehled Statistických Metod: Analýza a Metaanalýza dat. [Review of Statistical Methods: Data Analysis and Metaanalysis] 4., rozš. vyd; Portál: Prague, Czech Republic, 2012. [Google Scholar]
- Soukup, P. Nesprávná užívání statistické významnosti a jejich možná řešení. [Wrong use of statistical significance and its possible solutions]. Data Výzkum SDA 2010, 4, 77–104. [Google Scholar]
- Loftus, G.R. Psychology will be a Much Better Science when we Change the Way we Analyze Data. Curr. Dir. Psychol. Sci. 1996, 1, 161–171. [Google Scholar] [CrossRef]
- Robinson, D.H.J.; Levin, R. Reflections on statistical and substantive significance with a slice of replication. Educ. Res. 1997, 26, 21–27. [Google Scholar] [CrossRef]
- Schmidt, F. Statistical significance testing: Implications for the training of researchers. Psych. Methods 1996, 1, 115–129. [Google Scholar] [CrossRef]
- Cohen, B. Explaining Psychological Statistics, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2008. [Google Scholar]
- Moore, G.A. Crossing the Chasm. Marketing and Selling Disruptive Products to Mainstream Customers; HarperCollins Publishers: Pymble, Australia, 1999. [Google Scholar]
- Zakaria, Z. Factors Related to Information Technology Implementation in the Malaysian Ministry of Education Polytechnic. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2001. [Google Scholar]
- Valentín, A.; Mateos, P.M.; GonzáLez-Tablas, M.M.; Pérez, L.; López, E.; García, I. Motivation and learning strategies in the use of ICTs among university students. Comput. Educ. 2013, 61, 52–58. [Google Scholar] [CrossRef]
- Čeretková, S.; Melušová, J.; Šunderlík, J. Guide of Supporting Actions for Teachers in Promoting Inquiry-Based Learning. 2013. Available online: https://primas-project.eu/wp-content/uploads/sites/323/2017/11/FINAL_WP5_short-Guide-supporting-actions_licence_150708.pdf (accessed on 27 August 2019).
- Griffith, P.L. What is metacognition and what should be its role in literacy instruction? In Metacognition in Literacy Learning: Theory, Assessment, Instruction and Professional Development; Israel, S.E., Ed.; Lawrence Erlbaum Associates, Inc.: Mahwah, NJ, USA, 2005; pp. 3–18. [Google Scholar]
- Risko, V.J.; Roskos, K.; Vukelich, C. Reflection and the self-analytic turn of mind: Towards more robust instruction in teacher education. In Metacognition in Literacy Learning; Israel, S.E., Block, C.C., Bauserman, K.L., Kinnucan-Welsch, K., Eds.; Lawrence Erlbaum Associates, Inc.: Mahwah, NJ, USA, 2005; pp. 315–333. [Google Scholar]
- Hutton, L.A. The Impact of Reading Strategy Instruction on Struggling English Language Learners; University of California: Los Angeles, CA, USA, 2002. [Google Scholar]
- Pressley, M. Metacognition in literacy learning: Then, now and in the future. In Metacognition in Literacy Learning; Israel, S.E., Block, C.C., Bauserman, K.L., Kinnucan-Welsch, K., Eds.; Lawrence Erlbaum Associates, Inc.: Mahwah, NJ, USA, 2005; pp. 391–408. [Google Scholar]
- Anders, P.L.; Hoffman, J.V.; Duffy, G.G. Teaching teachers to teach reading: Paradigm shifts, persistent problems, and challenges. In Handbook of Reading Research; Kamil, M.L., Mosenthal, P.B., Pearson, P.D., Barr, R., Eds.; Lawrence Erlbaum Associates, Inc.: Mahwah, NJ, USA, 2000; Volume 3, pp. 719–742. [Google Scholar]
- Hunsaker, S.L.; Nielsen, A.; Bartlett, B. Correlates of Teacher Practices Influencing Student Outcomes in Reading Instruction for Advanced Readers. Gift. Child Q. 2010, 54, 273–282. [Google Scholar] [CrossRef]
- Cummins, C.; Stewart, M.T.; Block, C.C. Teaching several metacognitive strategies together increases students’ independent metacognition. In Metacognition in Literacy Learning; Israel, S.E., Block, C.C., Bauserman, K.L., Kinnucan-Welsch, K., Eds.; Lawrence Erlbaum Associates, Inc.: Mahwah, NJ, USA, 2005; pp. 391–408. [Google Scholar]
- Wenglinsky, H. How schools matter: The link between teacher classroom practices and student academic performance. Educ. Policy Anal. Arch. 2002, 10, 1–33. [Google Scholar] [CrossRef]
- Israel, G.D. Determining Sample Size. Fact Sheet PEOD-6 in Program Evaluation and Organizational Development, University of Florida. 1992. Available online: http://sociology.soc.uoc.gr/socmedia/papageo/metaptyxiakoi/sample_size/samplesize1.pdf (accessed on 15 August 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).