Abstract
Distance education has been gaining popularity for the last years. The proficiency in online environments of both learners and teachers explains the success of this methodology. An evaluation of graduate students’ performance within numerical analysis is discussed. In order to improve the marks obtained by the students, specific actions have been performed over the years and data from different classes has been analyzed using statistical tools. The results show that the actions proposed seemed to help the students in their learning process.
MSC:
97B40; 97N40; 62H99; 65-01
1. Introduction
The acronym STEM (science, technology, engineering, mathematics) has been growing in strength during the last few years in the academic community. There are several teaching institutions that are focusing their studies on this wide area that covers these disciplines in an integrated form. The intertwining of the four areas is achievable in different contexts, such as informal education [1], high-school [2] and university [3,4].
Mathematical subjects have been difficult to learn because of their inherent features, such as abstraction, prerequisites and technicalities, amongst others, which often leads to a lack of motivation. As cited in [5], this stimulus can be improved by increasing the efficiency of the mathematical learning in the first levels of early childhood. Self-efficacy, defined as learners’ judgments about their ability to successfully attain educational goals [6], has been analyzed in relation to its importance in university populations [7,8]. Moreover, the relationship between the motivation and both self-efficacy and teacher emotional support is highlighted elsewhere [9]. When the students reach university education, their fundamental problems remain, and, if they do not have a wide background, their motivation can fall dramatically.
For many years, it has not been questioned that the responsibility of the learning process is exclusively on the students’ shoulders [10]. There is an imbalanced deal between students and teachers. Therefore, when results are not as expected, teachers have the chance to start a two-step process, with the main questions being why and how. The former consists of an analysis of areas of failure: connection with students, mistakes in the platform, time devoted to self-learning, etc. The third example sets the spotlight on what actions can be considered to counter the inconveniences and boost the motivation of the students: including reinforcement sessions, reworking the teaching material, modifying the master lesson structure, etc.
The teaching strategy is essential. The first division reclassifies this strategy from student-centered to teacher-centered [11]. The former is the traditional way, which students pay attention to the teacher and collaboration in tasks is discouraged. In the latter, students and teachers interact equally, and group tasks are encouraged. There have been studies that analyzed the performances of students in courses with the same content but with different teaching methods [12]; they showed better results where the model was student-centered than teacher-centered.
Relating to the teaching strategies, Tourón and Martín present different teaching techniques [13], ranging from the low participation of the student, such as in a master class, to the inductive methodologies, such as project-based learning [14], problem-based learning [15,16] and challenge-based learning [17].
Project-based learning’s objective is the creation of a final product. To this end, multidisciplinary teams are formed in which the process is more important than the content. The seed of the project is a question, and students may search information for its solution. There have been some studies in higher education about the effectiveness of this learning methodology [18]. For instance, Hassan et al. [19] worked on a project with students—designing and developing a robot arm. The lecturer’s evaluation was performed by comparing the new methodology with the traditional one, and the authors concluded that students achievements increased. The students’ evaluation was performed by a survey about project-based learning. Students considered that this methodology was closer to the reality.
Problem-based learning (PBL) empowers students to conduct research, integrate theory into practice and apply skills to solve a problem [20]. It could be renamed problem-centered. The main benefits are an increase in motivation [21], a research attitude and the argumentation of the solution. On the part of the teacher, the problems should be well defined. They must integrate various contents of the subject that address different competences. Several authors [22,23,24,25] show how they have applied problem-based methodology to a course concerning numerical methods.
Challenge-based learning develops the applicability and transferability of concepts, given that the approach implies the use of inductive methodology. This kind of learning is fruitful when different teachers collaborate in the solution of the challenge, becoming mediators. Students generate questions and actions for getting such a solution, and get a roadmap in the learning process. Baloian et al. [26] established specific scenarios for the development of this learning model, giving details of the activities. Swiden [27] focused on students, analyzing their increased motivation and achievement.
Table 1 collects the main differences between these three models [13].

Table 1.
Comparison of dimensions in project-based, problem-based and challenge-based learning.
In this paper, the academic performance in a subject related to numerical analysis is reviewed over different years. Our learning method can be classified as problem-based learning. The results of the students were not as expected over the first few years. Therefore, the first step was the pondering of why these results were obtained. Different actions [13,20,28] applied on the diagnostics were implemented throughout the following years. The goal of the statistical study was to analyze whether the actions included collaborated to enhance the academic performances of the students, or, in return, whether new actions need to be drawn.
This paper is organized as follows. In Section 2 the online education course is introduced and analyzed. In addition, the problem is stated in terms of the course whose academic performance desires improvement, the student profile, the educational tools available, the methodology of the course, the problems detected and the actions undertaken. In Section 3 the methodology of the study is introduced. Section 4 shows the results of the statistical study we carried out to verify whether the actions taken have had an effect. Section 5 discusses the interpretation of the results obtained. Finally, Section 6 describes the conclusions of the research and what lines can be followed to anticipate problems in student performance.
2. Online Education
At the beginning of 21st century, Harasim [29] predicted that online education would go from peripheral to an integral part of mainstream society. In the early years of the century, many studies analyzed pros and cons of distance education [30,31], focusing the success on the self-motivated and self-disciplined students. Current studies [32,33] analyze the deployment of distance education, moving closer to the reality of online formative assessment. Moreover, instructors need to be proficient in computer-based learning. The combination of well prepared teachers and good digital resources generates good learning experiences for every student [34].
Blended and online education have been growing in popularity in recent years. In addition, massive open online courses (MOOC) are promoted in both institutional and social networks platforms [35]. However, we are focusing on direct communication with the student, unless the MOOC course is integrated in the classroom [36]. Several studies [37,38] remark on not only the web-based learning or the comfort of studying at home, but the instructional model being student-centered.
In the online world there are no barriers for learning, since a subject or a syllabus can reach anywhere. Nowadays, there are many online undergraduate and graduate Universities all around the world, mostly private. This new learning paradigm in distance education allows people to follow their first career, to carry on graduate studies or to improve some skills in their current job. Thus, the number of potential students is broadened.
Information and communication technologies (ICT) have been put at the service of the educational society. The main tool, the learning management system (LMS), is becoming increasingly important. A LMS integrates a large number of sections, such as forums, videoconferences, contents, resources or tasks. Some examples of the most used LMS platforms are Moodle, Sakai and Canvas. In traditional universities, LMS is relevant, but usually ends up being a repository of resources that the teacher provides to the student. In online universities, where the learning-teaching process is completely online, the LMS plays a fundamental role at the core of the course [39], because it is the place where teachers and students interact.
Below, some of the new trends in online education are analyzed and applied in order to improve the academic performance of the students. Therefore, the first step consists of the analysis of the context, which is undertaken below.
2.1. The Course
The subject under study is classified in the area of numerical analysis, as mentioned before, in a graduate course. The specific competences that students will acquire when they complete the course are:
- The ability to solve advanced mathematical problems, and plan their resolution according to available tools and time and resource constraints;
- The ability to understand and apply advanced computer knowledge and numerical or computational methods to engineering problems in order to solve them in the most appropriate way for each situation;
- The ability to choose and use computer applications, numerical and symbolic calculations or others, and to experiment in mathematics and solve complex problems.
The syllabus of the course includes the study of initial value problems, boundary value problems, partial differential equations and iterative methods for solving nonlinear equations and systems. Let us remark that these concepts are dealt with in the field of the numerical analysis. Therefore, the subject requires an effort on the part of the students both in the domain of mathematics and in that of computing.
2.2. The Students
The student profile is similar to that of the rest of graduate courses at the Engineering School. Regarding the specific subject, there are no differences in the profile compared to other subjects with high contents of mathematics or computer science.
The majority of the students are male, as represented in Figure 1. This imbalance does not affect the results, but ratifies the profile with respect to other studies.
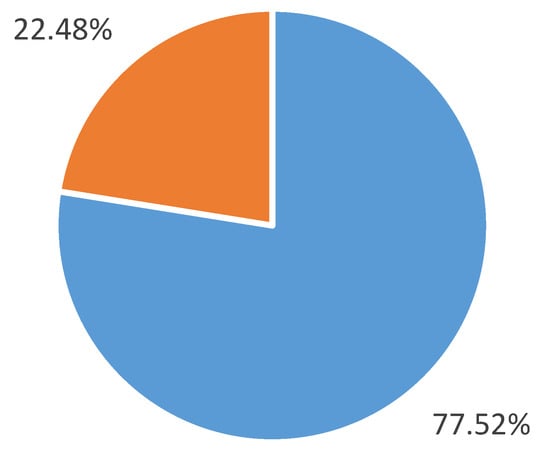
Figure 1.
Gender distribution of the students: male (blue) and female (orange).
The lessons are in Spanish. This fact discriminates among the students that enroll our studies. Therefore, the locations of the students are usually countries such as Spain, or Latin America. The location distribution of the students is represented in Figure 2. It can be seen that the main portion of the students is from Ecuador.
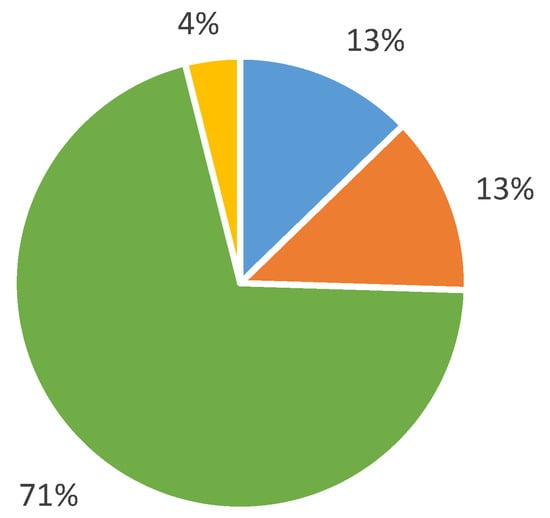
Figure 2.
Location distribution of the students: Spain (blue), Colombia (orange), Ecuador (green), rest of Latin America (yellow).
Finally, if we focus on the age groups, we find the percentage of the students by age in Figure 3. The range of ages above 25 is balanced. However, this is not very common in traditional teaching, because students tend to belong to the first range of ages.
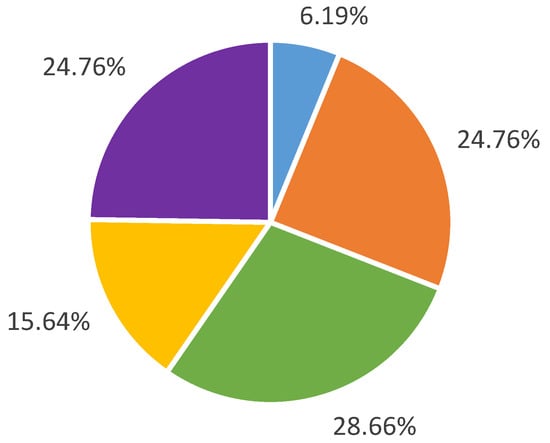
Figure 3.
Age distribution of the students: <24 (blue), 25–29 (orange), 30–34 (green), 35–39 (yellow), >40 (purple).
All students share a particularity that should be noted: they are working while studying. This common feature of the students indicates that they may not have much time to study for their final exams. In addition, 90% of the total number of students have family issues that require their attention. This contributes to the fact that after working, when they arrive at their homes, their time of allocation to study might be less than expected.
Therefore, the main characteristics of the students that allowed us to extract the first conclusions were
- Active employment situation;
- Family and personal issues to attend to;
- Age above the average of the students attending a face-to-face postgraduate course.
2.3. Educational Resources
Educational resources in an online teaching institution should mitigate the physical distance between students and the university. Most of these resources are common for every course in the institution. More details about these resources are provided below.
- The coach. Each student has the support of a coach, who contacts the student weekly. The coach guides the student through study techniques, collects their suggestions and transmits the most relevant comments to the teachers of the subject.
- The instructors. The professors of the subject have wide experience in the teaching of the contents. In addition, part of their research is focused on the aspects that are dealt with in the subject. As recommended by [34], these teachers are trained in the use of digital resources.
- The LMS. The platform on which interactions take place integrates multiple tools. On the static side, students can find a textbook, the slides used in the live lessons or the deliverable activities. Let us remark that this part can be modified along the course. On the dynamic side, there are forums for general queries or doubts, or links to join the live lessons.
- The course software. Given the characteristics of the subject—in which mathematics and computing are combined—the use of specialized software is required. Students have access to a license for downloading the software in their desktops. They also have the support of the coach if they have any problem in this process.
- The textbook. The teacher of the subject, prior to its teaching, is responsible for the writing of the textbook. The book details the contents, theoretical ideas, examples with solutions and external resources for further information.
- The live lessons. There are online live lessons, that can be classified in two groups: general and laboratory sessions. In general sessions, the concepts of the textbook are explained and exercises are solved step-by-step. Students may participate at any time, requesting additional explanation or clarification. The instructors share their screen with the students to see how the exercises are implemented in the software. In laboratory sessions, the teachers introduce one or more problems to solve. Students work together in groups to solve the exercise. When students are in doubt, they can ask for the instructor’s help, who gives them an idea of the path they should follow. A critical part is that the students have to work afterwards on the lessons.
- The forums. This part of the LMS is where the general queries, doubts or problems are transmitted to the rest of the students and teachers. It is useful for students because they can raise a question that worries other participants as well. These questions are answered by teachers within 48 h. Moreover, it is also helpful for teachers in order to broadcast, for instance, unexpected events.
2.4. Methodology of the Course
Implementing a flipped classroom model was considered at first. However, this method that arranges the lecturing part of the teaching as homework often generates tensions. As [40] discusses, the tensions generated in a flipped classroom scenario are between the expectation of the students to be taught and the discipline to prepare the lesson before attending when a heavy workload is expected in parallel courses. Due to our experience in online education, the flipped model is hardly acceptable for students who combine study and work. Although educational resources are within their reach, they do not feel comfortable with this effort prior to the live lesson. However, we asked the students if the were willing to work under a flipped classroom approach and they answered that this method did not suit to their circumstances.
Under these circumstances, we believe that the optimal methodology for developing subject content is problem-based learning. Since the subject is taught within the applied mathematics context, it is essential to solve and apply real problems, as well as understand theoretical models. In addition, this approach was to help us to introduce and solve new problems that could help the students in their learning process. Taking into account the personal circumstances of the students, we agreed that the best teaching strategy ranged from teacher-centered to student-centered. In the theoretical part and the step-by-step solving of the sessions, the focus was on the teacher. In the laboratory sessions, the students took the leading role.
The subject included a continuous assessment and a final exam on site, following the teaching model of the university. The continuous assessment comprised deliverable problems that deepened the main problems of the subject, and interaction in forums with specific content. The problems to be solved had the structure of the problem solving process, with a scheme similar to that of [24] adapted to the content of the course. The final exam on site consisted of three problems to solve with the help of computers, and students were allowed to bring all teaching materials and personal notes to the exam table, under the same conditions as in laboratory sessions. There was only one constraint: students were unable to communicate with each other during the exam, and, consequently, they could not connect to the Internet.
Although the students’ performance in the continuous assessment seemed to be good, their performance in the final exam was poor. Henceforth, only the results of the final exam on site are analyzed.
2.5. The Problems
After the first few academic years, the rate of success was not as expected. Therefore, an roadmap was designed including two main lines. The first one was to initiate a process of self-criticism with the staff about our teaching methods. The problems founded were:
- i
- The teaching approach. We agreed that a student-centered approach would be more suitable for the students than a teacher-based centered approach. As mentioned before, two possibilities were considered: the flipped classroom approach and the problem-based learning approach.
- ii
- The contents of the textbook were too theoretical.
- iii
- Students needed to solve more exercises.
Later, students’ were directly asked for their opinions in different contexts: alone with the coach, alone with the director of the subject or in group with other students and the staff of the subject. Below there are some of the main findings:
- iv
- The students thought that the contents of the course were difficult.
- v
- The students requested a shorter final exam or an increase in time to solve it.
- vi
- The book had many misprints and not every piece of content was well developed.
- vii
- Many students needed more examples to verify their capabilities to solve exercises and to internalize the concepts.
2.6. Actions
Taking into account the main results of the comments of the learners and the analyses of the teachers, some actions were carried out in order to improve the results of the students. The highlighted actions were the following ones.
- Continuous assessment activities. The activities of the continuous assessment are explained in the online lessons. The explanation involves the techniques to be used for solving the exercises and what is expected in each answer: table of results, implementation code, discussion of the results, representation of functions, etc.
- Improvement of the feedback process. The feedback process was improved, taking into account the seven rules about feedback of [13] and principle 6 of [41].
- Reedited version of the book. The book’s contents were completely revisited and rewritten. Based on the previous book, the misprints were corrected and the information that was less relevant was eliminated. In addition, some clarifications were included, using specifically, bibliography [42,43,44,45]. Finally, more problems with detailed solutions were provided.
- Overview seminar. Before the final exam, a seminar of 30 h was imparted. The attendance for students was optional but highly recommended, since different problems were going to be solved. Moreover, the students had the chance to send activities and receive individual feedback.
- Update of activities. The activities of the continuous assessment were updated. That way, the questions were more specific, and the structure of the activities was more similar to their structure in the final exam.
All actions were related to one or more detected problems, and each problem was expected to be resolved by one or more actions. These dependencies are listed in Table 2. Let us note that, although the time to solve the exam was not increased, we planned to solve the problem by making the students feel more confident.

Table 2.
Relationships between problems and actions.
3. Methodology of the Study
Since it is impossible to implement all changes at once, the actions described in Section 2 were carried out gradually. This allowed us to analyze whether the activities and changes really improved the students’ performances. The following methodology was applied:
- The groups were formed by four consecutive classes: “Class 1”, “Class 2”, “Class 3” and “Class 4”. The actions and changes described in Section 2 were gradually implemented over two years, as follows.
- Students of the Class 1 learned with problem-based learning lessons.
- Students of the Class 2 received a detailed explanation of the activities of the continuous assessment before they had to develop them as well as complete feedback based on [13,41].
- From Class 2 to Class 3 the major change was applied, because the full contents of the book were readdressed. This change consisted of correcting the misprints, including more examples solved step-by-step, descriptions of many pseudo-codes for implementing the programs that students need and inclusion of the complete code for particular cases. In these major changes, the activities of the continuous assessment were updated, taking into account the difficulties of comprehension that concerned students.
- Finally, besides all the aforementioned changes, we decided to include an overview seminar for students of Class 4.
- In this experiment, no control group was considered. This is due to ethical issues: since the marks scored by Class 1 students were very low, we considered that improving all students’ learning was more important than conducting a more reliable experiment. Consequently, there was no random selection, so we conducted a quasi experimental design.
- In all classes, assessment was carried out by the same evaluator.
- Since we were interested in analyzing the student’s improvements during the teaching period of the subject, we only considered the exam results obtained immediately after the course ended. The results of the rest of the activities were not considered since they were the improvement elements, whose real influence we wanted to determine.
- To guarantee independence, repeating students were removed from the following classes; that is, we only considered the marks of their first exam.
- A one-way ANOVA test was performed to determine whether the means of marks scored by the students of the classes were equal between groups [46]; that is, we wanted to find out if the hypothesis “the means are equal” could be accepted or not. The significance level was set at 0.05%.
- When the null hypothesis of the ANOVA test was rejected, it was important to explore differences between means. To know which specific means differed from the rest, the post hoc Bonferroni test was used [47]. This test performed multiple comparisons and the p-value was adjusted in order to control the type I error. This error was reduced at the expense of a type II error, so we have to take into account that when the number of comparisons is large, the test may become too conservative and no significant differences will be found. In this study, we did not have to perform a large amount of comparisons and, since we were interested in controlling the type I error, it was appropriate to use Bonferroni test.
4. Results
First, a basic descriptive statistics analysis was performed to have a view of the data based on central and dispersion measures. Table 3 shows the means of marks and standard deviations obtained. Figure 4 shows the means of marks over the time.

Table 3.
Means of marks and standard deviations.
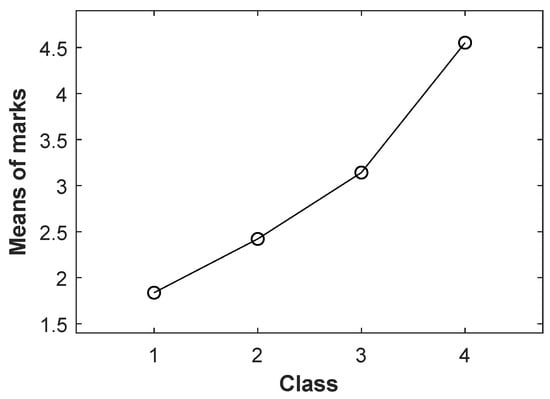
Figure 4.
Means of marks scored by the students of the classes.
As represented in Figure 4, there is an upward trend in the mean values as we move through the groups. Let us remark that values evolved from less than 2 to more than 4.5.
However, to determine if the increase in the means of the marks was significant through the different classes, a hypothesis test had to be performed. The results of the one-way ANOVA test are displayed in Table 4.

Table 4.
One-way ANOVA test results.
The reported p-value in Table 4 indicated that we could not accept the hypothesis of equal means. Thus, it was necessary to carry out a post-hoc analysis, in order to determine which groups had different means than others. Bonferroni post-hoc test results are shown in Table 5.

Table 5.
Bonferroni post-hoc test results.
Table 5 shows that the mean corresponding to Class 4 is significantly different from the means of marks obtained by Class 1 and Class 2 to students. The mean scored by Class 3 students is significantly different from the mean corresponding to Class 1 but it is not different from the mean corresponding to Class 2. So, the monotonous growth of the means implies significant differences between non-correlative groups.
5. Discussion
The new teaching methodologies deal with the old problems: difficulty in teaching abstract subjects, different competence levels within each class and lack of time or resources on the part of the students. We have to take into account that the demand on STEM competencies is continuously increasing, so as teaching professionals, we need to learn how to face these challenges.
Our learning methods can be classified as problem-based learning. And although the methodology was applied as recommended by experts, the first analytical study of the results was not as expected.
The students’ assessments for Class 1 were very unsatisfactory, both for teachers and students, despite students who already had a degree and who liked mathematics.
Consequently, a series of changes aimed at improving the learning process were implemented. The changes were very different: to propose a model of continuous evaluation, to improve the feedback to the student, to reedit the book, to offer an overview seminar and to update the activities. In general, it can be seen that the approach was not focused on one single aspect, but rather, the problem was attacked by proposing different types of changes.
The results displayed in Section 4 show that students’ mean performance follows an increasing monotonic curve and the p-value of the ANOVA test allowed us to reject the hypothesis of equality of means, which seemed to indicate that the changes were producing the desired effect. Although the quasi-experimental design does not allow us to affirm that the improvement was due to the changes introduced, as the profiles of the students are homogeneous, assessments were carried out by the same evaluator and the samples were independent. We did not find any other factor that could explain the change.
Although differences between standard deviations were not observed, the differences between the means of marks are considerable, since the average rating has been multiplied by approximately 2.5 from the beginning.
The results of the post hoc tests are also noteworthy: between two consecutive classes the differences in the means are not significant, but they are significant between non-consecutive classes: the average of Class 1 is significantly lower than the average of Classes 3 and 4, and the means scored by students of Classes 2 and 4 are significantly different.
In summary, we can conclude that it is important to make a continuous reflections on the learning process of students and continually question whether the methodology we apply is the most appropriate or not: in short, it is about getting everyone to learn as much as possible and this cannot be achieved by applying canned formulas. It is necessary to analyze where the learning problems are and also to reflect on them in the most global way possible so as not to leave any important aspect without contemplation. In addition, the analysis will be more complete if instead of being carried away by intuitions, we make a design for data processing and then analyze the results. That way, we can make decisions based on data that will always be more objective.
6. Conclusions and Future Work
Once it was statistically seen that the students’ success rate was greatly improved, we could only assume that this improvement was due to the different actions taken in the classes as described among others in [13]. We concluded that the actions we took collaborated to enhance the academic performance of the students in a problem-based methodology within a course concerning numerical methods.
In the future, we will continue working in order to improve students’ performances. We will keep introducing changes and analyzing their impacts. Although assessments seem to have improved, we must try to obtain an average mark above 5. Thus, we plan to introduce collaborative work during the course and reinforcement resources to allow them to review the basic ideas before starting the course. Moreover, we will apply what has been learned in this experiment to other subjects and vice versa: we also want to learn from the changes introduced by our colleagues to improve the quality of teaching.
Author Contributions
The individual contributions of the authors are as follows: conceptualization, F.I.C.; methodology, E.G.; software, Í.S.; formal analysis, E.G.; data curation, Í.S.; writing—original draft preparation, F.I.C., E.G. and Í.S.; writing—review and editing, F.I.C., E.G. and Í.S.; project administration, F.I.C.
Funding
The first author has been supported by PGC2018-095896-B-C22 (MCIU/AEI/FEDER/UE).
Acknowledgments
We would like to express our thankfulness to the anonymous reviewers for their comments to improve the final version of this research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Burrows, A.; Lockwood, M.; Borrowczak, M.; Janak, E.; Barber, B. Integrated STEM: Focus on Informal Education and Community Collaboration through Engineering. Educ. Sci. 2018, 8, 4. [Google Scholar] [CrossRef]
- Wiswall, M.; Stiefel, L.; Schwartz, A.E.; Boccardo, J. Does attending a STEM high school improve student performance? Evidence from New York City. Econ. Educ. Rev. 2014, 40, 93–105. [Google Scholar] [CrossRef]
- Grout, I. Remote laboratories as a means to widen participation in STEM education. Educ. Sci. 2017, 7, 85. [Google Scholar] [CrossRef]
- Nakakoji, Y.; Wilson, R. First-Year mathematics and its application to science: Evidence of transfer of learning to Physics and Engineering. Educ. Sci. 2018, 8, 8. [Google Scholar] [CrossRef]
- Orcos, L.; Hernández-Carrera, R.M.; Espigares, M.J.; Magreñán, Á.A. The Kumon method: Its importance in the improvement on the teaching and learning of mathematics from the first levels of early childhood and primary education. Mathematics 2019, 7, 109. [Google Scholar] [CrossRef]
- Elias, S.M.; MacDonald, S. Using past performance, proxy efficacy, and academic self-efficacy to predict college performance. J. Appl. Soc. Psychol. 2007, 37, 2518–2531. [Google Scholar] [CrossRef]
- Robbins, S.B.; Lauver, K.; Le, H.; David, D.; Langley, R. Do psychosocial and study skill factors predict college outcomes? A meta-analysis. Psychol. Bull. 2004, 130, 261–288. [Google Scholar] [CrossRef]
- Honicke, T.; Broadbent, J. The influence of academic self-efficacy on academic performance: A systematic review. Educ. Res. Rev. 2016, 17, 63–84. [Google Scholar] [CrossRef]
- Skaalvik, E.M.; Federici, R.A.; Klassen, R.M. Mathematics achievement and self-efficacy: Relations with motivation for mathematics. Int. J. Educ. Res. 2015, 72, 129–136. [Google Scholar] [CrossRef]
- Stipek, D.; Givvin, K.B.; Salmon, J.M.; Macgyvers, V.L. Can a teacher intervention improve classroom practices and student motivation in mathematics? J. Exp. Educ. 1998, 66, 319–337. [Google Scholar] [CrossRef]
- Killen, R. Effective Teaching Strategies: Lessons from Research and Practice; CENGAGE Learning: Boston, MA, USA, 2006. [Google Scholar]
- Jukic, L.; Dahl, B. What affects retention of core calculus concepts among university students? In Proceedings of the VII Congress of the European Society for Research in Mathematics Education, Rzeszów, Poland, 9–13 February 2011; pp. 2033–2042. [Google Scholar]
- Tourón, J.; Martín, D. Aprender y Enseñar en la Universidad Hoy; UNIR Editorial: Logroño, Spain, 2019. [Google Scholar]
- Kilpatrick, W.H. The Project Method: The Use of the Purposeful Act in the Education Process. Teach. Coll. Rec. 1918, 19, 319–335. [Google Scholar]
- Barrows, H.S.; Tamblyn, R.M. Problem-Based Learning: An Approach to Medical Education; Springer: Berlin, Germany, 1980. [Google Scholar]
- Savin-Banden, M.; Major, C.H. Foundations of Problem-Based Learning; McGraw Hill: New York, NY, USA, 2004. [Google Scholar]
- Johnson, L.F.; Smith, R.S.; Smythe, J.T.; Varon, R.K. Challenge-Based Learning: An Approach for Our Time; Technical Report; The New Media Consortium: West Lake Hills, TX, USA, 2009. [Google Scholar]
- Kokotsaki, D.; Menzies, V.; Wiggins, A. Project-based learning: A review of the literature. Improv. Sch. 2016, 19, 267–277. [Google Scholar] [CrossRef]
- Hassan, H.; Domínguez, C.; Martínez, J.M.; Perles, A.; Albaladejo, J.; Capella, J.V. Integrated Multicourse Project-based Learning in Electronic Engineering. Int. J. Eng. Educ. 2008, 24, 581–591. [Google Scholar]
- Savery, J.R. Overview of problem-based learning: Definitions and distinctions. In Essential Readings in Problem-Based Learning; Purdue University Press: West Lafayette, IN, USA, 2015; pp. 5–15. [Google Scholar]
- Laforce, M.; Noble, E.; Blackwell, C. Problem-Based Learning (PBL) and Student Interest in STEM Careers: The Roles of Motivation and Ability Beliefs. Educ. Sci. 2017, 7, 92. [Google Scholar] [CrossRef]
- Miranda, J.L.; Biscaia, H.E.C. A Problem-Based Learning Approach to Numerical Methods: Interface Behaviour in Glass FRP Strips Bonded to Reinforced Concrete Beams. In Proceedings of the International Conference on Engineering Education, Budapest, Hungary, 28–31 July 2008; pp. 1–10. [Google Scholar]
- Ketcheson, D.I. Teaching numerical methods with IPython notebooks and inquiry-based learning. In Proceedings of the 13th Python in Science Conference, Austin, TX, USA, 6–13 July 2014; pp. 20–26. [Google Scholar]
- Kortemeyer, J.; Biehler, R. The interface between mathematics and engineering–problem solving processes for an exercise on oscillating circuits using ordinary differential equations. In Proceedings of the X Congress of the European Society for Research in Mathematics Education, Dublin, Ireland, 1–5 February 2017; pp. 2153–2160. [Google Scholar]
- Cao, J.; Zhao, R. Research about problem-based learning mode in education reformation of numerical computation method course. Int. J. Electr. Eng. Educ. 2008, 56, 285–292. [Google Scholar] [CrossRef]
- Baloian, N.; Hoeksema, K.; Hoope, U.; Mirlad, M. Technologies and educational activities for supporting and implementing challenge-based learning. In Education for the 21st Century: Impact of ICT and Digital Resources; Springer: Boston, MA, USA, 2006; pp. 7–16. [Google Scholar]
- Swiden, C.L. Effects of Challenge Based Learning on Student Motivation and Achievement. Master’s Thesis, Montana State University, Bozeman, MT, USA, 2013. [Google Scholar]
- Gargallo, B.; Sánchez, F.; Ros, C.; Ferreras, A. Estilos docentes de los profesores universitarios. La percepción de los alumnos de los buenos profesores. Rev. Iberoam. Educ. 2010, 51, 1–16. [Google Scholar]
- Harasim, L. Shift happens: Online education as a new paradigm in learning. Internet High. Educ. 2000, 3, 41–61. [Google Scholar] [CrossRef]
- Hongmei, L. Distance education: Pros, cons, and the future. In Proceedings of the Annual Meeting of the Western States Communication Association, Long Beach, CA, USA, 2–5 March 2002; pp. 1–37. [Google Scholar]
- Taylor, R.W. Pros and cons of online learning—A faculty perspective. J. Eur. Ind. Train. 2002, 26, 24–37. [Google Scholar] [CrossRef]
- Gaylard, Z. Online formative assessment in higher education: Its pros and cons. Electron. J. E-Learn. 2015, 13, 228–236. [Google Scholar]
- Versteijlen, M.; Perez, F.; Groesbeek, M.J.; Counotte, A. Pros and cons of online education as a measure to reduce carbo emissions in higher education in the Netherlands. Curr. Opin. Environ. Sustain. 2017, 28, 80–89. [Google Scholar] [CrossRef]
- Sheninger, E.C.; Murray, T.C. Learning Transformed: 8 Keys to Designing Tomorrow’s Schools, Today; ASDC: New Delhi, India, 2017. [Google Scholar]
- Vázquez-Cano, E.; López, E.; Sevillano, M.L. The impact of the MOOC movement on social networks. A computational and statistical study on Twitter. Rev. Esp. Pedagog. 2017, 75, 47–64. [Google Scholar]
- Castaño-Garrido, C.; Garay, U.; Maiz, I. Factors for academic success in the integration of MOOCs in the university classroom. Rev. Esp. Pedagog. 2017, 75, 65–82. [Google Scholar]
- Hung, M.L.; Chou, C. Students’ perceptions of instructors’ roles in blended and online learning environments: A comparative study. Comput. Educ. 2015, 81, 315–325. [Google Scholar] [CrossRef]
- Rasheed, R.A.; Kasmin, A.; Abdullah, N.A. Challenges in the online component of blended learning: A systematic review. Comput. Educ. 2020, 144, 103701. [Google Scholar] [CrossRef]
- Balderas, A.; De-La-Fuente-Valentin, L.; Ortega-Gomez, M.; Dodero, J.M.; Burgos, D. Learning Management Systems Activity Records for Students’ Assessment of Generic Skills. IEEE Access 2018, 6, 15958–15968. [Google Scholar] [CrossRef]
- Fredriksen, H.; Hadjerrouit, S.; Monaghan, J.; Rensaa, R.J. Exploring tensions in a mathematical course for engineers utilizing a flipped classroom approach. In Proceedings of the X Congress of the European Society for Research in Mathematics Education, Dublin, Ireland, 1–5 February 2017; pp. 2057–2064. [Google Scholar]
- Lucariello, J.; Graham, S.; Nastani, B.; Dwyer, C.; Skiba, R.; Plucker, J.; Pitoniak, M.; Brabeck, M.; DeMaire, D.; Pritzker, S. Top 20 Principles from Psychology for preK-12 Teaching and Learning; American Psychological Association: Washington, DC, USA, 2015. [Google Scholar]
- Burden, R.L.; Faires, J.D. Numerical Analysis; CENGAGE Learning: Boston, MA, USA, 2010. [Google Scholar]
- Cordero, A.; Hueso, J.L.; Torregrosa, J.R. Cálculo Numérico: Teoría y Problemas; Editorial Universitat Politècnica de València: València, Spain, 2004. [Google Scholar]
- Chapra, S.; Canale, R. Numerical Methods for Engineers; McGraw Hill: New York, NY, USA, 2010. [Google Scholar]
- Cordero, A.; Hueso, J.L.; Martínez, E.; Torregrosa, J.R. Problemas Resueltos de Métodos Numéricos; Thomson-Paraninfo: Madrid, Spain, 2006. [Google Scholar]
- Heiberger, R.M.; Neuwirth, E. One-Way ANOVA. In R Through Excel; Springer: New York, NY, USA, 2009; pp. 165–191. [Google Scholar]
- Shaffer, J.P. Multiple Hypothesis Testing. Annu. Rev. Psychol. 1995, 46, 561–584. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).