Generalized High-Order Classes for Solving Nonlinear Systems and Their Applications
Abstract
1. Introduction
2. The GH Family for Solving Systems of Nonlinear Equations
- (a)
- , being , , and denotes the space of linear mappings from X to itself,
- (b)
- , where and .
- (c)
- , for and .
- (i)
- , , and .
- (ii)
- , , and .
3. Numerical Experience
3.1. Application of Family (3) to Fisher’s Equation
3.2. Application of Family GH to Nonlinear Test Systems
- (a)
- , where
- (b)
- , such that
- (c)
- , where
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Petković, M.S.; Neta, B.; Petković, L.D.; Džunić, J. Multipoint Methods for Solving Nonlinear Equations: A survey. App. Math. Comput. 2014, 226, 635–660. [Google Scholar]
- Cordero, A.; Torregrosa, J.R. On the Design of Optimal Iterative Methods for Solving Nonlinear Equations. In Advances in Iterative Methods for Nonlinear Equations; Amat, S., Busquier, S., Eds.; Springer: Cham, Switzerland, 2016; pp. 79–111. [Google Scholar]
- Kung, H.T.; Traub, J.F. Optimal order of one-point and multipoint iteration. J. Assoc. Comput. Math. 1974, 21, 643–651. [Google Scholar] [CrossRef]
- Cordero, A.; Gómez, E.; Torregrosa, J.R. Efficient high-order iterative methods for solving nonlinear systems and their application on heat conduction problems. Complexity 2017, 2017, 6457532. [Google Scholar] [CrossRef]
- Sharma, J.; Arora, H. Improved Newton-like methods for solving systems of nonlinear equations. SeMA J. 2017, 74, 147–163. [Google Scholar] [CrossRef]
- Amiri, A.; Cordero, A.; Darvishi, M.; Torregrosa, J. Stability analysis of a parametric family of seventh-order iterative methods for solving nonlinear systems. App. Math. Comput. 2018, 323, 43–57. [Google Scholar] [CrossRef]
- Cordero, A.; Hueso, J.L.; Martínez, E.; Torregrosa, J.R. A modified Newton-Jarratt’s composition. Numer. Algor. 2010, 55, 87–99. [Google Scholar] [CrossRef]
- Chicharro, F.I.; Cordero, A.; Garrido, N.; Torregrosa, J.R. Wide stability in a new family of optimal fourth-order iterative methods. Comput. Math. Methods 2019, 1, e1023. [Google Scholar] [CrossRef]
- Artidiello, S. Diseño, Implementación y Convergencia de Métodos Iterativos Para Resolver Ecuaciones y Sistemas No Lineales Utilizando Funciones Peso. Ph.D. Thesis, Servicio de publicaciones Universidad Politécnica de Valencia, Valencia, Spain, 2014. [Google Scholar]
- Ortega, J.M.; Reinhboldt, W.C. Iterative Solution of Nonlinear Equations in Several Variables; Academic Press: Cambridge, MA, USA, 1970. [Google Scholar]
- Fisher, R.A. The wave of advance of advantageous genes. Ann. Eugen. 1933, 7, 353–369. [Google Scholar] [CrossRef]
- Sharma, J.; Guha, R.; Sharma, R. An efficient fourth order weighted-Newton method for systems of nonlinear equations. Numer. Algor. 2013, 62, 307–323. [Google Scholar] [CrossRef]
- Ostrowski, A. Solution of Equations and Systems of Equations; Prentice-Hall: Upper Saddle River, NJ, USA, 1964. [Google Scholar]
- Soleymani, F.; Lotfi, T.; Bakhtiari, P. A multi-step class of iterative methods for nonlinear systems. Optim. Lett. 2014, 8, 1001–1015. [Google Scholar] [CrossRef]
- Cordero, A.; Torregrosa, J.R. Variants of Newton’s method using fifth order quadrature formulas. Appl. Math. Comput. 2007, 190, 686–698. [Google Scholar] [CrossRef]
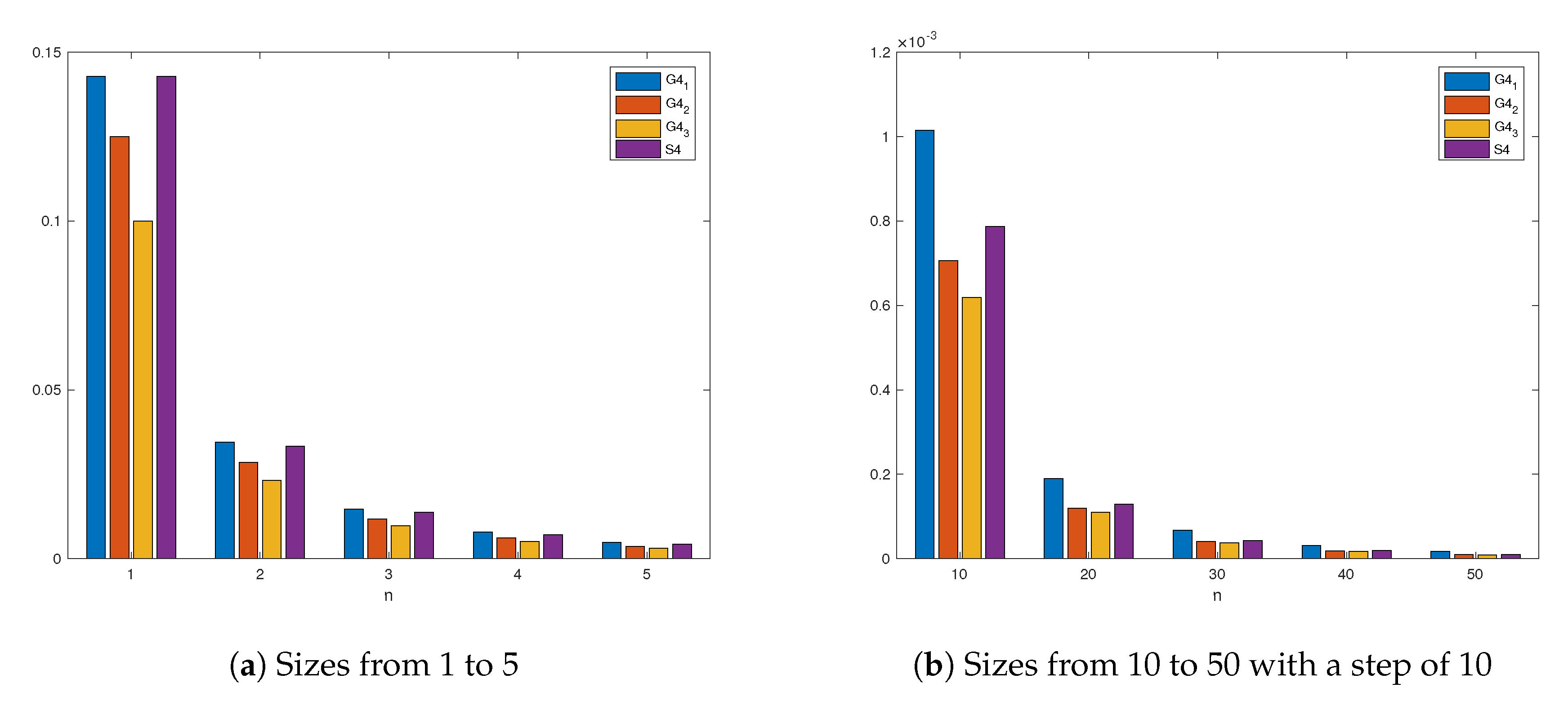
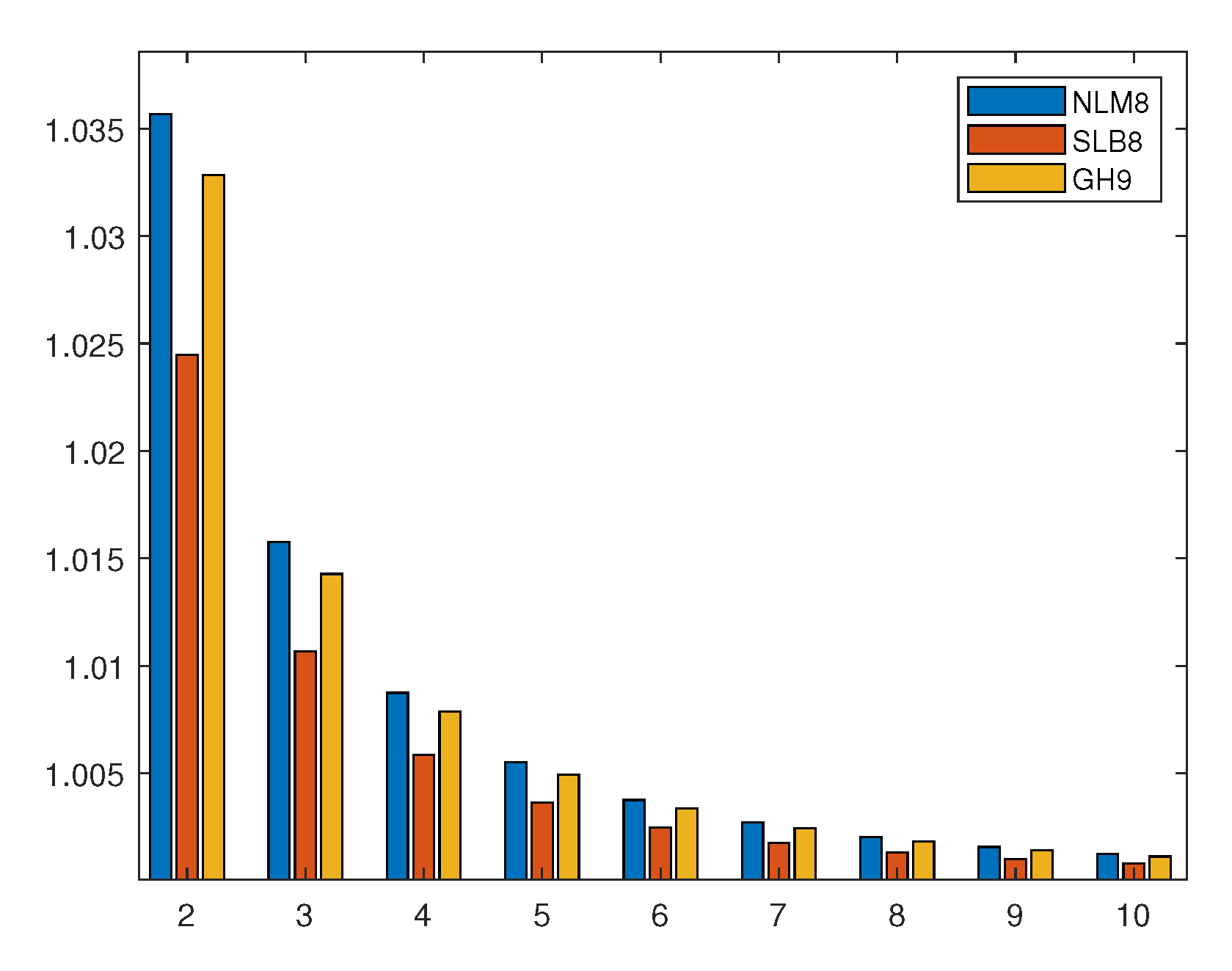
| Method | F | nDD | d | s1 | s2 | Mv | op | Order | CE | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 3 | 0 | 2 | 4 | ||||
| 1 | 1 | 1 | 3 | 2 | 1 | 4 | ||||
| 1 | 1 | 1 | 3 | 3 | 2 | 4 | ||||
| 1 | 2 | 0 | 2 | 1 | 1 | 4 |
| Method | nt | iter | e-time | ||
|---|---|---|---|---|---|
| 100 | 16.0 | 9.6054 (−7) | 397.1095 | ||
| 2.0 | 9.233 (−19) | 93.5890 | |||
| 200 | 15.0 | 7.8637 (−7) | 781.0227 | ||
| 2.0 | 7.2024 (−21) | 152.5548 | |||
| 500 | 13.0 | 8.4237 (−7) | 1.6520(03) | ||
| 2.0 | 1.179 (−23) | 515.5332 | |||
| Method | nt | iter | e-time | ||
| 100 | 17.96 | 8.1801 (−7) | 838.7530 | ||
| 2.0 | 1.6217 (−16) | 205.8390 | |||
| 200 | 16.37 | 6.6969 (−7) | 880.8873 | ||
| 2.0 | 1.2656 (−18) | 211.5296 | |||
| 500 | 14.592 | 7.1745 (−7) | 1.9021(03) | ||
| 2.0 | 2.0725 (−21) | 518.8443 | |||
| Method | nt | iter | e-time | ||
| 100 | 19.5 | 7.2062 (−7) | 529.8552 | ||
| 2.0 | 2.4203 (−14) | 106.0159 | |||
| 200 | 17.98 | 9.6415 (−7) | 965.8759 | ||
| 2.0 | 1.8728 (−16) | 209.1218 | |||
| 500 | 16.11 | 6.3074 (−7) | 2.0914(03) | ||
| 2.0 | 3.0515 (−19) | 513.5127 |
| Method | F | nDD | d | s1 | s2 | Mv | op | Order | CE | |
|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 2 | 0 | 7 | 0 | 2 | 8 | ||||
| 3 | 2 | 0 | 2 | 9 | 6 | 8 | ||||
| 2 | 1 | 2 | 8 | 0 | 6 | 9 |
| Method | Iter | ACOC | ||
|---|---|---|---|---|
| [7 7] | 3 | 1.929 (−201) | 6.9500 | |
| 3 | 1.433 (−378) | 7.8627 | ||
| 3 | 4.151 (−343) | 8.2992 | ||
| [4 −4.5] | 47 | 1.255 (−865) | 6.0711 | |
| 36 | 3.522 (−203) | 7.7505 | ||
| 20 | 1.164 (−1218) | 7.9956 | ||
| [−10 −7.5] | 20 | 3.371 (−501) | 6.4336 | |
| 5 | 6.248 (−1248) | 8.0000 | ||
| 4 | 1.722 (−416) | 8.1830 |
| Method | Iter | ACOC | ||
|---|---|---|---|---|
| [−1.5 −1.5 −1.5] | 4 | 7.484 (−633) | 6.3006 | |
| 4 | 3.902 (−1402) | 7.9274 | ||
| 4 | 7.286 (−1127) | 8.0749 | ||
| [0 −1 −1.5] | 5 | 9.291 (−1174) | 5.892 | |
| 4 | 2.557 (−1318) | 7.9291 | ||
| 4 | 1.064 (−425) | 8.5315 | ||
| [3 4 5] | 5 | 1.200 (−958) | 5.9817 | |
| 5 | 1.306 (−839) | 8.0606 | ||
| 4 | 3.982 (−350) | 8.3187 |
| Method | Iter | ACOC | ||
|---|---|---|---|---|
| [−1 1 2] | 4 | 2.587 (−412) | 7.8793 | |
| 13 | 2.419 (−854) | 7.9973 | ||
| 4 | 6.575 (−616) | 8.0173 | ||
| [−0.6 0.8 2.7] | 34 | 1.393 (−290) | 7.7554 | |
| 14 | 7.066 (−785) | 7.9959 | ||
| 4 | 2.445 (−511) | 8.0092 | ||
| [−2.5 −1 1] | 15 | 1.667 (−420) | 7.9179 | |
| 5 | 7.361 (−1165) | 7.9992 | ||
| 4 | 2.522 (−325) | 8.3981 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chicharro, F.I.; Cordero, A.; Garrido, N.; Torregrosa, J.R. Generalized High-Order Classes for Solving Nonlinear Systems and Their Applications. Mathematics 2019, 7, 1194. https://doi.org/10.3390/math7121194
Chicharro FI, Cordero A, Garrido N, Torregrosa JR. Generalized High-Order Classes for Solving Nonlinear Systems and Their Applications. Mathematics. 2019; 7(12):1194. https://doi.org/10.3390/math7121194
Chicago/Turabian StyleChicharro, Francisco I., Alicia Cordero, Neus Garrido, and Juan R. Torregrosa. 2019. "Generalized High-Order Classes for Solving Nonlinear Systems and Their Applications" Mathematics 7, no. 12: 1194. https://doi.org/10.3390/math7121194
APA StyleChicharro, F. I., Cordero, A., Garrido, N., & Torregrosa, J. R. (2019). Generalized High-Order Classes for Solving Nonlinear Systems and Their Applications. Mathematics, 7(12), 1194. https://doi.org/10.3390/math7121194








