Stage-Dependent Structured Discrete-Time Models for Mosquito Population Evolution with Survivability: Solution Properties, Equilibrium Points, Oscillations, and Population Feedback Controls
Abstract
1. Introduction
2. The Proposed Model, Its Basic Properties, and Worked Examples
2.1. The Model and Its Well-Posedness
- (i)
- Assume thatandare finite. Then,is bounded with;if and only if the sequenceis such thatis non-negative, which is equivalent to;. A necessary condition for that is that;.In addition,ifis positive for anyand, implying that, which is equivalent to;and.The above results keep valid ifis stage-dependent withfor all.The sequenceis strictly decreasing if and only ifis positive, that is, if and only if;. A necessary condition for that is;.
- (ii)
- Assume thatandare finite. Then,and
2.2. Stability and Convergence of the Solution
- (1)
- ; for some,
- (2)
- ,
- (3)
- .
- (i)
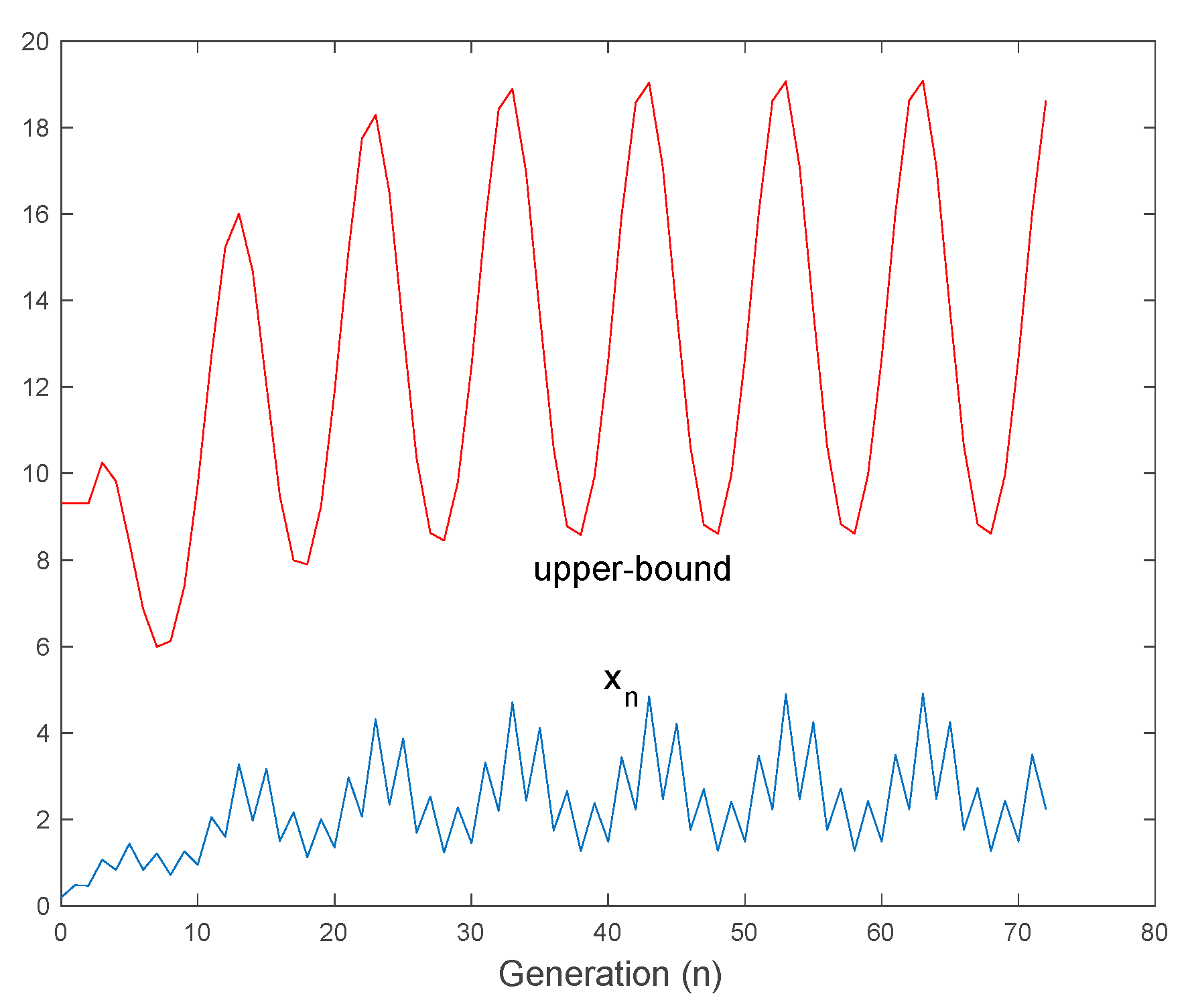
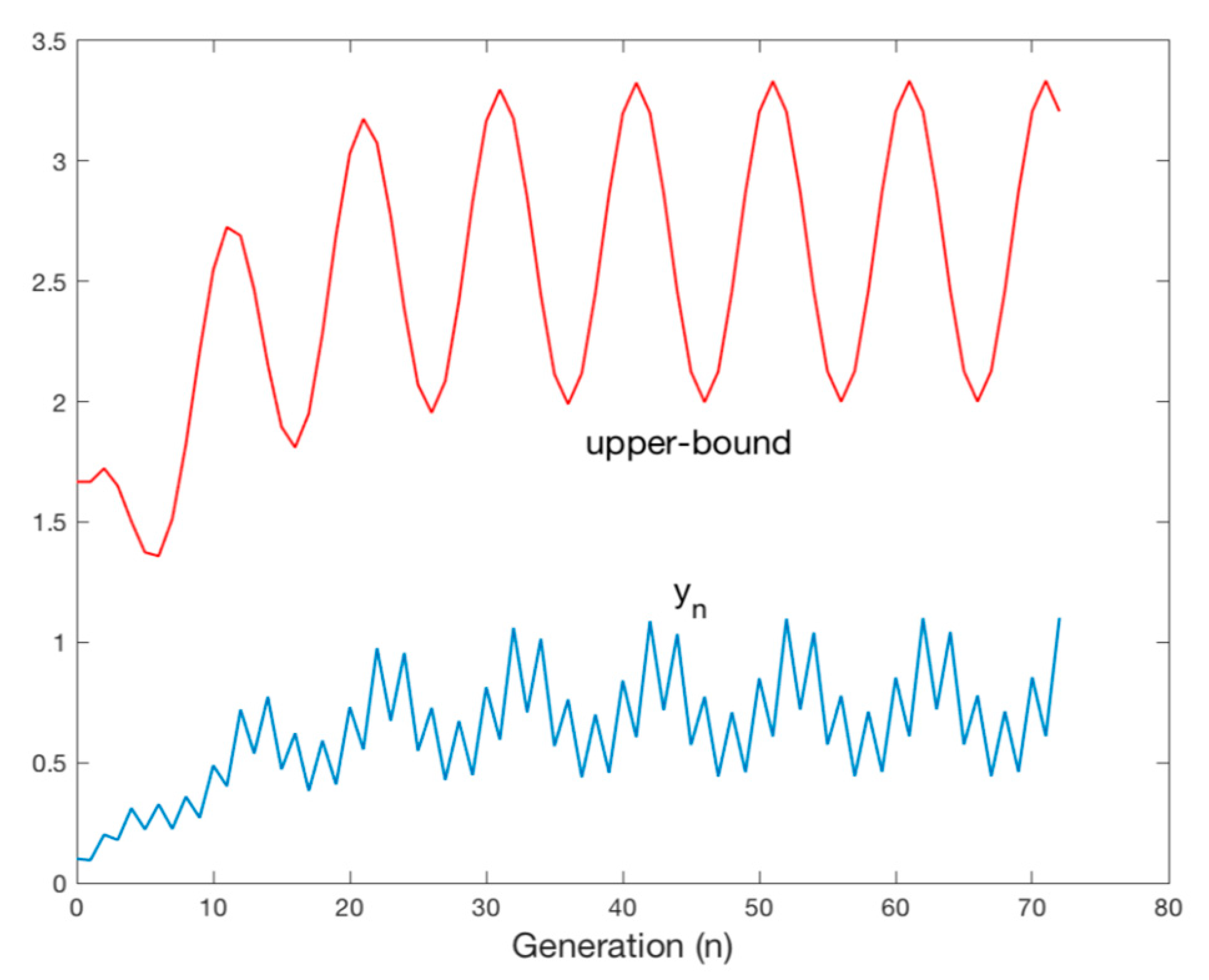
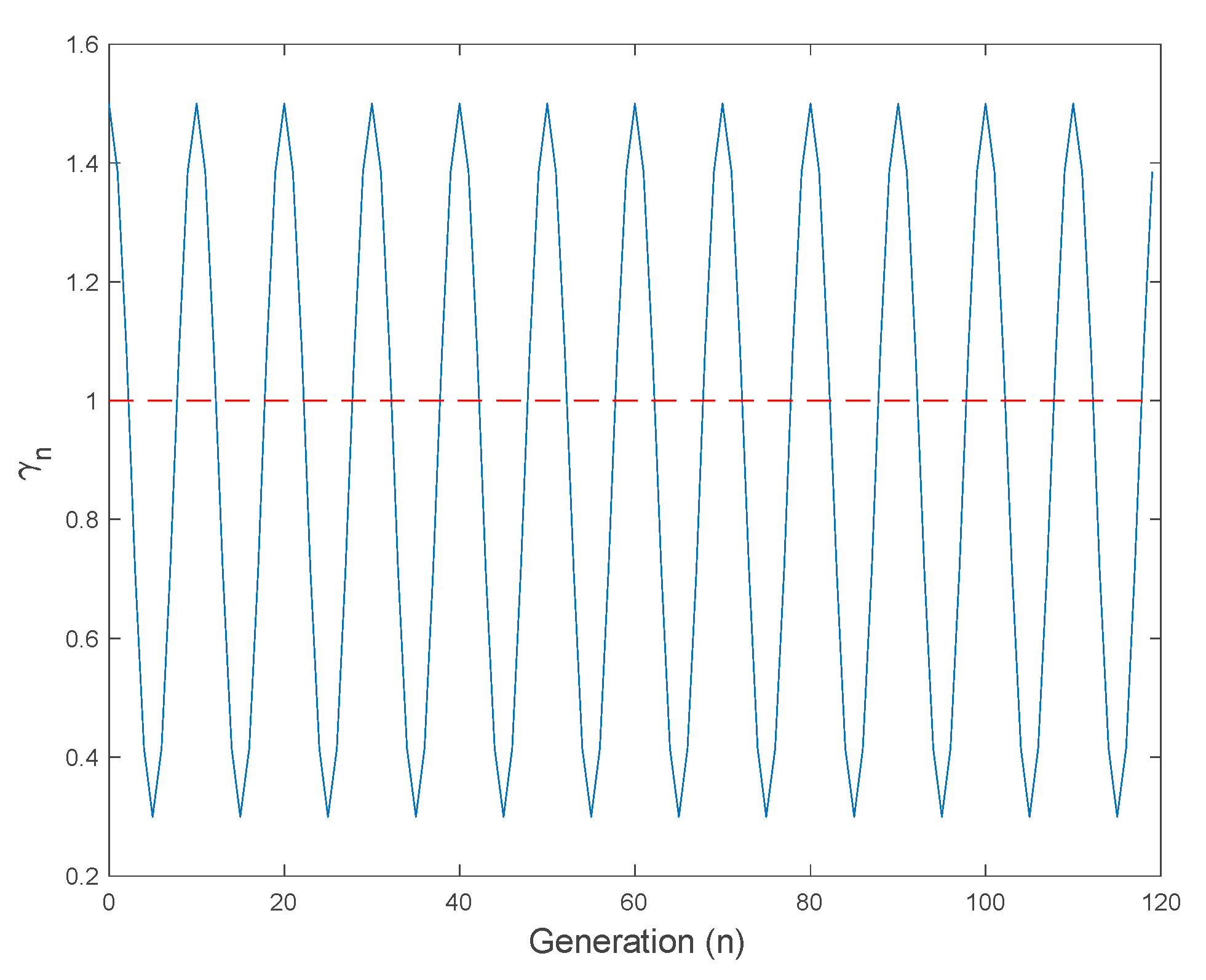
- Assume that for each given, there exist finiteand,such that eitherandorand. Then, the mosquito larvae evolution solution is oscillatory.The solutionis strictly oscillatory if in each of the above double conditions at least one of the inequalities is strict.The oscillatory solutionis periodic of, in general, a time-varying (or stage-dependent) oscillation period, if and only if there exists a strictly increasing sequencewith,such that;.
- (ii)
- A sufficient condition for the solutionto be oscillatory is that for any fixed non-negative integer number or any set of non-negative integer numbers (depending on the available computational possibilities)forand each:
- (iii)
- Different alternative sufficiency-type conditions for the solutionto be oscillatory are obtained with any of the following replacements in the sufficiency-type conditions of Property (ii):or by the alternative use of any of the combination of minima appearing in their definitions,or by the alternative use of any of the combination of maxima appearing in their definitions.
2.3. Worked Examples
- (a)
- Ifthen.
- (b)
- Ifthen.
- (a)
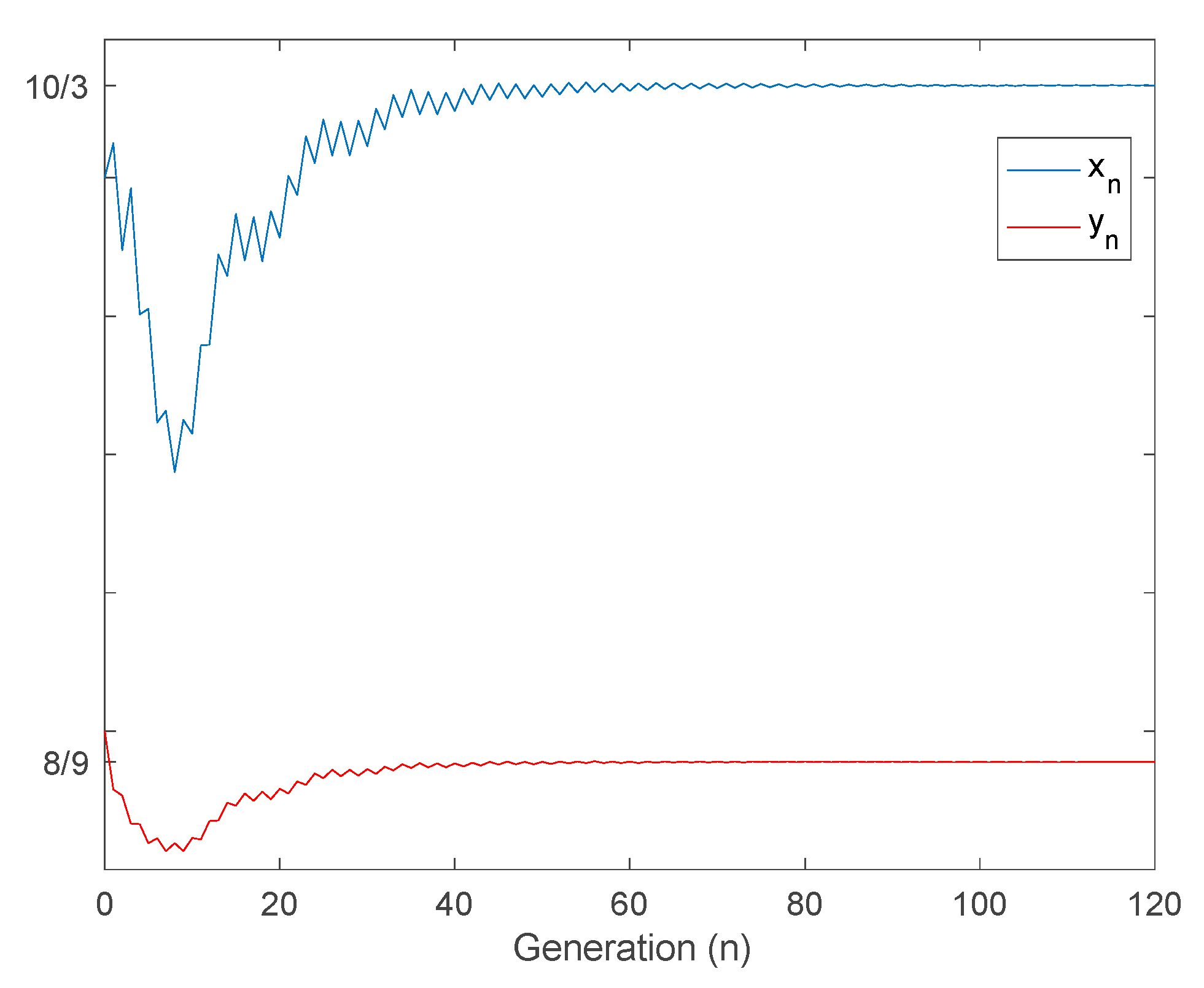
- At the equilibrium point,so thatandcan be either identical or distinct.
- (b)
- If a cycle of a two-stage period being distinct of an equilibrium point occurs, thenso that.
3. Monitored Control of the Mosquito Populations
- (a)
- The physical space of intervention;
- (b)
- The intensity and periodicity of the intervention, taking into account general details and information, such as seasonality influencing temperature, density, and larval food amounts availability;
- (c)
- The appropriate period of the day of intervention, for instance, at nights, for the case of Anopheles, where mosquitoes are more active;
- (d)
- The use of large allowed amounts of insecticide compatible with the ecosystem preservation and limited health influence damage.
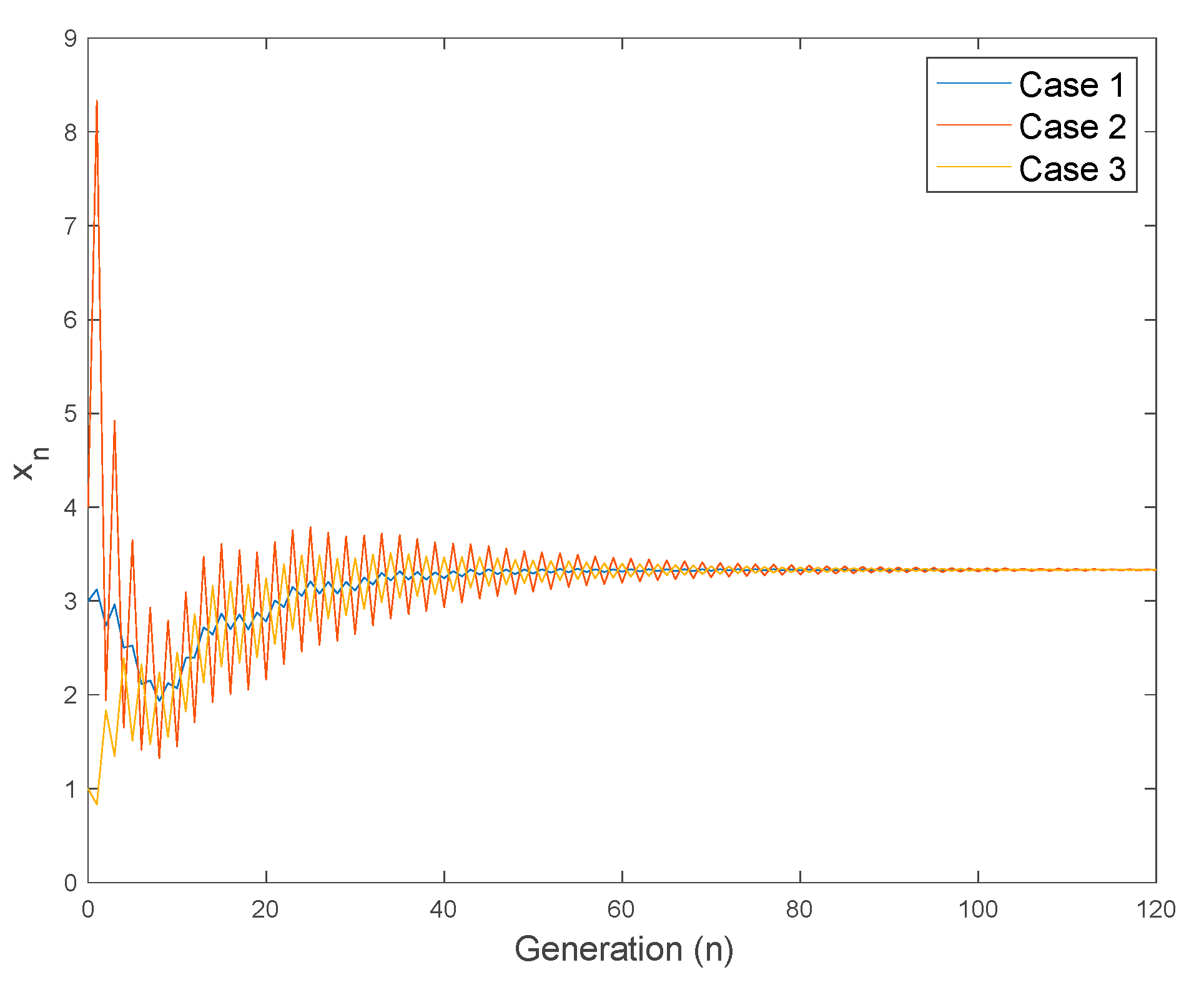
- (a)
- One-stage-ahead minimization population monitoring: One gets from (1) that (26) holds. So, given the current values ofand, one concludes that their minimum values at the next stage (i.e., the respective maxima of their inverses) for,are the subsequent ones:
- (b)
- Two-stage ahead minimization population monitoring: One concludes from (30) and (31) that, given, thenand then, for alreadygivenand, one hasHowever, note that
4. Simulation Examples
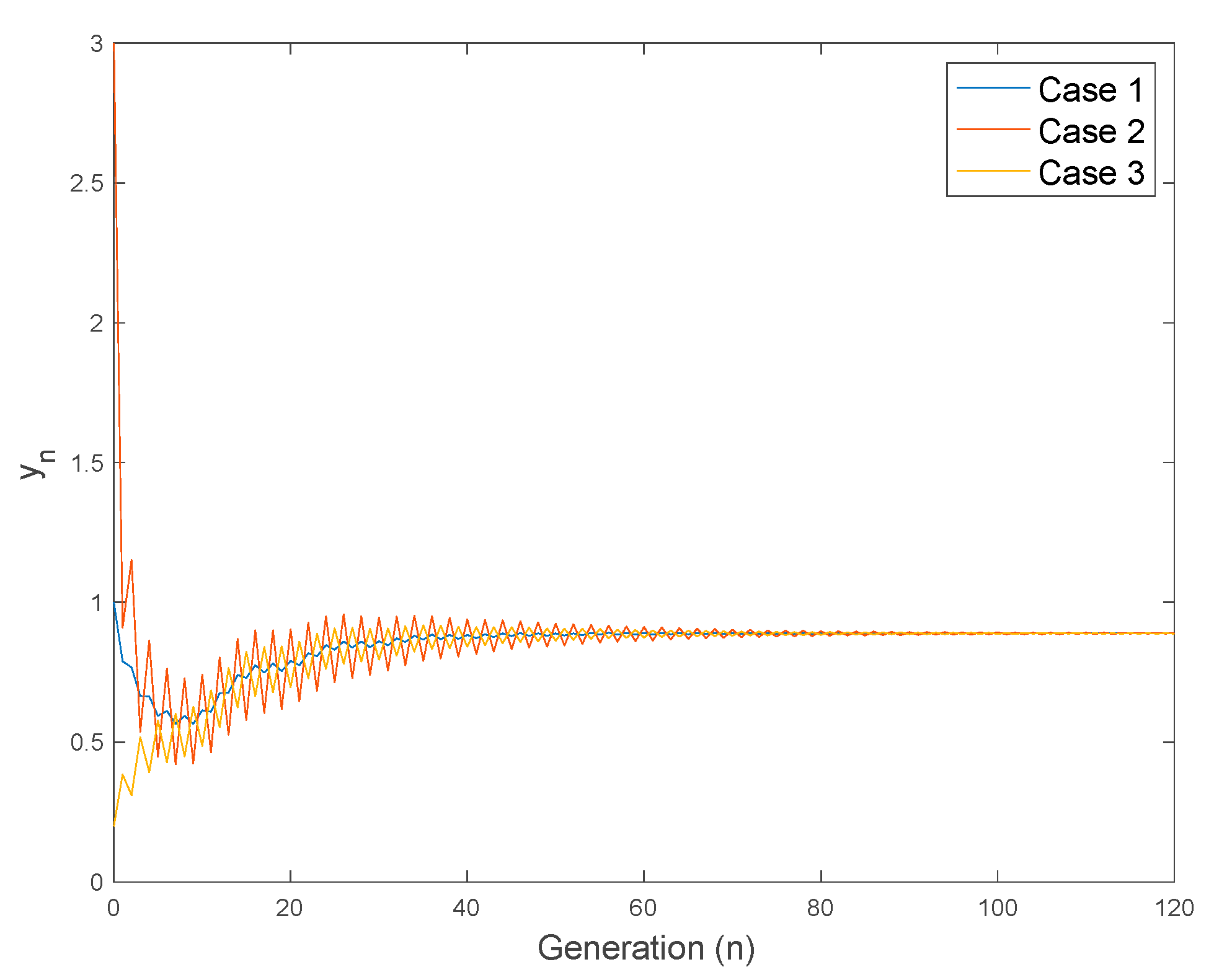
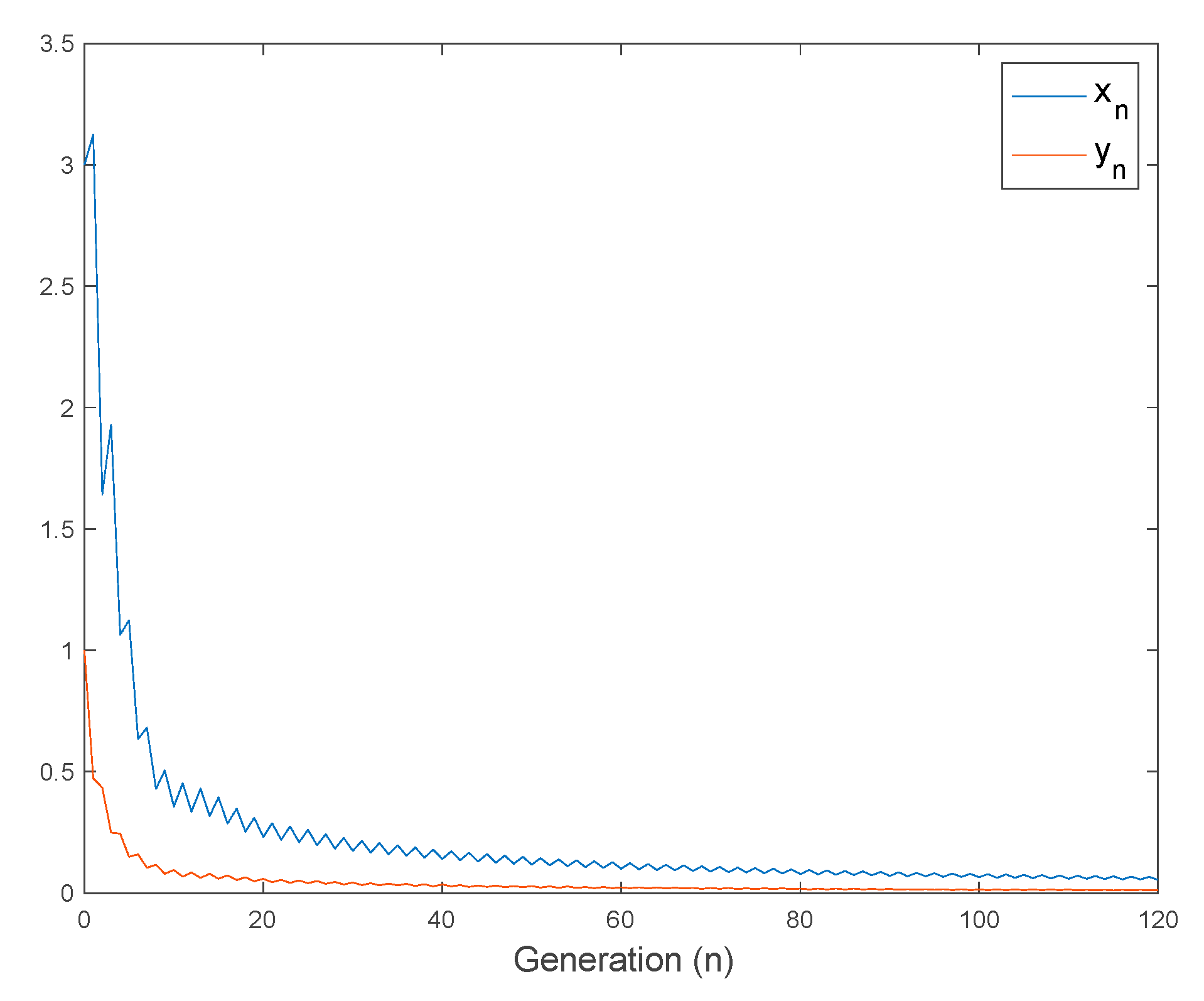
4.1. Non-Negativeness, Boundedness, and Location of Equilibrium Points
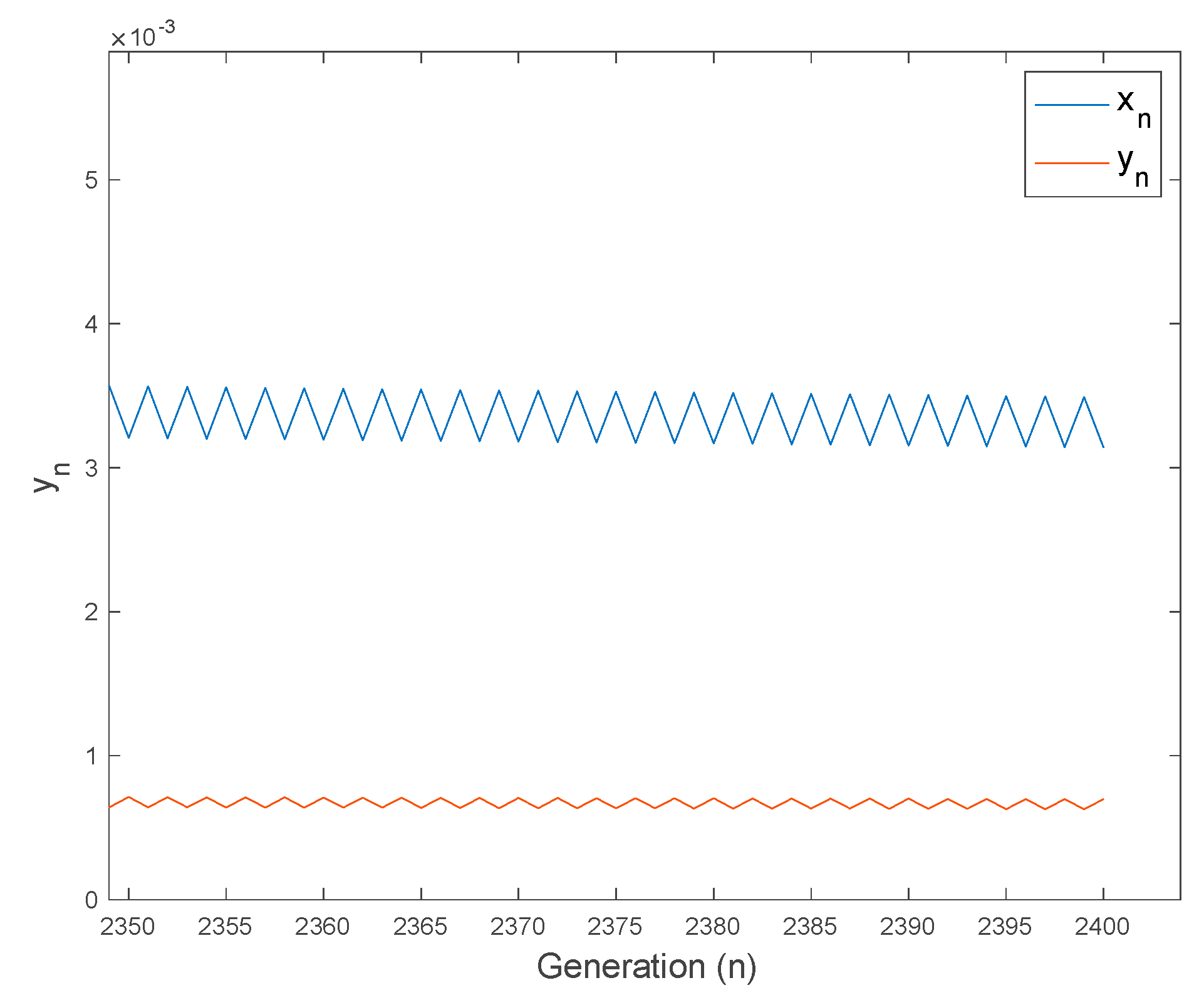
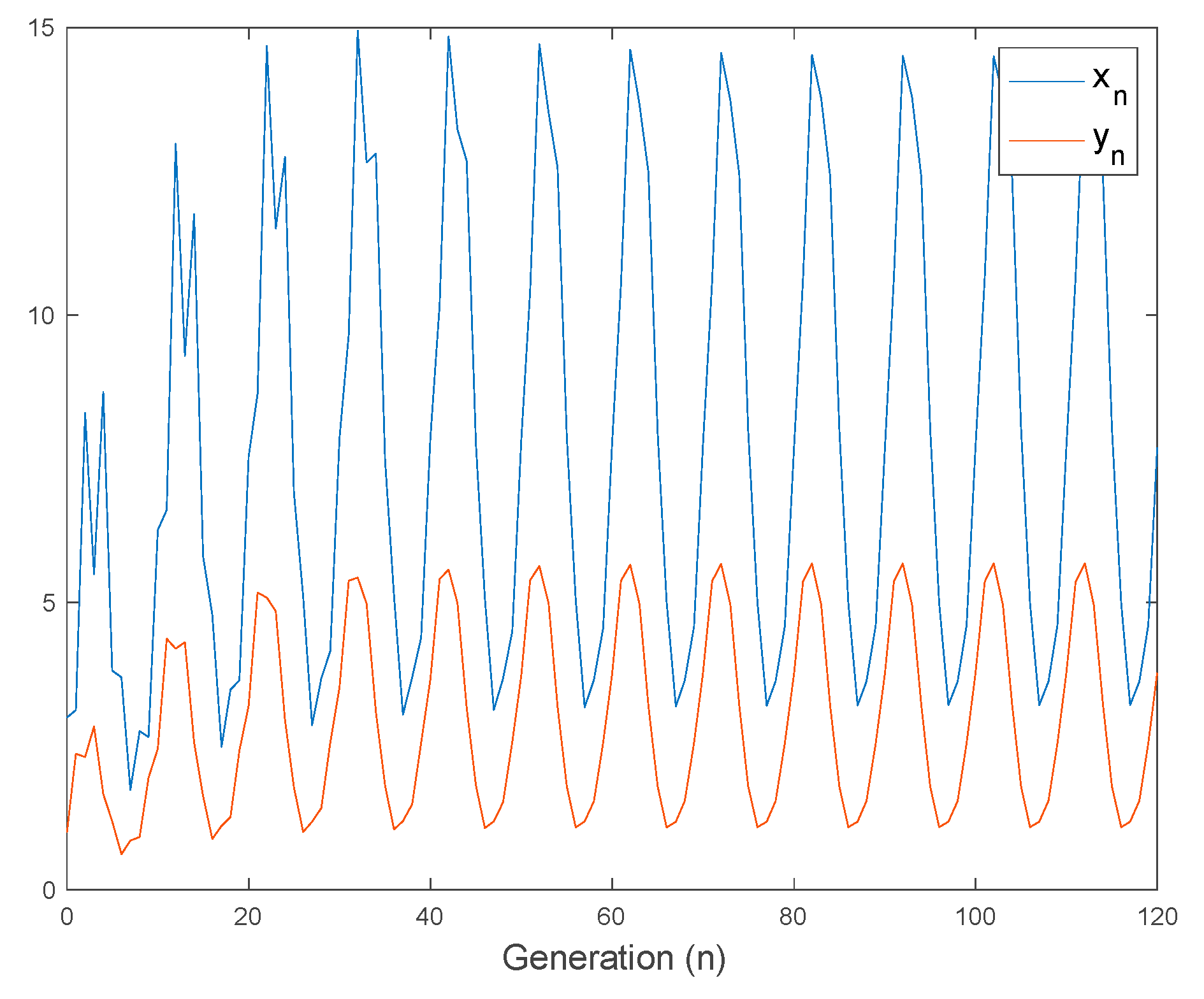
4.2. Oscillatory Solutions
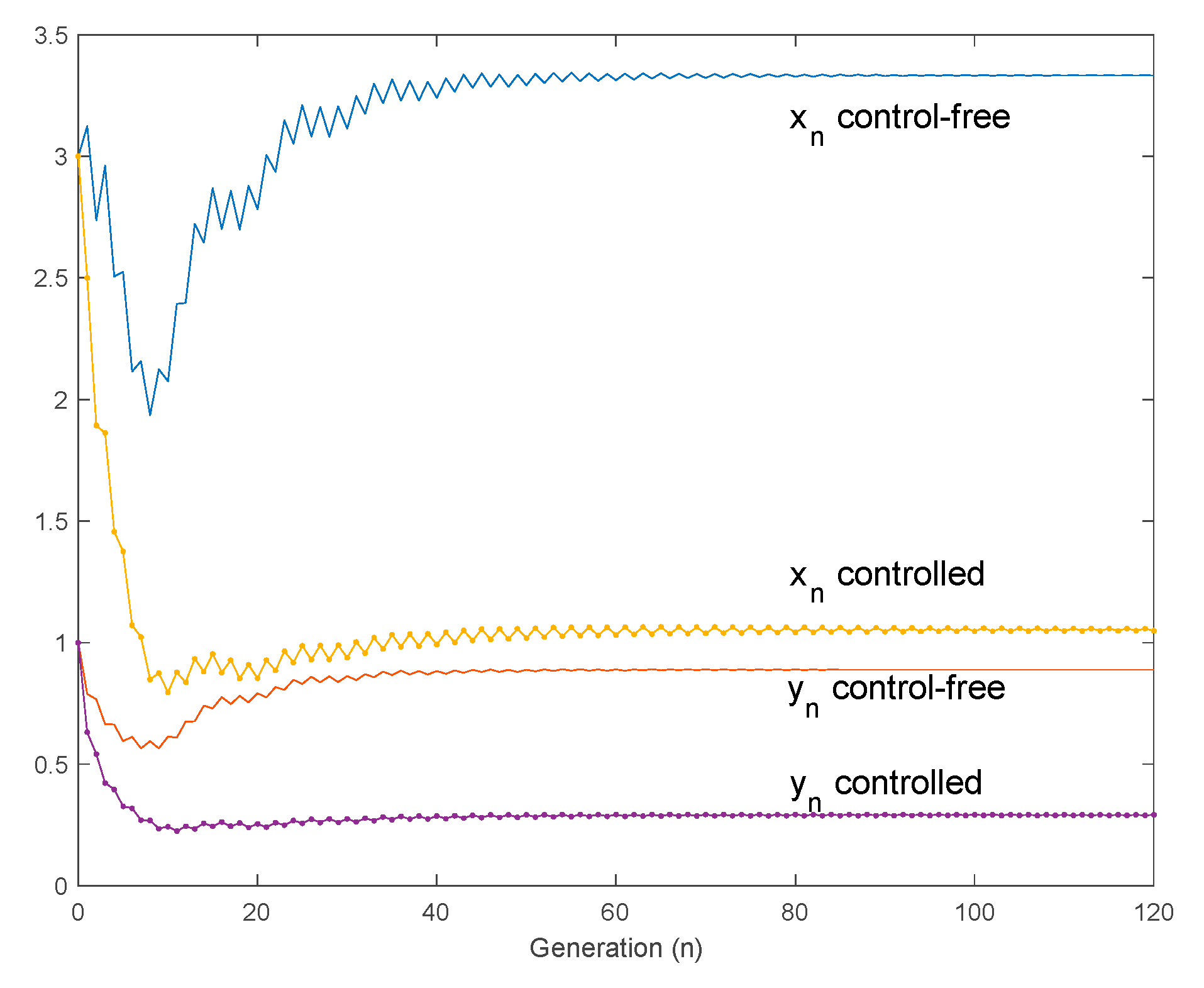
4.3. Use of Controls to Reduce the Larvae and Adult Mosquito Populations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Mathematical Proofs
- If , then , equivalently, and then or , and or . Each of those combinations of limits either leads to a contradiction or both sequences jointly converge to zero as proven as follows:
- (1a)
- and imply (from the first equation of (1)) and does not diverge (from the second equation of (1)) since ; are positive and bounded. However, this contradicts . Then, and is impossible if .
- (1b)
- and imply as from the first equation of (1) so that: 1) either and , and then (so, both sequences jointly converge to zero), or 2) , which contradicts and . Then, if , then and imply that and .
- (1c)
- and is impossible from the first equation of (1) so that if then implying the necessary constraint . On the other hand, if , then from the second equation of (1) and from the first equation of (1). However, then . Then, and as from (8). Since , then . Since and , then and, from the second equation of (1), .
- (1d)
- and implies from the second equation of (1) and as from the first equation of (1). As a result, and .
- If , then , equivalently, and then or and or . Each of those combinations either leads to a contradiction or both sequences jointly diverge to infinity as proven as follows:
- (2a)
- and imply is bounded (from the second equation of (1)). Thus, from the first equation of (1) . Since and implies is positive and bounded, then is bounded and is also bounded from the second equation of (1), so that is bounded. Then, bounded and imply that , while bounded and imply that is bounded so that is impossible. Thus, the joint conditions and are impossible if .
- (2b)
- and imply bounded and, since from the first equation of (1), either and is bounded (which together with bounded implies that is bounded) or does not converge to zero so that is unbounded. However, this is impossible, even if is unbounded from the second equation of (13). So, and imply that is bounded, so that is impossible, and (which implies that from the second equation of (1)) and is also bounded. Then, and are impossible if .
- (2c)
- and are compatible with , so with .
- (2d)
- and imply that and . Also, the second equation of (13) rewritten as leads to , implying , a contradiction to . Thus, and are impossible if . □
- (a)
- If , then , if and only if , but extinction needs the constraint , so a contradiction exists, and then the zero equilibrium point is not locally asymptotically stable.
- (a)
- If with , then , if and only if and (since ), that isor, equivalently,and both constraints jointly hold if and only if the, more restrictive, first one holdsequivalently, if and only if,
References
- Li, Y.; Li, J. Stage-structured discrete-time models for interacting wild and sterile mosquitoes with Beverton- Holt survivability. Math. Biosci. Eng. 2019, 16, 572–602. [Google Scholar] [CrossRef] [PubMed]
- Fister, K.R.; McCarthy, M.L.; Oppenheimer, S.F.; Collins, C. Optimal control of insects through sterile insect release and habitat modification. Math. Biosci. 2013, 244, 201–212. [Google Scholar]
- Flores, J.C. A mathematical model for wild and sterile species in competition: Immigration. Physica A 2003, 328, 214–224. [Google Scholar] [CrossRef]
- Li, Y.; Li, J. Discrete-time models for releases of sterile mosquitoes with Beverton-Holt type for survivability. Richerche Di Mat. 2018, 67, 141–162. [Google Scholar] [CrossRef]
- Li, J. Malaria model with stage-structured mosquitoes. Math. Biosci. Eng. 2011, 8, 753–768. [Google Scholar] [CrossRef]
- Stevic, S. A short proof of the Cushing-Henson conjecture. Discret. Dyn. Nat. Soc. 2006, 2006, 1–5. [Google Scholar] [CrossRef]
- de la Sen, M.; Alonso-Quesada, S. Control issues for the Beverton-Holt equation in ecology by locally monitoring the environment carrying capacity: Non-adaptive and adaptive cases. Appl. Math. Comput. 2009, 215, 2616–2633. [Google Scholar] [CrossRef]
- de la Sen, M.; Alonso-Quesada, S. Model-matching-based control of the Beverton-Holt equation in ecology. Discret. Dyn. Nat. Soc. 2008, 2008, 2616–2633. [Google Scholar] [CrossRef]
- de la Sen, M.; Alonso-Quesada, S. A control theory point of view on Beverton-Holt equation in population dynamics and some of its generalizations. Appl. Math. Comput. 2008, 215, 464–481. [Google Scholar] [CrossRef]
- Cushing, J.M.; Henson, S.M. A periodically forced Beverton-Holt equation. J. Differ. Equ. Appl. 2008, 8, 1119–1120. [Google Scholar] [CrossRef]
- de la Sen, M. The environment carrying capacity is not independent of the intrinsic growth rate for subcritical spawning stock biomass in the Beverton-Holt equation. Ecol. Model. 2007, 204, 2171–2273. [Google Scholar] [CrossRef]
- Hui, Y.; Lin, G.; Sun, Q. Oscillation threshold for a mosquito population suppression model with time delay. Math. Biosci. Eng. 2019, 16, 7362–7374. [Google Scholar] [CrossRef] [PubMed]
- Takahasi, S.E.; Miura, Y.; Miura, T. On convergence of a recursive sequence xn+1 = f(xn−1, xn). Taiwan. J. Math. 2006, 10, 631–638. [Google Scholar] [CrossRef]
- Stevic, S. On the recursive sequence xn+1 = xn−1/g(xn). Taiwan. J. Math. 2002, 6, 405–414. [Google Scholar]
- Verma, R.; Sehgal, V.K.; Nitin, V. Computational stochastic modelling to handle the crisis occurred during community epidemic. Ann. Data. Sci. 2016, 3, 119–133. [Google Scholar] [CrossRef]
- Iggidr, A.; Souza, M.O. State estimators for some epidemiological systems. Math. Biol. 2019, 78, 225–256. [Google Scholar] [CrossRef]
- Yang, H.M.; Ribas-Freitas, A.R. Biological view of vaccination described by mathematical modellings: From rubella to dengue vaccines. Math. Biosci. Eng. 2018, 16, 3185–3214. [Google Scholar]
- Koivu-Jolma, M.; Annila, A. Epidemic as a natural process. Math. Biosci. 2018, 299, 97–102. [Google Scholar] [CrossRef]
- Meyers, L. Contact network epidemiology: Bond percolation applied to infectious disease prediction and control. Bull. Am. Math. Soc. 2007, 44, 63–86. [Google Scholar] [CrossRef]
- de la Sen, M. On the design of hyperstable feedback controllers for a class of parameterized nonlinearities. Two application examples for controlling epidemic models. Int. J. Environ. Res. Public Health 2019, 16, 2689. [Google Scholar]
- de la Sen, M. Parametrical non-complex tests to evaluate partial decentralized linear-output feedback control stabilization conditions for their centralized stabilization counterparts. Appl. Sci. 2019, 9, 1739. [Google Scholar] [CrossRef]
- Cai, L.; Ai, S.; Li, J. Dynamics of mosquitoes populations with different strategies for releasing sterile mosquitoes. SIAM J. Appl. Math. 2014, 74, 1786–1809. [Google Scholar] [CrossRef]
- Li, J.; Yuan, Z. Modelling releases of sterile mosquitoes with different strategies. J. Biol. Dyn. 2015, 9, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Pryce, J.; Choi, L.; Malone, D. Insecticide space spraying for preventing malaria transmission. Cochrane DB. Syst. Rev. 2017, 2017, CD012689. [Google Scholar] [CrossRef][Green Version]
- Smith, D.L.; Battle, K.E.; Hay, S.I.; Barker, C.M.; Scott, T.W.; McKenzie, F.E. Ross, McDonald and a theory for the dynamics and control of mosquito-transmitted pathogens. Plos Pathogens 2012, 8, e1002588. [Google Scholar] [CrossRef]
- Couret, J.; Dotson, E.; Benedict, M.Q. Temperature, larval diet and density effects on development rate and survival of aedes aegypti (Dipta: Culicidae). PLoS ONE 2014, 9, e87468. [Google Scholar] [CrossRef]
- Ackleh, A.S.; Jang, S.R.J. A discrete two-staged population model: Continuous versus seasonal reproduction. J. Differ. Equ. Appl. 2007, 13, 261–274. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De la Sen, M.; Ibeas, A.; Garrido, A.J. Stage-Dependent Structured Discrete-Time Models for Mosquito Population Evolution with Survivability: Solution Properties, Equilibrium Points, Oscillations, and Population Feedback Controls. Mathematics 2019, 7, 1181. https://doi.org/10.3390/math7121181
De la Sen M, Ibeas A, Garrido AJ. Stage-Dependent Structured Discrete-Time Models for Mosquito Population Evolution with Survivability: Solution Properties, Equilibrium Points, Oscillations, and Population Feedback Controls. Mathematics. 2019; 7(12):1181. https://doi.org/10.3390/math7121181
Chicago/Turabian StyleDe la Sen, Manuel, Asier Ibeas, and Aitor J. Garrido. 2019. "Stage-Dependent Structured Discrete-Time Models for Mosquito Population Evolution with Survivability: Solution Properties, Equilibrium Points, Oscillations, and Population Feedback Controls" Mathematics 7, no. 12: 1181. https://doi.org/10.3390/math7121181
APA StyleDe la Sen, M., Ibeas, A., & Garrido, A. J. (2019). Stage-Dependent Structured Discrete-Time Models for Mosquito Population Evolution with Survivability: Solution Properties, Equilibrium Points, Oscillations, and Population Feedback Controls. Mathematics, 7(12), 1181. https://doi.org/10.3390/math7121181






