1. Introduction
Apéry’s proof [
1] of the irrationality of the number
(where
,
) is based on the second order difference equation (three-term recurrence relation)
where the two independent solutions, namely, the sequence of integers
defined by the initial conditions
and
, (more specifically
[
2,
3]) and the sequence of rationals
determined by the initial conditions
,
, form rational approximants
to the number
. This sequence of approximants can be expressed as the sequence of convergents of the corresponding continued fraction. Such a sequence shows the irrationality of
. Indeed, the inclusions
, where
denotes the least common multiple of
, together with the prime number theorem,
for any
, and Poincaré’s theorem [
4,
5,
6] yield for the error-term sequence
, the estimate
In [
7] the proof is addressed from the perspective of Hermite-Padé approximation problem involving multiple orthogonal polynomials [
8,
9,
10], but that proof was not connected with Equation (
1). A natural question arises: Do the coefficients in (
1) depend on other integers as well as
n in order that the derived sequences
and
guarantee the irrationality of
? Following this perspective, the primary goal of this paper was to obtain a second order holonomic difference equation as an alternative to the Equation (
1) by using rational approximation techniques in the context of Hermite-Padé approximation. In this paper we use the term "holonomic" to indicate that the coefficients in the linear difference equation depend on other parameters as well as
n (see [
11,
12] for this notion in the context of differential equations involving some Krall-type and Sobolev-type orthogonal polynomials). The holonomic character of Equation (
36) leads to infinitely many sequences of rational approximants to
. This is because the holonomic sequences that are produced depend on up to three integer parameters (almost freely selected). Usually, the deduction of the Equation (
1) makes use of the algorithm of creative telescoping due to Gosper and Zeilberger [
13]. However, the use of this technique is combinatorially more complicated when dealing with holonomic sequences that depend on several parameters.
Our goal was to find and solve a set of second order holonomic difference equations (see (
36))
with initial conditions
and
, respectively. The expressions for the coefficients
,
, and
are given in
Section 3.
represents a set of integer parameters involved in the polynomial solutions of the approximation problems (
5) and (
6). Let
, where
and
,
, and
denote the sets of all positive integers, integer numbers, and rational numbers, respectively.
For a given integer or a combination of given integers as in (
3) we found the corresponding holonomic solutions
and
, which form the numerator and denominator sequences of the rational approximants to
. Indeed, we give a correspondence from the set
to the set of bi-sequences
that are solutions of the holonomic three-term recurrence relations (
2) with variable coefficients depending on integer parameters.
The paper is structured as follows. In
Section 2 we introduce Hermite-Padé approximation problems near infinity with polynomial solutions. These solutions depend on integer parameters
that satisfy a set of conditions. In
Section 3 we compute the Casorati determinants for sequences of numerators and denominators of the rational approximants to
. Different series representations of the number
are derived. Moreover, from the Casorati determinant we deduce the second order holonomic difference equation satisfied by the sequences of both numerators and denominators of the rational approximants. In
Section 4 we asymptotically estimate the error-term sequence of our approximations by using steepest descent method. Then, we verify that the generated rational approximants (in
Section 2.1) and reprove the irrationality of
. In
Section 5 several comparisons (computations) involving rational approximants and Apéry’s approximants are given. We make concluding remarks in
Section 6.
2. Hermite-Padé Approximation
We derived a set of rational approximants classified in twelve types depending on certain parameters, which can be used to generate infinitely many rational approximants to . For that purpose, we formulated and solved the following problem:
For the system of polylogarithms
,
, find the polynomials
, and
such that the following interpolation conditions at infinity
hold, provided the following extra conditions involving the coefficients of polynomials (
4) are fulfilled
where
and
with
,
,
,
.
Condition (
7) implies the following relation
since
,
, while conditions (
8)–(
10) introduce certain dependence of parameters in the coefficients of polynomials (
4), and consequently, in the coefficients of polynomials
and
, respectively (see expressions (
17) and (
18) below).
For each pair
, the interpolation problems (
5) and (
6), together with (
7) and (
8), leads to a linear system of equations for the unknown coefficients of
,
,
, and
, which are uniquely determined (see [
10]).
Focusing on the polynomial solutions of (
5) and (
6), we show that such solutions can be derived from the orthogonality relations (
12) with conditions (
7) and (
8), instead of solving the aforementioned linear system of equations. Let
and
be two polynomials, such that
and
are as in (
9). Let
be subject to the conditions (
7) and (
8). These relations lead to a linear system of equations for the unknown coefficients of
and
, respectively. As a consequence of (
12) we have
where
and
are arbitrary polynomials of degree at most
and
, respectively.
Denoting
Equation (
13) implies that
and
. Now, setting
in Equations (
13) and using (
9), one obtains
where
Therefore, the above system of functions (
16) and polynomials (
4), (
17), and (
18) represent the simultaneous rational approximation problem near infinity (
5) and (
6). Notice that the orthogonality conditions (
12) along with (
7) and (
8) are equivalent to the interpolation conditions at infinity, (
5) and (
6). The solution of this problem depends only on the coefficients of the polynomials
and
, since the coefficients for
in the Laurent series expansion of
and for
in the series expansion of
vanish, while the coefficients for
coincide with the corresponding coefficients of
and
, respectively.
2.1. Explicit Expressions for Coefficients of the Vector Polynomial
We determined the common vector denominator
for the vector type II approximation problems (
14) and (
15). Define
Thus, we have the following sequences of rational functions
and
where
The expressions (
20) and (
21) represent the analytic continuation of the two functions given in (
19), respectively.
From the orthogonality conditions (
13), as well as from (
7) and (
8), it follows that
and
,
, is the Pochhammer symbol.
Hence, the coefficients in (
20) are as follows
and
where
denotes the Harmonic Number
k of order
r (
and
). In addition, the following relation holds
where
,
,
. Observe that if
denotes the least common multiple of
, and
,
, the following inclusions
hold.
We now derive an explicit expression for the sequences involved in (
11). From expressions (
11), (
18), and (
23)–(
25) one gets
where
Finally, since
as
, we have
which is in accordance with (
7).
3. Second Order Holonomic Difference Equation
We begin by obtaining an explicit expression for the Casorati determinant involving the above functions (
19)–(
21) and sequences (
23)–(
27); i.e.,
Lemma 1. The following relationholds. Proof. Consider the integral
Let
represent the generic dependence of the parameters
,
,
,
, and
defined in (
3). Using formulas (
13) and the fact that
, one gets
On the other hand,
where
Hence,
Equating (
30) and (
31), one obtains (
29). □
The first-order linear inhomogeneous difference equation with variable coefficients involved in the Casorati determinant (
29) can be written as follows
where
,
,
. Observe that its solution is given by
Hence, from (
32) we have
and
Expression (
34) gives a different representation for the sequences of numerators (
28) of the rational approximants to the number
provided one is able to explicitly compute (
29). Moreover, both from Theorem 2 (see
Section 4) and from Theorem 1 below
. Therefore, from Equation (
33) the series
converges, which leads to different series representations of this number for different sequences
.
Example 1. Let and . From Equation (29) we see thatwhere The right hand side of the above expression is a polynomial of degree 2 in , whose zeros and are non-integers depending on n. Therefore, for , and . Indeed,and and . Finally, from (35)where,
.
Theorem 1. The sequences , , and satisfy the following second order holonomic difference equationwhereand is a polynomial of degree in the variable n. The initial values and are given in (27) and (28). Proof. From Lemma 1, we have
where
. Thus, multiplying the first equation by
, the second one by
, and adding, one gets
Multiplying this equation by an integer constant
, we have
where
, and
. Since for
,
, there exists
such that
. Moreover,
This leads to the second order recurrence relation
satisfied by the sequences
,
and
. Furthermore, from (
40) one can write
From (
39) we see that there exists a positive integer
p such that the sequence
converges when
. Thus, by setting
in relation (
39) we obtain a linear system of equations for determining explicitly the coefficients of
. The solution of the resulting system gives us the coefficient
given in (
36) and (
37), where
. This completes the proof of the theorem. □
Example 2. Consider the sequences , , and . We show that the second order recurrence relationholds, whereand the initial values and are given in (27) and (28). Then, from (38), setting , we havewhere and are given in (42), and Denoting and setting in relation (43) we obtain a linear system of equations for determining its coefficients explicitly. Finally, one obtains the coefficient given in (42). Observe that the characteristic equation for the above equation with coefficients (42) is , which coincides with the one derived from (1). Using Poincaré’s Theorem [6] the asymptotic estimates and hold. In Section 4 a more accurate asymptotic expression for general cases, when , and , are studied. An interesting consequence of Theorem 1 is the continued fraction representation of the number . Below we present one of a number of possible continued fraction representations that follows from our results.
Example 3. Let . The following continued fraction expansion holds:whereand Recall that two continued fractionsare said to be equivalent if there exists a non-zero sequence , with , such that (see [14], p. 20) Furthermore, if and are two sequences such that , and the Casorati determinant is different from zero for , then there exists a unique continued fractionwhose n-th numerator is and n-th denominator is , for each . More precisely (see [14], p. 31) Now, by setting , in the case , one gets Moreover, from the recurrence relation (
41), one has
Thus, we have constructed the elements of the continued fraction (45) which satisfy (46); i.e., With the choice , , and , for , we obtain the continued fraction (44). 5. Discussion of Results
We discuss our results with the aid of graphics and tables. Denote
, where the integers
i,
j are such that
,
. By
we denote the Apéry’s approximants, where
In
Figure 1, a comparison between twelve selected rational approximants from the set
corresponding to different choices of parameters and Apéry’s approximants
is given. This comparison is depicted by means of a rectangular array of squares formed by thirteen rows and nine columns in a grayscale output, in which the color of each square is determined by the value of the function
ranges from
to
. The values close to the minimum of (
50) are shown as white squares while its maxima are shown as dark squares. Indeed, ten iterations (see columns in
Figure 1) are enough to show the accuracy of our results in the approximation to
. Clearly, in
Figure 1 the darkness decreases as the number of iterations grows, which is in accordance with the analytical results on the asymptotic behavior of the remainders discussed in
Section 4. In addition, in
Table 1 and
Table 2, we compare the rates of convergence of four selected cases among infinitely many options of the studied holonomic rational approximants versus
; namely,
for
,
for
, and
for
.
In the above discussions the computational software [
15] was used.
6. Concluding Remarks
The main point of interest in this paper is the deduction in
Section 3 of the holonomic difference Equation (
36). The non-holonomic equation (Equation (
1)) was the cornerstone of Apéry’s original proof [
1], which seemed unrelated to constructive approximation. The holonomicity is a consequence of the Hermite-Padé approximation problems formulated near infinity (
5) and (
6) along with some extra conditions for the vector polynomials involved. In the present contribution, we used a straightforward technique involving Casorati determinants to obtain the recurrence coefficients in the holonomic difference equation. A set of holonomic rational approximants with good rates of convergence to
is discussed in
Section 4 and
Section 5. In
Section 4, most of the used techniques are standard in the field, but we present them for completeness of the study; in particular, the use of the steepest descent method.
In the study of rational approximants for the Euler constant [
16], the authors also used Casorati determinants to reduced 10-term recurrence relations (which involved Hermite-Padé approximants) to the 4-term recurrences.
Other techniques for deriving recurrence relations rely on the algorithm of creative telescoping. The use of these techniques is more complicated in our context due to the dependence of integer parameters (up to three) in addition to the non-holonomic variable
n. In the literature, several results connect recurrence relations, continued fractions, and irrationality as well as the use of contiguous relations of hypergeometric series to derive rational approximants; however, similar results involving a holonomic phenomenon are absent. This paper focuses on the study of such a situation in the well known case of
(an early draft of our work can be found in [
17], also contained in the Ph. D. Thesis of the second author).
The other approach to the irrationality of
deals with the perturbation of the rational function
,
, introduced by Beukers in ([
18], p. 97) and by Nesterenko in [
19,
20]. In the next example, for a couple of rational perturbations of
, the generated sequences of rational approximants differ from the Apéry’s approximants given in (
49). Nevertheless, such sequences (as will be discussed) might not guarantee a priori that reproving the irrationality of
is possible. Alternatively, we propose deriving the perturbed rational functions (as in expression (
22)) from a Hermite-Padé approximation problem along with extra conditions.
Consider the following two perturbations:
and
where
,
. For (
51) and (
52), the derived corresponding sequences
and
,
, fail to prove the irrationality of
because: (1) The multiplication by
in the resulting linear form
will not eliminate the rational terms in the sequences
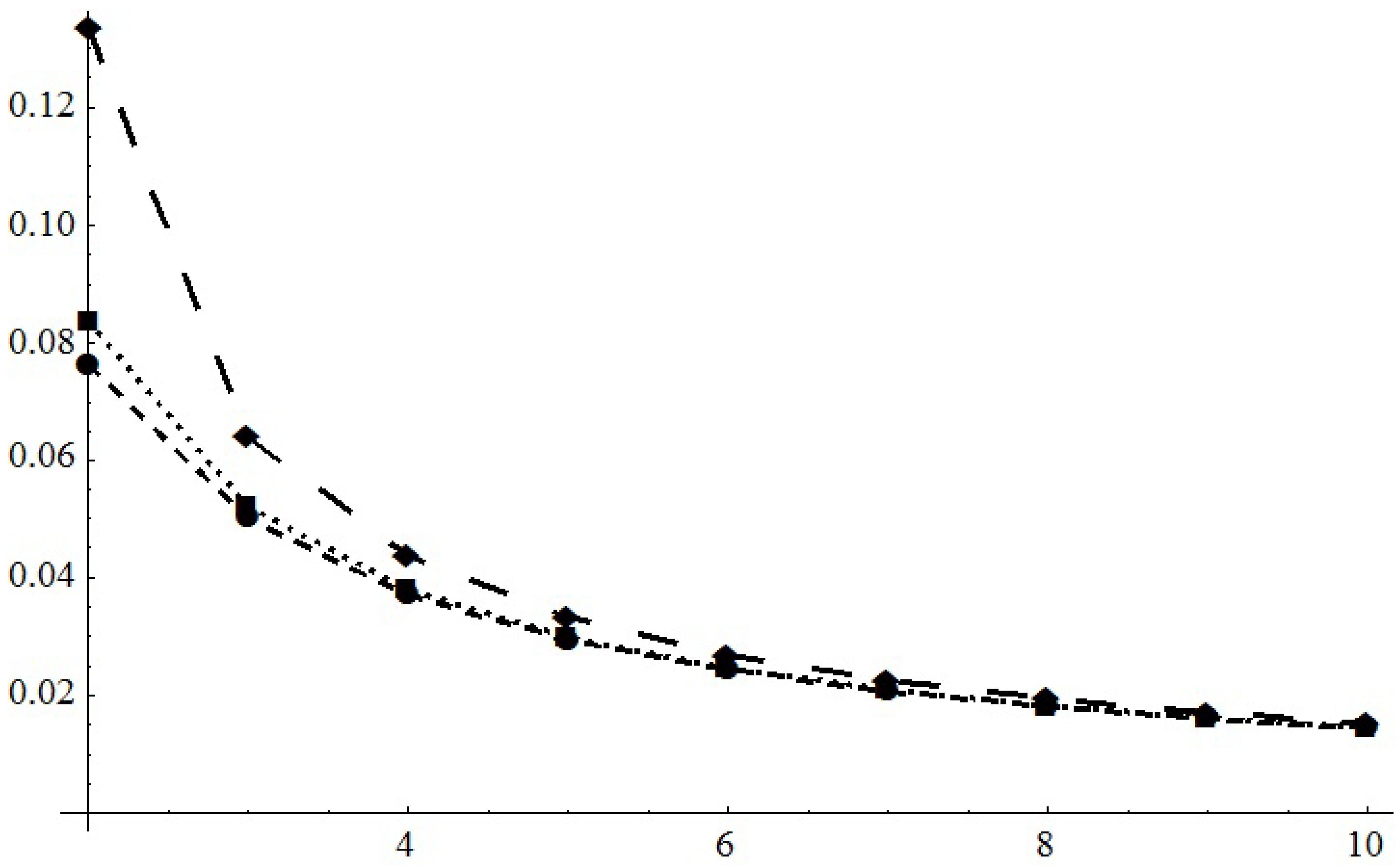
. (2) The additional requirements to transform them into integers cause the error-term sequence to diverge. However, the convergence of
to the number
is good, as it is depicted in
Figure 2, and their rates of convergence are as reasonable as Apéry’s approximants.