Fast Computation of Integrals with Fourier-Type Oscillator Involving Stationary Point
Abstract
1. Introduction
2. Evaluation Procedure
2.1. Levin Quadrature
2.2. Chebyshev Differentiation Matrix and Its Approximation
2.3. Chebyshev–Levin Quadrature
2.4. Adaptive Splitting
- If is used to compute the integral having a stationary point, then Chebyshev–hybrid quadrature is given by
- If is used for computing the integral having stationary point, then Chebyshev–Haar quadrature can be written as
- ;
- ; (Slitting parameter.)
- ;
- , for ; (where r(x) is the amplitude function of (1).)
- ; (The coefficient matrix of the ODE (8) and I is the identity matrix.)
- ; (The approximate solution of the ODE (8).)
- ; (Approximate Chebshev solution of integral having no stationary point.)
- ; (Approximate hybrid solution of the integral having stationary point.)
- ChQ = App1 + App2; (Solution of integral (1)).
3. Error Bounds
- i.
- or
- ii.
- and is monotonic.
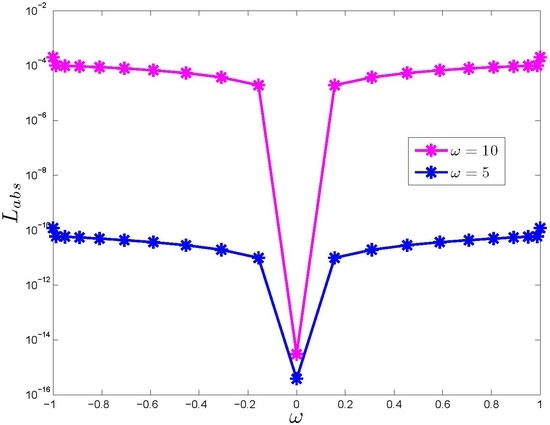
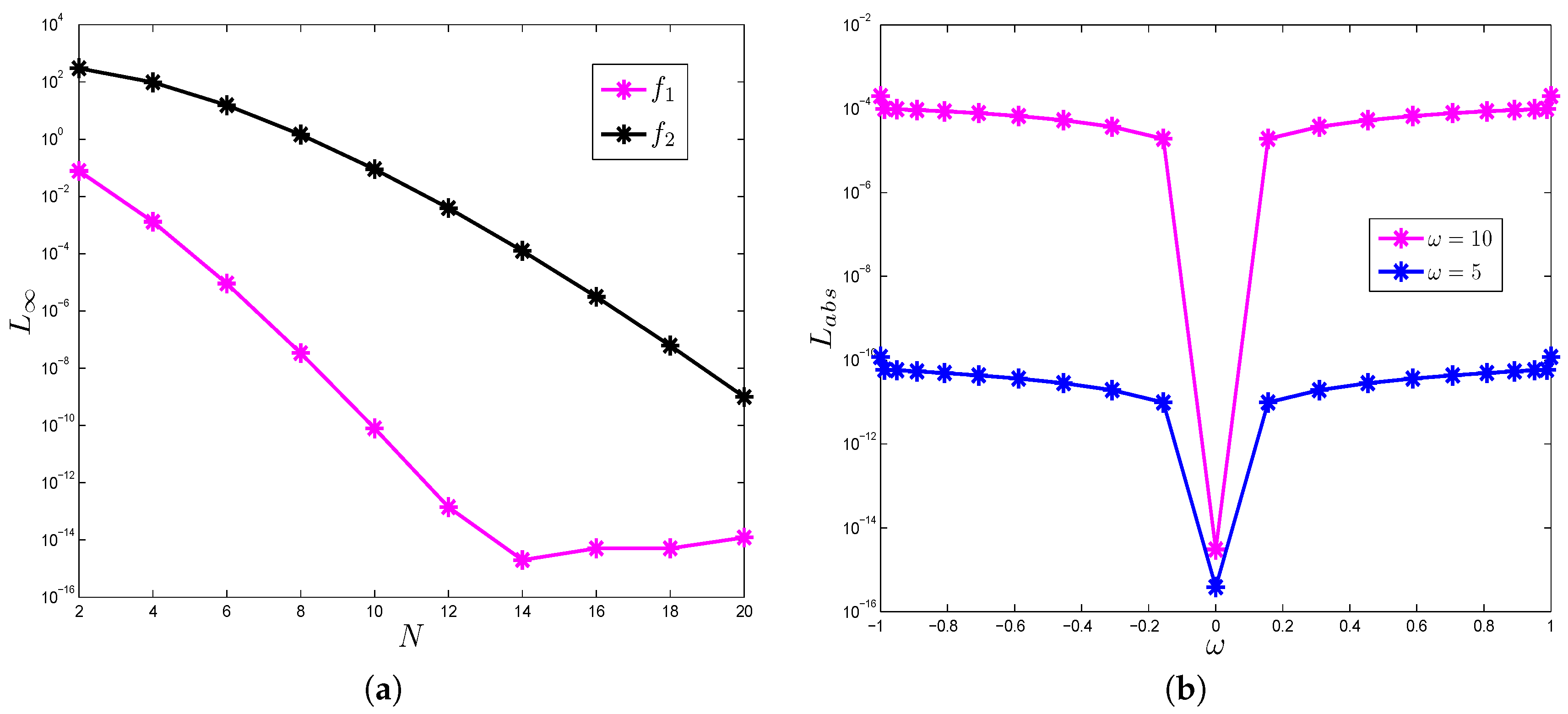
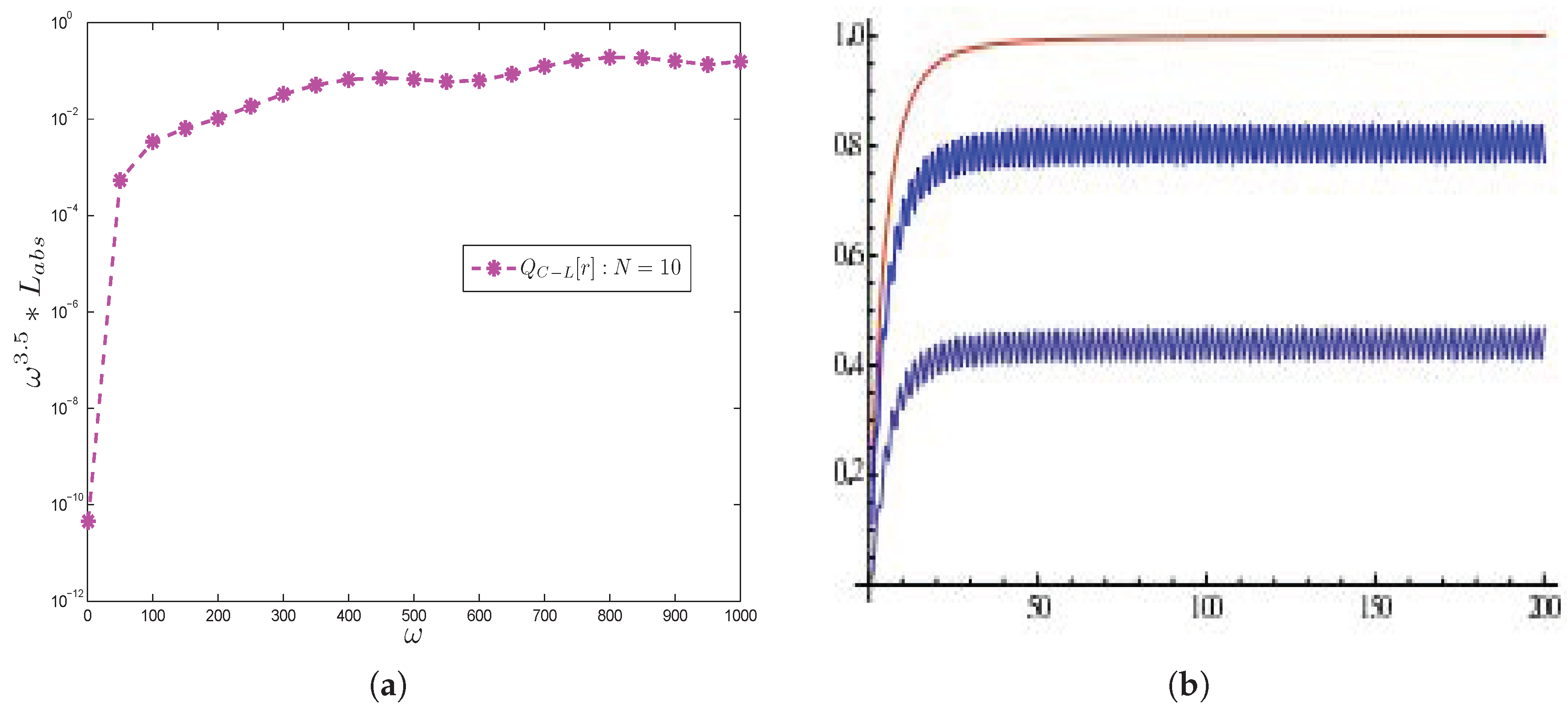
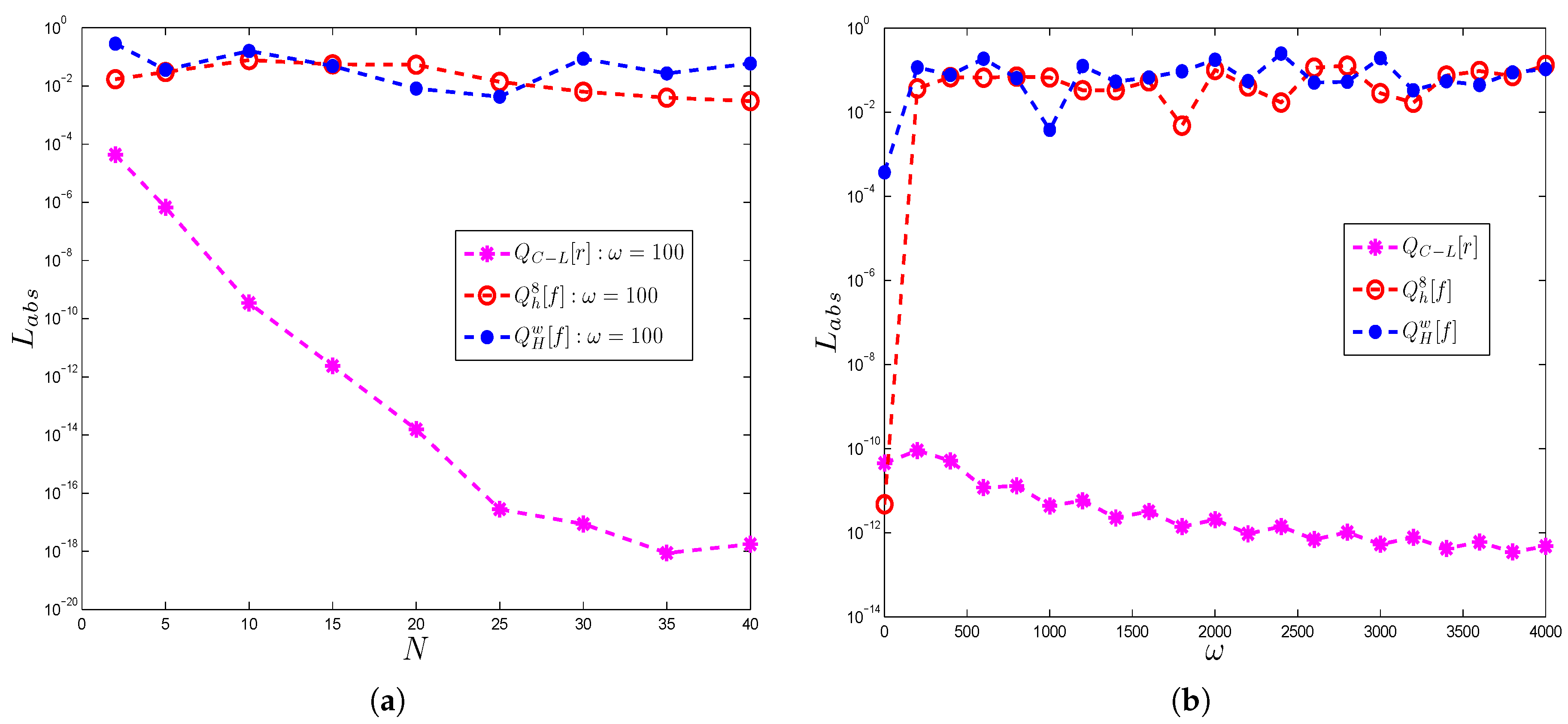
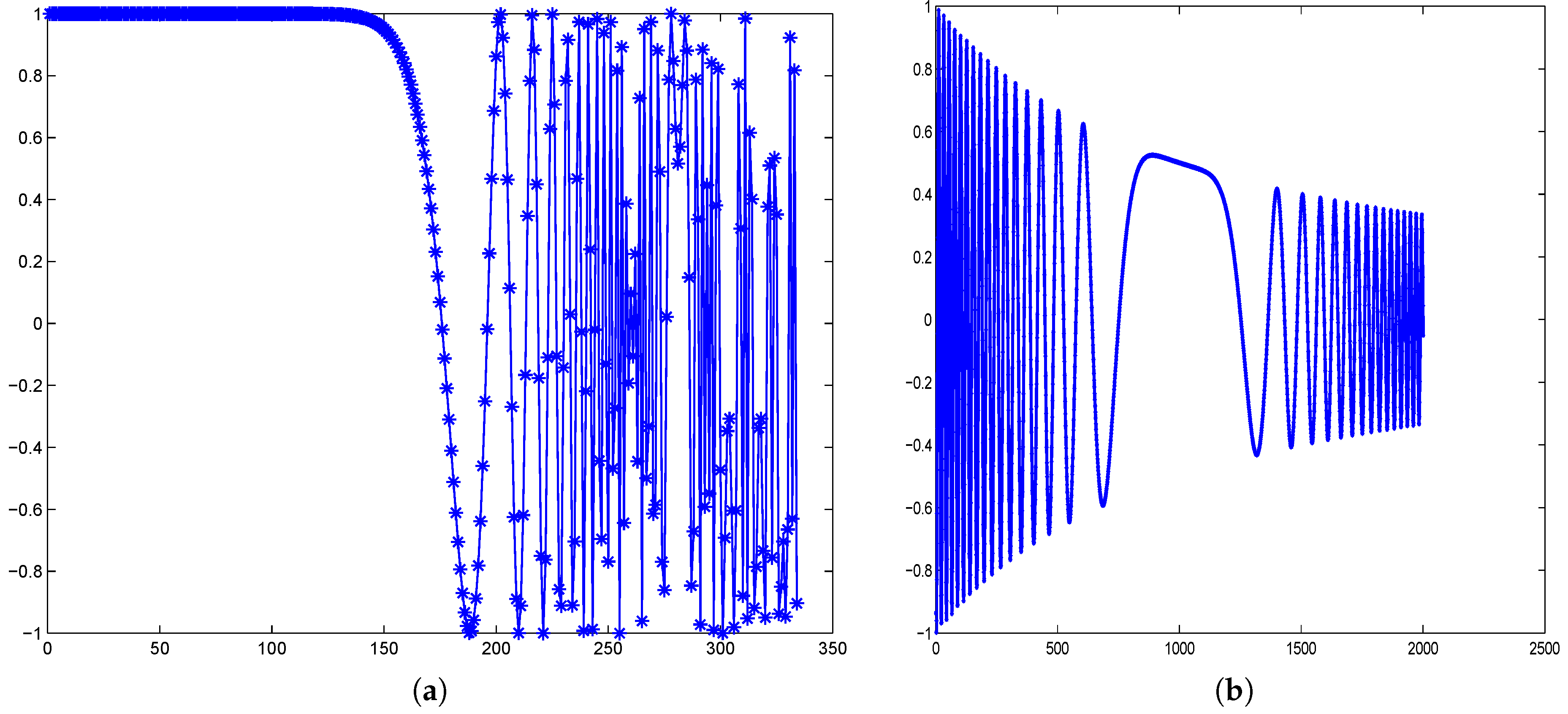
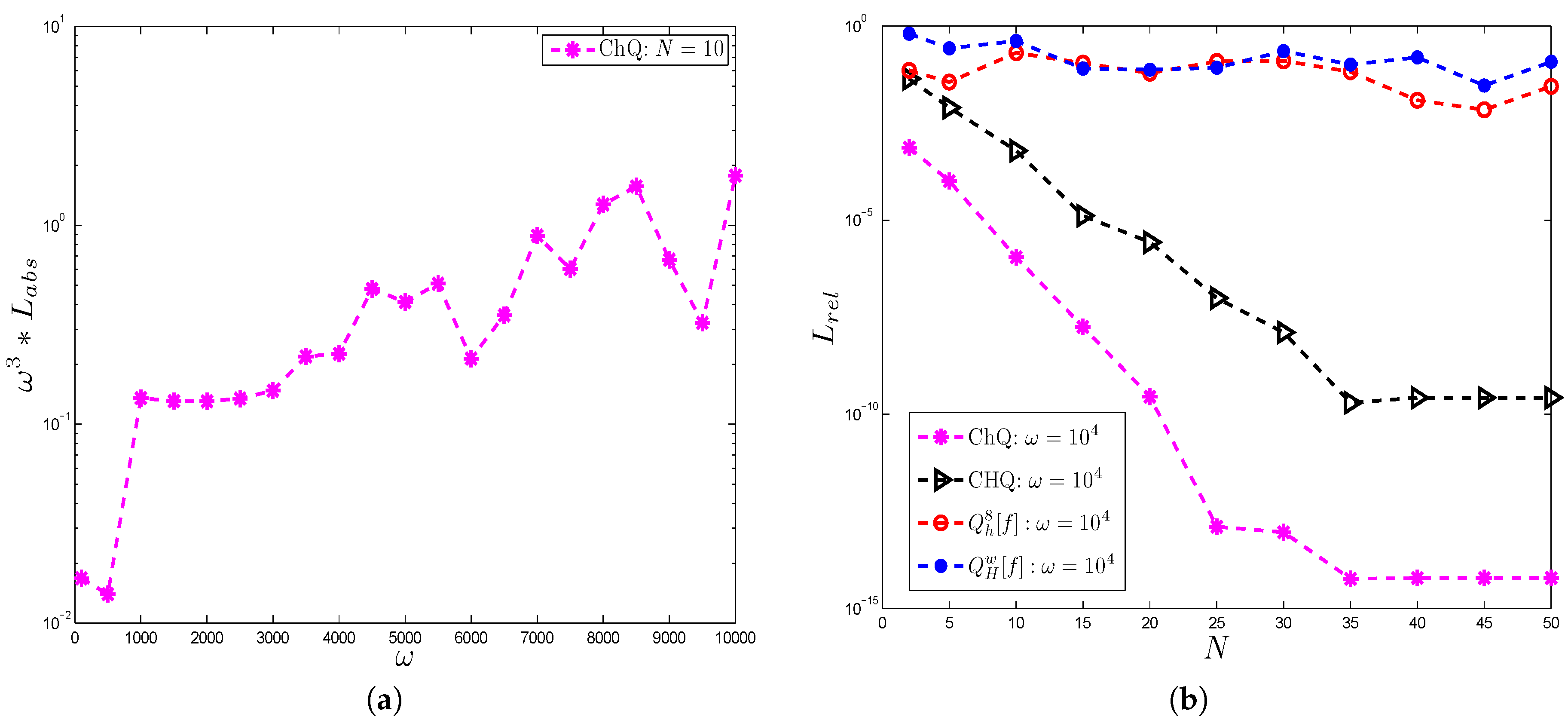
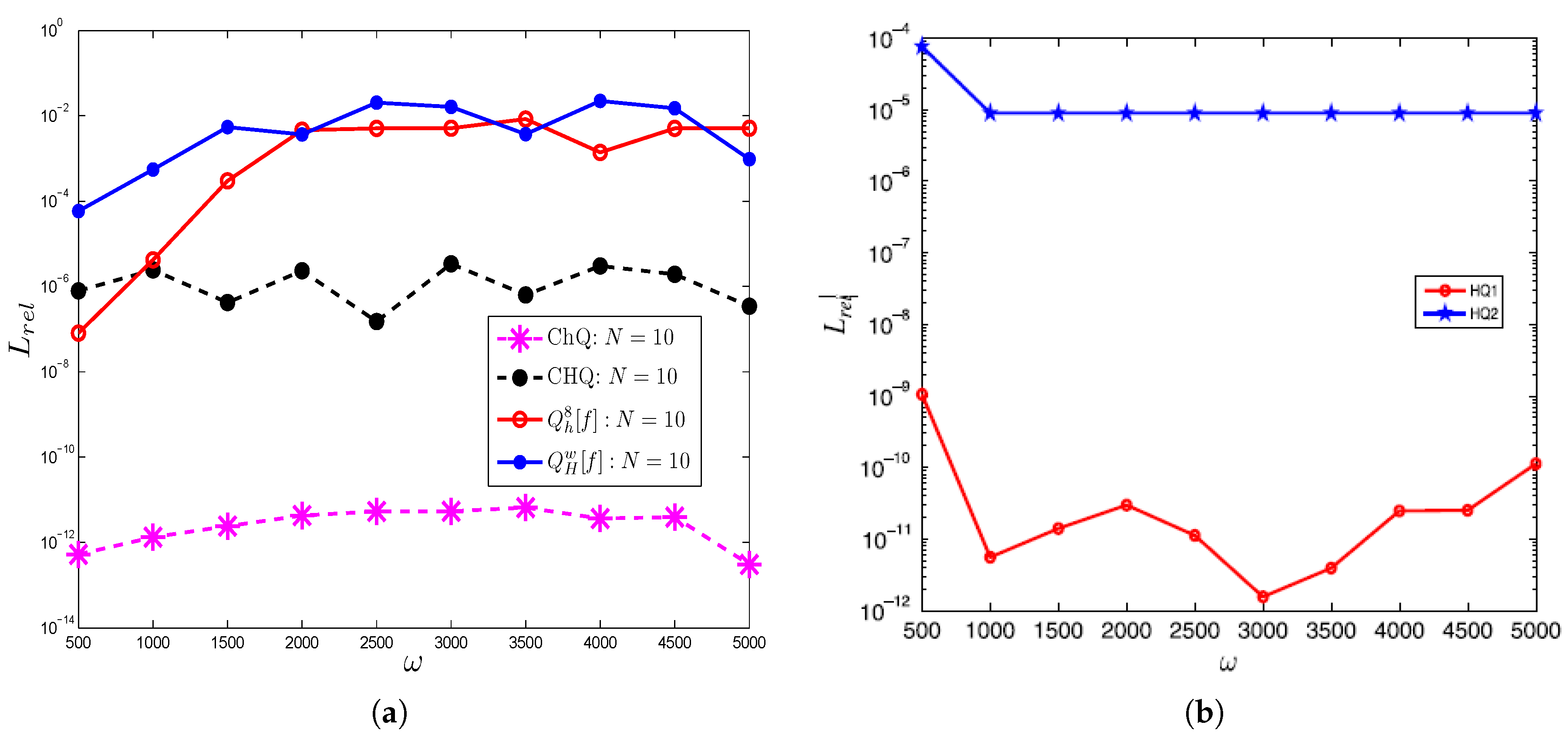
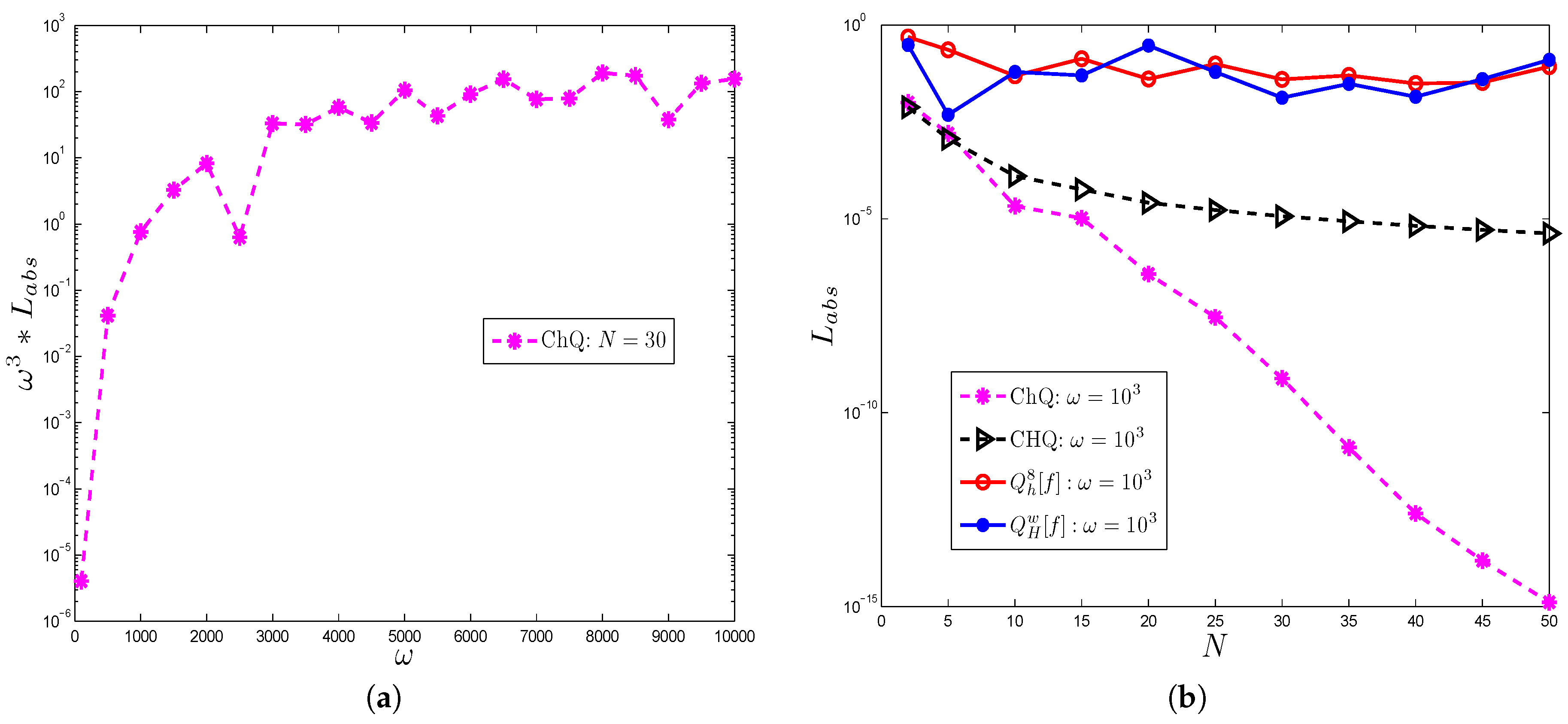
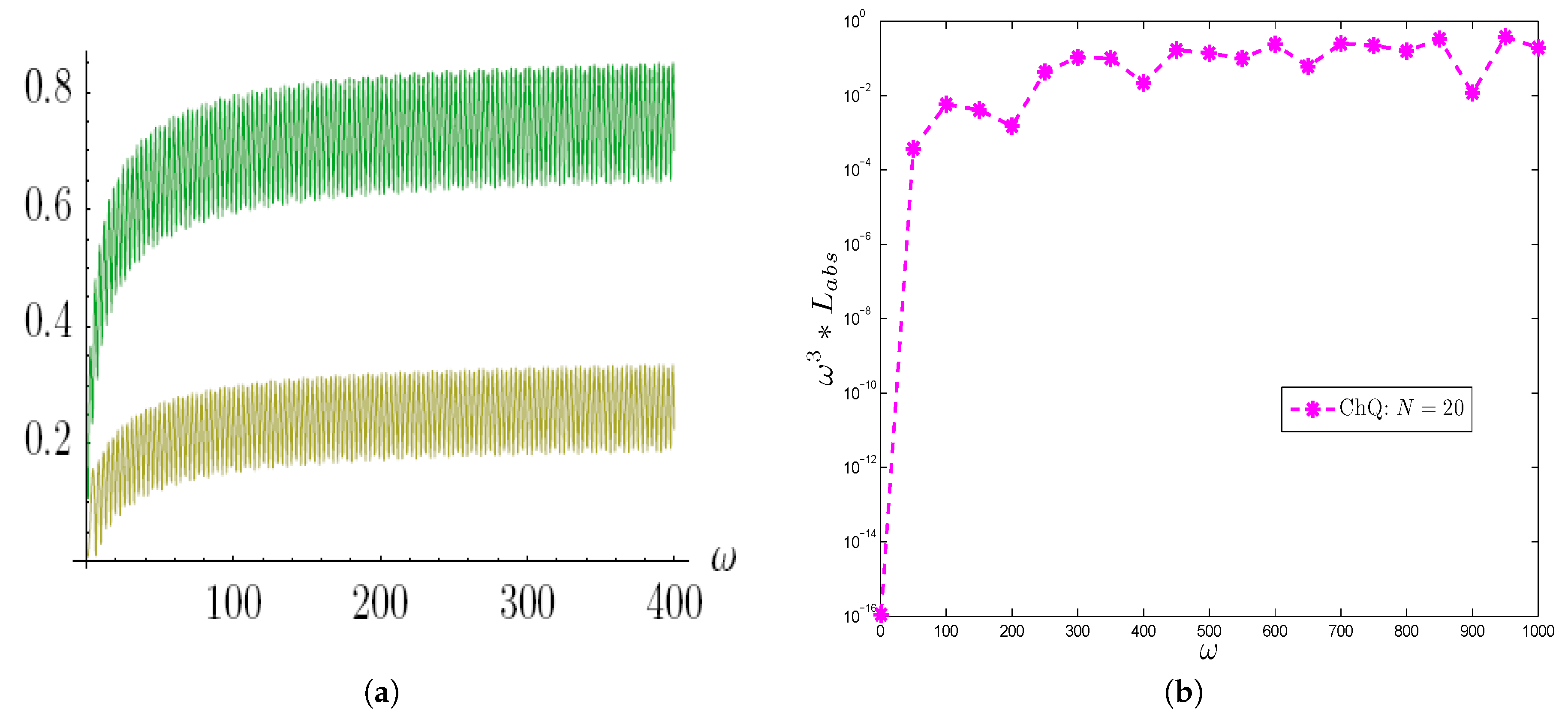
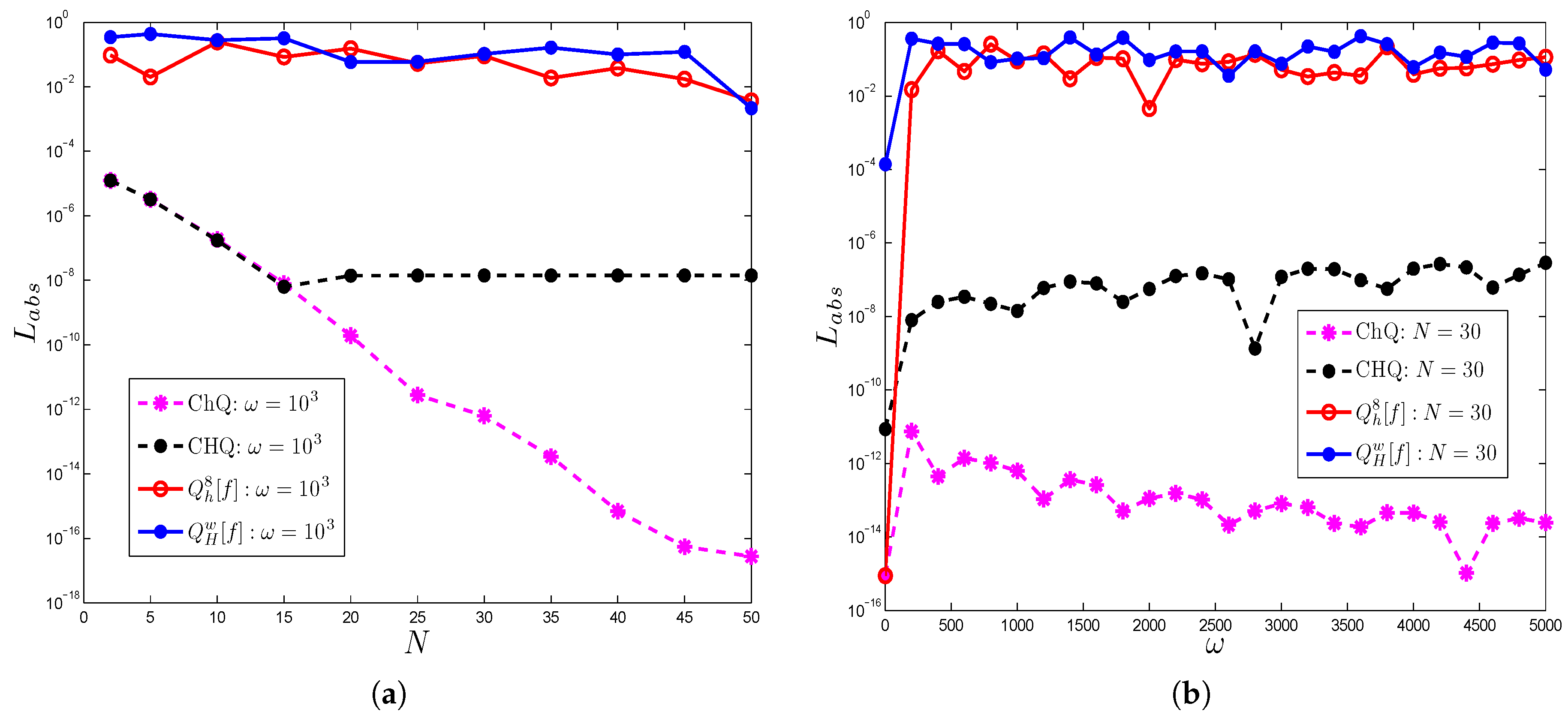
4. Numerical Examples and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
| Symbols | Discription |
| Chebyshev–Levin quadrature | |
| Quadrature based on hybrid functions | |
| Quadrature baed on Haar wavelet | |
| ChQ | Splitting procedure with Chebyshev–hybrid quadrature |
| CHQ | Splitting procedure with Chebyshev–Haar quadrature |
| Splitting parameter | |
| k | Order of the stationary point |
References
- Ishimaru, A. Wave Propagation and Scattering in Random Media; Academic Press: New York, NY, USA, 1978; Volume 2. [Google Scholar]
- Shariff, K.; Wray, A. Analysis of the radar reflectivity of aircraft vortex wakes. J. Fluid. Mech. 2002, 463, 121–161. [Google Scholar] [CrossRef]
- Singh, D.; Singh, M.; Hakimjon, Z. Signal Processing Applications Using Multidimensional Polynomial Splines; Springer: Singapore, 2019. [Google Scholar]
- Fang, C.; He, G.; Xiang, S. Hermite-Type Collocation Methods to Solve Volterra Integral Equations with Highly Oscillatory Bessel Kernels. Symmetry 2019, 11, 168. [Google Scholar] [CrossRef]
- Iserles, A.; Norsett, S.P. On the computation of highly oscillatory multivariate integrals with stationary points. BIT Numer. Math. 2006, 46, 549–566. [Google Scholar] [CrossRef]
- Singh, D.; Zaynidinov, H.; Lee, H. Piecewise-quadratic Harmut basis functions and their application to problems in digital signal processing. Int. J. Commun. Syst. 2010, 23, 751–762. [Google Scholar] [CrossRef]
- SAIRA; Xiang, S.; Liu, G. Numerical Solution of the Cauchy-Type Singular Integral Equation with a Highly Oscillatory Kernel Function. Mathematics 2019, 7, 872. [Google Scholar]
- SAIRA; Xiang, S. Approximation to Logarithmic-Cauchy Type Singular Integrals with Highly Oscillatory Kernels. Symmetry 2019, 11, 728. [Google Scholar]
- Iserles, A.; Norsett, S.P. Efficient quadrature of highly oscillatory integrals. Proc. R. Soc. A 2005, 461, 1383–1399. [Google Scholar] [CrossRef]
- Filon, L.N.G. On a quadrature formula for trigonometric integrals. Proc. R. Soc. Edinb. 2005, 49, 38–47. [Google Scholar] [CrossRef]
- Olver, S. Fast and numerically stable computation of oscillatory integrals with stationary points. BIT Numer. Math. 2010, 50, 149–171. [Google Scholar] [CrossRef]
- Levin, D. Procedures for computing one and two-dimensional integrals of functions with rapid irregular oscillations. Math. Comp. 1982, 158, 531–538. [Google Scholar] [CrossRef]
- Li, J.; Wang, X.; Wang, T.; Xiao, S. An improved Levin quadrature method for highly oscillatory integrals. J. Appl. Numer. Math. 2010, 60, 833–842. [Google Scholar] [CrossRef]
- Siraj-ul-Islam; Al-Fhaid, A.S.; Zaman, S. Meshless and wavelets based complex quadrature of highly oscillatory integrals and the integrals with stationary points. Eng. Anal. Bound. Elem. 2013; 37, 1136–1144. [Google Scholar]
- Siraj-ul-Islam; Aziz, I.; Khan, W. Numerical integration of multi-dimensional highly oscillatory, gentle oscillatory and non-oscillatory integrands based on wavelets and radial basis functions. Eng. Anal. Bound. Elem. 2012, 36, 1284–1295. [Google Scholar] [CrossRef]
- Siraj-ul-Islam; Zaman, S. New quadrature rules for highly oscillatory integrals with stationary points. J. Comp. Appl. Math. 2015, 278, 75–89. [Google Scholar] [CrossRef]
- Iserles, A. On the numerical quadrature of highly-oscillatory integrals ii: Irregular oscillators. IMA J. Numer. Anal. 2005, 25, 25–44. [Google Scholar] [CrossRef]
- Olver, S. Moment-free numerical integration of highly oscillatory functions. IMA J. Numer. Anal. 2006, 26, 213–227. [Google Scholar] [CrossRef]
- Xiang, S. Efficient quadrature for highly oscillatory integrals involving critical points. J. Comp. Appl. Math. 2007, 206, 688–698. [Google Scholar] [CrossRef][Green Version]
- Guo, H.; Xiang, S. An improved algorithm for the evaluation of Cauchy principal value integrals of oscillatory functions and its application. J. Comput. Appl. Math. 2015, 280, 1–13. [Google Scholar]
| y | ||||
|---|---|---|---|---|
| mp | ||||
| mp | mp |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaman, S.; Hussain, I.; Singh, D. Fast Computation of Integrals with Fourier-Type Oscillator Involving Stationary Point. Mathematics 2019, 7, 1160. https://doi.org/10.3390/math7121160
Zaman S, Hussain I, Singh D. Fast Computation of Integrals with Fourier-Type Oscillator Involving Stationary Point. Mathematics. 2019; 7(12):1160. https://doi.org/10.3390/math7121160
Chicago/Turabian StyleZaman, Sakhi, Irshad Hussain, and Dhananjay Singh. 2019. "Fast Computation of Integrals with Fourier-Type Oscillator Involving Stationary Point" Mathematics 7, no. 12: 1160. https://doi.org/10.3390/math7121160
APA StyleZaman, S., Hussain, I., & Singh, D. (2019). Fast Computation of Integrals with Fourier-Type Oscillator Involving Stationary Point. Mathematics, 7(12), 1160. https://doi.org/10.3390/math7121160